Abstract
A new scheme using macroscopic coherence is proposed to experimentally determine the neutrino mass matrix, in particular the absolute value of neutrino masses, and the mass type, Majorana or Dirac. The proposed process is a collective, coherent Raman scattering followed by neutrino-pair emission from \(|e\rangle \) of a long lifetime to \(|g\rangle \); \(\gamma _0 + | e\rangle \rightarrow \gamma + \sum _{ij} \nu _i \bar{\nu _j} + | g\rangle \) with \( \nu _i \bar{\nu _j}\) consisting of six massive neutrino-pairs. Calculated angular distribution has six (ij) thresholds which show up as steps at different angles. Angular locations of thresholds and event rates of the angular distribution make it possible to experimentally determine the smallest neutrino mass to the level of less than several meV, (accordingly all three masses using neutrino oscillation data), the mass ordering pattern, normal or inverted, and to distinguish whether neutrinos are of Majorana or Dirac type. Event rates of neutrino-pair emission, when the mechanism of macroscopic coherence amplification works, may become large enough for realistic experiments by carefully selecting certain types of target. The problem to be overcome is macro-coherently amplified quantum electrodynamic background of the process, \(\gamma _0 + | e\rangle \rightarrow \gamma +\gamma _2 + \gamma _3+ | g\rangle \), when two extra photons, \(\gamma _2, \gamma _3\), escape detection. We illustrate our idea using neutral Xe and trivalent Ho ion doped in dielectric crystals.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Remaining major problems in neutrino physics are determination of the absolute neutrino mass value and the nature of neutrino mass, either of Dirac type or of Majorana type. These problems are key important issues to clarify the origin of baryon asymmetry of our universe and to construct the ultimate unified theory beyond the standard theory. Despite of many year’s experimental efforts [1] no hint of these issues is found so far. It is necessary, in our opinion, to establish new experimental schemes based on targets besides nuclei having a few to several MeV energy release used in most of past experiments, since solution of these problems requires high sensitivity to the expected, much smaller, sub-eV neutrino mass range.
One possibility of new experimental approaches is the use of atoms/ions or molecules whose energy levels can be chosen to be almost arbitrarily close to small neutrino masses [2,3,4]. The process is atomic de-excitation from a metastable state \( |e \rangle \) to the ground state \( |g \rangle \), \(|e \rangle \rightarrow | g\rangle + \gamma + \nu _i \bar{\nu _j} \) where \(\gamma \) is detected photon accompanying invisible neutrino pair \( \nu _i \bar{\nu _j} \, ( i,j = 1,2,3) \) of mass eigenstates (anti-neutrino \(\bar{\nu _i}\) is distinguishable from neutrino \(\nu _i \) in the Dirac neutrino, while \(\bar{\nu _i} = \nu _i\) in the Majorana neutrino). Necessary rate enhancement mechanism of atomic de-excitation using a coherence of macroscopic number of atoms (macro-coherence) has been proposed in [5] and its principle has been experimentally confirmed in weak QED (Quantum ElectroDynamic) process [6,7,8]. The enhancement factor reached \(10^{18}\) orders over the spontaneous emission rate. The coherently amplified neutrino-pair emission is called RENP (Radiative Emission of Neutrino Pair), yet to be discovered.
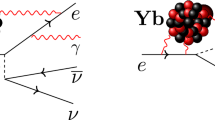
One of the problems in the original RENP scheme is a difficulty of distinguishing a detected photon from triggered photons (necessary to stimulate the weak process) which happens to have the same frequency and the same emitted direction. In the present work we study the process as depicted in Fig. 1, \( \gamma _0 + |e \rangle \rightarrow \gamma + | g\rangle + \nu _i \bar{\nu _j} \), in which the detected photon \(\gamma \) has different energy and different emitted direction from the trigger photon \(\gamma _0\). Doubly resonant neutrino-pair emission becomes possible and massive neutrino-pair thresholds appear in the angular distribution of detected photon \(\gamma \).
a Feynman diagram of \( \gamma _0 + |e \rangle \rightarrow \gamma + | g\rangle + \nu _i \bar{\nu _j} \). There are five more diagrams that contribute off resonances, as in Eq. (3). b Corresponding energy levels indicating absorption and emission of photons and a neutrino-pair
The paper is organized in such a way to first present the general idea and principles of macro-coherent neutrino-pair emission stimulated by Raman scattering. For brevity we call the process RANP (RAman stimulated Neutrino-Pair emission). There are three key issues to make the RANP project of neutrino mass spectroscopy successful: (1) mass determination and Majora/Dirac distinction [4] is clearly possible or not, (2) event rate is large enough or not, (3) macro-coherently amplified QED processes that may become backgrounds are controllable or not. Even if these issues are not ideally solved, the final question is (4) how technological improvements may be foreseeable. We study the general idea by using interesting examples of Xe and trivalent lanthanoid ions doped in crystals [9], for an interesting scheme of axion search in rare earth doped crystals, see [10], both of which have large target densities typically of order \(10^{20}\, \hbox {cm}^{-3}\) helping for a realistic detection and have small optical relaxation rates for the macro-coherence amplification. There may be other, hopefully better, candidate atoms or ions realizing the general idea, but the atomic or ion density in a laser excited state must be large enough, close to a value of atomic density in solids for realistic detection.
We use the natural unit of \(\hbar = c = 1\) throughout the present paper unless otherwise stated.
2 Double resonance condition and Raman stimulated neutrino-pair emission
Our experimental scheme uses two counter-propagating lasers of frequencies, \(\omega _i\,, i = 1,2\) for excitation to \(| e\rangle \) from the ground state and one trigger laser of frequency \(\omega _0\) for Raman excitation, as illustrated in Fig. 2. These excitation lasers are irradiated along the same axis unit vector \(\mathbf {e}_z \), hence \(\omega _1 + \omega _2 = \epsilon _{eg} \) and \(\omega _1 - \omega _2 = r\epsilon _{eg}\,, -1 \le r \le 1 \). At excitation a spatial phase \(e^{i \mathbf {p}_{eg}\cdot \mathbf {x} }, \, \mathbf {p}_{eg} = r \epsilon _{eg} \mathbf {e}_z\), is imprinted to target atoms, each at position \(\mathbf {x}\).
Suppose that a collective body of atoms, when they have a common spatial phase imprinted at excitation [11], de-excite emitting plural particles, which can be either photons or neutrino-pair. Quantum mechanical transition amplitude, if the phase of atomic part of amplitudes, \({{{\mathcal {A}}}}_a = {{{\mathcal {A}}}}\), is common and uniform, is given by a formula,
with n the assumed uniform density of excited atoms/ions. Equality to the right hand side is valid in the continuous limit of atomic distribution. This gives rise to the mechanism of macro-coherent amplification of rate \(\propto n^2 V\) with V the volume of target region. Thus, in the macro-coherent process depicted in Fig. 1, both the energy and the momentum conservation (equivalent to the spatial phase matching condition) hold [2, 3];
where \(E_i = \sqrt{p_i^2 + m_i^2}\) with \(m_i, i =1,2,3\) neutrino masses. From the energy and the momentum conservation one derives the kinetic region of (ij) neutrino-pair emission: \( ( \omega _0 + \epsilon _{eg} - \omega )^ 2 - ( \mathbf {k}_0 + \mathbf {p}_{eg} - \mathbf {k} )^ 2 \ge (m_i+m_j)^2\). This may be regarded as a restriction to emitted photon energy \(\omega \) and its emission angle. At the location where the equality holds, the neutrino-pair is emitted at rest. On the other hand, when atomic phases of \({{{\mathcal {A}}}}_a\) at sites a are random in a given target volume V, the rate scales with nV without the momentum conservation law, which gives much smaller rates.
The amplitude corresponding to Fig. 1 and related five more diagrams is given by
neglecting coupling constant factors \(G_F/\sqrt{2}\). Here \(\mathbf {\sigma } = 2\mathbf {S}\) is the electron spin operator, \(\mathbf {d} \) the electric dipole operator, and \(\mathbf {{{{\mathcal {N}}}}}_{ij} = \nu _i ^{\dagger }\mathbf {\sigma } (1-\gamma _5) \nu _j \) is the (ij) neutrino-pair emission current arising from the spatial part of axial vector charged current and neutral current interaction [2, 3]. When magnetic dipole transitions are dominant, the electric dipole operator \(\mathbf {d}\) should be replaced by the magnetic dipole operator \(\mathbf {\mu } \). Note that the magnetic dipole operator is odd under time reversal, while the electric dipole operator is even. The formula, Eq. (3), is written for convenience of the level ordering \(\epsilon _p> \epsilon _q > \epsilon _e \), but other cases may also be considered. The energy conservation \(\omega - \omega _0 = \epsilon _{eg} - E_1 - E_2 \) can be used to rewrite energy denominators, for instance \(\omega - \omega _0 + \epsilon _{qe} = - ( E_1+E_2 - \epsilon _{qg})\).
We find from Eq. (3) that double resonance occurs at \(\omega _0 = \epsilon _{pe} \) and \( E_1+E_2 = \epsilon _{qg} \) giving one diagram of Fig. 1 dominant (another possibility of \(\omega - \omega _0 = \epsilon _{pg} \) is not considered due to a difficulty of meeting the condition of McQ3 rejection). The condition implies that \(\omega = \epsilon _{pq}\). Thus, the doubly resonant process occurs via a series of real transitions: first trigger photon absorption at \(|e \rangle \rightarrow | p \rangle \), followed by a photon emission at \(|p \rangle \rightarrow | q\rangle \), then by the neutrino-pair emission at \(|q \rangle \rightarrow | g\rangle \). In the double resonance scheme the energy denominator \(\epsilon _{ab} \) should include the width factor, \(\epsilon _{ab} - i (\gamma _a + \gamma _b)/2\).
Let us take the same state for \(| q\rangle = | e \rangle \). A feature of this scheme is that a macro-coherence exists for the last step of neutrino-pair emission, \(| q \rangle \rightarrow | g \rangle \). One could take a view that the process is a macro-coherent neutrino-pair emission \( | e\rangle \rightarrow | g \rangle +\nu {\bar{\nu }} \), induced by elastic Raman scattering \( \gamma _0 (\mathbf {k}_0) + | e \rangle \rightarrow \gamma (\mathbf {k}) + | e \rangle \) of frequency \(\omega _0 = \omega \), but of \(\mathbf {k}_0 \ne \mathbf {k}\).
3 Event rate of neutrino-pair emission and angular spectrum
The differential spectrum rate in the double resonance scheme consists of a sum over contributions of massive (ij) neutrino-pair production [2, 3]:
Dependence \(n^2 V \) on the excited target number density is a result of macro-coherence amplification. The atomic part and the neutrino-pair emission part \( F_{ij} \) are factorized in the differential rate formula, Eq. (4). The step function \(\varTheta \left( {{{\mathcal {M}}}}^2 (\omega _{pe}, \theta ) - (m_i +m_j )^2\right) \) determines locations of (ij) neutrino-pair production thresholds. The squared neutrino pair current \(\mathbf {\mathcal{N}_{ij}}\cdot \mathbf { {{{\mathcal {N}}}}_{ij}}^{\dagger } \) is summed over neutrino helicities and their momenta. We used in the formula experimentally measurable A-coefficients \(\gamma _{ab} = (d_{ab}^2\, \mathrm{or} \,\mu _{ab}^2)\epsilon _{ab}^3/(3\pi )\) and the total width \(\gamma _{a} = \sum _b \gamma _{ab} \) instead of dipole moments. We denote the Raman trigger spectrum function by \(I(\omega _0) \) with width \(\varDelta \omega _0\) and its power \(E_0^2 = \omega _0 n_0 = \omega _0 n \eta \) where \(n_0\) is the photon number density. The dynamical factor denoted by \( \eta \) is actually time dependent, and is calculable using the Maxwell–Bloch equation [2, 3], the coupled set of partial differential equations of fields and atomic density matrix elements in the target region. This calculation is beyond the scope of this work, and we shall assume an ideal case later on.
The quantity that appears in the formula, Eq. (5), is calculated as
using methods of [2, 3]. \(\delta _M =0 \) for Dirac neutrino and \(=1 \) for Majorana neutrino due to identical fermion effect [4]. The \(3 \times 3\) unitary matrix \((U_{ei} )\,, i = 1,2,3,\) refers to the neutrino mass mixing [1]. In the double resonance scheme the detected photon energy is fixed at \(\omega = \epsilon _{pq} \), and six thresholds (ij) of neutrino pair production appear in the angular distribution at angles \(\theta _{ij}\) of \({{{\mathcal {M}}}}^2 (\omega _{pe}, \theta _{ij}) =(m_i +m_j)^2 \).
A more practical formula for rate estimate is obtained by integrating over the detected photon energy and convoluting with the trigger laser power. The convolution integral over a power spectrum \( I(\omega _0)\) is
with \(E_0^2 = \omega _0 \times \) the trigger photon number density, while the integration over the detected photon energy is
since the region of detected photon energy
\(\varDelta \omega \gg \sqrt{ \gamma _{e}^2+ \gamma _{q}^2 } \). We obtain the practical formula,
We shall estimate RANP rate stimulated by elastic Raman scattering. Taking partial decay rates and total decay rates to be of the same order, one may derive a total RANP rate scale \(\varGamma _0 \) by taking a typical value of the neutrino-pair phase space integration \(\epsilon _{eg}^2/24 \) from Eq. (6) approximated in the massless neutrino limit,
The rate formula calculated this way contains, besides detector and laser related quantities, four important factors, and these appear in the rate as
rate = Raman scattering rate (\( \gamma _{pe}^2/(\sqrt{ \gamma _{p}^2 + \gamma _{e}^2 + (\varDelta \omega _0)^2} )\,) \times \) lifetime of \(|e \rangle ( = | q\rangle )\) state (\(1/\gamma _e\)) \(\times \) neutrino-pair emission rate (\(G_F^2\epsilon _{eg}^2/ \epsilon _{pe}^3) \times \) coherence amplification factor (\(n^3 V \eta \)),
in the neutrino-pair emission stimulated by elastic Raman scattering. From Eq. (8) it becomes very important for target selection how large a dimensionless combination of decay rate, lifetime and energy differences, \(\gamma _{pe}^2 \epsilon _{eg}^2/ (\gamma _e \epsilon _{pe}^3 ) \) is.
4 Amplified QED backgrounds
The macro-coherent amplification necessary for RANP rate enhancement may also amplify QED processes which may give rise to serious backgrounds. These amplified QED processes are termed as McQn (macro-coherent QED n-th order photon emission) [12]. We shall first consider how to get rid of MacQn (n \(=\) 2, 3) backgrounds.
The quantity \({{{\mathcal {M}}}}^2 = (\omega _0 + \epsilon _{eg} - \omega )^2 - ( \mathbf {k}_0 + \mathbf {p}_{eg} - \mathbf {k})^2 \) is equal to \((E_1 + E_2)^2 - (\mathbf {p}_1 + \mathbf {p}_2)^2\) using variables of unseen \((\nu _1, \nu _2)\) and is important for discussion of backgrounds. In terms of Raman scattering variables it reads as
where \(\theta \) is the \(\gamma \) emission angle measured from the excitation axis. When a photon of 4-momentum \(k = (\omega , \mathbf {k})\) is emitted instead of the neutrino-pair, this quantity vanishes at some angle satisfying \({{{\mathcal {M}}}}^2 (\theta ) (= \omega ^2 - \mathbf {k}^2) = 0 \). In this case a serious amplified McQ3 background exists. On the other hand, if this quantity is arranged to be positive at all angles and is taken close to neutrino mass thresholds, \((m_i+m_j)^2 \), neutrino-pair emission occurs without the McQ3 background. With a proper choice of the imprinted phase r and trigger frequency \( \omega _0\), one may readily work out the parameter region that excludes QED backgrounds of McQ3. The other background, McQ2 (Paired Super-Radiance) \( |e\rangle \rightarrow |g \rangle + \gamma _0 +\gamma \), is rejected unless \(r = - 1 + 2\omega _0/\epsilon _{eg}\), which we shall assume to be valid in the following.
In the case of elastic RANP (\(\omega = \omega _0\)) the first angular threshold rise occurs at pair production of smallest neutrino mass \(m_1\) at an angle,
The formula may be used in other situations. A light hypothetical particle X such as axion and hidden photon [13] can be searched as an angular peak given by the angle \(\theta _X\) obtained by replacing \(4 m_1^2\) in Eq. (10) by the squared X-mass \(m_X^2\)
Without McQ2 and McQ3 events the largest amplified QED background arises from McQ4, \(\gamma _0 + | e\rangle \rightarrow \gamma +\gamma _2 + \gamma _3+ | g\rangle \), obtained by replacing the neutrino-pair \(\nu _i \bar{\nu _j} \) in \(|q \rangle \rightarrow |g\rangle \) by two photons, \(\gamma _2 \gamma _3\). It is difficult to kinetically reject McQ4 events when two extra photons escape detection, since the two-photon system has its squared pair-mass coincident to RANP events. The crucial question is how big the McQ4 background rate is. Disregarding the macro-coherent amplification factor common to RANP and McQ4 event rates,
one should compare two quantities, the RANP rate function \(I _{2\nu } = G_F^2 \sum _{ij} F_{ij}/2\) already given and McQ4 rate function, which has two possibilities, either E1 (electric dipole) \(\times \) M1 (magnetic dipole) or E1 \(\times \) E1. Macro-coherent E1 \(\times \) E1 rate function (one electric dipole d replaced by the magnetic dipole \(\mu \) for E1 \(\times \) M1) \(I _{2\gamma } \) to be compared with the factor of RANP function \(I _{2\nu }\) is
for elastic RANP (otherwise \(\epsilon _{eg} \rightarrow \epsilon _{eg} + \omega _{0} - \omega \)) with \(\mathbf {P} = \mathbf {p}_{eg} + \mathbf {k}_0 - \mathbf {k} \). The result of calculation is given by
where the relation \(\mathbf {P}^2= \epsilon _{eg}^2 - {{{\mathcal {M}}}}^2\) was used. Upper energy states \(| n \rangle \) in Eq. (12) must be connected to lower energy states by the combination of E1 \(\times \) E1 for Xe case and E1 \(\times \) M1 for trivalent lanthanoid ion, which restricts states of large contributions.Footnote 1
5 Numerical rate estimate for Xe and \(\hbox {Ho}^{3+}\) doped in crystals
In this section we apply theoretical formulas given in the preceding sections to real target atoms/ions. An exhaustive study of RANP and background rates is beyond the scope of this work. We shall restrict to two interesting cases of a trivalent lanthanoid ion and Xe atom whose relevant energy levels are depicted in Fig. 3. As shown there, there are a number of Stark states (degenerate states lifted by crystal field) that may contribute to RANP process: 11 theoretically expected and 9 experimentally detected levels for \(|p \rangle = ^5\!\!\hbox {I}_7\), and 13 theoretically expected and 9 experimentally detected levels for \(|g\rangle = ^5\!\!\hbox {I}_8\) [14, 15]. Trivalent lanthanoid ions have a number of 4f electrons shielded by outer 6s electrons, giving rise to sharp line widths, when they are doped in dielectric crystals [9]. Xe has two metastable excited states, \(2^-\) (lifetime \(\sim 43\) s) and \(0^-\) (lifetime \(\sim 0.13\) s), suitable for RENP [2, 3] and RANP. Both targets can be prepared to have large number densities.
Relevant energy levels of trivalent Ho ion in YLF and neutral Xe. a Ho in the unit of \(\hbox {cm}^{-1}\) (\(10^4\,\mathrm{cm}^{-1} = 1.24\,\mathrm{eV} \) in the natural unit). There are a number of split Stark states under crystal field that contribute as states, \(|q \rangle \) and \( | g \rangle \). b Xe in eV unit
5.1 Lanthanoid case: example of \(\hbox {Ho}^{3+}\) doped in YLF
We first comment on the important quantum number of state classification in solids. Without a magnetic field application (and even in the presence of an internal magnetic field of nucleus) time-reversal symmetry holds, but parity may be violated in the presence of the crystal field. Unlike the state classification in terms of parity in the free space (vacuum) one should use time-reversal quantum number, even or odd, or T quantum number in short. Hence optical transitions between two Stark states of definite T quantum numbers, either inter- or intra-J manifolds, should be classified according to relative T quantum numbers, even or odd. Following this classification T-odd single photon emission goes via M1, while T-even emission goes via E1 or E2 (electric quadrupole). Transitions among states made of 4f electrons in the free space are mainly M1, but parity violating effects caused by crystal field make E1 often dominant in crystals, as shown in [14,15,16,17], the idea of relevant parity violating effect in crystals goes back to [18].
The last step in the resonant path, \(|q \rangle \rightarrow | g \rangle \), must be M1 due to the nature of neutrino-pair emission operator, the spin of electron \(\mathbf {S}_e \). In the trivalent Ho ion transition paths of M1 nature are limited:
\(^5\mathrm{\!I}_7 \rightarrow ^5\mathrm{\!\!I}_8\,, ^5\mathrm{\!\!I}_6 \rightarrow ^5\mathrm{\!\!I}_7 \,, ^5\mathrm{\!I}_5 \rightarrow ^5\mathrm{\!\!I}_6, ^5\mathrm{\!I}_4 \rightarrow ^5\mathrm{\!\!I}_5, ^5\mathrm{\!F}_4 \rightarrow ^5\mathrm{\!\!F}_5\) from the list of [14, 15]. Other steps, \(| e \rangle \rightarrow | p \rangle \) and \(|p \rangle \rightarrow | q \rangle \), should be chosen from large listed A-coefficients, often from E1 transitions.
We first discuss McQ4 background whose amplitude is obtained by replacing neutrino-pair emission at \(|q \rangle \rightarrow | g \rangle \) by two-photon emission. T-odd two-photon emission occurs dominantly via M1 \(\times \) E1. Parity violating effect due to crystal field and consequent weak E1 decay rate calculation was formulated in [16,17,18], and decay rates among J-manifolds has been given in [14, 15] where we can find almost all data we need for our calculation. In trivalent Ho ion there are not many common levels \(|n \rangle \) that have E1 and M1 coupling to \(|q \rangle \,, | g \rangle \). From the point of background rejection it is desirable to search for \(|q \rangle , | g \rangle \) which have no sizable M1 \(\times \) E1. Indeed, there are a few candidates of this property. Another consideration we have to focus on is to choose the rate factor, \(\gamma _{pe}\gamma _{pq}/\sqrt{\gamma _e^2 + \gamma _q^2}\), as large as possible.
A choice of RANP path considering McQ3 rejection and large RANP rate is for neutrino-pair emission stimulated by elastic Raman scattering,
The useful relation in the natural unit is \(10^4\mathrm{cm}^{-1} = 1.24 \mathrm{eV} \). Energy values are taken from [14, 15]. Lowest energy Stark levels of J-manifolds are chosen to make effects of phonon emission minimal. We are not informed of T quantum numbers, hence if some of them do not match T-odd or T-even rule, different Stark levels in the vicinity must be changed to. To the calculation accuracy of [14, 15] M1 \(\times \) E1 two-photon emission in \(|e\rangle \rightarrow |g \rangle \) transition is forbidden, hence there is no McQ4 background to this accuracy.
Mass squared \({{{\mathcal {M}}}}^2(\theta ; r)\) vs r for three angles: \(\theta = 0\) in solid black, \(\theta = \pi /2\) in dashed red, and \(\theta = \pi \) in dash-dotted blue. The line \({{{\mathcal {M}}}}^2(\theta ; r) = 4 (60\,\mathrm{meV})^2\) (expected (33) mass square \({{{\mathcal {M}}}}^2\) assuming the smallest neutrino mass \(\ll \) 10 meV ) is shown in dotted black as a guide. It is concluded that no McQ3 is expected for \(r \le -\,0.36532\) as shown in the shaded region where \({{{\mathcal {M}}}}^2(\theta ; r) >0 \) for all angles. At \(r = - \epsilon _{pe}/\epsilon _{eg} \) there is no dependence of rates on emission angle
Rate vs neutrino-pair mass \(\sqrt{ \mathcal{M}^2(\theta ; r)} \) with \(r = -\,0.36532\) of trivalent Ho. Cases of NO Majorana of smallest neutrino mass 1 meV in solid black, NO Majorana of 50 meV in dotted black, NO Dirac 1 meV in dashed red, and NO Dirac 50 meV in dash-dotted blue. Two arrows indicate the largest threshold rises of (12) and (33) pair-production
RANP angular distribution with \(r = -\,0.36532\) of trivalent Ho. Cases of NO Majorana of smallest neutrino mass 1 meV in solid black, NO Majorana of 50 meV in dotted black, NO Dirac 1 meV in dashed red, and NO Dirac 50 meV in dash-dotted blue. The absolute rate is obtained by multiplying a factor \(5.1 \times 10^{-6}\,\hbox {s}^{-1}\) assuming \(n^3 V \eta = (10^{17} )^3\,\hbox {cm}^{-6}\). This rate unit is applied to Figs. 5, 7 and 8 as well
We first show the angular distribution given by
\(\sum _{ij} F_{ij} (\omega _{pe}, \cos \theta ) \) of Eq. (6) with \({{{\mathcal {M}}}}^2\) of Eq. (9). The angular spectrum is sensitive to an adopted value of the imprinted phase factor r. We investigated this dependence for a few trivalent lanthanoid ions doped in crystals by calculating the squared mass \({{{\mathcal {M}}}}^2 (\theta ; r)\) and searched for the parameter r to optimize the shape of angular spectrum clearly showing neutrino-pair threshold rises. The search is illustrated in Fig. 4, which gives an optimal value, \( r= -\,0.36532\). We show for this r choice the squared mass \({{{\mathcal {M}}}}^2\) distribution in Fig. 5 and the angular distribution in Figs. 6, 7 and 8. The two largest threshold rises appear at the pairs, (12) and (33), where \(|b_{12}|^2 = 0.405\,, |b_{33}|^2 = 0.227 \), making up most of the weight sum \(\sum _{ij} | b_{ij}|^2 = 3/4\).Footnote 2 The smallest neutrino mass of order 1 meV is best determined by measurements around (12) threshold, as is made evident in Figs. 5 and 6, while the Majorana/Dirac distinction is better studied after (33) threshold opens. The mass ordering pattern [1], normal ordering (NO) vs inverted ordering (IO) distinction, is relatively easy as seen in Fig. 7.
The unique feature of RENP and RANP experiments is that there is a sensitivity to determine CP violation phases intrinsic to Majorana neutrinos. We have not, however, studied this sensitivity in the present work.
With the r choice of these figures, frequencies of two excitation lasers are \(\omega _1 = 202. 366\) meV \(, \omega _2 =435.329\) meV, while the Raman trigger and detected photon have energies, \(\omega _0 = \omega = 435.33 \, \)meV. In Fig. 8 we show contributions from inelastic RANP paths arising from different, wide spread, Stark states for \(|q \rangle \) which should be separately detectable with a high resolution of detected photon energy. These inelastic Raman paths (contributions beside the one in solid black of Fig. 8) give rise to pair production at finite neutrino velocities. These contributions refer to production far away from thresholds, hence they are not sensitive to neutrino mass determination. But they are important to identify the process of macro-coherent neutrino-pair emission in atoms/ions. Other paths from Stark states in manifolds, \(^5\hbox {I}_7\) and \(^5\hbox {I}_8\), of the same T quantum numbers should equally contribute to RANP photon angular distributions.
The RANP rate scale \(\varGamma _0\) can be calculated using the formula, Eq. (8), with
\(\epsilon _{eg} = 631\, \mathrm{meV}\,, \epsilon _{pe} =431\, \mathrm{meV}\,, \gamma _{pe} = 14.2\, \mathrm{s}^{-1} \,, \gamma _{e} = 69.9\, \mathrm{s}^{-1}\) (the lifetime \(1/\gamma _{e} \) including non-radiative contributions at 10 K) for the relevant path. The result is
We assumed that laser related factors can give the combination \( n^3 V \eta \) of order \( (10^{17})^3\, \mathrm{cm}^{-6}\), having in mind 10 mJ (\(= 1.6 \times 10^{17}\) eV) lasers. Whether this \( n^3 V \eta \) value is a reasonable assumption or not has to be verified by detailed simulations. The rate unit for the Ho figures in the present work is \(24 \varGamma _0/\epsilon _{eg}^2 = 5.1 \times 10^{-6} \,\mathrm{s}^{-1}\,\mathrm{eV}^{-2} \), assuming \( n^3 V \eta \) of order \( (10^{17})^3\, \mathrm{cm}^{-6}\) and \(\varDelta \omega _0/2\pi = 100\,\mathrm{Hz}\). The very small rate value is due to small combination factors, \(\gamma _{pe}^2/\gamma _e \), in particular a small A-coefficient \(\gamma _{pe} \). A possible way to get larger rates is to use multiple identical laser systems of order 10, each system capable of producing \((10^{17})^3\,\hbox {cm}^{-6}\) of \( n^3 V \eta \), within the allowed range of target excitation to \((10^{20})^3\,\hbox {cm}^{-6}\), which may enhance the rate unit \(24 \varGamma _0/\epsilon _{eg}^2\) to \(5.1 \times 10^{-3}\,\hbox {s}^{-1}\,\hbox {eV}^{-2}\) due to \(\varGamma _0 \propto n^3 V\eta \). A search for better lanthanoid candidates is highly recommended.
5.2 Xe case
Xe RANP angular distribution with \(r = 0.32304\). Cases of NO Majorana of smallest neutrino mass 1 meV in solid black, NO Majorana of 50 meV in dotted black, NO Dirac 1 meV in dashed red, and NO Dirac 50 meV in dash-dotted blue. The absolute rate is obtained by multiplying a factor \(0.12\,\hbox {s}^{-1}\) assuming \(n^3 V \eta = (10^{17} )^3\,\hbox {cm}^{-6}\)
Four lowest excited energy states of Xe are \(^3\mathrm{P}_{2,1,0}\) and \(^1\mathrm{P}_1\) in LS coupling scheme, although energy spacings are better described by intermediate coupling scheme close to JJ scheme. The following RANP path is used:
where energy values in the free space are taken from NIST data [19]. We have in mind using Xe in the free space so that parity is a good quantum number, and spin-parity \(J^P\) changes in Xe RANP path are \(0^- \rightarrow 1^+ \rightarrow 0^- \rightarrow 1^-\). In the proposed scheme of \(r= 0.32304 \), excitation lasers have \(\omega _{1}=6.2495eV, \omega _{2}=3.1976eV\) with trigger and detection \(\omega _0 = \omega = 0.3421\) eV.
Xe RANP angular distribution with \(r= 0.32304\). Cases of NO Majorana of smallest neutrino mass 20 meV in solid black, NO Dirac of 20 meV in dotted black, IO Majorana 20 meV in dashed red, and IO Dirac 20 meV in dash-dotted blue. The absolute rate is obtained by multiplying a factor \(0.12\, \hbox {s}^{-1}\) assuming \(n^3 V \eta = (10^{17} )^3\,\hbox {cm}^{-6}\)
Xe RANP scale unit is much larger than trivalent Ho ion: first, the figure of merits factor \(F= \gamma _{pe}^2 \epsilon _{eg}^2/ (\gamma _e \epsilon _{pe}^3 )\) are
Xe RANP units are \(\varGamma _0 = 5 \times 10^{-3}\,\hbox {s}^{-1}\) and \(24 \varGamma _0/\epsilon _{eg}^2 = 0.12\,\hbox {s}^{-1}\,\hbox {eV}^{-2}\) using the same value of \(n^3V \eta = (10^{17})^3\hbox {cm}^{-6}\). Angular distributions are shown in Figs. 9 and 10. Sensitivity to the neutrino mass and Dirac/Majorana distinction is better than the ordinary \(2^-\) RENP [2, 3].
The problem of Xe scheme is a large McQ4 event rate. Relevant two-photon emission at \(|q\rangle \rightarrow | g \rangle \) occurs via E1 \(\times \) E1 unlike smaller E1 \(\times \) M1 in \(\hbox {Ho}^{3+}\) doped crystal. Xe value of McQ4 integral is \(I_{2\gamma } = 3.1\times 10^{-22}\,\hbox {eV}^{-2}\) (zero at calculation accuracy for \(\hbox {Ho}^{3+}\) case) to be compared the RANP value, \(I_{2\nu } = 2.3 \times 10^{-49}\,\hbox {eV}^{-2}\). A solution is to use photonic crystal for suppression of strayed McQ4 event [20]. Due to a large level spacing the excitation to Xe \(0^-\) is more complicated than a simple two-photon excitation, which has to be studied.
6 Summary
In summary, we proposed a general scheme of macro-coherent neutrino-pair emission stimulated by Raman scattering, in order to measure important neutrino properties, the unknown smallest neutrino mass to the level of less than 1 meV, NO/IO distinction, and
Majorana/Dirac distinction. The general scheme was illustrated using \(\hbox {Ho}^{3+}\) doped crystal and Xe atom. Xe has a larger rate than lanthanoid ions, while its QED background is much more severe. Both theoretical and experimental works on QED background rejection are needed to make the general scheme realistic.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The datasets publicly available from the cited website.]
Notes
We assume that major McQn \((n=5, 6)\) events of smaller rates can be identified by extra photons and are subtracted from data for RANP, while McQn (\(n\ge 7\))’s are negligible with very small rates. Needless to say, higher order spontaneous emission rates without macro-coherence amplification are completely negligible.
Parameters determined from neutrino oscillation experiments [1] and used this work are squared mixing matrix elements, \( |U_{ei}|^2, i = 1,2,3\) directly derived from experimental data, and mass differences, \(\delta m^2_{ij} = m_i^2 - m_j^2 \). The smallest neutrino mass is assumed in each calculation. Three CP violation phases are not known in oscillation experiments, and assumed vanishing, for simplicity, in the present work.
References
Particle Data Group Collaboration, M. Tanabashi et al., Phys. Rev. D 98, 030001 (2018)
A. Fukumi et al., Prog. Theor. Exp. Phys. 2012 04D002 (2012)
D.N. Din, S.T. Petcov, N. Sasao, M. Tanaka, M. Yoshimura, Phys. Lett. B 719, 013812 (2012)
M. Yoshimura, Phys. Rev. D 75, 113007 (2007)
M. Yoshimura, N. Sasao, M. Tanaka, Phys. Rev. A 86, 013812 (2012)
Y. Miyamoto et al., PTEP, 2014 113C01 (2014)
Y. Miyamoto et al., PTEP, 2015 081C01 (2015)
T. Hiraki et al., J. Phys. B Atom. Mol. Opt. Phys. 52, 045401 (2019)
M. Eichhorn, Appl. Phys. B 93, 269–316 (2008)
C. Braggio et al., Sci. Rep. 7, 15168 (2017)
M. Tanaka, K. Tsumura, N. Sasao, S. Uetake, M. Yoshimura, Phys. Rev. D 96, 113005 (2017)
M. Yoshimura, N. Sasao, M. Tanaka, PTEP, bf 2015 053B06 (2015)
J. Jaeckel, A force beyond the standard model—status of the quest for hidden photons (2013). arXiv:1303.1821v1
B.M. Walsh, G.W. Grew, N.P. Barnes, J. Phys. Condens. Matter 17, 7643 (2005)
B.M. Walsh, N.P. Barnes, B. Di Bartolo, J. Appl. Phys. 83, 2772 (1998)
B.R. Judd, Phys. Rev. 127, 750 (1962)
G.S. Ofelt, J. Chem. Phys. 37, 511 (1962)
J.H. Van Vleck, J. Chem. Phys. 41, 67 (1937)
https://www.nist.gov/pml/atomic-spectra-database. Accessed 1 Mar 2019
M. Tanaka, K. Tsumura, N. Sasao, M. Yoshimura, PTEP, 2017 043B03 (2017)
H. Hara, N. Sasao, M. Yoshimura, Divalent lanthanoid ions in crystals for neutrino mass spectroscopy (to appear)
Acknowledgements
We thank S. Uetake at Okayama, and C. Braggio, G. Carugno, and F. Chiossi at Padova for useful discussions. This research was partially supported by Grant-in-Aid 17K14363(HH) and 17H02895(MY) from the Ministry of Education, Culture, Sports, Science, and Technology.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Hara, H., Yoshimura, M. Raman stimulated neutrino pair emission. Eur. Phys. J. C 79, 684 (2019). https://doi.org/10.1140/epjc/s10052-019-7148-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-7148-y