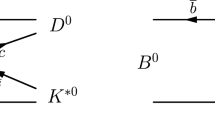New physics signature in $D^0 (\bar{D}^0)\rightarrow f$ effective width asymmetries

Abstract

Violation of charge conjugation-parity ($\mathrm CP$) symmetry plays a major rule in the dominance of matter in our universe. A kind of $\mathrm CP$ violation results from the asymmetry of the life time measured in $M^0$ and ${\bar{M}}^0$, here M is a heavy meson, decays to final states which is referred in the literature as $A_{\Gamma }^f$. In this paper, we give an estimation of the upper bound on $|A_{\Gamma }^f|$ for the Cabibbo Favored $D^0 \rightarrow K^- \pi ^+$ decay process in different models. We show that in the standard model, $|A_{\Gamma }^f| \lesssim {\mathcal {O}} (10^{-10})$. Recently a bound on $A_{\Gamma }^f$ has been obtained: $(A^f_{\Gamma })^{Exp.}= (1.6 \pm 1)\times 10^{-4}$. This result motivates further studies on $A_{\Gamma }^f$ in beyond standard model physics. In the framework of two Higgs doublet model with generic Yukawa structure, we show that $|A_\Gamma ^{f}|\lesssim {\mathcal {O}} (10^{-7})$ which is several orders of magnitude smaller than the current experimental value. Finally, in the framework of left-right symmetric models in which the mixing between the left and the right gauge bosons is allowed and the left-right symmetry is not manifest at unification scale, we find that $A_{\Gamma }^f$ can be as large as $|A_{\Gamma }^f|\lesssim {\mathcal {O}} (10^{-5})$ which is one order of magnitude smaller than the experimentally measured value by LHCb collaborators.

1 Introduction

Symmetries play an important rule in particle physics. In the standard model (SM), masses of quarks, charged leptons and weak gauge bosons can be attributed to the breaking of the electroweak symmetry. On the other hand, the difference between the decay rates of particle and its antiparticle can be an indication of direct violation of charge-parity (CPV) symmetry. Weak decays of hadrons can serve as a probe for CPV. This remark can be understood as in SM CPV originates from the presence of complex couplings in the Cabibbo–Kobayashi–Maskawa (CKM) matrix which appears only in the quark sector in the interactions of quarks and the charged weak gauge bosons $W^\pm$ [1, 2].

Direct CPV has been confirmed in the weak decays of K and B mesons [3,4,5,6]. On the other hand, the remarkable experimental progress in D mesons has leaded to the observation of $D^0-D^0$ meson mixing [7,8,9,10] and measurements of direct CP asymmetries in D mesons decays, with precision of O($10^{-3})$ [11]. A sensitive probe of CP violation in the weak decays of $D^0$ meson is given by the direct CP asymmetry difference, $\Delta A_{CP}$, between $D^0\rightarrow \pi ^+\pi ^-$ and $D^0\rightarrow K^+K^-$ which can be expressed as

$$\begin{aligned} \Delta A_{CP} = A_{CP}(K^-K^+) - A_{CP}(\pi ^-\pi ^+) \end{aligned}$$

(1)

The first observation of $\Delta A_{CP}$ was reported in 2011 by the LHCb Collaboration [12] and later confirmed by CDF [13] and Belle [14]. Recently, the LHCb collaboration has presented new measurements at Moriond 2019 and the combined value with previous LHCb results leads to [15]

$$\begin{aligned} \Delta A_{CP} = (-15.6 \pm 2.9) \times 10^{-4} \end{aligned}$$

(2)

which is 5.3 standard deviations away from zero and thus confirm direct CPV in these particular weak decays of $D^0$ mesons. This progress motivates further search and further studies of CP violation in D meson decays.

Indirect CP violation has been searched also in the decays of $D^0$ and ${\bar{D}}^0$ to final states $K^+K^-$, $\pi ^+\pi ^-$ and $K^-\pi ^+$ modes [16]. This kind of CP violation results from the asymmetry of the life time measured in $D^0$ and ${\bar{D}}^0$ decays to the same final states or equivalently the asymmetry in effective decay widths and usually denoted by $A_{\Gamma }$. The latest measurements are given as [16]

$$\begin{aligned} A_{\Gamma }(K^-K^+)= & {} \left( -0.30\pm 0.32\pm 0.10 \right) \times 10^{-3} \nonumber \\ A_{\Gamma }(\pi ^-\pi ^+)= & {} \left( 0.46 \pm 0.58 \pm 0.12 \right) \times 10^{-3}\nonumber \\ A_{\Gamma }(K^-\pi ^+)= & {} (0.16 \pm 0.10)\times 10^{-3} \end{aligned}$$

(3)

The first two processes are single Cabibbo suppressed (SCS) and the Standard Model (SM) contributions to these asymmetries are expected to be of order $10^{-4}$ [17,18,19,20]. On the other hand, the last one is Cabibbo favored (CF) with very suppressed direct CP asymmetry in the framework of the SM [21]. So any observation of CPV in these CF channels will be a strong hint for New Physics. At present time, all results are compatible with no direct or indirect CPV [16, 22,23,24,25,26,27].

In the literature, the study of the interference between direct CPV and mixing has been performed through the introduction of a non-universal weak phase defined as $\delta _f \equiv -\arg (\bar{A}_f/ A_f)$ where $A_f$ is the $A(D^0 \rightarrow f)$ amplitude [28,29,30]. It is important to notice that this weak phase is irrelevant for the direct CPV as direct CPV is proportional to $|A_f|^2-|{\bar{A}}_f|^2$. To get non vanishing direct CPV it is necessary to write the amplitude, $A_f$, as a sum of at least two amplitudes with different relative weak and strong phases.

The mass eigenstates of the neutral D mesones, denoted as $|D_{1,2}>$ with masses (total widths) $m_{1,2}$ ($\Gamma _{1,2}$), are linear combinations of the flavor eigenstates $|D^0>$ and $|{\overline{D}}^0>$ and can be defined as follows:

$$\begin{aligned} |D_{1,2}>= p|D0> \pm q|{\overline{D}}^0> \end{aligned}$$

(4)

with the imposed normalization condition $|p|^2+|q|^2=1$. We consider the decay modes $D^0\rightarrow f({\bar{f}})$ and ${\overline{D}}^0\rightarrow f({\bar{f}})$, with $f \equiv K^-\pi ^+$ and ${\bar{f}} \equiv K^+\pi ^-$. These modes are examples of $D^0$ and ${\bar{D}}^0$ decays to final non-CP eigenstate modes. In the following we denote the decay amplitudes as, $A_f=A(D^0\rightarrow f)$, ${\bar{A}}_f=A({{\overline{D}}}^0\rightarrow f)$, $A_{{\bar{f}}} =A(D^0\rightarrow {\bar{f}})$ and ${\bar{A}}_{\bar{f}}=A({{\overline{D}}}^0\rightarrow {\bar{f}})$. Moreover, we follow Ref. [31] and express the amplitudes as

$$\begin{aligned} A_f= & {} A^T_{f} e^{+i\phi ^T_{f}}[1+r_fe^{i(\delta _f+\phi _f)}],\nonumber \\ {\overline{A}}_{{{\overline{f}}}}= & {} A^T_{f} e^{-i\phi ^T_{f}}[1+r_fe^{i(\delta _f-\phi _f)}],\nonumber \\ A_{{{\overline{f}}}}= & {} A^T_{{{\overline{f}}}} e^{i(\Delta _{f}+\phi ^T_{{{\overline{f}}}})} [1+r_{{{\overline{f}}}} e^{i(\delta _{{{\overline{f}}}}+\phi _{{{\overline{f}}}})}] ,\nonumber \\ {\overline{A}}_f= & {} A^T_{{{\overline{f}}}} e^{i(\Delta _{f}-\phi ^T_{\overline{f}})} [1+r_{{{\overline{f}}} }e^{i(\delta _{{{\overline{f}}}}-\phi _{\overline{f} })}]. \end{aligned}$$

(5)

here $A^T_{f} e^{ i\phi ^T_{f}}$ and $A^T_{\overline{f}} e^{i(\Delta _{f}+\phi ^T_{{{\overline{f}}}})}$ represent SM tree-level contribution, the phases $\phi _f^T$ and $\phi ^T_{{{\overline{f}}}}$ represent weak CP violating phases while $\Delta _f$ represent strong CP conserving one all generated at tree-level. It should be noted that, upon neglecting small terms of order $|(V_{ub}V_{cb})/(V_{us}V_{cs})|\sim 10^{-3}$, $\phi ^T_f=\phi ^T_{{{\overline{f}}}}$. In Eq. (5), the quantities $r_f$ and $r_{{\bar{f}}}$ express the relative magnitudes of subleading contributions that can arise from new physics or from SM amplitudes with suppressed CKM factors. Moreover, the phases $\phi _{f,{{\overline{f}}}}$ and $\delta _{f,{{\overline{f}}}}$ denote the relative weak and strong CP violating phases respectively that account for the difference between the phases generated by the subleading contributions and the tree-levels ones.

Using the general formalism for $D^0-{\overline{D}}^0$ mixing, it is possible to compute the widths as a function of time. The time-dependent decay rates can be expressed as [31, 32]

$$\begin{aligned}&\Gamma (D^0(t)\rightarrow f) = \big |A_f(t)\big |^2 \nonumber \\&\quad = \big | g_+(t) A_f(t)+{q\over p}g_-(t){\bar{A}}_f(t)\big |^2 \nonumber \\&\quad = \big |A_f(t)\big |^2 \big [ |g_+(t)|^2+|g_-(t)\lambda _f|^2 \nonumber \\&\qquad +2\mathrm{Re}\big (g_+^*(t) g_-(t)\lambda _f\big )\big ] = {e^{-\Gamma t}\over 2}\big |A_f(t)\big |^2 \nonumber \\&\qquad \times \, \big [ (1+|\lambda _f|^2)\cosh (y\Gamma t)+(1-|\lambda _f|^2)\cos (x\Gamma t)\nonumber \\&\qquad +2\mathrm{Re} \lambda _f \sinh (y\Gamma t) -2\mathrm{Im} \lambda _f \sin (x\Gamma t) \big ],\nonumber \\&\qquad \Gamma ({\overline{D}}^0 \rightarrow f) (t) = \big |\bar{A}_f(t)\big |^2= \big | {p\over q}g_-(t)A_f(t) \nonumber \\&\qquad +g_+(t){\bar{A}}_f(t) \big |^2 = \big |{\bar{A}}_f(t)\big |^2 \big |g_+(t)+ g_-(t)\lambda ^{-1}_f\big |^2 \nonumber \\&\quad = \big |{\bar{A}}_f(t)\big |^2 \big [ |g_+(t)|^2\nonumber \\&\qquad +|g_-(t)\lambda ^{-1}_f|^2+2\mathrm{Re}\big (g_+^*(t) g_-(t)\lambda ^{-1}_f\big ) \big ] \nonumber \\&\quad ={e^{-\Gamma t}\over 2} \big |{\bar{A}}_f(t)\big |^2 \big [ \big (1+|\lambda ^{-1}_f|^2\big )\cosh (y\Gamma t)\nonumber \\&\qquad +\big (1-|\lambda ^{-1}_f|^2\big )\cos (x\Gamma t)+2\mathrm{Re}\big (\lambda ^{-1}_f\big ) \sinh (y\Gamma t) \nonumber \\&\qquad - 2\mathrm{Im}\big (\lambda ^{-1}_f\big ) \sin (x\Gamma t) \big ]. \end{aligned}$$

(6)

here $\Gamma = (\Gamma _1+\Gamma _2)/2$ is the mean $D^0$ width and

$$\begin{aligned} g_{\pm }(t)= & {} {1\over 2}\bigg (\mathrm{e}^{-i m_2 t-\frac{1}{2}\Gamma _2 t}\pm \mathrm{e}^{-i m_1 t-\frac{1}{2}\Gamma _1 t} \bigg )\nonumber \\ x= & {} \frac{\Delta m}{\Gamma }, \ y=\frac{\Delta {\Gamma }}{2\Gamma }\nonumber \\ \lambda _f= & {} {q{\bar{A}}_f\over p A_f}, \end{aligned}$$

(7)

The experimental values for the mixing and CPV parameters in D neutral mesons are given as [33]

$$\begin{aligned} x= & {} 0.41_{-0.15}^{+0.14} \% \end{aligned}$$

(8)

$$\begin{aligned} y= & {} 0.63_{-0.08}^{+0.07} \% \end{aligned}$$

(9)

$$\begin{aligned} a_{CP}^D= & {} -0.71_{-0.95}^{+0.92} \end{aligned}$$

(10)

$$\begin{aligned} |q/p|= & {} 0.93_{-0.08}^{+0.09} \end{aligned}$$

(11)

$$\begin{aligned} \phi= & {} -8.7_{-9.1}^{+8.7} \end{aligned}$$

(12)

where the fit assuming all floating parameters is used and $\phi =arg(q/p)$ is expressed in degree.

The expressions of the time-dependent decay rates into a final state ${\bar{f}}$ can be obtained via the substitutions $f\rightarrow {\bar{f}}$ in the above expressions [31]. Due to the small values of the mixing parameters x and y and $|\lambda _f| \ll 1$ and $|\lambda ^{-1}_{ {\bar{f}}}|\ll 1$, these approximations are experimentally confirmed for the decay modes under consideration [34], one can expand the expressions of the time-dependent decay rates of $D^0\rightarrow f$ and ${\overline{D}}^0\rightarrow {\bar{f}}$ and keep the terms up to first order in time. Thus, we get

$$\begin{aligned}&\Gamma \big [D^0(t)\rightarrow f\big ] \simeq \mathrm{e}^{-\Gamma t}\left| A_f\right| ^2 \left\{ 1+ \bigg [y\, Re(\lambda _{f}) \right. \nonumber \\&\left. \quad - x \, Im (\lambda _{f})\bigg ]\Gamma t \right\} \simeq \left| A_f\right| ^2 \mathrm{e}^{-t\,{\hat{\Gamma }}_{D^0\rightarrow f}} \nonumber \\&\Gamma \big [{{\overline{D}}}^0(t)\rightarrow {{{\overline{f}}}}\big ] \simeq \mathrm{e}^{-\Gamma t}\left| {\bar{A}}_{{{\overline{f}}}}\right| ^2 \left\{ 1+ \bigg [y\, Re(\lambda ^{-1}_{{{\overline{f}}}}) \right. \nonumber \\&\left. \quad - x \, Im (\lambda ^{-1}_{{{\overline{f}}}})\bigg ]\Gamma t \right\} \simeq \left| {\bar{A}}_{{{\overline{f}}}}\right| ^2 \mathrm{e}^{ -t\,{\hat{\Gamma }}_{{\overline{D}}^0\rightarrow {{\overline{f}}}}} \end{aligned}$$

(13)

Upon defining [28, 31]

$$\begin{aligned} \lambda _f\equiv \frac{q}{p}\frac{{\overline{A}}_f}{A_f}= & {} -R_m R_f e^{i(\Phi +\Delta _f+\delta \phi _{\lambda _f})},\nonumber \\ \lambda _{{{\overline{f}}}}\equiv \frac{q}{p}\frac{{\overline{A}}_{\overline{f}}}{A_{{{\overline{f}}}}}= & {} -R_mR_f^{-1}e^{i(\Phi -\Delta _f+\delta \phi _{\lambda _{{{\overline{f}}}}})}. \end{aligned}$$

(14)

where $R_m\equiv |q/p|$, $\Phi =\phi - \phi ^T_f-\phi ^T_{{{\overline{f}}}}$, $R_f\equiv |\frac{{\overline{A}}_f}{A_f}|$. The phases $\delta \phi _{\lambda _f}$ and $\delta \phi _{\lambda _{{{\overline{f}}}}}$, to first order in $r_f$ and $r_{{{\overline{f}}}}$, are given as [28]

$$\begin{aligned} \delta \phi _{\lambda _f}= & {} - r_f \sin (\delta _f+\phi _f)+r_{{{\overline{f}}}} \sin (\delta _{\overline{f}}-\phi _{\overline{f}})\nonumber \\ \delta \phi _{\lambda _{{{\overline{f}}}}}= & {} -r_{{{\overline{f}}}} \sin (\delta _{{{\overline{f}}}}+\phi _{{{\overline{f}}}})+r_f \sin (\delta _f-\phi _f) \end{aligned}$$

(15)

Using the above definitions of $\lambda _f$ and $\lambda _{{{\overline{f}}}}$, we find that the effective widths ${\hat{\Gamma }}_{D^0\rightarrow f}$ and ${\hat{\Gamma }}_{{\overline{D}}^0\rightarrow {{\overline{f}}}}$ in Eq.(13) can be expressed as

$$\begin{aligned} {\hat{\Gamma }}_{D^0\rightarrow f}= & {} \Gamma \left[ 1+R_m R_f\left( y\cos \phi _{\lambda _f}-x\sin \phi _{\lambda _f}\right) \right] \nonumber \\ {\hat{\Gamma }}_{{\overline{D}}^0\rightarrow {{\overline{f}}}}= & {} \Gamma \left[ 1+\frac{R_f}{R_m}\left( y\cos \phi _{\lambda _{\overline{f}}}+x\sin \phi _{\lambda _{{{\overline{f}}}}}\right) \right] \end{aligned}$$

(16)

here $\phi _{\lambda _f}$ and $\phi _{\lambda _{{{\overline{f}}}}}$ are the arguments of $-\lambda _f$ and $-\lambda _{{{\overline{f}}}}$ respectively. Now, one can define the following CP observable, the asymmetry in effective decay widths $A_{\Gamma }^f$, for the $D^0$ and ${{\overline{D}}}^0$ decays to final two-body non-CP eigenstate mode f [31]:

$$\begin{aligned} A_\Gamma ^f= & {} \frac{{\hat{\Gamma }}_{{\overline{D}}^0\rightarrow \overline{f}}-{\hat{\Gamma }}_{D^0\rightarrow f}}{2\,\Gamma } \end{aligned}$$

(17)

Thus, using Eq. (16), we obtain

$$\begin{aligned} A_\Gamma ^f= & {} {1\over 2} \frac{R_f}{R_m} (y\cos \phi _{\lambda _{\overline{f}}}+x\sin \phi _{\lambda _{{{\overline{f}}}}}) \nonumber \\&-{1\over 2} R_m R_f\left( y\cos \phi _{\lambda _f}-x\sin \phi _{\lambda _f}\right) \end{aligned}$$

(18)

Upon substitution of the expressions of $\phi _{\lambda _f}$ and $\phi _{\lambda _{{{\overline{f}}}}}$ we get

$$\begin{aligned} A_\Gamma ^f= & {} \frac{R_f}{2} \{[R_m (x \cos (\Delta _f+\delta \phi _{\lambda _f}) + y \sin (\Delta _f+\delta \phi _{\lambda _f}) ) \nonumber \\&+R^{-1}_m (x \cos (\Delta _f-\delta \phi _{\lambda _{{{\overline{f}}}}}) + y \sin (\Delta _f-\delta \phi _{\lambda _{{{\overline{f}}}}}) )] \nonumber \\&\times \sin \Phi -[R_m (y \cos (\Delta _f+\delta \phi _{\lambda _f})\nonumber \\&-\,x \sin (\Delta _f+\delta \phi _{\lambda _f}) ) -R^{-1}_m (y \cos (\Delta _f-\delta \phi _{\lambda _{{{\overline{f}}}}}) \nonumber \\&-\,x \sin (\Delta _f-\delta \phi _{\lambda _{{{\overline{f}}}}}) )] \cos \Phi \} \end{aligned}$$

(19)

In the models where $r_f$ and $r_{{{\overline{f}}}}$ are so small, $\delta \phi _{\lambda _f}\simeq \delta \phi _{\lambda _{\overline{f}}}\simeq 0$ and hence $A_\Gamma ^f$ reduces to

$$\begin{aligned}&A_\Gamma ^f|_{r_f=r_{{{\overline{f}}}}=0} = \frac{R_f}{2} (R_m+R^{-1}_m) \big (x \cos \Delta _f + y \sin \Delta _f \big ) \sin \Phi \nonumber \\&\quad - \frac{R_f}{2} (R_m-R^{-1}_m)\big (y \cos \Delta _f- x \sin \Delta _f\big ) \cos \Phi \end{aligned}$$

(20)

This expression is in agreement with the result in first line of Eq. (23) in Ref. [31]. At tree-level, the amplitudes of the decay processes under concern have no $\mathrm CP$ violating weak phases and thus $\phi ^T_f=\phi ^T_{{{\overline{f}}}}=0$ implying that $\Phi =\phi - \phi ^T_f-\phi ^T_{{{\overline{f}}}}=\phi$. Thus, for $\phi =0$ and $R_m = 1$, i.e. no $\mathrm CP$ violation in $D^0-{{\overline{D}}}^0$ mixing, we find that

$$\begin{aligned} A_\Gamma ^f= & {} -\frac{R_f}{2} \{y (\cos (\Delta _f+\delta \phi _{\lambda _f}) - \cos (\Delta _f-\delta \phi _{\lambda _{\overline{f}}})) \nonumber \\&- x (\sin (\Delta _f+\delta \phi _{\lambda _f})-\sin (\Delta _f-\delta \phi _{\lambda _{\overline{f}}}))\} \end{aligned}$$

(21)

The quantities $\delta \phi _{\lambda _{f}}$ and $\delta \phi _{\lambda _{{{\overline{f}}}}}$ are expected to be small and thus we can expand $A_\Gamma ^f$ in the preceding equation and keep terms up to linear order in $\delta \phi _{\lambda _{f}}$ and $\delta \phi _{\lambda _{{{\overline{f}}}}}$. Thus, we obtain

$$\begin{aligned} A_\Gamma ^f\simeq & {} \frac{R_f}{2} \big (\delta \phi _{\lambda _f}+\delta \phi _{\lambda _{{{\overline{f}}}}}\big ) \big (y \sin \Delta _f + x \cos \Delta _f\big ) \nonumber \\ {}\simeq & {} - R_f \big (r_f \cos \delta _f\sin \phi _f+r_{{{\overline{f}}}} \cos \delta _{{{\overline{f}}}}\sin \phi _{{{\overline{f}}}}\big ) \nonumber \\&\quad \times \big (y \sin \Delta _f + x \cos \Delta _f\big ) \end{aligned}$$

(22)

In the SM, the contributions to the amplitudes of the CF $D^0\rightarrow K^-\pi ^+$ and the DCS $D^0\rightarrow K^+\pi ^-$ decays originate from integrating out the $W^\pm$ boson mediating the tree-level diagrams. These contributions are proportional to the Fermi coupling constant, $G_F$, and CKM matrix elements $V_{U D}$ where $U=u,c,t$ and $D=d,s,b$. For the scenarios in which subleading contributions to the tree-level amplitudes arise from new physics with particles heavier than $m_W$ or from SM amplitudes with suppressed CKM factors, one finds that $R_f\simeq |\frac{A^T_{{{\overline{f}}}}}{A^T_{f}}|\simeq \frac{V_{cd}V^*_{us}}{V_{ud}V^*_{cs}}\simeq {\mathcal {O}} (10^{-2})$. In the SM also, the values of x, y can be as high as $x, y = {\mathcal {O}} (10^{-2})$ [35,36,37]. On the other hand, x can be close to the experimental limit in some classes of NP models [31, 38, 39]. As a consequence, we deduce from Eq. (22) that $A_\Gamma ^f$ is at least suppressed by a factor $x\, R_f \simeq {\mathcal {O}} (10^{-3})$. Other suppression factors can originate from $r_f$ and $r_{{{\overline{f}}}}$. The weak CP violating and the strong CP conserving phases may also generate suppression factors in $A_\Gamma ^f$. To obtain upper bound on $|A_\Gamma ^f |$, it is sufficient to find upper bounds on $r_f$ and $r_{{{\overline{f}}}}$ assuming no suppressions from the weak and the strong phases in a treatment similar to the one adopted in Section IV in Ref. [31] although the treatment there is for direct CP asymmetry.

As discussed in Ref. [31], and in the presence of new contributions to the QCD penguin and dipole operators, one can use the QCD factorization as a framework to obtain order-of-magnitude estimates for the amplitudes. However, for hadronic D decays, the $1/m_c$ expansion is not expected to work very well [31]. This can be understood as the mass of the charm quark is of order 1.5 GeV which is not heavy enough to allow for a sensible heavy quark expansion like the case of $1/m_b$ expansion in B meson decay. Thus, as proposed in Ref. [31], see appendix A for details, one can ignore ${\mathcal {O}} (\alpha _s)$ corrections to the matrix elements, as they are negligible compared to the overall theoretical uncertainties and work primarily at leading order in $\Lambda _{QCD}/m_c$, using naive factorization (NF) for tree and QCD penguin operators in the effective Hamiltonian governs the decay process. Thus, in the following we adopt NF in our analysis to give an estimation of the upper bounds on $r_f$ and $r_{{{\overline{f}}}}$ for the CF decay mode $D^0 \rightarrow K^- \pi ^+$ in the framework of the SM and classes of NP models.

2 The effective time-integrated CP asymmetry in the SM

In the SM, the total amplitudes of $D^0\rightarrow K^-\pi ^+$ and $D^0\rightarrow K^+\pi ^-$ decay processes can be expressed as [21, 40]

$$\begin{aligned} A^{SM}_{D^0\rightarrow K^-\pi ^+}= & {} -i{G_F\over \sqrt{2}}V_{cs}^*V_{ud} \left[ (a_1+\Delta a_1) X^{\pi ^+}_{D^0 K^-} \right. \nonumber \\&\left. + (a_2+\Delta a_2) X^{D^0}_{K^-\pi ^+} \right] ,\nonumber \\A^{SM}_{D^0\rightarrow K^+\pi ^-}= & {} -i{G_F\over \sqrt{2}}V_{us}V^*_{cd} \left[ (a_1+\Delta a'_1) X^{K^+}_{D^0 \pi ^-} \right. \nonumber \\&\left. + (a_2+\Delta a'_2) X^{D^0}_{K^+\pi ^-} \right] , \end{aligned}$$

(23)

with $X^{P_1}_{P_2P_3}$ is given by

$$\begin{aligned} X^{P_1}_{P_2P_3}= if_{P_1}\Delta _{P_2P_3}^2 F_0^{P_2P_3}(m_{P_1}^2),\ \Delta _{P_2P_3}^2=m_{P_2}^2-m_{P_3}^2 \end{aligned}$$

(24)

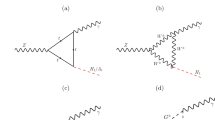
here $f_{P}$ is the P meson decay constant and $F_0^{P_2 P_3}$ is the form factor. In Eq. (23) $a_1 = c_1+ c_2/N_C$ and $a_2=-( c_2+c_1/N_C)$ where $N_C$ is the color number account for the tree-level contributions to the amplitudes. These coefficients originate from integrating out the $W^\pm$ boson mediating the tree-level diagrams. On the other hand, and in the same equation, $\Delta a_{1,2}$ and $\Delta a'_{1,2}$ express the contributions to the amplitudes resulting from integrating out the $W^\pm$ boson mediating the box and di-penguin diagrams. These loop contributions are essential for generating the weak phase required for having non-vanishing $A_{\Gamma }^f$ as the tree-level contributions are real. Their expressions are given as

$$\begin{aligned} \Delta a_1\simeq & {} -{G_Fm_W^2\over \sqrt{2}\ \pi ^2V_{c s}^*V_{u d}N } {{\mathcal {B}}}_x \nonumber \\&- {G_F \alpha _S\over 4\sqrt{2} \pi ^3V_{c s} ^* V_{u d}}\left[ {\kappa \over 2}\left( 1-{1\over N^2}\right) \right] {{\mathcal {P}}}_g \nonumber \\ \Delta a_2\simeq & {} -{G_Fm_W^2\over \sqrt{2}\ \pi ^2V_{c s}^*V_{u d} } {{\mathcal {B}}}_x \nonumber \\&- {G_F \alpha _S\over 4\sqrt{2} \pi ^3V_{c s} ^* V_{u d}}{3 m_{d} m_c\over 8 N }\chi ^{D^0} {{\mathcal {P}}}_g \end{aligned}$$

(25)

where $\kappa =(m_D^2+m_K^2)/2+3m_\pi ^2/4$ and

$$\begin{aligned} \chi ^{D^0} = {m_{D^0}^2\over (m_c+m_u)(m_s-m_d)}, \end{aligned}$$

(26)

The quantities ${{\mathcal {B}}}_x$ and ${{\mathcal {P}}}_g$ originate from the box and di-penguin diagrams respectively and their expressions are given as

$$\begin{aligned} {{\mathcal {B}}}_x= & {} V_{c D}^*V_{u D} V_{U s}^*V_{U d} f(x_U,\ x_D)\nonumber \\ {{\mathcal {P}}}_g= & {} \left[ V_{c D}^*V_{u D} E_0(x_D)\right] \left[ V_{U s}^*V_{U d} E_0(x_U)\right] \end{aligned}$$

(27)

with $U=u,\ c,\ t$ and $D=d,\ s,\ b$, $x_q=(m_q/m_W)^2$ and $f_{UD} \equiv f(x_U,x_D)$ where [41]

$$\begin{aligned} f(x,\ y)= & {} {7xy-4\over 4(1-x)(1-y)} \\&+{1\over x-y}\bigg [ {y^2\log y\over (1-y)^2}\left( 1-2x+{xy\over 4}\right) \\&- {x^2\log x\over (1-x)^2}\left( 1-2y+{xy\over 4}\right) \bigg ] \end{aligned}$$

and the Inami function $E_0(x)$ is given as

$$\begin{aligned} E_0(x)= & {} {1\over 12(1-x)^4} [ x(1-x)(18-11x-x^2) \nonumber \\&-2(4-16x+9x^2)\log (x)] \end{aligned}$$

(28)

Turning now to $\Delta a'_{1,2}$ we find that their expressions are given as

$$\begin{aligned} \Delta a'_1 \simeq&-{G_Fm_W^2\over \sqrt{2}\ \pi ^2V_{cd}^*V_{us}N }\,{{\mathcal {B}}}'_x \nonumber \\&- {G_F \alpha _S\over 4\sqrt{2} \pi ^3 V_{cd}^*V_{us}}\left[ {q^2\over 2}\left( 1-{1\over N^2}\right) \right] {{\mathcal {P}}}'_g \nonumber \\ \Delta a'_2 \approx&-{G_Fm_W^2\over \sqrt{2}\ \pi ^2V_{cd}^*V_{us} } \,{{\mathcal {B}}}'_x - {G_F \alpha _S\over 4\sqrt{2} \pi ^3 V_{cd}^*V_{us}}{5m_s m_D^2\over 8N m_d} \mathcal{P}'_g \end{aligned}$$

(29)

where the quantities ${{\mathcal {B}}}'_x , {{\mathcal {P}}}'_g$ can be obtained from the expressions of ${{\mathcal {B}}}_x , {{\mathcal {P}}}_g$, given in Eq. (27), via the replacement $d \leftrightarrow s$.

Using $a_1= 1.2 \pm 0.1$, $a_2 = - 0.5 \pm 0.1$ $, | F_0^{K\pi }(m^2_{D^2})|= 0.5$ and $Arg(F_0^{K\pi }(m^2_{D^2}))= 75^\circ$ [42], $F^{D\pi }_0 (m_K^2)=0.6$, $F^{D K}_0 (m_\pi ^2)=0.75$ [43], $f_D= 212.15 \pm 1.45$ MeV [44] and $f_K= 157.5 (2.4)$ MeV [44, 45], we find that $|\Delta a_{1,2} | \lesssim \mathcal {O} (10^{-8})$ and $|\Delta a'_{1,2} |\lesssim \mathcal {O} (10^{-6})$ leading to $r_f \lesssim \mathcal {O} (10^{-8})$ and $r_{{\overline{f}}} \lesssim \mathcal {O} (10^{-6})$. Clearly, $A^{f\,SM}_{\Gamma }$ is suppressed at least by a factor of $\mathcal {O} (10^{-10})$ resulting from the product $x\,R_f\,r_{{\overline{f}}}$ leading to the prediction $|A^{f\,SM}_{\Gamma }|\lesssim \mathcal {O} (10^{-10})$.

3 The effective time-integrated CP asymmetry in NP models

In this section we consider two particular extensions of the SM based on their potentials to enhance CP violation due to the presence of new complex couplings. The first model is based on extending the scalar sector of the SM to include new Higgs doublet. The other model is based on extending the gauge symmetry of the SM to include new gauge group. In both models, the new interactions can provide new sources for the weak CP violating phases essential for CP violation as we showed in our earlier studies in Refs. [21, 40]. Based on the studies and due to the strong constraints on the parameter space of the two models, $r_{{\overline{f}}}$ are expected to be small compared to $r_f$ and thus in the following we give an estimation of the upper bound on $r_f$ only.

3.1 Models with charged Higgs contributions

Two Higgs doublet models (2HDM) are simple extensions of the SM. In 2HDM, only the scalar sector of the SM is extended to include extra Higgs doublet [46, 47]. In the literature, 2HDM have been classified, according to their couplings to quarks and leptons, into: 2HDM type I, II or III (for a review see Ref. [48]). The 2HDM type III (2HDM III) is of a particular interest to our study due to the presence of complex couplings of Higgs to quarks which are relevant for generating the desired CP violating weak phases. The model has five physical mass eigenstates; heavy CP-even Higgs ($H_0$), light CP-even Higgs ($h_0$), CP-odd Higgs ($A_0$) and finally the charged Higgs ($H^{\pm }$). In the model also, both Higgs doublets can couple to up-type and down-type quarks implying that the couplings of the neutral Higgs mass eigenstates can lead to flavor violation in neutral currents at tree-level. As a result, flavor changing neutral current processes can be used to strongly restraint these couplings [49, 50]. We turn now to the charged Higgs couplings to the quarks. The interaction Lagrangian in this case is given as [49, 50]

$$\begin{aligned} \mathcal {L}^{eff}_{H^\pm } = \bar{u}_f {\Gamma _{u_f d_i }^{H^\pm \,LR\,\mathrm {eff} } }P_R d_i + \bar{u}_f {\Gamma _{u_f d_i }^{H^\pm \,RL\,\mathrm {eff} } }P_L d_i\, , \end{aligned}$$

(30)

where

$$\begin{aligned} {\Gamma _{u_f d_i }^{H^\pm \,LR\,\mathrm {eff} } }= & {} \sum \limits _{j = 1}^3 {\sin \beta \, V_{fj} \left( \frac{m_{d_i }}{v_d} \delta _{ji}- \epsilon ^{ d}_{ji}\tan \beta \right) , } \nonumber \\ {\Gamma _{u_f d_i }^{H^ \pm \,RL\,\mathrm {eff} } }= & {} \sum \limits _{j = 1}^3 {\cos \beta \, \left( \frac{m_{u_f }}{v_u} \delta _{jf}- \epsilon ^{ u\star }_{jf}\tan \beta \right) V_{ji}} \end{aligned}$$

(31)

where $v_u$ and $v_d$ denote the vacuum expectations values of the neutral component of the Higgs doublets, tan $\beta = v_u/v_d$ and V is the CKM matrix. Extensive study of all possible constraints that can be imposed on the parameters $\epsilon ^{ u,d}_{jf}$ has been carried in Ref. [50]. We also have studied the constraints on $\epsilon ^{ u,d}_{jf}$ relevant to the process $D^0\rightarrow K^-\pi ^+$ in a previous work in Ref. [21]. Based on our study in Ref. [21], the total amplitude, including Higgs contribution, can be written as

$$\begin{aligned} A^{SM+H^\pm }_{D^0\rightarrow K^-\pi ^+}\simeq & {} -i{G_F\over \sqrt{2}}V_{cs}^*V_{ud} \left[ (a_1+\Delta a^{H^\pm }_1) X^{\pi ^+}_{D^0 K^-} \right. \nonumber \\&\left. + (a_2+\Delta a^{H^\pm }_2) X^{D^0}_{K^-\pi ^+} \right] , \end{aligned}$$

(32)

Keeping only the dominant contributions to $\Delta a^{H^\pm }_{1,2}$ we find that

$$\begin{aligned} \Delta a^{H^\pm }_1\simeq & {} \frac{\sin 2\beta m_{d }\epsilon ^{ u}_{22}\tan \beta \,\chi ^{\pi ^+} }{ \sqrt{2} \, G_F m^2_H v_d},\nonumber \\ \Delta a^{H^\pm }_2\simeq & {} \frac{\sin 2\beta m_{d }\epsilon ^{ u}_{22}\tan \beta \,\chi ^{D} }{ 2 \sqrt{2} \, G_F m^2_H v_d\,N} \end{aligned}$$

(33)

where

$$\begin{aligned} \chi ^{\pi ^+} = {m_{\pi }^2\over (m_c-m_s)(m_u+m_d)} \end{aligned}$$

(34)

A recent analysis has set the bound $m_{H^\pm }\gtrsim 600$ GeV independent of $\tan \beta$ in 2HDM II [51]. This result has been obtained after considering the most recent constraints from flavour physics and direct charged and neutral Higgs boson searches at LEP and the LHC. It should be noted that the obtained bound must be respected also for the charged Higgs mass in 2HDM III [49], Thus, for $\tan \beta = 50$ and $m_{H^\pm } = 600$ GeV we find that

$$\begin{aligned} \Delta a^{H^\pm }_1\simeq & {} 1.1\times 10^{-3} \, Im(\epsilon ^{ u}_{22})I \nonumber \\ \Delta a^{H^\pm }_2\simeq & {} 2.3\times 10^{-3}\, Im(\epsilon ^{ u}_{22}) I \end{aligned}$$

(35)

where we kept only the imaginary parts required for generating the weak phases and neglected the real parts of $\Delta a^{H^\pm }_1$ and $\Delta a^{H^\pm }_2$ as they are much smaller than the SM contributions and they are not relevant for generating weak phases. The most dominant constraints on $Im(\epsilon ^{ u}_{22})$ arise from the electric dipole moment of the neutron [50]. The resultant bound reads $-0.16 \lesssim \, Im(\epsilon ^{ u}_{22})\, \lesssim 0.16$. Thus, From Eq. (35), we find that $|a^{H^\pm }_{1,2}|$ of $\mathcal {O} (10^{-4})$. Thus, we obtain $r_f\lesssim \mathcal {O} (10^{-4})$ resulting in this model $|A_\Gamma ^{f}|\lesssim \mathcal {O} (10^{-7})$ which still very small compared to the current experimental value.

3.2 A new charged gauge boson as left right models

Possible extensions of the SM include models based on the gauge group $SU(2)_L \times SU(2)_R \times U(1)_{B-L}$ [52,53,54,55,56,57,58,59,60,61]. In these class of models, new complex couplings can arise due to the interactions of quarks and leptons with the new charged boson. In turn, this can affects CP violation in meson and lepton sectors. Previous analyses showed that large direct CP violation can be generated in the Charm and muon sectors if the mixing between the left and the right gauge bosons is allowed and the left-right symmetry is not manifest at unification scale [21, 62, 63]. Motivated by this finding, we study the impact of the new complex couplings in such particular setup of LRS model on $A_{\Gamma }^f$ of the decay process $D^0\rightarrow K^-\pi ^+$. The charged current mixing matrix can be parameterized as [59, 62, 64]

$$\begin{aligned} \left( \begin{array}{c} W^\pm _L \\ W^\pm _R \end{array}\right)&= \left( \begin{array}{cc} \cos \xi &{} -\sin \xi \\ \mathrm{e}^{i\omega }\sin \xi &{} \mathrm{e}^{i\omega }\cos \xi \end{array}\right) \left( \begin{array}{c} W^\pm _1 \\ W^\pm _2 \end{array}\right) \nonumber \\&\simeq \left( \begin{array}{cc} 1 &{} - \xi \\ \mathrm{e}^{i\omega }\xi &{} \mathrm{e}^{i\omega } \end{array}\right) \left( \begin{array}{c} W^\pm _1 \\ W^\pm _2 \end{array}\right) \end{aligned}$$

(36)

here $\xi$ is a mixing angle, $W^\pm _1$ and $W^\pm _2$ denote the mass eigenstates and $\omega$ is a weak CP violating phase. This mixing results in interactions between charged quarks and charged W bosons that reads

$$\begin{aligned} {{\mathcal {L}}}\simeq & {} -{1\over \sqrt{2}} {\bar{U}} \gamma _\mu \left( g_LVP_L+g_R\xi {\bar{V}}^RP_R\right) DW_1^\dagger \nonumber \\&- {1\over \sqrt{2}} {\bar{U}} \gamma _\mu \left( -g_L\xi VP_L+g_R\bar{V}^RP_R\right) DW_2^\dagger \end{aligned}$$

(37)

where ${\bar{V}}^R=\mathrm{e}^{i\omega }V^R$. Upon integrating out $W_1$ in the usual way and neglecting $W_2$ contributions, given its mass is much higher, we can express the total amplitude of $D^0\rightarrow K^-\pi ^+$ as

$$\begin{aligned} A^{SM+LRS}_{D^0\rightarrow K^-\pi ^+}\simeq & {} -i{G_F\over \sqrt{2}}V_{cs}^*V_{ud} \left[ (a_1+\Delta a^{LRS}_1) X^{\pi ^+}_{D^0 K^-} \right. \nonumber \\&\left. + (a_2+\Delta a^{LRS}_2) X^{D^0}_{K^-\pi ^+} \right] , \end{aligned}$$

(38)

with

$$\begin{aligned} \Delta a^{LRS}_1\simeq & {} {g_R\over g_L }\xi \left( \bar{V}^R_{ud}-{\bar{V}}^{R*}_{cs} \right) a_1 \nonumber \\ \Delta a^{LRS}_2\simeq & {} {2 g_R\over g_L }\xi \left( {\bar{V}}^R_{ud}-{\bar{V}}^{R*}_{cs} \right) \chi ^{D^0} a_2 \end{aligned}$$

(39)

The measurement of the muon decay parameter $\rho$, which governs the shape of the overall momentum spectrum, performed by the TWIST collaboration [65, 66] can set constraint on the left right mixing angle $\xi$. The $\rho$ parameter can be linked to $\xi$ via [65]:

$$\begin{aligned} \rho \simeq \frac{3}{4}\bigg [1- 2\, \big (\frac{g_R}{g_L} \xi \big )^2\bigg ] \end{aligned}$$

(40)

Upon defining $\zeta = \frac{g_R}{g_L} \xi$ and using the TWIST value, from their latest global fit given in Table VII in Ref. [66], $\rho = 0.74960 \pm 0.00019$ we obtain

$$\begin{aligned} 3.7\times 10^{-3} \lesssim \zeta \lesssim 2.3\times 10^{-2} \end{aligned}$$

(41)

which represents the allowed $2 \sigma$ range of the mixing parameter $\zeta$. We move now to discuss the allowed values of ${\bar{V}}^R_{ud}, {\bar{V}}^R_{cs}$. The real parts of these quark mixing matrix elements will be always suppressed by a factor $\zeta$ and thus can be neglected compare to the SM contributions. This will be the case also for the imaginary parts of $\bar{V}^R_{ud}, {\bar{V}}^R_{cs}$ where they are also suppressed by the same factor $\zeta$. However, they provide new source of the desired weak CP violating phases and thus can not be neglected.

Recently, the authors of Ref. [67] have investigated the possible bounds that can be imposed on the complex couplings of the $W^\pm$ boson to right-handed quarks using low-energy precision measurements, flavor physics and collider physics. These bounds can be applied to the couplings in general left-right symmetric model that allows mixing between the charged gauge bosons of the $S U(2)_R$ and $S U(2)_L$ as the one we consider here. The findings of the study in Ref. [67], imply that the experimental value of $(\epsilon '/ \epsilon )_K$ and the stringent bounds on the electric dipole moment of the neutron can allow $Im(\bar{V}^R_{ud})$ to be as large as $9\times 10^{-4}$. Moreover, the dominant constraint on $\zeta Im({\bar{V}}^R_{c s})$ arise from the process $K_L\rightarrow \pi ^0\, e^+\, e^ -$ and can allow $\zeta \, Im({\bar{V}}^R_{c s})$ to have a maximum value $7\times 10^{-3}$. Consequently, with the range of $\zeta$ in Eq. (41), $Im({\bar{V}}^R_{c s})$ can have a value $\simeq {{\mathcal {O}} }(1)$ without violating the imposed constraints from the process $K_L\rightarrow \pi ^0\, e^+\, e^ -$. Taking these values into account, we obtain $|\Delta a^{LRS}_1|\simeq \mathcal {O} (10^{-2})$ and $|\Delta a^{LRS}_2|\simeq \mathcal {O} (10^{-1})$. As a consequence, we find that $r_f \lesssim \mathcal {O} (10^{-2})$ and hence, in this class of NP models $|A_{\Gamma }^f|\lesssim \mathcal {O} (10^{-5})$. The result is one order of magnitude smaller than the experimentally measured value by LHCb collaborators.

4 Conclusion

In this work we have studied the CP asymmetry in the time-integrated effective widths, $A_{\Gamma }^f$, for the Cabibbo Favored $D^0 \rightarrow K^- \pi ^+$ decay process within different models. This asymmetry is very sensitive to both the scale and the weak phases of the amplitudes generated from the radiative corrections to the SM tree-level amplitude or from the New Physics contributions. In the SM, due to the suppression of the radiative corrections to the tree-level amplitude, we have shown that $|A_{\Gamma }^f| \lesssim \mathcal {O} (10^{-10})$ which is very suppressed compared to the recently measured value $(A^f_{\Gamma })^{Exp.}= (1.6 \pm 1.0)\times 10^{-4}$. It should be noted that, this experimental result shows only a $1.6\, \sigma$ deviation from zero and the mode served only as a control channel in Ref. [16], where its consistence with zero has been used as a justification of the main result of that paper.

Regarding the prediction in the framework of 2HDM III, we have found that $|A_\Gamma ^{f\,SM+H^\pm }|\lesssim \mathcal {O} (10^{-7})$ which is several orders of magnitude smaller than the current experimental value. Finally, in a general left-right symmetric models, allowing the mixing between the left and the right gauge bosons and adopting the scenario that the left-right symmetry is not manifest at unification scale can lead to a value $|A_{\Gamma }^f|\lesssim \mathcal {O} (10^{-5})$ which is one order of magnitude smaller than the experimentally measured value by LHCb collaborators.