1 Introduction

The standard model (SM) of particle physics has been describing phenomena over the wide range of energy scale from eV to TeV scale. Despite of such enormous success, the anomalous magnetic moment of the muon, \((g-2)_\mu \), shows a long-standing discrepancy between experimental observations [1, 2] and theoretical predictions [3,4,5,6],

$$\begin{aligned} \Delta a_\mu \equiv \Delta a_\mu ^{\mathrm {exp}} - \Delta a_\mu ^{\mathrm {th}} = (28.8 \pm 8.0) \times 10^{-10}, \end{aligned}$$
(1)

where \(a_\mu = (g-2)_\mu /2\). This difference reaches to \(3.6\sigma \) deviation from the prediction and seems not to be resolved within the SM. The on-going and forthcoming experiments will verify the discrepancy with high statistics, which will reduce the uncertainties by a factor of four [8, 9]. Then, when the discrepancy is confirmed by the these experiments, it must be a firm evidence of physics beyond the SM.

Many extensions of the SM have been proposed to resolve the discrepancy so far (See for a review [7]). Among them, one of the minimal extensions is to add a new U(1) gauge symmetry to the SM. When muon is charged under the symmetry, the deviation of \((g-2)_\mu \) can be explained by a new contribution from the associated gauge boson of the symmetry through loop diagrams. The \(L_\mu - L_\tau \) gauge symmetry is particularly interesting in this regard because it is anomaly free extension and can also explain the neutrino mass and mixings simultaneously [10,11,12]. In this model, it was shown in Refs. [13,14,15] that the deviation of \((g-2)_\mu \) can be resolved when the gauge boson mass is of order 10 MeV and the gauge coupling constant is of order \(10^{-4}\). Such a light and weakly interacting gauge boson is still allowed from experimental searches performed in past. Interestingly, it was also shown that the gauge boson with similar mass and gauge coupling can also explain the deficit of cosmic neutrino flux reported by IceCube collaboration [16,17,18,19,20]. Many experimental searches have been prepared and on-going for such a light particles in meson decay experiment [21], beam dump experiment [22] and electron-positron collider experiment [23]. Theoretical studies on search strategy at collider experiment are also proposed (see e.g. [24,25,26,27] for \(L_\mu - L_\tau \) model Footnote 1).

As mentioned above, the \(L_\mu - L_\tau \) gauge boson has a mass, hence the symmetry must be broken. This implies that at least one new complex scalar, which is singlet under the SM gauge group, should exist to break the symmetry and give a mass to the gauge boson. Then, from the gauge symmetry, there must exist an interaction of two gauge bosons and one real scalar by replacing the scalar field with its vacuum expectation value (VEV). Since this interaction is generated after the symmetry breaking, the confirmation of the interaction by experiments is a crucial to identify the model. The VEV of the scalar can be estimated as about 10–100 GeV from the gauge boson mass and the gauge coupling. Thus, naively one can expect that the physical CP-even scalar emerging after the symmetry breaking has a mass of the same order. Such a heavy scalar can not be directly searched at low energy experiments, and hence should be searched at high energy collider experiments, i.e. the Large Hadron Collider (LHC) experiment and future International Linear Collider (ILC) experiment [28, 29]. In this paper, we study signatures for the scalar as well as the light gauge boson using \(Z'\)-\(Z'\)-\(\phi \) vertex at the LHC experiment and Z-Z-\(\phi \) vertex at the ILC experiments.

This paper is organized as follows. In Sect. 2, we briefly review the minimal gauged \(L_\mu - L_\tau \) model and give the partial decay widths of the scalar and gauge bosons. In Sect. 3, we show the allowed parameter space of the model. Then we show our results on the signatures of the scalar and the gauge boson production at the LHC and ILC experiments in Sect. 4. Section 5 is devoted to the summary and discussion.

Table 1 Contents of scalar fields and their charge assignments under \(SU(2)_L\times U(1)_Y \times U(1)_{L_\mu -L_\tau }\)
Full size table

2 Model

We begin our discussions with reviewing a model with gauged \(U(1)_{L_\mu - L_\tau }\) symmetry under which muon (\(\mu \)) and tau (\(\tau \)) flavor leptons are charged among the SM leptons. As a minimal setup, we introduce a SM singlet scalar field \(\varphi \) to break the \(L_\mu - L_\tau \) symmetry spontaneously. The gauge charge assignment for the lepton and scalar fields are given in Table 1, and the quark sector is the same as that of the SM. In the table, \(L_{e},~L_{\mu },~L_{\tau }\) and \(e_R,~\mu _R,~\tau _R\) denote the left and right-handed leptons, and H denotes the \(SU(2)_L\) doublet scalar field, respectively. The Lagrangian of the model is given by

$$\begin{aligned} {\mathcal {L}}&= {\mathcal {L}}_{\mathrm{SM}} +|D_\mu \varphi |^2 - V - \frac{1}{4} Z'_{\mu \nu } Z'^{\mu \nu } - \frac{\epsilon }{2} B_{\mu \nu } Z'^{\mu \nu } \nonumber \\&\quad + g' Z'_\mu J^\mu _{Z'}, \end{aligned}$$
(2)
$$\begin{aligned} J^\mu _{Z'}&= {\bar{L}}_\mu \gamma ^\mu L_\mu + {\bar{\mu }}_R \gamma ^\mu \mu _R - {\bar{L}}_\tau \gamma ^\mu L_\tau - {\bar{\tau }}_R \gamma ^\mu \tau _R, \end{aligned}$$
(3)
$$\begin{aligned} V&= -\mu _H^2 H^\dagger H - \mu _\varphi ^2 \varphi ^* \varphi + \frac{\lambda _H}{2} (H^\dagger H)^2 + \frac{\lambda _\varphi }{2} (\varphi ^* \varphi )^2 \nonumber \\&\quad + \lambda _{H \varphi } (H^\dagger H)(\varphi ^* \varphi ), \end{aligned}$$
(4)

where \({\mathcal {L}}_{\mathrm{SM}}\), \(J_{Z'}\) and V represent the SM Lagrangian, the \(U(1)_{L_\mu - L_\tau }\) current and the scalar potential, respectively. The gauge fields and its field strengths corresponding to \(U(1)_{L_\mu - L_\tau }\) and \(U(1)_Y\) are denoted by \(Z'\) and B. In Eq. (3), \(D_\mu = \partial _\mu - i g' Z'_\mu \) is the covariant derivative, and \(g'\) and \(\epsilon \) represent the \(L_{\mu }- L_{\tau }\) gauge coupling constant and the kinetic mixing parameter, respectively. In the following discussions, we assume that the quartic couplings of the scalar fields, \(\lambda _H,~\lambda _\varphi \) and \(\lambda _{H\varphi }\), are positive to avoid runaway directions. In Eq. (4), \(\mu _H^2\) and \(\mu _\phi ^2\) are the tachyonic masses of H and \(\varphi \).

The scalar fields H and \(\varphi \) can be expanded as

$$\begin{aligned} H = \begin{pmatrix} H^+ \\ \frac{1}{\sqrt{2}} (v + {\tilde{H}} + i A) \end{pmatrix}, \quad \varphi = \frac{1}{\sqrt{2}} (v_\varphi + {{\tilde{\phi }}} + i a), \end{aligned}$$
(5)

where \(H^+\), A and a are massless Nambu–Goldstone bosons which should be absorbed by the gauge bosons \(W^+\), Z and \(Z'\), while \(\tilde{H}\) and \({\tilde{\phi }}\) represent the physical CP-even scalar bosons.

The VEVs of the scalar fields, v and \(v_\varphi \), are obtained from the stationary conditions \(\partial V/ \partial v = \partial V/ \partial v_\varphi = 0\);

$$\begin{aligned} v = \sqrt{\frac{2 (\lambda _\varphi \mu _H^2 - \lambda _{H \varphi } \mu _\varphi ^2 )}{\lambda _H \lambda _\varphi - \lambda _{H \varphi }^2 }}, \quad v_\varphi = \sqrt{\frac{2 ( \lambda _H \mu _\varphi ^2 - \lambda _{H \varphi } \mu _H^2) }{\lambda _H \lambda _\varphi - \lambda _{H \varphi }^2 }}.\!\!\!\!\nonumber \\ \end{aligned}$$
(6)

Without loss of generality, the VEVs are taken to be real-positive by using the degree of freedom of the gauge symmetries to rotate the scalar fields. Inserting Eq. (5) into Eq. (4), the squared mass terms for CP-even scalar bosons are given by

$$\begin{aligned} {\mathcal {L}} \supset \frac{1}{4} \begin{pmatrix} {\tilde{H}} \\ {{\tilde{\phi }}} \end{pmatrix}^T \begin{pmatrix} \lambda _H v^2 &{} \lambda _{H \varphi } v v_\varphi \\ \lambda _{H \varphi } v v_\varphi &{} \lambda _\varphi v_\varphi ^2 \end{pmatrix} \begin{pmatrix} {\tilde{H}} \\ {{\tilde{\phi }}} \end{pmatrix}. \end{aligned}$$
(7)

The above squared mass matrix can be diagonalized by an orthogonal matrix. The mass eigenvalues are given by

$$\begin{aligned} m_{h,\phi }^2 = \frac{\lambda _H v^2 +\lambda _\varphi v_\varphi ^2 }{4} \pm \frac{1}{4} \sqrt{\left( \lambda _H v^2 -\lambda _\varphi v_\varphi ^2 \right) ^2 + 4 \lambda _{H \varphi }^2 v^2 v_\varphi ^2 },\!\!\!\!\nonumber \\ \end{aligned}$$
(8)

and the corresponding mass eigenstates h and \(\phi \) are obtained as

$$\begin{aligned} \begin{pmatrix} h \\ \phi \end{pmatrix} = \begin{pmatrix} \cos \alpha &{} \sin \alpha \\ - \sin \alpha &{} \cos \alpha \end{pmatrix} \begin{pmatrix} {\tilde{H}} \\ {\tilde{\phi }} \end{pmatrix}, \quad \tan 2 \alpha = \frac{2 \lambda _{H \varphi } v v_\varphi }{\lambda _H v^2 - \lambda _\varphi v_\varphi ^2},\!\!\!\!\nonumber \\ \end{aligned}$$
(9)

where \(\alpha \) is the mixing angle. When \(\alpha \ll 1\), h is identified as the SM-like Higgs boson. Note that the scalar quartic couplings, \(\lambda _\varphi \) and \(\lambda _{H\varphi }\), are smaller than unity in our discussion. In fact, the typical order of these couplings are \({\mathcal {O}}(10^{-2})\) and \({\mathcal {O}}(10^{-3})\), respectively, when we take \(\sin \alpha =0.05\) and \(m_\phi ={\mathcal {O}}(100)\) GeV, \(m_{Z'} = 100\) MeV. Therefore the perturbative unitarity and stability of the potential are maintained at least up to 10 TeV.

After the spontaneous breaking of the electroweak and \(L_\mu -L_\tau \) symmetries, the gauge bosons acquire masses. The neutral components of the gauge bosons mix each other due to the kinetic mixing while the charged ones remain the same as those of the SM. Assuming \(\epsilon \ll 1\), the mass eigenvalues of the neutral components, \(Z_{1,2,3}\), are obtained after diagonalizing the mass term as well as the kinetic term,

$$\begin{aligned} m_{Z_1}^2&= 0, \end{aligned}$$
(10a)
$$\begin{aligned} m_{Z_2}^2&= m_Z^2 (1 - 2 \epsilon ^2 \sin ^2 \theta _W) + {\mathcal {O}}(\epsilon ^4 m_Z^2), \end{aligned}$$
(10b)
$$\begin{aligned} m_{Z_3}^2&= m_{Z'}^2 + {\mathcal {O}}(\epsilon ^6 m_Z^2), \end{aligned}$$
(10c)

where \(m_Z\) and \(\theta _W\) are the Z boson mass and the Weinberg angle in the SM, respectively, and

$$\begin{aligned} m_{Z'} = g' v_\varphi \end{aligned}$$
(11)

The corresponding mass eigenstates of the gauge bosons are given by

$$\begin{aligned} Z_1^\mu&= A^\mu , \end{aligned}$$
(12a)
$$\begin{aligned} Z_2^\mu&\simeq Z^\mu , \end{aligned}$$
(12b)
$$\begin{aligned} Z_3^\mu&\simeq Z'^\mu - \epsilon \sin \theta _W Z^\mu , \end{aligned}$$
(12c)

up to \({\mathcal {O}}(\epsilon ^2)\). Thus, \(Z_1\) is the photon, and \(Z_2\) and \(Z_3\) are almost Z and \(Z'\), respectively. We denote \(Z_1\) and \(Z_2\) as Z and \(Z'\) in the rest of this paper. Note that \(\rho \)-parameter in our model is shifted from 1 as

$$\begin{aligned} \rho = \frac{m_{Z}^2}{m_{Z_2}^2} \simeq 1 + 2 \epsilon ^2 \sin ^2 \theta _W \simeq 1 + \frac{1}{2} 10^{-6} \left( \frac{\epsilon }{10^{-3}} \right) ^2, \end{aligned}$$
(13)

where the experimental observation is given by \(\rho = 1.0004^{+0.0003}_{-0.0004}\) [30] with \(2 \sigma \) error. Thus we can avoid the constraint from \(\rho \)-parameter for \(\epsilon \lesssim 3.7 \times 10^{-2}\).

The Yukawa and gauge interactions of the SM fermions and \(\phi \) in mass-basis are given by

$$\begin{aligned}&{\mathcal {L}} \supset \sum _{f} \frac{m_f}{v} \sin \alpha \phi {\bar{f}} f + \frac{m_{Z'}^2}{v_\varphi } \cos \alpha \phi Z'_\mu Z'^\mu \nonumber \\&\quad + \frac{m_Z^2}{v} \sin \alpha \phi Z_\mu Z^\mu + \frac{2 m_W^2}{v} \sin \alpha \phi W^+_\mu W^{-\mu } \nonumber \\&\quad + Z'_\mu (-e \epsilon \cos \theta _W J_{\mathrm{EM}}^\mu + g' J_{Z'}^\mu ) + {\mathcal {O}}(\epsilon ^2), \end{aligned}$$
(14)

where \(m_f\) and \(J_{\mathrm{EM}}\) represent the mass of the fermions f and the electromagnetic currents of the SM, and e and \(\theta _W\) are the electric charge of the proton and the Weinberg angle, respectively. In Eq. (14), the interactions between \(Z'\) and \(J_{\mathrm{EM}}\) are induced through the kinetic mixing.Footnote 2 In the LHC and lepton collider experiments, the scalar \(\phi \) can be mainly produced via the gluon fusion and associate Z production processes. One can see from Eq. (14) that the relevant interactions are proportional to the scalar mixing, \(\sin \alpha \). Therefore the production cross section increases as \(\sin \alpha \) becomes larger.

For the SM-like Higgs boson, the gauge and scalar interactions in mass-basis are also obtained by inserting Eq. (9) into the Lagrangian. The relevant interactions in our discussions are given by

$$\begin{aligned} {\mathcal {L}} \supset \frac{m_{Z'}^2}{v} \sin \alpha h Z'_\mu Z'^\mu - \frac{1}{2} g_{h \phi \phi } h \phi \phi + {\mathcal {O}}(\epsilon ), \end{aligned}$$
(15)

where \(g_{h \phi \phi }\) is the constant given by

$$\begin{aligned} g_{h \phi \phi }&= 3 \sin \alpha \cos \alpha ( \lambda _H v \sin \alpha + \lambda _\varphi v_\varphi \cos \alpha ) \nonumber \\&\quad +\lambda _{H\varphi } (v \cos ^3\alpha + v_\varphi \sin ^3\alpha - 2 v_\varphi \sin \alpha \cos ^2 \alpha \nonumber \\&\quad - 2 v \sin ^2 \alpha \cos \alpha ). \end{aligned}$$
(16)

There exist other gauge and scalar-self interactions involving h. However, those are negligible when the mixing angle \(\alpha \) and the kinetic mixing parameter \(\epsilon \) is much smaller than the unity. Note that \(\lambda _{H \varphi }\) is written in terms of \(\alpha \) from Eq. (9). Therefore \(g_{h \phi \phi }\) becomes proportional to \(\alpha \) when \(\alpha \) is small enough.

In the end of this section, we show the decay widths of \(\phi \), \(Z'\) and h. As we will explain in the next section, we focus our discussions on the situation that the \(Z'\) gauge boson has a mass lighter than \(2m_\mu \), while the scalar boson \(\phi \) has a mass of order 10–100 GeV. Thus, the \(\phi \) can decay into \(Z'\) as well as the SM fermions and the gauge bosons. The partial decay widths of \(\phi \) are given by

$$\begin{aligned} \Gamma _{\phi \rightarrow Z' Z'}&= \frac{{g'}^2 \cos ^2 \alpha }{8 \pi } \frac{m_{Z'}^2}{m_\phi } \sqrt{1 - \frac{4 m_{Z'}^2}{m_\phi ^2}}\nonumber \\&\quad \times \left( 2 + \frac{m_\phi ^4}{4 m_{Z'}^4} \left( 1 - \frac{2 m_{Z'}^2 }{m_\phi ^2} \right) ^2 \right) , \end{aligned}$$
(17)
$$\begin{aligned} \Gamma _{\phi \rightarrow f {\bar{f}}}&= \frac{m_\phi }{8 \pi } \left( \frac{m_f}{v} \right) ^2 \sin ^2 \alpha \left( 1 - \frac{4 m_f^2}{m_\phi ^2} \right) ^{\frac{3}{2}}, \end{aligned}$$
(18)
$$\begin{aligned}&\Gamma _{\phi \rightarrow Z Z(W^+W^-)} \nonumber \\&\quad = \frac{\sin ^2 \alpha }{8 \pi } \frac{m_{Z(W)}^3}{v^2} \frac{m_{Z(W)}}{m_\phi } \sqrt{1 - \frac{4 m_{Z(W)}^2}{m_\phi ^2}}\nonumber \\&\qquad \times \left( 2 + \frac{m_\phi ^4}{4 m_{Z(W)}^4} \left( 1 - \frac{4 m_{Z(W)}^2 }{m_\phi ^2} \right) ^2 \right) , \end{aligned}$$
(19)

where \(m_{Z,W^\pm }\) are the mass of the gauge bosons, respectively. Here we have assumed final states are on-shell. It is important to mention that \(\phi \) dominantly decays into \(Z' Z'\) when \(Z'\) mass is light since its partial decay width is enhanced by \(m_\phi ^4/m_{Z'}^4\) factor.

Fig. 1
figure 1

\(BR(Z' \rightarrow ff)\) as a function of \(\epsilon /g'\) where red and blue lines correspond to \({\bar{\nu }}_{\mu ,\tau } \nu _{\mu ,\tau }\) and \(e^+e^-\) mode respectively. The mass of \(Z'\) is fixed to 100 MeV

Full size image

The \(Z'\) boson can decay into \({\bar{\nu }}_{\mu ,\tau } \nu _{\mu , \tau }\) or \(e^+ e^-\) modes because \(m_{Z'} < 2 m_\mu \). Then the partial decay widths of \(Z'\) are obtained as

$$\begin{aligned} \Gamma _{Z' \rightarrow \nu {\bar{\nu }}}&= \frac{g'^2}{24 \pi } m_{Z'}, \end{aligned}$$
(20)
$$\begin{aligned} \Gamma _{Z' \rightarrow e^+ e^-}&=\frac{e^2 \epsilon ^2 \cos ^2 \theta _W}{12 \pi } m_{Z'} \left( 1 + 2 \frac{m_e^2}{m_{Z'}^2} \right) \sqrt{1 - \frac{4 m_e^2}{m_{Z'}^2}}, \end{aligned}$$
(21)

where we have ignored the neutrino masses and mixing. The branching ratio (BR) can be parametrized by the ratio of \(L_\mu - L_\tau \) gauge coupling and kinetic mixing parameter, \(\epsilon /g'\). We show \(BR(Z' \rightarrow ff)\) as a function of \(\epsilon /g'\) in Fig. 1 where red and blue curves respectively correspond to \({\bar{\nu }}_{\mu ,\tau } \nu _{\mu ,\tau }\) and \(e^+e^-\) mode. The mass of \(Z'\) is fixed to 100 MeV, however the branching ratio is almost independent of the \(Z'\) mass when \(m_{Z'} \gg m_e\). It is seen in Fig. 1 that \(Z'\) mainly decays into neutrinos for \(\epsilon /g'<1\). For later use, the branching ratio is about 0.07 for \(\epsilon /g' = 1\).

The SM-like Higgs boson can decay into not only \(Z'\) but also \(\phi \) when \(m_\phi < m_h/2\). The partial widths of these decays are given by

$$\begin{aligned}&\Gamma _{h \rightarrow Z' Z'} \nonumber \\&\quad = \frac{{g'}^2 \sin ^2 \alpha }{8 \pi } \frac{m_{Z'}^2}{m_{h}} \sqrt{1 - \frac{4 m_{Z'}^2}{m_{h}^2}} \left( 2 + \frac{m_{h}^4}{4 m_{Z'}^4} \left( 1 - \frac{2 m_{Z'}^2 }{m_{h}^2} \right) ^2 \right) , \end{aligned}$$
(22a)
$$\begin{aligned}&\Gamma _{h \rightarrow \phi \phi } =\frac{g_{h \phi \phi }^2}{32\pi m_{h}} \sqrt{1 - \left( \frac{2m_\phi }{m_{h} } \right) ^2}. \end{aligned}$$
(22b)
Fig. 2
figure 2

The branching ratio of the Higgs invisible decays, \(h \rightarrow Z'Z'\) and \(h \rightarrow \phi \phi \)

Full size image

As we mentioned above, \(\phi \) dominantly decays into \(Z'\), and \(Z'\) mainly decays into neutrinos for \(\epsilon /g' < 1\). Therefore these decays are invisible. The branching ratio of the invisible decays in our model is given by

$$\begin{aligned} BR(h \rightarrow \mathrm {invisibles}) \equiv \frac{\Gamma _{h \rightarrow Z'Z'} + \Gamma _{h \rightarrow \phi \phi }}{\Gamma _{\mathrm {SM}} + \Gamma _{h \rightarrow Z'Z'} + \Gamma _{h \rightarrow \phi \phi }}, \end{aligned}$$
(23)

where \(\Gamma _{\mathrm {SM}}\) is the total width of the Higgs boson in the SM.Footnote 3 When \(m_\phi \ge m_{h}/2\), \(\Gamma _{h \rightarrow \phi \phi }\) should be dropped in Eq. (23). The invisible decay of the Higgs boson has been searched at the LHC experiment in the production via gluon fusion [32], vector boson fusion [32,33,34,35], and in association with a vector boson [32, 33, 35,36,37,38]. We employ \(BR(h \rightarrow \mathrm {invisibles}) \le 0.25\) given in [35]. In Fig. 2, the branching ratio is shown in \(m_{Z'}\)-\(g'\) plane. The blue, green and red lines correspond to \(BR(h \rightarrow \mathrm {invisibles}) =0.25, 0.05\) and 0.001, respectively. The scalar mass is taken as \(m_\phi = 30\) GeV (solid) and \(m_\phi \ge m_h/2\) (dashed), and the scalar mixing is fixed to \(\sin \alpha = 0.03\) for reference. The SM-like Higgs mass and its total decay width is taken as 125 GeV [39] and 4.07 MeV [40], respectively. From the figure, we can see that \(g'\) should be smaller than \(2 \times 10^{-3}\) for \(m_{Z'} \le 2 m_\mu \), to avoid the upper bound from the LHC experiment. This region of \(g'\) is consistent with the favored region to resolve \((g-2)_\mu \) discrepancy.

3 Allowed parameter space

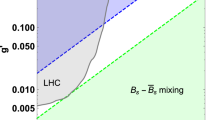
In this section, we show the allowed parameter space of \(g'\), \(\epsilon \) and \(m_{Z'}\), \(\alpha \). The parameters of \(Z'\) are tightly constrained by experiments such as beam dump experiments [41, 42], meson decay experiments [21, 43,44,45,46], neutrino-electron scattering measurements [47], electron-positron collider experiment [48, 49], neutrino trident production process [50, 51]. A hadron collider experiment such as the LHC also constrains the gauge interaction for heavier \(Z'\) region [25,26,27] although we will not discuss such a heavy \(Z'\). The parameters can be further constrained by requiring that the \(Z'\) gauge boson gives enough contributions to \((g-2)_\mu \).

As we mentioned in the introduction, the deviation of \((g-2)_\mu \) between the experimental observations and the theoretical prediction are

$$\begin{aligned} 12.8~(4.8) \le \Delta a_\mu ^{Z'} \times 10^{10} \le 44.8~(52.8). \end{aligned}$$
(24)

within \(2\sigma ~(3\sigma )\). The contribution from \(Z'\) to the anomalous magnetic moment is given by

$$\begin{aligned} \Delta a_\mu ^{Z'} = \frac{(g'+\epsilon e \cos \theta _W)^2}{8 \pi ^2} \int ^1_0 dx \frac{2 m_\mu ^2 x^2 (1-x)}{x^2 m_\mu ^2 + (1-x)m_{Z'}^2}. \end{aligned}$$
(25)

The favored region of the gauge coupling and the \(Z'\) mass to explain the deviation were studied in [52,53,54,55]. The region is summarized as

$$\begin{aligned}&2 \times 10^{-4} \le ~ g' \le 2 \times 10^{-3}, \end{aligned}$$
(26)
$$\begin{aligned}&5 \le ~ m_{Z'} \le 210~ \mathrm {MeV} . \end{aligned}$$
(27)

The VEV of \(\varphi \) is estimated from Eqs. (26) and (27) as

$$\begin{aligned} v_\varphi = \frac{m_{Z'}}{g'} \simeq 10 - 1000~\mathrm {GeV}. \end{aligned}$$
(28)

Since the mass of \(\phi \) is roughly given by \(\lambda _{\varphi } v_\varphi \), it is naturally expected that \(m_\phi \) is the same order of \(v_\varphi \). The most stringent bound on the kinetic mixing parameter is set by NA64 [21]. Based on the analysis in [54], the constraint from the meson decay is obtained by

$$\begin{aligned} \epsilon \cos \theta _W \sqrt{BR(Z' \rightarrow e^+ e^-)} \le \epsilon _{\mathrm {MD}}, \end{aligned}$$
(29)

where \(\epsilon _{\mathrm {MD}}\) is the upper bound in [21], which depends on \(m_{Z'}\). For \(m_{Z'} = 100~(5)\) MeV, the favored region of \(\epsilon \) is obtained as

$$\begin{aligned} \frac{\epsilon }{g'} \le 2~(0.6), \end{aligned}$$
(30)

respectively.

Fig. 3
figure 3

The allowed region of the parameters in \(m_{Z'}\)-\(g'\) plane. In the left and right panels, \(m_\phi \) is taken as 30 GeV and larger than \(m_{h}/2\), respectively. The blue, green, red and brown lines represents the upper bound on the invisible Higgs decays. The values of \(\sin \alpha \) corresponding to each line are shown in the figures. The favored regions of \((g-2)_\mu \) within \(2\sigma \) and \(3\sigma \) are indicated by the orange and purple bands. The gray area is excluded by the neutrino trident production process

Full size image

On the other hand, the scalar mixing and the invisible Higgs decay branching ratio, \(BR_{\mathrm {invis}}\), are also constrained by analysis of data from the LHC experiment [56, 57] as

$$\begin{aligned} \sin \alpha&\le 0.3, \end{aligned}$$
(31)
$$\begin{aligned} BR_{\mathrm {invis}}&\le 0.25, \end{aligned}$$
(32)

In Fig. 3, we show the allowed region of \(\sin \alpha \) in \(m_{Z'}\)-\(g'\) plane. In the left and right panels, \(m_\phi \) is taken as 30 GeV and larger than \(m_{h}/2\), respectively, and \(\epsilon /g' = 1\) is assumed. The blue, green, red and brown lines indicate \(BR(h \rightarrow \mathrm {invisibles}) \le 0.25\) for various values of \(\sin \alpha \) shown in the figure. The area below lines is allowed. The constraint on \(g'\) becomes tight as \(\sin \alpha \) increases since the decay widths of the invisible Higgs decays Eq. (22) are proportional to \(\alpha \) when \(\alpha \ll 1\). The orange and purple regions are the favored region of \((g-2)_\mu \) within \(2\sigma \) and \(3\sigma \). From the right panel, we can see that the scalar mixing, \(\sin \alpha \), should be between \(1.7\times 10^{-3}\) and \(7.5\times 10^{-2}\) to explain \((g-2)_\mu \). This range of \(\sin \alpha \) becomes slightly shifted to \(2.5\times 10^{-3}\) and \(1.1\times 10^{-1}\) for \(m_\phi \gtrsim m_h/2\), as shown in the left panel. Note that for lighter \(m_{Z'}\), \(\epsilon /g' = 1\) is excluded by NA64. However, when we use \(\epsilon /g' = 0.6\), the \((g-2)_\mu \) favored region and the excluded region are slightly shifted upward in this case. Therefore, the result does not change so much. In the following analysis, we fix \(m_{Z'} = 100\) MeV, \(\epsilon /g' = 1\) and \(\sin \alpha = 0.05\), and discuss the observation possibilities at the LHC and the ILC collider experiments.

4 Signature of extra scalar boson and \(Z'\) in collider experiments

In this section, we discuss signature of \(\phi \) and \(Z'\) in collider experiments; the LHC and the ILC. We consider the mass of \(\phi \) and \(Z'\) are \(O(10-100)\) GeV and O(100) MeV, respectively. The scalar boson \(\phi \) can be produced in collider experiments through the mixing with the SM Higgs boson, and dominantly decays into \(Z'\) bosons. As we showed in the previous section, \(Z'\) dominantly decays into \(\nu \bar{\nu }\), and subdominantly into \(e^+ e^-\) for \(\epsilon /g' < 1\). We investigate possibilities to search for the signature of \(\phi \) and \(Z'\) in collider experiments in this situation.

4.1 Signatures at the LHC

In the parameter space of our choice, the gauge boson \(Z'\) is mainly produced from \(\phi \) decay at the LHC because \(Z'\) interacts with quarks only through the kinetic mixing. The main production of \(\phi \) is gluon fusion through the mixing with the SM Higgs.

To identify the gauge and scalar bosons, \(Z'\) should decay into \(e^+e^-\) because \(Z'\) and \(\phi \) are electrically neutral. However, \(e^+e^-\) pair from \(Z'\) decay will be highly collimated due to lighter \(Z'\) mass than GeV scale. Here we estimate the degree of collimation; if \(Z' \rightarrow e^+ e^-\) decay system is boosted with velocity of \(v_{Z'} \sim \sqrt{m_\phi ^2/4-m_{Z'}^2}/(m_\phi /2)\) which is induced by decay of \(\phi \rightarrow Z' Z'\), the angle between \(e^+\) and \(e^-\) is approximately \(\theta \sim \cos ^{-1} (1-8m_{Z'}^2/m_\phi ^2)\) where we assumed \(e^\pm \) direction before boost is z-direction and \(\mathbf {v}_{Z'}\) is perpendicular to the direction. Then the angle is \(\sim 1^\circ \) for \(m_{Z'} = 100\) MeV and \(m_\phi = 50\) GeV. It is discussed in [60, 61] that reconstruction of such a collimated \(e^+e^-\) pair is experimentally challenging due to angle resolution with the ATLAS detector. The reconstruction of \(e^+ e^-\) pair is possible for \(m_{Z'} \ge 15\) GeV, which is already excluded for muon \((g-2)\) to be explained. Even for \(\mu ^+ \mu ^-\) pair, the reconstruction has been simulated only above \(m_{Z'} \ge 1\) GeV. A new analysis would be needed for the reconstruction of \(e^+\) and \(e^-\) momenta. However such a new analysis is beyond the scope of this paper and we do not discuss here. From this fact, lepton colliders are more suitable to search for \(\phi \) in our parameter choice because it can use missing energy search due to the precise knowledge of the initial energy.

Although the light \(Z'\) is hard to observe at the LHC, for future reference, we show the production cross section of \(\phi \) via gluon fusion process \(gg \rightarrow \phi \) through the mixing with the SM Higgs boson. The relevant effective interaction for the gluon fusion is given by [58]

$$\begin{aligned} {{\mathcal {L}}}_{\phi gg} = \frac{\alpha _s}{16 \pi } \frac{\sin \alpha }{v} A_{1/2}(\tau _t) \phi G^a_{\mu \nu } G^{a \mu \nu }, \end{aligned}$$
(33)

where \(G^a_{\mu \nu }\) is the field strength for gluon and \(A_{1/2}(\tau _t) = -\frac{1}{4} [\ln [(1+\sqrt{\tau _t})/(1-\sqrt{\tau _t})] - i \pi ]^2\) with \(\tau _t = 4 m_{t}^2/m_\phi ^2\). This effective interaction is induced from \({\bar{t}} t \phi \) coupling via the mixing effect where we take into account only top Yukawa coupling since the other contributions are subdominant. In Fig. 4, we show the production cross section estimated by MADGRAPH5 [59] implementing the effective interaction by use of FeynRules 2.0 [63], which is multiplied by scaling factor \(\kappa _\alpha \equiv (0.05 /\sin \alpha )^2\) since the cross section is proportional to \(\sin ^2 \alpha \). We also included K-factor of \(K_{gg} = 1.6\) for gluon fusion process which comes from NLO correction [64]. We can see that the production cross section is \({\mathcal {O}}(0.01 - 0.1)\) pb for \(70 \le m_\phi \le 190\) GeV. Assuming the integrated luminosity 300 fb\(^{-1}\) (LHC) and 3000 fb\(^{-1}\) (HL-LHC), the number of \(\phi \) produced is \({\mathcal {O}}(10^3-10^4)\) and \({\mathcal {O}}(10^4-10^5)\), respectively. Therefore we have sizable number of events, and background estimation as well as analysis on the collimated \(e^+ e^-\) pair will be important.

Fig. 4
figure 4

The cross section for \(pp \rightarrow \phi \) as a function of \(m_\phi \) which is multiplied by scaling factor \(\kappa _\alpha = (0.05/\sin \alpha )^2\), and \(\sqrt{s} = 13\) TeV is applied

Full size image

4.2 Signatures at the ILC

Here we discuss \(\phi \) production processes and possibility to search for its signature at the ILC experiment. In lepton collider experiments, \(\phi \) can be produced by the processes such that \(e^+ e^- \rightarrow Z \phi \), \(e^+ e^- \rightarrow \nu {\bar{\nu }} \phi \) and \(e^+ e^- \rightarrow e^+ e^- \phi \) where the second process is W boson fusion and the third process is Z boson fusion; these processes are induced by the interactions in Eq. (14). Remarkably, polarized electron and positron beams will be available at ILC where possible combinations of \((e^+, e^-)\) polarization is \((-+, +-, ++, --)\). In our following analysis, we apply fractions of \((45 \%, 45 \%, 5 \%, 5 \%)\) with the total integrated luminosity \(L = 2000\) fb\(^{-1}\), and \(\pm 80(30) \%\) polarization for the electron(positron) beam as a realistic value [29]. To simplify the analysis, we only consider \((e^+, e^-)\) polarizations \((+,-)\) and \((-,+)\) with the integrated luminosity of 900 fb\(^{-1}\) where we respectively denote these cases as LL and RR polarizations hereafter.

Fig. 5
figure 5

The cross section for \(\phi \) production processes in \(e^+e^-\) collider for two polarization cases LL and RR as a function of \(m_\phi \). The scaling factor \(\kappa _\alpha = (0.05/\sin \alpha )^2\) is multiplied with the cross section

Full size image
Fig. 6
figure 6

Distribution of invariant mass for \(\ell ^+ \ell ^-\) with only basic cuts where left-, middle- and right-panels correspond to signal, \(\ell ^+\ell ^- \nu {\bar{\nu }}\) BG and \(\tau ^+ \tau ^-\) BG events. Here \(\kappa _\alpha =1\) is applied

Full size image

In Fig. 5, we show the production cross sections for \(\sqrt{s}=250\) GeV for two polarization cases calculated by CalcHEP 3.6 [62] implementing relevant interactions, which is scaled by \(\kappa _\alpha = (0.05/\sin \alpha )^2\) factor. The figure shows that \(e^+ e^- \rightarrow Z \phi \) mode gives the largest cross section for \(m_\phi \lesssim 160\) GeV for the LL and RR polarizations. In our following analysis, we thus focus on the \(Z \phi \) mode since cross sections for the other modes are small. Then we consider two cases; (1) Z decays into two leptons, \(\ell ^+ \ell ^-\) (\(\ell = e, \mu \)) and (2) Z decays into two jets, jj. In both cases, \(\phi \) decays as \(\phi \rightarrow Z' Z' \rightarrow \nu \nu {\bar{\nu }} {\bar{\nu }}\) which is the dominant decay mode. Therefore our signals are

(34)

for cases (1) and (2) respectively where denotes missing energy. Note that we can reconstruct mass of \(\phi \) in lepton collider experiments using energy momentum conservation even if \(\phi \) becomes missing energy.

Hereafter we perform a simulation study of our signal and background (BG) processes in both cases (1) and (2); the events are generated via MADGRAPH/MADEVENT 5 [59], where the necessary Feynman rules and relevant parameters of the model are implemented by use of FeynRules 2.0 [63], the PYTHIA 6 [66] is applied to deal with hadronization effects, the initial-state radiation (ISR) and final-state radiation (FSR) effects and the decays of the SM particles, and Delphes [67] is used for detector level simulation.

4.2.1 The case of signal

Here we discuss the ”” signal and corresponding BG events. We then estimate the discovery significance applying relevant kinematical cuts. In this case we consider following BG processes:

  • \(e^+ e^- \rightarrow \ell ^+ \ell ^- \nu {\bar{\nu }}\)  ,

  • \(e^+ e^- \rightarrow \tau ^+ \tau ^+\),

where the first process mainly comes from \(e^+e^- \rightarrow ZZ/W^+W^-\) followed by leptonic decays of \(Z/W^\pm \) while the second process gives evens via leptonic decay of \(\tau ^\pm \). Signal and BG events are generated with basic cuts implemented in MADGRAPH/MADEVENT 5 as

$$\begin{aligned} p_T(\ell ^\pm ) > 7 \ \mathrm{GeV}, \quad |\eta (\ell ^\pm )| < 2.5, \end{aligned}$$
(35)

where \(p_T\) denotes transverse momentum and \(\eta = -\ln (\tan \theta /2)\) is the pseudo-rapidity with \(\theta \) being the scattering angle in the laboratory frame. With the basic cuts, the cross sections for the BG processes are obtained such as

$$\begin{aligned}&\sigma (e^+ e^- \rightarrow \ell ^+ \ell ^- \nu {\bar{\nu }}) = 1.99 (0.186) \ \mathrm{pb} \nonumber \\&\quad \text {for LL(RR) polarization}, \end{aligned}$$
(36)
$$\begin{aligned}&\sigma (e^+ e^- \rightarrow \tau ^+ \tau ^+) = 2.36 (1.94) \ \mathrm{pb}\nonumber \\&\quad \text {for LL(RR) polarization}, \end{aligned}$$
(37)

where detector efficiency is not applied here. Note that \(\ell ^+ \ell ^- \nu {\bar{\nu }}\) background is small for RR polarization since \(W^+ W^-\) production cross section is suppressed.

Fig. 7
figure 7

Distribution of reconstructed \(\varphi \) mass after imposing basic and \(M_{\ell ^+ \ell ^-}\) cuts where left-, middle- and right-panels correspond to signal, \(\ell ^+\ell ^- \nu {\bar{\nu }}\) BG and \(\tau ^+ \tau ^-\) BG events. Here \(\kappa _\alpha =1\) is applied

Full size image
Table 2 The number of events for signal (\(N_S\)), BG (\(N_{BG}\)) and significance (\(S_{cl}\)) for RR polarization case after each cut where we have adopted \(m_\phi = (30, 65)\) GeV as reference values. The integrated luminosity is taken as 900 fb\(^{-1}\), and \(N_S(S_{cl})\) is given by the products of scaling factor \(k_\alpha \) and the value for \(\kappa _\alpha =1\)
Full size table

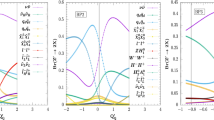
We then investigate kinematic distributions for signals and BGs, and also efficiency of kinematical cutoff. Plots in Fig. 6 show \(\ell ^+ \ell ^-\) invariant mass distributions where left-, middle- and right-panels correspond to events from the signal, \(\ell ^+\ell ^- \nu {\bar{\nu }}\) BG and \(\tau ^+ \tau ^-\) BG with only basic cuts in Eq. (35). Here we show distribution for both LL and RR polarizations in \(\ell ^+ \ell ^- \nu {\bar{\nu }}\) BG, and those for only LL polarization are shown in the other plots since RR case present almost the same behavior. We find that the distribution for signal events shows a clear peak at Z boson mass. On the other hand the distribution for \(\ell ^+ \ell ^- \nu {\bar{\nu }}\) BG has a peak at Z mass and continuous region coming from \(e^+e^- \rightarrow W^+W^-\) process. Note that continuous region is much suppressed in RR case since contribution from \(e^+ e^- \rightarrow W^+ W^-\) is small. The distribution for \(\tau ^+ \tau ^-\) BG has broad bump peaked around 80 GeV. To reduce the BG events, we thus impose the \(\ell ^+ \ell ^-\) invariant mass cuts as

$$\begin{aligned} m_Z - 10 \ \mathrm{GeV}< M_{\ell ^+ \ell ^-} < m_Z + 10 \ \mathrm{GeV}. \end{aligned}$$
(38)

Furthermore we reconstruct the mass of \(\phi \) using energy momentum conservation. The reconstructed mass is given by

$$\begin{aligned} M_{\phi _\ell }^{rec} = \sqrt{s + m_Z^2 -2 (E_{\ell ^+} + E_{\ell ^-}) \sqrt{s} } \end{aligned}$$
(39)

where \(E_{\ell ^\pm }\) is energy of final state \(\ell ^\pm \). Plots in Fig. 7 show the distribution of \(M_\phi ^{rec}\) for the signal and BGs. As in the \(M_{\ell ^+ \ell ^-}\) distribution, we show the distribution for both LL and RR polarizations in \(\ell ^+ \ell ^- \nu {\bar{\nu }}\) BG and show only those for RR polarization in the other plots. We see that the mass of \(\phi \) is indeed reconstructed giving clear peaks. Note also that \(\ell ^+ \ell ^- \nu {\bar{\nu }}\) BG has a peak at Z boson mass which comes from \(e^+ e^- \rightarrow ZZ\) process due to energy momentum conservation. Then we also impose kinematical cuts for \(M_\phi ^{rec}\) such that

$$\begin{aligned} m_\phi - 10 \ \mathrm{GeV}< M_{\phi _\ell }^{rec} < m_\phi + 10 \ \mathrm{GeV}. \end{aligned}$$
(40)

Table 2 summarizes the effect of kinematical cuts to signal and BGs for RR polarization as an example where cut efficiency has similar behavior in LL polarization. We see that the number of events for the BGs can be highly reduced by the \(M_{\ell ^+ \ell ^-}\) and \(M_{\phi _\ell }^{rec}\) cuts while that of the signal events does not change significantly. Note that the number of the BG events is large in the region \(M_{\phi _\ell }^{rec} \gtrsim 80\) GeV. It would be difficult to search for our signal if \(m_\phi \) is in the region.

Finally we estimate the discovery significance by

$$\begin{aligned} S_{cl} = \frac{N_S}{\sqrt{N_{BG}}}, \end{aligned}$$
(41)

where \(N_S\) and \(N_{BG}\) respectively denote the number of events for the signal and total BG. The significances before and after kinematical cuts are shown in the last column of Table 2 for RR polarization. We see that cut for \(M_{\phi _\ell }^{rec}\) can reduce the BG events significantly while keeping signal events. In addition, we compare the significances in RR and LL polarizations, and sum of them after all kinematical cuts in Table. 3. Then we find that the events from only RR polarization provides the largest significance since \(\ell ^+ \ell ^- \nu {\bar{\nu }}\) background in LL polarization is large and hence decrease the significance. We can obtain discovery significance of 2.2(2.5) for \(m_\phi = 65(30)\) GeV with \(\kappa _\alpha = 1\) corresponding to \(\sin \alpha = 0.05\) in RR polarization. Thus small scalar mixing as \(\sin \alpha =0.05\) will be constrained when mass of \(\phi \) is as light as 65 GeV for RR polarization. Furthermore if \(\sin \alpha \sim 0.1\) we can get discovery significance larger than \(S_{cl} = 5\) since \(\kappa _\alpha \sim 1/4\). Note that more detailed kinematical cuts will improve the significance [69] but it is beyond the scope of this paper.

Table 3 The number of events for signal (\(N_S\)), BG (\(N_{BG}\)) and significance (\(S_{cl}\)) for RR and LL polarizations with integrated luminosity of 900 fb\(^{-1}\) each and for sum of events from two polarizaitons, where we show cases for \(m_{\phi } = 65(30)\) GeV with all kinematical cuts imposed
Full size table
Fig. 8
figure 8

Distribution of invariant mass for two jets with only basic cuts where left-, middle- and right-panels correspond to signal, \(jj \nu {\bar{\nu }}\) BG and \(\tau ^+ \tau ^-\) BG events. Here \(\kappa _\alpha =1\) is applied

Full size image

4.2.2 The case of signal

Here we discuss the ”” signal and corresponding BG events and estimate discovery significance applying relevant kinematical cuts. In this case we consider following BG processes:

  • \(e^+ e^- \rightarrow j j \nu {\bar{\nu }}\)  ,

  • \(e^+ e^- \rightarrow \tau ^+ \tau ^+\),

where the first process mainly comes from \(e^+e^- \rightarrow ZZ\) followed by Z decay into jets/neutrinos and the second process gives events due to miss-identification of \(\tau \)-jet as hadronic jets with missing energy. Signal and BG events are generated with basic cuts for jets in final states implemented in MADGRAPH/MADEVENT 5 as

$$\begin{aligned} p_T(j) > 20 \ \mathrm{GeV}, \quad \eta (j) < 5.0 \, . \end{aligned}$$
(42)

With the basic cuts, the cross sections for BG processes are obtained such as

$$\begin{aligned}&\sigma (e^+ e^- \rightarrow j j \nu {\bar{\nu }}) = 0.398 (0.158) \ \mathrm{pb}\nonumber \\&\quad \text {for LL(RR) polarization}, \end{aligned}$$
(43)

where efficiency at the detector is not applied here and cross section for \(\tau ^+ \tau ^-\) is the same as Eq. (37).

Fig. 9
figure 9

Distribution of reconstructed \(\varphi \) mass after imposing basic and \(M_{jj}\) cuts where left-, middle- and right-panels correspond to signal, \(jj \nu {\bar{\nu }}\) BG and \(\tau ^+ \tau ^-\) BG events. Here \(\kappa _\alpha =1\) is applied

Full size image
Table 4 The number of events for signal (\(N_S\)), BG (\(N_{BG}\)) and significance (\(S_{cl}\)) for RR polarization after each cut where the setting is the same as Table. 2
Full size table

As in the case, we investigate kinematical distributions for the signal and BGs to find relevant kinematical cuts. Plots in Fig. 8 show distributions of invariant mass of two jets where left-, middle- and right-panels correspond to events from signal, \(jj\nu {\bar{\nu }}\) BG and \(\tau ^+ \tau ^-\) BG with only basic cuts in Eq. (42). To compare with ”” case we show distribution for both LL and RR polarization in \(jj \nu {\bar{\nu }}\) BG, and we find the behaviors are not significantly different in these polarizations since the BG comes from ZZ production; the distributions for the other plots have also similar behavior in LL and RR polarizations. The distribution for signal shows Z peak which is slightly broader than that in \(\ell ^+\ell ^-\) case above and the position of peak is slightly smaller than Z boson mass; this is due to the fact that jet energy resolution is worse than that of charged leptons. The \(jj \nu {\bar{\nu }}\) BG case also shows distribution peaked around Z boson mass. The distribution for \(\tau ^+ \tau ^-\) BG shows broad bump peaked around 160 GeV. In reducing BG events, we thus impose jj invariant mass cuts such that

$$\begin{aligned} m_Z - 20 \ \mathrm{GeV}< M_{jj} < m_Z + 5 \ \mathrm{GeV}. \end{aligned}$$
(44)

We also reconstruct the mass of \(\phi \) as in the case of charged lepton final state with energy momentum conservation. Similarly we obtain the reconstructed mass as

$$\begin{aligned} M_{\phi _j}^{rec} = \sqrt{s + m_Z^2 -2 (E_{j_1} + E_{j_2}) \sqrt{s} } \end{aligned}$$
(45)

where \(E_{j_i}\) is energy of a jet in final state \(j_i\). Plots in Fig. 9 show the distribution of \(M_{\phi _j}^{rec}\) for signal and BGs. We see that the reconstructed mass of \(\phi \) tends to larger than actual value of \(m_\phi \) and peak for \(jj \nu {\bar{\nu }}\) BG is also larger than \(m_Z\). This is due to energy loss of two jets due to initial/final state radiation which is stronger than the case of charged lepton final states. Then we impose kinematical cuts for \(M_{\phi _j}^{rec}\) such that

$$\begin{aligned} m_\phi - 15(10) \ \mathrm{GeV}< M_{\phi _j}^{rec} < m_\phi + 25(50) \ \mathrm{GeV}, \end{aligned}$$
(46)

for \(m_\phi = 65(30)\) GeV. Table 4 summarizes the effect of kinematical cuts to signal and BGs for RR polarization. We find that \(\tau ^+ \tau ^-\) BG is highly suppressed by \(M_{jj}\) and \(M_{\phi _j}^{rec}\) cuts, and main BG after cuts is \(jj \nu {\bar{\nu }}\) one.

Finally we estimate the discovery significance using Eq. (41) which is shown in the last column of Table 4 for RR polarization. In addition, for comparison, we show significances for RR, LL and sum of LL and RR polarizations in Table 5 for \(m_{\phi } = 65(30)\) GeV. Significance tends to higher than that of ”” case; this is due to the facts that higher number of signal events by \(BR(Z \rightarrow jj) > BR(Z \rightarrow \ell ^+ \ell ^-)\) and \(e^+ e^- \rightarrow W^+W^-\) process does not contribute to \(jj \nu {\bar{\nu }}\) final state. We then obtain significance much larger than 5 for \(m_\phi = 30\) GeV with \(\kappa _\alpha =1\) corresponding to \(\sin \alpha =0.05\); \(S_{cl} \sim 5\) can be obtained with \(\sin \alpha =0.04\). Note also that we have the largest significance when we sum up events from LL and RR polarizations simply due to increase of the number of signal events.

Table 5 The number of events for signal (\(N_S\)), BG (\(N_{BG}\)) and significance (\(S_{cl}\)) for RR and LL polarizations with integrated luminosity of 900 fb\(^{-1}\) each and for sum of events from two polarizaitons, where we show cases for \(m_{\phi } = 65(30)\) GeV with all kinematical cuts imposed
Full size table

Before closing this section, let us discuss the potential of the other lepton colliders and possibility of testing scalar mixing in future Higgs measurement. In addition to the ILC, the CEPC [70] and FCC-ee [71, 72] can investigate our scenario; the CEPC at \(\sqrt{s} = 240\) GeV can provide data with integrated luminosity of 5 ab\(^{-1}\) while at the FCC-ee integrated luminosity can be 10(5) ab\(^{-1}\) for \(\sqrt{s} = 160(\sim 250)\) GeV and that of 1.5 ab\(^{-1}\) is possible for \(\sqrt{s}= 350\) GeV. Then these experiments also have the potential to find the signature of our model which would give similar significance as our analysis since the energy and integrated luminosity are not significantly different from the case of the ILC. Thus combining the analysis of these experiments we can further improve the test of our model. Moreover the lepton colliders can significantly improve measurements of the SM Higgs coupling which can constrain the scalar mixing. The couplings of hZZ interaction can be measured with the most strong sensitivity of \(\sim 0.1 \%\) error and the other coupling can be also measured with few \(\%\) error in each future lepton colliders [29, 70, 71]. In our case, the SM Higgs coupling is given by \(\cos \alpha \times C_{{h VV/ h{\bar{f}} f}}^{SM}\) where \(C_{hVV/ h{\bar{f}} f}^{SM}\) is the SM Higgs coupling with vector bosons/fermions. Thus divination from the SM is given by \(1 - \cos \alpha \simeq 0.0013 \times (\sin \alpha /0.05)^2\) which would be tested by hZZ coupling measurement. The more stringent constraint can be obtained from future measurement of invisible decay branching ratio of the SM Higgs. For example, the ILC at \(\sqrt{s}=250\) GeV with integrated luminosity of 2 ab\(^{-1}\) can explore the branching ratio up to \(0.32 \%\) [29]. Therefore, comparing with Fig. 2, wide parameter region can be explored which will be good complimentary test of our model.

5 Summary and discussion

We have studied a model with \(U(1)_{L_\mu - L_\tau }\) gauge symmetry which is spontaneously broken by a VEV of SM singlet scalar field with non-zero \(L_\mu - L_\tau \) charge. In this model \(Z'\) boson and new CP-even scalar boson \(\phi \) are obtained after spontaneous symmetry breaking. Then we have focused on parameter region which can explain muon \(g-2\) by one-loop contribution where \(Z'\) boson propagates inside a loop, taking into account current experimental constraints. In the parameter region \(Z'\) mass range is 5 MeV \(\lesssim m_{Z'} \lesssim \) 210 MeV, and mass of \(\phi \) is typically \({\mathcal {O}}(100)\) GeV. We have also found that \(\phi \) dominantly decays into \(Z'Z'\) mode and \(Z'\) decays into \(e^+e^-\) or \({\bar{\nu }}_\ell \nu _\ell \) modes depending on the ratio between \(U(1)_{L_\mu - L_\tau }\) gauge coupling constant and kinetic mixing parameter.

Then we have investigated signatures of \(\phi \) production processes in collider experiments. Firstly gluon fusion production of \(\phi \) at the LHC has been discussed considering mixing between the SM Higgs boson and \(\phi \); the cross section is thus proportional to \(\sin ^2 \alpha \) with mixing angle \(\alpha \). In principle we can obtain sizable number of events from \(pp \rightarrow \phi \rightarrow Z' Z'\) followed by decay of \(Z' \rightarrow e^+ e^-\) even if Higgs-\(\phi \) mixing is as small as \(\sin \alpha \lesssim 0.1\). However \(e^+e^-\) pair from light \(Z'\) decay is highly collimated and it is very challenging to analyze the signal events at the LHC requiring improved technology.

Secondly we have investigated \(\phi \) production at \(e^+ e^-\) collider such as the ILC. In \(e^+ e^-\) collider, \(\phi \) can be produced via \(e^+e^- \rightarrow Z \phi \), W boson fusion and Z boson fusion processes through the mixing with the SM Higgs boson. Among them \(Z \phi \) mode can give the largest cross section if kinematically allowed and we have focused on the process. One advantage of \(e^+e^-\) collider compared with hadron colliders is that we can use energy momentum conservation and \(\phi \) mass can be reconstructed even if final state includes missing energy. In addition, we can use polarized electron/positron beam at the ILC experiment. We have then considered the process \(e^+e^- \rightarrow Z \phi \) where \(\phi \) decays into missing energy as \(\phi \rightarrow Z' Z' \rightarrow 4 \nu \) since \(BR(Z' \rightarrow \nu {\bar{\nu }}) \gg BR(Z' \rightarrow e^+ e^-)\) in the parameter region to give sizable muon \(g-2\). For Z boson decay, we have discussed two cases (1) \(Z \rightarrow \ell ^+ \ell ^- (\ell = e, \mu )\) and (2) \(Z \rightarrow j j\) giving “” and “” signal events respectively. Numerical simulation study has been carried out for these cases generating signal events and the SM background events. In our analysis, we have applied two polarization case in which \((e^-, e^+)\) beams are polarized as \((- 80 \%, + 30 \%)\) and \((+ 80 \%, - 30 \%)\) denoted by LL and RR polarizations respectively. We have investigated relevant kinematical cuts to reduce the backgrounds showing corresponding distributions. Finally we have estimated discovery significance for our signal taking into account the effects of kinematical cuts. The significance of 2.2(2.5) has been obtained for “” signal when we take \(\sin \alpha =0.05\), \(m_\phi =65(30)\) GeV and integrated luminosity of 900 fb\(^{-1}\) for RR polarization. Remarkably, we have the largest significance from RR polarization which is even larger than sum of LL and RR events since BG from \(e^+ e^- \rightarrow W^+ W^- \rightarrow \ell ^+ \ell ^- \nu {\bar{\nu }}\) process is suppressed in RR polarization. Furthermore the significance of 2.4(9.7) has been obtained for ”” signal when we take \(\sin \alpha =0.05\) and \(m_\phi =65(30)\) GeV, which is larger than the case with charged lepton final state. In this case, we have find the largest significance can be obtained by simply summing up events from events LL and RR polarization. In addition, we can obtain larger significance for larger \(\sin \alpha \) although muon \(g-2\) tends to become smaller. Therefore we can search for the signal of \(\phi \) at \(e^+e^-\) collider with sufficient integrated luminosity, and combining together with results from future muon \(g-2\) measurements our \(U(1)_{L_{\mu }- L_{\tau }}\) model will be further tested. Note also that the significance would be improved by more sophisticated cuts and further analysis will be given elsewhere. For the last comment, we discuss displaced vertex of \(Z'\) decay into \(e^+ e^-\). From Eq. (20), the order of the lifetime can be estimated as \(\tau _{Z'} \simeq 24 \pi /(g'^2 m_{Z'}) \sim 4 \times 10^{-14}\) sec., where we assumed \(g' = 10^{-4}\) and \(m_{Z'} = 100\) MeV. The decay length is \(c \tau _{Z'} \sim 1\) cm which is comparable with the radius of an innermost vertex tracker at the ILC. Therefore displaced vertices of \(Z'\) decaying into \(e^+ e^-\) might be measured if enough number of \(Z'\) is produced.