Extensions of modified Chaplygin gas from Geometrothermodynamics

Abstract

We derive modified classes of Chaplygin gas by using the formalism of Geometrothermodynamics. In particular, our strategy gives us extended versions of Chaplygin gas, providing a novel thermodynamic explanation. Thus, we show that our models correspond to systems with internal thermodynamic interaction. Bearing this in mind, we find new free parameters which are derived from thermodynamics and we give them an interpretation. To this end, we predict the range of values that every term can take in the context of homogeneous and isotropic universe. We also show that our new versions of modified Chaplygin gas can be interpreted as unified dark energy models, independently from the introduction of our new additional terms. Finally, we compare our theoretical scenarios through a fit on a grid based on the Union 2.1 compilation and we evaluate the growth factor of small perturbations. In this respect, we show that our model better adapts to the theoretical $\varLambda$CDM value, namely $\gamma _{\varLambda CDM}=\frac{6}{11}$, than previous versions of modified Cgaplygin gas. We show numerical constraints at late and early redshift domains, which turn out to be compatible with previous results on standard versions of Chaplygin gas models.

1 Introduction

A growing number of data surveys indicate that the observable universe is undergoing a phase of accelerated expansion [1,2,3,4,5,6,7,8,9,10]. The most popular explanation for the cosmic speed up states that the fluid pushing up the universe to accelerate is due to a vacuum energy cosmological constant [11]. Alternatively, non-equilibrium barotropic fluids may originate dark energy, representing an alternative paradigm which does not make use of the cosmological constant. Among all the possible mechanisms of dark energy production, unified dark energy models have reached a large consensus during last years [12]. The underlying philosophy of these approaches consists in assuming a single-component fluid, which behaves as dust and dark energy at different regimes. A famous prototype, which goes toward unified scenarios, is dubbed Chaplygin gas, which has definitively attracted great interest during last years [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. Chaplygin proposed his equation of state to study the lifting forces on a plane wing in aerodynamics, which has been modified accordingly to recent variants like $p = A \rho - \frac{B}{\rho ^{\alpha }}$, where A, B and $\alpha$ are universal positive constants [33]. As $A \rightarrow 0$ and $\alpha \rightarrow 1$, one recovers the original formulation made by Chaplygin. Alternative models with $A = 0$ and $\alpha > 0$ are known as generalized Chaplygin gases [34, 35]. Unified dark energy models and, in particular, the modified Chaplygin gas has the remarkable property of describing the dark sector of the universe through a single dark fluid, which passes from a matter-dominated era to a cosmological constant-dominated era [36,37,38]. Although several papers discuss the behavior of the modified Chaplygin gas to reconcile the standard cosmological model with observations  [39,40,41,42], a full explanation of the mechanism behind the origin of unified dark energy model is still lacking. In other words, if dark energy is not under the form of a genuine vacuum energy fluid, what is the mechanism enabling matter to behave anti-gravitationally?¹

In this work, we demonstrate that a possible solution to the aforementioned issue may be found in Geometrothermodynamics (GTD), which represents a formalism that has been developed during the past few years to describe ordinary thermodynamics by using differential geometry [46]. This formalism has encoded diverse applications in black hole thermodynamics [47], relativistic cosmology [48], mathematical chemistry [49], and others. Here, we show that it is possible to get the modified Chaplygin models by means of GTD and we obtain a new modification of the Chaplygin gas, with additional free parameters. Each parameter holds its own physical significance since it comes from GTD considerations and describes different thermodynamic properties. Hence, we show that the class of models we get is mathematically equivalent to previous versions of modified Chaplygin gas, albeit physically different.

In particular, we combine thermodynamic and geometric considerations in the GTD framework, and find out a new equation of state of the modified Chaplygin gas, which explains the recent cosmological observations. In so doing, we give an explanation to the mechanism which produces unified dark energy models by using a pure thermodynamic approach. Further, we analyze the kinematics of the model by means of cosmography and fix limits over the new free constants, providing flat priors over them. Thus, we compare our paradigm with the standard cosmological model and show the main differences.

The work is organized as follows. In Sect. 2, we briefly review fundamental topics on GTD. Later, we show how to build up our cosmological model and discuss its thermodynamic and kinematic properties. In Sect. 3, we develop a numerical analysis making use of cosmic data surveys and compare our results with the ones obtained from the standard cosmological model. Finally, in Sect. 4, we discuss the conclusions and perspectives of our work.

2 From geometrothermodynamics to extended modified Chaplygin gas

The main purpose of this section is to show how to reproduce the dark energy contribution by means of GTD and how to handle it in view of the universe expansion history. In particular, we study the possibility that GTD can be seen as a method to generate unified dark energy models. To do so, we first analyze the whole framework of GTD as a differential geometric formalism for thermodynamics. Then, we show how to get from GTD the corresponding equation of state for the modified Chaplygin gas.

2.1 Basics of Geometrothermodynamics

The starting point of Geometrothermodynamics is a $(2 n + 1)$-dimensional contact manifold $\mathcal{T}$, called phase space, which is endowed with a Riemanian metric G and a contact 1-form $\varTheta$. A set of coordinates $\{Z^A \}_{A=1, \ldots , 2n+1} = \{\varPhi , E^a, I^a \}_{a=1, \ldots ,n}$ is introduced, where $\varPhi$ represents the thermodynamic potential and $E^a$ and $I^a$ represent extensive and intensive thermodynamic variables, respectively. An important property of GTD is that all its geometric objects are constructed such that they are invariant with respect to Legendre transformations. In classical thermodynamics, this is equivalent to saying that the physical properties of a particular thermodynamic system do not depend on the choice of thermodynamic potential used for its description. A particular GTD metric G, which is invariant with respect to partial and total Legendre transformations, can be written as (summation over all repeated indices is implied)

$$\begin{aligned} G = \varTheta ^2 + \varLambda \left( E_a I_a dE^a dI^a \right) \end{aligned}$$

(1)

where the fundamental Gibbs 1-form is $\varTheta = d \varPhi - \delta _{ab} I^a dE^b$ and $\varLambda$ is a real constant, which can be set equal to one without loss of generality. The equilibrium n-dimensional submanifold $\mathcal{E} \in \mathcal{T}$ is defined by the smooth map,

$$\begin{aligned} \varphi :&\mathcal{E} \longrightarrow \mathcal{T} \nonumber \\&\{E^a \} \longrightarrow \{\varPhi (E^a), E^a, I^a (E^a) \} \end{aligned}$$

(2)

such that the condition $\varphi ^{\star } (\varTheta ) = 0$ is satisfied, implying that the first law of thermodynamics is satisfied on $\mathcal{E}$. Applying the pullback $\varphi ^{\star }$ to the metric G, we get the induced thermodynamic metric g given by:

$$\begin{aligned} g = \varphi ^{\star } (G)= & {} \left( E_a \frac{\partial \varPhi }{\partial E^a} \right) ~\frac{\partial ^2 \varPhi }{\partial E^b \partial E^c} \delta ^{ab} dE^a dE^c \end{aligned}$$

(3)

According to the GTD prescription, one only needs to specify the fundamental equation $\varPhi = \varPhi (E^a)$ in order to find explicitly the metric g of the equilibrium submanifold $\mathcal{E}$.

2.2 A new derivation of modified Chaplygin gas from GTD

To derive the modified Chaplygin gas, we choose the entropy $S = S \left( U,V \right)$ to be the thermodynamic potential and U, V to be the extensive variables. Then, the corresponding thermodynamic phase space $\mathcal{T}$ is a five dimensional space endowed with the set of independent coordinates $Z^A = \{S, U, V, \frac{1}{T}, \frac{P}{T} \}$. The Gibbs’ fundamental 1-form $\varTheta _S$ is given by:

$$\begin{aligned} \varTheta _S= & {} d S - \frac{1}{T} d U - \frac{P}{T} d V. \end{aligned}$$

(4)

By defining the space of equilibrium states $\mathcal{E}$ by $\varphi ^{\star }_S (\varTheta _S ) = 0$, we obtain both the first law of thermodynamics,

$$\begin{aligned} d S = \frac{1}{T} d U + \frac{P}{T} d V, \end{aligned}$$

(5)

and the equilibrium conditions,

$$\begin{aligned} \frac{\partial S}{\partial U} = \frac{1}{T},\quad \frac{\partial S}{\partial V} = \frac{P}{T}\,. \end{aligned}$$

(6)

To derive the modified Chaplygin gas, we consider the Nambu-Goto system of differential equations

$$\begin{aligned} \Box Z^A = \frac{1}{\sqrt{\mathrm{det}(g)}} \left( \sqrt{\mathrm{det}(g)} g^{ab} Z^A_{,a} \right) _{,b} + \varGamma ^{A}_{\, BC} Z^B_{,b} Z^C_{,c} g^{bc}=0, \end{aligned}$$

(7)

where $\Box$ is the d’Alembert operator and $\varGamma ^{A}_{\, BC}$ are the Christoffel symbols associated with the metric $G_{AB}$ of the phase space. The above system of differential equations follows from the variational principle $\delta \int _\mathcal{E} \sqrt{\mathrm{det}(g)} d^n E =0$, which implies that the equilibrium space $\mathcal{E}$ with metric g constitutes an extremal subspace of the phase space $\mathcal{T}$. A relevant solution of the Nambu-Goto differential equations is the fundamental equation

$$\begin{aligned} S= & {} c_0 \ln V + \frac{c_1}{1+\beta } ~\ln \left( U^{\alpha +1} + c_2 V^{\beta +1} \right) , \end{aligned}$$

(8)

where $c_0$, $c_1$, $c_2$, $\alpha$ and $\beta$ are real constants. Now, according to Eq. (2), the induced metric in the space of equilibrium states $\mathcal{E}$ is given as follows

$$\begin{aligned} g= & {} g_{U U} dU^2 + 2 g_{U V} dU dV + g_{V V} dV^2, \end{aligned}$$

(9)

where the components of the thermodynamic metric g can be expressed as

$$\begin{aligned} g_{U U} = \,&c_1^2 \left( \frac{1 + \alpha }{1 + \beta }\right) ^2 \mathcal F_{\alpha _1,-1}^{(\alpha ,\beta ,c_2)}\,f^{2}, \end{aligned}$$

(10)

$$\begin{aligned} g_{U V} =&- \frac{c_1}{2}\frac{1 + \alpha }{1+\beta }fU^\alpha \mathcal F_{1,0}^{(\alpha ,\beta ,c_2)}\left( c_0+f\,\mathcal F_{1+\beta ,c_1(1+\alpha )}^{(\alpha ,\beta ,c_2)}\right) ,\end{aligned}$$

(11)

$$\begin{aligned} g_{V V} =&- \frac{1}{V^2} \left( c_0 + c_1 f\,\mathcal F_{1,0}^{(\alpha ,\beta ,c_2)}\right) \nonumber \\&\left( c_0+c_1f^2\mathcal F_{1,0}^{(\alpha ,\beta ,c_2)}\mathcal F_{1,\beta }^{(\alpha ,\beta ,c_2)}\right) , \end{aligned}$$

(12)

in which we used the auxiliary functions ${f}\equiv {f}^{(\alpha ,\beta ,c_2)}$, $\mathcal F^{(\alpha ,\beta ,c_2)}_{\sigma _1,\sigma _2}$

$$\begin{aligned}&f^{(\alpha ,\beta ,c_2)}\equiv \left( U^{1+\alpha }+c_2V^{1+\beta }\right) ^{-1}, \end{aligned}$$

(13)

$$\begin{aligned}&\mathcal F_{\sigma _1,\sigma _2}^{(\alpha ,\beta ,c_2)}\equiv \sigma _1c_2V^{1+\beta }+\sigma _2 U^{1+\alpha }. \end{aligned}$$

(14)

Using the induced metric, we obtain the scalar curvature for the particular case $\beta = \alpha$ as:

$$\begin{aligned} R = \frac{N \left( U,V \right) }{D \left( U,V \right) }, \end{aligned}$$

(15)

where $N \left( U,V \right)$ and $D \left( U,V \right)$ are given in “Appendix A”. The Legendre invariant scalar curvature is in general non-vanishing, which indicates the presence of internal thermodynamic interaction.

2.3 Extending the modified Chaplygin gas

From the fundamental Eq. (6), we obtain the the equilibrium conditions

$$\begin{aligned} \frac{\partial S}{\partial U}= & {} \frac{c_1 (1+ \alpha )}{1+ \beta } \frac{U^\alpha }{U^{1+\alpha } + c_2 V^{1+\beta }} = \frac{1}{T}\,, \end{aligned}$$

(16)

$$\begin{aligned} \frac{\partial S}{\partial V}= & {} \frac{c_0}{V} + c_1 c_2 \frac{V^\beta }{U^{1+\alpha } + c_2 V^{1+\beta }} = \frac{P}{T}\,, \end{aligned}$$

(17)

which lead to the equation of state

$$\begin{aligned} P = \frac{c_0}{c_1} \left( \frac{1+\beta }{1+\alpha } \right) \rho + c_2 \left( \frac{1+\beta }{1+\alpha } \right) \left( 1+ \frac{c_0}{c_1} \right) \frac{V^{-(\alpha -\beta )}}{\rho ^\alpha } . \end{aligned}$$

(18)

This is a generalization of the equation of state proposed by hand by Chaplygin and of the other modifications investigated so far in the literature. Consequently, the GTD formulation is able to generate models of unified dark energy in terms of an equation of state, which contains the results of previous approaches and extensions of them. We will see that the generality of this new fundamental equation is constrained by a degeneration between parameters. In particular, it is not possible to constrain arbitrarily $c_0$ and $c_1$, but the ratio $\frac{c_0}{c_1}$ only. Further, a multiplicative degeneration occurs among $c_0,\ c_1,\ \alpha$ and $\beta$. These degenerations suggest the existence of theoretical limits on the applicability of each particular case, as we will discuss below.

2.3.1 Limits on the modified Chaplygin gas and variable Chaplygin gas

Through the following recasting

$$\begin{aligned}&A \rightarrow \frac{c_0}{c_1} \left( \frac{1+\beta }{1+\alpha }\right) , \end{aligned}$$

(19)

$$\begin{aligned}&B \rightarrow - c_2 \left( A + \frac{1+\beta }{1+\alpha } \right) , \end{aligned}$$

(20)

Equation (18) can be written as

$$\begin{aligned} P = A ~\rho - \frac{B V^{-(\alpha -\beta )}}{\rho ^{\alpha }}\,. \end{aligned}$$

(21)

Consequently, we have two possibilities:

• $\beta = \alpha$. This corresponds to a genuine modified Chaplygin gas.

• $\beta \ne \alpha$. This corresponds to the variable modified Chaplygin gas.

Assuming that $\rho$, as a function of time, can be represented as a function of the scale factor $\rho (a)$, the conservation law can be integrated and so we assume the GTD equation of state to get the final solution for the Hubble rate.

The models are formally equivalent to the ones provided in the literature. However, since each new parameter has its own physical interpretation, as we underline later in the manuscript, our approach differs from the ones of standard Chaplygin models. For each model, we can find its physical properties, investigating the corresponding effective thermodynamics and kinematics to check its goodness.

2.3.2 Thermodynamics

One of the advantages of knowing the fundamental Eq.  (8) explicitly is that it can be used to derive the complete thermodynamic information of the system. In particular, two thermodynamic quantities are important for the cosmological model under consideration, namely, the temperature and specific heats.

Dark temperature:   Equation (16) takes the form:

$$\begin{aligned} T= \frac{1}{c_1} \left( \frac{1+\alpha }{1+\beta } \right) \rho V \left( 1 + c_2 \rho ^{-\alpha -1} V^{\beta -\alpha }\right) \,. \end{aligned}$$

(22)

Heat capacity:  

$$\begin{aligned} C_V=-\frac{\left( \frac{\partial S}{\partial U}\right) ^2}{\frac{\partial ^2 S}{\partial U^2}} = c_1\left( \frac{1+\alpha }{1+\beta }\right) \frac{1}{1-\alpha c_2 \rho ^{-\alpha -1} V^{\beta -\alpha }}\ .\nonumber \\ \end{aligned}$$

(23)

The arbitrary parameters which enter Eq. (22) must be chosen such that the temperature is always positive definite. Moreover, from the heat capacity one can infer the phase transition structure of the system. Indeed, for a phase transition to take place ($C_V\rightarrow \infty$), the condition

$$\begin{aligned} \frac{c_2}{ \rho ^{\alpha +1} V^{\alpha -\beta }} = \frac{1}{\alpha } \end{aligned}$$

(24)

must be satisfied.

2.3.3 Cosmological dynamics

We consider a homogeneous and isotropic universe pictured by the cosmological principle. The maximally symmetric spacetime which accounts for the cosmological principle is described by the Friedmann-Lemaître-Robertson-Walker (FLRW) line element

$$\begin{aligned} ds^2 = - dt^2 + a^2 (t) \left[ \frac{dr^2}{1 - k r^2} +r^2 d \varOmega ^2_{D-1} \right] \,, \end{aligned}$$

(25)

where the whole dynamics is encapsuled into a(t), i.r. the scale factor. Spatial curvature is described by $k = 0, \pm 1$, respectively for spatially flat, closed or open universes. In agreement with recent Planck measurements, we assume $k=0$ and we take into Einstein’s equations the one-component perfect fluid through the requirement $T_{\mu \nu } = Pg_{\mu \nu } + \left( \rho + P \right) ~ u_{\mu } u_{\nu }$. This leads to the most general Friedmann equations:

$$\begin{aligned}&H^2 = \frac{2 ~\rho }{(D-1) (D-2)} - \frac{k}{a^2}, \end{aligned}$$

(26)

$$\begin{aligned}&\dot{H} = \frac{1}{D-2} ( \rho + P ) + \frac{k}{a^2}, \end{aligned}$$

(27)

and to the conservation law:

$$\begin{aligned} \dot{\rho } + (D-1) ~H ( \rho + P) = 0, \end{aligned}$$

(28)

where $H \equiv \frac{\dot{a}}{a}$ is the Hubble parameter and $c = 8 \pi G = 1$. Under the hypothesis $D=4$, we get:

$$\begin{aligned}&H^2 = \left( \frac{\dot{a}}{a}\right) ^2 = \frac{1}{3}\rho \,, \end{aligned}$$

(29)

$$\begin{aligned}&\dot{H}+H^2 = \frac{\ddot{a}}{a} = -\frac{1}{6}\left( \rho +3 P\right) . \end{aligned}$$

(30)

The final solution for the normalized Hubble rate thus becomes

$$\begin{aligned} \mathcal E^{2(1+\alpha )}(a)=-c_2\,a^{3(\alpha +\beta )}+(1 + c_2) a^{-\frac{3 (c_0 + c_1 + c_1 \alpha + c_0 \beta )}{c_1}}\,,\nonumber \\ \end{aligned}$$

(31)

where $\mathcal E\equiv H/H_0$. It is evident from the above relation that one can assume $c_1=1$, without losing generality. Moreover, the limit to the concordance paradigm is found assuming the set: $\alpha \rightarrow 0, \beta \rightarrow 0, c_2 \rightarrow \varOmega _{m,0} - 1, c_0 \rightarrow 0$.

2.3.4 Kinematics of our model

The kinematics of the universe consists in writing the scale factor in terms of observable quantities and to expand it around time, making use of the cosmological principle only. The corresponding definition of kinematic quantities is model-independent and furnishes a set of quantities which can be fixed by using cosmic data directly. Likely, the most suitable kinematic definitions are the deceleration and jerk parameters:

$$\begin{aligned} q&= -\frac{1}{H^2} \frac{\ddot{a}}{a}\rightarrow q(t)=-\frac{\dot{H}}{H^2} -1\, \end{aligned}$$

(32)

$$\begin{aligned} j&= \frac{1}{H^3} \frac{a^{(3)}}{a}\rightarrow j(t)=\frac{\ddot{H}}{H^3}-3q-2\,, \end{aligned}$$

(33)

or in terms of the Hubble rate

$$\begin{aligned}&q(t)=-\frac{\dot{H}}{H^2} -1\,, \end{aligned}$$

(34)

$$\begin{aligned}&j(t)=\frac{\ddot{H}}{H^3}-3q-2\,. \end{aligned}$$

(35)

At current time, these parameters enter the a(t) expansion in the form

$$\begin{aligned} \frac{a(t)-1}{H_0 \varDelta t} = 1 - \frac{1}{2} q_0 H_0 \varDelta t +\frac{1}{6} j_0 H_0^2\varDelta t^2 + \ldots \,, \end{aligned}$$

(36)

in which the subscript 0 indicates the value of the coefficients at present time, i.e., at $z=0$.

The deceleration parameter q provides the sign of the cosmic expansion, i.e., if the universe accelerates or decelerates. The sign of the jerk parameter j indicates whether the universe passes through a decelerated phase before acceleration or not. Current limits on $q_0$ and $j_0$ are essentially given by

$$\begin{aligned}&q_0 \quad \in [-1,0]\,, \end{aligned}$$

(37)

$$\begin{aligned}&j_0 \quad \ge 0\,, \end{aligned}$$

(38)

which are bounds useful for fixing constraints over our free constants defined in our extensions of the modified Chaplygin gas.

We compute the deceleration at present time and obtain

$$\begin{aligned} q_0=\frac{3 c_0 (1 + c_2) (1 + \beta ) + c_1 (1 + \alpha + 3 c_2 (1 + \beta ))}{2 c_1 (1 + \alpha )} \end{aligned}$$

(39)

and the jerk parameter which is reported in “Appendix A”. We use the intervals defined in Eq. (37) to combine the constants $c_0,\ c_2,\ \alpha$ and $\beta$ to show which limits might be imposed on them.

2.3.5 Bounds on the extra parameters

The aforementioned theoretical predictions define suitable bounds over the involved new coefficients, namely $\alpha ,\ \beta ,\ c_0,c_1$ and $c_2$. In particular, we discuss below the physical priors which come from their definitions.

$\alpha >\beta$ :

As the universe increases its size, namely at current time, the right part of $P(\rho )$ turns out to be negligible with respect to the left one. This implies that $\alpha -\beta >0$, i.e., $\alpha$ is always larger than $\beta$, although the sign of $\alpha$ will be fixed later.

$1+\alpha >0$ :

The requirement that $1+\alpha >0$ guarantees that the asymptotic behavior of the specific heat at constant volume is not extensive with respect to the density $\rho$. Again, this does not fix the sign of $\alpha$ which is arbitrary inside the interval $\alpha >-1$.

Signs of $\alpha$ and $c_2$:

The two parameters, $\alpha$ and $c_2$ have the same sign. This is a direct consequence of Eq. (24). In fact, since $\rho$ and V are positive definite the signs of $\alpha$ and $c_2$ is the same.

$c_1$ is arbitrary:

The sign and value of $c_1$ is unfixed. This is due to the degeneracy between $c_1$ and $c_0$. Hence, for simplicity hereafter we fix $c_1=1$.

$c_0$ is negative definite:

The limit to the $\varLambda$CDM model guarantees that $c_0\left( \frac{1+\beta }{1+\alpha }\right) <0$. In fact, the concordance paradigm is recover as $\alpha \rightarrow 0,\beta \rightarrow 0$ with $c_0\rightarrow -1$ and $B\rightarrow 0$. As the volume increases, however, the dominant term continues being the one $\propto \rho$. Thus, conventionally one can assume $-1<c_0<0$ without losing generality.

Arbitrariness on $c_2$:

The term $c_2\left( A+\frac{1+\beta }{1+\alpha }\right)$ is not bounded a priori. The only speculation that can be done is over the $c_2$ sign, which is arbitrary. As a consequence, we here take $c_2<0$, whose choice limits the intervals over $\alpha$ and $\beta$. In particular, by means of Eq. (37), we take $\alpha <0$ and $\beta <0$, implying $(1+c_0)\left( \frac{1+\beta }{1+\alpha }\right) >0$. Bearing this in mind, we take $1+\beta >0$, showing that $\alpha$ and $\beta$ are closed to each other, but different.

Positive T:

The temperature T is positive definite. This implies that $c_2$ is limited inside a particular set of values, albeit it is unbounded.

The above discussion means that only for this particular choices of the free parameters, a physical phase transition can occur and the Chaplygin scenarios are reproduced. Below we fix limits over the form of the free coefficients. To do so, we focus on $H_0$, $c_0$ and $c_2$.

3 Numerical constraints

We here test through our model with the Union 2.1 SNe of type Ia compilation. To do so, we employ the theoretical distance modulus,

$$\begin{aligned} \mu _{th}(z)=25+5\log _{10}[d_L(z)]\ , \end{aligned}$$

(40)

often parameterized by $\mu _{obs}=m_B-(M_B-\tilde{\alpha }X_1+\tilde{\beta }C)\ ,$, with absolute magnitude:

$$\begin{aligned} M_B= {\left\{ \begin{array}{ll} M, &{} \quad \text {if}\ M_{host}<10^{10}M_{Sun}\\ M+\varDelta _M, &{} \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(41)

Here, $M_{host}$ is the host stellar mass and {M, $\varDelta _M$, $\tilde{\alpha }$, $\tilde{\beta }$} are the nuisance parameters. We here assume that the nuisance parameters do not influence the analysis and we neglect their effects. Thus, to perform our analysis we consider a fit on a grid, performed over a discretization of phase-space, having as likelihood the following

$$\begin{aligned} \mathcal {L}=\mathcal {L}_{SN}\,, \end{aligned}$$

(42)

in which we assume that all probabilities are independent. We thus assume uniform priors as given by (see 1), showing our numerical outcomes 2. For our joint analysis, we produce in Fig. 1 the marginalized 2D $1\sigma$ and $2\sigma$ regions for the cosmological parameters.

Table 1 Flat priors provided for our numerical analysis. $H_0$ values are given in units of Km/s/Mpc, while $r_d$ values in units of Mpc

Table 2 68% and 95% confidence level parameters got from SNe, in which we fixed $\alpha$ and $\beta$. $H_0$ values are given in units of Km/s/Mpc, while $r_d$ values in units of Mpc. The result over $H_0$ is compatible with the assumptions of Union 2.1 in which its value is fixed

The fitting procedure shows that at least at 1$\sigma$ our model extends Chaplygin gas, obeying the properties emphasizing above for each free parameters. One may notice that the whole test, involving all free constants free to vary, suffers from a deep degeneration over the coefficients. Thus, a refined analysis would be useful to better underline the bounds over the entire sets of coefficients, in order to check the departures of our model from a genuine Chaplygin gas.

Fig. 1

Contours at 1$\sigma$ and 2$\sigma$ over the free parameters of our model

4 Perturbations and growth index

On sub-horizon scales, the first order perturbations of matter $\delta =\frac{\delta \rho _{m}}{\rho _{m}}$ are given by²

$$\begin{aligned} \ddot{\delta }+2H\dot{\delta }-4\pi G\rho _{m}\delta =0. \end{aligned}$$

(43)

This defines the evolution of $\delta \rho _{m}$, i.e. matter fluctuations in linear approximation.

Immediately, it is possible to compute the evolution equation for the growth index. It is thus defined by:

$$\begin{aligned}&f^\prime +a^{-2}f^2+\nonumber \\&\left[ 2a^{-1}+{1\over 2}(2\ln E)^\prime \right] f={3\over 2}\varOmega _m \mathcal {E}^{-2}a^{-4}\,, \end{aligned}$$

(44)

which has been obtained by replacing the time derivative by $\frac{d}{dt}\rightarrow H\frac{d}{d\ln a}$, in terms of the prime derivative ${}^\prime$ i.e. with respect to the scale factor a(t). Furthermore, we assume that a solution of Eq. (43) is given by:

$$\begin{aligned} \delta _m\sim D(a)\,, \end{aligned}$$

(45)

whose expression is given by:

$$\begin{aligned} D(a)=\exp \Big [\int _{(1+z)^{-1}}^{1}\frac{\varOmega _m^\gamma }{\xi }d\xi \Big ]\,, \end{aligned}$$

(46)

in which we have used the usual assumption:

$$\begin{aligned} f(a)\equiv \frac{d\ln \delta _m}{d\ln a}\simeq \varOmega ^\gamma _m(a)\,. \end{aligned}$$

(47)

To insert the information coming from the Chaplygin equation of state, we need to consider the normalized matter, $\varOmega _m(a)$, and the corresponding equation of state. For the standard modified Chaplygin gas, with equation of state $\omega$, we simply obtain [50]:

$$\begin{aligned}&3\omega \varOmega _{m}(1-\varOmega _{m})\frac{d f}{d \varOmega _{m}}+f^{2} +f\left[ \frac{1}{2}-\frac{3}{2}\omega (1-\varOmega _{m}(a))\right] \nonumber \\&\quad =\frac{3}{2}\varOmega _{m}(a). \end{aligned}$$

(48)

Thus, in the case of a genuine modified Chaplygin gas, one argues that

$$\begin{aligned} \gamma =\frac{3(1-\omega )}{5-6\omega }+(1-\varOmega _{m})\frac{3(1-\omega )(1-\frac{3\omega }{2})}{125(1-\frac{6\omega }{5})^{3}}. \end{aligned}$$

(49)

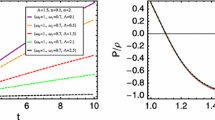
In our version of the Chaplygin gas, we can use the assumptions that we have made on the free constants coming from GTD. To do so, let us soon notice that in the case of our approach, the pressure becomes:

$$\begin{aligned} P = \frac{c_0}{c_1} \left( \frac{1+\beta }{1+\alpha } \right) V^{-3} + c_2 \left( \frac{1+\beta }{1+\alpha } \right) \left( 1+ \frac{c_0}{c_1} \right) V^{-\frac{21}{10}}\,, \end{aligned}$$

(50)

in which we have plugged the behavior of the density in terms of the volume and the information on $\alpha$ and $\beta$ on the exponents of the above relation. Approximatively this can be viewed as two evolving fluids whose net pressure evolves like $P\sim a^{-9}+a^{-6}$. Clearly, as the volume becomes smaller, i.e. at the regime of small perturbations and high redshifts, we have that the term $\sim V^{-3}$ becomes dominant. This implies that our fluid behaves like the $\omega$CDM model as the redshift increases. Plugging this expression in (44), we immediately get

$$\begin{aligned} \gamma \simeq \frac{3\Big [c_0 (1 + \beta )-c_1 (1 + \alpha )\Big ]}{ 6 c_0 (1 + \beta )-5 c_1 (1 + \alpha ) }\,, \end{aligned}$$

(51)

in which we have considered the zero-order term of $\gamma$ in approximating it with our equation of state for the modified version of Chaplygin gas inferred from GTD.

In order to check the goodness of our approach with previous paradigms, let us conventionally define a discrepancy as:

$$\begin{aligned} \varDelta \varGamma \equiv \Big |\gamma _i-\gamma _{\varLambda CDM}\Big |\,, \end{aligned}$$

(52)

whose aim is to evaluate how different models³ depart from an arbitrary fiducial scenario, that here we assume to be the theoretical expectation coming from the standard cosmological model, i.e. $\gamma _{\varLambda CDM}$. The discrepancies have been reported in Table 3.

Table 3 Discrepancies with respect to previous Chaplygin models. We considered, in particular, the modified version of the Chapygin gas, namely MCG, the variable modified Chaplygin gas VMCG and our model, here indicated as GTD. The percentages reported on the right side of the table are defined by $\varDelta \varGamma /\gamma _{\varLambda CDM}$. They represent the percentage discrepancies among the various models. The values of $\gamma _i$ for the modified and variable modified Chaplygin gas have been taken from [51]

The results have been obtained using Eq. (49) and $\gamma _{\varLambda CDM} = \frac{6}{11}$, by means of numerical values of $\gamma _i$ respectively for the modified and variable modified Chaplygin gas got from [51], i.e. $\gamma _{MCG}=0.562$ and $\gamma _{VMCG}=0.564$. It soon comes evident that our model generalizes the standard Chaplygin approaches even at the level of small perturbations. The discrepancy between our approach and the fiducial one are mostly smaller than modified scenarios of Chaplygin fluids. The model is thus expected to work better at the level of small perturbations than previous Chaplygin scenarios. This is prevalently due to the fact that our model has been built up in terms of two counterparts: the first proportional to a quintessence-like fluid, namely $P\sim \omega \rho$, whereas the second proportional to a variable modified Chaplygin gas. Thus the fluid has two possible regimes, at separate redshift domains, behaving differently at distinct epochs of the universe expansion. The second advantage of our approach is clearly due to the fact that the free constants entering the model are intertwined among them. By construction, in fact, A and B depend upon $\alpha$, $\beta$ and on $c_0,c_1,c_2$. Even though this leads to a degeneracy problem as one fits the free constants, it “calibrates” the corresponding values to precise outcomes which turn out to be compatible with current numerical bounds on the growth index. It is, however, evident that a more refined analysis, which combines small and large scales, will better focus on the arbitrariness of $c_2$. This would heal the degeneracy on coefficients, increasing the precision on the whole set of free constants, without fixing $\alpha$ and $\beta$ to any theoretical values.

5 Final outlooks and perspectives

In this work, we employed the formalism of GTD to build up a new version of the modified Chaplygin gas describing the dark sector. The model shows up new physical constants which cannot escape a physical interpretation, since they represent a byproduct of our method. The advantage consists in handling pure extensive thermodynamic quantities to provide the equation of state, pushing up the universe to accelerate. Our scenario defines all the physical properties of the system by using thermodynamic standard laws, providing a fundamental GTD equation. Naturally, we obtain an equation of state which is then used to integrate the Friedmann equations of relativistic cosmology. By analyzing the physical properties of the resulting model, we conclude that from GTD it is possible to obtain fundamental equations for thermodynamic systems that can be used to develop physically reasonable cosmological models.

In particular, under certain conditions our formalism constructs a generalization of the modified Chaplygin gas cosmological model. To get this result, we inferred a particular fundamental equation that determines an equilibrium space embedded in the phase space by means of a map. This procedure satisfies the Nambu-Goto variational principle and relates the entropy of a thermodynamic system with its internal energy and volume. It turned out that our fluid corresponds to an equilibrium space with non-zero thermodynamic curvature, indicating the presence of internal thermodynamic interaction. The so-obtained pressure depends explicitly on the volume and has a non-vanishing small temperature associated to the dark fluid itself.

We showed the limiting cases of our approach with respect to the previous versions of modified Chaplygin gas and we performed a detailed analysis of its behavior. Dark energy and dark matter have been unified under our scheme by properly choosing the constants involved in the model. We discussed the role played by each constant and we finally gave priors over their evolution. As a final check, we forecasted a simple numerical analysis and showed that the limits over the free parameters of our model fulfill the basic requirements imposed by our theoretical priors. To do so, we assume the SNe data based on Union 2.1 catalog and baryonic acoustic observations. We thus discussed the main properties of our model in view of the cosmic evolution of each thermodynamic quantity.

Last but not least, we provided refined results on the growth factor $\gamma$ in the regime of linear perturbations. We compared our expectations, got from the numerical values that we obtained through our fit, with the ones obtained from previous approaches. We demonstrated that, under the numerical bounds found in this work, the $\gamma$ factor matches well the theoretical predictions of the standard $\varLambda$CDM model up to a $\sim 1\%$ discrepancy. Future developments will focus on refined numerical analyses with additional data sets of SNe Ia and also with joint analyses making use of early time data sets. Moreover, we will clarify the role of each parameter even at the level of small perturbations, in order to check the goodness of our approach in view of structure formation. In particular, this will alleviate the arbitrariness of $c_2$ and will refine the degeneracy among all the other coefficients.

Appendix A

The functions $N \left( U,V \right)$ and $D \left( U,V \right)$ are below reported. For simplicity they have been written in the case $\alpha =\beta$.

$$\begin{aligned}&N \left( U,V \right) \nonumber \\&\quad = -8 (\alpha +1)^2 c_2 V^{\alpha +1} \left( c_2 V^{\alpha +1}+U^{\alpha +1}\right) ^3 (c_2^3 (c_0+c_1) \nonumber \\&\qquad \times \left[ (3 \alpha -5) c_0^2+(9 \alpha -5) c_0 c_1+4 \alpha c_1^2\right] U^{\alpha +1} V^{3 (\alpha +1)}\nonumber \\&\qquad + c_0 c_2 \left[ (\alpha -7) c_0^2-(\alpha -1) c_1^2-2 c_0 c_1 \right] U^{3 (\alpha +1)} V^{\alpha +1}\nonumber \\&\qquad -2 c_0^2 (c_0-c_1) U^{4 (\alpha +1)}\nonumber \\&\qquad +c_2^4 (c_0+c_1)^2 \left[ (\alpha -1) c_0+4 \alpha c_1 \right] V^{4 (\alpha +1)} \nonumber \\&\qquad +3 c_0 c_2^2 (c_0+c_1) \left[ (\alpha -3) c_0+(\alpha -1) c_1 \right] U^{2 (\alpha +1)} V^{2 (\alpha +1)} ), \nonumber \\&D \left( U,V \right) \nonumber \\&\quad =c_1 (c_2^2 \Big [ c_0^2(\alpha ^2+14 \alpha -11) -2 c_0 c_1 (\alpha ^2-6 \alpha +5) \nonumber \\&\qquad +c_1^2 (\alpha ^2+6 \alpha +1) \Big ] ~U^{2 (\alpha +1)} V^{2 (\alpha +1)}\nonumber \\&\qquad + c_2^4 (c_0+c_1)^2 (\alpha ^2+6 \alpha +1) ~V^{4 ( \alpha +1)} \nonumber \\&\qquad + 2 c_2^3 (c_0+c_1) \left[ c_0 (\alpha ^2+8 \alpha -1)- c_1 (\alpha -1)^2 \right] \nonumber \\&\quad U^{\alpha +1} ~V^{3 (\alpha +1)}\nonumber \\&\qquad -4 c_0^2 U^{4 (\alpha +1)}+4 c_0 c_2 \left[ c_0 (\alpha -3) +c_1 (\alpha -1) \right] \nonumber \\&\quad U^{3 (\alpha +1)} V^{\alpha +1} )^2 ~~~~~~~~~~. \end{aligned}$$

(53)

The jerk parameter reads

$$\begin{aligned} j= \frac{j_1 +j_2}{2 c_1^2 (1 + \alpha )^2}\,, \end{aligned}$$

(54)

with the auxiliary functions

$$\begin{aligned} j_1&=-9 c_0^2 (1 + c_2) (-1 + c_2 \alpha ) (1 + \beta )^2 \\&\quad - 9 c_0 c_1 (1 + c_2) (1 + \beta ) (-1 + \alpha (-1 + 2 c_2 (1 + \beta )))\,,\\ j_2&= c_1^2 (2 + 2 \alpha ^2 - 9 c_2 \beta (1 + \beta ) \\&\quad - \alpha (-4 + 9 c_2 \beta (1 + \beta ) + 9 c_2^2 (1 + \beta )^2)) \end{aligned}$$