1 Introduction

At the LHC energies a typical proton–proton (pp) collision involves several parton–parton interactions with transverse momentum transfer of a few GeV, leading to the production of several minijets, which are referred to as multiparton interactions (MPI). Successful Monte Carlo (MC) models of pp inelastic interaction at the LHC, such as the models implemented in the event generators Pythia [1] and Herwig [2], have to tame the perturbative growth of the QCD parton–proton scattering cross section below \(p_T \sim 4~\hbox {GeV}\). Within these models, the taming has to strengthen with the increase of the invariant energy of collision. Minijets give an important contribution to the production of relatively soft hadrons that give a main contribution to the so called underlying event (UE) with respect to the hard processes. It is generally accepted that characteristics of the UE are measured in the direction perpendicular to the momentum of a high-\(p_{\mathrm{T}}\) jet [3]. However, a direct observation of minijets is challenging since it is very difficult to separate them. Over the last decade, intensive theoretical and experimental studies of double parton scattering (DPS) were performed [4,5,6,7,8]; a comprehensive review was recently compiled in Ref. [9].

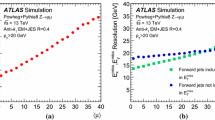
In particular, a number of experimental analyses have been performed, aiming at finding an optimal kinematics where the ratio of the cross sections of DPS to the competing leading twist processes are somewhat enhanced. Except for the case of double charm production [10,11,12], the best kinematics still corresponds to the DPS being a correction to the LT contribution. Hence, the identification of DPS events is rather sensitive to the particular model adopted to describe LT processes, which are usually rather involved. To illustrate this point, Fig. 1 shows the DPS fraction of the total cross section of dijet production within \(\vert \eta \vert <~2\) and \(p_{\mathrm{T}}^{\mathrm{jet}} \ge 50 \, \hbox {GeV}\) plus a charged particle, which originates from the different parton interaction, obtained with Pythia 8 Monash model [13]. The charged particle has an azimuthal angle difference with respect to the leading jet within \(80^o< {\varDelta }\phi < 100^o\), as a function of the pseudorapidity interval between the leading jet and the charged particle \({\varDelta }\eta \), and of the transverse momentum, \(p_{\mathrm{T}}\), of the charged particle. The fraction of the cross section due to DPS presented in Fig. 1 is computed as a difference between the standard collision simulation and one with MPI mechanism switched-off, divided by the former one. One can see from Fig. 1 that the DPS contribution is significant but not dominant, hence a relatively small uncertainty in the calculation of the LT contribution leads to a pretty large uncertainty in the determination of the DPS contribution to the experimental cross section. Traditionally the DPS cross section is parameterized in the following form:

$$\begin{aligned} \sigma ^{\mathrm{DPS}} = \frac{\sigma _1\,\sigma _2}{\sigma _{\mathrm {eff}}} , \end{aligned}$$
(1)

where \(\sigma _i\) are the cross sections of binary pp collisions, and \(\sigma _{\mathrm {eff}}\) is the effective cross section, widely used to characterize the effective transverse area of hard partonic interactions in pp collisions [14, 15].

Fig. 1
figure 1

Fraction of dijet + a charged particle cross section due to the DPS as a function of the \(p_{\mathrm{T}}\) of the charged particle and the pseudorapidity interval between the leading jet and the charged particle, \({\varDelta }\eta \). The result is obtained using Pythia 8 Monash model [13]

Full size image

In QCD one expects \(\sigma _{\mathrm {eff}}\) to depend on the Bjorken x’s of the colliding partons, their flavors, as well as the hardnesses of the subprocesses. We will not write this dependence explicitly in the following.

The LHC data are consistent with \(\sigma _{\mathrm {eff}}\sim 20 \, \hbox {mb}\) for production of two pairs of jets with \(p_{\mathrm{T}}^{\mathrm{jet}} \ge 50 \, \hbox {GeV}\) [16]. In this paper we use the formalism for the description of MPI developed in [4, 6, 8, 12]; see the review and references in Ref. [17], which takes into account both the mean field contributions as well pQCD-induced parton–parton correlations and small x soft correlations. This formalism allows to describe all existing LHC data except double \(J/\psi \) production [18]. For smaller virtualities this formalism predicts \(\sigma _{\mathrm {eff}}\sim 30 \, \hbox {mb}\), which is consistent with the recent Monte Carlo analyses [19]. The model also explains an increase of \(\sigma _{\mathrm {eff}}\) from \(\sim 14 \) to 20 mb between the Tevatron and LHC energies for the kinematical ranges in which measurements were performed.

Though the LHC data strongly suggest the presence of the MPI effects in pp scattering, no accurate determinations of the MPI cross section were reported so far (a notable exception is the charm production [10,11,12]). To a large extent, this is due to insufficient accuracy of modeling higher order leading twist (LT) contributions to multijet production.

We suggest that a way out is to study MPI in proton–nucleus collisions as a function of the centrality of the collision. The suggested procedure is based on the observation made a long time ago [20] that MPI are enhanced in proton–nucleus collisions, leading to a parametric enhancement of MPI by the factor \(\propto A^{1/3}\) as compared to the LT contribution due to hard scattering off two nucleons. The enhancement strongly increases with centrality of the collision. Hence, the study of the rate of the MPI candidate events as a function of centrality would allow to separate DPS and LT processes and provide an unambiguous measurement of DPS.

Fig. 2
figure 2

Sketch of double parton collisions with production of four jets (arrows on the plot) occurring on a single nucleon (a) or on two different nucleons (b) in the target nucleus. In both illustrations, hard-interacting nucleons are depicted in blue, soft-interacting (wounded) nucleons in red, and spectator nucleons in light grey. The reddish tube represents the incoming proton, and its transverse size is proportional to the pN total cross section

Full size image

We study the centrality dependence of the different contributions to DPS in pA collisions at LHC energies, within a high-accuracy implementation of the Glauber Monte Carlo model. Our model makes use of realistic nucleus configurations including NN correlations [21] and neutron skin in lead, the target nucleus [22]. Other implementations of the Monte Carlo Glauber model for soft processes exist, for example the one in Ref. [23]. In the treatment of the individual soft pN collisions, we also include the color fluctuation effect [24], which takes into account the possibility for the incoming proton to fluctuate in different quantum states with substantially different pN interaction strength; this effect is important for an accurate description of the dependence of the hadron production on centrality [25]; see discussion in Sect. 4. The main effect of smearing of centrality which we take into account is due to the experimental definition of centrality classes, based on the measured transverse energy distribution \(\sum E_{\mathrm{T}}\). Eventually, we implement an algorithm for a double hard trigger in each Monte Carlo Glauber event, based on the extension to two hard interactions of an existing model for single hard trigger [26].

We organized the paper as follows.

In Sect. 2 we describe the basic idea and summarize the relevant information from the previous studies. In Sect. 3 we describe the development of a Monte Carlo event generator for calculating the inclusive rate of DPS. In Sect. 4 we describe an extension to the case of DPS of the existing Monte Carlo procedure for the calculation of the probability distribution over the number of the wounded nucleons in events with single hard interaction. In Sect. 5 we include the effect of smearing over impact parameter for the transverse energy of hadrons for centrality characterization. Based on this calculation we outline the proposed procedure for comparing events of different centrality classes in order to measure the DPS cross section.

2 Basic idea

In the optical approximation, which does not include NN correlations and considers the nucleon size much smaller than the internucleon distance, the cross section of DPS in pA collisions for large A can be written as follows [20]:

$$\begin{aligned} \sigma ^{DPS}_{\mathrm pA} = A\,\frac{\sigma _1\,\sigma _2}{\sigma _{eff}} + \sigma _1\,\sigma _2\,\int d^2b\,T^2(b) , \end{aligned}$$
(2)

where b is the impact parameter of the proton, and \(T(b) = \int _\infty ^\infty \rho (b, z) dz\) is the standard nuclear profile function obtained from the nuclear density \(\rho (b,z)\), which is normalized as \(\int d^3r\rho (r) =A\). The first term in Eq. (2) is the contribution of the impulse approximation, in which two partons of the proton interact with two partons of a single nucleon of the target nucleus (Fig. 2a). The second term describes the interaction of two partons in the proton with two partons of two different nucleons of the nucleus, neglecting parton–parton correlations in the projectile proton (Fig. 2b).

Here and below we shall use the notation \(1N\rightarrow 2N\) for the processes where two partons from one projectile nucleon interact with different nucleons from the target, and notation \(1N\rightarrow 1N\) for the processes where two partons from the projectile nucleon interact with one nucleon from the target (i.e. a conventional NN DPS process).

Using realistic nuclear densities (see e.g. [27]) to calculate \( \int d^b T^2(b)\), for \(A\ge 40\) one can calculate the ratio of the DPS contributions in pA and pp scattering as follows [17]:

$$\begin{aligned} r(A)=\frac{\sigma _{pA}^{DPS}}{\,A\sigma _{pp}^\mathrm{DPS}}= 1 + 1.1\,\left( \frac{\sigma _{\mathrm {eff}}}{\text{15 } \text{ mb }}\right) \,\left( \frac{A}{40}\right) ^{0.39}\,(1 + R_{\mathrm{corr}}) .\nonumber \\ \end{aligned}$$
(3)

In Eq. (3), \(R_{\mathrm{corr}} = f(x_1,x_2,Q^2) / f(x_1)f(x_2)-1\) where \(f(x,Q^2)\) and \( f(x_1, x_2,Q^2)\) are the the single and double parton distribution functions (dPDFs). \(R_{\mathrm{corr}}\) accounts for the longitudinal correlations of the constituents of the projectile proton due to the pQCD evolution [28]. In the pp case, correlation effects leads to a decrease of \(\sigma _{\mathrm {eff}}\) by the factor \((1+5 R_{\mathrm{corr}})\) as compared to the uncorrelated (mean field) model. The function

$$\begin{aligned} f(x_1,x_2)\equiv G(x_1,x_2,Q^2,Q^2,\mathbf {0}) \end{aligned}$$
(4)

is the double generalized parton distributions (DGPD) at zero transferred momenta [6]. Numerical calculations were performed under the assumption that the DGPD are factorized at the scale \(Q_0^2\) [6]. For different models of double parton correlations at a low resolution scale, see Ref. [29] and references therein. It was found that for large \(p_{\mathrm{T}}\), the factor \(5 R_{\mathrm{corr}} = 0.5 \div 1\) allows to reproduce the measured values of \(\sigma _{\mathrm {eff}}(NN)\); see [17] and references therein. For the kinematics we discuss in this work, a typical value is \(R_{\mathrm{corr}} \sim 0.15\), see Fig. 3. Taking \(\sigma _{\mathrm {eff}}= 20 \, \hbox {mb}\) leads to the expectation that the ratio of DPS to LT contributions is enhanced in pPb collisions by a factor \(r(200) \sim 4\). For minijets with \(p_{\mathrm{T}}\) of a few GeV, one expects \(\sigma _{\mathrm {eff}}\sim 30~ \hbox {mb}\), leading to \(r(200) \sim 5\). However this enhancement is somewhat reduced due to the leading twist shadowing effect which requires a detailed modeling of the particular kinematic domains [30], hence this effect will be considered elsewhere.

Fig. 3
figure 3

Correlation factor as a function of \({\varDelta }\eta \) and \(p_{\mathrm{T}}\) for different starting points of the QCD evolution, namely \(Q_0^2 = 0.5 \, {\hbox {GeV}}^2\) (a), and \(Q_0^2 = 1.0 \, {\hbox {GeV}}^2\) (b)

Full size image

One can try to observe the predicted enhancement of DPS in pA scattering at the LHC by comparing pp and pA data. However this would require comparing two different sets of data in a somewhat different kinematics. An alternative strategy we suggest in this paper is to explore the strong dependence of the DPS/LT ratio on the impact parameter of the pA collision.

Let us rewrite Eq. (2) in the differential form

$$\begin{aligned} \frac{d^2 \sigma ^{DPS}_{\mathrm pA}\,}{d^2b} =\,\frac{\sigma _1\,\sigma _2}{\sigma _{eff}}T(b) + \sigma _1\,\sigma _2\,T^2(b) , \end{aligned}$$
(5)

Then ratio of the second term in Eq. (5), corresponding to the specific to pA mechanism when two gluons from the incoming proton interact with two nucleons of the nuclei at the same impact parameter b, and the first term, corresponding to conventional nucleon–nucleon DPS is given by

$$\begin{aligned} \sigma _{\mathrm{DPS}}\,^{1N \rightarrow 2N}(b)/\sigma _{\mathrm{DPS}}\,^{1N \rightarrow 1N}(b) = \sigma _{\mathrm{eff}}\,T(b) , \end{aligned}$$
(6)

which corresponds to a very large enhancement of DPS for central pA collisions.

In experiment we however usually measure total four jet cross section (or any other cross section to which DPS contributes), that is the sum of the leading twist (LT) contribution (i.e. 2–4 gluons cross section) and DPS which is of the next to leading twist. Adding the LT contribution to Eq. 5 we can write

$$\begin{aligned} \frac{d\sigma _{pA}^{\mathrm{LT+DPS}}}{d^2b} = \sigma _{pN}\,T(b)\,+ \,\sigma _1\,\sigma _2\,T^2(b) . \end{aligned}$$
(7)

In Eq. (7), we removed the superscript (DPS) in the first term on the right hand side to indicate that \(\sigma _{pN}\) includes the leading twist contribution to the cross section of a process to which both LT and DPS contribute. This is possible because the LT cross section is also linear in T(b). Hence, Eq. (7) gives a model-independent prediction for the b-dependence of DPS in terms of the elementary DPS pp cross section, \(\sigma _1\) and \(\sigma _2\), and of T(b).

Obviously, one cannot fix the impact parameter of the collision, but one can still define centrality classes, for example using the method adopted by the ATLAS collaboration [31]. An evidence of the validity of such a procedure is that it reproduces correctly the rate of jet production in the kinematics where the parton of the proton carries a moderate Bjorken x, like \(x \le 0.1\).

To make realistic predictions for the DPS-related observables we perform the calculation in several steps, extending the existing Monte Carlo generator for the production of dijets [24, 26, 32], which allows to calculate the interaction probability distribution as a function of the number of wounded nucleons and of the pA centrality. We take into account the finite transverse spread of the parton distribution in nucleons, and correlations between nucleons in the nucleus [21].

3 Inclusive DPS beyond mean field approximation

The generalized double parton distributions necessary for the calculation of the DPS off nuclei were calculated in Ref. [28] as sum of two terms, as in Eq. (3) and as illustrated in Fig. 2.

Fig. 4
figure 4

Sketch of the transverse geometry of the the double parton collisions. The incoming proton, \(P_{\mathrm{proj}}\), is displaced in transverse space by the vector \(\mathbf {b}\) from the nucleus center, while the i-th nucleon in the target, \(N^{i}_{\mathrm{target}}\), is displaced in transverse space by the vector \(\mathbf {b}_i\) from the nucleus center. In this work, the hard interaction points \(g^{(1,2)}_{\mathrm{hard}}\), pointed by \(\rho _1\) and \(\rho _2\) from \(P_{\mathrm{proj}}\), are integrated over the whole transverse plane, event-by-event. The remaining vector notations are self-explanatory

Full size image

The first term in Eq. (3) term accounts for the scattering off two partons of the same nucleon. It can be calculated by a convolution of two double nucleon GPDs plus the pQCD induced correlations, and corresponds to the impulse approximation. The second term in Eq. (3) corresponds to scattering of two partons of the projectile off two partons belonging to two different nucleons of the nucleus. Figure 4 shows the notations used for the various quantities used in this work. Separating the contribution of scattering off the same nucleon is necessary to account in an economic way for the existence of parton–parton correlations in the nucleons. To calculate the DPS cross section accounting for a finite transverse spread of the parton distributions we introduce the quantity \(f_N(x, Q^2, \rho )\), describing the transverse distribution of partons in the nucleon, defined as follows:

$$\begin{aligned} f_N(x,Q^2, \rho ) = \frac{g(x, Q^2, \rho )}{f(x, Q^2)} , \end{aligned}$$
(8)

where \(g(x, Q^2, \rho )\) is the diagonal generalized single parton distribution and \(f(x, Q^2)\) is the parton distribution. The \(\rho \) dependence of the generalized parton distribution is given by the Fourier transform of the two gluon form factor of the nucleon, \(F_{2g}(t)\), which is determined from the analysis of \(J/\psi \) exclusive photoproduction [33]. For simplicity we will use an exponential parameterization of \(F_{2g}(t)=\exp (Bt/2)\), and will not write explicitly the dependence of B and \(f_N\) on x and \(Q^2\). Thus the transverse distribution of partons takes the form:

$$\begin{aligned} f_N(\rho ) = \frac{1}{2\,\pi \,B}\,\exp ( - \rho ^2 /2B) . \end{aligned}$$
(9)

The value of B in Eq. (9) can be extracted from the analysis of the exclusive \(J/\psi \) photoproduction.

The geometric factor entering to the DPS cross section can be written as

$$\begin{aligned}&D^{1N\rightarrow 1N+1N\rightarrow 2N}(b) \nonumber \\&\quad =\,\int d\varvec{\rho }_1d\varvec{\rho }_2 \,f_p(\rho _1)\,f_p(\rho _2)\,\psi _A^2(r_t^{(i)},z_i, r_t^{(k)},z_k) \nonumber \\&\qquad \times \sum ^A_{i=1}\,f_{N} ( |\varvec{\rho }_1+\varvec{b}- \varvec{r}^{(i)}_t | ) \sum ^A_{k=1}\,f_{N} ( |\varvec{\rho }_2+\varvec{b}- \varvec{r}^{(k)}_t | ) ,\nonumber \\ \end{aligned}$$
(10)

which includes both interactions with two different nucleons (\(1N\rightarrow 2N\)) and the same nucleon (\(1N\rightarrow 1N\)) of the target nucleus. The geometric factor for the same nucleon case is given by:

$$\begin{aligned}&D^{1N\rightarrow 1N}(b) \nonumber \\&\quad = \int d\varvec{\rho }_1d\varvec{\rho }_2 \psi _A^2(r_t^{(i)},z_i) \,f_p(\rho _1)\,f_p(\rho _2) \nonumber \\&\qquad \times \sum ^A_{i=1}\,f_{N} ( |\varvec{\rho }_1+\varvec{b}- \varvec{r}^{(i)}_t | ) \,f_{N} ( |\varvec{\rho }_2+ \varvec{b}-\varvec{r}^{(i)}_t |) . \end{aligned}$$
(11)

The factor for the interaction with two different nucleons, which replaces the \(T^2(b)\) factor in the optical approximation, Eq. (2), is simply given by the difference \(D^{1N\rightarrow 1N+1N\rightarrow 2N}(b) - D^{1N\rightarrow 1N}(b)\):

$$\begin{aligned}&D^{1N\rightarrow 2N}(b) \nonumber \\&\quad = \int d\varvec{\rho }_1d\varvec{\rho }_2 \psi _A^2(r_t^{(i)},z_i, r_t^{(k)},z_k,) \,f_p(\rho _1)\,f_p(\rho _2) \nonumber \\&\qquad \times \sum ^A_{i=1}\,f_{N} ( |\varvec{\rho }_1+\varvec{b}-\varvec{r}^{(i)}_t | ) \,\sum ^A_{k\ne i}\,f_{N} ( |\varvec{\rho }_2+\varvec{b}-\varvec{r}^{(k)}_t |),\nonumber \\ \end{aligned}$$
(12)

For our numerical studies, we choose \(B = 3 \, {\hbox {GeV}}^{-2}\), which corresponds to \(x \sim 0.01\) for \(Q^2 \sim \) a few \({\hbox {GeV}}^2\). The effective cross section, \(\sigma _{\mathrm {eff}}\) in Eq. (1), is expressed through B as \(\sigma _{\mathrm {eff}}= 8\pi B\), leading to \(\sigma _{\mathrm {eff}}= 30~ \hbox {mb}\) for \(B = 3 \, {\hbox {GeV}}^{-2}\). Smaller values of \(\sigma _{\mathrm {eff}}\) at large virtualities result in this approach from pQCD induced correlations [4, 6, 8].

The code developed to calculate Eqs. (10–12) thus allows to obtain the separate contributions due to the DPS with one (Eq. (12)) and two (Eq. (11)) nucleons, both as a function of pA centrality and of the number of wounded nucleons.

Our numerical results for the b-distributions for DPS off two and single nucleon can be compared with the optical model approximation. In Fig. 5 we compare \(D^{1N\rightarrow 2N}(b)\) and \(T^2(b)\). We find that the b-dependent distribution accounting for the finite nucleon size is a bit broader and the total contribution of the \(1N\rightarrow 2N\) term is somewhat smaller than in the optical approximation. For example, for pPb scattering, \(\int d^2b D^{1N\rightarrow 2N}(b) / \int d^2b T^2(b) = 0.95\), accounting for finite size, accurate treatment of the surface region of matter distribution (neutron skin effect, as described in Ref. [22]), and NN correlations. This suppression factor is close to the correction found in the mean field approximation for the nucleus wave function accounting for the finite nucleon size: \(\approx (1 - 2 r_N^2/R_A^2)\) [28].

Fig. 5
figure 5

The impact parameter distributions for scattering off two nucleons in optical approximation, \(T^2(b)\), and with finite radius of interaction with and without NN correlations, \(D^{1N\rightarrow 2N}(b)\), as defined in Eq. (12)

Full size image

The impulse approximation term \(\propto D^{1N\rightarrow 1N}(b)\) obviously does not introduce any corrections to the cross section integrated over b. However, since the elementary cross section corresponds to the interaction of two nucleons at a finite impact distance, the b-distribution of \(D^{1N\rightarrow 1N}(b)\) should be somewhat broader than for T(b).

The distribution over b for the leading twist distribution is given by

$$\begin{aligned} S(b)= & {} \int d\varvec{\rho }_1\,f_p(\rho _1) \nonumber \\&\times \sum ^A_{i=1}\,\psi _A^2(r_t^{(i)},z_i ) \,f_{N} ( |\varvec{\rho }_1+\varvec{b}-\varvec{r}^{(i)}_t | ) . \end{aligned}$$
(13)

The difference of S(b) and T(b) is very small, so we do not present the corresponding plot. The double scattering in NN interactions corresponds to a smaller average transverse distance than a single scattering [4, 6, 8, 34]. So in this case the deviation of the b-distribution from T(b) is even smaller. Hence, in the following we will neglect the small difference between S(b) and \(D^{1N\rightarrow 2N}(b)\).

4 Distribution over the number of wounded nucleons

In order to calculate the distribution over the number of wounded nucleons we need to distinguish events in which the two interacting partons of the nucleus belong either to the same nucleon or to two different nucleons. In the first class of events, which is described by \(D^{1N\rightarrow 1N}(b)\) in Eq. (11), we need to calculate the distribution over the number of soft interactions excluding the nucleon involved in the hard interaction. Analogously, we exclude two nucleons in the case of hard interactions with partons from two different nucleons in the nucleus. The procedure is a straightforward extension of the one we developed for dijet production [26]. For each of the two interacting partons of the proton, we assign one particular nucleon as the one involved in a hard interaction, with probabilities given by:

$$\begin{aligned} P_j= {g_N^{(j)}(\rho ) \over \sum _{k=1}^A g_N^{(j)}(\rho )}. \end{aligned}$$
(14)

Now we need to generate the distribution over the number of nucleons involved in soft interactions. We do it in two ways. The first approach is based on the standard Glauber model with an accurate treatment of the distribution of the probability of the inelastic NN interaction over the relative impact parameter. Another approach includes in addition effects of fluctuations of the strength of interaction of the projectile proton with the target nucleus from event to event, which we refer to as color fluctuations. These fluctuations take into account presence of the inelastic diffraction and provide an effective implementation of the high energy Gribov–Glauber picture of hadron–nucleus scattering. We follow closely the procedure discussed in our paper [26]. We assign to each incoming proton interaction strength \(\sigma \) with probability \(P(\sigma )\) – for a detailed discussion see Ref. [26] and calculate averages over a large sample of the events. The variance of the distribution over \(\sigma \), \(\omega _\sigma = \left\langle \sigma ^2\right\rangle / \left\langle \sigma \right\rangle ^2 -1\) is given by the Miettinen–Pumplin relation [35] which expresses \(\omega _\sigma \) through the ratio of inelastic and elastic NN cross sections at \(t=0\). For the LHC energies we estimate \(\omega _\sigma \approx 0.1\).

We follow the procedure developed by ATLAS to define centrality classes [31]. They use the transverse energy, \(\sum E_{\mathrm{T}}\), in the pseudorapidity interval \(-3.2\ge \eta \ge -4.9\) (i.e. along the nucleus direction) as a measure of centrality. The centrality intervals were defined in terms of percentiles of the \(\sum E_{\mathrm{T}}\) distribution. It was shown in Ref. [36] that \(\sum E_{\mathrm{T}}\) in this kinematics is not sensitive to production of hadrons at forward rapidities. The Authors calculated the distribution over the number of wounded nucleons, \(\nu \), using Glauber model or a color fluctuation model and developed a model to describe the distribution over \(\sum E_{\mathrm{T}}\) as a function of \(\nu \), see Refs. [25, 31, 36]. Centrality classes are defined as corresponding ranges in \(\sum E_{\mathrm{T}}\). For example, the centrality class \(0\div 10\%\) includes 10% of the events with the highest \(\sum E_{\mathrm{T}}\). Authors studied centrality dependence of the multiplicity distribution of charged-particle production for three values of \(\omega _\sigma =0, 0.11, 0.2\). It is remarkable that the best description was found for \(\omega _\sigma =0.11\). For such \(P(\sigma )\) they also found that the ratio of the observed charge particle production in bins and the impulse approximation expectation, \(R_{pPb}\), is close to one for \(p_{\mathrm{T}}\ge 2\div 3 \,\text{ GeV }\) and a wide range of rapidities.

Since we count nucleons which were involved in both soft and hard interaction only once, the distribution for the double nucleon term obviously starts at \(\nu =2\), with \(\nu \) the total number number of interacting nucleons.

The results of the calculation for the distribution over \(\nu \) for the no correlation scenario with account of color fluctuations (\(\sigma _{\mathrm {eff}}= 30 \, \hbox {mb}\)) are presented in Fig. 6 for several centrality classes. One can see from the figure that centrality classes correspond to rather narrow ranges of \(\nu \). In Fig  6a we present the distribution for soft events for different centrality classes while in Fig. 6b we present the distribution for inelastic events with two hard dijets (which serve as double hard trigger). For large \(\nu \) the account of color fluctuations leads to broadening of the distribution over \(\nu \).

Fig. 6
figure 6

Left: the centrality distribution of the number of soft (minimum-bias) collisions. Right: the centrality distribution of the number of inelastic collisions with the double hard trigger (i.e. with two dijets). Note that the distributions depend only on the transverse spread of individual DGPDs but not on specific of reaction

Full size image

One can see that for DPS events distribution over \(\nu \) is much broader. Parton–parton correlations lead to an enhancement of the impulse approximation the \(1N\rightarrow 2N\) term in Eq. (11) by a factor \(\sigma _{\mathrm {eff}}(m.f.)/ \sigma _{exp}= 1+ 5 R_{\mathrm{corr}}\), and of the double nucleon term by a factor \(1+R_{\mathrm{corr}}\) [28]. For the kinematics discussed in this work (presented in Fig. 4), \(R_{\mathrm{corr}}\sim 0.15\) (Fig. 3). Hence, its effect for the double scattering term is pretty small, and we will neglect its residual dependence on impact parameter.

Note that the distributions depend only on the transverse spread of individual DGPDs but not on specific characteristics of the reaction.

To take into account parton–parton correlations in the calculation of the distribution over \(\nu \), it is sufficient to take the impulse approximation term \(D^{1N\rightarrow 2N}(b)\) with an additional factor \((1 + 5R_{\mathrm{corr}}) /(1 + R_{\mathrm{corr}}) \sim 1.5\) and normalize to the inclusive cross section where the \(D^{1N\rightarrow 2N}(b)\) term is also enhanced by the same factor.

5 Transverse energy distribution and extraction of the DPS signal

Let us consider a process in which DPS contributes: for example production of four jets in a special configuration, or production of two jets and a hadron with a sufficiently large \(p_{\mathrm{T}}\) from the underlying event. The main challenge is that the LT process can also contribute to this special configuration (cf. Fig. 1), leading to the need to rely on a Monte Carlo simulation for a rather complicated final state.

If we choose a kinematics where soft contributions (including very soft minijets) can be neglected, there are three contributions to the final state: the leading twist contribution, DPS due to the interaction with one nucleon and DPS due to the interaction with two nucleons. The first two contributions are proportional to roughly the number of nucleons along the projectile path. In the events with a dijet trigger they would result in the same multiplicity of a second dijet (hadron) for different centralities. At the same time the DPS due to the interaction with two nucleons should lead to a contribution which grows with centrality much faster (roughly the square of the number of nucleons along the projectile path). Hence, it is convenient to consider the ratio of the multiplicity N of the candidate DPS final state (for example dijet plus a pion) and the multiplicity of the inclusive dijet production in the same kinematics:

$$\begin{aligned} N^{D/I} = N(\mathrm{dijet + pion})/ N(\mathrm{dijet}) . \end{aligned}$$
(15)

For such a ratio, deviations from linearity in the number of collisions, which were found in Ref. [26], practically cancel out. The dependence of \(N^{D/I}\) on centrality is only due to the double nucleon interaction term. We follow the procedure developed by ATLAS to define centrality classes [31] described in the previous section.

We choose the bins in \(\sum E_{\mathrm{T}}\) as in Refs. [24, 32], and use the 10–20% (second) bin, in which the first term of Eq. (2) (linear in A) dominates, and build the ratio of the differences in multiplicities in the \(i^{th}\) centrality bin as follows:

$$\begin{aligned} {\mathcal {R}}_{i} = \frac{N^{D/I}_i - N^{D/I}_2}{N^{D/I}_3 - N^{D/I}_2} . \end{aligned}$$
(16)

We substruct the value of the second bin since there are significant uncertainties in modeling the most peripheral bin, in particular due to the contribution of diffraction /rapidity gaps. In the differences \(N^{D/I}_i - N^{D/I}_2\) the contribution of the terms linear in A cancels out and the \(\sum E_{\mathrm{T}}\) dependence originates solely from the geometry of the process. Thus, the dependence of \({\mathcal {R}}_{i}\) on the momenta of the jets (hadrons) is expected to be universal (i.e. does not depend on the momenta of jets and hadrons). This would provide a crucial test of the overall picture of the double scattering process. The predicted dependence of \({\mathcal {R}}_{i}\) on centrality is very strong, as it is illustrated in Fig. 7 for the Color Fluctuation and Glauber models. One can see that color fluctuations somewhat reduce \({\mathcal {R}}_{i}\) for most central bin due to additional smearing over impact parameter. Anyway, the predicted effect is large and should be pretty straightforward to observe. Note that in our considerations we assumed that both components of DPS events originate from the leading twist QCD processes. So one needs to select the kinematics where for both subprocesses \(R_{p Pb}\) is close to one. Based on the analysis of ATLAS [25] use of the color fluctuation model with \(\omega _\sigma \sim 0.1\) appears to be preferable. Note also that in the kinematics where deviations of \(R_{pPb}\) from one for both subprocesses are small one can estimate related corrections for \({\mathcal {R}}_{i}\).

An important test of the picture is that \({\mathcal {R}}_{i}\) should be a universal function of \(\sum E_{\mathrm{T}}\), independent on the angle between the dijet and the hadron, and the hadron transverse momentum.

Fig. 7
figure 7

Centrality dependence of DPS multiplicity enhancement as a function of \(\sum E_{\mathrm{T}}\) measured in \(-3.2\ge \eta \ge -4.9\) (along the nucleus direction) which corresponds centrality bins denoted in the plot

Full size image

Let us now consider an example of a process which can be studied using this procedure, the production of a dijet at forward rapidities, in the range \(y = 2 \, \div \, 4\), and a hadron from an underlying event with a tight cut on the emission angle \(\theta = 90^o \pm 10^o\). We performed the calculations using the Pythia model of the contribution of DPS to the underlying multiplicity. The results of the calculation were shown in Fig. 1. One can see that in a wide range of hadron momenta DPS contributes on the scale of 30% \(\div \) 40% to the pp cross section. In the kinematics where the DPS/total ratio is 1 / 3 for pp collisions, we expect a large enhancement of DPS \(1N\rightarrow 2N\) contribution. For example taking \(\sigma _{eff} = 25 \, \hbox {mb}\) and using \(T_{Pb}(b\sim 0)= 2.0 fm^{-2}\) we find the ratio of\(1N\rightarrow 2N \) and \(1N\rightarrow 1N\) DPS contributions (see Eq. 6): \(\approx \sigma _{eff} T(b\sim 0) \sim 5\), leading to the change of the DPS/LT ratio from 0.5 to 3.0. The multiplicity enhancement due to DPS can be increased by suppressing the LT contribution. For instance, imposing additional requirement on the dijet momentum imbalance \((p_{\mathrm{T, 1}} - p_{\mathrm{T, 2}})/(p_{\mathrm{T, 1}} + p_\mathrm{T, 2})<\) 0.1, where \(p_{\mathrm{T, 1}}\) and \(p_{\mathrm{T, 2}}\) are the transverse momenta of the leading and subleading jets respectively, would increase the DPS contribution to 35-50%. Also due to a relatively high rate of the discussed process an accurate subtraction procedure should be possible both for the narrow angle window we discuss, and for a wider range of the angles. The minimal \(p_{\mathrm{T}}\) of the hadrons for which our calculations are applicable follow from the requirement that \(R_{pPb}\), the ratio of the rate of the observed dijet production and the rate calculated in the impulse approximation, should be close to one. Depending on the rapidity of the hadron it corresponds to \( p_{\mathrm{T}}(hadron) \ge \text{2 } \div \text{5 } \text{ GeV }\) [25]. Also, one has to impose a restriction to the fraction of the momentum of proton, \(x_p\), carried by the parton involved in the dijet production \(x_p \le 0.1\), since for large \(x_p\) the centrality dependence is gradually changing [37]. This may be due to selection of smaller size configurations by a large \(x_p\) trigger, see discussions in [24, 32].

A clean separation of the \(1N\rightarrow 2N\) contribution would allow to perform a direct measurement of the parton–parton correlations (\(R_{\mathrm{corr}}\)) (cf. Eq. (3)). Knowing the \(A^{4/3}\) term it would be possible to measure correlation effects for two partons of the projectile proton involved in the process (cf. Eq. (3)). Also it would make it easier to extract \(\sigma _{\mathrm {eff}}\) from the linear term. In this case \(\sigma _{\mathrm {eff}}\) is the only parameter which could be adjusted and it could be determined from the condition that the dependence of the hadron emission on the azimuthal angle with the respect to the dijet should disappear (we make here a natural assumption valid in the leading order that DPS gives a flat distribution in the azimuthal angle relative to the prime dijet in difference of the LT contributions \(2\rightarrow 3, 2\rightarrow 4 ,\ldots \)).

6 Conclusions

We developed an algorithm for the calculation of the DPS cross section in pA scattering as a function of centrality. We suggested a method to use the centrality to determine the cross section of DPS due to scattering off two different nucleons. In the long run this would allow to study parton–parton correlations in nucleons as a function of virtuality and x’s. It would be possible also to look for triple parton scattering [20] using a similar strategy.