Circular motion around a rotating black hole in quintessential dark energy

Abstract

This paper investigates the circular motion of neutral test particles orbiting near Kerr–Newman black hole in the presence of quintessential dark energy and cosmological constant. We limit our analysis to the equatorial plane and explore the properties of both time-like and null geodesics. The behavior of the specific energy and the angular momentum of the co-rotating as well as the counter rotating particles is analyzed. We also discuss the stable regions with respect to the horizons, radius of photon sphere and the so called static radius. We have shown that the stable points are always less than the static radius while they exceed the radius of photon orbit. The energy extraction, negative energy state and energy gain during the Penrose process is also discussed. It is found that more energy can be gained during the Penrose process in the presence of dark energy as compared to the charge and spin of the said black hole.

1 Introduction

It is believed that the dark matter (DM) and dark energy (DE) remain two unresolved issues in cosmology as well as astrophysics. Recent cosmic observations indicate that the DE is responsible for the accelerated expansion of the Universe. The DE is about $70\%$ of the observable Universe [1, 2] and can be represented by a repulsive cosmological constant $\Lambda >0$ (vacuum density) or by a quintessential field [3,4,5,6,7,8,9,10,11,12]. The cosmological constant can be considered as homogeneous and vacuum energy having negative pressure, fully characterized by its value ($\Lambda \approx 1.3\times 10^{-56} \mathrm{cm}^{-2}$) which remains the same everywhere in space [13]. The vicinity of the cosmological constant alters the asymptotic structure of naked singularity or black hole (BH) backgrounds as such backgrounds become asymptotically de Sitter (dS) spacetime. The cosmological horizon always exits in such type of spacetimes.

The quintessence is an inhomogeneous and dynamical scalar field having negative pressure, fully defined by the equation $\rho =\omega p$, where $\rho$ and p represents the energy density and pressure, respectively. There are three cases according to the value of state parameter $\omega$, i.e., $\omega <-1$, $\omega =-1$ and $-1<\omega <-1/3$, corresponds to the phantom energy, the cosmological constant and the quintessence, respectively [14].

In recent years, the particle motion around a BH has been an important issue in astrophysics. The analysis of geodesics helps us to understand the gravitational field around a BH. They may display a rich structure and convey important information on the background geometry. Stuchlik and Hledik [15] studied photon motion around Kerr Newman (KN) BH with non-zero cosmological constant and found that there are always two unstable circular photon orbit outside the outer horizon. Jamil et al. [16] discussed particle dynamics near Schwarzschild-like BH in the background of quintessence and concluded that innermost stable circular orbit shifts near to the event horizon due to presence of DE in comparison with the Schwarzschild BH. Shanjit and Singh [17] explored the geodesics in KN anti-dS (KNAdS) spacetime and found that the stable circular orbits exist in the region of $0<r<r_{-}$, where $r_{-}$ is the inner horizon of BH. Sharif and Shahzadi [18] studied the geodesics around Kerr modified BH. They also investigated the neutral particle motion around Schwarzschild BH in modified gravity [19]. Some important concepts of geodesics can be found in [20,21,22,23,24,25,26].

The extraction of energy from a rotating BH is remained the topic of interest in general relativity (GR). Penrose [27, 28] proposed a process through which energy can be extracted from a BH and the maximum efficiency of the Penrose process is about 0.207 [29]. The accretion efficiency can be higher than 1.0 around Kerr naked singularities [30]. In 1985, the Penrose process for the Kerr BH immersed in magnetic was considered [31]. It was shown that only the magnetic version of the Penrose process can be significantly efficient [32] and it can be much higher that 1.0 [33]. It is believed that the necessary and sufficient condition for the extraction of energy from a rotating BH is the particle absorption with negative energy as well as angular momentum. Nozawa and Maeda [34] proposed that the higher dimensional BHs could be the source of excessive energy extraction as compared to the 4D Kerr BH. Mukherjee [35] explored the Penrose process for spinning particles near Kerr BH and found the high energy extraction in comparison to the case of non-spinning particles.

The energy gain in the Penrose process can be explained by the negative energy of the ergosphere (where the trapped particle absorbed by the BH). Pradhan [36] found that the energy gain decreases with the increasing values of the NUT parameter around KN-Tab-Nut BH. Toshmatov et al. [37] explored the Penrose process near a rotating regular BH and concluded the decrease in efficiency of energy extraction with the increase of electric charge. Sharif and Iftikhar [38] examined the Penrose process for the dyonic KN BH with cosmic string and concluded that energy gain may not be affected by the string parameter.

In this paper, we examine the circular geodesics as well as energy extraction through Penrose process around KN BH in the presence of quintessential DE and a cosmological constant (KNdSQ BH) (We confine our study to the case of positive cosmological constant (case of de-Sitter solution)). The outline of this paper is as follows. In Sect. 2, we describe the geometry of KNdSQ BH and explore the time-like as well as null geodesics. We derive the expressions for energy and angular momentum for circular orbits and also find the equation for circular photon orbit. In Sect. 3, we investigate the stability of orbits through the analysis of the effective potential. The negative energy state and energy gain via Penrose process has been discussed in Sect. 4. The last section provides the summary of our results.

2 Equatorial circular geodesics

Dark energy is an exotic type of matter which responsible for the accelerated expansion of the universe. It is also believed that content filled with DE such as cosmological constant and quintessence can alter the BH structure. There are many well-known models of DE that explains the expansion through cosmological constant term, however the quintessential field in one of the most promising candidates of DE [39]. The cosmological constant has a significant effect on the properties of accretion disc around the BHs in quasars as well as active galactic nuclei [13]. The spherically symmetric and axially symmetric spacetimes influenced by cosmological constant are described as Schwarzschild as well as Kerr dS BHs [13, 40]. Kiselev [41] obtained a class of spherically symmetric BHs parameterized by quintessence charge $\omega _{q}$. Later on, Xu and Wang [42] generalized this solution by including rotation as well as charge parameters and extended quintessence KN BH for the case of the cosmological constant. There is a large body of literature available for various important aspects (test particle motion, AdS/CFT correspondence, quasinormal modes, etc.) of BHs parameterized by cosmological constant and quintessential DE [43,44,45,46,47,48,49,50,51].

Motivated by the previous works, we study the particle dynamics around KNdSQ BH. In this section, we explore that geodesics for both null and time-like particles. The said BH is the solution of Einstein–Maxwell equations and the line element corresponding to this BH is given as [42]

$$\begin{aligned} ds^{2}= & {} \frac{\rho ^{2}}{\Delta _{r}}dr^{2}+\frac{\rho ^{2}}{\Delta _{\theta }}d\theta ^{2} +\frac{\Delta _{\theta }\sin ^{2}\theta }{\rho ^{2}}\nonumber \\&\quad \times \left( a\frac{dt}{\Sigma } -(r^{2}+a^{2})\frac{d\phi }{\Sigma }\right) ^{2}\nonumber \\&\quad -\frac{\Delta _{r}}{\rho ^{2}} \left( \frac{dt}{\Sigma }-a\sin ^{2}\theta \frac{d\phi }{\Sigma }\right) ^{2}, \end{aligned}$$

(1)

where

$$\begin{aligned}&\Delta _{r}=r^{2}+a^{2}+Q^{2}-2Mr-\alpha r^{1-3\omega }-\frac{\Lambda }{3}(r^{2}+a^{2})r^{2},\\&\Delta _{\theta }=1{+}\frac{a^{2}}{3}\Lambda \cos ^{2}\theta , \quad \Sigma =1{+}\frac{a^{2}}{3}\Lambda , \quad \rho ^{2}{=}r^{2}{+}a^{2}\cos ^{2}\theta , \end{aligned}$$

here, M is the gravitational mass of BH, a denotes the spin parameter, $\Lambda$ is the cosmological constant and Q represents the electric charge of BH. The quintessence parameter $\alpha$ describes the intensity of the quintessence field related to BH. The parameter $\omega$ represents the equation of state as $p=\omega \rho$, in which $\omega \in (-1, -\frac{1}{3})$, where p and $\rho$ denotes the pressure as well as energy density of the quintessence, respectively. For $\Lambda =\alpha =0$, the metric (1) reduces to the KN metric, furthermore, $\Lambda =\alpha =Q=0$, leads to Kerr metric. Moreover, $\Lambda =\alpha =Q=a=0$, describes the Schwarzschild metric and for $\Lambda =\alpha =a=0$, we recover RN metric. The horizons for (1) can be obtained by solving $\Delta _{r}=0$.

The motion of a test particle can be described by the following Lagrangian

$$\begin{aligned} \mathcal {L}=\frac{1}{2}g_{\mu \sigma }\dot{x}^{\mu }\dot{x}^{\sigma }, \end{aligned}$$

where, $\dot{x^\mu }=u^\mu =\frac{dx^\mu }{d\tau }$ ($\tau$ represents the proper time) is the 4-velocity of particle.

The study of circular geodesics in the equatorial plane is of fundamental interest in BH physics as well as the accretion disc theory to determine the importance features of the spacetime. It has been shown that the Lense-Thirring effect causes gradual transition of the tilted accretion disc to the equatorial plane [55]. The stability of orbits in latitudinal and radial motion has been studied in detail in [56]. Other evolutionary studies such as wave fronts and equatorial orbits and analysis of circular equatorial orbits [52, 57,58,59,60].

We consider the particle motion near an equatorial plane, i.e., $\theta =\frac{\pi }{2}, \dot{\theta }=0$ and following the technique of Chandrasekhar [29]. For KNdSQ BH, the Lagrangian takes the form

$$\begin{aligned} 2\mathcal {L}= & {} -\left( \frac{\Delta _{r}-a^{2}}{r^{2}\Sigma ^{2}} \right) \dot{t}^{2}-2a\left( \frac{r^{2} +a^{2}-\Delta _{r}}{r^{2}\Sigma ^{2}}\right) \dot{t}\dot{\phi }\nonumber \\&+\frac{r^{2}}{\Delta _{r}}\dot{r}^{2} +\frac{r^{2}}{\Delta _{\theta }}\dot{\theta }^{2}+\left( \frac{(r^{2}+a^{2})^{2}-a^{2}\Delta _{r}}{r^{2}\Sigma ^{2}}\right) \dot{\phi }^{2}. \end{aligned}$$

(2)

From Eq. (2), it is clear that t and $\phi$ are the cyclic co-ordinates which corresponds to two constants of motion, the total energy, E and angular momentum, L which remain conserved along geodesics. The generalized momenta are given as

$$\begin{aligned} -p_{t}= & {} -\left( \frac{\Delta _{r}-a^{2}}{r^{2}\Sigma ^{2}}\right) \dot{t} -a\left( \frac{r^{2}+a^{2}-\Delta _{r}}{r^{2}\Sigma ^{2}}\right) \dot{\phi }=E,\nonumber \\ \end{aligned}$$

(3)

$$\begin{aligned} p_{\phi }&{=}&\left( \frac{(r^{2}{+}a^{2})^{2}{-}a^{2}\Delta _{r}}{r^{2}\Sigma ^{2}}\right) \dot{\phi }{-}a\left( \frac{r^{2}{+}a^{2}{-}\Delta _{r}}{r^{2}\Sigma ^{2}}\right) \dot{t}{=}L,\nonumber \\ p_{r}= & {} \frac{r^{2}}{\Delta _{r}}\dot{r}. \end{aligned}$$

(4)

The Hamiltonian can be written as

$$\begin{aligned} H=p_{t}\dot{t}+p_{r}\dot{r}+p_{\phi }\dot{\phi }-\mathcal {L}. \end{aligned}$$

(5)

Using (1), Eq. (5) equation takes the form

$$\begin{aligned} 2H= & {} -\left[ \left( \frac{\Delta _{r}-a^{2}}{r^{2}\Sigma ^{2}}\right) \dot{t} -a\left( \frac{r^{2}+a^{2}-\Delta _{r}}{r^{2}\Sigma ^{2}}\right) \dot{\phi }\right] \dot{t} +\frac{r^{2}}{\Delta _{r}}\dot{r}^{2}\\&{+} \left[ \left( \frac{(r^{2}+a^{2})^{2}{-}a^{2}\Delta _{r}}{r^{2}\Sigma ^{2}}\right) \dot{\phi } -a\left( \frac{r^{2}+a^{2}-\Delta _{r}}{r^{2}\Sigma ^{2}}\right) \dot{t}\right] \dot{\phi }\\= & {} -E\dot{t}+L\dot{\phi }+\frac{r^{2}}{\Delta _{r}}\dot{r}^{2}=\epsilon =\text {constant}, \end{aligned}$$

where $\epsilon =-1, 0, 1$ specify the time-like, null (lightlike) and spacelike geodesics. Solving Eqs. (3) and (4), we have

$$\begin{aligned} \dot{t}&{=}&\frac{\Sigma ^{2}}{r^{2}\Delta _{r}}\left[ a L\left( r^{2}{+}a^{2}{-}\Delta _{r}\right) {-}E\left( (r^{2}{+}a^{2})^{2} -a^{2}\Delta _{r}\right) \right] , \end{aligned}$$

(6)

$$\begin{aligned} \dot{\phi }= & {} \frac{\Sigma ^{2}}{r^{2}\Delta _{r}}\left[ a \left( E(r^{2}+a^{2})-aL\right) -\Delta _{r}\left( a E-L\right) \right] . \end{aligned}$$

(7)

Substituting Eqs. (6) and (7) into (5), we obtain the radial equation of motion

$$\begin{aligned} \dot{r}^{2}{=}\frac{\Sigma ^{2}}{r^{4}}\left[ \left( E\left( r^{2}{+}a^{2}\right) {-}aL\right) ^{2}{-}\Delta _{r}(a E-L)^{2}\right] -\frac{\Delta _{r}}{r^{2}}\epsilon . \end{aligned}$$

Inserting the value of $\Sigma$ and neglecting higher powers of $\Lambda$, the above equation takes the form

$$\begin{aligned} \dot{r}^{2}= & {} E^{2}+\frac{2M}{r^{3}}(L-a E)^{2}+\frac{\Lambda }{3}\left( L-a E\right) ^{2}\nonumber \\&-\frac{Q^{2}}{r^{4}}\left( L-a E\right) ^{2}+\alpha (L-a E)^{2}r^{-3(1+\omega )}\nonumber \\&-\frac{1}{r^{2}}\left( L-a E\right) [a E+L-\frac{\Lambda }{3}\left( L-a E\right) a^{2}]-\frac{\Delta _{r}}{r^{2}}\epsilon .\nonumber \\ \end{aligned}$$

(8)

Equations (6)–(8) are useful to analyze several features associated with the particle motion. In the following, we discuss the null as well as time-like geodesics.

2.1 Null geodesics

In this section, we study the null geodesics by taking $\epsilon =0$. In this case, Eq. (8) takes the form

$$\begin{aligned} \dot{r}^{2}= & {} E^{2}+\frac{2M}{r^{3}}(L-a E)^{2}+\frac{\Lambda }{3}\left( L-a E\right) ^{2}\nonumber \\&-\frac{Q^{2}}{r^{4}}\left( L-a E\right) ^{2}+\alpha (L-a E)^{2}r^{-3(1+\omega )}\nonumber \\&-\frac{1}{r^{2}}\left( L-a E\right) [a E+L-\frac{\Lambda }{3}\left( L-a E\right) a^{2}]. \end{aligned}$$

(9)

It is useful to introduce an impact parameter $D=\frac{L}{E}$ instead of L. Firstly, we consider a specific case $L=aE$ for which $D=a$. Thus, Eqs. (6), (7) and (9) reduce to

$$\begin{aligned} \dot{t}=\frac{\Sigma ^{2}}{\Delta _{r}}E\left( r^{2}+a^{2}\right) , \quad \dot{\phi }=\frac{\Sigma ^{2}}{\Delta _{r}}Ea, \quad \dot{r}=\pm E. \end{aligned}$$

The equations governing t and $\phi$ turns out to be

$$\begin{aligned} \frac{dt}{dr}=\pm \frac{\Sigma ^{2}}{\Delta _{r}}\left( r^{2}+a^{2}\right) , \quad \frac{d\phi }{dt}=\pm \frac{a}{r^{2}+a^{2}}. \end{aligned}$$

We distinguish the orbits with impact parameter less or greater than the certain critical value $D_{c}$. For $D>D_{c}$, there are two types of orbits: those of the first type that arriving from infinity and having perihelion distance greater than $r_{c}$ (radius of unstable circular orbit) and those of the second type that having aphelion distances less than $r_{c}$. For $D=D_{c}$, the both type of orbits coalesce. For $D <D_{c}$, there is one type of orbit arriving from infinity which crosses the horizons and terminate at singularity.

Now, as the general case, we consider $L\ne aE$ and determine the radius of the unstable photon orbit for which $E=E_{c}$, $L=L_{c}$ and $D_{c}=L_{c}/E_{c}$. We first consider the case when $\omega =-\frac{2}{3}$ (for the sake of simplicity). Therefore, Eq. (9) and its derivative takes the following form

$$\begin{aligned}&r_{c}^{2}+\frac{1}{r_{c}^{2}}(a-D_{c})^{2}\left[ 2Mr_{c}-Q^{2}+\alpha r_{c}^{3}+\frac{\Lambda }{3}r_{c}^{2}(r_{c}-a^{2})\right] \nonumber \\&+(a^{2}-D_{c}^{2})=0, \end{aligned}$$

(10)

$$\begin{aligned}&r_{c}-\frac{1}{r_{c}^{4}}(a-D_{c})^{2}\left[ Mr_{c}^{2}-Q^{2}r_{c}-r_{c}^{4}\left( \alpha +\frac{\Lambda }{3}\right) \right] =0. \end{aligned}$$

(11)

From Eq. (11), we obtain

$$\begin{aligned} D_{c}=a{\mp }\sqrt{\frac{r_{c}^{5}}{Mr_{c}^{2}-Q^{2}r_{c} -r_{c}^{4}(\alpha +\frac{\Lambda }{3})}}, \end{aligned}$$

(12)

where ${\mp }$ corresponds to the counter as well as co-rotating orbits, respectively. Substituting Eq. (12) into Eq. (10), we have

$$\begin{aligned}&r_{c}^{2}(6Q^{2}+r_{c}(-9M+r_{c}(3+a^{2}\Lambda ))) \nonumber \\&\pm 2\sqrt{3}a\sqrt{r_{c}^{4}[3Mr_{c}-3Q^{2}-r_{c}^{3}(3\alpha +\Lambda )]}=0, \end{aligned}$$

(13)

here, $r_{c}=r_{po}$ represents the positive real root of Eq. (13) that gives the radius of photon orbit for KNdSQ BH for $\omega =-\frac{2}{3}$.

Next, we consider $\omega =-\frac{1}{2}$, in this case

$$\begin{aligned}&r_{c}^{2}+\frac{1}{r_{c}^{2}}(a-D_{c})^{2}\left[ 2Mr_{c}-Q^{2}+\alpha r_{c}^{5/3} +\frac{\Lambda }{3}r_{c}^{2}(r_{c}-a^{2})\right] \nonumber \\&\quad +(a^{2}-D_{c}^{2})=0, \end{aligned}$$

(14)

$$\begin{aligned}&r_{c}-\frac{1}{r_{c}^{4}}(a-D_{c})^{2} \left[ Mr_{c}^{2}{-}Q^{2}r_{c} {-}\frac{r_{c}^{4}}{2}\left( \frac{\alpha }{2 r^{1/2}}{+}\frac{\Lambda }{3}\right) \right] =0.\nonumber \\ \end{aligned}$$

(15)

From Eq. (15), we obtain

$$\begin{aligned} D_{c}=a{\mp }\sqrt{\frac{r_{c}^{5}}{Mr_{c}^{2}-Q^{2}r_{c} -\frac{r_{c}^{4}}{2}\left( \frac{\alpha }{2 r^{1/2}}+\frac{\Lambda }{3}\right) }}, \end{aligned}$$

(16)

where ${\mp }$ corresponds to the counter(co-rotating) orbits, respectively. Substituting Eq. (12) into Eq. (10), we have

$$\begin{aligned}&r_{c}\left( r_{c} \left( 4 \left( a^2 \Lambda +3\right) -6 r_{c} (2 \alpha +\Lambda )+3\alpha \sqrt{r_{c}}\right) -36 M\right) \nonumber \\&\quad +24 Q^2 \nonumber \\&\quad \pm 4 a \sqrt{36 M r_{c}-36 Q^2-9 \alpha r_{c}^{5/2}+6 \Lambda r_{c}^3}=0. \end{aligned}$$

(17)

here, $r_{c}=r_{po}$ represents the positive real root of Eq. (17) which gives the radius of photon orbit for KNdSQ BH for $\omega =-\frac{1}{2}$. Tables 1, 2, 3 and 4 describe the behavior of circular photon orbit with the variation of a, Q and $\alpha$.

Table 1 Photon orbits $r_{po1}$ (direct rotating) for $\omega =-\frac{2}{3}$

Table 2 Photon orbits $r_{po2}$ (counter rotating) for $\omega =-\frac{2}{3}$

Table 3 Photon orbits $r_{po1}$ (direct rotating) for $\omega =-\frac{1}{2}$

2.2 Time-like geodesics

Here, we discuss timelike geodesics ($\epsilon =-1$). In this case, Eqs. (6) and (7) remain the same and (8) takes the following form

$$\begin{aligned} \dot{r}^{2}= & {} E^{2}+\frac{2M}{r^{3}}(L-a E)^{2}+\frac{\Lambda }{3}\left( L-a E\right) ^{2}\nonumber \\&-\frac{Q^{2}}{r^{4}}\left( L-a E\right) ^{2}+\alpha (L-a E)^{2}r^{-3(1+\omega )}\nonumber \\&-\frac{1}{r^{2}}\left( L-a E\right) \left[ a E+L-\frac{\Lambda }{3}\left( L-a E\right) a^{2}\right] \nonumber \\&-\frac{\Delta _{r}}{r^{2}}. \end{aligned}$$

(18)

Table 4 Photon orbits $r_{po2}$ (counter rotating) for $\omega =-\frac{1}{2}$

For special case $L=aE$, the above equation reduces to

$$\begin{aligned} r^{2}\dot{r}^{2}=E^{2}r^{2}-\Delta _{r}. \end{aligned}$$

(19)

Integrating Eq. (19), we get

$$\begin{aligned} \tau =\int \left( E^{2}-\frac{\Delta _{r}}{r^{2}}\right) ^{-\frac{1}{2}}dr. \end{aligned}$$

Now, we consider a general case $(L\ne aE)$, substituting $x=L-aE$ in Eq. (18), it follows that

$$\begin{aligned} F(r)=r^{4}\dot{r}^{2}=x^{2}(a^{2}-\Delta _{r})-2aEr^{2}x+r^{4}E^{2}-r^{2}\Delta _{r}.\nonumber \\ \end{aligned}$$

(20)

Differentiating with respect to r, the above equation takes the form

$$\begin{aligned} F'(r)=-4aErx+4r^{3}E^{2}-r^{2}\Delta _{r}'-2r\Delta _{r}-x^{2}\Delta _{r}'. \end{aligned}$$

(21)

Combining Eqs. (20), (21) and taking $F(r)=0=F'(r)$, we have

$$\begin{aligned}&\left( \Delta _{r}-\frac{r\Delta _{r}^{'}}{2}-a^{2}\right) x^{2}+E^{2}r^{4} -\frac{r^{3}\Delta _{r}^{'}}{2}=0, \end{aligned}$$

(22)

$$\begin{aligned}&E=\frac{1}{r^{2}ax}\left[ \left( a^{2}-\Delta _{r}+\frac{r\Delta _{r}^{'}}{4}\right) x^{2} +\frac{r^{3}\Delta _{r}^{'}}{4}-\frac{r^{2}\Delta _{r}}{2}\right] .\nonumber \\ \end{aligned}$$

(23)

Inserting the value of E in Eq. (22), we obtain

$$\begin{aligned}&\left[ 2\left( a^{2}-\Delta _{r}+\frac{r}{4}\Delta _{r}'\right) ^{2}+a^{2} \left( 4\Delta _{r}-4a^{2}\frac{r}{2}\Delta _{r}'\right) \right] x^{4}\nonumber \\&\quad + \left[ \left( 4a^{2}-4\Delta _{r}'+r\Delta _{r}'\right) \nonumber \right. \\&\left. \quad \times \left( \frac{r^{3}}{2}\Delta _{r}'-r^{2}\Delta _{r}\right) -2r^{3}a^{2}\Delta _{r}'\right] x^{2}\nonumber \\&\quad +\left( r^{2}\Delta _{r}-\frac{r^{3}}{3}\Delta _{r}'\right) ^{2}=0. \end{aligned}$$

(24)

The above equation leads to the following discriminant

$$\begin{aligned} \mathcal {D}=8r^{4}\Delta _{r}^{2}a^{2}\left( a^{2}+\frac{r}{2}\Delta _{r}'-\Delta _{r}\right) . \end{aligned}$$

Thus the solution of Eq. (24) is found as

$$\begin{aligned} x=-\frac{r}{\sqrt{\chi _{{\mp }}}}\left( a\pm \sqrt{a^{2}+ \frac{r\Delta _{r}^{'}}{2}-\Delta _{r}}\right) , \end{aligned}$$

(25)

here, the lower and upper signs lead to prograde and retrograde orbits, respectively and

$$\begin{aligned} \chi _{{\mp }}=2\left( \Delta _{r}-a^{2}-\frac{r}{4}\Delta _{r}'\right) {\mp } a\sqrt{4\left( a^{2}-\Delta _{r}\right) +2r\Delta _{r}'}. \end{aligned}$$

Inserting the value of x in Eq. (22), we obtain the energy of circular orbit

$$\begin{aligned} E=\frac{1}{r\sqrt{\chi _{{\mp }}}}\left( \Delta _{r}-a^{2}{\mp }\sqrt{a^{4} -a^{2}\Delta _{r}+\frac{a^{2}r}{2}\Delta _{r}'} \right) . \end{aligned}$$

(26)

Using the above equation, we find angular momentum related to the circular orbit

$$\begin{aligned} L=x+aE= & {} \frac{1}{r\sqrt{\chi _{{\mp }}}}\left[ {\phantom {\left. {{\mp }}\left( r^{2} +a^{2}\right) \sqrt{a^{2}+\frac{r}{2}\Delta _{r}'-\Delta _{r}}\right] }}\left( \Delta _{r}-a^{2}-r^{2}\right) a\right. \nonumber \\&\left. {{\mp }}\left( r^{2} +a^{2}\right) \sqrt{a^{2}+\frac{r}{2}\Delta _{r}'-\Delta _{r}}\right] . \end{aligned}$$

(27)

Equations (26) and (27) give the energy and angular momentum of a particle specifying a circular orbit of reciprocal radius u. The angular velocity for test particles turns out to be

$$\begin{aligned} \Omega =\frac{\dot{\phi }}{\dot{t}}=\frac{{\mp }\sqrt{a^{2}+\frac{r}{2}\Delta _{r}'-\Delta _{r}}}{r^{2}{\mp }\sqrt{a^{4}-a^{2}\Delta _{r}+\frac{r}{2}a^{2}\Delta _{r}'}}. \end{aligned}$$

By taking into account Eqs. (26) and (27), we found two reality conditions for the existence of the circular orbits. The first one is given as the following relation

$$\begin{aligned} y\le y_{s}\equiv \frac{1}{2} r^{-4 - 3 w} (\alpha r - 2 Q^{2} r^{3 w} + 2 r^{1 + 3 w} + 3 \alpha r), \end{aligned}$$

(28)

here, $y=\frac{\Lambda M^2}{3}$ and $M=1$ (for the sake of simplicity). The above equation establish the notion of “static radius” which can be obtained from

$$\begin{aligned} -4 Q^2 + 2 r (2 + \alpha r^{-3 w} (1 + 3 w)) = 4 r^4 y \end{aligned}$$

(29)

and the second restriction on existence of circular orbits is given by

$$\begin{aligned} 2\left( \Delta _{r}-a^{2}-\frac{r}{4}\Delta _{r}'\right) {\mp } a\sqrt{4\left( a^{2}-\Delta _{r}\right) +2r\Delta _{r}'}\ge 0. \end{aligned}$$

(30)

The equality of the this equation leads to the radii of the circular photon orbits. For $\alpha =0$, $Q=0$, Eqs. (28)–(30) correspond to the Kerr-dS BH [52].

Fig. 1

Plots of energy of a particle as a function of r (left for direct orbits and right for retrograde orbits). Here, the ascending and descending parts corresponds to stable and unstable orbits

Fig. 2

Plots of angular momentum of a particle as a function of r, here left and right plots are for direct orbits $(L>0)$ and retrograde orbits $(L<0)$, respectively. The ascending parts of $L>0$ and descending parts of $L<0$ correspond to stable orbits while the descending parts of $L>0$ and ascending parts of $L<0$ lead to unstable orbits

The graphical behavior of energy is depicted in Fig. 1. The left and right graphs are plotted for direct and retrograde motion, respectively. The top panel shows the variation of energy against the different values of spin parameter a. We observe the decrease in energy profile with the increase of spin parameter, in the case of direct motion while it increases with the increasing values of spin in the retrograde motion. The middle graphs represent the variation of Q. It is noted that energy for co-rotating orbits decreases with the increasing value of Q but in the case of counter rotating orbits, it increases for large values of Q and we observe a small change at a large radial distance r. The third panel shows that the particles with direct as well as retrograde motion has less energy in the presence of DE (as compared to its absence) as it decreases gradually with the increase of $\alpha$. In the last panel, the solid and dashed line correspond to the Kerr and KN BHs, respectively. It can be seen that for direct orbits, Kerr BH has greater energy as compared to KN and KN dS BHs while for retrograde orbits, Kerr BH has less energy in comparison with the KN and KN dS BHs. The analysis of angular momentum is shown in Fig. 2. The left and right graphs are plotted for direct and retrograde motion, respectively. The upper panel shows that the large values of Q correspond to increase in the angular momentum in retrograde motion while in the case of direct motion, it decreases as Q increases and attain higher values with the increase of radial distance r. The next panel represent the behavior of angular momentum against different values of a. We observe that the angular momentum corresponding to co-rotating orbits increase with the increase of the rotation of a BH but for counter rotating orbits, we have opposite behavior. The third panel shows that the particles in retrograde motion have more angular momentum in the presence of DE while for direct motion, angular momentum has decreasing behavior. In the last panel, solid and dashed lines correspond to the Kerr and KN BHs, respectively. It is noted that, for direct orbits angular momentum for KNdSQ BH takes higher values as compared to the case of Kerr and KN BHs while for retrograde orbits, it has small values.

3 Behavior of effective potential

Fig. 3

Plots of effective potential for null geodesics as a of function of r for $\omega =-\frac{2}{3}$

Fig. 4

Plots of effective potential for null geodesics as a function of r for $\omega =-\frac{1}{2}$

In this section, we discuss the stable as well as the unstable motion of the circular orbits by the analysis of the effective potential for KNdSQ BH. The radial equation of motion can be written as [69]

$$\begin{aligned} \left( \frac{dr}{d\tau }\right) ^{2} + U_{eff} = E^{2} \end{aligned}$$

where

$$\begin{aligned} U_{eff}= & {} \frac{1}{r^{2}}\left( L-a E\right) \left[ a E+L-\frac{\Lambda }{3}\left( L-a E\right) a^{2}\right] \nonumber \\&-\frac{2M}{r^{3}}(L-a E)^{2}\\&-\frac{\Lambda }{3}\left( L-a E\right) ^{2}+\frac{Q^{2}}{r^{4}}(L-a E)^{2}\nonumber \\&-\alpha (L-a E)^{2}r^{-3(1+\omega )} +\frac{\Delta _{r}}{r^{2}}\epsilon , \end{aligned}$$

is the effective potential. For circular motion (at constant radius $r=r_{0}$) of particles, the initial velocity $\dot{r}$ must be zero. The effective potential must attain minimum values for the case of stable circular orbits, i.e.,

$$\begin{aligned} \frac{\partial ^{2} U_{eff}}{\partial ^{2} r}|_{r=r_{0}}>0. \end{aligned}$$

For null geodesics, the radial equation for the specific case ($L=aE$) is $r=\pm E$. Thus, the effective potential of photon for $L\ne aE$ takes the form

$$\begin{aligned} U_{eff}= & {} \frac{1}{r^{2}}\left( L-a E\right) \left[ a E+L-\frac{\Lambda }{3}\left( L-a E\right) a^{2}\right] \nonumber \\&-\frac{2M}{r^{3}}\left( L-a E\right) ^{2}-\frac{\Lambda }{3}\left( L-a E\right) ^{2}\nonumber \\&+\frac{Q^{2}}{r^{4}}\left( L-a E\right) ^{2}-\alpha (L-a E)^{2}r^{-3(1+\omega )}. \end{aligned}$$

Figures 3 and 4 represent the graphical analysis of effective potential for null particles with $\omega =-\frac{2}{3}$ and $\omega =-\frac{1}{2}$, respectively. In both figures, the top panel, left graph is plotted for varying values of a. In Fig. 3, the curves have local maxima (unstable orbit) with $U_{eff}=0.84,0.46, 0.25, 0.13$ as well as in Fig. 4, $U_{eff}=0.88,0.48, 0.27, 0.16$ corresponding to $a=0.3,0.3,0.2,0$. In both figures, the curves tends to decrease near $r \approx 1.99$. The right graphs are plotted for the varying values of $\alpha$ and the maximum values $U_{eff}=1.76, 1.72, 1.56$ (Fig. 3) and $U_{eff}=1.52, 1.69, 1.76$ (Fig. 4) appear for $\alpha =0, 0.05, 0.16$ which are the points where orbit become unstable. The gradual decrease in $U_{eff}$ (for the increasing values of radius) leads to the stable motion of particles. In the lower panel, left and right graphs are plotted for different values of L and Q, respectively. It is noted that initially, the orbits exhibit unstable behavior for large values of angular momentum, but the motion becomes stable with the increases of radial distance r. For $Q=0.4, 0.3, 0$ the effective potential attains maximum values (unstable orbit) $U_{eff}=1.19,1.33,1.47$ (Fig. 3) and $U_{eff}=1.19,1.31,1.45$ (Fig. 4). However at $r\approx 1.6$ the curves coincide and diverging values leads to stable orbits.

Fig. 5

Plots of effective potential for time-like geodesics as a of function of r for $\omega =-\frac{2}{3}$

Fig. 6

Plots of effective potential for time-like geodesics as a function of r for $\omega =-\frac{1}{2}$

The analysis of effective potential for time-like particles with $\omega =-\frac{2}{3}$ and $\omega =-\frac{1}{2}$ is shown in Figs. 5 and 6, respectively. For the variation of a the curves coincide near $r\approx 2.6$ (Fig. 5) and $r\approx 2.3$ (Fig. 6) leading to unstable orbits. In Fig. 5, for $\alpha =0, 0.05, 0.16$, the curves attain maximum values $U_{eff}=0.79, 0.69, 0.49$ near $r\approx 0.81, 0.82,0.89$ and minimum values $U_{eff}=0.62, 0.52, 0.33$ near $r\approx 1.63, 1.7, 1.8$. Here, the particle remain marginally bound between two extreme values. In the left plot of bottom panel, there is a minimum point near $r\approx 0.7$ for $L=1.4$, also, the particle remain trapped in the region (between two turning points) $r=0.51-1.4$, $r=0.4-1.7$ and $r=0.25-1.73$ for $L=1.3,1.2,1.1$. The right graph in the bottom panel, plotted for the variation of $Q=0,0.3,0.4$. Near $r=0.1, 1,1,1.2$, effective potential has its maximum $U_{eff}=0.61,0.50,0.43$ and minimum $U_{eff}=0.51,0.48, 0.4$ near $r\approx 1.5,1.6,1.62$, showing the marginally bound orbit. The curves coincide at $r\approx 2.5$ and tend to increase.

In Fig. 6, left plot in the upper panel, maximum values $U_{eff}=0.82,0.71,0.51$ appear near $r\approx 0.79, 0.8,0.88$ (corresponding to $\alpha =0, 0.05, 0.16$) and minimum values $U_{eff}=0.60, 0.44$ exist near $r\approx 1.64, 1.72$ (for $\alpha =0, 0.05$). The marginally bound orbits are for $\alpha =0, 0.05$ and for $\alpha =0.16$ the curve diverges. In the left plot of the bottom panel, there is a minimum point $r\approx 0.86$ for $L=1.4$ and between two turning points, the particle is bound within the region $r=0.64-1.33$, $r=0.52-1.44$, $r=0.4-1.6$ and $r=0.25-1.72$ for $L=1.4,1.3,1.2,1.1$. In the right graph of bottom panel ($Q=0,0.3,0.4$), the particle confines in the region $r=0.88-1.37$, $r=1.1-1.42$ and $r=1.21-1.61$.

Next, we discuss the stability of orbits with respect to horizon, radius of photon sphere and the static radius.

In view of Figs. 3,  4 and using Tables 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10:

• For the variation of a, the stable points ($r\approx 1.99$) lie in the region $r_{h-}<r_{h+}<r<r_{po_1}<r_{po_2}<r_{s}<r_{c}$

• For the variation of $\alpha$, the stable points ($r\approx 2.6$) lie in the region $r_{h-}<r_{h+}<r_{po_1}<r<r_{po_2}<r_{s}<r_{c}$, when $\omega =\frac{-2}{3}$, $\alpha =0,0.0005,0.05$ and $r_{h-}<r_{h+}<r<r_{po_1}<r_{po_2}<r_{s}<r_{c}$, when $\omega =\frac{-2}{3}$, $\alpha =0.16$ as well as $r_{h-}<r_{h+}<r<r_{po_1}<r_{po_2}<r_{s}<r_{c}$, when $\omega =\frac{-1}{2}$, $\alpha =0,0.0005,0.05$ and $r_{h-}<r_{h+}<r_{po_1}<r<r_{po_2}<r_{s}<r_{c}$, when $\omega =\frac{-1}{2}$, $\alpha =0.16$

• For the variation of Q, the stable points ($r\approx 2.67$) lie in the region $r_{h-}<r_{h+}<r_{po_1}<r<r_{po_2}<r_{s}<r_{c}$, when $\omega =\frac{-2}{3}$, $Q=0,0.3,0.4$ whereas $r_{h-}<r_{h+}<r<r_{po_1}<r_{po_2}<r_{s}<r_{c}$, when $\omega =\frac{-2}{3}$, $Q=0.5$ and $r_{h-}<r_{h+}<r_{po_1}<r<r_{po_2}<r_{s}<r_{c}$, when $\omega =\frac{-1}{2}$

• For the variation of $L=1.1$ and $L=1.2,1.3,1.4$, the stable points $r\approx 0.7$ and $r\approx 1.65$ lie in the region $r_{h-}<r<r_{h+}<r_{po_1}<r_{po_2}<r_{s}<r_{c}$, when $\omega =\frac{-2}{3}$ and $\omega =\frac{-1}{2}$

  In view of Figs. 5, 6 and using Tables 5, 6, 7, 8, 9 and 10:

• For the variation of $\alpha$, the stable points ($r\approx 1.63,1.7,1.8$) lie in the region $r_{h-}<r<r_{h+}<r_{s}<r_{c}$, when $\omega =\frac{-2}{3},~\frac{-1}{2}$

• For the variation of Q, the stable points ($r\approx 1.5,1.6,1.62$) lie in the region $r_{h-}<r<r_{h+}<r_{s}<r_{c}$ when $\omega =\frac{-2}{3},~\frac{-1}{2}$

• For the variation of L, the stable points ($r\approx 0.42,0.6,0.75,0.8$) lie in the region $r_{h-}<r<r_{h+}<r_{s}<r_{c}$ when $\omega =\frac{-2}{3},~\frac{-1}{2}$

4 Energy extraction by penrose process

The process of energy extraction from rotating BHs is one of the topic of fundamental interest in GR. There are many other processes that are used to discuss the extraction of energy. The Penrose process is the most important among all of such process. In this procedure, when a particle with positive energy moves to the ergoregion (a region between stationary limit and the outer horizon), split into two parts, such that one of them with negative energy absorbed by the BH, while the other part escape to infinity. The escape one has more energy than that of the falling particle. The energy gain in this process is explained by the negative energy of the ergosphere-trapped particle absorbed by the BHs. In the next sections, we discuss the state of negative energy and the original Penrose process for the KNQdS BH.

4.1 The state of negative energy

The existence of particle with negative energy is a distinct feature of the ergoregion of any rotating source. Therefore, it is convenient to identify the limits on energy which a particle can posses at some particular location. Using the radial equation, we get

$$\begin{aligned}&E^{2}((r^{2}+a^{2})^{2}-a^{2} \Delta _{r})-2aEL(r^{2}+a^{2}-\Delta _{r})\nonumber \\&\quad -L^{2}(\Delta _{r}-a^{2})+\epsilon r^{2}\Delta _{r}=0. \end{aligned}$$

(31)

Solving Eq. (31) for E and L, we have

$$\begin{aligned} E= & {} \frac{a L\left( r^{2}+a^{2}-\Delta _{r}\right) \pm r \sqrt{\Delta _{r}\left( L^{2}r^{2}-\epsilon \left( \left( r^{2}+a^{2}\right) ^{2} -a^{2}\Delta _{r}\right) \right) }}{\left( r^{2}+a^{2}\right) ^{2}-a^{2}\Delta _{r}},\nonumber \\ \end{aligned}$$

(32)

$$\begin{aligned} L= & {} \frac{-a E\left( r^{2}+a^{2}-\Delta _{r}\right) \pm r \sqrt{\Delta _{r}\left( E^{2}r^{2}+\epsilon \left( \Delta _{r}-a^{2}\right) \right) }}{\Delta _{r}-a^{2}}. \end{aligned}$$

(33)

The following identity has been used to find the above results

$$\begin{aligned}&\left[ (r^{2}+a^{2})^{2}-a^{2}\Delta _{r}\right] \left[ \Delta _{r}-a^{2}\right] \nonumber \\&\quad =r^{4}\Delta _{r}-a^{2}\left( r^{2}+a^{2}-\Delta _{r}\right) ^{2}. \end{aligned}$$

(34)

From Eq. (32), we can inferred the conditions under which energy can be negative. First, we consider $E=1$ (with unit rest mass at infinity). We consider positive sign of Eq. (32) which requires $L<0$ for $E<0$ and

$$\begin{aligned}&a^{2}L^{2}\left( r^{2}+a^{2}-\Delta _{r}\right) ^{2}\nonumber \\&\quad >r^{2}\Delta _{r} \left[ L^{2}r^{2}-\epsilon \left( \left( r^{2}+a^{2}\right) ^{2}-a^{2}\Delta _{r}\right) \right] . \end{aligned}$$

(35)

Using Eq. (32), we can write

$$\begin{aligned} \left[ \left( r^{2}+a^{2}\right) ^{2}-a^{2}\Delta _{r}\right] \left[ L^{2}\left( \Delta _{r}-a^{2}\right) -\epsilon r^{2}\Delta _{r}\right] <0. \end{aligned}$$

It is clear from the above inequality that $L<0$ corresponds to $E<0$ and

$$\begin{aligned} \left( \frac{\Delta _{r}-a^{2}}{r^{2}}\right) <\frac{\epsilon \Delta _{r}}{L^{2}}. \end{aligned}$$

We observe that only counter rotating particles possess negative energy and it is essential that the particle must remain inside the ergosphere $r<a+M$. Figure 7 represents the nature of negative energy as a function of r. In the upper panel, the left and right graphs are plotted for different values of a and L, respectively. We also note that there is less negative energy with the increase of a. The variation of angular momentum leads to decrease in the negative energy and for the small values of angular momentum, it takes higher values. The left and right graphs in the lower panel are depicted for different values of $\alpha$ as well as Q, respectively. It is observed that negative energy shows decreasing behavior as $\alpha$ increases and it takes higher values for increasing values of $\alpha$. In the Penrose process, the produced particle has more negative energy in the presence of DE as compared to its absence. The right graph represents that the produced particles may have less negative energy for large values of Q.

Table 5 Static radius for $\omega =\frac{-2}{3}$

Table 6 Static radius for $\omega =\frac{-1}{2}$

Table 7 Inner($r_{h-}$) and outer ($r_{h+}$) for $\omega =\frac{-2}{3}$

Table 8 Inner ($r_{h-}$) and outer ($r_{h+}$) horizons for $\omega =\frac{-1}{2}$

Table 9 Cosmological horizon $r_{c}$ for $\omega =\frac{-2}{3}$

Table 10 Cosmological horizon $r_{c}$ for $\omega =\frac{-1}{2}$

Fig. 7

Negative energy as a function of r

4.2 The original penrose process

In the Penrose process, when a particle decompose into two photons, one of them is attracted towards the BH whereas the other escapes to infinity. We assume that the photon that is captured by the BH, possesses negative energy while the other (that escapes to infinity) has more energy than the original particle (that came from infinity). We assume that $E^{(x)}=1$, $L^{(x)}$; $E^{(y)}$, $L^{(y)}$ and $E^{(z)}$, $L^{(z)}$ represent the energies and angular momenta of the original particle coming from infinity and the two photons (one that escapes to infinity and the other which enters the event horizon). Using Eq. (33) and assuming $E=1$ and $\epsilon =1$, the angular momentum of the particle coming from infinity is obtained as

$$\begin{aligned} L= & {} \frac{-a (r^{2}+a^{2}-\Delta _{r})\pm r \sqrt{\Delta _{r}(r^{2}-\Delta _{r}+a^{2})}}{\Delta _{r}-a^{2}}\nonumber \\= & {} a^{(x)}. \end{aligned}$$

(36)

The relation between energy and angular momentum of photons (one which escapes to infinity and other that enters the event horizon) can be obtained by choosing the negative and positive signs in Eq. (33) as

$$\begin{aligned} L^{(y)}= & {} \frac{-a E^{(y)}(r^{2}+a^{2}-\Delta _{r})- E^{(y)} r^{2} \sqrt{\Delta _{r}}}{\Delta _{r}-a^{2}}\nonumber \\= & {} a^{(y)}E^{(y)}, \end{aligned}$$

(37)

$$\begin{aligned} L^{(z)}= & {} \frac{-a E^{(z)}(r^{2}+a^{2}-\Delta _{r})- E^{(z)} r^{2} \sqrt{\Delta _{r}}}{\Delta _{r}-a^{2}}\nonumber \\= & {} a^{(z)}E^{(z)}. \end{aligned}$$

(38)

From the conservation of energy as well as angular momentum, we have

$$\begin{aligned} E^{(x)}= & {} E^{(y)}+E^{(z)}, \end{aligned}$$

(39)

$$\begin{aligned} L^{(x)}= & {} a^{(x)}=L^{(y)}+L^{(z)}=a^{(y)}E^{(y)}+a^{(z)}E^{(z)}. \end{aligned}$$

(40)

Solving the Eqs. (39) and (40), we obtain

$$\begin{aligned} E^{(y)}=\frac{a^{(x)}-a^{(z)}}{a^{(y)}-a^{(z)}}, \quad E^{(z)}=\frac{a^{(y)}-a^{(x)}}{a^{(y)}-a^{(z)}}. \end{aligned}$$

Substituting the values of $a^{(x)}$, $a^{(y)}$ and $a^{(z)}$ from Eqs. (36)–(38), we obtain

$$\begin{aligned}&E^{(y)}=-\frac{1}{2}\left( \sqrt{\frac{\left( r^{2}+a^{2}\right) -\Delta _{r}}{r^{2}}}-1\right) ,\\&E^{(z)}=\frac{1}{2}\left( \sqrt{\frac{\left( r^{2}+a^{2}\right) -\Delta _{r}}{r^{2}}}-1\right) . \end{aligned}$$

The escaping photon has more energy in comparison with the original particle. The gained energy can be found as

$$\begin{aligned} \Delta E=\frac{1}{2}\left( \sqrt{\frac{\left( r^{2} +a^{2}\right) -\Delta _{r}}{r^{2}}}-1\right) =-E^{(x)}. \end{aligned}$$

According to the Penrose process, maximum energy can be achieved at the event horizon

$$\begin{aligned} \Delta E\le \frac{1}{2}\left( \sqrt{1+\frac{a^{2}-\Delta _{r}}{r_{+}^{2}}}-1\right) . \end{aligned}$$

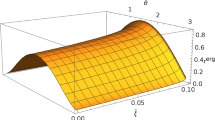
The graphical behavior of energy gain as a function of r is shown in Fig. 8. In the top panel, left graph is drawn for different values of Q. We found that there is a less energy gain for large values of Q but it takes higher values as the radius incresae. The right plot shows that the more energy can be gained during the Penrose process in the presence of DE. The lower graph is plotted for different values of a. It is noted that more energy can be gained when BH rotates rapidly.

Fig. 8

Plots of energy gain as a function of r

5 Summary and conclusion

In this work, we have explored the circular geodesics and energy extraction by Penrose process near a KNQdS BH. Geodesics play a significant role to illustrate the motion of particles near a BH. Circular geodesics are the fascinating one among different kinds of geodesics and are useful to understand the galaxy dynamics, accretion disk theory and planetary motion. The circular null geodesics are also very interesting as they transfer the astrophysical information from accretion disk to the observer.

We have explored both null as well as time-like geodesics and derived some important expressions for specific energy and angular momentum of a particle describing the motion in circular orbits. We have analyzed graphically the behavior of energy and angular momentum for both direct and retrograde motion. The graphs of energy have monotonic behavior and the descending and the rising curves correspond to the unstable and stable orbits slightly similar to Kerr dS BH [52]. We observe that for direct motion of orbits, the energy shows decreasing behavior with the increase of spin, but in the case of retrograde motion, it increases as rotation increases. This result contrasts with [53], where the energies of the quintessential rotating BH for co-rotating and counter rotating particle circular orbits initially decrease and then increase slightly for the large radius. We observe that particles for both direct and retrograde motion has less energy in the presence of DE as compared to its absence. The plots of angular momentum indicate that, it monotonically increases(decreases) for the direct(counter rotating) motion corresponding to stable orbits. However, the graphs do not contain turning points as compared to Kerr-dS BH [52]. It is worthily to mention that angular momentum corresponding to co-rotating orbits increases with large values of a, but for the counter rotating orbits, it has opposite behavior. There is less angular momentum for direct orbit as compared to the retrograde orbits in the presence of DE which agrees with quintessential rotating BH [53].

We have investigated the stability of orbits for both null and time-like particles by analyzing the effective potential. In both cases, we observe relative maxima(minima) which shows the existence of unstable(stable) orbits. However, the maximum as well as minimum values appear only once in a curve as compared to Kerr-dS BH [52]. We note that the presence of DE leads to the stable motion of particles and stability increases as DE increases. We observe that the particles can move in a stable region in the absence of charge. Moreover, the stability of orbits decreases as a increases. We note that orbits for time-like particles become more unstable with a small increase of DE while for null particles, it does not change much more. It is interesting to note that stability of orbits increases as Q increases.

We also discuss the stability regions with respect to photon orbits, static radius and the inner, outer as well as cosmological horizons. The properties of test particle motion around Schwarzschild-de Sitter as well as anti-de Sitter with respect to static radius are discussed in [61]. The static radius describe the scale for cosmic repulsion which plays a critical role in geodesic motion [62]. It has been observed that the so called static radius has a important role in dealing with small as well as large magellanic clouds [63]. Other important aspects are discussed in [64, 65]. We observe that the stable points (where the effective potential attains minimum values) never exceed the static radius in both null as well as time-like geodesics. In the case of null geodesics, by increasing the spin parameter, the stable pint lie near $r\approx 1.99$ (out side $r_{h-}$), whereas in KN NUT BH stable region came to exist by increasing the spin that lies in $r=0$ to $r_{h-}$ [66]. The stable and unstable photon orbits corresponding to the maxima and minima of the effective potential for both BH and naked singularity have been discuss in [67], however, in this paper we only concentrate on the stable as well as unstable rgions of the BH spacetime. For the variation of a, the stable points always exceeds photon orbit (direct rotating) similar to the case of marginally stable orbits [68] where the stability regions for photons orbits are discussed in detail.

We have discussed the Penrose process for KNdSQ BH. We have also analyzed the negative energy state and gain in energy during Penrose process. It is observed that the particles have more negative energy in the presence of DE but for large values of Q negative energy can be minimum. We note that the negative energy E decreases for the variation of $\alpha$ but for non-Kerr BH [54], it increases with the increase of deformation parameter. We also observe that the gain energy ($\Delta E$) gradually decreases to the increasing value of the charge which is similar to the dyonic KN BH [38]. However, the parameter $\alpha$ tends to increase the gain energy which resembles the non-Kerr BH [54] (where the maximum efficiency enhanced due to deformation parameter) and contrasts with the KN-Tuab NUT BH [36]. It is worthwhile to mention that, for $a=1$ and $\alpha =Q=\Lambda =0$, our result reduces to the extreme Kerr BH, i.e., $\Delta E=20.7\%$ [29]. It is concluded that more energy can be gained during the Penrose process in the vicinity of DE. There is a less energy gain for the large values Q but more energy could be gained with the increase of BH rotation.