Odderon effects in the differential cross-sections at Tevatron and LHC energies

Abstract

In the present paper, we extend the Froissaron-Maximal Odderon (FMO) approach at t different from 0. Our extended FMO approach gives an excellent description of the 3266 experimental points considered in a wide range of energies and momentum transferred. We show that the very interesting TOTEM results for proton–proton differential cross-section in the range 2.76–13 TeV, together with the Tevatron data for antiproton–proton at 1.8 and 1.96 TeV give further experimental evidence for the existence of the Odderon. One spectacular theoretical result is the fact that the difference in the dip-bump region between ${\bar{p}}p$ and pp differential cross-sections is diminishing with increasing energies and for very high energies (say 100 TeV), the difference between ${\bar{p}}p$ and pp in the dip-bump region is changing its sign: pp becomes bigger than ${\bar{p}}p$ at |t| about 1 GeV$^2$. This is a typical Odderon effect. Another important – phenomenological – result of our approach is that the slope in pp scattering has a different behavior in t than the slope in ${\bar{p}}p$ scattering. This is also a clear Odderon effect.

1 Introduction

The Odderon is certainly one the most important problems in strong interaction physics. It was introduced [1] in 1973 on the basis of asymptotic theorems [2, 3] and was rediscovered later in QCD [4,5,6,7,8]. In spite of the fact that its theoretical status is very solid, its experimental evidence from half a century is still scarce. This situation is not astonishing, The clear evidence for Odderon has to come by comparing the data at the same energy in hadron-hadron and antihadron-hadron scatterings. But we have not such accelerators! We therefore have to limit our search for evidence for the Odderon only in an indirect way. The search for the Odderon is crucial in order to confirm the validity of QCD. It is very fortunate that the TOTEM datum $\rho ^{pp} = 0.1\pm 0.01$ at 13 TeV [9] is the first experimental discovery of the Odderon at $t=0$, namely in its maximal form [10]. Moreover, we checked recently that just the Maximal Odderon in FMO approach is preferred by the experimental data. We generalized the FMO approach by relaxing the $\ln ^2s$ constraints both in the even- and odd-under-crossing amplitude and we show that, in spite of a considerable freedom of a large class of amplitudes, the best fits bring us back to the maximality of strong interaction [11].

In the present paper, we extend the FMO approach at t different from 0. We show that the very interesting TOTEM results for proton–proton differential cross-section in the range 2.76–13 TeV, together with the D0 data for antiproton–proton at 1.96 TeV give further experimental evidence for the existence of the Odderon.

2 Extension of the FMO approach at t different from zero: general definitions

In general amplitude of pp forward scattering is

$$\begin{aligned} F_{pp}(s,t) = F_+(s,t) + F_-(s,t) \end{aligned}$$

(1)

and the amplitude of antiproton–proton scattering is

$$\begin{aligned} F_{{\bar{p}}p}(s,t) = F_+(s,t) - F_-(s,t). \end{aligned}$$

(2)

In this model we used the following normalization of the physical amplitudes.

$$\begin{aligned} \sigma _t(s)= & {} \dfrac{1}{\sqrt{s (s-4m^2 )}}\text {Im} F(s,0), \nonumber \\ \dfrac{d\sigma _{el}}{dt}= & {} \dfrac{1}{64\pi ks(s-4m^2)}|F(s,t)|^2 \end{aligned}$$

(3)

where $k=0.3893797\,\, \text {mb}\,\,\text {GeV}^2$. With this normalization the amplitudes have dimension $\text {mb}\,\,\text {GeV}^2$.

Strictly speaking crossing-even (CE), $F_+(s,t)$, and crossing-odd (CO), $F_-(s,t)$, parts of amplitudes are defined as functions of $z_t=(t+2s-4m^2)/(4m^2-t)$, where m is proton mass, with the property

$$\begin{aligned} F_{\pm } (-z_t,t)=\pm F_{\pm } (z_t,t). \end{aligned}$$

(4)

In the FMO model CE and CO terms of amplitudes are defined as sums of the asymptotic contributions $F^H(s,t)$, $F^{MO}(s,t)$ and Regge pole contributions which are important at the intermediate and relatively low energies

$$\begin{aligned} F_+(z_t,t)= & {} F^H(z_t,t)+F^{R_+}(z_t,t), \nonumber \\ F_-(z_t,t)= & {} F^{MO}(z_t,t)+F^{R_-}(z_t,t) \end{aligned}$$

(5)

where $F^H(z_t,t)$ denotes the Froissaron contribution and $F^{MO}(z_t,t)$ denotes the Maximal Odderon contribution. Their specified form will be defined below.

3 Regge poles and their double rescatterings

In the FMO model in the terms $F^{R_{\pm }}(s,t)$ we consider not only single Regge pole contributions but also their double rescatterings or double cuts. Their contributions, $F^R_{pp}(z_t,t), F^R_{{\bar{p}}p}(z_t,t)$, are the following

$$\begin{aligned} F^R_{pp}(z_t,t)= & {} F^{_+}(z_t,t)+F^{_-}(z_t,t),\nonumber \\ F^R_{{\bar{p}}p}(z_t,t)= & {} F^{_+}(z_t,t)-F^{_-}(z_t,t) \end{aligned}$$

(6)

where $z_t=-1+2s/(4m^2-t)\approx 2s/(4m^2-t)$. For convenience in further work with parameterizations in FMO model at $t=0$ and $t\ne 0$ contrary to standard definition of $z_t$ we put opposite sign for it.

$$\begin{aligned} F^{_+}(z_t,t)= & {} F^P(z_t,t)+F^{R_+}(z_t,t)+F^{PP}(z_t,t)\nonumber \\&+F^{OO}(z_t,t),\nonumber \\ F^{_-}(z_t,t)= & {} F^O(z_t,t)+F^{R_-}(z_t,t)+F^{PO}(z_t,t). \end{aligned}$$

(7)

Here $F^P(z_t,t), F^O(z_t,t)$ are simple j-pole Pomeron and Odderon contributions and $F^{R_+}(z_t,t), F^{R_-}(z_t,t)$ are effective f and $\omega$ simple j-pole contributions, where j is an angular momenta of these reggeons. $F^{PP}(z_t,t)$, $F^{OO}(z_t,t),$ $F^{PO}(z_t,t),$ are double PP, OO, PO cuts, correspondingly. We consider the model at $t\ne 0$ and at energy $\sqrt{s}> 19$ GeV, so we neglect the rescatterings of secondary reggeons with P and O. In the considered kinematical region they are small. Besides, because f and $\omega$ are effective, they can take into account small effects from the cuts. The standard Regge pole contributions have the form

$$\begin{aligned} F^{R_\pm }(z_t,t)=-\left( {\begin{array}{c}1\\ i\end{array}}\right) 2m^2C^{R_\pm }(t)(-iz_t)^{\alpha _\pm (t)} \end{aligned}$$

(8)

where $R_\pm = P,O,R_+,R_-$ and $\alpha _P(0)=\alpha _O(0)=1$. The factor $2m^2$ is inserted in amplitudes $F^{R_\pm }(z_t,t)$ in order to have the normalization for amplitudes and dimension of coupling constants (in mb) coinciding with those in [10]. The same is made for all other amplitudes, including Froissaron and Maximal Odderon (see below).

For the coupling function $C^{R_\pm }(t)$ we have considered two possibilities. The first one is a simple exponential form. It is used for the secondary reggeons, because we did not consider low energies where terms $R_{\pm }(s,t)$ are more important.

$$\begin{aligned} C^{R_\pm }(t)=C^{R_\pm }e^{b^{R_{\pm }}t}, \qquad C^{R_\pm }(0)=C^{R_\pm }. \end{aligned}$$

(9)

The second case is a linear combination of exponents for Standard Pomeron and Odderon terms which allow to take into account some possible effects of non-exponential behavior of coupling function.

$$\begin{aligned} C^{P,O}(t)= & {} C^{P,O}\left[ \varPsi ^{P,O}(t) \right] ^2, \nonumber \\ \varPsi ^{P,O}(t)= & {} d_{p,o}e^{b_1^{P,O}t}+(1-d_{p,o})e^{b_2^{P,O}t}. \end{aligned}$$

(10)

We have added as well the double pomeron and odderon cuts, PP, OO, PO in their exact form without any new parameters. Namely,

$$\begin{aligned} F^{PP}(z_t,t)= & {} -i\dfrac{(z_tC^P)^2}{16\pi s\sqrt{1-4m^2/s}} \left\{ \dfrac{d_p^2}{2B_1^p}\exp (tB_1^p/2)\right. \nonumber \\&+\dfrac{2d_p(1-d_p)}{B_1^p+B_2^p}\exp \left( t\dfrac{B_1^pB_2^p}{B_1^p+B_2^p} \right) \nonumber \\&\left. +\dfrac{(1-d_p)^2}{2B_2^p}\exp (tB_2^p/2) \right\} \end{aligned}$$

(11)

$$\begin{aligned} F^{OO}(z_t,t)= & {} -i\dfrac{(z_tC^O)^2}{16\pi s\sqrt{1-4m^2/s}} \left\{ \dfrac{d_o^2}{2B_1^o}\exp (tB_1^o/2)\right. \nonumber \\&+\dfrac{2d_o(1-d_o)}{B_1^o+B_2^o}\exp \left( t\dfrac{B_1^oB_2^o}{B_1^o+B_2^o} \right) \nonumber \\&+\left. \dfrac{(1-d_o)^2}{2B_2^o}\exp (tB_2^o/2) \right\} \end{aligned}$$

(12)

where $B_k^{p,o}=b_k^{P.O}+\alpha '_{P,0}\ln (-iz_t),\quad k=1,2 , \quad b_k^{P,O}$ are the constants from single pomeron and odderon contributions.

$$\begin{aligned} F^{PO}(z_t,t)= & {} \dfrac{z_t^2C^PC^O}{16\pi s\sqrt{1-4m^2/s}} \nonumber \\&\times \left\{ \dfrac{d_pd_o}{B_1^p+B_1^o}\exp \left( t\dfrac{B_1^pB_1^o}{B_1^p+B_1^o}\right) \right. \nonumber \\&+ \dfrac{d_p(1-d_o)}{B_1^p+B_2^o}\exp \left( t\dfrac{B_1^pB_2^o}{B_1^p+B_2^o}\right) \nonumber \\&+\dfrac{(1-d_p)d_o}{B_2^p+B_1^o}\exp \left( t\dfrac{B_2^pB_1^o}{B_2^p+B_1^o}\right) \nonumber \\&+\left. \dfrac{(1-d_p)(1-d_o)}{B_2^p+B_2^o}\exp \left( t\dfrac{B_2^pB_2^o}{B_2^p+B_2^o}\right) \right\} \nonumber \\ \end{aligned}$$

(13)

We have found that for a better description of the data it is reasonable to add to the amplitudes the contributions which mimic some properties of ”hard“ pomeron ($P^H$) and odderon ($O^H$). We take them in the simplest form

$$\begin{aligned} P^H(t)= & {} i\dfrac{C^{PH}z_t}{(1-t/t_P)^{\mu _P} }, \quad \mu _P\le 4. \end{aligned}$$

(14)

$$\begin{aligned} P^O(t)= & {} \dfrac{C^{OH}z_t}{(1-t/t_O)^{\mu _OP} }, \quad \mu _O\le 4. \end{aligned}$$

(15)

4 Froissaron and Maximal Odderon at $t\ne 0$

4.1 Partial amplitudes for Froissaron and Odderon

Let us start from the Froissaron amplitude in (s, t)-representation at high s. The amplitude can be expanded in the series of partial amplitudes $\phi (\omega ,t)$. In accordance with the standard definition of partial amplitude

$$\begin{aligned} F(z_t,t)=16\pi \sum \limits _{j=0}^{\infty }(2j+1)P_j(-z_t)\phi (j,t). \end{aligned}$$

(16)

With such definition partial amplitude satisfies the unitarity equation in the form

$$\begin{aligned} \text {Im}\phi (j,t)= & {} \rho (t)|\phi (j,t)|^2+\text {inelastic contribution},\nonumber \\ \rho (t)= & {} \sqrt{1-4m^2/t} \end{aligned}$$

(17)

We use of the Sommerfeld–Watson transform amplitude (here and in what follows $\omega =j-1$ and j is complex angular momentum) which can be written as follows

$$\begin{aligned} F^\zeta (z_t,t)= & {} 16\pi \sum \limits _{\xi =-1,1} \int \limits _C\dfrac{d\omega }{2\pi i} (2\omega +3)\dfrac{1-\xi e^{-i\pi \omega }}{-\sin (\pi \omega ) }\nonumber \\&\times \phi ^\xi (\omega ,t) P_{1+\omega }(z_t) \nonumber \\= & {} 16\pi \sum \limits _{\xi =-1,1} \int \limits _C\dfrac{d\omega }{2\pi i} (2\omega +3)\nonumber \\&\times e^{-i\pi \omega /2}\dfrac{e^{i\pi \omega /2}-\xi e^{-i\pi \omega /2}}{-\sin (\pi \omega )}\phi ^\xi (\omega ,t)P_{1+\omega }(z_t)\nonumber \\= & {} z_t\sum \limits _{\xi =-1,1} \int \limits _C\dfrac{d\omega }{2\pi i}e^{\omega \zeta }\varphi ^\xi (\omega ,t). \end{aligned}$$

(18)

where $\omega =j-1$, $\xi$ is the signature of the term, contour C is a straight line parallel to imaginary axis and at the right of all singularities of $\phi ^\xi (\omega ,t)$, $\zeta =\ln (z_t)-i\pi /2 \equiv \ln (-iz_t)$ and

$$\begin{aligned} \varphi ^\xi (\omega ,t)= & {} 16\pi (2\omega +3)\dfrac{e^{i\pi \omega /2}-\xi e^{-i\pi \omega /2}}{-\sin (\pi \omega )}\pi ^{-1/2}2^{ \omega +1}\nonumber \\&\times \dfrac{\varGamma (\omega +3/2)}{\varGamma (\omega +2)}\phi ^\xi (\omega ,t) \end{aligned}$$

(19)

Thus for crossing even amplitude ($\xi$=+1) we have

$$\begin{aligned} \varphi ^+(\omega ,t)=i32\sqrt{\pi }(2\omega +3)\dfrac{\varGamma (\omega +3/2)}{\varGamma (\omega +2)}2^\omega \dfrac{\phi ^+(\omega ,t)}{\cos (\pi \omega /2)}\nonumber \\ \end{aligned}$$

(20)

and for crossing odd amplitude ($\xi$=-1)

$$\begin{aligned} \varphi ^-(\omega ,t)=-32\sqrt{\pi }(2\omega +3)\dfrac{\varGamma (\omega +3/2)}{\varGamma (\omega +2)}2^\omega \dfrac{\phi ^-(\omega ,t)}{\sin (\pi \omega /2)}.\nonumber \\ \end{aligned}$$

(21)

Inverse transformation is

$$\begin{aligned} \varphi ^\pm (\omega ,t)=\int \limits _0^\infty d\zeta e^{-\omega \zeta } F^\pm (z_t,t), \qquad z_t=e^\zeta . \end{aligned}$$

(22)

One can show that in order to have maximal growth of total cross section $\sigma _{tot}(s)\propto \xi ^2$ at $s\rightarrow \infty$, to have a growing elastic cross section bounded by

$$\begin{aligned} \sigma _{el}(s)/\sigma _{tot}(s)\rightarrow const \quad \text {at}\quad s\rightarrow \infty \end{aligned}$$

and to provide the correct analytical properties of amplitude at $t\approx 0$ necessary to write the partial amplitude $\phi (\omega ,t)$ in the following form (more details are given in the Appendix A)

$$\begin{aligned} \varphi ^\pm (\omega ,t )=\left( {\begin{array}{c}i\\ -1\end{array}}\right) \dfrac{\beta ^\pm (\omega , t)}{[\omega ^2+r_\pm ^2q_{\perp }^2]^{3/2}}. \end{aligned}$$

(23)

where $r_\pm$ are some constants, $q_{\perp }^2=-t$ and $\beta (\omega ,t)$ has not singularity at $\omega ^2+R^2q_{\perp }^2=0$. In fact a choice of the sign in $\phi ^-(\omega ,t)$ does nor matter because the crossing odd terms contribute to pp and ${\bar{p}}p$ amplitude with the opposite signs. In order to have agreement with parametrization and parameters which we used in the papers devoted to analysis of the data at $t=0$, we should replace -1 for for +1 in front of $\phi ^-(\omega ,t)$.

At $\omega =0$, function $\varphi ^-(\omega ,t)$ has singularity in t if $\beta ^-(0,t) \ne 0$, namely, $\phi ^-(0,t)\propto (-t)^{3/2}$. One of arguments against the Maximal Odderon is that this singularity in partial amplitude means the existing of massless particle in the model. However as we seen above $\varphi ^-(\omega ,t)$ is not the real physical partial amplitude which is

$$\begin{aligned} \phi ^-(\omega ,t)= & {} \left[ 32\sqrt{\pi }(2\omega +3)\dfrac{\varGamma (\omega +3/2)}{\varGamma (\omega +2)}2^\omega \right] ^{-1}\nonumber \\&\times \sin (\pi \omega /2)\varphi ^-(\omega ,t) \end{aligned}$$

(24)

and it equals to 0 at $\omega =0$ because of $\sin (\pi \omega /2)$ coming from signature factor.

Now let us suppose that in accordance with the structure of the singularity of $\varphi _\pm (\omega ,t)$ at $\omega ^2+\omega _{0\pm }^2=0$ ($\omega _{0\pm }^2= R_\pm ^2q_{\perp }^2)$ the functions $\beta _\pm (\omega ,t)$, depending on $\omega$ through the variable $\kappa _\pm =(\omega ^2+\omega _{0\pm }^2) ^{1/2}$, can be expanded in powers of $\kappa _\pm$

$$\begin{aligned} \varphi ^\pm (\omega ,t)=\left( {\begin{array}{c}i\\ 1\end{array}}\right) \dfrac{\beta _1^{\pm }(t)+\kappa _\pm \beta _2^{\pm }(t)+ \kappa _\pm ^2 \beta _3^{\pm }(t)}{\kappa _\pm ^{3}} \end{aligned}$$

(25)

Then making use of the table integrals (see the Appendix A) we obtain the expressions for $F^\pm (z_t,t)$ which are written in the next section.

4.2 Froissaron and Maximal Odderon in (s, t)-representation

At $t=0$ Froissaron and Maximal Odderon have the universal form independently of any extension to $t\ne 0$:

$$\begin{aligned} F^H(z_t,t=0)= & {} iz[H_1\ln ^2(-iz_t)\nonumber \\&+H_2\ln (-iz_t)+H_3], \end{aligned}$$

(26)

$$\begin{aligned} F^{MO}(z_t,t=0)= & {} z[O_1\ln ^2(-iz_t)\nonumber \\&+O_2\ln (-iz_t)+O_3] \end{aligned}$$

(27)

where $z=2m^2z_t$. At $t=0$ we have $z_t=(s-2m^2)/(2m^2)$.

The Froissaron and the Maximal Odderon defined at $t=0$ by above Eqs. (26, 27) allow various extensions to analytical t-dependences. Probably it is impossible a priory to choose the best of them. In the present work we consider an extension of Eqs. (26, 27) in accordance with Eq. (25).

$$\begin{aligned} \dfrac{-1}{iz}F^H(z_t,t)= & {} H_1\zeta ^2\dfrac{2J_{1}(r_{+}\tau \zeta )}{r_{+}\tau \zeta }\varPhi ^{2}_{H,1}(t) \nonumber \\&+H_2\zeta \dfrac{\sin (r_{+}\tau \zeta )}{r_+\tau \zeta }\varPhi ^{2}_{H,2}(t)\nonumber \\&+H_3J_0(r_{+}\tau \zeta )\varPhi ^{2}_{H,3}(t) ,\nonumber \\ \varPhi _{H,i}(t)= & {} \exp (b^H_iq_+),\quad i=1.2,3 \nonumber \\&q_+=2m_{\pi }-\sqrt{4m_{\pi }^2-t} . \end{aligned}$$

(28)

$$\begin{aligned} \dfrac{1}{z}F^{MO}(z_t,t)= & {} O_1\zeta ^2\dfrac{2J_{1}(r_{-}\tau \zeta )}{r_{-}\tau \zeta }\varPhi ^{2}_{O,1}(t) \nonumber \\&+ O_2\zeta \dfrac{\sin (r_{-}\tau \zeta )}{r_{-}\tau \zeta }\varPhi ^{2}_{O,2}(t)\nonumber \\&+O_3J_0(r_{-}\tau \zeta )\varPhi ^{2}_{O,3}(t),\nonumber \\ \varPhi _{O,i}(t)= & {} \exp (b^O_iq_-), \quad i=1,2,3,\nonumber \\ q_-= & {} 3m_{\pi }-\sqrt{9m_{\pi }^2-t}. \end{aligned}$$

(29)

where $z=2m^2z_t, \quad \zeta =\ln (-iz_t), \quad \tau =\sqrt{-t/t_0}, \quad t_0=1\text {GeV}^2$.

Due to the factor z (instead of $z_t$) the amplitudes $F^H(z_t,t)$ and $F^{MO}(z_t,t)$ have the required normalization with additional factor $2m^2$.

5 Comparison of the FMO model with the data

We give here the results of the fit to the data in the following region of s and |t|.

$$\begin{aligned} \begin{array}{llllll} \text {for} \quad \sigma _{tot}(s), \rho (s) \quad &{} \text {at} \quad 5 &{} \text {GeV} &{} \le \sqrt{s} &{} \le 13 &{} \text {TeV}, \\ \text {for} \quad d\sigma (s,t)/dt \quad &{} \text {at} \quad 9 &{} \text {GeV} &{} \le \sqrt{s} &{} \le 13 &{} \text {TeV}\\ \text {and} &{} \text {at} \quad 10^{-4} &{} \text {GeV}^2 &{} \le |t| &{} \le 5 &{} \text {GeV}^2. \end{array} \end{aligned}$$

We add the recent data at $t=0$ of TOTEM Collaboration [9, 12,13,14] to data set published by Particle Data Group [15].

We have performed two alternative fits of the FMO model and experimental data from the above mentioned kinematic region.

In the Fit I we take into account all the data at t = 0, i.e. $\sigma _{tot}$ and $\rho$ are calculated from the FMO model, free parameters are determined from the fit to all t, chosen in such a way that we can ignore in given region the contribution of the Coulomb part of amplitudes which is less than  1% of the nuclear amplitude. Thus, t-region $0.0<|t|<0.05$ GeV$^2$ is excluded in the Fit I, and the Coulomb part of amplitudes put to zero.

In the Fit II all experimental data on $\sigma _{tot}$ and $\rho$ are excluded and fit is made at energies $\sqrt{s}> 19$ GeV and $0<|t|< 5$ GeV$^2$. Taking into account that in this kinematic region parameters of CE and CO secondary reggeons are badly determined, we put all the parameters of these contributions as fixed from the results of Fit I.

Fig. 1

Total cross sections and ratios $\rho$ in FMO model with the PP, PO, OO terms added

For 13 TeV TOTEM data we used the data at $t=0$ for $\sigma _{tot}$ [12] and $\rho$ [9], as well as the data on differential cross sections [14, 16,17,18]. We add also recently published data on $d\sigma /dt$ at $\sqrt{s}=2.76$ TeV obtained by TOTEM [19].

5.1 Coulomb amplitude, one of the simplest parameterizations

Coulomb terms in the pp and ${\bar{p}}p$ amplitudes are written in the well known form

$$\begin{aligned} {{\mathcal {F}}}_{CN}(s,t)=\pm 8\pi s\dfrac{\alpha }{t}F_1^2(t)\exp (i\alpha \phi (s,t)) \end{aligned}$$

(30)

where $\alpha =7.297352 \times 10^{-3} = 1/137.035$ is the fine-structure constant and

$$\begin{aligned} F_1(t)= & {} \dfrac{4m_p^2-2.79t}{4m_p^2-t}\dfrac{1}{(1-t/0.71)^2}, \end{aligned}$$

(31)

For the phase $\phi (s,t)$ we nave

$$\begin{aligned} \phi (s,t)=\pm \left[ \ln \left( \dfrac{B(s)}{2}|t|\right) +\gamma \right] \end{aligned}$$

(32)

where $\gamma =0.5772156649$ is the Euler constant.

Fig. 2

pp differential cross sections at $\sqrt{s}>19$ GeV

Fig. 3

${\bar{p}}p$ differential cross sections at $\sqrt{s}$ from 19 GeV up to 1.96 TeV

Fig. 4

pp differential cross sections at $\sqrt{s}=7, 8, 13$ TeV

Fig. 5

Differential pp cross sections at the lowest |t| and at ISR energies

Fig. 6

Differential pp cross sections at the lowest |t| and at LHC energies

Fig. 7

Differential ${\bar{p}}p$ cross sections at the lowest |t|

Fig. 8

pp and ${\bar{p}}p$ differential cross sections at $\sqrt{s}=53$ GeV

Fig. 9

Evolution of pp and ${\bar{p}}p$ differential cross sections with increasing energy

Fig. 10

pp and ${\bar{p}}p$ differential cross sections in and around the dip region

Fig. 11

Evolution of the ratio of differential cross sections $R_{\sigma }=(d\sigma ({\bar{p}}p)/dt)/(d\sigma (pp)/dt)$ with energy

Fig. 12

Partial contributions of the real and imaginary parts of even and odd terms to pp and ${\bar{p}}p$ scattering amplitudes at various energies

The slope B(s) is calculated through a fit making use of the equation

$$\begin{aligned} {}\langle B(s)\rangle= & {} (1/\varDelta _t)\int \limits _{t_{max}}^{t_{min}}dt \,\dfrac{d}{dt}(\ln (d\sigma (t)/dt))\nonumber \\= & {} (1/\varDelta _t )\left[ \ln \left( \dfrac{d\sigma (t_{min})/dt}{d\sigma (t_{max})/dt}\right) \right] \end{aligned}$$

(33)

where $\varDelta _t=t_{max}-t_{min}$. We put (in accordance with the TOTEM estimations [16]), $t_{max}=-0.07$ GeV$^2$, $t_{min}=-0.005$ GeV$^2$.

5.2 pp and ${\bar{p}}p$ differential cross sections $d\sigma /dt$

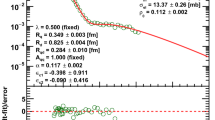
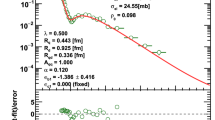
Here we present results for both methods of the data description. Fit I: FMO model without Coulumb term fitted to the whole set of data excluding lowest $|t|<0.05$ GeV$^2$. Fit II: FMO model with Coulomb term fitted to the whole set of the data at $t\ne 0$. In the legends of Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 ,10, 11 and 12 these fits are labeled as “FMO” and “FMO+C”, correspondingly. The curves shown at the Figs. 13, 14, 15 and 16 were calculated in the FMO model without Coulomb terms (Fit I).

Number of experimental points in pp and ${\bar{p}}p$ total cross sections $\sigma _t^{pp}, \sigma _t^{{\bar{p}}p}$, ratios $\rho ^{pp}, \rho ^{{\bar{p}}p}$ and differential cross sections used in the Fit I and quality of fit are shown in the Table 1.

Numbers of the data points and obtained values of $\chi {^2}$ in the Fit II are given in the Table 2.

The values of parameters and their errors obtained in these two fits within the FMO model are given in the Table 3 (parameters of the Froissaron and Maximal Odderon terms, of the standard Pomeron and Odderon, of the ”hard“Pomeron and Odderon, and of the secondary reggeons).

To avoid a possible negative cross sections in the large partial waves, j, (at the edge of the disk) we put in the fit the restriction $r_-\le r_+$. However, we observed that in the various considered modifications of the FMO model these parameters are almost equal each to other. Based on this fact we put $r_-= r_+$ in the model presented here. Also we have fixed the parameters $b^{\pm }$ at 0 because in all considered fits $b^+$ has the error comparable with the value of parameter and $b^-$ has value close to 0.

Figure 1 demonstrates a behavior of the pp and ${\bar{p}}p$ total cross sections and ratios real part to imaginary part of the amplitudes at $t=0$ obtained in the both Fit I and Fit II. We would like to notice the interesting odderon effect: the change of sign in the differences between total cross section and $\rho$’s between $\sqrt{s}\approx 50$ and $\sqrt{s}\approx 500$ GeV. Such a spectacular effect is allowed by asymptotic theorems. A detailed dynamic model for this effect was not yet invented.

Fig. 13

Slopes $B^{pp}(t)$ and $B^{{\bar{p}}p}(t)$ at increasing energy (left panel) and the s-dependence of the averaged slopes $<B^{pp}(s)>$, $<B^{{\bar{p}}p}(s)>$ together with experimental data (right panel)

Fig. 14

Slope B(s, t) for pp (left panel) and ${\bar{p}}p)$ (right panel) at selected energies

Fig. 15

Dependence on t of the slopes B(s, t) for pp scattering at 7 and 13 TeV and for ${\bar{p}}p$ scattering at 1.96 TeV

Fig. 16

${\bar{p}}p$ differential cross section at 1.18–1.96 TeV and pp differential cross section at 2.76 TeV

In Figs. 2 and 3 we show the differential cross-sections at energies bigger than 19 GeV. In Fig. 4 we show the differential cross-sections at the LHC energies 7, 8 and 13 TeV and in Figs. 5, 6, and 7 we show differential pp and ${\bar{p}}p$ at lowest |t|. In Fig. 8, we show in a magnified way the differential cross-sections at 53 GeV.

As one can see from these figures our description of the data in a wide range of energies is very good. In Fig. 9 we show the evolution of the dip-bump structure in pp and ${\bar{p}}p$ differential cross sections with increasing energy. In Fig. 10 we show in a magnified way the dip-bump region at different energies and in Fig. 11 we show the evolution of the ratio $R_\sigma = (d\sigma ({\bar{p}}p) /dt) / (d\sigma (pp)/dt)$ with increasing energy. A remarkable prediction can be seen from these last three figures: the difference in the dip-bump region between ${\bar{p}}p$ and pp differential cross sections is diminishing with increasing energies and, for very high energies (say 100 TeV, see Fig. 10), the ratio in the dip-bump region goes to 1. At ISR energies until $\sim 60$ GeV the ratio $R_\sigma > 1$ and then it becomes less than 1 but increases to maximum at some $t_m$. After maximum the value of $R_\sigma$ is decreasing and equals to 1 at some $t_1$ which is going to lower t with increasing energy. At higher t however $R_\sigma$ is oscillating around of 1 when t increases. This is a spectacular Odderon effect. One can see also the clear Odderon effects and their evolution with energy in Fig. 12.

6 Slope B(s, t)

The slope B(s, t) is a very interesting quantity in the search for Odderon effects. It is defined by

$$\begin{aligned} B(s,t)=\dfrac{d}{dt}\ln (d\sigma /dt). \end{aligned}$$

(34)

If we consider the dependence of slope on energy and compare this dependence with available experimental data we have to take into account that slopes in any realistic model depend on t. Dependence of slope on t at various energies in the FMO model is illustrated in Fig.  13 (left panel). Therefore we must to calculate the slope $\langle B(s)\rangle$ averaged in some interval of t. We did that in the interval $|t|\in (0.05, 0.2) \text {GeV}^2$ for GeV energies which approximately is in agreement to the intervals from which the experimental data on B are determined.

$$\begin{aligned} {}\langle B(s)\rangle= & {} (1/\varDelta _t)\int \limits _{t_{max}}^{t_{min}}dt \,\dfrac{d}{dt}(\ln (d\sigma (t)/dt))\nonumber \\= & {} (1/\varDelta _t )\left[ \ln \left( \dfrac{d\sigma (t_{min})/dt}{d\sigma (t_{max})/dt}\right) \right] \end{aligned}$$

(35)

where $\varDelta _t=t_{max}-t_{min}$.

Table 1 Number of experimental points and the quality of their description when the usual minimization in FMO model is applied

Table 2 Number of experimental points and the quality of their description when the fit with FMO+Coulomb terms is made. The data on $\sigma _{tot}(s)$ and $\rho (s)$ has been excluded from this fit

Table 3 Parameters of standard Pomeron and Odderon, of their double rescatterings, of secondary Reggeons and their errors in FMO model determined from the fits to the data on $d\sigma /dt$. Total cross sections $\sigma _{tot}$ and ratios $\rho$ were included in the fit without the Coulomb term

We show in Table 4 our predictions for the averaged slopes in the TeV region of energy as compared with experiments at Tevatron and LHC.

Table 4 Experimetal values of slopes of pp and ${\bar{p}}p$ differential cross sections at TeV energies and the averaged slopes calculated in FMO model

In Fig. 13 (right panel) we show the increasing of the averaged slopes at t=0 with increasing energy. One can see that the slopes are approaching the $\ln ^2s$ increase at high energies.

in pp and ${\bar{p}}p$ scatterings. We discover from the t-dependence of the slopes an extremely interesting phenomenon. The slope in pp scattering has a different behaviour in t than the slope in ${\bar{p}}p$ scattering. In the left panel of Fig. 14 we see that in pp scattering the slopes are first nearly constant and after that they fall sharply, they cut a first time the $B(t)=0$ line, reach a deep minimum negative value, after that they increase and cut a second time the $B(t)=0$ line and finally they reach an approximately constant value for higher t. The two crossing points of the $B(t)=0$ line move towards smaller t when energy increases. In the right panel of Fig. 14 we see a very different behaviour in ${\bar{p}}p$ scattering. In this case, at energies higher than ISR ones, B(t) marginally crosses zero, but no so deeply and sharply as in pp scattering. For completeness, we show in Fig. 15 the slope parameter for pp scattering at 7 and 13 TeV as compared with the slope parameter in ${\bar{p}}p$ scattering at 1.96 TeV, where we can see the same phenomenon.

This phenomenon is a clear Odderon effect. The odd-under crossing amplitude makes the difference between pp and ${\bar{p}}p$ scatterings and this amplitude is dominated at high energy by the Maximal Odderon.

7 Comparison with other approaches

To our knowledge, the present model is the only model which fits forward and non forward data in a wide range of energies (including TeV region), without theoretical defects (like the violation of the unitarity).

However, it is important to note that our results concerning the slopes are in complete agreement with those obtained recently by Csörgö et al. [20], who performed a very useful mirroring between the discontinuous experimental data (points) and continuous analytic functions (scattering amplitudes) by using an expansion in terms of Lévy polynomials. In such a way they get a very clear Odderon effect concerning the slopes. Their analysis have no dynamical content: it is a parametrization of experimental data in terms of big number of parameters.

This agreement is very important from two points of view. On one side, the Odderon existence is reinforced by two quite different analysis, one model-independent and the other one having a dynamical content.

On another side, the fact that the Maximal Odderon is in agreement with a model-independent analysis reinforce the status of the Maximal Odderon.

8 Conclusion

In our paper we present an extension of the Froissaron-Maximal Odderon (FMO) approach for t different from zero, which satisfies rigorous theoretical constraints. Our extended FMO approach gives an excellent description of the 3266¹ experimental points considered in a wide range of energies and momentum transferred. One spectacular theoretical result is the fact that the difference in the dip-bump region between ${\bar{p}}p$ and pp differential cross sections is diminishing with increasing energies and for very high energies (say 100 TeV), the difference in the dip-bump region between ${\bar{p}}p$ and pp is changing its sign: pp becomes bigger than ${\bar{p}}p$ at |t| about 1 GeV$^2$. This is a typical Odderon effect.

Another important – phenomenological – result of our approach is that the slope in pp scattering has a different behaviour in t than the slope in ${\bar{p}}p$ scattering. This is a clear Odderon effect.

Let us emphasize that the FMO model is in a good agreement with the data in a wide interval of energy. However, there is a some discrepancy of the data and model in a region around $\sqrt{s}$=2 TeV (it is illustrated in the Fig. 16). At the same time agreement with the data at lower and at higher energies is really very good. This problem requires a special investigation which we will perform after the publication of the common TOTEM/D0 paper [21].

New ways of detecting Odderon effects, e. g. in an Electron-Ion Collider, were recently explored on the basis of a general QCD light front formalism [22].

In Fig. 14 we plot the slopes as function of t

Appendix

1.1 General constraints

Let us reiterate here that the model with $\sigma _{t}(s)\propto \ln ^{2}s$ is not compatible with a linear pomeron trajectory having the intercept 1. Indeed, let us assume that

$$\begin{aligned} \alpha _{P}(t)=1+\alpha _{P}'t \end{aligned}$$

(36)

and the partial wave amplitude has the form

$$\begin{aligned} \varphi (j,t)= & {} \eta (j)\frac{\beta (j,t)}{\left[ j-1-\alpha _{P}'t\right] ^{n}}\approx \frac{i\beta (1,t)}{\left[ j-1-\alpha _{P}'t\right] ^{n}}, \end{aligned}$$

(37)

$$\begin{aligned} \eta (j)= & {} \frac{1+\xi e^{-i\pi j}}{-\sin \pi j}. \end{aligned}$$

(38)

For Pomeron (simple or double pole) and Froissaron signature is positive, $\xi =+1$.

In (s, t)-representation amplitude $\varphi (j,t)$ is transformed to

$$\begin{aligned} a(s,t)=\frac{1}{2\pi i}\int dj \varphi (j,t)e^{\xi j}, \quad \xi =\ln (s/s_{0}). \end{aligned}$$

(39)

Then, we have pomeron contribution at large s as

$$\begin{aligned} a(s,t)\approx -\tilde{\beta }(t)[\ln (-is/s_{0})]^{n-1}(-is/s_{0})^{1+\alpha '_{P}t} \end{aligned}$$

(40)

where

$$\begin{aligned} {{\tilde{\beta }}}(t)=\beta (t)/\sin (\pi \alpha _{P}(t)/2). \end{aligned}$$

(41)

If as usually ${{\tilde{\beta }}}(t)={{\tilde{\beta }}}\exp (bt)$ then we obtain

$$\begin{aligned} \sigma _{t}(s)&\propto \ln ^{n-1}s,\nonumber \\ \sigma _{el}(s)&\propto \frac{1}{s^{2}}\int \limits _{-\infty }^{0}dt|a(s,t)|^{2}\propto \ln ^{2n-3}s. \end{aligned}$$

(42)

According to the obvious inequality,

$$\begin{aligned} \sigma _{el}(s)\le \sigma _{t}(s) \end{aligned}$$

(43)

we have

$$\begin{aligned} 2n-3\le n-1 \qquad \Rightarrow \qquad n\le 2. \end{aligned}$$

(44)

Thus we come to the conclusion that the a model with $\sigma _{t}(s)\propto \ln ^{2}s$ (n=3) is incompatible with a linear pomeron trajectory. In other words the partial amplitude Eq. (37) with $n=3$ is incorrect.

If $n=1$ we have a simple j-pole leading to constant total cross section and vanishing at $s\rightarrow \infty$ elastic cross section. However such a behaviour of the cross sections is not supported by experimental data.

If $n=2$ we have the model of dipole pomeron ($\sigma _{t}(s)\propto \ln (s)$) and would like to emphasize that double j-pole is the maximal singularity of partial amplitude settled by unitarity bound (43) if its trajectory is linear at $t\approx 0$.

We would like to notice here that TOTEM data for the pp total cross section exclude the dipole pomeron model which is unable to describe with a reasonable $\chi ^2$ the high values of $\sigma ^{pp}_{tot}(s)$ at LHC energies.

Thus, constructing the model leading to cross section which increases faster than $\ln (s)$, we need to consider a more complicated case (we consider at the moment a region of small t and $j\approx 1$):

$$\begin{aligned} \varphi _+(j,t)= & {} \dfrac{\beta (j,t)}{\left[ j-1+r(-t)^{1/\mu }\right] ^{n}}\nonumber \\\approx & {} \dfrac{i\beta (1,t)}{\left[ j-1+r(-t)^{1/\mu }\right] ^{n}}. \end{aligned}$$

(45)

Making use of the same arguments as above, we obtain

$$\begin{aligned}&\sigma _{t}(s)\propto \ln ^{n-1}s, \end{aligned}$$

(46)

$$\begin{aligned}&\sigma _{el}(s)\propto \ln ^{2n-2-\mu }s \qquad \text{ and } \qquad \mu \ge n-1. \end{aligned}$$

(47)

However in this case amplitude a(s, t) has a branch point at $t=0$ which is forbidden by analyticity of amplitude a(s, t).

A proper form of amplitude leading to $t_{eff}$² decreasing faster than $\ln ^{-1}s$ (it is necessary for $\sigma _{t}$ rising faster than $\ln s$) is the following

$$\begin{aligned} \varphi _+ (j,t)=\dfrac{\beta (j,t)}{\left[ (j-1)^{m}-rt\right] ^{n}}. \end{aligned}$$

(48)

Now we have m branch points colliding at $t=0$ in j-plane and creating the pole of order mn at $j=1$ (but there is no branch point in t at $t=0$). At the same time $t_{eff}\propto 1/\ln ^{m}s$ and from $\sigma _{el}\propto \ln ^{2mn-2-m}s\le \sigma _{t}\propto \ln ^{mn-1}s\le \ln ^{2}s$ one obtains

$$\begin{aligned} \left\{ \begin{array}{ll} mn &{}\le m+1, \\ mn &{}\le 3. \end{array} \right. \end{aligned}$$

(49)

If $\sigma _{el}\propto \sigma _{t}$ then $n=1+1/m$. Furthermore, if $\sigma _{t}\propto \ln s$ then $m=1$ and $n=2$ which corresponds just to the dipole pomeron model. In the Froissaron (or tripole pomeron) model $m=2$ and $n=3/2$. It means that $\sigma _{t}\propto \ln ^{2}s$.

1.2 Partial amplitudes

As it follows from Eq.(49) for the dominating at $s\rightarrow \infty$ contribution in a Froissaron model with $\sigma _{t}(s)\propto \ln ^{2}(s)$, i.e. $n=2$, $m=3/2$, we have to take (here and in what follows we used a more convenient notations $\omega =j-1$ and $\omega _{0\pm }=r_\pm \tau =r_\pm \sqrt{-t/t_0},\quad t_0=1 \text {GeV}^2$). Then

$$\begin{aligned} \varphi _{\pm }(\omega ,t)= & {} \eta _{\pm } (\omega )\dfrac{\beta _{\pm }(\omega ,t)}{(\omega ^{2}+\omega _{0\pm }^2)^{3/2}}\nonumber \\= & {} \left( {\begin{array}{c}i\\ 1\end{array}}\right) e^{-i\pi \omega /2} \dfrac{\tilde{\beta }_\pm (\omega ,t)}{(\omega ^{2}+\omega _{0\pm }^2)^{3/2}} \end{aligned}$$

(50)

where

$$\begin{aligned} \eta _\pm (\omega )=\frac{1\mp e^{-i\pi \omega } }{\sin \pi \omega }. \end{aligned}$$

(51)

For even signature

$$\begin{aligned} {{\tilde{\beta }}}_+(\omega ,t)=\beta _+(\omega ,t)/\cos (\omega \pi /2) \end{aligned}$$

(52)

and for odd signature

$$\begin{aligned} {{\tilde{\beta }}}_-(\omega ,t)=\beta _-(\omega ,t)/\sin (\omega \pi /2). \end{aligned}$$

(53)

Now let us suppose that in agreement with the structure of the singularity of $\phi _\pm (\omega ,t)$ at $\omega ^2+\omega _{0\pm }^2=0$ the functions ${{\tilde{\beta }}}_\pm (\omega ,t)$ depend on $\omega$ through the variable $\kappa _\pm =(\omega ^2+\omega _{0\pm }^2) ^{1/2}$ and it can be expanded in powers of $\kappa _\pm$

$$\begin{aligned} \phi _\pm (\omega ,t)=\left( {\begin{array}{c}i\\ 1\end{array}}\right) e^{-i\pi \omega /2}\dfrac{\tilde{\beta }_{1\pm }(t)+\kappa _\pm {{\tilde{\beta }}}_{2\pm }(t)+ \kappa _\pm ^2 {{\tilde{\beta }}}_{3\pm }(t)}{\kappa _\pm ^{3}}.\nonumber \\ \end{aligned}$$

(54)

There are a different ways to add to partial amplitude $\varphi (j,t)$ terms which at $s\rightarrow \infty$ are small corrections (they can be named as subasymptotic terms).

Thus we can expand the “residue” $\beta (\omega ,t)$ in powers of $\omega$ (if $\beta (\omega ,t)$ has not branch point in $\omega$ at $\omega =0$) or in powers of $(\omega ^2+\omega _0^2)^{1/2}$. Then, for the first case

$$\begin{aligned} {{\tilde{\beta }}}(\omega ,t)={{\tilde{\beta }}}_1(t)+\omega \tilde{\beta }_2(t)+\omega ^2{{\tilde{\beta }}}_3(t), \end{aligned}$$

(55)

and in the second case we have (just this case is explored in the Sect. 4.2)

$$\begin{aligned} {{\tilde{\beta }}}(\omega ,t)={{\tilde{\beta }}}_1(t)+(\omega ^2+\omega _0^2)^{1/2} {{\tilde{\beta }}}_2(t)+(\omega ^2+\omega _0^2) {{\tilde{\beta }}}_3(t).\nonumber \\ \end{aligned}$$

(56)

Let us notice that the main terms in $\varphi (j,t)\equiv \varphi (\omega ,t)$ for both cases are coinciding having a pair of branch points colliding at $\omega _0=0\quad (t=0)$ and generating a triple pole in partial amplitude.

Taking into account the table integrals

$$\begin{aligned} \int \limits _{0}^{\infty } dx x^{\alpha -1}e^{-\omega x}{} \textit{J}_{\nu }(\omega _{0}x)=I_{\nu }^{\alpha }(\omega , \omega _0) \end{aligned}$$

(57)

where

$$\begin{aligned} I_{\nu }^{\nu +1}= & {} \dfrac{(2\omega _{0})^{\nu }}{\sqrt{\pi } \dfrac{\varGamma (\nu +1/2)}{(\omega ^{2}+\omega _{0}^{2})^{\nu +1/2}}},\nonumber \\ I_{\nu }^{\nu +2}= & {} 2\omega \dfrac{(2\omega _{0})^{\nu }}{\sqrt{\pi } \dfrac{\varGamma (\nu +3/2)}{(\omega ^{2}+\omega _{0}^{2})^{\nu +3/2}}}, \end{aligned}$$

(58)

one can find

$$\begin{aligned} \dfrac{1}{(\omega ^{2}+\omega _{0}^{2})^{3/2}}&=\dfrac{1}{\omega _{0}} \int \limits _{0}^{\infty } dx xe^{-x\omega }J_{1}(\omega _{0}x), \nonumber \\ \int \limits _C \dfrac{d\omega }{2\pi i} \dfrac{e^{\xi \omega }}{(\omega ^2+\omega _0^2)^{3/2}}&= \dfrac{J_1(\omega _0\xi )}{\omega _0\xi }. \end{aligned}$$

(59)

$$\begin{aligned} \dfrac{1}{\omega ^{2}+\omega _{0}^{2}}&=\dfrac{1}{\omega _{0}}\int \limits _{0}^{\infty } dx e^{-x\omega }\sin (x\omega _{0}), \nonumber \\ \int \limits _C \dfrac{d\omega }{2\pi i} \dfrac{e^{\xi \omega }}{\omega ^2+\omega _0^2}&= \dfrac{\sin (\omega _0\xi )}{\omega _0\xi }. \end{aligned}$$

(60)

$$\begin{aligned} \dfrac{1}{(\omega ^{2}+\omega _{0}^{2})^{1/2}}&=\int \limits _{0}^{\infty } dx e^{-x\omega }J_{0}(\omega _{0}x), \nonumber \\ \int \limits _C \dfrac{d\omega }{2\pi i} \dfrac{e^{\xi \omega }}{(\omega ^2+\omega _0^2)^{1/2}}&= J_0(\omega _0\xi ). \end{aligned}$$

(61)