1 Introduction

New heavy vector bosons V and light scalars a are common predictions of different scenarios of physics beyond the Standard Model (SM). The former appear in extensions of the SM gauge group, including theories of grand unification [1,2,3,4,5] and string constructions [6]. They are also natural in composite sectors [7,8,9,10] and their holographic relatives [11, 12]. Recently, new vectors at the TeV scale have been also proposed as a plausible explanation [13] of the anomalies observed in the branching fractions, angular distributions and lepton universality tests of the decays \(B^{+(0)}\rightarrow K^{+(*)}\ell ^+\ell ^-\) [14,15,16,17,18,19,20,21,22]. Models predicting ultralight scalars a have been studied [23] for collider phenomenology. Likewise, they have been also studied in light of the observed disagreement between the predicted and the observed values of the anomalous magnetic moment of the muon [24, 25].

Perhaps, the most traditional scenario involving both new scalars and vectors consists of a new strongly interacting sector extending the SM. In this case, V and a play the role of the \(\rho \) and \(\pi \) mesons in QCD. The separation of these scales is explained by the pseudo-Nambu Goldstone boson nature of the latter. We show that rare B decays can be naturally expected in this context. In the situation where the scalar decays to two muons, these include \(B^0_{(s)}\rightarrow aa\), which have already been searched for at LHCb [26], as well as \(B^{+/0} \rightarrow M aa\) with \(M=K^+, D^+, K^*\).

Fig. 1
figure 1

Diagrams of the decays \(B_s^0 \rightarrow aa\) (left) and \(B^+ \rightarrow K^+ a a\) (right) mediated by a heavy vector boson V

Full size image

In this article, we perform simulations to estimate the reach of the LHCb experiment to the aforementioned processes with the currently available data as well as with the anticipated upgrades. Our choice of parameters is motivated by the B and \((g-2)_\mu \) anomalies. However, our results are of much broader applicability. The paper is organized as follows. In Sect. 2 we introduce the generic Lagrangian we are interested in; we comment on constraints on the different parameters and compute the amplitudes for the different B decays. In Sect. 2.1, we match a particular composite Higgs model to the Lagrangian above. We study the new rare B meson decays in Sect. 3. We subsequently interpret these results in the model introduced before. Finally, we conclude in Sect. 4.

2 Generic Lagrangian

Let us extend the SM with a new vector boson V and a new scalar a with masses of the order of TeV and GeV, respectively. They are both singlets of the SM gauge group. At energies below the electroweak scale \(v\sim 246\) GeV, the Lagrangian we are interested in is

$$\begin{aligned} L&= \frac{1}{2}m_V^2 V_\mu V^\mu + \frac{1}{2}m_a^2 a^2 \nonumber \\&\quad +\,V_\mu \left[ g^u_{ij} (\overline{u_L^i}\gamma ^\mu u_L^j) + g^d_{ij} (\overline{d_L^i}\gamma ^\mu d_L^j) + \text {h.c.}\right] \nonumber \\&\quad +\, g_{ij}^ea \left[ \overline{l_L^i} e_R^j + \text {h.c.}\right] +g' V_\mu (a\partial ^\mu a). \end{aligned}$$
(2.1)

where \(u_L^i, d_L^i\) stand for the i-th family of left-handed up and down quarks, and \(l_L^i, e_R^i\) stand for the i-th family of left- and right-handed leptons, respectively. Inspired by recently observed flavour anomalies, we will focus mostly on the case in which the only non-vanishing g coupling is \(g_{23}^d\). To a lesser extent, we will also consider \(g_{13}^d\ne 0\). These couplings are constrained by measurements of \(\Delta M_s\) and \(\Delta M_d\) [27], respectively. Thus, for \(m_V = 1\) TeV, \(g_{23}^d \lesssim 0.002\) and \(g_{13}^d\) is bounded to be about one order of magnitude smaller.

Together with a non-vanishing \(g'\), these couplings trigger rare B decays as shown in Fig. 1. The decay width for \(B_s^0\rightarrow aa\) is

$$\begin{aligned} \Gamma = \frac{f_B^2}{32 \pi m_V^4} (g_{23}^d g')^2 m_B^3 \sqrt{1-\frac{4 m_a^2}{m_B^2}}, \end{aligned}$$
(2.2)

with \(f_B \sim 0.23\) GeV [28]. Similar expressions hold for other decay modes, e.g. \(B^0\rightarrow a a\).

The amplitude for \(B^+\rightarrow K^+ a a\) reads:

$$\begin{aligned} {\mathcal {M}} = \frac{g_{23}^d g'}{m_V^2} \langle K(p_3)|{\overline{s}}\gamma _\mu b|B(p)\rangle (p_1+p_2)^\mu \end{aligned}$$
(2.3)

with [29]

$$\begin{aligned}&\langle K(p_3)|{\overline{s}}\gamma _\mu b|B(p)\rangle \nonumber \\&\quad = f_+^P(q^2) \left[ (p+p_3)_\mu - \frac{m_{B}^2-m_K^2}{q^2}q_\mu \right] \nonumber \\&\qquad + \, f_0(q^2)\frac{m_{B}^2-m_K^2}{q^2}q_\mu . \end{aligned}$$
(2.4)

The transferred momentum is \(q^2 = (p-p_3)^2\), and varies between \(q^2_\text {min} = 4 m_a^2\) and \(q^2_\text {max} = (m_{B}-m_K)^2\). The contraction of this matrix element with \((p_1+p_2) = q\) in the amplitude annihilates the \(f_+^P(q^2)\) part. Altogether, we obtain

$$\begin{aligned} \frac{d\Gamma }{dq^2} = \frac{(g_{23}^d g')^2}{512\pi ^3 m_V^4 m_{B}^3} (m_{B}^2-m_K^2)^2 F(q^2), \end{aligned}$$
(2.5)

with

$$\begin{aligned} F(q^2)\equiv & {} \sqrt{m_{B}^4 + (m_K^2-q^2)^2 - 2m_{B^+}^2 (m_K^2+q^2)} \nonumber \\&\times \sqrt{1-\frac{4m_a^2}{q^2}} |f_0(q^2)|^2. \end{aligned}$$
(2.6)

In the approximation \(m_K,m_a\rightarrow 0\), \(f_0(q^2)\rightarrow 1\), one easily obtains

$$\begin{aligned} \Gamma \sim \frac{(g_{23}^d g')^2}{1024 \pi ^3 m_V^4} m_B^5. \end{aligned}$$
(2.7)

Following Ref. [29], we parametrize the form factor as \(f_0(q^2) = r_2/(1-q^2/m_\text {fit}^2)\), with \(r_2 = 0.330\) and \(m^2_\text {fit} = 37.46\) \(\hbox {GeV}^2\); see Fig. 2. Similar expressions hold for other processes, e.g. \(B^0\rightarrow K^{*0}a a\) or \(B_c^+\rightarrow D^+ a a\). The latter is however hard to test at the LHCb and we will not consider it. The reason is that the \(B_c^+\) production cross section is much smaller and the \(B_c^+\) width is larger (which reduces both the impact of the new interactions and the experimental efficiency).

Fig. 2
figure 2

Left: scalar momentum form factor for \(B^+\rightarrow K^+\) as a function of the transferred momentum \(q^2\). Right: differential branching ratio for \(B^+\rightarrow K^+ a a\) as a function of the momentum transferred \(q^2\). In both cases, we have fixed \(m_V = 1\) TeV, \(m_a = 1\) GeV, \(g_{23}=g'=1\)

Full size image

We note also that final states containing one meson and aa can probe effective operators containing four quarks and two light scalars (12 of these operators are present in the SM effective field theory extended with a [30]). One can easily estimate \(\Gamma (B^+\rightarrow K^+ a a)\sim (\text {few}\,\text {GeV})^9 /\Lambda ^8\), which is of the order of \(10^{-11}\) provided \(\Lambda \lesssim 1\) TeV. For this reason, we will also consider the channel \(B^+\rightarrow D^+ a a\). It tests operators such as \({\mathcal {O}}\sim 1/\Lambda ^4 a^2 (\overline{u_R}\gamma _\mu b_R) (\overline{d_R}\gamma ^\mu c_R)+\text {h.c.}\)

We will assume that a decays into muons with a width smaller than \(\sim 10\) MeV and a lifetime shorter than \(\sim 10\) fs. In this case, it will appear not to have any experimentally measurable flight distance and will appear to have zero width. This is easily achieved if a is muonphilic with \(10^{-5}\lesssim g_{22}^e\lesssim 1\). The processes discussed so far leads therefore to four-muon final states with and without additional mesons and with the muons forming pairs of two identical masses.

2.1 Explicit model

Light scalars are natural within CHMs, for they are approximate Nambu-Goldstone Bosons (NGBs) arising from the spontaneous symmetry breaking \({\mathcal {G}}/{\mathcal {H}}\) in the confinement of a new strong sector at a scale \(f\sim \) TeV. The simplest coset delivering the four Higgs degrees of freedom as well as a new scalar singlet a is SO(6) / SO(5) [31]. Interestingly, it can be UV completed in four dimensions [32].

In this model, the SM fermions do not couple directly to the Higgs boson. They rather mix with other composite resonances that do interact with the Higgs boson. Thus, the Yukawa Lagrangian depends on the quantum numbers of the aforementioned resonances. As a simple yet realistic example, we assume that the second generation leptons mix with two fundamental representations \({\mathbf {6}}\) of SO(6). An equivalent description is the embedding of the elementary leptons into incomplete fundamental representations of SO(6). The most general such embedding depends on a single positive parameter \(\gamma \) to give

$$\begin{aligned} \text {L}_L= & {} (-\text {i}\mu _L, \mu _L, \text {i}\nu _L, \nu _L, 0, 0), \quad \nonumber \\ \text {L}_R= & {} (0, 0, 0, 0, \gamma \mu _R, \mu _R). \end{aligned}$$
(2.8)

Using the corresponding Goldstone matrix

$$\begin{aligned} \text {U}= & {} \left[ \begin{array}{cccc} 1_{3\times 3} &{} &{} &{} \\ &{}1-h^2/(f^2+\Pi ) &{} -ha/(f^2+\Pi ) &{} h/f\\ &{}-ha/(f^2+\Pi ) &{} 1 -a^2/(f^2+\Pi ) &{} a/f\\ &{}-h/f &{} -a/f &{} \Pi /f^2 \end{array}\right] , \nonumber \\ \Pi= & {} f^2\left( 1-\frac{h^2}{f^2}-\frac{a^2}{f^2}\right) ^{1/2}, \end{aligned}$$
(2.9)

one obtains the leading-order Yukawa Lagrangian

$$\begin{aligned} L =&-\frac{y_\mu }{\sqrt{2}} f\overline{(U^T \text {L}_L)_1} (U^T \text {L}_R)_1 + \text {h.c.} \nonumber \\ =&-\frac{1}{\sqrt{2}} y_\mu \overline{\mu _L} h\mu _R\left[ 1 + \frac{\gamma }{f}a + \cdots \right] + \text {h.c.} \end{aligned}$$
(2.10)

The coupling \(y_\mu \sim 6\times 10^{-4}\) stands for the muon Yukawa. The subindex in \((U^T \text {L}_R)_1 \) indicates the projection of the fundamental representation of SO(6) into the singlet of SO(5) according to the decomposition \({\mathbf {6}} = 1+ {\mathbf {5}}\). The ellipsis stands for terms containing higher powers of a. Likewise, the one-loop induced potential for a reads:

$$\begin{aligned} V&= c_R f^4 y_\mu ^2 (U^T\Lambda _R)_1 (U^T \Lambda _R)_1 \nonumber \\&\quad +\, c_L f^4 y_\mu ^2 (U^T\Lambda _L^I)_1 (U^T \Lambda _{I L})_1\nonumber \\&\sim c_R f^2 y_\mu ^2\left( \gamma ^2-1\right) a^2+\cdots \end{aligned}$$
(2.11)

where we have neglected terms not involving a. \(\Lambda _R\) stands for \(\hbox {L}_R/\mu _R\); analogously for \(\Lambda _L^I\) with I the flavour index. \(c_R\) is a free parameter encoding the details of the strong sectors. Its size can be estimated using naive power counting [33], \(c_R\sim g_*^2/(32\pi ^2)\), with \(1\lesssim g_*\lesssim \sqrt{4\pi }\) the typical coupling between resonances. All in all, we obtain

$$\begin{aligned} m_a&\sim \frac{g_\rho y_\mu }{4\pi } \sqrt{(\gamma ^2-1)}\, f, \end{aligned}$$
(2.12)
$$\begin{aligned} g_{22}^e&\sim \frac{m_\mu }{f}\gamma . \end{aligned}$$
(2.13)

The scalar a decays 100% into muons. The other fermions respect this phenomenology provided they do not break the shift symmetry \(a\rightarrow a+\text {constant}\), nor \(a\rightarrow -a\). These two conditions can hold simultaneously if the left (right) chiralities mix with e.g. \({\mathbf {6}}\) (1), \({\mathbf {6}}\) (\({\mathbf {15}}\)) or \({\mathbf {6}}\) (\(\mathbf {20'}\)).

The scalar defined above can explain the longstanding anomaly on the magnetic moment of the muon [25]. In this concrete model, we can fit the experimental measurement \((\Delta a_\mu )_\text {obs} = (2.74\pm 0.73)\times 10^{-9}\) [34] within two standard deviations for \(g_* = 2\) and \(f = 800\) GeV and \(\gamma \gtrsim 10\). Fitting the experimental observation within one standard deviation is in principle possible, but it requires even larger values of \(\gamma \), too small values of \(g_*\) (which would contradict the strongly coupled nature of the composite sector) and \(f \lesssim 800\) GeV (which is in tension with Higgs and electroweak precision data [35]). Therefore, the value \(m_a \sim 1\) GeV is a very likely value in this setup.

New composite vector bosons V explaining the observed anomalies in \(R_{K^{(*)}}\) appear also naturally in this framework [36,37,38,39,40,41,42,43,44,45]. These particles decay preferably into composite states [44], being too broad and too heavy to be directly detected unless very dedicated LHC analyses are performed for masses \(m_{V}\lesssim 3\) TeV [44].Footnote 1

The interaction with the SM fermions takes the form of Eq. 2.1, with \(g^d_{23}\sim 0.002\, m_V^2/\text {TeV}^2\) [44, 46]. Relying on these results, we consider for reference the benchmark point

$$\begin{aligned} \text {BP}: m_a = 1~\text {GeV}, ~ m_V = 4~\text {TeV}, ~ g_{23}^d \sim 0.03. \end{aligned}$$
(2.14)

For \(g' \lesssim 0.1\), this point satisfies all current constraints from LHC searches and measurements of \(\Delta M_s\). Constraints set by the latter observable could be competitive if the more recent predictions of the SM value are confirmed [46, 47]. However, we will show that a signal should be observable with the future upgrades of the LHCb experiment. In particular, we obtain \({\mathcal {B}}(B_s^0\rightarrow \mu ^+\mu ^-\mu ^+\mu ^-)\sim 4\times 10^{-9}\), \({\mathcal {B}}(B^+\rightarrow K^+\mu ^+\mu ^-\mu ^+\mu ^-)\sim 10^{-9}\). Note that the final state with \(K^+\) meson is of the same order of magnitude as the four body final state. Together with the fact that the \(B^+\) meson has a higher production cross section than \(B_s^{0}\) in pp collisions, this suggests that \(B^+\rightarrow K^+\mu ^+\mu ^-\mu ^+\mu ^-\) is a key signature to explore for this kind of models. This channel has not been experimentally explored though. Similar conclusions were pointed out in Ref. [48] in the context of dark sectors.Footnote 2

3 Reach of the LHCb

LHCb has searched for the decays \(B^0_{(s)} \rightarrow \mu ^+ \mu ^- \mu ^+ \mu ^-\) [26] and has set the limits \({\mathcal {B}}(B^0 \rightarrow \mu ^+ \mu ^- \mu + \mu ^-) < 7 \times 10^{-10}\) and \({\mathcal {B}}(B^0_s \rightarrow \mu ^+ \mu ^- \mu + \mu ^-) < 2.5 \times 10^{-9}\) with a \(3~\hbox {fb}^{-1}\) dataset at the collision energies of \(\sqrt{s} = 7\) and \(\sqrt{s}=8~\hbox {TeV}\). However, there is a limitation in this analysis as it places a veto on the mass of the muon pairs to be close to the \(\varphi \) or \(J/\psi \) mass, to avoid background from the decay \(B^0_s \rightarrow J/\psi \varphi \) followed by both vector mesons decaying to a pair of muons. As the a mass is likely very close to the \(\varphi \) mass, the current analysis is not sufficiently general. If a new analysis removes the veto around the \(\varphi \) mass, and instead imposes a requirement that two opposite muon combinations recombine to the same invariant mass, the limit should stay the same and the background from \(B^0_s \rightarrow J/\psi \varphi \) would still be avoided. This veto would also kill the non-resonant SM background, whose branching fraction is predicted to be of order \(3.5\times 10^{-11}\) before cuts [49].

Due to the four muons in the final state for the LHCb analysis, the combinatorial background to a possible signal is extremely low. As an essentially background free analysis, even in the far future, the branching fraction limit can be expected to scale inversely with the number of B mesons produced.

Fig. 3
figure 3

Upper left: normalised distribution of the transverse momentum of the hardest muon in the case \(B_s^0\rightarrow aa\) (solid black), \(B^+\rightarrow K^+ aa\) (dashed blue) and \(B^+\rightarrow D^+ aa\) (dotted green). Upper right: same as before but for the transverse momentum of the softest particle. Bottom left: same as before but for the pseudorapidity of the most central particle. Bottom right: same as before but for the pseudorapidity of the most forward particle

Full size image

In the run periods of Upgrade-I and Upgrade-II of LHCb, the collision energy will be \(\sqrt{s}=14~\hbox {TeV}\). As the b cross-section is scaling more or less in direct proportion to the collision energy, the amount of B mesons produced per inverse fb, can be expected to be around a factor \(14/7.7=1.8\) higher compared to the average Run-1 conditions of the LHC. Expectations below will be quoted for the end of LHCb (\(9~\hbox {fb}^{-1}\)), end of Upgrade-I (\(50~\hbox {fb}^{-1}\)) and end of upgrade-II (\(300~\hbox {fb}^{-1}\)). The naive scaling factors, compared to the current Run-1 for these, and taking the different b cross-sections into account, are for LHCb a factor 5.5, for Upgrade-I a factor 29, and for Upgrade-II a factor 180. Thus for the limits on \({\mathcal {B}}(B^0_s \rightarrow \mu ^+ \mu ^- \mu + \mu ^-)\) we should expect \(6 \times 10^{-10}\), \(9 \times 10^{-11}\) and \(1.4 \times 10^{-11}\), respectively. This assumes no changes to the trigger or tracking performance in the upgrades of LHCb.

Irreducible backgrounds to the decay have to be considered. The decay \(B^0_s \rightarrow \varphi \varphi \) with \(\varphi \rightarrow \mu ^+\mu ^-\) is one of these. Using the measured branching fractions [50, 51] we get \({\mathcal {B}}(B^0_s \rightarrow (\varphi \rightarrow \mu ^+\mu ^-) (\varphi \rightarrow \mu ^+\mu ^-)) = 1.84 \times 10^{-5} \times (2.89 \times 10^{-4})^2 = 1.5 \times 10^{-12}\). As can be seen from the expected limits above, even at the end of LHCb Upgrade II, this is not relevant. For the equivalent decay mode of the \(B^0\), the measured branching fraction limit for the \(B^0 \rightarrow \varphi \varphi \) decay is three orders of magnitude below the \(B^0_s\) mode and thus even less of a concern. The decay \(B^0_s \rightarrow \varphi \mu ^+ \mu ^-\) has a measured differential rate of \(2.6 \times 10^{-8}~\hbox {GeV}^{-2}\) in the region of the squared dimuon mass close to the \(\varphi \) mass [17]. Letting the \(\varphi \) decay to a muon pair and considering a mass region with width of around 20 MeV, corresponding to a realistic mass resolution, this will give a background at the \(10^{-13}\) level and is thus not relevant.

A simplified model for which limits the LHCb experiment can be made for similar decay modes. When comparing different B hadrons, the relative production fractions as measured at \(\sqrt{s}=7~\hbox {TeV}\) collisions in the LHCb acceptance [52] are taken into account. The relative production fractions are not expected to change significantly with collision energy as they are determined from the fragmentation process. From this, we conclude that the production of \(B^+\) and \(B^0\) are the same and that the production of \(B^0_s\) mesons is a factor 3.7 less common. For the reconstruction in LHCb, it is assumed that the efficiency is 95% per track inside the fiducial volume defined by the pseudorapidity \(2.5< \eta < 5.0\) and that tracks have a transverse momentum above \(0.5~\hbox {GeV}\) with respect to the beam axis to be reconstructed. For the trigger it is assumed that at least one reconstructed muon should have a transverse momentum above \(1.7~\hbox {GeV}\). The effect of these criteria is that final states with a larger number of particles have a lower efficiency, both due to the requirement that all tracks have to be reconstructed but also due to that the muons turn softer and the trigger efficiency thus is getting lower; see Fig. 3.

For the positive identification of muons, it is assumed that the efficiency is 100% for muons with a total momentum above 2.5 GeV. It is assumed that no or only very loose particle identification is required on the charged hadrons. For the \(D^{+}\) reconstruction, it is assumed that only the \(D^{+} \rightarrow K^{-}\pi ^{+}\pi ^{+}\) final state is used. This is the easiest decay mode to reconstruct and has a branching fraction of 9.0% [53]. The final state with a semileptonic decay of the \(D^+\) could also be considered, in an analysis similar to the \(B^+ \rightarrow \mu ^+\mu ^-\mu ^+\nu \) [54] analysis carried out by LHCb. However, to estimate the reconstruction efficiency of this five charged lepton final state with a neutrino would require a full detector level simulation which is beyond this paper. For the \(K^{*0}\) case, we consider the decay into \(K^+ \pi ^-\), which has a branching ratio of \(\sim 67\%\).

All overall efficiencies for a given final state are evaluated relative to the published analysis on the decays \(B^0_{(s)} \rightarrow \mu ^+ \mu ^- \mu ^+ \mu ^-\) [26]. As the trigger and main selection are the same for all these decays, this provides a robust normalisation method.

Simulations are carried out using Pythia 8 [55] for the production of B mesons in pp collisions and EvtGen [56] for the subsequent decays. The decays are assumed to be of the type \(B \rightarrow (M)aa\) with \(a \rightarrow \mu ^+ \mu ^-\) and with M a possible meson in the final state. The B meson decay is simulated with a flat phase space distribution. If the hadron is unstable, it is decayed to stable particles using the default model in EvtGen and with branching fractions taken from the PDG [53]. A summary of the expected limits that can be set are given in Table 1.

Table 1 Expected branching fraction limits for the different decays under consideration in units of \(10^{-11}\). It is assumed that the \(D^+\) meson is only reconstructed in the \(K^-\pi ^+\pi ^+\) final state
Full size table
Fig. 4
figure 4

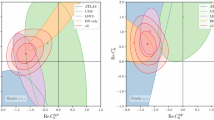
Upper left: region in the plane \((g_{23}^d, m_V)\) that can be tested at the current run of the LHCb (light) for \(g' = 0.1\) versus the area excluded by measurements of \(\Delta M_s\) (dark). Upper right: same as before but for \(g' = 0.5\). Bottom left: same as before but for the LHCb Upgrade II and \(g'=0.1\). Bottom right: same as before but for \(g'=0.5\). In all cases, the benchmark point defined in Sect. 2.1 is shown with a star for reference

Full size image

Translated to the plane \((g_{23}^d, m_V)\) for given values of \(g'\), the limits from \(B_s^0\rightarrow \mu ^+\mu ^-\mu ^+\mu ^-\) and \(B^+\rightarrow K^+\mu ^+\mu ^-\mu ^+\mu ^-\) are compared with those from \(\Delta M_s\) in Fig. 4. Interestingly, we see that scales of several tens of TeV not yet probed by current experiments could be tested in the Upgrade II of the LHCb with our analysis.

4 Conclusions

We have considered scenarios involving new heavy and flavour-violating vectors V as well as light scalars a. We have shown that these particles give rise to rare B meson decays that are not yet probed. As the preferred mass of the scalar a lies inside the window vetoed by current LHCb searches, namely [950, 1090] MeV, even the simplest decay mode \(B^0_{(s)}\rightarrow \mu ^+\mu ^-\mu ^+\mu ^-\) is not fully probed. Other decay modes of interest are \(B^+\rightarrow K^+(D^+) \mu ^+\mu ^-\mu ^+\mu ^-\) and \(B^0\rightarrow K^{*0}\mu ^+\mu ^-\mu ^+\mu ^-\). We have shown that the five-body final state can be as significant as the four-body. Relying on simulations, we have estimated the reach of the LHCb experiment for these processes in the current run and in Upgrades I and II. In the Upgrade II scenario we expect that branching fraction limits in the \(10^{-11}\) region can be reached.

Finally, we emphasize again that the decays into a meson and aa are the only sensible probe of different effective operators in the SM effective-field theory extended with a scalar singlet. We therefore encourage the experimental collaborations to consider these processes in future analyses.