Abstract
We describe how NNLO final state quark-pair corrections are computed in FDR by directly enforcing gauge invariance and unitarity in the definition of the regularized divergent integrals. We give details of our approach and show how virtual and real contributions can be merged together without relying, explicitly or implicitly, on dimensional regularization. As an example, we recompute the \({ H} \rightarrow b {\bar{b}} + {jets}\) and \(\gamma ^*\rightarrow {jets}\) inclusive rates at the NNLO accuracy in the large \(N_F\) limit of QCD. This demonstrates, for the first time, that physical results with intermediate infrared singularities can be obtained at NNLO using a fully four-dimensional procedure.
Similar content being viewed by others
1 Introduction
It is well known that calculations of observables in quantum field theory (QFT) are complicated by divergences in intermediate steps. On general grounds these divergences fall into two categories – ultraviolet (UV) divergences, associated with short wavelengths, and infrared (IR) divergences, associated with large wavelengths and/or collinear configurations. They show up in the form of integrals which do not exist in the four-dimensional physical space.
The customary way to deal with UV infinities is a two step procedure. Firstly, one regularizes the divergent integrals. Secondly, one reabsorbs the UV pieces into the free parameters of the Lagrangian. As for the IR infinities, they cancel when considering sufficiently inclusive observables, or can be reabsorbed in the parton densities. Depending on the approach, this cancellation can be achieved before or after integration. In the latter case, IR divergent integrals also need to be regulated.
When performing calculations of observables in QFT, the exact method of regulating the UV/IR divergences is arbitrary. Nevertheless, this freedom is not absolute as the chosen method should not interfere with two core tenets of QFT, that are
These general principles have concrete consequences in perturbative calculations. Gauge invariance implies a set of graphical identities (see e.g. [1]) that need to be fulfilled to all perturbative orders by the Feynman diagrams of the QFT. Unitarity, meanwhile, demands the validity of the cutting equations [2, 3] corresponding to the relation
for the T matrix [4]. Both (1) are essential to preserve the Ward/Slavnov-Taylor identities (WI) at the regularized level, known as the regularized quantum action principle [5].
The most commonly used technique is dimensional regularization [6, 7] (DReg). DReg exploits the fact that gauge invariance and unitarity are naturally preserved as they hold for the theory in all values of the dimensionality d of the space-time. Hence, the divergent integrals are analytically evaluated in d dimensions, and the asymptotic \(d \rightarrow 4\) limit is eventually taken. By doing so, UV/IR divergences are parametrized in terms of negative powers of a Laurent expansion in \((d-4)\). In this framework, one still has some freedom to define objects in intermediate steps. Hence, several variants of DReg exist such as conventional dimensional regularization [8], ’tHooft–Veltman [6], four-dimensional helicity [9] and dimensional reduction [10]. We refer to [11] for an exact definition of all of them.
In recent years, a considerable effort has been pursued by several groups to introduce more four-dimensional ingredients in the definition of regularization. The main motivation being an attempt to simplify analytical and numerical methods, as well as to try to consider different theoretical perspectives. This four-dimensional program has resulted in a number of methods such as the four-dimensional formulation of FDH [12], implicit regularization [13, 14], four-dimensional unsubtraction [15,16,17] and FDR [18,19,20,21,22]. They are described and compared in [23]. Whilst all approaches are different, FDR is the only method that does not rely on the customary UV renormalization procedure. Instead, the result of an FDR calculation is directly a renormalized quantity.
FDR treats UV divergences by performing a subtraction, extracting from the loop integrands the divergent parts which do not contain physical information – the so-called vacua. In the case of IR finite amplitudes, the validity of the FDR strategy has been explicitly demonstrated in [22]. In the presence of IR divergent configurations, the IR regulator should not interfere with principles (1). If this is achieved, the correct physical result is obtained for IR safe quantities. At NLO, it is known how to match real and one-loop contributions in the presence of final state IR singularities [21, 23], while, so far, no FDR NNLO calculation has been performed involving infrared divergent configurations. In this paper we bridge this gap and give the first example of such a computation. We describe how NNLO final state quark-pair corrections can be computed in FDR in a way that automatically respects the principles (1). In particular, we reproduce the \({\overline{\mathrm{MS}}}\) results for the \(N_F\) part of \({ H} \rightarrow b {\bar{b}} + {jets}\) and \(\gamma ^*\rightarrow {jets}\). Since DReg is never used, explicitly or implicitly, this represents, to our knowledge, the first example of a realistic fully four-dimensional NNLO calculation.
The structure of the paper is as follows. In Sect. 2 we present our definitions of the virtual and real integrals appearing when computing NNLO quark-pair corrections. In Sect. 3 we discuss the relevant renormalization issues. Sections 4 and 5 give a detailed description of the \({ H} \rightarrow b {\bar{b}} + {jets}\) and \(\gamma ^*\rightarrow {jets}\) calculations. Finally, in Sect. 6 we summarize our findings and discuss perspectives and directions opened by the procedures introduced in this work.
The lowest order amplitude (a), the IR divergent final-state virtual quark-pair correction (b) and the IR divergent real component (c). The blob stands for the emission of \(n-1\) particles. Additional IR finite corrections are created if the gluons with momenta \(q_1\) and \(k_{34}\) are emitted by an off-shell particle in the blob
2 Inclusive quark-pair corrections and FDR
Our aim is to compute the large \(N_F\) limit of cross sections including NNLO quark-pair corrections. The relevant contributions are the Born, Virtual and Real reactions given by
In (3), \(A^{(j)}_n\) represents the amplitude for the emission of n partons computed at the \(j^{th}\) perturbative order, while \(d \varPhi _m\) is the m-particle phase-space
with \(\delta _+(p^2_i):= \delta (p^2_i)\varTheta (p^0_i)\), in which P is the initial state momentum. The amplitude \(A^{(0)}_{n}\) is drawn in Fig. 1a, where the line with momentum p is an on-shell QCD parton and the blob denotes n-1 additional final-state particles. The NNLO amplitudes can be split into IR divergent and finite parts
The infrared singular contributions are depicted in Fig. 1b, c, while the finite pieces are created when the splitting gluons with momenta \(q_1\) and \(k_{34}\) are emitted by an off-shell particle contained in the blob.
Due to the presence of IR parts in (5), both \(\sigma _{V}\) and \(\sigma _{R}\) are IR divergent, although, as is well known, their combination in infrared safe quantities is IR finite. In addition, UV infinities are present in \(\sigma _{V}\) that are renormalized away when bare parameters are determined at the perturbative order appropriate to match the NNLO accuracy. In conclusion, the fully inclusive sum
is a physical quantity, although its parts are separately plagued by IR and UV divergences. Indeed, it is the simplest case of an infrared safe observable, which must give the same result when computed in any consistent scheme used to deal with the divergences.
In this section we use the four-dimensional FDR framework, and describe the procedures which allow one to compute \(\sigma ^{{ NNLO}}\). We put particular emphasis on the steps needed to cope with the simultaneous presence of IR and UV infinities at two loops, and on how to merge virtual and real components. Section 2.1 presents the steps needed to define \(\sigma _V\), while 2.2 deals with \(\sigma _R\). Section 2.3 contains an explicit example which guides the reader across both real and virtual procedures.
2.1 The NNLO definition of the virtual contribution
A generic two-loop integrand in \(A^{(2)}_{n,\mathrm IR}\) has the form
with internal loop momenta \(q_1\), \(q_2\) and \(q_{12}:= q_1 + q_2\). The denominator D collects all \(q_2\)-independent propagators
where k is the number of propagators in the blob of Fig. 1b, and N is the numerator of the integrand. The hats on Lorentz indices means that they are external to the divergent sub-diagram, as in Fig. 2. The difference between hatted and un-hatted indices can be ignored until equation (23). Here we just point out that hatted indices can be identified in more general cases as described in [22].
We now analyze all possible divergences generated upon loop integration. We do this to determine the form of the FDR UV subtractions and the structure of the IR regulator needed to define the FDR integration over (7) given in (35). \(J(q_1,q_2)\) is quadratically divergent when \(q_2 \rightarrow \infty \) at fixed \(q_1\). Given the presence of many propagators in D, this is the only possible UV sub-divergence. Depending on where the lower gluon reconnects to the blob, it may also generate global UV infinities. In addition, due to the on-shell condition \(p^2= 0\), a double collinear IR singularity arises when both \(q_1\) and \(q_2\) are proportional to p. A second potential IR divergent configuration is \(q^2_1 \rightarrow 0\) but \(q^2_2 \ne 0\). Nevertheless, this divergence is cancelled by the UV behavior of the \(q_2\) integration. This can be understood by noticing that a scaleless \(q_2\)-type sub-integral is generated in this case, that vanishes in FDR.Footnote 1 An additional double collinear IR singularity is created if the lower gluon is attached to a second external massless parton.
In FDR, a common unphysical scale \(\mu ^2\) is added to all propagators in order to regulate divergences. As is well known, performing this operation only in the denominator is contrary to the core principle (1a) of gauge invariance. As such, in FDR one performs a Global Prescription (GP) [18], also making the replacement in the numerator such that all integrand cancellations between numerator and denominator take place at the regulated level.Footnote 2 These cancellations are called “gauge cancellations”. In practice, one first determines the dependence of \(J(q_1,q_2)\) on \(q^2_1\), \(q^2_2\) and \(q^2_{12}\) generated by Feynman rules. This is the reason for the explicit \(q^2_1\) as an argument of F in (7). Subsequently, one adds an unphysical scale \(\mu ^2\) to all such self-contractions
We denote this procedure by the symbol \({\mathop {\rightarrow }\limits ^{\mathrm{GP}}}\). Therefore, the replacement \( f {\mathop {\rightarrow }\limits ^{\mathrm{GP}}}{\bar{f}}, \) applied to any function \(f(q^2_1, q^2_2, q^2_{12})\), produces a new function \({\bar{f}}\) with arguments replaced as in (9),
Note that \({\bar{f}}\) has the same functional form as f. Nevertheless, we keep the bar to make explicit that GP has been implemented on f. In the case at hand one has
with
and
In our calculation, we simplify the \({\bar{q}}^2_i\)s in \({\bar{N}}\) with the denominators of (11),
After this is done, \(\mu ^2\) only appears in the propagators.
The IR singularities of \(J(q_1,q_2)\) are now regulated by the addition of \(\mu ^2\) in the propagators. As we shall see, the asymptotic limit \(\mu ^2 \rightarrow 0\) will be eventually taken after integration. That generates logarithms of \(\mu ^2\) of IR origin. Nevertheless \(\bar{J}(q_1,q_2)\) is still UV divergent. The global UV infinities are subtracted by separating physical and non-physical scales in \({\bar{D}}_p\). That means using the identity
and noticing that the second term is more UV convergent than the original propagator. The same expansion has to be applied to the other propagators in \(1/{\bar{D}}\), until \({\bar{F}}/{\bar{D}}\) is written as follows
where \([{\bar{F}}/{\bar{D}}]_{V}\) do not depend on physical scales. Since also \({\bar{G}}^{\rho \sigma }\) does not contain physical scales, \([{\bar{F}}/{\bar{D}}]_{V}\) defines the global UV divergent behavior of \({\bar{J}}(q_1,q_2)\):
\([\bar{J}(q_1,q_2)]_{GV}\) is called a Global Vacuum (GV) and is written between square brackets, that is the standard FDR notation to indicate the vacuum part of an object. Note that \(({\bar{F}}/{\bar{D}})_{F}\) in (16) gives rise to a subtracted integrand which is globally UV convergent but still divergent when \(q_2 \rightarrow \infty \):
This is fixed by subtracting the Sub-Vacuum (SV) from \({\bar{G}}^{\rho \sigma }\) by means of the expansion
The final result has the form
so that the fully UV subtracted integrand
is integrable in four dimensions.Footnote 3 Upon integration, the vacua subtracted in (21) induce the appearance of logarithms of \(\mu ^2\) of UV origin, so that both IR and UV singularities are regulated by the same regulator.
The procedure leading to (21) is conveniently encoded in a linear integral operator
whose action on a two-loop integrand is defined by three subsequent operations:
-
subtract the vacua;
-
integrate over \(q_1\) and \(q_2\);
-
take the asymptotic limit \(\mu ^2 \rightarrow 0\).
The last operation means retaining only the logarithmic pieces in the asymptotic expansion, neglecting \(\mathcal{O}(\mu ^2)\) terms. Thus, the FDR two-loop integration over \({\bar{J}}(q_1,q_2)\) in (11) is defined as followsFootnote 4
In the following, we will often omit terms that integrate to zero in globally prescribed numerators. Hence, it is convenient to introduce a notation for that, that is \( {\bar{N}}^\prime \simeq {\bar{N}} \) if both numerators give the same result upon FDR integration.
Equation (23) defines a gauge-invariant object, in which the necessary gauge cancellations are preserved by the GP operation. By “gauge-invariant object” we mean that a calculation of \(\bar{I}\) in a different gauge will give the same result. It is instructive to check that no change in \(\bar{I}\) is produced if one shifts the numerator of the gluon propagator as
Thus, \({\bar{I}}\) gives the same result when computed in any gauge. Another consequence of the WIs is that the term proportional \(q_2^\rho q_1^\sigma +q_1^\rho q_2^\sigma \) in (13) should not contribute to \({\bar{I}}\) when contracted with \({\bar{F}}_{{\hat{\rho }} {\hat{\sigma }}}\). That is,
After taking into account the vanishing of scaleless integrals, this corresponds to the WI depicted in Fig. 3. Nevertheless, we keep this piece in (13), as we will explicitly show in our calculation that it never contributes.
The graphical version of the WI in (25). The scalar gluon, with coupling proportional to the gluon momentum, is denoted by a dashed arrow. The symbol \(\otimes \) indicates that it is emitted by the quark loop
Perturbative expansion of (2) for \(H \rightarrow b {\bar{b}} + jets\) in the large \(N_F\) limit
Let us now consider the unitarity properties of this prescription. Equation (2) relates different orders of perturbation theory, so a given divergent subgraph \(S_{\mathrm{G}}\) can appear embedded in loop diagrams of different orders \(\ell \). If the result of \(S_{\mathrm{G}}\) depends on \(\ell \) then the relation (2) will in general not survive. For a more concrete example relevant to the calculations of this paper, consider the consequence of (2) shown in Fig. 4. This specifies that the discontinuity of a two-loop graph is given in terms of a one-loop graph. As such, the higher loop regularization must be consistent with the lower loop one. In FDR this places strong constraints on the GP. In our example of Fig. 4 we see that on the left hand side, the momenta associated to the gluon lines take part in the GP, but this is not true for the right hand side. In FDR, this tension is resolved by enforcing “sub-integration consistency” (SIC) [22].
We now consider this procedure in detail for the integrand \(J(q_1, q_2)\). We analyze a subset of the full integrand, specifically the numerator of the gluonic self-energy of Fig. 2, \( q_2^{\rho } q_{12}^{\sigma } +q_{12}^\rho q_2^\sigma -g^{\rho \sigma } (q_2 \cdot q_{12}) \), which appears in (7). This is the piece that needs to be treated carefully to maintain SIC. We consider, in particular, the result of the contraction with a \(g_{{\hat{\rho }} {\hat{\sigma }}}\)Footnote 5 (potentially) contained in \(F_{{\hat{\rho }} {\hat{\sigma }}}\). It reads
where we have explicitly separated the contribution \( {\hat{q}}^2_2 :=g_{{\hat{\rho }} {\hat{\sigma }}} q^\rho _2 q^\sigma _2 \). From the point of view of the sub-diagram disconnected from the rest, \({\hat{q}}^2_2\) should not be globally prescribed, hence the GP replacement to be performed is
On the other hand, embedding this in the full diagram requires integrating over \(q_1\), therefore \(q^2_1\) needs to be barred
Nevertheless, \(\rho \) and \(\sigma \) are internal indices of the two-loop diagrams of Fig. 1b, so that GP is needed for \({\hat{q}}^2_2\) as well
which is the prescription used in (23). It is the mismatch among (27)–(29) which violates SIC. Our solution to this problem is modifying the integrand in (23) as follows:
-
we do not apply GP to \({\hat{q}}^2_2\) terms whose origin is a contraction with indices external to the UV divergent sub-diagram;Footnote 6
-
we replace back everywhere \({\bar{q}}^2_1 \rightarrow q^2_1\) after GV subtraction.
Note that the last operation is possible because barring \(q^2_2\) and \(q^2_{12}\) is sufficient to regulate the IR divergences. This is a consequence of the fact that the only IR divergent configuration is the double collinear limit. Furthermore, this solution does not affect any of the WIs and so still defines a gauge invariant object. In summary, after GV subtraction, (27) is maintained as it is also when embedded in a two-loop calculation. A comparison between this solution and the IR-free case in given in Appendix A.
Let us now return to the matter of enforcing SIC in the entirety of (23), and how one applies our solution. We enforce SIC by rewriting (23) as
where we have used the fact that \([{\bar{F}}/{\bar{D}}]_V\) is subtracted by the integral operator. The structure of the expansions needed to extract the GV is such that \({\bar{D}}\) can be always pulled out from the rest. Thus, it is possible to rewrite
Next, we introduce the numerator function
where the explicit dependence on \({\hat{q}}^2_2\) is generated by the l.h.s of (27). In practice, \({\bar{\mathcal{Z}}}({\bar{q}}^2_1,{\hat{q}}^2_2)\) is constructed from N in (7) as follows:
-
globally prescribe N, \( N {\mathop {\rightarrow }\limits ^{\mathrm{GP}}}{\bar{N}}\), leaving \({\hat{q}}^2_2\) unbarred;
-
perform GV subtraction and determine, for each term T in \({\bar{N}}\), the appropriate function \({\bar{H}}\) to be used in (32). The result of this will always have a factorized form. For instance, if (15) has to be used once to subtract the global vacuum, the contribution of T to \({\bar{\mathcal{Z}}}({\bar{q}}^2_1,{\hat{q}}^2_2)\) is \(-2(q_1 \cdot p)/{\bar{q}}^2_1 \times T\);
-
eliminates the bars from the \({\bar{q}}^2_1\)s;
-
identify \({\hat{q}}^2_2\) with \(q^2_2\).
We denote the last two operations with the symbol \({\mathop {\rightarrow }\limits ^{\mathrm{SIC}}}\). Thus, the change \( {\bar{f}} {\mathop {\rightarrow }\limits ^{\mathrm{SIC}}}{\tilde{f}}, \) applied to any globally prescribed and GV subtracted function \({\bar{f}}({\bar{q}}^2_1,{\hat{q}}^2_2)\), produces a new function defined as
In the equation above, \({\tilde{f}}\) has the same functional form as \({\bar{f}}\), but we use the tilded notation to denote that the SIC operation has been imposed on \({\bar{f}}\). Thus, the SIC compatible version of (32) reads
To continue to ensure gauge cancellations, we unbar also the propagators, that leads to
Equation (35) defines the SIC preserving four-dimensional integration over the integrand in (7). Note that, since the GV has been subtracted in it, \([d^4q_1]\) is replaced by a customary integration \(d^4q_1\). The asymptotic limit \(\mu ^2 \rightarrow 0\) is understood after taking the two integrations.
A first consequence of this definition is that external wave-function corrections vanish for massless particles, so that they can always be neglected in actual calculations. The proof is given in Appendix B.
2.2 The NNLO definition of the real component
Given the propagator structure of Fig. 1c, the integrands contributing to \(\sigma _R\) in (3) have the following form
where \(0 \le \alpha ,\beta \le 2\). The symbol S collects all the remaining propagators and \(N_R\) is the numerator of the amplitude squared. Depending on the value of the exponents \(\alpha \) and \(\beta \), \(J_R\) becomes IR divergent under integration over \(\varPhi _{n+2}\). These IR singularities must be regulated coherently with our treatment of the virtual component, without violating unitarity and gauge invariance. In this section, we determine a four-dimensional integration that achieves this.
Our starting point is the representation of \(\sigma _V\) and \(\sigma _R\) in terms of cut diagrams, in which we put the complex conjugate amplitudes on the right side. With this convention, normal Feynman rules are assumed on the left and complex conjugate ones on the right. The cuts generating IR divergent configurations are obtained by squaring the amplitudes in Fig. 1b, c and are depicted in Fig. 5. IR divergences manifest themselves as pinch singularities of the loop integrals in (a,b) and endpoint phase-space singularities in (c,d). These two kinds of singularities are related to each other by the identity
in which the poles of the propagator on the l.h.s. may create a pinch in the complex plane of the loop integration and the \(\delta _+(k^2)\) on the r.h.s. may induce a non-integrable end-point configuration. Dubbing \(\varSigma _{c}\) the sum over all cuts that appears in the r.h.s. of (2), the cutting equations [2, 3] ensure that the last term in (37) does not contribute to the singular part of each cut in \(\varSigma _{c}\), and that \(\varSigma _{c}\) is IR finite. This theorem implies a unitarity-preserving cancellation of the IR singularities if the Cutkosky relation
giving the possibility of a one-to-one integrand level identification of the infrared divergent parts contributing to different cuts in \(\varSigma _{c}\), is preserved. However, one should also prove that \(\varSigma _{c}= \sigma _R + \sigma _V\). The reason for this second requirement is the different origin of the potential numerators multiplying the two sides of (38a). In the case of a fermion line, that is the only cut relevant for this paper, the l.h.s. gets multiplied by the numerator of the propagator  , while the r.h.s. by
, while the r.h.s. by  . Hence, in addition to (38a), the identity
. Hence, in addition to (38a), the identity

must hold to guarantee the validity of (2). Equation (38b) states that the numerators of the loop propagators in Fig. 5a, b should be treated consistently with the sum over the spin polarizations of the cut lines in Fig. 5c, d. Note that (38b) also guarantees consistent gauge cancellations in all terms contributing to \(\varSigma _{c}\).
Let us consider how to make these relations consistent with the procedure from the previous section where we make two modifications to the integrand:
-
adding \(\mu ^2\) to the propagators with momenta \(q_2\) and \(q_{12}\);
-
SV and GV subtraction from the integrand.
We first study how FDR preserves (38a). We start dealing with the effect of the \(q_2^2 {\mathop {\rightarrow }\limits ^{\mathrm{GP}}}{\bar{q}}^2_2\) and \(q^2_{12}{\mathop {\rightarrow }\limits ^{\mathrm{GP}}}{\bar{q}}^2_{12}\) replacements in cuts (a,b). Equation (38a) is preserved if
with \(\bar{k}^2_{3,4}:= k^2_{3,4}-\mu ^2\). Thus, the \({\bar{q}}_2^2\) and \({\bar{q}}^2_{12}\) propagators in \(\sigma _V\) must correspond to external particles in \(\sigma _R\) obeying
Hence, we replace in (3) \(\varPhi _{n+2} \rightarrow \tilde{\varPhi }_{n+2}\), where the phase-space \(\tilde{\varPhi }_{n+2}\) is such that \(k^2_3=k^2_4= \mu ^2\) and \(k^2_i= 0\) when \(i \ne 3,4\). However, this is not enough. One also needs to show that (39) survives the SV subtraction of (21). We prove this explicitly in the case of the last term in (13). The proof is unchanged for the other contributions. The relevant expansion is
where SV is the term to be subtracted. We consider a piece of the finite part of (41) as a numerator factor \(\lambda \)
and observe that \(\lambda \rightarrow 1\) when \({\bar{q}}^2_{12}\rightarrow 0\). We therefore first put the \({\bar{q}}^2_{12}\) propagator on-shell, giving
When also \({\bar{k}}^2_3\) goes on-shell, one obtains the same result as applying (39) before subtracting the vacuum. Hence, the SV subtraction is “invisible” from the point of view of (39), and (38a) is fulfilled if \(k_{3,4}\) obey (40).
As for (38b), in order to preserve it, one must treat \(k^2_3\), \(k^2_4\) and \((k_3+k_4)^2= s_{34}\) in the numerator \(N_R\) of (36) using the same prescriptions imposed on \(q^2_2\), \(q^2_{12}\) and \(q^2_1\) in N of (7). This means replacing in \(N_R\)
where the last equalities are induced by the delta functions in (39). These changes should be performed everywhere in \(N_R\) except in contractions induced by the external indices \({\hat{\rho }}\) and \({\hat{\sigma }}\) in cuts (c,d). In this case
in accordance to the SIC preserving requirement we have used to construct \({\tilde{\mathcal{Z}}}(q^2_1,q^2_2)\) from N.Footnote 7 We denote all of this by introducing a globally prescribed and SIC preserving version of \(N_R\)
where the action of \({\mathop {\rightarrow }\limits ^{\mathrm{GS}}}\) on a function \( f(k^2_3,k^2_4,\hat{k}^2_3, \hat{k}^2_4) \) is defined to be
in which the tilde on \({\tilde{f}}\) expresses the fact that GS has been imposed. Only a dependence on \(\mu ^2\) is left in the r.h.s. of (46) because of the deltas in \(\tilde{\varPhi }_{n+2}\).
The only remaining propagator involved in our definition of the virtual component is in the top-left line of cut (a), that must correspond to the cut \(k_1\) propagator in (d) through the relationFootnote 8
Everything is massless in this case, so that (38b) is fulfilled and it is sufficient to check that GV subtraction does not alter (48). The proof is similar to the one used for the SV. In fact, if m expansions
are needed to subtract the vacuum in front of a term in \(\bar{\mathcal{Z}}({\bar{q}}^2_1,{\hat{q}}^2_2)\), this term gets multiplied by a factor \(\lambda ^m\) in \(\tilde{\mathcal{Z}}(q^2_1,q^2_2)\), where
But \(\lambda =1\) when the propagator goes on-shell. So that (48) survives the GV subtraction.
In summary, we define the four-dimensional integration over the integrand in (36) as follows
By doing that, unitarity preserving IR cancellations occur by construction between \(\sigma _R\) and \(\sigma _V\), without violating gauge invariance.
2.3 An example of cancellation
The integrals in (35) and (51) can be computed independently, and this is the strategy we adopt in this paper. In fact, term by term cancellations in \(\varSigma _c\) are difficult to find. The reason is that one can add to the numerator of the virtual piece arbitrary vanishing terms that nevertheless contribute to the real part, and vice-versa. This is due to the different structure of the deltas contained in \(d \varPhi _{n}\) and \(d \tilde{\varPhi }_{n+2}\). However, if the numerator of a term does not change – modulo a relabelling of the momenta – when multiplied by both phase-spaces, the IR cancellation must occur between integrals constructed one from the other via the replacement in (38a). In this section we illustrate this phenomenon by considering a piece of the full \(H \rightarrow b {\bar{b}} + {jets}\) calculation presented in the following section. This also serves us as a concrete example on how the procedures of Sects. 2.1 and 2.2 work in practice.
A cut contributing to \(H \rightarrow b {\bar{b}}\) at NNLO. Only the term proportional to \(g_{\rho \sigma }\) is considered in (52)
A cut contributing to \(H \rightarrow b {\bar{b}} q {\bar{q}}\). Only the \(g_{\rho \sigma }\) term is considered in (61)
The two-loop contribution to \(\sigma _V\) is depicted in Fig. 6. We focus on the term generated by the \(g_{\rho \sigma }\) piece of the internal trace. It reads
with \({D_i:=(q_1+p_i)^2}\). The numerator \({{\bar{N}}_V}\) is obtained via GP from its unbarred version
where we have neglected couplings and color factors, but not phases needed to compute the overall sign. We rewrite
with \(s= P^2\), that gives
This expression can be simplified by dropping terms which integrate to zero, for example \({\bar{q}}^2_2\) and \({\bar{q}}^2_{12}\) generate vacua and \({\bar{D}}_1\) gives a scale-less integral. Furthermore, \((P \cdot q_1 )\) does not contribute because it is antisymmetric when \(p_1 \leftrightarrow p_2\), while the denominator in (52) is symmetric. Thus \({\bar{N}}_{V} \simeq {\bar{N}}^\prime _{V}\), with
The GV in (52) is fully removed by the subtraction of the scale-less integral. Thus, \({\bar{\mathcal{Z}}_V}({\bar{q}}^2_1)= {\bar{N}}^\prime _{V}({\bar{q}}^2_1 )\) and
so that the physically relevant two-loop contribution reads
\(\tilde{\varGamma }_V\) develops IR divergences in the form of powers of
When splitting the result of the integration in a part which collects all terms containing powers of L, dubbed logarithmic part (L.P.), plus a remainder, one finds
These logarithms are cancelled by a term contributing to the four-particle cut-diagram in Fig. 7
where the IR behavior is now regulated by the two external massive lines \(k_{3}^2= k_{4}^2= \mu ^2\). \(\tilde{N}_R\) is obtained by applying the GS operation defined in (47) to the numerator of the diagram
the result reads
\(\tilde{N}_R\) does not depend on \(\mu ^2\) because in this case there are no contractions of \(k_{3,4}\) vectors with the external indices \({\hat{\rho }}\) and \({\hat{\sigma }}\).
We now can check that the integrand in (61) is the correct object to cancel the logarithms in (60). In fact, it can be obtained from (58) by means of the Cutkosky replacement in (38a), together with the relabellings
inferred by comparing Figs. 6 and 7, and the substitution
which is necessary because of the gluon propagator appearing on the r.h.s. of Fig. 7. Therefore, \(\tilde{\varGamma }_R\) must contain a contribution with the same singular behavior of \(-\tilde{\varGamma }_V\). We dub \(\tilde{\varGamma }_{R}^\prime \) such a contribution, and \(\tilde{N}_{R}^\prime \) its numerator function. The terms proportional to \(s_{234}\) or \(s_{134}\) in (63) give zero when evaluated at the two-particle cut: they cannot be “seen” by \(\tilde{\varGamma }_V\). This leads us to the conclusion that
which corresponds to \({\tilde{\mathcal{Z}}_V}(q^2_1)\) in (57), modulo the first replacement in (64). Thus, \(\tilde{\varGamma }_{R}^\prime \) is obtained by replacing \( \tilde{N}_{R} \rightarrow \tilde{N}_{R}^\prime \) in (61). An explicit calculation confirms that
3 Renormalization
In this section, we discuss and implement the FDR renormalization program in the context of our calculation. To do this we need to distinguish, at least conceptually, between UV regulator, IR regulator and renormalization scale. We denote them by \(\mu _{\mathrm{UV}}\), \(\mu _{\mathrm{IR}}\) and \(\mu _{\mathrm{R}}\), respectively.
In the case of IR free observables, the FDR integral operator in (22) subtracts the UV infinities before integration. For this reason, after taking the asymptotic limit \(\mu _{\mathrm{UV}}\rightarrow 0\), \(\mu _{\mathrm{UV}}\) can be directly interpreted as the finite renormalization scale \(\mu _{\mathrm{R}}\) [18]. In this sense, FDR directly produces a finite, renormalized result for the loop part: nothing needs to be subtracted from it. However, this result is arbitrary until bare parameters are fixed by experimental measurements. After doing so, if the theory is renormalizable, the scale \(\mu _{\mathrm{R}}\) gets replaced by physical scales, leading to an unambiguous prediction. This can be understood as a finite renormalization necessary to make the theory predictive [25].
In the presence of IR divergences, no distinction is made in the virtual component between \(\mu _{\mathrm{UV}}\) and \(\mu _{\mathrm{IR}}\). As a matter of fact, the procedure in Sect. 2.1 assumes \(\mu = \mu _{\mathrm{UV}}= \mu _{\mathrm{IR}}\), preventing one from setting \(\mu = \mu _{\mathrm{UV}}= \mu _{\mathrm{R}}\), as is possible in the IR free case. Our solution is fixing the bare parameters in terms of physical quantities before combining virtual and real components. After this is done, the \(\mu _{\mathrm{R}}\) scales get automatically replaced by physical scales, hence the left over \(\mu \)s are the \(\mu _{\mathrm{IR}}\)s which cancel the IR behavior of the real counterpart.
The bare parameters in our calculation are \(\alpha _S^0\) and the Yukawa coupling \(y_b^0\). In order to implement our renormalization program we need relations linking them to measured quantities at the appropriate perturbative order, which is one loop for \(\alpha _S^0\) and two loops for \(y_b^0\).
We are interested in corrections proportional to \(N_F\). Hence, \(\alpha _S^0\) can be linked to the customary \(\alpha _S^{{\overline{\mathrm{MS}}}}(s)\) by using the fact that the \(N_F\) contribution to the running coincides in FDR and \(\overline{\mathrm{MS}}\) [21]. As a consequence, we choose our renormalized strong coupling constant to be \(\alpha _S= \alpha _S^{{\overline{\mathrm{MS}}}}(s)\), that gives the relation
with
where L is given in (59).
The Yukawa coupling is renormalized by using its proportionality to the bottom mass. The corrected bottom propagator at the pole is proportional to

where \(m^0\) is the bare mass and the \({\varSigma }^{(j)}\)s are computed in Appendix C. This gives a relation between \(m^0\) and the pole mass m
which translates into
with
where
Equation (72) contains the bare QCD coupling. Inserting (68) gives the desired two-loop relation between bare and renormalized Yukawa coupling
4 \({ H} \rightarrow b {\bar{b}} + {jets}\)
In this section, we use FDR to reproduce the physical prediction for the inclusive decay width of the Higgs into two b jets up to the NNLO accuracy in the large \(N_F\) limit of QCD. That means computing the observable
where \(\varGamma _2^{(0)}(y_b)\) is the tree-level decay width and \(\delta \varGamma ^{N_F}\) collects all the NNLO terms proportional to \(\alpha _S^2N_F\).
The correction factor \(\delta \varGamma ^{N_F}\) receives contributions from processes with up to four final-state particles, namely:
-
\(H \rightarrow b {\bar{b}}\) up to two loops;
-
\(H \rightarrow b {\bar{b}} g\) at the tree level;
-
\(H \rightarrow b {\bar{b}} q {\bar{q}}\) at the tree level.
The tree- and one-loop two- and three-body decays in the above list contribute to \(\delta \varGamma ^{N_F}\) through renormalization. As a matter of fact, due to the scalar nature of the Yukawa coupling, \(\varGamma ^{\mathrm{NNLO}}(y_b)\) is a simple process in terms of the contributing tensor structures. Nevertheless, it requires the two-loop renormalization of (75).
In the following, we compute all components in the massless limit of QCD, namely with \(m\ne 0\) only in \(y_b\). Our notation is as follows. We dub \(V_i^{(j)}\) the H decay amplitudes into i final state partons computed at the \(j^{th}\) order of the QCD perturbative expansion. We shall omit for brevity the multiplication of the appropriate quark spinors in any expressions for the \(V_i^{(j)}\). The decay widths are obtained by squaring the amplitudes and are denoted by \(\varGamma _i^{(j)}\).
In this paper we focus on the new aspects of FDR at NNLO, namely the procedures presented in Sects. 2.1 and 2.2. For this reason we do not go into detail of the calculation of the NLO part. The corresponding expressions can be computed as described in references [21, 23]. However, we emphasize that FDR NLO formulae stay the same also when they contribute to a NNLO calculation. The same holds true for LO expressions multiplying higher order corrections. This is in contrast to d-dimensional regularization methods, in which higher powers in the \((d-4)\) expansion must be added.
4.1 \({ H} \rightarrow b {\bar{b}}\) up to two loops
In our conventions, the lowest order \({ H} \rightarrow b {\bar{b}}\) vertex is
where k and l are the color indices of the bottom quarks. Squaring \(V_2^{(0)}\) gives the LO \({ H} \rightarrow b {\bar{b}}\) decay width
in which \(N_C\) is the number of colors.
The one-loop correction is depicted in Fig. 8. Following reference [21] one obtains
with
The globally prescribed integral needed to compute the two-loop correction is given by left part of Fig. 6. It reads
with \({\bar{D}}_i\) given right after (52). Here we have replaced bare quantities with renormalized ones, because the difference is \(\mathcal{O}(\alpha ^3_S)\). In the following, we compute \({\bar{N}}_{A,B}\) starting form their unbarred counterparts \(N_{A,B}\), which can be obtained from (7) by taking  . By denoting
. By denoting  one finds
one finds

where the last term originates from the piece we have studied in detail in Sect. 2.3, with \(N_V\) given in (53). \(N_A\) does not contribute to \(\bar{V}_2^{(2)}\). In fact, a \(\bar{u}(p_1)\)(\(u(p_2)\)) is understood on the l.h.s.(r.h.s.), so that, by virtue of the Dirac equation, one can replace  , giving
, giving

which generates scale-less integrals. That explicitly proves the WI in (25). As for the \(N_B\) piece, there are several ways [19, 20] to deal with strings of \(\gamma \)-matrices to extract the dependence on \((q_i \cdot q_j)\) and \(q_i^2\) needed to implement GP. They are based on replacements of the type  , where the “masses” \(\mu _i\) serve as a bookkeeping tool. In this paper we find it more convenient to use Clifford algebra until we reach the configurationsFootnote 9
, where the “masses” \(\mu _i\) serve as a bookkeeping tool. In this paper we find it more convenient to use Clifford algebra until we reach the configurationsFootnote 9

By using this method one finds \(N_B {\mathop {\rightarrow }\limits ^{\mathrm{GP}}}{\bar{N}}_B \simeq {\bar{N}}^\prime _B\) with
\({\bar{N}}^\prime _B\) does not induce the appearance of global UV divergences in (81), hence the numerator function directly reads \( {\bar{\mathcal{Z}}}({\bar{q}}^2_1,{\hat{q}}^2_2)= {\bar{N}}^\prime _B({\bar{q}}^2_1,{\hat{q}}^2_2) \). Thus, the SIC preserving numerator function is \( {\tilde{\mathcal{Z}}}(q^2_1,q^2_2)= {\bar{N}}^\prime _B(q^2_1,q^2_2) \), and the two-loop correction is
In terms of the master integrals listed in Appendix D it reads
4.2 \({ H} \rightarrow b {\bar{b}} g\) and \(H \rightarrow b {\bar{b}} q {\bar{q}}\) at the tree level
The LO \({ H} \rightarrow b {\bar{b}} g\) decay width is obtained by squaring the \(V_3^{(0)}\) vertex drawn in Fig. 9 and integrating over a phase-space in which all final-state particles acquire a small mass \(\mu \), as described in reference [21]. The result is
with L defined in (59).
As for \(H \rightarrow b {\bar{b}} q {\bar{q}}\), two diagrams contribute to the amplitude \(V_4^{(0)}\). They can be read from Fig. 9 by allowing the gluon to split into a \(q {\bar{q}}\) pair. As described in Sect. 2.2, \(\varGamma _4^{(0)}\) is obtained by squaring \(V_4^{(0)}\) and integrating over a massive 4-particle phase-space \(\tilde{\varPhi }_4\) such that \(k_1^2= k_2^2= 0\) and \(k_3^2= k_4^2= \mu ^2\). Prior to integration, the integrand should be modified according to the GP and SIC replacements given in (46). As a result of this, the function to be integrated in (51) is a rational combination of the invariants \(s_{34}\), \(s_{134}\), \(s_{234}\) and \(\mu ^2\):
where the \(\mu ^2\) dependence is induced by (45). It is interesting to note this \(\mu ^2\) dependence factorizes. In particular, one finds
with
Therefore, (51) has the form of a massless-like matrix element \(\tilde{J_R^\prime }(s_{34},s_{134},s_{234})\), obeying all relevant WIs, times a global factor \(w(\mu ^2)\) integrated over a massive phase-space. We conjecture that a similar gauge-invariant structure should naturally appear also when dealing with more complicated cases involving, for instance, IR divergences induced by vector particles like gluons.
In terms of the integrals reported in Appendix E the result reads
4.3 The large \(N_F\) limit of the inclusive width
Here we gather all the calculated components and compute \(\varGamma ^{\mathrm{NNLO}}(y_b)\) in (76). The correction factor \(\delta \varGamma ^{N_F}\) receives contributions from processes with up to four partons
that are obtained by inserting the renormalization equations (68) and (75) in the amplitudes given in the previous sections.
One finds
where
Equations (94) are written in a form that highlights the contributions generated by renormalization. Collecting all the pieces gives the IR finite result
Equation (96) is written in terms of the pole mass m. It is possible to reabsorb the large logarithms of the ratio \(m^2/s\) in a new Yukawa coupling \(y^{{\overline{\mathrm{MS}}}}_b\) defined through the known two-loop relation between m and the \({\overline{\mathrm{MS}}}\) mass [26]. Using the \(N_F\) part of it gives
hence
Equation (98) coincides with the known \({\overline{\mathrm{MS}}}\) result [27, 28].
5 \(\gamma ^*\rightarrow {jets}\)
In this section we compute the large \(N_F\) limit of the inclusive \(e^+ e^- \rightarrow \gamma ^*\rightarrow jets\) production rate up to the NNLO accuracy. That is the observable
where \(\sigma _2^{(0)}\) is the tree-level \(e^+ e^- \rightarrow \gamma ^*\rightarrow q {\bar{q}}\) cross-section and \(\delta \sigma ^{N_F}\) contains the QCD corrections proportional to \(\alpha _S^2N_F\). QCD renormalization only involves \(\alpha _S\), in this case. Nevertheless, higher rank tensors contribute, so that preserving gauge cancellations and unitarity in such an environment provides a more stringent test for our procedures. In this respect, \(\gamma ^*\rightarrow jets\) is complementary to \(H \rightarrow b {\bar{b}} + jets\).
The processes which contribute to \(\delta \sigma ^{N_F}\) are
-
\(e^+ e^- \rightarrow q {\bar{q}}\) up to two loops;
-
\(e^+ e^- \rightarrow q {\bar{q}} g\) at the tree level;
-
\(e^+ e^- \rightarrow q {\bar{q}} q^\prime {\bar{q}}^\prime \) at the tree level,
where we understand a photon mediating the reactions. We dub \(V^{(j)\beta }_i\) the final-state current producing i partons computed at the \(j^{th}\) QCD order, where \(\beta \) is the Lorentz index of the virtual photon. The Feynman diagrams representing the vertices are obtained from those in the previous section by replacing the Higgs with a photon. Hence, we do not draw them. Contracting \(V^{(j)\beta }_i\) with the initial-state current, squaring and integrating over the phase-space gives the corresponding cross section, denoted by \(\sigma ^{(j)}_i\).
In the following, we describe the FDR computation of the various components.
5.1 \(e^+ e^- \rightarrow q {\bar{q}}\) up to two loops
The lowest order vertex is
where \(Q_q\) is the electric charge of the quark. The corresponding cross section reads
in which \(\alpha \) is the fine-structure constant.
The computation of \(V^{(1)\beta }_2\) is described in [23]. The result is
with \(a^0\) and \(L^\prime \) defined in (69) and (80), respectively.
The globally prescribed two-loop integral we need to compute \(V_2^{(2)\beta }\) reads
The unbarred \(N^\beta \) is obtained from (7) with  by using the fact that, according to the WI in (25), the term proportional to \(q^\rho _2 q^\sigma _1+q^\rho _1 q^\sigma _2\) in the fermion trace does not contribute.Footnote 10 Hence
by using the fact that, according to the WI in (25), the term proportional to \(q^\rho _2 q^\sigma _1+q^\rho _1 q^\sigma _2\) in the fermion trace does not contribute.Footnote 10 Hence

Using tensor decomposition and the \(p_1 \leftrightarrow p_2\) symmetry gives \(N^\beta {\mathop {\rightarrow }\limits ^{\mathrm{GP}}}{\bar{N}}^\beta \simeq \bar{M}^\beta \) with

where the factor \(-2(q_1 \cdot p_1)/{\bar{q}}^2_1\) multiplying the last term subtracts its GV. Thus, the SIC preserving numerator function is \( {\tilde{\mathcal{Z}}}^\beta (q^2_1,q^2_2)= \bar{M}^\beta (q_1^2,q^2_2) \), giving
In terms of the two-loop integrals in Appendix D one finds
5.2 \(e^+ e^- \rightarrow q {\bar{q}} g\) and \(e^+ e^- \rightarrow q {\bar{q}} q^\prime {\bar{q}}^\prime \) at the tree level
A NLO computation produces
with L is given in (59).
As for \(\sigma _4^{(0)}\), it is obtained by computing the amplitude squared, modifying it according to the prescription in (46) and integrating over the \(\tilde{\varPhi }_4\) phase-space. In terms of the integrals in Appendix E the result reads
5.3 The large \(N_F\) limit of the inclusive jet production rate
Here we collect all components needed to compute \(\sigma ^{\mathrm{NNLO}}\). The correction can be split as follows
where the various contributions are obtained by inserting (68) in the results of the previous sections. One has
with
Gathering all the pieces gives
which reproduces the \({\overline{\mathrm{MS}}}\) result [29, 30].
6 Conclusion and outlook
In this paper we have demonstrated that a fully four-dimensional framework to compute NNLO quark-pair corrections can be constructed based on the requirement of preserving the two principles given in (1). The FDR idea of enforcing gauge invariance and unitarity at the level of the UV subtracted integrands is at the base of the procedures we have used to define UV and IR divergent integrals.
A few advantages of such an approach that have appeared in our calculation are, for the UV part
-
no (explicit or implicit) UV counterterms have to be included in the Lagrangian;
-
lower-order substructures are used in higher-order calculations without any modification (see e.g. (79) and (102)).
For the IR sector
-
infrared divergences in the real component directly show up in terms of logarithms of a small cut-off parameter \(\mu _{\mathrm{IR}}\), with no need for a prior subtraction of \(1/(d-4)\) poles (see, for instance, the four-parton rates in (94) and (111));
-
one-to-one integrand correspondences can be written down between virtual and real contributions (see Sect. 2.3).
In this paper we have focused our attention on a special class of NNLO corrections. However, we believe that the basic principles that have guided us towards a consistent treatment of all the pieces contributing to the final NNLO answer will remain valid also when considering more complicated environments, with the final aim of constructing a completely general procedure including also initial state IR singularities. This is certainly the main subject of our future investigations. Other possible directions are: using \(\mu _{\mathrm{IR}}\) as a separation parameter in slicing-based subtraction methods at NNLO [31], or exploiting the virtual/real integrand correspondence to construct four-dimensional local counter-terms directly from the virtuals,Footnote 11 in the same spirit of the procedure presented at NLO in the FDR section of [23].
On a more general ground, we envisage that the intrinsic four-dimensionality of FDR can pave the way to new numerical methods and that there is room for fully exploiting its potential in NNLO calculations.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical paper with no external associated data.]
Notes
See Appendix B.
This, combined with the shift invariance of FDR integrals is sufficient to prove all Ward identities graphically [20].
The described procedure is quite general. For example, despite the fact that subtracting sub-divergences via (19) potentially re-introduces UV singularities due to \(q_1\), the expressions can be arranged in such a way that fully subtracted integrands can be always written down. Indeed, this has been automated in the case of two-loop off-shell QCD amplitudes in [22].
Due to the vacuum subtraction, \(q^2_i/{\bar{q}}^2_i \ne 1\) under FDR integration. This is the reason why we perform the explicit gauge cancellations of (14).
The analysis for terms like \(\gamma _{{\hat{\rho }}}\gamma _{{\hat{\sigma }}}\) is also required, but equivalent.
This reproduces the effect of the evanescent operators needed in the four-dimensional helicity scheme and dimensional reduction to restore renormalizability [24].
Although it does not occur in our calculation, it is worth mentioning what happens when loop propagators and cut lines refer to spin-1 particles. In this case (38b) is replaced by \(g^{\mu \nu }_\mathrm{prop} = g^{\mu \nu }_\mathrm{spin}\), which states that the metric tensor in the numerator of a loop propagator should be handled consistently with the one generated by the sum over polarizations. This is again achieved by treating the self contractions \(k^2_3\), \(k^2_4\), \((k_3+k_4)^2\) in \(\sigma _R\) exactly as their counterparts \(q^2_2\), \(q^2_{12}\), \(q^2_1\) in \(\sigma _V\), as done in (44) and (45).
The complex conjugate of (48) links cuts (b) and (c).
Note the invariance of the last term under
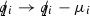 .
.The proof is analogous to the one given in Sect. 4.1.
A two-loop DReg algorithm along these lines has been recently proposed in [32].
Assuming the appropriate GV subtraction in the rest of the integral.
References
G.F. Sterman, An Introduction to Quantum Field Theory (Cambridge University Press, Cambridge, 1994)
R.E. Cutkosky, J. Math. Phys. 1, 429 (1960). https://doi.org/10.1063/1.1703676
M.J.G. Veltman, Physica 29, 186 (1963). https://doi.org/10.1016/S0031-8914(63)80277-3
G. ’t Hooft, M.J.G. Veltman, NATO Sci. Ser. B 4, 177 (1974)
D. Stöckinger, JHEP 0503, 076 (2005). https://doi.org/10.1088/1126-6708/2005/03/076
G. ’t Hooft, M. Veltman, Nucl. Phys. B 44, 189 (1972). https://doi.org/10.1016/0550-3213(72)90279-9
C.G. Bollini, J.J. Giambiagi, Nuovo Cim. B 12, 20 (1972). https://doi.org/10.1007/BF02895558
J.C. Collins, Renormalization (Cambridge University Press, Cambridge, 1984)
Z. Bern, D.A. Kosower, Nucl. Phys. B 379, 451 (1992). https://doi.org/10.1016/0550-3213(92)90134-W
W. Siegel, Phys. Lett. B 84, 193 (1979). https://doi.org/10.1016/0370-2693(79)90282-X
A. Signer, D. Stöckinger, Nucl. Phys. B 808, 88 (2009). https://doi.org/10.1016/j.nuclphysb.2008.09.016
R.A. Fazio, P. Mastrolia, E. Mirabella, W.J. Torres Bobadilla, Eur. Phys. J. C 74(12), 3197 (2014). https://doi.org/10.1140/epjc/s10052-014-3197-4
O.A. Battistel, A.L. Mota, M.C. Nemes, Mod. Phys. Lett. A 13, 1597 (1998). https://doi.org/10.1142/S0217732398001686
A.L. Cherchiglia, M. Sampaio, M.C. Nemes, Int. J. Mod. Phys. A 26, 2591 (2011). https://doi.org/10.1142/S0217751X11053419
R.J. Hernandez-Pinto, G.F.R. Sborlini, G. Rodrigo, JHEP 02, 044 (2016). https://doi.org/10.1007/JHEP02(2016)044
G.F.R. Sborlini, F. Driencourt-Mangin, R. Hernandez-Pinto, G. Rodrigo, JHEP 08, 160 (2016). https://doi.org/10.1007/JHEP08(2016)160
G.F.R. Sborlini, F. Driencourt-Mangin, G. Rodrigo, JHEP 10, 162 (2016). https://doi.org/10.1007/JHEP10(2016)162
R. Pittau, JHEP 11, 151 (2012). https://doi.org/10.1007/JHEP11(2012)151
A.M. Donati, R. Pittau, JHEP 04, 167 (2013). https://doi.org/10.1007/JHEP04(2013)167
A.M. Donati, R. Pittau, Eur. Phys. J. C 74, 2864 (2014). https://doi.org/10.1140/epjc/s10052-014-2864-9
R. Pittau, Eur. Phys. J. C 74(1), 2686 (2014). https://doi.org/10.1140/epjc/s10052-013-2686-1
B. Page, R. Pittau, JHEP 11, 183 (2015). https://doi.org/10.1007/JHEP11(2015)183
C. Gnendiger et al., Eur. Phys. J. C 77(7), 471 (2017). https://doi.org/10.1140/epjc/s10052-017-5023-2
C. Gnendiger, A. Signer, Private communication
R. Pittau, Fortschr. Phys. 63, 132 (2015). https://doi.org/10.1002/prop.201400079
A.V. Bednyakov, B.A. Kniehl, A.F. Pikelner, O.L. Veretin, Nucl. Phys. B 916, 463 (2017). https://doi.org/10.1016/j.nuclphysb.2017.01.004
S.G. Gorishnii, A.L. Kataev, S.A. Larin, L.R. Surguladze, Mod. Phys. Lett. A 5, 2703 (1990). https://doi.org/10.1142/S0217732390003152
S.G. Gorishnii, A.L. Kataev, S.A. Larin, L.R. Surguladze, Phys. Rev. D 43, 1633 (1991). https://doi.org/10.1103/PhysRevD.43.1633
K.G. Chetyrkin, J.H. Kuhn, A. Kwiatkowski, Phys. Rep. 277, 189 (1996). https://doi.org/10.1016/S0370-1573(96)00012-9
A. Gehrmann-De Ridder, T. Gehrmann, E.W.N. Glover, Nucl. Phys. B 691, 195 (2004). https://doi.org/10.1016/j.nuclphysb.2004.05.017
R. Boughezal, J.M. Campbell, R.K. Ellis, C. Focke, W.T. Giele, X. Liu, F. Petriello, Phys. Rev. Lett. 116(15), 152001 (2016). https://doi.org/10.1103/PhysRevLett.116.152001
L. Magnea, E. Maina, G. Pelliccioli, C. Signorile-Signorile, P. Torrielli, S. Uccirati, JHEP 12, 062 (2018). https://doi.org/10.1007/JHEP12(2018)062
J.A.M. Vermaseren, Comput. Phys. Commun. 83, 45 (1994). https://doi.org/10.1016/0010-4655(94)90034-5
Acknowledgements
R.P. acknowledges the financial support of the MINECO Project FPA2016-78220-C3-3-P and the hospitality of the CERN TH department during the completion of this work. Our figures are prepared with Axodraw [33].
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Sub-integration consistency with and w/o IR divergences
When no IR infinities are present, the mismatch between Eqs. (28) and (29) is cured by adding the so called extra-extra integrals (EEI) introduced in [22]. Their exact definition is not needed here. It suffices to say that terms proportional to the difference
are included. They multiply UV \(1/\mu ^2\) poles and generate logarithms of \(\mu ^2\) that restore the correct renormalization properties of the two-loop amplitude. Such contributions are missed by (29).
In the presence of IR divergences an additional complication is generated by the GP \(q^2_1 \rightarrow {\bar{q}}^2_1\) in (28) and (29). After GV subtraction, the difference
also hits \(1/\mu ^2\) poles of IR origin. This gives rise to different renormalization constants for processes with or without IR divergences, which is unacceptable. This leads to the choice of letting \(q^2_1\) unbarred, as discussed in Sect. 2.1. For the sake of consistency, also the EEIs part needs to be modified accordingly. The problem is that the EEIs become unregulated when unbarring \({\bar{q}}^2_1\) at the integrand level. The solution to this is replacing EEIs with the difference of two ordinary FDR integrals, generated by the combination
which is sometimes referred as an extra-integral (EI). One shows that EEIs and EIs share the same logarithmic content, which fixes the correct UV behavior. In addition, EIs admit the \({\bar{q}}^2_1 \rightarrow q^2_1\) limit that matches the rest of the calculation.
In summary, the solution presented in Sect. 2.1 is equivalent to the following procedure:
-
apply GP;
-
subtract GV;
-
downgrade \({\bar{q}}^2_1 \rightarrow q^2_1\) in the result;
-
identify the EEIs to be added (using the same algorithm as in the IR-free case);
-
replace each EEI with the corresponding EI.
It would be interesting to establish whether this strategy works also for IR finite two-loop calculations. That would make unnecessary the use of the EEIs. We leave this to further investigations.
Appendix B: Massless wave-function corrections
Wave function corrections are generated when the lower gluon in Fig. 1b reconnects to the emitting massless parton. In this appendix, we use the results of Sect. 2.1 to demonstrate that they vanish.
The relevant integrand is obtained by taking  in (7), that gives \(N = N_A+N_B\) with
in (7), that gives \(N = N_A+N_B\) with

Furthermore, \(D = q^4_1 D_p\), so that the integrals we have to consider are
One finds

Only the third term contributes to \({\bar{I}}_{A}\). All the others generate vacua or result from contractions of antisymmetric combinations of \(\gamma \)-matrices with symmetric integrals. Thus

\({\bar{I}}_{A}\) only depends on \(p^2= 0\). In addition, it is both UV divergent and logarithmically IR divergent, so that it is a scale-less integral. Such integrals vanish in FDR as a consequence of an exact cancellation between UV and IR singularities, therefore \({\bar{I}}_{A}=0\), as required by (25). In the same way, \({\bar{I}}_{B}\) is fully scale-less

so that self-energy corrections \({\bar{I}}_{A} +{\bar{I}}_{B}\) vanish.
The proof that scale-less integrals do not contribute can be found in [20]. Here we prove that they vanish also when \(q^2_1\) is unbarred, as in (35). We concentrate on first term of (B.8)

The proof is unchanged for all the other contributions. A GV subtraction is needed in front of  . This is achieved by using twice the identity in (15)
. This is achieved by using twice the identity in (15)
The  piece is less UV divergent, so that a single subtraction is sufficient
piece is less UV divergent, so that a single subtraction is sufficient
The vacua are subtracted by the integral operator. That defines the numerator function associated with \({\bar{N}}_C\)

Hence

which produces

\(\tilde{I}_{C}\) diverges logarithmically in the double collinear configuration in the absence of regulator. The barred \(q_2\)-type denominators are sufficient to regulate this. That is a consequence of the fact that (B.10) and (B.11) do not alter the IR power counting. By tensor decomposition  , so that it vanishes on-shell. In summary, the GV subtraction does not leave finite pieces in scale-less integrals.
, so that it vanishes on-shell. In summary, the GV subtraction does not leave finite pieces in scale-less integrals.
Appendix C: Correcting the bottom propagator
To renormalize the Yukawa coupling, we need the one- and two-loop QCD corrections of Fig. 10 computed at the value  . We dub them
. We dub them  .
.
One finds
with \({L^{\prime \prime }}\) in (74).
As for the second order contribution, one has

with \( D_p= q_1^2+2 (q_1 \cdot p)\). The unbarred  is given by (7) with
is given by (7) with  . The result reads
. The result reads  , where
, where

When barring \(N_A\) one obtains a vanishing contribution to \(i \bar{\varSigma }^{(2)}\). As for \(N_B\), one computes  . Using tensor decomposition gives
. Using tensor decomposition gives

with

To subtract the GV from \({\bar{N}}^\prime _B\) we expand \(1/{\bar{D}}_p= 1/{\bar{q}}^2_1+\bar{\lambda }/{\bar{D}}_p\) with \(\bar{\lambda }= -2(q_1 \cdot p)/{\bar{q}}^2_1\), that gives the numerator function
Hence
where \(\lambda = -2\frac{(q_1 \cdot p)}{q^2_1}\). In summary, the two-loop correction is
with \({\tilde{I}_{4,5}}\) written in Appendix D.
Appendix D: The virtual master integrals
In this appendix we sketch out the computation of the two-loop integrals appearing in our calculation.
The \(q_2\) integration is performed first.Footnote 12 This means computing
As for B, we use the expansion in (41) to subtract its sub-vacuum. Then we use Feynman parametrization and integrate over the UV finite remainder. The result is
with
To determine \(B^{\alpha }\) we use tensor decomposition
The first two terms cancel each other due to the \(q^2_2 \leftrightarrow q^2_{12}\) symmetry of the integral. Thus
Finally, tensor decomposition gives
The coefficients are obtained by subtracting the SV by means of (19), and integrating over the finite part. The result reads
When inserting these results in Eqs. (86) and (106) one finds that the two-loop vertex corrections can be expressed in terms of three master integrals
where \({\tilde{I}}_2\) is UV finite because \(p_1^2= 0\). Integrating over \(q_1\) and x and neglecting \(\mathcal{O} (\mu ^2)\) terms gives
with \(L^\prime \) given in (80).
Finally, the two-loop integrals in (C.22) are
Their asymptotic expansions read
with \({L^{\prime \prime }}\) in (74).
Appendix E: The real integrals
The real component of the NNLO corrections computed in this paper can be expressed in terms of the following eight integrals
with \(w(\mu ^2)\) given in (91).
To compute the \({\tilde{R}}_i\)s it is convenient to use the following phase-space parametrization
where \( z = {s_{34}}/{s} \), \( y = {s_{234}}/{s} \), \( x = {s_{134}}/{s} \), and \( \epsilon ^2 = {\mu ^2}/{s} \). The asymptotic \(\mu ^2 \rightarrow 0\) behavior can be extracted with the change of variable \( \tau = 4\epsilon ^2/z, \) to be used when \(\lim _{\epsilon \rightarrow 0}\) cannot be taken before integration.
The first three integrals are IR finite
As for the remaining ones, (E.35) gives
with L written in (59).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Page, B., Pittau, R. NNLO final-state quark-pair corrections in four dimensions. Eur. Phys. J. C 79, 361 (2019). https://doi.org/10.1140/epjc/s10052-019-6865-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-6865-6












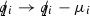 .
.