Stability and bifurcation analysis of interacting f(T) cosmology

Abstract

The present work deals with dynamical system analysis of Interacting f(T) cosmology. Einstein field equations are second order non-linear differential equations. So it is very difficult to solve them analytically. We can draw the vector field and analyze the stability of the universe in different phase by dynamical system analysis. By suitable transformation of variables the Einstein field equations are converted to an autonomous system. The critical points are determined and the stability of the equilibrium points are examined by center manifold theory. Possible bifurcation scenarios have also been explained.

1 Introduction

Several cosmological observations of the Supernovae type Ia [1,2,3], cosmic microwave background radiation [4, 5], large scale structure [6,7,8], baryon acoustic oscillations [9, 10] and weak lensing [11,12,13,14,15,16,17,18] suggest the fact that our universe is now experiencing an accelerated expansion. Many theories are formulated to explain this late-time acceleration. However, these theories can be divided mainly in two categories fulfilling the criteria of a homogeneous and isotropic universe. First kind of theory assumes a mysterious matter component with negative pressure, dubbed as dark energy (DE) [11,12,13,14,15,16,17,18] which accounts for about 70% of total energy. This model of exotic fluid seems to have an equation of state $\omega$ close to $-1$ which gives birth of “anti-gravity” [19, 20] and makes it phenomenologically analogous to a cosmological $\Lambda$-term or to a vacuum energy. The observations have shown that about 5% of universe’s energy content is baryonic matter. However, observations of rotation galaxy curves, galaxy clustering and galaxy X-ray emission have shown that 26% of the matter in the universe is dark matter. Cosmologists are inclined to suspect dark energy and dark matter are thought to be responsible for the current acceleration of the universe and the dynamics of the galaxy respectively.

It is not achievable to derive explicit form of the interaction between dark energy (DE) and dark matter (DM) from first principle. A specific coupling has to be considered relating to the phenomena. Moreover, the inevitable interaction between the dark components is natural to consider in the framework of the field theory and to diminish the possibility of coincidence problem an appropriate interaction between DE and DM has to be taken care of. On the other hand, it was revealed that the late integrated Sachs–Wolfe effect has the unique ability to provide insight into the coupling between dark sectors. Further, the dark energy decays into matter at a rate proportional to Hubble length. So, it is customary to consider a phenomenological form of interaction between dark matter and dark energy since they are dominant components of the cosmic configuration now a days. In fact, the rate of exchange of energy density in the dark sector is given by the interaction term.

However, standard cosmological framework of general relativity (GR) does not match with the overwhelming abundance of observational evidences for cosmic speed up [21]. To solve this paradox, one could follow in search for solution of the accelerating cosmic expansion enigma is to develop several modified theories of which f(R)-gravity theory gets much attention [22,23,24,25,26,27,28]. The first inferred f(R) models proposed rely on negative power of R, which become dominant at small curvature, in the gravitational action to generate the late-time de-Sitter stage, but suffered from severe instabilities in the presence of matter. In the f(R)-gravity theory the geometric Lagrangian density is replaced by a suitably chosen algebraic function f(R), where R is the variable.

An equivalent formulation represented by teleparallelism [25,26,27,28] where instead of curvature torsion is responsible for the gravitational interaction. This model was first proposed by Einstein for unifying electromagnetism and gravity on Weitzenböck non-riemannian manifold. Ferraro and Fiorini [29] proposed a possible generalization of teleparallel gravity to describe the gravitational interaction as well as the accelerated expansion of our universe. This approach is known as f(T)-gravity [30,31,32,33,34,35,36]. In this approach, the Levi–Civita connection is replaced by the Weitzenböck connection with torsion scalar T. Compared with the f(R) theory leading to the fourth order equations, the field equations of the f(T) theory are in the form of second order differential equations. However this modified theory breaks the invariance under Local Lorentz Transformation complicating the interpretation of the relationship between all inertial frames of the tangent space to the differentiable manifold (space-time) [37, 38]. Hence all 16 components of the vierbien are independent and one can not fix six of them by a gauge choice. In addition if certain condition are satisfied , the behavior of f(T) cosmologies is similar to several popular dark energy models, such as quintessence, phantom, DGP model and transient acceleration. Thus starting from teleparallel equivalent of GR (TEGR), in which Lagrangian is the torsion scalar T, one can extend T to f(T) resulting to f(T)-gravity which proves to be very interesting both for early time as well as late-time universe evolution, while black hole solutions in this framework also lead to interesting features. One of the important features of both general relativity and modified gravity is that the nonlinear nature of the corresponding cosmological equations. So one can not determine exact analytical solutions. Nevertheless, one can apply dynamical system analysis which allows to extract the global behavior of the scenario, independently of the initial condition and by passing the complexity of the equations. The dynamical system analysis method serves as an useful technique to analyze and classify various features of cosmological models [21, 39,40,41,42,43,44,45,46]. In particular, the Einstein-field equations are transformed into an autonomous system of equations by suitable change of variables and we get the following set of ordinary differential equations.

$$\begin{aligned} \frac{dx}{dt}=f(x,\lambda ), \end{aligned}$$

where $x=(x_1,\ldots ,x_n)$ are variables needed to characterize the system and the functions $f(x)=(f_1(x_1,\ldots ,x_n),\ldots ,f_n(x_1,\ldots ,x_n))$ are determined by the system for parameter value $\lambda$. Next we determine the hyperbolic and non-hyperbolic critical points of the corresponding autonomous system. Hartman–Grobman theorem [47] can be used to characterize the hyperbolic critical point. To analyze the non-hyperbolic critical points there are various tools. Center Manifold [48,49,50,51,52,53] theory is an important and useful tool to study the qualitative behavior and stability of non-hyperbolic critical points. However, behavior of the critical points may depend on the parameter value $\lambda$. In this situation bifurcation [48,49,50,51,52, 54, 55] may occur for some values of the parameter.

2 Basic equations

In f(T)-gravity torsion is responsible for generating the gravity and the field equations which are only second order. In f(T) gravity theory the action can be expressed as,

$$\begin{aligned} A=\frac{1}{2\kappa ^2}\int {d^{4}x~\bigg [\sqrt{-g}~\bigg (T+f(T)\bigg ) +A_m\bigg ]}, \end{aligned}$$

(1)

where T is the torsion scalar, f(T) is a differentiable function of the torsion, $A_m$ corresponds to the matter Lagrangian and $\kappa ^2=8\pi G$. The torsion scalar is defined as

$$\begin{aligned} T=S_{\alpha }{}^{\mu \nu } T^{~\alpha }{}_{\mu \nu }, \end{aligned}$$

(2)

where

$$\begin{aligned} S_{\alpha }{}^{\mu \nu }= & {} \frac{1}{2}\bigg (K^{~\mu \nu }{}_{\alpha } + \delta ^{~\mu }{}_{\alpha }T^{~\beta \mu }{}_{\alpha }-\delta ^{~\nu }{}_{\alpha }T^{~\beta \mu }{}_{\beta }\bigg ), \end{aligned}$$

(3)

$$\begin{aligned} K^{~\mu \nu }{}_{\alpha }= & {} -\frac{1}{2}\bigg (T^{~\mu \nu }{}_{\alpha }-T^{~\nu \mu }{}_{\alpha }-T_{\alpha }{}^{\mu \nu }\bigg ), \end{aligned}$$

(4)

$$\begin{aligned} T^{~\theta }{}_{\mu \nu }= & {} \Gamma ^{~\theta }{}_{\nu \mu }-\Gamma ^{~\theta }{}_{\mu \nu }. \end{aligned}$$

(5)

We consider the metric in the form of a flat Friedmann–Lemaitre–Robertson–Walker metric

$$\begin{aligned} ds^2=dt^2-a(t)^2(dx^i dx_i), \quad (i=1,2,3) \end{aligned}$$

(6)

where a(t) is cosmological scale factor.

The matter is chosen as dark matter in the form of dust (having energy density $\rho _m$) interacting with the dark energy which is chosen as a minimally coupled scalar field $\phi$ having self interacting potential $V(\phi )$. So the energy density and pressure corresponding to this scalar field are

$$\begin{aligned} \rho _{\phi }= & {} \frac{1}{2}{\dot{\phi }}^2 + V(\phi ), \end{aligned}$$

(7)

$$\begin{aligned} P_{\phi }= & {} \frac{1}{2}{\dot{\phi }}^2 - V(\phi ). \end{aligned}$$

(8)

We start with the Friedmann equation for f(T) model

$$\begin{aligned} H^2=\frac{1}{2f_T +1}\bigg (\frac{1}{3}(\rho _\phi + \rho _m)-\frac{f}{6}\bigg ). \end{aligned}$$

(9)

The second FRW equation is

$$\begin{aligned} {\dot{H}}=-\frac{1}{2}\bigg (\frac{\rho _m+\rho _\phi +p_\phi }{1+f_T+2Tf_{TT}} \bigg ). \end{aligned}$$

(10)

The energy-balance equations corresponding to dark energy and dark matter are,

$$\begin{aligned} \dot{\rho _m}+3H\rho _m= & {} Q, \end{aligned}$$

(11)

$$\begin{aligned} {\dot{\rho }}_{\phi } +3H(1+\omega _{\phi })\rho _{\phi }= & {} -Q , \end{aligned}$$

(12)

where the interaction term Q corresponds to energy exchange between dark energy and dark matter.

The function Q has dependencies on the energy densities of the dark matter and dark energy and Hubble parameter. The positive Q implies a transfer of energy from dark energy to dark matter and it is assume that Q does not change sign during the cosmic evolution. Due to the unknown nature of two dark components, the precise form of the interaction term can not be determined. Thus doctrinally, Q can be chosen as

• (i) Q=Q(H$\rho _m$),

• (ii) Q=Q(H$\rho _{\phi }$),

• (iii) Q=Q(H$\rho _m$,H$\rho _{\phi }$).

f is redefinition of Newton’s constant when linear in T and in particular, constant f(T) acts like a cosmological constant. A sensible choice of f(T) should agree with primordial nucleosynthesis and cosmic microwave background constraints i.e $\frac{f}{T} \rightarrow 0$ at early times (a $\ll$ 1) and at late time there will be de Sitter phase asymptotically. A straightforward choice of f is polynomial in T

$$\begin{aligned} f(T)=\beta (-T)^n, \end{aligned}$$

(13)

where $\beta$ is arbitrary constant. For the restriction ‘$n \ll 1$’, f(T) appears to be a viable model compared to current observed data set and also $f_T$ acts as the Newton’s constant. The effective DE equation of state parameter varies from $\omega =-1+n$ in early phase to $\omega =-1$ in late phase. So we consider $f(T)=\beta \sqrt{T}$, where $\beta$ is arbitrary constant and for simplicity Q is chosen as $Q=\alpha H\rho _m$, where the coupling parameter is ‘$\alpha$’. By combining (3), (4) and (5) one can obtain

$$\begin{aligned} T=S^{\alpha \mu \nu }T_{\alpha \mu \nu }=-6H^2, \end{aligned}$$

(14)

where $H=\frac{{\dot{a}}}{a}$ is the Hubble parameter and dot represents derivative with respect to t.

Now, using Eqs. (7), (8) and (12) we get modified Klein–Gordon equation

$$\begin{aligned} \ddot{\phi }+3H{\dot{\phi }}+\frac{dV(\phi )}{d\phi }=-\frac{Q}{{\dot{\phi }}}. \end{aligned}$$

(15)

It is very hard to extract exact solution analytically from this complicated form of evolution equation. So we perform suitable transformation of variables to construct an autonomous system from the evolution equation. For this we introduce new variables as follows [21],

$$\begin{aligned} x=\frac{{\dot{\phi }}}{\sqrt{6}H},\quad y=\frac{\sqrt{V(\phi )}}{\sqrt{3}H},\quad \Omega _m=\frac{\rho _m}{3H^2}, \end{aligned}$$

where $\Omega _m$ is the density parameter for DM. As a result, the evolution equations reduce to the following autonomous system as follows,

$$\begin{aligned} \frac{dx}{dN}= & {} \frac{1}{2}(\alpha -3)x-\frac{\alpha }{2x}(1-y^2)-\frac{3}{2}xy^2\nonumber \\&-\left( \sqrt{\frac{3}{2}\lambda }\right) y^2+\frac{3}{2}x^3, \end{aligned}$$

(16)

$$\begin{aligned} \frac{dy}{dN}= & {} \left( \sqrt{\frac{3}{2}}\lambda \right) xy + \frac{3}{2}y + \frac{3}{2}x^2y-\frac{3}{2}y^3 , \end{aligned}$$

(17)

$$\begin{aligned} \frac{d\Omega _m}{dN}= & {} \alpha \Omega _m + 3x^2 \Omega _m -3y^2 \Omega _m , \end{aligned}$$

(18)

where we choose $\frac{V'(\phi )}{V(\phi )}=\lambda$ which is a constant such that $V(\phi )=e^{\lambda \phi }$. The independent variable is N = ln a, which is called the e-folding parameter.

Further, using the normalize variables in the first Friedman equation the density parameter of dark matter is restricted to

$$\begin{aligned} x^2+y^2+\Omega _m=1 \end{aligned}$$

(19)

where $0<\Omega _m<1$, so the above paraboloid will be confine finitely in the phase space [21].

The equation of state parameter ($\omega _{\phi }$) and the density parameter ($\Omega _{\phi }$) of the scalar field can be expressed by the newly defined variables as

$$\begin{aligned} \omega _{\phi }= & {} \frac{p_{\phi }}{\rho _{\phi }}, \end{aligned}$$

(20)

$$\begin{aligned} \Omega _{\phi }= & {} \frac{\rho _{\phi }}{3H^2}=x^2+y^2 . \end{aligned}$$

(21)

We can also express $\omega _{total}$ in terms of newly defined variables by using Eqs. (7), (8) and (19) as

$$\begin{aligned} \omega _{total}:= & {} \frac{p}{\rho }=\frac{p_{\phi }}{\rho _{\phi }+\rho _m}\nonumber \\= & {} \frac{x^2-y^2}{x^2+y^2+\Omega _m}=x^2-y^2=\omega _{Tot}~(say). \end{aligned}$$

(22)

The deceleration parameter can be expressed by $\omega _{total}$ as follows

$$\begin{aligned} q=\frac{1}{2}(1+3\omega _{Tot}). \end{aligned}$$

(23)

On the other hand, the explicit form of ‘q’ is as follows

$$\begin{aligned} q=-1-\frac{{\dot{H}}}{H^2}=-1+\frac{3}{2}(2x^2+\Omega _m). \end{aligned}$$

(24)

The critical points of the autonomous system (16–18) and the corresponding cosmological parameters are presented in Table 1.

Table 1 Critical points (CPs) and corresponding cosmological parameters

Table 2 Eigenvalues of the Jacobian matrix at CPs and corresponding non-hyperbolic constrains

In the present work we analyze the non-hyperbolic critical points of the above system. The hyperbolic critical points are analyzed in paper [21]. The non-hyperbolic critical points are important to analyze bifurcation scenarios which indicate the phase transition of the universe. We only analyze non-hyperbolic critical points by center manifold theory, while hyperbolic CPs are already discussed in paper [21] using Hartman–Grobman theorem. It is to be noted that $P_7$ and $P_8$ appear to be same as the critical points $P_1$ and $P_2$ respectively for $\alpha =-3$ (non-hyperbolic case). So we skip the CPs $P_7$ and $P_8$. The conditions for non-hyperbolicity of the critical points $P_1$ to $P_6$ are mentioned in Table 2.

Fig. 1

Vector field near $P_1$ for $\alpha =-3$ and $\lambda \ne -\sqrt{6}$

3 Stability analysis

In this section, We investigate the stability of non-hyperbolic critical points for some choices of $\alpha$ and $\lambda$. Most of the cases stability of non-hyperbolic critical points can be determined by center manifold (CM) theory. For this we first perform coordinate transformation so that the critical point moves to the origin.

3.1 Critical point $P_1$

We shift the critical point $P_1$ to the origin by the coordinate transformation $x \rightarrow X+1$, $y \rightarrow Y$, $\Omega _m \rightarrow {\bar{\Omega }}_m$. The system of Eqs. (16–18) changes to

$$\begin{aligned} \frac{dX}{dN}= & {} \bigg (\alpha + 3\bigg )X - \bigg (\frac{\alpha -9}{2}\bigg )X^2\nonumber \\&+ \bigg (\frac{\alpha -3}{2}-\sqrt{\frac{3}{2}}\lambda \bigg )Y^2- \bigg (\frac{\alpha + 3}{2}\bigg )XY^2 \nonumber \\&+\bigg (\frac{\alpha +3}{2}\bigg )X^3 + \text {higher power terms}, \end{aligned}$$

(25)

$$\begin{aligned} \frac{dY}{dN}= & {} \bigg (3+\sqrt{\frac{3}{2}}\lambda \bigg )Y + \bigg (3 + \sqrt{\frac{3}{2}}\lambda \bigg )XY \nonumber \\&+ \frac{3}{2}X^2Y-\frac{3}{2}Y^3 , \end{aligned}$$

(26)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} \bigg (\alpha +3\bigg ){\bar{\Omega }}_m+ 3\bigg (X^2+2X-Y^2\bigg ){\bar{\Omega }}_m . \end{aligned}$$

(27)

Origin is a critical point of this system of equations. The eigenvalues of the Jacobian Matrix at the origin are $\lambda _1= \alpha +3$, $\lambda _2 = 3+ \sqrt{\frac{3}{2}}\lambda$, $\lambda _3= \alpha +3$. The vector field is undetermined when $\alpha =-3$ and $\lambda =-\sqrt{6}$ at a time as all the eigenvalues of Jacobian matrix are 0.

$\bullet$ The critical point is non-hyperbolic for $\alpha =-3$. As Hartman–Grobman Theorem can not be used to analyze the critical point, we shall use center manifold theory (CMT).

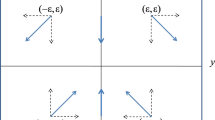
By CMT there exits a continuously differentiable function $h:{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ such that $Y=h(X,{\bar{\Omega }}_m)=aX^2+bX{\bar{\Omega }}_m +c{\bar{\Omega }}_m^2 + \text {higher power terms}$, where $a,b,c\in {\mathbb {R}}$ [56]. We only concern about the non-zero coefficients of the lowest power terms in CMT as we analyze arbitrary small neighborhood of the origin.

Now differentiating both side with respect to N, we get

$$\begin{aligned} \frac{dY}{dN}&= [\, 2aX+b{\bar{\Omega }}_m \quad bX+2c{\bar{\Omega }}_m \,]\begin{bmatrix} \frac{dX}{dN} \\\\ \frac{d{\bar{\Omega }}_m}{dN} \end{bmatrix} . \end{aligned}$$

(28)

Comparing L.H.S. and R.H.S. of (28) we get center manifold Y = 0. This two dimensional center manifold coincides with the two dimensional center subspace (X-${\bar{\Omega }}_m$)-plane near the origin. The flow on the CM is determined by the following equations

$$\begin{aligned} \frac{dX}{dN}= & {} 6X^2 + \text {higher power terms}, \end{aligned}$$

(29)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} 3(X^2+2X){\bar{\Omega }}_m + \text {higher power terms}. \end{aligned}$$

(30)

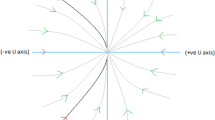
We take $r^2=X^2+{\bar{\Omega }}_m^2$ in arbitrary small neighborhood of the origin. Differentiating with respect to N, we get ${\dot{r}}=6Xr$. For $X<0$ one has ${\dot{r}}<0$, while ${\dot{r}}>0$ for $X>0$. Thus the behavior of the vector field depends on the change of X and Y coordinates. If we project the vector field on the plane which is parallel to XY-plane, the origin is a saddle-node and unstable in nature for $\alpha =-3$ and $\lambda >-\sqrt{6}$ (Fig. 1a) or $\lambda <-\sqrt{6}$ (Fig. 1b).

• The critical point is non-hyperbolic for $\lambda =-\sqrt{6}$. So by CMT there exists a continuously differentiable function $h:{\mathbb {R}}\rightarrow {\mathbb {R}}^2$ such that

$$\begin{aligned} h(Y)= \begin{bmatrix} X\\ \Omega _m \end{bmatrix}&= \begin{bmatrix} a_1Y^2 + a_2Y^3+ \text {higher power terms}\\\\ b_1Y^2 + b_2Y^3+ \text {higher power terms} \end{bmatrix}. \end{aligned}$$

(31)

Differentiating both side with respect to N, we get

$$\begin{aligned} {\dot{X}}= & {} (2a_1Y+3a_2Y^2){\dot{Y}} + \text {higher power terms}, \end{aligned}$$

(32)

$$\begin{aligned} \dot{{\bar{\Omega }}}_m= & {} (2b_1Y+3b^2Y^2){\dot{Y}} + \text {higher power terms}. \end{aligned}$$

(33)

Comparing coefficients corresponding to power of Y we get $a_1=-\frac{1}{2}$ and $b_i=0$ for i = 1,2,..., that is,

$$\begin{aligned} X= & {} -\frac{1}{2}Y^2 + \text {higher power terms}, \end{aligned}$$

(34)

$$\begin{aligned} {\bar{\Omega }}_m= & {} 0. \end{aligned}$$

(35)

This implies that one dimensional center manifold lies on the (X–Y)-plane and tangent to the center subspace (Y-axis) at the origin. The flow on the CM near the origin is determined by

$$\begin{aligned} \frac{dY}{dN}=-\frac{3}{2}Y^3+ \text {higher power terms}. \end{aligned}$$

(36)

If we see the vector field in the 3D-space, the origin is saddle-node for $\alpha >-3$ and $\lambda =-\sqrt{6}$ (Fig. 2a) and unstable in nature. The origin is stable-node for $\alpha <-3$ and $\lambda =-\sqrt{6}$ (Fig. 2b) and stable in nature.

3.2 Critical point $P_2$

We shift the critical point $P_2$ to the origin by the coordinate transformation $x \rightarrow X-1$, $y \rightarrow Y$, $\Omega _m \rightarrow {\bar{\Omega }}_m$. The system of Eqs. (16–18) changes to

$$\begin{aligned} \frac{dX}{dN}= & {} \bigg (\alpha + 3\bigg )X+ \bigg (\frac{\alpha -9}{2}\bigg )X^2-\bigg (\frac{\alpha + 3}{2}\bigg )XY^2 \nonumber \\&+ \bigg (\frac{\alpha +3}{2}-\sqrt{\frac{3}{2}}\lambda \bigg )Y^2+\bigg (\frac{\alpha +3}{2}\bigg )X^3 \nonumber \\&+\text {higher power terms}, \end{aligned}$$

(37)

$$\begin{aligned} \frac{dY}{dN}= & {} \bigg (3-\sqrt{\frac{3}{2}}\lambda \bigg )Y - \bigg (3 - \sqrt{\frac{3}{2}}\lambda \bigg )XY \nonumber \\&+ \frac{3}{2}X^2Y-\frac{3}{2}Y^3, \end{aligned}$$

(38)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} \bigg (\alpha +3\bigg ){\bar{\Omega }}_m+ 3\bigg (X^2-2X-Y^2\bigg ){\bar{\Omega }}_m . \end{aligned}$$

(39)

• The critical point is non-hyperbolic for $\alpha =-3$. Similar to the point $P_1$, we get the center manifold Y = 0. This two dimensional center manifold coincide with the two dimensional center subspace (X-${\bar{\Omega }}_m$)-plane near the origin. The flow on the CM is determined by the following equations

$$\begin{aligned} \frac{dX}{dN}= & {} -6X^2 + \text {higher power terms}, \end{aligned}$$

(40)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} -6X{\bar{\Omega }}_m + \text {higher power terms}. \end{aligned}$$

(41)

We take $r^2=X^2+{\bar{\Omega }}_m^2$ in arbitrary small neighborhood of the origin. Differentiating with respect to N, we get ${\dot{r}}=-6Xr$. For $X<0$ one has ${\dot{r}}>0$, while ${\dot{r}}<0$ for $X>0$. Thus the behavior of the vector field depends on the change of X and Y coordinates. If we project the vector field on the plane which is parallel to XY-plane, the origin is a saddle-node and unstable in nature for $\alpha =-3$ and $\lambda <\sqrt{6}$ (Fig. 3a) or $\lambda >\sqrt{6}$ (Fig. 3b).

Fig. 2

Vector field near $P_1$ for $\alpha \ne -3$ and $\lambda =-\sqrt{6}$. All center manifolds (blue curves) lie on (X-Y)-plane

Fig. 3

Vector field near $P_2$ for $\alpha =-3$ and $\lambda \ne \sqrt{6}$

• The critical point is non-hyperbolic for $\lambda =\sqrt{6}$. By similar procedure as stated for $P_1$, the center manifold at the origin is

$$\begin{aligned} X= & {} -\frac{1}{2}\bigg (\frac{\alpha -3}{\alpha +3}\bigg )Y^2 + \text {higher power terms} \end{aligned}$$

(42)

$$\begin{aligned} {\bar{\Omega }}_m= & {} 0 \end{aligned}$$

(43)

The flow on the center manifold near the origin is determined by

$$\begin{aligned} \frac{dY}{dN}=- \frac{3}{2}Y^3 + \text {higher power terms.} \end{aligned}$$

(44)

For $\lambda =\sqrt{6}$ we get three different phase diagrams near the origin (shifted system) depending on $\alpha$. The origin is a saddle for $-3<\alpha <3$ (see Fig. 4a) so unstable in nature, stable node for $\alpha <-3$ (see Fig. 4b) and saddle in nature for $\alpha >3$ (see Fig. 4c).

Next we consider $\lambda \ne 0$ for the existence of the critical points $P_3$ to $P_6$ and to make the corresponding autonomous system continuously differentiable. For this, we consider $-\sqrt{6}<\lambda <\sqrt{6}$ same as $\lambda \in (-\sqrt{6},0) ~\cup ~(0,\sqrt{6})$.

3.3 Critical point $P_3$

We shift the critical point $P_3$ to the origin by the coordinate transformation $x \rightarrow X-\frac{\lambda }{\sqrt{6}}$, $y \rightarrow Y + \sqrt{1-\frac{\lambda ^2}{6}}$, $\Omega _m \rightarrow {\bar{\Omega }}_m$. The system of Eqs. (16–18) changes to

$$\begin{aligned} \frac{dX}{dN}= & {} \bigg (\lambda ^2 +\alpha -3 \bigg )X\nonumber \\&-\sqrt{1-\frac{\lambda ^2}{6}}\bigg (\sqrt{6}\frac{\alpha }{\lambda } +\sqrt{ \frac{3}{2}}\lambda \bigg )Y -\sqrt{\frac{3}{2}}\bigg (\frac{\alpha }{\lambda }+\frac{\lambda }{2}\bigg ) Y^2 \nonumber \\&+ \sqrt{\frac{3}{2}}\bigg (\frac{\alpha }{\lambda }-\frac{3\lambda }{2}\bigg ) X^2 -3\sqrt{1-\frac{\lambda ^2}{6}}\bigg (1+\frac{2\alpha }{\lambda ^2}\bigg )XY \nonumber \\&+ \text {higher power terms}, \end{aligned}$$

(45)

$$\begin{aligned} \frac{dY}{dN}= & {} \bigg (\frac{\lambda ^2}{2}-3\bigg )Y + \frac{3}{2}\sqrt{1-\frac{\lambda ^2}{6}}X^2 \nonumber \\&- \frac{9}{2}\sqrt{1-\frac{\lambda ^2}{6}}Y^2 -\frac{3}{2}Y^3 + \frac{3}{2}X^2Y, \end{aligned}$$

(46)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} \bigg (\lambda ^2 + \alpha -3\bigg ){\bar{\Omega }}_m \nonumber \\&+ \bigg (3X^2-3Y^2-\sqrt{6}\lambda X -6\sqrt{6-\lambda ^2}Y\bigg ){\bar{\Omega }}_m. \end{aligned}$$

(47)

$P_3$ is a non-hyperbolic critical point for $\alpha + \lambda ^2=3$ (considering $-\sqrt{6}<\lambda < \sqrt{6}$). By CMT there exits a continuously differentiable function $h:{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ such that $Y=h(X,{\bar{\Omega }}_m)=aX^2+bX{\bar{\Omega }}_m +c{\bar{\Omega }}_m^2 + \text {higher power terms}$, where $a,b,c\in {\mathbb {R}}$. We only concern about the non-zero coefficients of the lowest power terms in CMT as we analyze arbitrary small neighborhood of the origin.

Fig. 4

Vector field near $P_2$ for $\alpha \ne \pm 3$ and $\lambda = \sqrt{6}$. All center manifolds (blue curves) lie on (X–Y)-plane

Now differentiating both side with respect to N, we get

$$\begin{aligned} \frac{dY}{dN}&= [\, 2aX+b{\bar{\Omega }}_m \quad bX+2c{\bar{\Omega }}_m \,] \begin{bmatrix} \frac{dX}{dN} \\\\ \frac{d{\bar{\Omega }}_m}{dN} \end{bmatrix} \end{aligned}$$

(48)

Comparing the coefficients corresponding to the $X^2$, $X{\bar{\Omega }}_m$ and ${\bar{\Omega }}_m^2$ we get $a=\frac{1}{2}\frac{1}{\sqrt{1-\frac{\lambda ^2}{6}}}$, b=0, c=0.

So the center manifold is

$$\begin{aligned} Y= \frac{1}{2}\frac{1}{\sqrt{1-\frac{\lambda ^2}{6}}}X^2 + \text {higher power terms.} \end{aligned}$$

(49)

The flow on the center manifold near the origin is determined by

$$\begin{aligned} \frac{dX}{dN}= & {} -\sqrt{6}\lambda X^2 + \text {higher power terms,} \end{aligned}$$

(50)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} -\sqrt{6}\lambda X{\bar{\Omega }}_m - \frac{3}{4}\frac{1}{1-\frac{\lambda ^2}{6}}X^4{\bar{\Omega }}_m \nonumber \\&+ \text {higher power terms.} \end{aligned}$$

(51)

We take $r^2=X^2+{\bar{\Omega }}_m^2$ in arbitrary small neighborhood of the origin. Differentiating with respect to N, we get ${\dot{r}}=-\sqrt{6}\lambda Xr$ (ignoring higher power terms). Thus the nature of stability depends only on the change of X and Y coordinates and $\lambda$.

If we project the vector field on the plane which is parallel to XY-plane, the origin is a saddle-node and unstable in nature for $\alpha + \lambda ^2 =3$ and $-\sqrt{6}<\lambda <\sqrt{6}$ (Figs. 5, 6).

For $\lambda = \pm \sqrt{6}$ the critical point $P_3$ becomes identical to $P_1$ and $P_2$ respectively. So we skip this case. On the other hand, $P_3$ does not exist for $\lambda >\sqrt{6}$ or $\lambda <-\sqrt{6}$.

Fig. 5

Critical point $P_3$ for $\alpha + \lambda ^2=3$ and $-\sqrt{6}<\lambda <0$

Fig. 6

Critical point $P_3$ for $\alpha + \lambda ^2=3$ and $0>\lambda >\sqrt{6}$

3.4 Critical point $P_4$

We shift the critical point $P_4$ to the origin by the coordinate transformation $x \rightarrow X-\frac{\lambda }{\sqrt{6}}$, $y \rightarrow Y - \sqrt{1-\frac{\lambda ^2}{6}}$, $\Omega _m \rightarrow {\bar{\Omega }}_m$. The system of Eqs. (16–18) changes to

$$\begin{aligned} \frac{dX}{dN}= & {} \bigg (\lambda ^2 + \alpha -3\bigg )X \nonumber \\&+ \sqrt{1-\frac{\lambda ^2}{6}} \bigg (\sqrt{6}\frac{\alpha }{\lambda } +\sqrt{\frac{3}{2}}\lambda \bigg )Y- \sqrt{\frac{3}{2}}\bigg (\frac{\alpha }{\lambda } + \frac{\lambda }{2}\bigg )Y^2 \nonumber \\&+ \sqrt{\frac{3}{2}}\bigg (\frac{\alpha }{\lambda } - \frac{3\lambda }{2}\bigg ) + 3\sqrt{1+\frac{\lambda ^2}{6}}\bigg (1+\frac{2\alpha }{\lambda ^2}\bigg ) \nonumber \\&+ \text {higher power terms,} \end{aligned}$$

(52)

$$\begin{aligned} \frac{dY}{dN}= & {} \bigg (\frac{\lambda ^2}{2}-3\bigg )Y - \frac{3}{2}\sqrt{1-\frac{\lambda ^2}{6}}X^2 \nonumber \\&+ \frac{9}{2}\sqrt{1-\frac{\lambda ^2}{6}}Y^2 -\frac{3}{2}Y^3 + \frac{3}{2}X^2Y \end{aligned}$$

(53)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} \bigg (\lambda ^2 + \alpha -3\bigg ){\bar{\Omega }}_m \nonumber \\&+ \bigg (3X^2-3Y^2-\sqrt{6}\lambda X +6\sqrt{6-\lambda ^2}Y\bigg ){\bar{\Omega }}_m . \end{aligned}$$

(54)

$P_4$ is a non-hyperbolic critical point for $\alpha + \lambda ^2=3$ (considering $-\sqrt{6}<\lambda < \sqrt{6}$). We put forward similar argument as we have mentioned for the analysis of $P_3$ and we get the center manifold

$$\begin{aligned} Y= -\frac{1}{2}\frac{1}{\sqrt{1-\frac{\lambda ^2}{6}}}X^2 + \text {higher power terms.} \end{aligned}$$

(55)

The flow on the center manifold near the origin is determined by

$$\begin{aligned} \frac{dX}{dN}= & {} -\sqrt{6}\lambda X^2 + \text {higher power terms} , \end{aligned}$$

(56)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} -\sqrt{6}\lambda X{\bar{\Omega }}_m - \frac{3}{4}\frac{1}{1-\frac{\lambda ^2}{6}}X^4{\bar{\Omega }}_m \nonumber \\&+ \text {higher power terms}, \end{aligned}$$

(57)

We take $r^2=X^2+{\bar{\Omega }}_m^2$ in arbitrary small neighborhood of the origin. Differentiating with respect to N, we get ${\dot{r}}=-\sqrt{6}\lambda Xr$ (ignoring higher power terms). Thus, similar to $P_3$, the nature of stability depends only on the change of X and Y coordinates and $\lambda$.

If we project the vector field on the plane which is parallel to XY-plane, the origin is a saddle-node and unstable in nature for $\alpha + \lambda ^2 =3$ and $-\sqrt{6}<\lambda <\sqrt{6}$ (Figs. 7, 8).

For $\lambda = \pm \sqrt{6}$ the critical point $P_4$ becomes identical to $P_1$ and $P_2$ respectively. So we skip this case. On the other hand, $P_4$ does not exist for $\lambda >\sqrt{6}$ or $\lambda <-\sqrt{6}$.

Fig. 7

Critical point $P_4$ for $\alpha + \lambda ^2=3$ and $-\sqrt{6}<\lambda <0$

Fig. 8

Critical point $P_4$ for $\alpha + \lambda ^2=3$ and $0>\lambda >\sqrt{6}$

3.5 Critical point $P_5$

$P_5$ is a non-hyperbolic critical point for any values of $\alpha$ and $\lambda$. We shift the critical point $P_5$ shifted to the origin by the coordinate transformation $x \rightarrow X+ \frac{\alpha -3}{\sqrt{6}\lambda }$, $y \rightarrow Y + \sqrt{\frac{\alpha }{3}+\frac{(\alpha -3)^2}{6\lambda ^2}}$, $\Omega _m \rightarrow {\bar{\Omega }}_m+\frac{3-\alpha }{3}(1-\frac{3-\alpha }{\lambda ^2})$. The system of Eqs. (16–18) changes to

$$\begin{aligned} \frac{dX}{dN}= & {} A_1X+A_2Y+ A_3 X^2 + A_4 Y^2 + A_5 XY \nonumber \\&+ \text {higher power terms}, \end{aligned}$$

(58)

$$\begin{aligned} \frac{dY}{dN}= & {} B_1X+B_2Y+ B_3 X^2 -3 B_3 Y^2 + B_4 XY \nonumber \\&+ \text {higher power terms}, \end{aligned}$$

(59)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} C_1X+C_2Y+C_3 X^2 - C_3 Y^2 \nonumber \\&+ C_4 X{\bar{\Omega }}_m + C_5 Y{\bar{\Omega }}_m + \text {higher power terms}. \end{aligned}$$

(60)

where

$$\begin{aligned} A_1= & {} 3\frac{\lambda ^2 \alpha }{(3-\alpha )^2}-\frac{\alpha ^2 \lambda ^2}{(\alpha -3)^2}+\frac{(\alpha -3)^2}{2\lambda ^2} -\frac{1}{2}(3+\alpha ),\\ A_2= & {} \sqrt{\frac{\alpha }{3}+\frac{(\alpha -3)^2}{6\lambda ^2}} \bigg (\sqrt{6}\frac{\alpha \lambda }{\alpha -3}-\sqrt{\frac{3}{2}}\frac{\alpha -3}{\lambda } -\sqrt{6}\lambda \bigg ),\\ A_3= & {} -3\sqrt{6}\frac{\alpha \lambda ^3}{(\alpha -3)^3}\bigg (1 -\frac{\alpha }{3}-\frac{(\alpha -3)^2}{6\lambda ^2}\bigg )+ \frac{9}{2}\frac{\alpha -3}{\sqrt{6}\lambda },\\ A_4= & {} \sqrt{\frac{3}{2}}\frac{\alpha \lambda }{\alpha -3}-\frac{3}{2}\frac{\alpha -3}{\sqrt{6}\lambda } -\sqrt{\frac{3}{2}}\lambda ,\\ A_5= & {} -2\sqrt{\frac{\alpha }{3}+\frac{(\alpha -3)^2}{6\lambda ^2}} \bigg (\frac{3}{2}+\frac{3\alpha \lambda }{\alpha -3} \bigg ),\\ B_1= & {} \sqrt{\frac{3}{2}}\sqrt{\frac{\alpha }{3}+\frac{(\alpha -3)^2}{6\lambda ^2}}\bigg (\lambda +\alpha -3\bigg ),\\ B_2= & {} -\frac{(\alpha -3)^2}{2\lambda ^2},\\ B_3= & {} \frac{3}{2}\sqrt{\frac{\alpha }{3}+\frac{(\alpha -3)^2}{6\lambda ^2}},\\ B_4= & {} \sqrt{\frac{3}{2}}\bigg (\lambda +\frac{\alpha -3}{\lambda }\bigg ),\\ C_1= & {} -\sqrt{\frac{2}{3}}\frac{(\alpha -3)^2}{\lambda } \bigg (1+\frac{\alpha -3}{\lambda ^2}\bigg ),\\ C_2= & {} 2\bigg (\alpha -3\bigg )\bigg (1+\frac{\alpha -3}{\lambda ^2}\bigg ) \sqrt{\frac{\alpha }{3}+\frac{(\alpha -3)^2}{6\lambda ^2}},\\ C_3= & {} \bigg (3-\alpha \bigg )\bigg (1-\frac{3-\alpha }{\lambda ^2}\bigg ),\\ C_4= & {} \sqrt{6}\bigg (\frac{\alpha -3}{\lambda }\bigg ),\\ C_5= & {} -6\sqrt{\frac{\alpha }{3}+\frac{(\alpha -3)^2}{6\lambda ^2}}. \end{aligned}$$

Here we consider $\alpha \ne 3$ to ensure the system to be continuously differentiable.

The Jacobian matrix at the origin is given by

$$\begin{aligned} J_{origin}= \begin{bmatrix} A_1&A_2&0\\ B_1&B_2&0\\ C_1&C_2&0 \end{bmatrix} . \end{aligned}$$

(61)

The eigenvalues are $\lbrace \lambda _1, \lambda _2,0 \rbrace$ (see Table 2). For mathematical simplicity, let us first consider $\alpha =-3$ which is something of a special case because for $\alpha =-3$ all critical points $P_1$ to $P_4$ become non-hyperbolic. For this case, we also consider $\lambda \in [-\sqrt{6},0)$ or $\lambda \in (0,\sqrt{6}]$ because outside these intervals the critical point $P_5$ does not exists. For $\alpha =-3$, the eigenvalues $\lambda _1$ and $\lambda _2$ are as follows

$$\begin{aligned} \lambda _1= & {} \frac{1}{2}\sqrt{\frac{\lambda ^4}{4}-4\bigg \lbrace -\frac{324}{\lambda ^4}-\bigg (\frac{6}{\lambda ^2}-1\bigg ) \bigg (\frac{9}{\lambda }-\frac{3}{2}\lambda \bigg )\bigg (\lambda -6\bigg ) -9\bigg \rbrace }\nonumber \\&-\frac{\lambda ^2}{4}, \end{aligned}$$

(62)

$$\begin{aligned} \lambda _2= & {} -\frac{1}{2}\sqrt{\frac{\lambda ^4}{4}-4\bigg \lbrace -\frac{324}{\lambda ^4}-\bigg (\frac{6}{\lambda ^2}-1\bigg ) \bigg (\frac{9}{\lambda }-\frac{3}{2}\lambda \bigg )\bigg (\lambda -6\bigg ) -9\bigg \rbrace }\nonumber \\&-\frac{\lambda ^2}{4}. \end{aligned}$$

(63)

For all values of $\lambda$ we get $\lambda _2<0$. But $\lambda _1>0$ for $\lambda \in (-\sqrt{6},0)$ or $\lambda \in (0,\sqrt{6})$. So for these $\lambda$, $P_5$ is saddle and unstable in nature.

Now we analyze the system for $\alpha =-3$ and $\lambda =\pm \sqrt{6}$. In this case, we get $\lambda _1=0$ , $\lambda _2=-3$ and $A_1=0$, $A_2=0$, $B_1=0$, $B_2=-3$, $C_1=0$ and $C_2=0$. Thus the Jacobian matrix takes the form as follows

$$\begin{aligned} J_{origin}(\alpha =-3,\lambda =\pm \sqrt{6})= \begin{bmatrix} 0&0&0\\ 0&-3&0\\ 0&0&0 \end{bmatrix}. \end{aligned}$$

(64)

By CMT there exits a continuously differentiable function $h:{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ such that $Y=h(X,{\bar{\Omega }}_m)=aX^2+bX{\bar{\Omega }}_m +c{\bar{\Omega }}_m^2 + \text {higher power terms}$, where $a,b,c\in {\mathbb {R}}$. As previously mentioned we only concern about the non-zero coefficients of the lowest power terms.

Now differentiating both side with respect to N, we get

$$\begin{aligned} \frac{dY}{dN}&= [\, 2aX+b{\bar{\Omega }}_m \quad bX+2c{\bar{\Omega }}_m \,]\begin{bmatrix} \frac{dX}{dN} \\\\ \frac{d{\bar{\Omega }}_m}{dN} \end{bmatrix}. \end{aligned}$$

(65)

Equating both sides with the coefficients of $X^2$, $X^2{\bar{\Omega }}_m$ and $X{\bar{\Omega }}_m^2$ in the identity (28) we get

$$\begin{aligned}&a=\frac{B_3}{3}, \end{aligned}$$

(66)

$$\begin{aligned}&bA_3 + 2cC_3 + bC_4=B_4c, \end{aligned}$$

(67)

$$\begin{aligned}&2cC_4=B_4c \end{aligned}$$

(68)

respectively. Now for $\alpha =-3$ and $\lambda =\sqrt{6}$, $A_3=-6$, ,$B_3=0$, $B_4=0$, $C_3=0$, $C_4=-6$ and $A_4=0$. This implies a=0 , b=0 and c=0.

By brute force calculation it is possible to show that all higher power coefficients are also zero. This yields the center manifold to be Y = 0. The flow on the center manifold for $\lambda =-\sqrt{6}$ at the origin is determined by

$$\begin{aligned} \frac{dX}{dN}= & {} 6X^2 + \text {higher power terms}, \end{aligned}$$

(69)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} 6X{\bar{\Omega }}_m +\text {higher power terms}. \end{aligned}$$

(70)

This yields ${\dot{r}}=6Xr$. So for $X>0$ implies ${\dot{r}}>0$ and for $X<0$ implies ${\dot{r}}<0$. So $P_5$ is saddle-node for $\alpha =-3,\lambda =- \sqrt{6}$ and that it is unstable in nature.

The flow on the center manifold for $\lambda =\sqrt{6}$ at the origin is determined by

$$\begin{aligned} \frac{dX}{dN}= & {} -6X^2 + \text {higher power terms}, \end{aligned}$$

(71)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} - 6X{\bar{\Omega }}_m +\text {higher power terms}. \end{aligned}$$

(72)

This yields ${\dot{r}}=-6Xr$. So, $X>0$ implies ${\dot{r}}<0$ and for $X<0$ implies ${\dot{r}}>0$. Hence $P_5$ is saddle-node for $\alpha =-3,\lambda =\sqrt{6}$ and that it is unstable in nature.

Next we analyze the system for arbitrary $\alpha$. In this case, the eigenvalues of Jacobian matrix become very complicated to characterize. For this reason we state some ranges of $\alpha$ and corresponding character of the vector field.

The discriminant is $D=(A_1+B_2)^2-4(A_1B_2-B_1A_2)$. Now the eigenvalues $\lambda _1$ and $\lambda _2$ can be following three types

• $D>0$: distinct real eigenvalues (see Table 3).

• $D<0$: complex conjugate eigenvalues (see Table 4).

• $D=0$: real equal eigenvalues (see Table 5).

Table 3 $D>0$: ranges of $\alpha$ and $\lambda$ for distinct real eigenvalues

Table 4 $D<0$: ranges of $\alpha$ and $\lambda$ for complex conjugate eigenvalues

Table 5 $D=0$: values of $\alpha$ and $\lambda$ for $\lambda _1$=$\lambda _2$

The Tables 3, 4 and 5 present the values of $\alpha$ and $\lambda$ for different character of eigenvalues. But all these critical points are not cosmologically viable as there is no phase transition of the evolution of the universe at these critical points. So we skip the discussion of these critical points in detail.

3.6 Critical point $P_6$

$P_6$ is a non-hyperbolic critical point for any values of $\alpha$ and $\lambda$. We shift the critical point $P_6$ to the origin by the coordinate transformation $x \rightarrow X+ \frac{\alpha -3}{\sqrt{6}\lambda }$, $y \rightarrow Y - \sqrt{\frac{\alpha }{3}+\frac{(\alpha -3)^2}{6\lambda ^2}}$, $\Omega _m \rightarrow {\bar{\Omega }}_m+\frac{3-\alpha }{3}(1-\frac{3-\alpha }{\lambda ^2})$. The system of Eqs. (16–18) changes to

$$\begin{aligned} \frac{dX}{dN}= & {} A_1X-A_2Y+ A_3 X^2 + A_4 Y^2 - A_5 XY \nonumber \\&+ \text {higher power terms}, \end{aligned}$$

(73)

$$\begin{aligned} \frac{dY}{dN}= & {} -B_1X+B_2Y- B_3 X^2 +3 B_3 Y^2 + B_4 XY \nonumber \\&+ \text {higher power terms}, \end{aligned}$$

(74)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} C_1X-C_2Y+C_3 X^2 - C_3 Y^2 + C_4 X{\bar{\Omega }}_m \nonumber \\&- C_5 Y{\bar{\Omega }}_m + \text {higher power terms}. \end{aligned}$$

(75)

The Jacobian matrix at the origin is given by

$$\begin{aligned} J_{origin}= \begin{bmatrix} A_1&-A_2&0\\ -B_1&B_2&0\\ C_1&-C_2&0 \end{bmatrix} . \end{aligned}$$

(76)

The eigenvalues are $\lambda _1$, $\lambda _2$ and 0 where

$$\begin{aligned} \lambda _1= & {} \frac{(A_1+B_2) + \sqrt{(A_1+B_2)^2 -4(A_1B_2-A_2B_1)}}{2},\\ \lambda _2= & {} \frac{(A_1+B_2) - \sqrt{(A_1+B_2)^2 -4(A_1B_2-A_2B_1)}}{2}. \end{aligned}$$

It is to be noted that the eigenvalues are same as $P_5$. Thus we forge ahead with the same analysis as of $P_5$ and we get center manifold Y=0. The flow on the center manifold for $\lambda =-\sqrt{6}$ at the origin is determined by

$$\begin{aligned} \frac{dX}{dN}= & {} 6X^2 + \text {higher power terms}, \end{aligned}$$

(77)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} 6X{\bar{\Omega }}_m +\text {higher power terms}. \end{aligned}$$

(78)

This yields ${\dot{r}}=6Xr$. So, $X>0$ implies ${\dot{r}}>0$ and for $X<0$ implies ${\dot{r}}<0$. Hence $P_6$ is saddle-node for $\alpha =-3,\lambda =- \sqrt{6}$ and that it is unstable in nature.

The flow on the center manifold for $\lambda =\sqrt{6}$ at the origin is determined by

$$\begin{aligned} \frac{dX}{dN}= & {} -6X^2 + \text {higher power terms}, \end{aligned}$$

(79)

$$\begin{aligned} \frac{d{\bar{\Omega }}_m}{dN}= & {} - 6X{\bar{\Omega }}_m +\text {higher power terms}. \end{aligned}$$

(80)

This yields ${\dot{r}}=-6Xr$. So $X>0$ implies ${\dot{r}}<0$ and for $X<0$ implies ${\dot{r}}>0$. Hence $P_6$ is saddle-node for $\alpha =-3,\lambda =\sqrt{6}$ and that it is unstable in nature.

4 Bifurcation analysis and cosmological upshot

In this section, we find the change of stability of all critical points of the autonomous system (16–18) by varying the parameters $\alpha$ and $\lambda$. We prepare bifurcation diagram corresponding to the sudden changes of stability of the critical points for small perturbation of the parameters and identify the phase transition of the universe. Finally we categorize the evolution of the universe corresponding to the evolutionary path without singularity.

For the sake of convenience to draw bifurcation diagrams we first summarize stability of the critical points for the change of parameters by tabular form as follows (Tables 6, 7, 8).

Table 6 Stability of $P_1$ and $P_2$ according to range of parameters

Table 7 Stability of $P_3$ and $P_4$ according to range of parameters

Table 8 Stability of $P_5$ and $P_6$ according to range of parameters

Fig. 9

Bifurcation diagram from Table 6 for $P_1$ varying parameters $\alpha$ and $\lambda$

The local bifurcation diagram for the critical point $P_1$ is shown in Fig. 9. The transition is visible in this diagram for the line $\alpha =-3$ where for $\lambda >-\sqrt{6}$, $P_1$ undergoes stable-node to saddle via non-hyperbolic saddle-nodes (blue line) and for $\lambda <-\sqrt{6}$, it passes through non-hyperbolic saddle-nodes (blue line) from stable-node to saddle. The another transition is visible in this diagram for the line $\lambda =-\sqrt{6}$ where for $\alpha <-3$, $P_1$ undergoes a change from saddle-node to stable-node via non-hyperbolic stable nodes (black line) and a change from unstable to saddle via non-hyperbolic saddle (red line) for $\alpha >-3$. Thus $\alpha =-3$ and $\lambda =-\sqrt{6}$ are lines of bifurcation values and $P_1$ is a bifurcation point.

The cosmological parameters corresponding to $P_1$ are $\Omega _m=0$, $\Omega _{\phi }=1$, $\omega _{\phi }=1$, $\omega _{total}=1$, q=2 and ${\dot{H}}<0$. Thus the universe is open and continue for scalar field dominated decelerating expansion. We also note that, in this case the self interacting potential vanishes.

Fig. 10

Bifurcation diagram from Table 6 for $P_2$ varying parameters $\alpha$ and $\lambda$

Figure 10 represents the local bifurcation diagram for $\alpha =-3$ line and $\lambda =\sqrt{6}$ line. The phase transition is visible for the line $\alpha =-3$ where for $\lambda >\sqrt{6}$, $P_2$ undergoes stable-node to saddle via non-hyperbolic saddle-nodes (blue line) and for $\lambda <\sqrt{6}$, it passes through non-hyperbolic saddle-nodes (blue line) from saddle-node to unstable-node. The another transition is visible in this diagram for the line $\lambda =\sqrt{6}$ where for $\alpha <-3$, $P_2$ undergoes a change from saddle to unstable-node via non-hyperbolic stable nodes (black line) and a change from unstable to saddle via non-hyperbolic saddle (red line) for $\alpha >-3$. Cosmological evolution at $P_2$ is same as of $P_1$.

Another local bifurcation is shown in Fig. 11 for the critical points $P_3$ and $P_4$ which exist for $-\sqrt{6}<\lambda <\sqrt{6}$. The transition is visible in this diagram for the curve $\alpha +\lambda ^2=3$. $P_3$ and $P_4$ undergo a change from stable-node ($\alpha +\lambda ^2<0$) to saddle ($\alpha +\lambda ^2>0$) via non-hyperbolic curve $\alpha +\lambda ^2=3$. On this curve $P_3$ and $P_4$ are saddle-node in nature. Thus $\alpha +\lambda =3$ is a curve of bifurcation values. In particular, ($\alpha ,\lambda$)=(3, 0) is a bifurcation value.

For $-\sqrt{6}<\lambda <\sqrt{6}$ , we note that, $-1\leqslant \omega _{\phi }<1$, $-1\leqslant q <2$, $\Omega _m=0$ and $\Omega _{\phi }=1$. For $\lambda =0$ the critical point $P_3$ represents dark energy dominated cosmological constant era with vanishing kinetic energy. It also represents exponential de-Sitter expansion of the universe. For $-2<\lambda <0$ or $0<\lambda <2$ the critical point represents phantom divide line in the cosmic evolution with accelerating power law expansion. For $\lambda <-\sqrt{6}$ or $\lambda >\sqrt{6}$, we get $\omega _{\phi }>1$, $\omega _{total}>1$ and $q>2$ which are not feasible cosmologically. For $\lambda =\pm \sqrt{6}$, we get $\omega _{\phi }=1$, $\omega _{total}=1$, $\Omega _{\phi }=1$ and q=2 which implies decelerating expansion of the universe with a free scalar field.

Fig. 11

Bifurcation diagram from Table 7 for $P_3$ and $P_4$ varying parameters $\alpha$ and $\lambda$

Fig. 12

Bifurcation diagram of the local stability of points $P_1$ to $P_6$ for $\alpha =-3$

Table 9 Different phase-generic evolution -decelerating to accelerating evolution

Furthermore, combining Figs. 9, 10 and 11 with Table 8 and fixing $\alpha =-3$ we can notice that bifurcation takes place for $\lambda =\pm \sqrt{6}$. This phenomenon is shown in Fig. 12. In this diagram $P_1$ and $P_2$ overlap by their Y-coordinates but their stability is opposite for $\lambda <\sqrt{6}$ and $\lambda >\sqrt{6}$: $P_1$ is stable-node (green line) and $P_2$ is unstable-node (red dotted line) for $\lambda <-\sqrt{6}$ and in turn, the stability is reverse for $\lambda >\sqrt{6}$.

When $\lambda$ crosses $-\sqrt{6}$ from left, $P_1$ becomes unstable and two stable and two unstable fixed points appear in the picture. It is so to speak a combination of the sub-critical and supercritical pichfork bifurcation: the fixed points $P_1$, $P_3$ and $P_4$ behave like supercritical pichfork bifurcation, while the fixed points $P_1$, $P_5$ and $P_6$ behave like sub-critical pichfork bifurcation. Similar behavior of dynamics can be found for $\lambda =\sqrt{6}$ also.

At $P_5$ and $P_6$ we have $\omega _{total}=-\frac{\alpha }{3}$ and $q=\frac{1-\alpha }{2}$, so for $\alpha =3$ the critical point represents cosmological constant era with exponential de-Sitter expansion. For $-3<\alpha <3$ the critical point represents phantom phase of the universe and for $\alpha >3$ the universe would be in the case of Big-Rip singularity. The universe experiences accelerating expansion for $\alpha >1$ and decelerating expansion for $\alpha <1$.

Finally, we can divide the evolution of the universe with respect to the critical points into two groups: representing generic and non-generic evolution. The generic evolution occurs,when there exists a family of solutions satisfying given initial conditions, while the non-generic evolution takes place if one particular solution exists for given initial conditions. To be specific, when a family of trajectory comes out of a unstable point in the early equilibrium (like unstable node/focus or saddle-node) representing a phase and then finishes in a stable point also representing the same phase is called generic evolution [57]. We mention some generic and non-generic evolution of the universe in tabular form (see Tables 9, 10). It is speculated that non-generic evolution occurs at the bifurcation values.

Table 10 Non-generic evolution at bifurcation values

Fig. 13

Phase transition of the universe at the bifurcation value $\alpha =3$

Fig. 14

Phase transition of the universe at the bifurcation values $\lambda =\pm \sqrt{6}$

Figure 13 presents the local phase transition of cosmological evolution for $\lambda =0$ and $\alpha =3$. The only transition of the cosmological solution is visible from non-phantom model to phantom one via vanishing kinetic energy for $\alpha =3$. So the cosmological model is structurally unstable in the case of non-generic evolution of the universe. On the other hand, Fig. 14 presents the universe passes through a free scalar field stiff fluid era for $\lambda =\pm \sqrt{6}$ and $\alpha =-3$ to transit non-vanishing scalar field to non-vanishing one.

5 Discussion

An unstable fixed point may be considered as an initial position of the universe and a small perturbation scamper the start of the trajectory of the universe. The initial position of the universe drives a unique trajectory which starts from an arbitrary close neighborhood of an unstable critical point (CP) and stops to an arbitrary close neighborhood of a stable critical point or goes to infinity. As our phase space is finite region of infinite paraboloid, so we skip the infinity case. The qualitative global behavior of the trajectory of the universe is described by inspecting the local behavior of critical points.

The critical points $P_1$ to $P_4$ are shown to be non-hyperbolic equilibrium points for certain choices of the parameters $\alpha$ and $\lambda$. The critical point $P_1$ is non-hyperbolic in nature for the choices $\alpha =-3$ or $\lambda =-\sqrt{6}$ or both. However, $\alpha =-3$ and $\lambda =-\sqrt{6}$ is not chosen simultaneously as the vector field is undetermined. From Figs. 1a, b, we see that for $\alpha =-3$ and $\lambda \ne -\sqrt{6}$ the critical point $P_1$ is a saddle-node and unstable in nature while for $\lambda =-\sqrt{6}$, $P_1$ is unstable saddle for $\alpha >-3$ and stable node for $\alpha <-3$. Cosmologically, the critical point is not interesting as it represents a scalar field dominated decelerating era. Note that the critical point $P_2$ has identical behavior as $P_1$ from the cosmological point of view. The non-hyperbolic critical point $P_3$ is analyzed for the parametric restriction $\alpha +\lambda ^2=3$ and $\lambda ^2 \ne 6$ so that we have unstable saddle-node as shown in Figs. 5 and 6. From cosmological point of view, the equilibrium points $P_3$ and $P_4$ are equivalent and both of them are dark energy dominated. The model represents accelerated era of expansion for $\lambda ^2<2$ while it will be in decelerating phase for $\lambda ^2>2$. The equilibrium points $P_5$ and $P_6$ are non-hyperbolic in nature without any restriction on the parameters $\alpha$ and $\lambda$. Both the critical points represent cosmological scaling solution. The effective single fluid will be of quintessence nature if $1<\alpha <3$ while phantom nature is characterized by the restriction $\alpha >3$.

The application of bifurcation theory allows us to distinguish some classes of non-generic and generic evolutionary scenarios for either cosmological constant or free scalar field. There are non-singular evolutionary paths from decelerating phase to accelerating phase of the universe. There are two types of initial state from which the universe starts evolution. In the first scenario, the universe is emergent from decelerating expansion with free scalar field and in second one, the universe is emergent from the exponential de Sitter expansion with cosmological constant era. From the bifurcation analysis, we have obtained a lines of bifurcation values varying $\alpha$ and $\lambda$. We also notice phase transition of the universe at the bifurcation value $\alpha =3$ or $\lambda =\pm \sqrt{6}$.