Abstract
We present the first performance results obtained with microwave multiplexed Transition Edge Sensors prototypes specifically designed for the HOLMES experiment, a project aimed at directly measuring the electron neutrino mass through the calorimetric measurement of the \(^{163}\)Ho electron capture spectrum. The detectors required for such an experiment feature a high energy resolution at the Q–value of the transition, around \(\sim \) 2.8 keV, and a fast response time combined with the compatibility to be multiplexed in large arrays in order to collect a large statistics while keeping the pile-up contribution as small as possible. In addition, the design has to be suitable for future ion-implantation of \(^{163}\)Ho. The results obtained in these tests allowed us to identify the optimal detector design among several prototypes. The chosen detector achieved an energy resolution of (4.5 ± 0.3) eV on the chlorine K\(_\alpha \) line, at \(\sim \) 2.6 keV, obtained with an exponential rise time of 14 \(\upmu \)s. The achievements described in this paper pose a milestone for the HOLMES detectors, setting a baseline for the subsequent developments, aiming to the actual ion-implantation of the \(^{163}\)Ho nuclei. In the first section the HOLMES experiment is outlined along with its physics goal, while in the second section the HOLMES detectors are described; the experimental set-up and the calibration source used for the measurements described in this paper are reported in Sects. 3 and 4, respectively; finally, the details of the data analysis and the results obtained are reported in Sect. 6.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 HOLMES experiment
Measuring the value of the absolute neutrino mass would represent a major breakthrough with profound consequences in cosmology and particle physics [1]. Indeed, due to their abundance as big-bang relics, massive neutrinos strongly affect the large-scale structure and dynamics of the universe [2, 3]. In addition, the knowledge of the scale of neutrino masses, together with their hierarchy pattern, is invaluable to clarify the origin of fermion masses beyond the Higgs mechanism [4, 5].
The HOLMES experiment [6] aims at directly measuring the electron neutrino mass with a sensitivity [7] around 2 eV/c\(^2\) through the calorimetric measurement [8] of the energy released in the decay of \(^{163}\)Ho [9]. This isotope decays via electron capture to an atomic excited state of \(^{163}\)Dy which in turn relaxes mostly by emitting Auger electrons, with a fluorescence yield less than 10\(^{-3}\) [9]. This decay is characterized by a relatively short half-life of about 4570 years, and features an advantageous low energy end-point of \((2833\pm 30_{{\text{ stat }}}\pm 15_{{\text{ sys }}})\) eV [10]. This low value, along with the proximity of the M1 de-excitation line to the end-point, ensures a relatively large fraction of events in the region of interest. The effect of a finite neutrino mass can be appreciated solely in the high energy end of the spectrum, where, unfortunately, only a small fraction of events lies.
One major limiting factor to the achievable statistical sensitivity with the calorimetric approach [7] is the background due to undetected event pile-up: two events of energies \(E_1\) and \(E_2\) occurring within a time interval shorter than the time resolution of the detector are recorded and processed as a single event with an energy \(E{{\text{ tot }}}\simeq E_1+E_2\). The pile-up events for which \(E{{\text{ tot }}}\) is close to the end-point of the decay add a background in the spectrum, impairing the signal due the neutrino mass in the region of interest. Since the fraction of events affected by undetected pile-up is given by \(f_{{\text{ pp }}}\approx \) \(A_{{\text{ EC }}}\)\(\tau _{{\text{ R }}}\) [11], where \(A_{{\text{ EC }}}\) is the \(^{163}\)Ho activity per detector and \(\tau _R\) is the time resolution, the detectors must feature a very fast response, and a trade-off between the activity per detector and pile-up has to be found.
Besides, given the strong dependence of the experimental sensitivity on the total statistics [7], a large number of detectors working in parallel is necessary. Since the dependence of the sensitivity is stronger on the number of events rather than on the pile-up fraction, it pays off to increase the activity of each detector in spite of a larger pile-up contribution. However, the maximum activity per detector might be constrained by the implantation concentration, i.e. the number of implanted nuclei per volume, and by the bearable pile-up.Footnote 1.
The baseline of HOLMES foresees the deployment of 1000 microwave multiplexed [13] microcalorimeters coupled to transition edge sensors (TES) [14, 15] capable of energy and time resolutions of 1 eV FWHM and 1 \(\upmu \)s, respectively, at the Q-value of the decay (\(\sim 2.8\) keV).
2 Detector design
Each of the HOLMES detector features a \(200\times 200\times 2~\upmu \hbox {m}^3\) gold absorber coupled to a TES thermometer; about \(6.5\times 10^{13}\) \(^{163}\)Ho atoms will be ion-implanted in each absorber providing an activity of \(\sim 300\) Bq per detector. The ion implantation will take place in a 1 \(\upmu \)m thick gold layer which will be then covered by a second 1 \(\upmu \)m thick layer for full containment of decay products. This method of embedding the \(^{163}\)Ho in metallic absorbers was firstly demonstrated by the ECHo collaboration [16, 17]. The total thickness of the absorber was chosen after extensive GEANT-4 [18] based Monte Carlo simulations to provide full containment of the 99.99% (96.73%) of the most energetic electrons (photons) produced in the decay, which have an energy around 2 keV. Each absorber is coupled to a Mo/Cu bi-layer TES tuned to have a transition temperature \(T_{{\text{ c }}}\approx 100\) mK. The entire structure is suspended on a Si\(_2\)N\(_3\) membrane. Although in the initial configuration [19] a bismuth absorber was to be placed atop of the TES, tests have shown that this material affects the detector response causing an undesirable tail on the low energy side of a monochromatic energy peak. The same behavior concerning bismuth absorbers was found in different TES microcalorimeters [20]. Furthermore, by replacing the bismuth with gold and maintaining the same design, the transition shape showed suppression of the \(T_{{\text{ c }}}\) due to proximity effects of the superconductor beneath the gold layer [21]: this is reflected in an undesirable kink in the transition shape which in turn causes strong non-linearity in the detector response. It was then decided to place the absorber besides the TES and to couple them through a copper link. In the final array configuration the detectors will be packed as closely as possible to maximize the geometrical filling, which strongly affects the \(^{163}\)Ho embedding efficiency.
2.1 Holmium-163 embedding
The isotope embedding process will finally allow us to implant as many as 6.5\(\times 10^{13}\) \(^{163}\)Ho nuclei per detector, corresponding to an activity of about 300 Bq. \(^{163}\)Ho embedding will be performed using a custom ion implantation system produced by Danfysik which is composed of five main components: (1) a sputter ion source containing \(^{163}\)Ho; (2) an acceleration section with a maximum potential of 50 kV, which allows to achieve an implantation depth of the order of few tens of nanometers; (3) a dipole magnet mass analyzer; (4) a focusing electrostatic triplet; (5) a magnetic XY scanning stage.
The magnetic mass selection is required to avoid contaminants that can not be separated chemically. \(^{163}\)Ho is produced by neutron irradiation of erbium enriched in \(^{162}\)Er [22]. Yet, other isotopes in the erbium sample provide path to the production of \(^{166m}\)Ho. For example, the enriched erbium sample contains also \(^{164}\)Er which undergoes neutron capture to \(^{165}\)Er. \(^{165}\)Er decays \(\beta \) to \(^{165}\)Ho which in turn undergoes neutron capture to \(^{166m}\)Ho. For each \(^{163}\)Ho MBq produced, a contamination of the order of the kBq of \(^{166m}\)Ho is expected. Since \(^{166m}\)Ho decays \(\beta \) with a Q-value of about 1856 keV, its presence along with \(^{163}\)Ho is deleterious for the neutrino mass measurement: in fact the decay of this isotope in the detector absorber causes a background concealing the effect due to a non-vanishing neutrino mass. For this reason, along the beam line a dipole magnet is placed and tuned to eliminate any eventual trace of \(^{166m}\)Ho.
Schematics of the readout used for HOLMES. The orange portion of the drawing is the bias circuit with the sensors, the shunt resistors and the coupling inductors to the rf-SQUIDs (purple). These, in turn, are coupled to the flux-rump modulation line (green) and to the resonators belonging to the multiplexing board (black). All these components are kept at few tens of millikelvin
The ion implantation system includes a chamber where the detectors being implanted are hosted and which is equipped with an ion beam assisted sputtering system. The sputtering device allows the in-situ deposition of the final 1 \(\upmu \)m gold layer on the detector absorbers thereby avoiding any risk of oxidation for the \(^{163}\)Ho ions: in fact the chemical environment and in particular the holmium oxidation state might induce a chemical shift of the spectrum end-point by affecting the available decay energy Q. Moreover the system allows the co-deposition of gold during the ion implantation process which is crucial for two purposes. First of all it compensates for the sputtering of the detector absorber caused by the impinging holmium ion beam which limits the maximum embeddable \(^{163}\)Ho activity to few becquerels as shown by our SRIM [23] simulations; simulations carried independently by the ECHo collaboration reached similar conclusions [24]. Second it can be used to control the local holmium concentration in the gold absorber: in fact too high concentrations might give rise to an excess heat capacity due to hyperfine level splitting [25].
3 Experimental set-up
HOLMES will be set-up in a dilution refrigerator (Oxford Instruments, model Triton 200), used to maintain the detectors at few tens of mK. At this cryogenic temperatures, the heat load introduced by the electrical wires used for the operation of the detectors becomes comparable with the cooling power of the fridge, so the cabling must be done with great care and limiting the number of wires as much as possible. Reading-out each of the 1000 detectors independently would dramatically increase the number of wires, and hence the heat load, far beyond the available cooling power. For this reason a multiplexing scheme will be adopted in HOLMES: each of the voltage biased TES is coupled to a rf-SQUID which is in turn coupled to a quarter wavelength resonator which oscillates in the GHz range. Each resonator is designed to ring at a unique characteristic frequency so all the resonators can be coupled to a common feedline and read-out independently using a comb of tones. In order to linearize the periodic rf-SQUID response, a flux ramp modulation runs through a common line inductively coupled to each rf-SQUID. The electrical diagram is shown in Fig. 1.
Prior to the implantation of \(^{163}\)Ho in the TESs absorbers, we carried out work aimed at selecting the optimal detector configuration among several different designs and at testing the read-out chain. We finally focused on 4 slightly different alternatives (Fig. 2) of the same baseline design (a): all the variants display the gold absorber placed besides the temperature sensor; the two parts are connected with each other by means of a copper link. The sensor is also connected to a copper bar structure surrounding the whole detector and intended to increase the thermal conductance toward the heat bath by phonon irradiation. We investigated two temperature sensor variants, the first one adopted by the detectors (a), (c), (d) features two copper bars used for the noise suppression [26]; as for the sensor used for the geometry (b), three bars are used. Besides, different TES-absorber thermal couplings were considered: (a) and (b) have a single copper stem, while (c) and (d) display a triangular shaped coupling. Finally, (d) is characterized by a higher heat capacity, \(\sim \) 1 pW/K instead of \(\sim \) 0.8 pW/K of the other designs, due to a higher copper mass used for the radiation bars coupled to the sensor. Even though a higher heat capacity may reduce the pulse height, and ultimately the energy resolution, such a characteristic can be favourable in terms of a wider dynamic range and a smaller slew rate of the detector response, if required. It is worth noticing that all the detectors share the same perimeter length of the radiation bars, setting the thermal conductance G towards the bath to a value around 600 pW/K. This relatively large value is intended for shortening the decay time of the pulses [27] and hence the dead time (see note 1) of each detector after an energy deposition. Assuming pulses lasting over a time interval of 300 \(\upmu \)s, the dead time of the system would be of the order of 10% with a 300 Hz counting rate. On the other hand, the rise time of each detector, at the first order, is set by the electrical cutoff of \(L/R_0\), where \(R_0\) is the resistance of the sensor at the working point, and L is a selectable stray inductance. In the measurements described here \(R_0\) is of the order of the m\(\Omega \), while L was chosen to be 50 nH in order to tune the rise time at the desired value of \(\sim \) 10 \(\upmu \)s.
The four detector variants that have been tested: the baseline design a displays a gold absorber (light purple) thermally linked by means of a copper element (orange) to the temperature sensor (yellow); the latter is connected to the bias and read-out circuit through electrical contacts (dark purple). The sensor is also linked to a copper structure that is intended to extend the external perimeter in order to increase the thermal conductance toward the thermal bath and hence shortening the fall time of the pulses. The entire structure is suspended by means of a \(\hbox {Si}_2\hbox {N}_3\) membrane (light gray). In b the sensor has one extra bar in the meander. The design c differs from a for the different thermal coupling between absorber and sensor. Finally, the d version differs from c for an increased mass of copper in the radiating structure: this increases the heat capacity by maintaining the thermal conductivity constant
4 Calibration source
A fluorescence source was employed to test the detectors: this was composed of a primary \(^{55}\)Fe source faced to a target containing calcium carbonate, sodium chloride and aluminum, so that the most intense characteristic X-ray lines of these elements were available, see Table 1.
The X-rays were collimated on the absorbers by a micro-machined silicon collimator placed above the detector chip to shadow the TES sensors and the membranes. The entrance window of the detector holder (Fig. 3a) for the X-rays was covered by a 6 \(\upmu \)m light-tight aluminum foil in order to stop the Auger electrons coming from the source and the thermal radiation emitted by the surroundings from hitting the detectors.
5 Detector read-out
The bias and ramp signals were carried by Nb–Ti superconducting twisted cables, while the microwave signals were fed to the multiplexing chip through coaxial cables made of different materials, chosen according to their characteristic thermal conductivity and signal attenuation: both on the input and output lines Cu–Be cables were employed between room temperature down to 4 K because of the low thermal conductivity ensured by this material in this temperature range; on the input line between the 4 K and the multiplexing chip stainless steel was chosen instead. Two 20 dB attenuators were placed on the input side at 4 K and at the base temperature stages to match the temperature noise. With the aim of minimizing the signal loss, the connection between the output of the multiplexing chip and the low-noise High Electron Mobility Transistor (HEMT) amplifier (Low Noise Factory model LNC4_8A), which is placed on the 4 K stage, was performed with superconducting Nb–Ti cables. Finally, to avoid signal reflection due to possible minor impedance mismatches, two cryogenic circulators (Quinstar model QCY–060400C000) configured as isolators were mounted at the input and output of the multiplexing chip.
a Detector holder with the multiplexing (green rectangle), detectors (red) and bias (purple) chip mounted. This last chip is glued on a PCB board responsible to distribute the bias and ramp signals to the bias and mux chips, respectively. Atop of the detector chip a collimator is mounted, in order to prevent direct interactions in the TES and in the membrane. b Detail of the mux chip with 6 of the 33 resonators: in the top part of the picture the common feedline running horizontally is visible. The resonant frequency, set by the length of the “trumpet”–shaped transmission line, is designed to be unique for each resonance; at the bottom end of each trumpet the SQUIDs are visible
The detectors were sampled at a ramp frequency of 500 kHz, which is also the effective signal sampling rate [13], and the ramp amplitude was chosen so that the SQUIDs swept through two entire oscillations within a ramp period. The read-out electronics of HOLMES exploits a ROACH2-based [28, 29] digital acquisition system combined with a fast ADC/DAC peripheral board. The DAC generates the comb of tones in base-band frequency [0–512 MHz]: these are up-converted via IQ-mixing (Marki model IQ0318) in the [4–8 GHz] frequency range to probe the resonators. The signal transmitted through the feedline is then amplified by the HEMT, characterized by a gain of + 45 dB and a noise temperature of 2 K, placed on the 4 K stage of the fridge, and a second time at room temperature (amplifier Mini-Circuits model ZVA-183+), where the signals are down-converted and digitized by the ADC, which is characterized by a bandwidth \(f_{{\text{ ADC }}}\) matching the DAC base-band frequency range. The ROACH FPGA (Xilinx Virtex6) takes care of the channelization and of the flux ramp demodulation, allowing a real-time reconstruction and triggering of the events. The maximum number of detectors readable with a single ROACH2 board (\(n_{{\text{ TES }}}\)) depends on the ramp frequency (\(f_{{\text{ RAMP }}}\)) and on the number of SQUID cycles per ramp period (\(n_{\phi _0}\)): \(n_{{\text{ TES }}}=f_{{\text{ ADC }}}/(2\cdot f_{{\text{ RAMP }}}\cdot n_{\phi _0}\cdot g_{{\text{ f }}})\), where \(g_{{\text{ f }}}\) is a guard factor defined as the ratio between the separation among two adjacent tones (\(\Delta f\)) and the bandwidth of a single resonance (\(f_{{\text{ BW }}}\)). In the case of HOLMES, \(\Delta f=14\) MHz and \(f_{{\text{ BW }}}=2\) MHz, so \(g_{{\text{ f }}}=7\). With such parameters 36 detectors could be simultaneously read-out with the same ROACH2 board. In the final configuration, though, this number will be reduced to 32 for practical reasons, related to the geometrical filling of the detector chip. It is worth noticing that the limiting factor for the maximum speed of the detectors is represented by \(f_{{\text{ ADC }}}\), which limits the width of the resonances and hence the maximum sampling rate of each pixel. In the future, leveraging new and faster ADCs, the stray inductance used for slowing down the response of the detectors could be eventually reduced, with a clear improvement in pile-up discrimination ability.
6 Data analysis
The amplitude of the pulses is evaluated with the optimal filtering technique [12]. The temperature of the thermal bath was stabilized using a resistive heater regulated by a PI (proportional and integrative) loop tuned to match the thermal constants of our cryogenic system: both the heater and the thermometer were placed on the detector holder in order to operate the detectors in stable and controlled conditions. Still, residual instabilities and drifts, consequent to bath temperature or bias voltage fluctuations, are visible in the data. These instabilities can degrade the best achievable energy resolution, if not corrected: given the strict correlation that occurs between the pre-trigger value of a pulse, which is related to the detector base temperature and bias voltage, and the amplitude of signals that follow the detection of a monochromatic X-ray, an off-line correction can be performed to mitigate the consequences of these effects.
The empirical second order calibration curve used to convert the output units of the SQUID (\(\phi _0\)) into energy units for the detector a: E [keV] = \(0.11927 \phi _0^2 + 2.7345 \phi _0 + 0.041166\). The errors are compatible with the dimensions of the points. It is possible to appreciate how the wide energy range considered for the calibration introduces an non-negligible error in evaluating the energies. This systematic error, though, will be reduced by great margin in the analysis of actual HOLMES data, because of the narrower energy range considered
Also, given the exiguity of number of samples (\(\sim \) 20) on the rising edge of the signal, the evaluation of the amplitude of the pulses can be affected by the arrival time of the pulses. These effects can be avoided by performing a smoothing of the signal [30] by means of a moving average. After evaluating the amplitude of every pulse an energy calibration of each detector is performed. The calibration function is a second order polynomial determined empirically, see Fig. 4.
To evaluate the energy resolutions properly, each characteristic X-ray line was fitted keeping into account its intrinsic width with a procedure which is described in Ferri et al. [31]. The Mn \(\hbox {K}{_{\alpha }}\) lines (Fig. 5), instead, were fitted keeping into account their complex intrinsic structure [32]. With these analysis procedures we obtained the energy resolutions reported in Table 2, while in Fig. 6 it is possible to appreciate the full energy spectra of the four detectors under study in raw units.
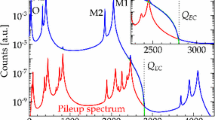
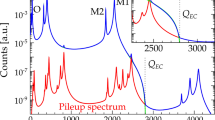
Full energy range spectra obtained with the 4 designs in flux quanta units: due to the inductive coupling in our design, 1 \(\phi _0\) is equal to \(\sim \) 11 \(\upmu \)A of current flowing in the TES. From the left to the right, the energy peaks are due characteristic X-ray of aluminum, chlorine, calcium and manganese. In the case of detectors (c) the manganese peak is not present because of limited dynamic range of this particular detector operated at this working point. The smaller pulse height of the detector (d) is due to the larger heat capacity respect to the other geometries, while for detector (b) the different design of the sensor might affect the conversion of heat into current signal
The contribution to the energy resolution due to the electrical noise (Fig. 7) was evaluated with the following process. The noise is calculated applying the optimum filter to empty data samples; the RMS value of these records is then converted into energy units with the same calibration curve used to convert the amplitude of the peaks into energy. The SQUID contribution to the total noise is limited by the noise temperature of the HEMT amplifier noise. The contribution to the energy resolution purely due to the noise for the investigated detectors are: (a) 3.3 eV; (b) 4.1 eV; (c) 4.1 eV; (d) 6.2 eV. With respect to the others, the design (b) appears to perform poorly in terms of peak energy resolution (Table 2) compared to its noise limit for unknown reasons. The performance of detector design (d) is limited by the smaller signal amplitude caused by the larger heat capacity: for this detector the peak FWHM is dominated by the electrical noise at all energies.
Noise power spectral density measured with the detector a with all its individual contributions [14]. The SQUID noise (green) is limited by the HEMT amplifier noise; \(R_{{\text{ TES }}}\) (dark blue) and \(R_{{\text{ LOAD }}}\) (light blue) are contributions caused by the Johnson noise of the TES resistance and of the load resistance of the bias circuit, respectively; finally, the noise contribution labeled as “G” (black) is the thermal fluctuation noise across the finite thermal conductance G. The peak at 62.5 kHz and its harmonics are due to an artifact of the demodulation algorithm. Nevertheless, these peaks do not contribute to the energy resolution thanks to the optimal filtering
Example of single event pulses due to the chlorine X-rays (\(\approx \) 2.6 keV) for the four different detector under study. The difference in amplitude among the four designs is explained in Fig. 6
A further analysis was performed to investigate the time response of the detectors, especially at the X-ray energy line of the chlorine, which is the closest in energy to the end-point of \(^{163}\)Ho. To this aim, the pulses (Fig. 8) were fitted with a function characterized by three exponentials, one on the rising edge and two on the decay: the two time constants on the fall of the pulses are necessary because of the existence of a weakly coupled subsystem in the absorber which causes the appearance of a long decay time constant [33]. Nevertheless, the long component of the pulses accounts just for few percent of the total event energy as calculated from the ratio of the integrals of the exponentials. The results of this analysis are reported in Table 3.
7 Conclusions
We have characterized four detector designs in order to identify the most suitable design for the needs of HOLMES, with particular care for rise time and energy resolution, which are crucial factors in achieving the desired sensitivity on the neutrino mass. The detectors analyzed in this contribution have shown very good energy resolution and time response performances; among these, we choose the design (c) as final detector prototype for HOLMES. From simulations, whose details are described in Ferri et al. [34], it is possible to establish that an exponential rise time of 15 \(\upmu \)s and a sampling frequency of 500 kHz allow an effective time resolution of 3 \(\upmu \)s by applying a Wiener filter to the pulses. This value might improve by a factor two with a singular value decomposition-based algorithm [35].
Respect to the baseline performances of HOLMES detectors, namely \(\Delta E_{{\text{ FWHM }}}=1\) eV, \(\tau _{{\text{ R }}}= 1 \upmu \)s, with the measured detector performances the expectations of HOLMES in terms of statistical sensitivity on the neutrino mass, for a fixed number of recorded events equal to 3\(\times \)10\(^{13}\), would be degraded of a factor \(\sim \) 20% according to simulations [7].
These results conclude the first phase of the HOLMES detector development. A second phase is already in progress, during which several aspects have to be optimized to get to the final detectors for HOLMES. After the embedding procedure is finalized and optimized the detectors will have to be tested with several different \(^{163}\)Ho concentrations, to verify that the implantation process, and the holmium concentration, do not spoil the baseline performances presented in this paper. During this phase, a two-step fabrication will be also implemented: the first step, made at NIST, foresees the deposition of the TES and of the first \(\upmu \)m of the gold absorber; during the second step, at INFN of Genova, the absorber are ion-implanted [36] and the gold absorber is finalized with the deposition of another \(\upmu \)m of gold. Finally, the silicon underneath the detector is etched away in order to release the membrane [37].
In this paper we presented the first application of microwave multiplexing of TESs where a large bandwidth budget is exploited for reading out highly energy resolving pixels designed to be very fast, with characteristic times of the order of tens of microseconds. In spite of this unusual and extreme design, in the case described in this paper the energy resolution is limited just by the signal to noise ratio: its value might be further improved by reducing the mass of the absorber for applications where such stopping power is not required. The ability of managing fast rise and decay times, with high speed transient digitizers, fast processors, and matching firmware and software is of great interest for all high counting rate applications which also demand high energy resolution.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The energy resolutions and the signals time constants are all reported as tables and figures.]
Notes
Even when two events are distant enough to be separated by the off-line analysis, they can cause pile-up if they are closer than the detector temperature relaxation time (i.e. the pulse decay time, \(\tau _{{\text{ dec }}}\)) In this case the safest analysis approach is to discard both events: the second pulse is altered because it is not starting from the quiescent operating temperature of the detector, whereas the first one can not be processed correctly because of the non-causality of the optimal filtering [12]. Therefore identifiable pile-up causes a dead-time due to the loss of a fraction of events of about few times \(A_{{\text{ EC }}}\)\(\tau _{{\text{ dec }}}\).
References
C. Giunti, C.W. Kim, Fundamentals of Neutrino Physics and Astrophysics (Oxford University Press, Oxford, 2007)
S. Hannestad, Prog. Part. Nucl. Phys. 65, 185 (2010). https://doi.org/10.1016/j.ppnp.2010.07.001
D. Boyanovsky, H.J. de Vega, N.G. Sanchez, Phys. Rev. D 77, 043518 (2008). https://doi.org/10.1103/PhysRevD.77.043518
R.N. Mohapatra et al., Rep. Prog. Phys. 70, 1757 (2007). https://doi.org/10.1088/0034-4885/70/11/R02
R.N. Mohapatra, A.Y. Smirnov, Annu. Rev. Nucl. Part. Sci. 56, 569 (2006). https://doi.org/10.1146/annurev.nucl.56.080805.140534
B. Alpert et al., Eur. Phys. J. C 75, 112 (2015). https://doi.org/10.1140/epjc/s10052-015-3329-5
A. Nucciotti, Eur. Phys. J. C 74, 3161 (2014). https://doi.org/10.1140/epjc/s10052-014-3161-3
A. Nucciotti, Adv. High Energy Phys. 2016, 9153024 (2016). https://doi.org/10.1155/2016/9153024
A. de Rújula, M. Lusignoli, Nucl. Phys. B 219, 277 (1983). https://doi.org/10.1016/0550-3213(83)90642-9
S. Eliseev et al., Phys. Rev. Lett. 115, 062501 (2015). https://doi.org/10.1103/PhysRevLett.115.062501
A. Nucciotti, E. Ferri, O. Cremonesi, Astropart. Phys. 34, 80 (2010). https://doi.org/10.1016/j.astropartphys.2010.05.004
E. Gatti, P.F. Manfredi, Riv. Nuovo Cim. 9, 1 (1986). https://doi.org/10.1007/BF02822156
O. Noroozian et al., Appl. Phys. Lett. 103, 202602 (2013). https://doi.org/10.1063/1.4829156
K.D. Irwin, G.C. Hilton, Transition-Edge Sensors, ed. by C. Enss. Cryogenic Particle Detection (Springer, Berlin, Heidelberg, 2005), pp. 63–150. https://doi.org/10.1007/10933596_3
J.N. Ullom, D.A. Bennet, Sucpercond. Sci. Technol. 28, 084003 (2015). https://doi.org/10.1088/0953-2048/28/8/084003
L. Gastaldo et al., Eur. Phys. J. Special Top. 226, 1623 (2017). https://doi.org/10.1140/epjst/e2017-70071-y
F. Schneider et al., Nucl. Instrum. Methods Phys. Res. B 376, 388 (2016). https://doi.org/10.1016/j.nimb.2015.12.012
S. Agostinelli et al., Nucl. Instrum. Methods Phys. Res. A 506, 250 (2003). https://doi.org/10.1016/S0168-9002(03)01368-8
M. Faverzani et al., IEEE Trans. Appl. Supercond. 26, 2100204 (2016). https://doi.org/10.1109/TASC.2016.2540242
H. Tatsuno et al., J. Low Temp. Phys. 184, 930 (2016). https://doi.org/10.1007/s10909-016-1491-2
M. Faverzani et al., J. Low Temp. Phys. 184, 922 (2016). https://doi.org/10.1007/s10909-016-1540-x
S. Heinitz et al., PLoS One 13, e0200910 (2018). https://doi.org/10.1371/journal.pone.0200910
www.srim.org. www.srim.org . Accessed 1 Apr 2019
L. Gamer et al., Nucl. Instrum. Methods Phys. Res. A 854, 139 (2017). 10.1016/j.nima.2017.02.056
K. Prasai et al., Rev. Sci. Instrum. 84, 083905 (2013). https://doi.org/10.1063/1.4816640
J.N. Ullom et al., Appl. Phys. Lett. 847, 4206 (2004). https://doi.org/10.1063/1.1753058
J.P. Hays-Wehle, D.R. Schmidt, J.N. Ullom, D.S. Swetz, J. Low Temp. Phys. 184, 492 (2016). https://doi.org/10.1007/s10909-015-1416-5
R. Duan et al., Proc. SPIE 7741, 77411V (2010). https://doi.org/10.1117/12.856832
S. McHugh et al., Rev. Sci. Instrum. 83, 044702 (2012). https://doi.org/10.1063/1.3700812
J.W. Fowler, B.K. Alpert, W.B. Doriese et al., J. Low Temp. Phys. 184, 374 (2016). https://doi.org/10.1007/s10909-015-1380-0
E. Ferri, S. Kraft-Bermuth, A. Monfardini, A. Nucciotti, D. Schaeffer, M. Sisti, Eur. Phys. J. A 48, 131 (2012). https://doi.org/10.1140/epja/i2012-12131-5
G. Hölzer et al., Phys. Rev. A 56, 4554 (1997). https://doi.org/10.1103/PhysRevA.56.4554
D.A. Bennet et al., Appl. Phys. Lett. 97, 102504 (2010). https://doi.org/10.1063/1.3486477
E. Ferri et al., J. Low Temp. Phys. 184, 405 (2016). https://doi.org/10.1007/s10909-015-1466-8
B. Alpert et al., J. Low Temp. Phys. 184, 263 (2016). https://doi.org/10.1007/s10909-015-1402-y
G. Gallucci et al., J. Low Temp. Phys. (2018). https://doi.org/10.1007/s10909-018-2086-x
A. Orlando et al., J. Low Temp. Phys. 193, 771 (2018). https://doi.org/10.1007/s10909-018-1968-2
Acknowledgements
The HOLMES experiment is funded by the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007–2013)/ERC Grant Agreement no. 340321. We also acknowledge support from the NIST Innovations in Measurement Science program. Mention of commercial products is for information only and does not imply recommendation or endorsement.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Alpert, B., Becker, D., Bennet, D. et al. High-resolution high-speed microwave-multiplexed low temperature microcalorimeters for the HOLMES experiment. Eur. Phys. J. C 79, 304 (2019). https://doi.org/10.1140/epjc/s10052-019-6814-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-6814-4