Models of charged compact objects with generalized polytropic equation of state

Abstract

In this work, we have studied the combined effect of charge and anisotropy on gravitational interaction of compact sources by making use of generalized polytropic equation of state (GPEoS). We have utilized four different values of polytropic index to ascertain the solution of Einstein–Maxwell field equations and develop a new class of spherically symmetric charged polytropic models. Further, we regain the masses of realistic strange stars 4U 1820-30, PSR J1614-2230, PSR J1903+327, Vela 4U and Vela X-1 that shows viability of the present study. Stability of presented models is analyzed by determining speed of sound that indicates the viability of newly generated models.

1 Introduction

The well known Lane–Emden equation (LEe) named after Lane [1] whose contribution is fundamental in establishing structure of stellar objects in the form of polytropes. Polytropes represent general solution of LEe playing vital role in the modeling of compact gravitational sources. The polytropic models has gained much attention in recent times because of their elementary equation of state (EoS). After the seminal work of Lane, the major contribution towards theory of polytropes in Newtonian regime was done by Chandareskhar [2], he developed the theoretical weak field models using polytropic EoS. In this context, Tooper [3,4,5] presented the general frame work for perfect fluid spheres by taking adiabatic and radiative models in context of general relativity. Kovetz [6] reviewed the work on distorted polytropes [7] and concluded that Chandareskhar’s work is free of discrepancies pointed in [8].

Discussion of white dwarfs in perspective of polytropes is made in [9], while Abramowicz [10] introduced the concept of higher dimensional polytropes and described the evolution of modified LEe in cylindrical, spherical and planner geometry. Komatsu et al. [11] explored the applications of rapidly rotating gravitating sources to uniformly rotating polytropes by using numerical techniques. Cook et al. [12] determined maximum mass and spin rate to diagnose stability for rotating polytropes. Azam et al. [13,14,15] constructed general framework to study the physical attributes of charged cylindrical and spherical sources via GPEoS. Matter configuration and physical parameters pertaining the kinematics of gravitating systems are vital in the study of stability analysis, in fact matter distribution is essential in modeling of physical problems. Bowers and Liang [16] considered anisotropy factor to study mass and surface redshift and conclude their results by presenting the comparison with isotropic stars. Cosenza et al. [17] presented general framework for handling of anisotropic gravitating sources. Many people [18,19,20,21,22,23,24,25] incorporate the pressure anisotropy to study the polytropic models with the help of different techniques such as perturbation approach, use of effective variables and Tolman mass etc.

Charge is another important factor that affects number of properties in polytropic models that is why significant contribution on impact of heat flux is found in literature. Bekenstien [26] studied gravitational collapse using hydrostatic equilibrium equation in charged compact objects. Bonor [27, 28] discussed mass and equilibrium configurations of charged compact objects, he explained that forces of repulsion due to charge may also effect gravitational collapse in realistic stars. Patiño and Rago [29] obtained exact solutions of the Einstein–Maxwell field equations (EMFEs) for static spherically symmetric distribution of charged matter through the extension of a method used for neutral configurations that are matched to the Reissner-Nordström exterior metric. Koppar et al. [30] explained the process to detect charge generalization in relativistic charged spheres. Ray et al. [31] discussed charged compact objects and observed that high density stars can have charge up to $10^{20}$ coulomb. Varela et al. [32] discussed analytical solutions of gravitating systems by extending Krori and Barua’s method for charged anisotropic configuration with linear or nonlinear EoS. Takisa and Maharaj [33] developed some new charged polytropic models. Azam et al. [34,35,36] found instability regions of charged compact objects through local density perturbations.

Isotropic coordinates are of great importance in making spacetime such as much Euclidean space that is vital in the studies related to static spherically symmetric sources. Boutros [37] used isotropic coordinates to find solution of relativistic EFEs for perfect fluid with of polytropic EoS. Mak and Harko [38] employed isotropic coordinates to split EFEs into two independent Riccati-type equations and established three new models of exact solutions. Crothers [39] explained gravitational interaction in detail by utilizing isotropic coordinates. Govender and Thirukkanesh [40] developed general framework for exact solution of EFEs by introducing pressure anisotropy and linear EoS in isotropic coordinates.

For modeling of any compact object a proper EoS is of fundamental importance. Chavanis [41, 42] modified usual polytropic EoS ($P_{r}=K\rho ^{1+\frac{1}{n}}$, where $P_{r}$ is radial pressure, K denotes polytropic constant and n stands for the polytropic index) and combined it with linear EoS ($P_{r}=\beta \rho _{0}$) to form GPEoS ($P_{r}=\beta \rho +\alpha \rho ^{1+\frac{1}{n}}$) which he used to explain number of cosmological situations and gave concept of late universe for $n<0$ and early universe for $n>0$. Freitas and Goncalves [43] developed model of universe using GPEoS and discussed primordial quantum fluctuations. Modeling of gravitating sources is quite significant in establishing of instability problems. Bondi [44] developed hydrostatic equilibrium equations to elaborate stability of gravitating sources. Various developments have been made in recent past to explain stellar structure either by using Schwarzschild or isotropic coordinates for polytropic index ranging from $1<n<5$. Pandey et al. [45] explained properties of polytropic models with index $\frac{1}{2}<n<3$, different values of polytropic indices have been chosen in [46] to study effect of anisotropic factor on spherically symmetric exact solutions. Ngubelanga and Maharaj [47, 50] found new classes of polytropic models and generate physically acceptable models for different values of polytropic indices. Azam et al. [49,50,51] calculated the cracking points of compact objects through local density perturbations.

In this manuscript, we have worked out the role of charge on recent contribution [46] to develop well behaved solutions of EMFEs. We have taken charged anisotropic spherically symmetric metric in isotropic coordinates with GPEoS. By taking different values of n, we develop four mathematical models that are physically viable. This article is organized in a way that Sect. 2 contains EMFEs and general model of polytropes, which gives us the exact values of matter variables and charge quantities. Integration of the system is described in Sect. 3. Properties of generalized polytropic models with $n=1, 2, \frac{2}{3}, \frac{1}{2}$ are discussed in Sect. 4. Section 5 contains properties and graphs for the model with $n=1$, in which we have used speed of sound for analysis followed by discussion and concluding remarks in the last section.

2 Einstein–Maxwell field equations

We consider static spherically symmetric spacetime

$$\begin{aligned} ds^2=-A^{2}(r)dt^{2}+B^{2}(r)[d r^{2}+r^2(d\theta ^{2}+sin^2\theta d \phi ^{2})],\nonumber \\ \end{aligned}$$

(1)

in isotropic coordinates $x^{a}$ = $t, r, \theta , \phi$. In Eq. (1) the metric functions A(r) and B(r) represents gravitational potential. The energy momentum tensor with charge for anisotropic fluid is as follows:

$$\begin{aligned} T_{i j}=diag\left( -\rho -\frac{1}{2} E^2,P_{r}-\frac{1}{2} E^2,P_{t} +\frac{1}{2} E^2,P_{t}+\frac{1}{2} E^2\right) ,\nonumber \\ \end{aligned}$$

(2)

where energy density, radial pressure, tangential pressure and electric field intensity are represented by $\rho$, $P_{r}$, $P_{t}$ and respectively. Equations (1) and (2) yields EMFEs

$$\begin{aligned} 8\pi \rho +\frac{1}{2}E^2= & {} -\frac{1}{B^2}\left[ 2\frac{B^{\prime \prime }}{B} -\frac{B^\prime }{B}\left( \frac{B^\prime }{B}-\frac{4}{r}\right) \right] , \end{aligned}$$

(3)

$$\begin{aligned} 8\pi p_r-\frac{1}{2}E^2= & {} 2\frac{A^{\prime }}{A}\left( \frac{B^\prime }{B^3} +\frac{1}{r}\frac{1}{B^2}\right) +\frac{B^\prime }{B^3} \left( \frac{B^\prime }{B}+\frac{2}{r}\right) , \nonumber \\\end{aligned}$$

(4)

$$\begin{aligned} 8\pi p_r+\frac{1}{2}E^2= & {} 2\frac{1}{B^2}\left[ \frac{B^{\prime \prime }}{B} -\frac{B^\prime }{B}\left( \frac{B^\prime }{B}-\frac{1}{r}\right) \right] \nonumber \\&+\frac{1}{B^2}\left( \frac{A^{\prime \prime }}{A}+\frac{1}{r}\frac{A^\prime }{A}\right) ,\end{aligned}$$

(5)

$$\begin{aligned} \sigma= & {} \frac{1}{4\pi r^2}\left( r^2 E\right) ^\prime , \end{aligned}$$

(6)

where $\sigma (r)$ denotes the charge density and prime represents derivative with respect to the radial coordinate. The above system of Eqs. (3)–(6), contains of six variables (A(r), B(r), $\rho$, $P_{r}$, E, $P_{t}$) with four equations. So for simplicity let us define new variables [50]

$$\begin{aligned} x\equiv r^2,~~~~~~~~~L\equiv B^{-1},~~~~~~~~~G\equiv LA, \end{aligned}$$

(7)

to express the onset of of EMFEs in equivalent form. Applying above transformation in Eqs. (3)–(6), we have

$$\begin{aligned} 8\pi \rho +\frac{1}{2}E^2= & {} 4\left[ 2xLL_{xx}-3(x L_x-L)L_x\right] , \end{aligned}$$

(8)

$$\begin{aligned} 8\pi p_r+\frac{1}{2}E^2= & {} 4L(L-2x L_x)\frac{G_x}{G}-4(2L-3x L_x)L_x, \nonumber \\\end{aligned}$$

(9)

$$\begin{aligned} 8\pi p_t+\frac{1}{2}E^2= & {} 4x L^2\frac{G_{xx}}{G}+4L(L-2x L_x)\frac{G_x}{G}\nonumber \\&-\,4(2L-3x L_x)L_x-8x L L_{xx}, \end{aligned}$$

(10)

$$\begin{aligned}&\sigma ^{2}=\frac{1}{4\pi ^{2}x}L^{2}(E+xE_{x})^{2}. \end{aligned}$$

(11)

Here subscript x denotes the derivative with respect to x and units are used here in such a way that the values for speed of sound and gravitational constant is unity. We assume that matter distribution satisfies the GPEoS which is of the form [13]

$$\begin{aligned} P_r =\beta \rho +\alpha \rho ^\Gamma , \end{aligned}$$

(12)

where $\Gamma$=$1+\frac{1}{n}$, and n represents polytropic index. The above equation is a combination of linear ($P_{r}=\beta \rho$) and polytropic ($P_{r}=\alpha \rho ^\Gamma$) The system of Eqs. (8)–(11) with (12) becomes

$$\begin{aligned} 8\pi \rho= & {} 4[2xLL_{xx}-3(xL_{x}-L)L_{x}]-\frac{1}{2}E^2, \end{aligned}$$

(13)

$$\begin{aligned} P_{r}= & {} \frac{\beta }{16\pi }[8(2xLL_{xx}-3(xL_{x}-L)L_{x})-E^2] \nonumber \\&+\frac{\alpha }{(16\pi )^{1+\frac{1}{n}}}\nonumber \\&[8(2xLL_{xx}-3(xL_{x}-L) L_{x})-E^2]^{1+\frac{1}{n}}, \end{aligned}$$

(14)

$$\begin{aligned} \Delta= & {} 4xL^2\frac{G_{xx}}{G}+4L(L-2xL_{x})\frac{G_{x}}{G} -4(2L-3xL_{x})L_{x} \nonumber \\- & {} 8xLL_{xx}-\frac{1}{2}E^2 \nonumber \\&-\frac{\beta }{2}[8(2xLL_{xx} -3(x L_{x}-L)L_{x})-E^2] \nonumber \\&-\frac{8\pi \alpha }{(16\pi )^{1+ \frac{1}{n}}}[8(2xLL_{xx} -3(x L_{x}-L)L_{x})-E^2]^{1+\frac{1}{n}}, \nonumber \\ \end{aligned}$$

(15)

$$\begin{aligned} \frac{G_{x}}{G}= & {} \frac{\beta }{4L(L-2xL_{x})}[8(2xLL_{xx} -3(xL_{x}-L)L_{x})-E^2]\nonumber \\&+\frac{2\pi \alpha }{L(L-2xL_{x})}\nonumber \\&\left[ \frac{8(2xLL_{xx}-3(xL_{x}-L) L_{x})-E^2}{16\pi }\right] ^{1+\frac{1}{n}}, \end{aligned}$$

(16)

$$\begin{aligned} \sigma ^2= & {} \frac{1}{4\pi ^2x}L^2(E+xE_{x})^2, \end{aligned}$$

(17)

where $\Delta =8\pi (P_{t}-P_{r})$ is measure of anisotropy. It is worth mentioning here that the system of Eqs. (13)–(17) is non linear in L and G, it contains six independent variables ($\rho$, $\Delta$, E, $\sigma$, L, G) and five equations. In order to solve this system, we need to define two variables in a single variable for exact solution. The gravitational mass function is defined as [50]

$$\begin{aligned} m(x)=2\pi \int _{0}^{x}\frac{1}{\sqrt{\tau }}\left[ \tau \rho (\tau ) +\frac{E^{2}}{8\pi }\right] d\tau . \end{aligned}$$

(18)

3 Fundamental equation for polytropic models

To obtain exact solution for matter variables in Eqs. (13)–(17), different authors have used the specific choices of L and E to formulated viable solutions with different equation of states [47,48,49]. These choices are physical acceptable, since the solutions obtained with some fixed values of parameters correspond to recent observations of compact objects like PSR J1614-2230, Vela X-1, PSR J1903+3217, and 4U 1820-30 [47,48,49]. These quantities are defined as

$$\begin{aligned} L=bx+a, \end{aligned}$$

(19)

where a and b are constants. A physically acceptable choice for the electric field is

$$\begin{aligned} E^2=x^s(c+dx)^q, \end{aligned}$$

(20)

where s and q takes on the constant values. Equations (19) and (20) together with (13) yield

$$\begin{aligned} 8\pi \rho =\left( \frac{24ab-c}{2}\right) -\frac{1}{2}dx, \end{aligned}$$

(21)

above equation represents energy density. Similarly, radial pressure turns out to be

$$\begin{aligned} P_{r}=\beta \left( \frac{24ab-c-dx}{16\pi }\right) +\alpha \left( \frac{24ab-c-dx}{16\pi }\right) ^{1+\frac{1}{n}}, \end{aligned}$$

(22)

where $\alpha$ and $\beta$ are constants, while the charge density takes the form

$$\begin{aligned} \sigma ^2=\frac{(a+bx)^2(2c+3dx)^2}{16\pi ^2x(c+dx)}. \end{aligned}$$

(23)

Thus Eq. (16) with Eqs. (19) and (20) becomes

$$\begin{aligned} \frac{G_{x}}{G}= & {} \frac{1}{8(a+bx)(a-bx)}\Big [16\pi \alpha \Big (\frac{24ab-c-dx}{16\pi }\Big )^{1+\frac{1}{n}} \nonumber \\&+2\beta (24ab-c-dx)+(16ab-c)-(8b^2+dx)\Big ],\nonumber \\ \end{aligned}$$

(24)

which is a first order linear differential equation. This is the fundamental equation which on integration (with $s=0, q=1$) yields exact solutions for particular values of polytropic indices $n= 1, \frac{1}{2}, \frac{2}{3}, 2$.

4 Generalized polytropic models

In this section, we will solve Eq. (24) corresponding to particular values of polytropic polytropic indices $n= 1, \frac{1}{2}, \frac{2}{3}, 2$ for generalized polytropic models [50].

4.1 Model 1 for index n=1

On integrating Eq. (24) for n=1, we get

$$\begin{aligned} G(r)=K(a-br^{2})^{P} (a+br^{2})^{H} e^{N(r)}, \end{aligned}$$

(25)

where K is integration constant and other parameters mentioned are

$$\begin{aligned} P= & {} \frac{1}{256\pi ab^3} \left[ \alpha (24ab^2-bc+ad)^2 \right. \nonumber \\&\left. +32\pi b\beta (24ab^2-bc+ad)\right. \nonumber \\&\left. +16\pi b(24ab^2-bc+ad) \right] , \end{aligned}$$

(26)

$$\begin{aligned} H= & {} \frac{1}{256\pi ab^3} \left[ 16\pi b(ad+bc-8ab^2) \right. \nonumber \\&\left. -32\pi b\beta (24ab^2-bc+ad) \right. \nonumber \\&\left. -\alpha (24ab^2-bc+ad)^2 \right] , \end{aligned}$$

(27)

$$\begin{aligned} N(r)= & {} -\frac{d^2\alpha r^2}{128b^2\pi }. \end{aligned}$$

(28)

The anisotropy parameter

$$\begin{aligned} \Delta= & {} \frac{4bP(a+br^{2})}{(a-br^{2})^{2}} \left[ b(P-1)(a+br^{2}) -2(a-br^{2}) \right. \nonumber \\&\left. (b H+(a+br^{2})N^{'}) \right] \nonumber \\&-\frac{24ab-c-dr^{2}}{2} \left[ \beta +\frac{\alpha }{16\pi } \left( 24ab-c-dr^{2} \right) \right] \nonumber \\&-\frac{(c+dr^{2})}{2}\nonumber \\&+4b^{2}R^{2} \left[ 1+H(H-1) \right] \nonumber \\&+4(a+br^{2}) \left[ a+b(2H-1)r^{2}+(a+br^{2})r^{2}N^{'} \right] N^{'} \nonumber \\&-4b \left[ 2a+a(P-H)+b(P+H)r^{2} \right] . \end{aligned}$$

(29)

Consequently, Eq. (1) gives

$$\begin{aligned} ds^{2}= & {} -K(a-br^{2})^{2P}(a+br^{2})^{2(H-1)}e^{2N(r)}dt^{2} \nonumber \\&+(a+br^{2})^{-2} \left[ dr^{2}+r^{2}\left( d\theta ^{2}+sin^{2}\theta d\phi ^{2} \right) \right] .\nonumber \\ \end{aligned}$$

(30)

This solution corresponds to quadratic EoS $p_{r}=\beta \rho +\alpha \rho ^{2}$.

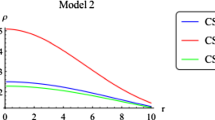
4.2 Model 2 for index n=2

Integrating Eq. (24) for index $n=2$ yields

$$\begin{aligned} G(r)=K\left( a-br^2 \right) ^{P} \left( a-br^2 \right) ^{H} [U(r)]^\Omega [V(r)]^\Upsilon e^{N(r)}, \end{aligned}$$

(31)

where

$$\begin{aligned} P= & {} \frac{1}{16ab^{2}}\left( -2\beta \left( a \left( -24b^2+d \right) +bc \right) \right. \nonumber \\&\left. -\left( a \left( -8b^2+d \right) +bc \right) \right) , \end{aligned}$$

(32)

$$\begin{aligned} H= & {} \frac{1}{16ab^{2}}\left( 2\beta \left( a\left( 24b^2+d \right) -bc \right) \right. \nonumber \\&\left. + \left( a \left( 24b^2+d \right) -bc \right) \right) , \end{aligned}$$

(33)

$$\begin{aligned} N(r)= & {} \frac{d\alpha }{16b^2}\left[ \frac{f(r)}{\pi }\right] ^{\frac{1}{2}},\end{aligned}$$

(34)

$$\begin{aligned} \Omega= & {} \frac{\alpha }{64a}\left[ \frac{\left[ a \left( 24b^2-d \right) -bc \right] ^3}{\pi b^5}\right] ^{\frac{1}{2}},\end{aligned}$$

(35)

$$\begin{aligned} \Upsilon= & {} \frac{\alpha }{64a}\left[ \frac{\left[ a \left( 24b^2+d \right) -bc \right] ^3}{\pi b^5}\right] ^{\frac{1}{2}},\end{aligned}$$

(36)

$$\begin{aligned} f(r)= & {} 24ab-c-dr^2,\end{aligned}$$

(37)

$$\begin{aligned} U(r)= & {} \frac{\left[ a \left( 24b^2-d \right) -bc \right] ^{\frac{1}{2}}+[b f(r)]^{\frac{1}{2}}}{\left[ a \left( 24b^2-d \right) -bc \right] ^{\frac{1}{2}}-[b f(r)]^{\frac{1}{2}}},\end{aligned}$$

(38)

$$\begin{aligned} V(r)= & {} \frac{ \left[ a \left( 24b^2-d \right) -bc \right] ^{\frac{1}{2}}-[b f(r)]^{\frac{1}{2}}}{ \left[ a \left( 24b^2-d \right) -bc \right] ^{\frac{1}{2}}+[b f(r)]^{\frac{1}{2}}}. \end{aligned}$$

(39)

The measure of degree of anisotropy is given by

$$\begin{aligned} \Delta= & {} \frac{4bP \left( a+br^{2} \right) }{ \left( a-br^{2} \right) ^{2}}\nonumber \\&\left[ b(P-1) \left( a+br^{2} \right) -2\left( a-br^{2} \right) \right. \nonumber \\&\left. \left( b H+ \left( a+br^{2} \right) N^{'} \right) \right] \nonumber \\&+4\left[ \left( a-br^{2} \right) ^{2}-2b \left( a(P-H)+b(P+H)r^{2} \right) r^{2}\right] \nonumber \\&\frac{\left( a+br^{2} \right) }{ \left( a-br^{2} \right) }\left[ \Omega \frac{U^{'}}{U} +\Upsilon \frac{V^{'}}{V}\right] \nonumber \\&+4\Omega r^{2}(a+br^{2})^{2}\left[ \frac{U^{''}}{U}+(\Omega -1) \left( \frac{U^{'}}{U}\right) ^{2}+2N^{'}\frac{U^{'}}{U}\right] \nonumber \\&+4\Upsilon r^{2}(a+br^{2})^{2}\left[ \frac{V^{''}}{V}+(\Upsilon -1) \left( \frac{V^{'}}{V}\right) ^{2}+2N^{'}\frac{V^{'}}{V}\right] \nonumber \\&+4r^{2} \left( a+br^{2} \right) ^{2}\left[ N^{''}+(N^{'})^{2}+2\Omega \Upsilon \frac{U^{'}V^{'}}{UV}\right] \nonumber \\&-\frac{24ab-c-dr^{2}}{2}\left[ \beta +\frac{\alpha }{16\pi } \left( 24ab-c-dr^{2} \right) \right] \nonumber \\&-\frac{(c+dr^{2})}{2} \nonumber \\&+4b^{2}R^{2} \left[ 1+H(H-1) \right] \nonumber \\&+4(a+br^{2})\left[ a+b(2H-1)r^{2} +(a+br^{2})r^{2}N^{'} \right] N^{'} \nonumber \\&-4b \left[ 2a+a(P-H)+b(P+H)r^{2} \right] . \end{aligned}$$

(40)

The polytropic EoS ($p_{r}=\beta \rho +\alpha \rho ^{\frac{3}{2}}$) reads the following line element

$$\begin{aligned} ds^{2}= & {} -K(a-br^{2})^{2P}(a+br^{2})^{2(H-1)}\nonumber \\&\times \left[ U(r)\right] ^{2\Omega } \left[ V(r)\right] ^{2\Upsilon }e^{2N(r)}dt^{2} \nonumber \\&(a+br^{2})^{-2} \left[ dr^{2}+r^{2}(d\theta ^{2}+sin^{2}\theta d\phi ^{2})\right] . \end{aligned}$$

(41)

4.3 Model 3 for index n=$\frac{2}{3}$

For $n=\frac{2}{3}$, integration of Eq. (24) implies

$$\begin{aligned} G(r)=K(a-br^2)^{P} (a+br^2)^{H}[U(r)]^\Omega [V(r)]^\Upsilon e^{N(r)},\nonumber \\ \end{aligned}$$

(42)

where

$$\begin{aligned} P= & {} \frac{1}{16ab^{2}}\left( 2\beta \left( a \left( 24b^2-d \right) -bc \right) \right. \nonumber \\&\left. +\, \left( a \left( 8b^2-d \right) -bc \right) \right) ,\end{aligned}$$

(43)

$$\begin{aligned} H= & {} \frac{1}{16ab^{2}} \left( 2\beta \left( a \left( 24b^2+d \right) -bc \right) \right. \nonumber \\&\left. + \left( a \left( 24b^2+d \right) -bc \right) \right) ,\end{aligned}$$

(44)

$$\begin{aligned} N(r)= & {} \frac{d\alpha }{768b^2} \left[ \frac{f(r)}{\pi ^3} \right] ^{\frac{1}{2}} [7(24ab-c)-dr^2],\end{aligned}$$

(45)

$$\begin{aligned} \Omega= & {} \frac{\alpha }{1024a} \left[ \frac{ \left[ a \left( 24b^2-d \right) -bc \right] ^5}{\pi ^3 b^7} \right] ^{\frac{1}{2}},\end{aligned}$$

(46)

$$\begin{aligned} \Upsilon= & {} \frac{\alpha }{1024a}\left[ \frac{\left[ a \left( 24b^2+d \right) -bc \right] ^5}{\pi ^3 b^7} \right] ^{\frac{1}{2}},\end{aligned}$$

(47)

$$\begin{aligned} f(r)= & {} 24ab-c-dr^2,\end{aligned}$$

(48)

$$\begin{aligned} U(r)= & {} \frac{\left[ a \left( 24b^2-d \right) -bc \right] ^{\frac{1}{2}}+ \left[ b f(r) \right] ^{\frac{1}{2}}}{\left[ a \left( 24b^2-d \right) -bc \right] ^{\frac{1}{2}}-[b f(r)]^{\frac{1}{2}}},\end{aligned}$$

(49)

$$\begin{aligned} V(r)= & {} \frac{\left[ a \left( 24b^2+d \right) -bc \right] ^{\frac{1}{2}}-[b f(r)]^{\frac{1}{2}}}{\left[ a \left( 24b^2+d \right) -bc \right] ^{\frac{1}{2}}+[b f(r)]^{\frac{1}{2}}}. \end{aligned}$$

(50)

The measure of degree of anisotropy for $n=\frac{2}{3}$ is

$$\begin{aligned} \Delta= & {} \frac{4bP(a+br^{2})}{(a-br^{2})^{2}}\left[ b(P-1)\Big (a+br^{2}\right) \nonumber \\&-2 \left( a-br^{2} \right) \left( b H+ \left( a+br^{2} \right) N^{'} \right) \Big ]\nonumber \\&+4 \left[ \left( a-br^{2} \right) ^{2}-2b \left( a(P-H)+b(P+H)r^{2} \right) r^{2} \right] \nonumber \\&\frac{\left( a+br^{2} \right) }{\left( a-br^{2} \right) } \left[ \Omega \frac{U^{'}}{U} +\Upsilon \frac{V^{'}}{V} \right] \nonumber \\&+4\Omega r^{2}(a+br^{2})^{2} \left[ \frac{U^{''}}{U}+(\Omega -1) \left( \frac{U^{'}}{U} \right) ^{2}+2N^{'}\frac{U^{'}}{U} \right] \nonumber \\&+4\Upsilon r^{2}(a+br^{2})^{2} \left[ \frac{V^{''}}{V} +(\Upsilon -1) \left( \frac{V^{'}}{V} \right) ^{2}+2N^{'}\frac{V^{'}}{V} \right] \nonumber \\&+4r^{2}(a+br^{2})^{2} \left[ N^{''}+(N^{'})^{2}+2\Omega \Upsilon \frac{U^{'}V^{'}}{UV} \right] \nonumber \\&-\frac{24ab-c-dr^{2}}{2} \left[ \beta +\frac{\alpha }{16\pi }\left( 24ab-c-dr^{2}\right) \right] -\frac{(c+dr^{2})}{2} \nonumber \\&+4b^{2}R^{2}[1+H(H-1)]\nonumber \\&+4 \left( a+br^{2} \right) \left[ a+b(2H-1)r^{2}+(a+br^{2})r^{2}N^{'} \right] N^{'} \nonumber \\&-4b \left[ 2a+a(P-H)+b(P+H)r^{2} \right] . \end{aligned}$$

(51)

The line element corresponding to polytropic EoS $p_{r}=\beta \rho +\alpha \rho ^{\frac{5}{2}}$ takes the form

$$\begin{aligned} ds^{2}= & {} -K(a-br^{2})^{2P}(a+br^{2})^{2(H-1)}\nonumber \\&\times \Big [U(r)\Big ]^{2\Omega }\Big [V(r)\Big ]^{2\Upsilon }e^{2N(r)}dt^{2} \nonumber \\&+(a+br^{2})^{-2} \left[ dr^{2}+r^{2}(d\theta ^{2}+sin^{2}\theta d\phi ^{2})\right] . \end{aligned}$$

(52)

4.4 Model 4 for index $n =\frac{1}{2}$

After integrating Eq. (24) for $n=\frac{1}{2}$, we have

$$\begin{aligned} G(r)=K \left( a-br^2 \right) ^{P} \left( a+br^2 \right) ^{H} e^{N(r)}, \end{aligned}$$

(53)

where

$$\begin{aligned} P= & {} \frac{1}{4096ab^{4}\pi ^2} \left( \alpha \left( a \left( 24b^2+d \right) -bc \right) \right. \nonumber \\&\left. +256\pi ^2b^2 \left( a \left( -8b^2+d \right) +bc \right) \right. \nonumber \\&\left. +512\pi ^2b^2\beta \left( a \left( -8b^2+d \right) +bc \right) \right) , \end{aligned}$$

(54)

$$\begin{aligned} H= & {} \frac{1}{4096ab^{4}\pi ^2} \left( \alpha \left( a \left( 24b^2+d \right) -bc \right) ^3 \right. \nonumber \\&\left. + 256\pi ^2b^2 \left( a \left( 24b^2+d \right) -bc \right) \right. \nonumber \\&+ \left. 512\pi ^2b^2\beta \left( a \left( 24b^2+d \right) -bc \right) \right) ,\end{aligned}$$

(55)

$$\begin{aligned} N(r)= & {} \frac{d^2\alpha \left[ 6(c-24ab)+dr^2 \right] r^2}{4096\pi ^2b^2}. \end{aligned}$$

(56)

The measure of degree of anisotropy is given as

$$\begin{aligned} \Delta= & {} \frac{4bP(a+br^{2})}{(a-br^{2})^{2}}\nonumber \\&\left[ b(P-1)(a+br^{2})-2(a-br^{2})(b H+(a+br^{2})N^{'}) \right] \nonumber \\&-\frac{24ab-c-dr^{2}}{2} \left[ \beta +\frac{\alpha }{16\pi } \left( 24ab-c-dr^{2} \right) \right] \nonumber \\&-\frac{(c+dr^{2})}{2} \nonumber \\&+4b^{2}R^{2}\Big [1+H(H-1)\Big ]\nonumber \\&+4(a+br^{2}) \left[ a+b(2H-1)r^{2}+ \left( a+br^{2} \right) r^{2}N^{'} \right] N^{'} \nonumber \\&-4b \left[ 2a+a(P-H)+b(P+H)r^{2} \right] . \end{aligned}$$

(57)

In this case line element (1) becomes

$$\begin{aligned} ds^{2}= & {} -K(a-br^{2})^{2P}(a+br^{2})^{2(H-1)}e^{2N(r)}dt^{2} \nonumber \\&+(a+br^{2})^{-2}\Big [dr^{2}+r^{2}(d\theta ^{2}+sin^{2}\theta d\phi ^{2})\Big ]. \end{aligned}$$

(58)

5 Properties of solution

In this section, we analyze the physical analysis of the obtained solution in the previous section. For simplicity, we take model 1 corresponding to $n=1$ to study the properties of polytropes in detail. The radial pressure for n=1 is

$$\begin{aligned} P_{r}=\beta \rho +\alpha \rho ^{2}, \end{aligned}$$

(59)

and the energy density

$$\begin{aligned} 8\pi \rho = \left( 12ab-\frac{1}{2}c \right) -\frac{1}{2}dr^{2}. \end{aligned}$$

(60)

Consequently, Eq. (59) with above equation takes the form

$$\begin{aligned} P_r=\beta \left( \frac{24ab-dr^2}{16\pi }\right) +\alpha \left( \frac{24ab-dr^2}{16\pi }\right) ^{2}. \end{aligned}$$

(61)

Similarly, the charge density turns out to be

$$\begin{aligned} \sigma ^{2}=\frac{(a+br^{2})(2c+3dr^{2})^{2}}{16\pi ^{2}r^{2}(c+dr^{2})}. \end{aligned}$$

(62)

The above equation shows that charge density has singularity at r = 0, to avoid this we put parameter c = 0, so charge density reads as

$$\begin{aligned} \sigma ^{2}=d\left[ \frac{3(a+br^{2})}{4\pi }\right] ^{2}, \end{aligned}$$

(63)

Fig. 1

Energy density $\rho$ with $n=1, \alpha =0.025$ and $d=0.0804$

Fig. 2

Radial pressure $P_r$ with $n=1, \alpha =0.025$ and $d=0.0804$

Fig. 3

Mass function m with for $n=1, \alpha =0.025$ and $d=0.0804$

Table 1 Mass (m), central density $(\rho _{0})$ and central radial pressure $(P_{r_{0}})$ for $\alpha =0.025$ and $d=0.0804$

with the choice $c=0$, the physical quantities mass function, energy density and radial pressure does not have singularity at $r=0$ and can be written as (Figs. 1, 2, 3)

$$\begin{aligned} m(r)= & {} 2abr^{3}+\frac{d}{2}r^3-\frac{d}{28}r^7, \end{aligned}$$

(64)

$$\begin{aligned} 8\pi \rho= & {} 12ab-\frac{1}{2}dr^{2}, \end{aligned}$$

(65)

$$\begin{aligned} P_r= & {} \beta \left( \frac{24ab-dr^2}{16\pi }\right) +\alpha \left( \frac{24ab-dr^2}{16\pi }\right) ^{2}, \end{aligned}$$

(66)

where r is the radial coordinate. All the physical quantities are well behaved i.e., charge density $(\sigma )$, energy density $(\rho )$ and electric charge (E) are finite at the center of star. The central energy density ($\rho _0$) and radial pressure ($P_{r_{0}}$) at the center becomes

$$\begin{aligned} \rho _0= & {} \frac{3ab}{2\pi }, \end{aligned}$$

(67)

$$\begin{aligned} P_{r_{0}}= & {} \beta \left( \frac{3ab}{2\pi } \right) +\alpha \left( \frac{3ab}{2\pi } \right) ^{2}. \end{aligned}$$

(68)

Similarly, the charge density and electric charge at center are

$$\begin{aligned} \sigma _0^{2}= & {} d \left( \frac{3a}{4\pi } \right) ^{2}, \end{aligned}$$

(69)

$$\begin{aligned} E_0^{2}= & {} 0, \end{aligned}$$

(70)

which are constant. The speed of sound is defined as

$$\begin{aligned} \upsilon ^{2}=\frac{dp_{r}}{d\rho }. \end{aligned}$$

(71)

For stable configuration of a star, we requires radial pressure to be zero at the boundary. We set r=1 to obtain the relation

$$\begin{aligned} \beta =\alpha \left( \frac{d-24ab}{16\pi } \right) , \end{aligned}$$

(72)

to give finite values of density and pressure at surface.

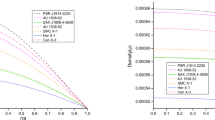
Table 1 provides the estimated values of model parameters for the considered strange stars, the masses of stars mentioned in column 1 have been regained in column 2 by varying the values of parameters ab and $\beta$ as given in column 3 and 4, while $\alpha$ and d have fixed values. In last two columns of Table 1, represents the values of $P_{r_{0}}$ and $\rho _{0}$.

Table 2 Variation in physical parameters from center to the surface for the realistic star $4U 1820-30$

Table 2 elaborates the variation in the values of physical parameters such as energy density, radial pressure, mass function and gradient of radial pressure from center to the surface of realistic star $4U 1820-30$. In order to study the general properties of the model, we have plotted the physical quantities corresponding to $n=1$, $ab=0.772$, $\alpha =0.025$, $\beta =-0.00917508$ and $d=0.0804$. The graphical representation of energy energy density $\rho$, radial pressure $P_r$ and speed of sound v displays monotonically decreasing behavior from center to the surface, while tangential pressure $(P_t)$, mass function (m), electric field (E) and anisotropy $(\Delta )$ are increasing satisfying the desire physical behavior against defined values of the parameters involved in the model (Figs. 4, 5, 6, 7).

Fig. 4

Electric intensity E with $n=1, \alpha =0.025$ and $d=0.0804$

Fig. 5

Speed of sound v with $n=1, \alpha =0.025$ and $d=0.0804$

6 Summary and discussion

We have found exact solutions of EMFEs by employing GPEoS to obtain some new polytropic models. Modeling of highly dense stars is of much importance in general relativity because of their similarity to relativistic astrophysics. For this, we have formulated EMFEs for spherically symmetric static spacetime with anisotropic matter distribution. In order to calculate the exact solution of onset of EMFEs we define some new variables as in [50] and applied GPEoS ($P_{r}=\beta \rho +\alpha \rho ^{1+\frac{1}{n}}$) on the gravitating system. Generic value of polytropic index n leads to complexities in finding exact solution through integration, that is why four different values of n ($1, 2, \frac{2}{3}, \frac{1}{2}$) have been incorporated here that leads to a new class of charged polytropic models.

Fig. 6

tangential pressure $P_t$ with $n=1, \alpha =0.025$ and $d=0.0804$

We have chosen physically acceptable form of gravitational potential $L=bx+a$, and electric field $E^2=x^s(c+dx)^q$ have been taken into account that allows us to find exact solution of constituting system for constant values of model parameters $``a''$, $``b''$, $``s''$ and $``q''$ with the help of GPEoS. Consideration of charged parameter helped in the development of better and simple mathematical model with linear choice of gravitational potential L, instead of quadratic form as in [54]. It is worth mentioning here that specific selections for electric and gravitational potentials and their parametric entries are presumed in a way that system do not face any singularity and physical viability of the model remains intact. For these parametric values generated models satisfy all the physical conditions, i.e., energy density $(\rho )$ and radial pressure $P_{r}$ maintain positivity within the gravitating source and vanishes at the boundary and monotonic decrease in $(\rho )$ and ($P_{r}$) from center of star to its surface. Whereas tangential pressure $(P_t)$ gains maximum value at the boundary and vanishes at $r=0$, being a monotonically increasing function. Anisotropy measure $(\Delta )$ is increasing which indicates negativity of the pressure gradient $(\frac{dP_{r}}{dr})$. Also, $\Delta$ vanishes at $r=0$, on initial working singular point was observed at $r=0$ in charge density that was removed by taking suitable value of parameter “c”, metric functions remain positive and central density continues to be finite.

Fig. 7

Anisotropy $\Delta$ with $n=1, \alpha =0.025$ and $d=0.0804$

Regaining the mass of realistic stars strengthens the importance of exact solution, herein, Table 1 elaborates the masses of five stars PSR J1614-2230, Vela X-1, Vela 4U, PSR J1903+327 and 4U 1820-30 that we have regained for the physically reasonable choice of model parameters. For any mathematical model stability analysis is the most important step in development of that model. We have found values radial pressure $(P_{r})$ and energy density $(\rho )$ for all stars which are satisfying the energy density regularity conditions in presence of charge.

We have discussed the properties of exact model for polytropic index $n=1$ in detail and studied the variation in charge and physical quantities from center to the surface for one star 4U 1820-30 given in Table 2. We have used speed of sound as stability criterion for compact sources. The attributes of energy density, radial pressure, mass, speed of sound and electric field are demonstrated by their graphical representation for unit radius. Plotting of these parameters indicate monotonic decrease in $\rho$ and $P_{r}$ with vanishing values at the boundary, while mass (m), charge (E), $P_t$ and $\Delta$ are zero at the center and increase monotonically towards surface. Positivity of speed of sound indicates the viability of newly developed polytropic models.