Relative particle yield fluctuations in $\text{ Pb--Pb }$ collisions at $\sqrt{s_\mathrm{{NN}}} =2.76\hbox { TeV}$

Abstract

First results on $\hbox {K}/\pi$, $\hbox {p}/\pi$ and K/p fluctuations are obtained with the ALICE detector at the CERN LHC as a function of centrality in $\text{ Pb--Pb }$ collisions at $\sqrt{s_\mathrm{{NN}}} =2.76\hbox { TeV}$. The observable $\nu _{\mathrm{dyn}}$, which is defined in terms of the moments of particle multiplicity distributions, is used to quantify the magnitude of dynamical fluctuations of relative particle yields and also provides insight into the correlation between particle pairs. This study is based on a novel experimental technique, called the Identity Method, which allows one to measure the moments of multiplicity distributions in case of incomplete particle identification. The results for $\hbox {p}/\pi$ show a change of sign in $\nu _{\mathrm{dyn}}$ from positive to negative towards more peripheral collisions. For central collisions, the results follow the smooth trend of the data at lower energies and $\nu _{\mathrm{dyn}}$ exhibits a change in sign for $\hbox {p}/\pi$ and K/p.

1 Introduction

The theory of strong interactions, Quantum Chromodynamics (QCD), predicts that at sufficiently high energy density nuclear matter transforms into a deconfined state of quarks and gluons known as Quark–Gluon Plasma (QGP) [1, 2]. One of the possible signatures of a transition between the hadronic and partonic phases is the enhancement of fluctuations of the number of produced particles in the hadronic final state of relativistic heavy-ion collisions [3,4,5]. Event-by-event fluctuations and correlations may show critical behaviour near the phase boundary, including the crossover region where there is no thermal singularity, in a strict sense, associated with the transition from a QGP phase to a hadron-gas phase. A correlation analysis of event-by-event abundances of pions, kaons and protons produced in $\text{ Pb--Pb }$ collisions at LHC energies may provide a connection to fluctuations of globally conserved quantities such as electric charge, strangeness and baryon number, and therefore shed light on the phase structure of strongly interacting matter [6].

In view of the predicted criticality signals at crossover for vanishing net-baryon densities [7], event-by-event fluctuations of relative particle yields are studied using the fluctuation measure $\nu _\mathrm{dyn}[A,B]$ [8] defined in terms of moments of particle multiplicity distributions as

$$\begin{aligned} \nu _\mathrm{dyn}[A,B]= & {} \dfrac{\langle N_{A}(N_{A}-1) \rangle }{{\langle N_{A} \rangle }^{2}} + \dfrac{\langle N_{B}(N_{B}-1) \rangle }{{\langle N_{B} \rangle }^{2}} \nonumber \\&- 2\dfrac{\langle N_{A}N_{B} \rangle }{\langle N_{A} \rangle \langle N_{B} \rangle }, \end{aligned}$$

(1)

where $N_{A}$ and $N_{B}$ are the multiplicities of particles A and B measured event-by-event in a given kinematic range. The $\nu _\mathrm{dyn}[A,B]$¹ fluctuation measure contrasts the relative strength of fluctuations of species A and B to the relative strength of correlations between these two species. It vanishes when the particles A and B are produced in a statistically independent way [8, 9].

This study at LHC energies is of particular importance for establishing the energy and system size dependence of $\nu _{\mathrm{dyn}}$ in order to understand the trend observed at lower collision energies from the RHIC Beam Energy Scan (BES) results reported by the STAR collaboration [10]. Furthermore, the advantage of this fluctuation measurement is its robustness against non-dynamical contributions such as those stemming from participant nucleon fluctuations and finite particle detection efficiencies [8, 11]. Measurements of the $\nu _{\mathrm{dyn}}$ observable for net-charge fluctuations were already published by ALICE [12]. Moreover, for identified particles, it was measured at the Super Proton Synchrotron (SPS) [13] and at the Relativistic Heavy-Ion Collider (RHIC) [10] in $\text{ Pb--Pb }$ and Au–Au collisions, respectively. The ALICE detector at the LHC is ideally suited to extend these measurements to higher collision energies. In particular, the excellent charged-particle tracking and particle identification (PID) capabilities in the central barrel of the detector allow for a precise and differential event-by-event analysis at midrapidity and low transverse momentum ($p_{\mathrm{T}}$).

The paper is organized as follows. In Sect. 2, details about the ALICE detector setup and the dataset are given. Section 3 discusses the event and track selection criteria, particle identification procedure, and the analysis method. Estimates of statistical and systematic uncertainties are given in Sect. 4. Results on $\nu _{\mathrm{dyn}}[\pi ,\mathrm {K}]$, $\nu _{\mathrm{dyn}}[\pi ,\mathrm {p}]$ and $\nu _{\mathrm{dyn}}[\mathrm {p},\mathrm {K}]$ in $\text{ Pb--Pb }$ collisions at $\sqrt{s_\mathrm{{NN}}} =2.76\hbox { TeV}$ are presented in Sect. 5, and finally Sect. 6 summarizes the measurements presented in this paper.

2 Experimental setup and dataset

ALICE is a general-purpose detector system designed, in particular, for the study of collisions of heavy ions at the LHC. The design, components, and performance of the ALICE detector have been reported elsewhere [14, 15]. The ALICE detector is comprised of several detector components organized into a central barrel detection system and forward/backward detectors. The main tracking and PID devices in the central barrel of the experiment are the Inner Tracking System (ITS) and the Time Projection Chamber (TPC), which are operated inside a large solenoidal magnet with $B=0.5$ T. Two forward scintillator arrays V0-A and V0-C are located on either side of the interaction point and cover the pseudorapidity ($\eta$) intervals $2.8<\eta <5.1$ and $-3.7<\eta <-1.7$. The V0 detectors and the two neutron Zero Degree Calorimeters (ZDC), placed at ± 114 m from the interaction point, were used for triggering and event selection.

The ITS-TPC tracking system covers the midrapidity region and provides charged-particle tracking and momentum reconstruction down to $p_{\mathrm{T}} =100\,\hbox {MeV}/c$. The ITS is employed to reconstruct the collision vertex with high precision and to reject charged particles produced in secondary vertices.

The analysis presented in this paper is based on about 13 million minimum-bias $\text{ Pb--Pb }$ collisions at $\sqrt{s_\mathrm{{NN}}} =2.76\hbox { TeV}$ collected in the year 2010. The minimum-bias trigger condition is defined by the coincidence of hits in both V0 detectors. In the offline event selection, V0 and ZDC timing information is used to reject beam-gas background and parasitic beam-beam interactions. The definition of the collision centrality is based on the charged-particle multiplicity measured in the V0 detectors [14], which can be related to collision geometry and the number of participating nucleons through a Monte-Carlo (MC) simulation based on a Glauber model [16].

3 Data analysis

3.1 Event and track selection

Charged particles reconstructed in the TPC with full azimuthal acceptance and in the pseudorapidity range of $|\eta |< 0.8$ were used in this analysis. The momentum range was restricted to $0.2<p<1.5\hbox { GeV}/c$ in order to minimize systematic uncertainties arising from the overlap of the $\hbox {d}E/\hbox {d}x$ distributions. Furthermore, the following track selection criteria were applied to guarantee optimal $\hbox {d}E/\hbox {d}x$ and momentum resolution, which are crucial for precise particle identification. Charged-particle tracks were accepted in this analysis when they have at least 80 out of a maximum of 159 reconstructed space points in the TPC, and the $\chi ^{2}$ per space point from the track fit is less than 4. Daughter tracks from reconstructed secondary weak-decay kink topologies were rejected. Additional suppression of secondary particles was achieved by restricting the distance-of-closest-approach (DCA) of the extrapolated trajectory to the primary vertex position to less than 2 cm along the beam direction. In the transverse plane the restriction in the DCA depends on $p_{\mathrm{T}}$ in order to take into account the $p_{\mathrm{T}}$ dependence of the impact parameter resolution [17]. The remaining contamination after the DCA cuts is typically less than 10% for the momentum range covered in this work [18].

3.2 Identity method

The standard approach of finding the moments $\langle N_{A} \rangle$, $\langle N_{B} \rangle$, $\langle N_{A}(N_{A}-1) \rangle$ and $\langle N_{B}(N_{B}-1) \rangle$ is to count the number of particles $N_{A}$ and $N_{B}$ event-by-event and calculate averages over the dataset. However, this approach suffers from incomplete particle identification due to overlapping $\hbox {d}E/\hbox {d}x$ distribution functions, which could be circumvented by either selecting suitable phase-space regions or by using additional detector information such as time-of-flight measurements. These procedures reduce the overall phase-space coverage and detection efficiencies. The present study is based on the Identity Method [19,20,21] which overcomes the misidentification problem.

Fig. 1

Distributions of $\omega$ and W for pions (top), kaons (middle) and protons (bottom) in the momentum interval of $0.3<p<0.8\hbox { GeV}/c$ for 0–5% central $\text{ Pb--Pb }$ events

The Identity Method was proposed in Ref. [19] as a solution to the misidentification problem for the analysis of events with two different particle species. In Ref. [20], the method was developed further to calculate the second moments of the multiplicity distributions of more than two particle species. Subsequently, in Ref. [21], it was generalized to the first and higher moments of the multiplicity distributions for an arbitrary number of particle species. The first experimental results using the Identity Method were published by the NA49 collaboration [13].

Instead of counting every detected particle event-by-event, the Identity Method follows a probabilistic approach using two basic experimental per-track and per-event observables, $\omega$ and W, respectively. They are defined as

$$\begin{aligned} \omega _{j}(x_{i})= & {} \dfrac{\rho _{j}(x_{i})}{\rho (x_{i})} \in [0,1],\nonumber \\ \quad \rho (x_{i})= & {} \sum _{j}\rho _{j}(x_{i}), \quad W_{j} \equiv \sum _{i=1}^{N(n)} \omega _{j}(x_{i}), \end{aligned}$$

(2)

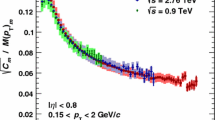
where $x_{i}$ stands for the $\hbox {d}E/\hbox {d}x$ of a given track i, $\rho _{j}(x)$ is the $\hbox {d}E/\hbox {d}x$ distribution of particle species j within a given phase-space bin and N(n) is the number of tracks in the nth event. The quantity $\omega _{j}(x_{i})$ represents the probability that particle i is of type j. Thus, in case of perfect particle identification, one expects $W_{j} = N_{j}$, while this does not hold in case of overlapping $\hbox {d}E/\hbox {d}x$ distributions. Figure 1 shows the $\omega$ and W distributions for pions, kaons and protons in the momentum interval of $0.3<p<0.8$ GeV/c. The W distribution of protons shows a discrete structure because proton $\hbox {d}E/\hbox {d}x$ distributions have the least overlap.

The moments of the W distributions can be constructed directly from experimental data. The Identity Method calculates the moments of the particle multiplicity distributions by unfolding the moments of the W distributions with the following matrix operation

$$\begin{aligned} \langle \overrightarrow{N} \rangle = \text {A}^{-1} \langle \overrightarrow{W} \rangle , \end{aligned}$$

(3)

where $\langle \overrightarrow{W} \rangle$ and $\langle \overrightarrow{N} \rangle$ are the vectors of the moments of W quantities and unknown true multiplicity distributions, respectively. The response matrix $\text {A}$ is defined by the $\omega$ quantities. A detailed description of the technique and a demonstration of its robustness can be found in Refs. [20, 21].

The $\hbox {d}E/\hbox {d}x$ measurements used as the only input for the Identity Method are obtained from the TPC, which provides a momentum resolution of better than 2% and a single-particle detection efficiency of up to 80% for the kinematic range considered in this paper [14]. The Identity Method employs fits of inclusive $\hbox {d}E/\hbox {d}x$ distributions for the calculation of the $\omega$ probabilities entering Eq. 3. Since the overlap regions in the $\hbox {d}E/\hbox {d}x$ distributions are also properly taken into account, a very good description of the inclusive $\hbox {d}E/\hbox {d}x$ spectra, and therefore an excellent understanding of the TPC detector response, is required over the full momentum range covered in this analysis. To this end, the $\hbox {d}E/\hbox {d}x$ distributions of pre-selected samples of pions, protons and electrons, identified by the reconstruction of $\mathrm {K}_{S}^{0}$ and $\varLambda$ decays and photon conversions, were fitted with a generalized Gaussian function of the form:

$$\begin{aligned} f(x) = A e^{- {\left( |x-\mu |/\sigma \right) }^{\beta }} {\left( 1+\text {erf} \left( \alpha \dfrac{|x-\mu |}{\sigma \sqrt{2}} \right) \right) } \end{aligned}$$

(4)

where A, $\mu$, $\sigma$, $\alpha$ and $\beta$ stand for the abundance, mean, width, skewness and kurtosis of the distribution, respectively. The detector response functions obtained in this way were used later to fit the inclusive $\hbox {d}E/\hbox {d}x$ spectra. To cope with the dependencies of the $\hbox {d}E/\hbox {d}x$ on the track angle and particle multiplicity, fits were performed over the entire pseudorapidity range of $|\eta |<0.8$ in steps of 0.1 units for each centrality class. Moreover, the momentum intervals were chosen narrow enough to minimize the effect of the momentum dependence on $\hbox {d}E/\hbox {d}x$, most particularly at low momenta where the magnitude of $\hbox {d}E/\hbox {d}x$ varies rapidly with the momentum. An example of a $\hbox {d}E/\hbox {d}x$ distribution in a given phase-space bin and the corresponding fits are shown in Fig. 2.

Fig. 2

Distributions of the TPC $\hbox {d}E/\hbox {d}x$ signal of pions, kaons, electrons and protons fitted with the generalized Gaussian function in a given phase-space bin. The residuals are defined as the difference between data points and the total fit function normalized to the statistical error of the data points

4 Statistical and systematic uncertainties

The statistical uncertainties were determined by the number of events in this analysis and the finite number of tracks in each event. The number of events also affects the uncertainty of the shape of the inclusive $\hbox {d}E/\hbox {d}x$ spectra, which is determined by a fit. This uncertainty enters the calculation of $\omega$ and W, and finally the computation of the moments of multiplicity distributions with the Identity Method. Since standard error propagation is impractical given the rather complicated numerical derivation of the final result, the subsample method was chosen to evaluate the statistical uncertainties. To this end, the data set was subdivided into $n=$ 25 random subsamples i. The $\nu _{\mathrm{dyn}}$ values were reconstructed for each subsample and the statistical uncertainty was obtained according to

$$\begin{aligned} \sigma _{\langle \nu _{\mathrm {dyn}} \rangle } = \dfrac{\sigma }{\sqrt{n}}, \end{aligned}$$

(5)

where

$$\begin{aligned} \sigma = \sqrt{\dfrac{\sum _{i} (\nu _{\mathrm {dyn},i} - \langle \nu _{\mathrm {dyn}} \rangle )^2}{n-1}}, \,\,\langle \nu _{\mathrm {dyn}} \rangle = \dfrac{1}{n}\sum _{i} \nu _{\mathrm {dyn},i}. \end{aligned}$$

(6)

The summary of all sources of systematic uncertainties is shown in Table 1 and in the next paragraphs the main contributors to the systematics are detailed.

The largest contribution to the total systematic uncertainty is from the fits of the measured particle $\hbox {d}E/\hbox {d}x$ distributions. The quality of the fits was monitored by Kolmogorov–Smirnov (K–S) and $\chi ^{2}$ tests. To study the influence of possible systematic shifts in the fit parameters on $\nu _{\mathrm{dyn}}$, the fit parameters of each particle in the overlap regions were varied by about ± 0.5 %, which defines the boundaries where the K–S test fails at 90% confidence level. The observed maximum variations range from about 7% to 15% for $\nu _{\mathrm{dyn}}[\pi ,\mathrm {p}]$ and $\nu _{\mathrm{dyn}}[\pi ,\mathrm {K}]$, respectively.

Even though $\nu _{\mathrm{dyn}}$ is known to be robust against detection-efficiency losses, it may show an explicit dependence if the detector response functions differ from Binomial or the efficiencies exhibit large variations with detector occupancy [8]. Therefore, one also has to investigate the uncertainty resulting from the detection efficiency losses. For that, the $\nu _{\mathrm{dyn}}$ results reconstructed from a full Monte Carlo simulation of HIJING [22, 23] events employing a GEANT3 [24] implementation of the ALICE detector were compared to the analysis at the generator level, where in both generated and reconstructed levels perfect PID information was used. The resulting systematic uncertainty from the finite tracking efficiency is less than 6%.

Table 1 List of contributions to the systematic uncertainty of the particle ratio fluctuations

Table 2 Numerical values of $\nu _{\mathrm{dyn}}$ results for different particle pairs. The first uncertainty is statistical and the second systematic

The systematic uncertainties due to the track selection criteria were estimated by a variation of the selection ranges. The systematics from contamination of weak decays and other secondary particles were obtained by varying the DCA cuts. Other contributions to the total systematic uncertainty arise from the cuts applied on the maximum distance of the reconstructed vertex to the nominal interaction point along the beam axis, the number of required TPC space points per track and the $\chi ^{2}$ per degree of freedom of the track fit. Moreover, the effect of the magnetic field polarity was investigated by separate analyses of data taken under two polarities. Neither of these contributions to the total systematic uncertainty exceeds 5%. The total systematic uncertainty was obtained by adding in quadrature the individual maximum systematic variations from these different contributions.

5 Results

5.1 Centrality dependence and comparison to models

In this section, the results are presented as a function of collision centrality and compared to calculations with the HIJING [22, 23] and AMPT [25] models. The unscaled values of $\nu _{\mathrm{dyn}}$ for different combinations of particles in each centrality class, together with the final statistical and systematic uncertainties, are given in Table 2. Due to the intrinsic multiplicity dependence of $\nu _{\mathrm{dyn}}$, discussed in Refs [26, 27], the values of $\nu _{\mathrm{dyn}}$ were scaled further by the charged-particle multiplicity density at midrapidity, $\hbox {d}N_{\mathrm{ch}}/\hbox {d}\eta$. The fully corrected experimental $\hbox {d}N_{\mathrm{ch}}/\hbox {d}\eta$ values were taken from Ref. [18]. Figure 3 shows measured values of $\nu _{\mathrm{dyn}}$ scaled by $\hbox {d}N_{\mathrm{ch}}/\hbox {d}\eta$ as a function of the collision centrality expressed in terms of $\hbox {d}N_{\mathrm{ch}}/\hbox {d}\eta$. The values for $\nu _{\mathrm{dyn}}$ and $\hbox {d}N_{\mathrm{ch}}/\hbox {d}\eta$ for HIJING and AMPT were calculated by using corresponding particle multiplicities at the generator level within the same experimental acceptance. A flat behaviour is expected in this representation if a superposition of independent particle sources is assumed, as in the Wounded Nucleon Model (WNM) [28].

Measured values of $\nu _{\mathrm{dyn}}[\pi ,\mathrm {K}]$ and $\nu _{\mathrm{dyn}}[\mathrm {p},\mathrm {K}]$ are positive across the entire centrality range, while $\nu _{\mathrm{dyn}}[\pi ,\mathrm {p}]$ is negative for the most peripheral collisions and changes sign at mid-central collisions. The centrality dependencies observed in $\nu _{\mathrm{dyn}}[\mathrm {p},\mathrm {K}]$ and $\nu _{\mathrm{dyn}}[\pi ,\mathrm {p}]$ are similar in shape, being flat from central to mid-central collisions and systematically decreasing for the most peripheral ones. In contrast, $\nu _{\mathrm{dyn}}[\pi ,\mathrm {K}]$ is almost independent of centrality from most peripheral to mid-central collisions and rises as the centrality increases. A similar qualitative behaviour is also observed for $\nu _{\mathrm{dyn}}[\pi ,\mathrm {K}]$ within the kinematic range of $|\eta |<1$ and $0.2<p<0.6\hbox { GeV}/c$ as measured in Au–Au collisions at $\sqrt{s_\mathrm{{NN}}} =200\hbox { GeV}$ by the STAR collaboration. The difference in the absolute values is, to a large extent, due to the increase in $\hbox {d}N_{\mathrm{ch}}/\hbox {d}\eta$ by almost a factor of two between the two collision energies. The same argument holds true for the most central STAR data at $62.4\hbox { GeV}$, although the centrality dependence is rather flat in this case [27]. The overall behaviour is defined by the interplay between correlation and fluctuation terms encoded in the definition of the $\nu _{\mathrm{dyn}}$ observable. To disentangle these terms, one needs a dedicated study focusing on separate charge combinations, which also makes it possible to investigate contributions from resonance decays and global charge conservations.

Fig. 3

Results for $\nu _{\mathrm{dyn}}[\pi ,\mathrm {K}]$, $\nu _{\mathrm{dyn}}[\pi ,\mathrm {p}]$ and $\nu _{\mathrm{dyn}}[\mathrm {p},\mathrm {K}]$ scaled by the charged-particle density $\hbox {d}N_{\mathrm{ch}}/\hbox {d}\eta$. The ALICE data are shown by red markers while the coloured lines indicate the HIJING [22, 23] and AMPT [25] model calculations. The data are shown as a function of the collision centrality, expressed in terms of $\hbox {d}N_{\mathrm{ch}}/\hbox {d}\eta$

An important characteristic of HIJING is that it treats nucleus-nucleus collisions as an independent superposition of nucleon-nucleon interactions. As such, it does not incorporate mechanisms for final-state interactions among the produced particles and therefore phenomena such as equilibrium and collectivity do not occur. The AMPT calculations are performed with three different settings including (1) string melting, (2) hadronic rescattering, and (3) string melting and hadronic rescattering. All three versions of the AMPT model presented here use hard minijet partons and soft strings from HIJING as initial conditions. Partonic evolution is described by Zhang’s parton cascade (ZPC) [29] which is followed by a hadronization process. In the last step, hadronic rescattering and the decay of resonances takes place. In the default AMPT model, after minijet partons stop interacting with other partons, they are combined with their parent strings to form excited strings, which are then converted to hadrons according to the Lund string fragmentation model [25]. However, in the string melting scenario, instead of employing the Lund string fragmentation mechanism, hadronization is modeled via a quark coalescence scheme by combining two nearest quarks into a meson and three nearest quarks (antiquarks) into a baryon (antibaryon). This ultimately reduces the correlation between produced hadrons.

HIJING produces positive values for the three particle pair combinations and does not exhibit any non-monotonic behaviour as a function of centrality, even though it implements exact global conservation laws. In contrast, hadronic rescattering produces additional resonances at the hadronization phase thereby introducing additional correlations between particles [25]. Consequently, the AMPT configuration with hadronic rescattering drives the $\nu _{\mathrm{dyn}}$ results towards negative values as the collision centrality increases. In particular, for $\nu _{\mathrm{dyn}}[\pi ,\mathrm {p}]$, contrary to the data, it predicts negative values. On the other hand, the AMPT version with string melting shows a weak centrality dependence for the three particle pair combinations. None of the models investigated in this work give a reasonable quantitative description of the measured data.

5.2 Energy dependence

Values of $\nu _{\mathrm{dyn}}$ measured in this work for the most central Pb–Pb collisions were compared to NA49 and STAR data in Fig. 4. Measurements from NA49 and STAR show a smooth evolution of $\nu _{\mathrm{dyn}}$ with collision energy and do not reveal any indications for critical behaviour in