1 Introduction

The holographic nature of spacetime can be manifestly disclosed by AdS/CFT correspondence [1,2,3,4]. Recently it has been proposed that the exponential growth of the interior of a black hole can be described by a quantity in the quantum field theory on the boundary [5]. Specifically, it has been conjectured that the quantum computational complexity is equal to the volume of Einstein-Rosen Bridge (ERB) (CV conjecture) [5]. An outstanding model has been considered in the AdS-Schwarzschild geometry, where the maximal volume of codimension-one surface \(\Sigma \) bounded by the boundary time \(t_{L}\) and \(t_{R}\) (where L and R label the left and the right boundary, respectively.) is dual to the quantum computational complexity of a boundary state \(|(t_{L},t_{R})\rangle \) relative to the reference state \(|TFD\rangle \):

$$\begin{aligned} C(t_{L},t_{R})&=\frac{V_{\Sigma }(t_{L},t_{R})}{G_{N}l},\nonumber \\ |TFD(t_{L},t_{R})\rangle&=U(t_{L})U(t_{R})|TFD\rangle . \end{aligned}$$
(1)

where \(U(t_{L})\), \(U(t_{R})\) are quantum gates with U labelling the time evolution operator in the boundary theory. \(G_N\) is the gravitational constant and l is a certain length scale.

Because of the ambiguity of choosing the radius l, it has been further conjectured that the quantum computational complexity is equal to the gravitational action on the Wheeler DeWitt (WDW) patch (CA conjecture) [6]:

$$\begin{aligned} C(t_L,t_R)=\frac{A_{WDW}(t_L,t_R)}{\pi \hbar }. \end{aligned}$$
(2)

The WDW patch is the domain of dependence of a cauchy slice anchored at some boundary time \(t_L\) and \(t_R\).

These two conjectures have been extensively testified in literature. On the gravity side, the growth behavior of the action as well as the maximal volume has firstly been investigated in the late time limit [7,8,9,10], and then for the full-time period [11,12,13,14,15,16,17]. See the generalizations of the conjectures to CV2.0 and CA2.0 in [18,19,20]. Others see [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39].

On the boundary field theory side, basically there are two ways to understand the complexity of quantum fields. The one is “path-integral complexity” [40,41,42,43,44] and the other is “geometric complexity” [45,46,47,48,49,50,51,52,53,54], based on different understandings on quantum gates in field theory. Currently, one puzzle is that in most holographic work one usually focuses on the evolution of the complexity beginning at a TFD state, however in QFT one usually considers the evolution relative to a vacuum state. These two processes may be different in principle and further investigation is needed. Recently, the complexity between the vacuum and the thermal state has been studied by a holographic quench in Vaidya-AdS spacetime [55, 56, 58, 86].

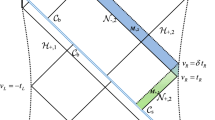
Above CV and CA conjectures on the complexity are originally proposed for global spacetime. Sequently they have been generalized to be applicable for the subregion in [59] and [60]. Given a boundary subregion \({\mathcal {A}}\) on a time slice \(\mathcal {\sigma }\), one can construct the corresponding entanglement wedge \(W[{\mathcal {A}}]\) and the Wheeler-DeWitt patch \(W_{WDW}[\mathcal {\sigma }]\). Then the subregion CA conjecture tells us that the complexity of a boundary state (which corresponds to the subregion \({\mathcal {A}}\)) equals the action of the intersecting region \(W[{\mathcal {A}}]\cap W_{WDW}[\mathcal {\sigma }]\). While the subregion CV conjecture tells us that the complexity of a boundary state is equal to the volume of codimension-one extremal hypersurface \(\Gamma _{{\mathcal {A}}}\), which is bounded by the boundary subregion \({\mathcal {A}}\) and the corresponding Hubeny-Rangamani-Takayanagi (HRT) surface \(\gamma _{{\mathcal {A}}}\). The formula is given by

$$\begin{aligned} C_{{\mathcal {A}}}=\frac{V(\Gamma _{{\mathcal {A}}})}{8\pi l_{AdS}G_{N}} \end{aligned}$$
(3)

where \(l_{AdS}\) is the AdS radius. In addition, some attempts to understand the dual complexity of mixed states are recently suggested in [61]. (See [37, 62,63,64,65,66,67,68,69,70,71,72] for related works on the subregion complexity.)

The evolution of the holographic subregion complexity has been investigated over the Vaidya-AdS spacetime in [62]. This dynamical process is dual to the thermal quench in CFT on the boundary, and can be modelled holographically by collapsing a thin shell of null matter from the AdS boundary to form an AdS black brane. We intend to know more details about this process and provide more physical understanding on the results obtained in numerics. It is also desirable to provide more information about the subregion complexity in the boundary field theory.

In this paper we will explore the evolution of the subregion complexity with CV conjecture over the background in Einstein-Born-Infeld theory. The subregion we choose here is an infinitely long strip with the width l. This evolution process is dual to the process of a quench which is not only thermal, but also electromagnetic in the sense that it is modelled holographically by collapsing a null-like thin shell with mass M and charge Q from the AdS boundary to form Born-Infeld-AdS (BI-AdS) black brane [73].

Born-Infeld (BI) electrodynamics was firstly introduced by Born and Infeld in the 1930’s [74]. They proposed a non-linear modification to Maxwell theory to regularize the divergence of self-energy of a point-like charged particle. Recently BI electrodynamics becomes more intriguing in superstring theory. The low energy behavior of the vector modes of open strings and dynamics of D-branes are given by the BI action and its similar non-Abelian version respectively.(See [75, 76] for related works.) Further, BI theory plays an important role in the modified gravity [77] and inspires a new approach to avoid spacetime spacetime singularities in the high energy or highly curved regime.

Here we desire to capture more general features of the evolution of complexity caused by BI electrodynamics that may not appear in Einstein theory. On the one hand, in the limit of \(b\rightarrow 0\), this framework covers Einstein-Maxwell theory and can be applied to explore the thermalization process of a strongly coupled system with chemical potential. In [78], it was found that the thermalization time for the two-point function, Wilson loop and entanglement entropy are increased with the charge (or the chemical potential). Thus it also deserves to find out the effect of chemical potential on the subregion complexity. On the other hand, for non-zero parameter b more interesting effects caused by the nonlinearity of electrodynamics will be disclosed. The parameter b was found to have the opposite effect against the charge Q. That is to say, as the parameter b grows, the thermalization time for above non-local probes is decreased (see [73]). Inspired by the former works, we intend to explore what will happen to the subregion complexity during the holographic quench process with nonlinear electrodynamics.

We organize the paper as follows. In Section 2, we introduce the general setup for the bulk geometry with Vaidya-type black brane solutions in Einstein-Born-Infeld theory. Then we derive the holographic entanglement entropy(HEE) and the subregion complexity for a strip on the boundary. In Section 3 we numerically calculate the evolution of the holographic subregion complexity as well as the holographic entanglement entropy. The impact of the charge Q and the inverse of BI parameter b on the evolution is investigated. Section 4 is the conclusions and outlooks.

2 The setup

In this section we will briefly review the Einstein-Born-Infeld theory which contains a non-linear term of electrodynamics, and then present a Vaidya-type black brane background, which is holographically dual to the quench process from a vacuum state to a thermal state on the boundary. Given a strip on the boundary, we will derive the analytical expressions for its HEE and the holographic subregion complexity.

2.1 Einstein-Born-Infeld theory

The action for \((d+1)\)-dimensional Einstein gravity minimally coupled to Born-Infeld electrodynamics can be expressed as [79] (see also [80,81,82])

$$\begin{aligned} S = \frac{1}{16\pi G}\int d^{d+1}x \sqrt{-g}\big [R-2\Lambda +L_{BI}(F)\big ]\ , \end{aligned}$$
(4)

where \(L_{BI}(F)\) is given by

$$\begin{aligned} L_{BI}(F) = 4b^{-2}\left( 1-\sqrt{1+\frac{F_{\mu \nu }F^{\mu \nu }}{2}b^{2}}\right) \ . \end{aligned}$$
(5)

The constant b is the inverse of the ordinary BI parameter (for numerical convenience). In the limit \(b\rightarrow 0\), the action goes back to Einstein-Maxwell theory. And here we choose \(16\pi G=1\). The metric of BI-AdS solution with a planar horizon can be expressed as

$$\begin{aligned} ds^2 = -U(r)dt^2+\frac{dr^2}{U(r)}+ r^2\sum _{i=1}^{d-1}dx_i^2\ , \end{aligned}$$
(6)

where

$$\begin{aligned} U(r)=&-\frac{M}{r^{d-2}}+\left[ \frac{4b^{-2}}{d(d-1)}+1\right] r^2\nonumber \\&-\frac{2\sqrt{2}b^{-1}}{d(d-1)r^{d-3}}\sqrt{2b^{-2}r^{2d-2}+(d-1)(d-2)Q^2}\nonumber \\&+\frac{2(d-1)Q^2}{dr^{2d-4}}{}_{2}F_1\left[ \frac{d-2}{2d-2},\frac{1}{2};\frac{3d-4}{2d-2};\right. \nonumber \\&\left. -\frac{(d-1)(d-2)Q^2b^{2}}{2r^{2d-2}}\right] , \end{aligned}$$
(7)

and the AdS radius is set to 1. The event horizon is defined by \(U(r_h)=0\) and since the horizon is planar, we should regard this spacetime as a black brane as mentioned in [73]. In the next subsection we will generalize it to a time-dependent background which is so-called the Vaiyda-BI-AdS spacetime.

2.1.1 Vaidya-BI-AdS Metric

To obtain Vaidya-BI-AdS metric, we firstly rewrite the metric (6) in Eddington-Finkelstein coordinate system by the following transformations

$$\begin{aligned} dv&=dt+dr/U(r),\\ z&=1/r. \end{aligned}$$

Then the metric is expressed as

$$\begin{aligned} ds^2 =\frac{1}{z^2}\left[ -f(z)dv^2-2dvdz+\sum _{i=1}^{d-1}dx_i^2\right] \ , \end{aligned}$$
(8)

where

$$\begin{aligned} f(z) = z^2 U\left( \frac{1}{z}\right) . \end{aligned}$$
(9)

In addition, from the metric in (6), one can derive the Hawking temperature as

$$\begin{aligned} T&= \frac{1}{4\pi r_h}\left[ \left( \frac{4b^{-2}}{d-1}+d\right) r_h^2\right. \nonumber \\&\left. \quad -\frac{2\sqrt{2}b^{-1}}{(d-1)r_h^{d-3}}\sqrt{2b^{-2}r_h^{2d-2}+(d-1)(d-2)Q^2}\right] .\nonumber \\ \end{aligned}$$
(10)

In particular, when Hawking temperature \(T=0\), we obtain an extremal black brane. Under this condition, the charge takes the maximal value \(Q=Q_{ext}\) which is

$$\begin{aligned} Q_{ext}^2 = \frac{d}{(d-2)}\left[ 1+\frac{d(d-1)b^2}{8}\right] r_h^{2d-2} . \end{aligned}$$
(11)

Now we extend it to the Vaidya-BI-AdS metric in which both the mass and the charge of the black brane are treated as functions of v. That is

$$\begin{aligned} m(v)&=\frac{M}{2}\left( 1+\tanh \frac{v}{v_{0}}\right) , \nonumber \\ q(v)&=\frac{Q}{2}\left( 1+\tanh \frac{v}{v_{0}}\right) , \end{aligned}$$
(12)

where M and Q are the parameters of the BI-AdS black brane and \(v_0\) denotes the thickness of the shell. This extension leads to the following dynamical background

$$\begin{aligned} ds^{2}= & {} \frac{1}{z^{2}}\left[ -f(v,z)dv^{2}-2dzdv+dx^{2}+\sum _{i=1}^{d-2}dy_{i}^{2}\right] ,\nonumber \\ f(v,z)= & {} 1+\frac{2(d-1)}{d}{}_2 F_1\left[ \frac{1}{2},\frac{d-2}{2d-2},\frac{4-3d}{2-2d},\right. \nonumber \\&\left. -\frac{b^2}{2}(d-2)(d-1)q(v)^2 z^{2(d-1)}\right] q(v)^2 z^{2(d-1)} \nonumber \\&+\frac{4}{b^2d(d-1)}-m(v)z^d\nonumber \\&-\frac{2z^{d-1}}{b(d-1)d}\sqrt{2(2-3d+d^2)q(v)^2+\frac{4z^{2-2d}}{b^2}}.\nonumber \\ \end{aligned}$$
(13)

Since in Eq. (12) we have changed mass M and charge Q into a time-dependent form, it is obvious that the metric in Eq. (13) is not a solution of the original action as shown in Eq. (4). Therefore, to guarantee that Eq. (12) could be a solution to Einstein equations, we need add some external source term \(S_{ex}\) to provide a variation of M and Q. Taking \(S_{ex}\) into account, the equations of motion can be expressed as

$$\begin{aligned}&R_{\mu \nu }-\frac{1}{2}Rg_{\mu \nu }-2b^{-2}g_{\mu \nu }\left( 1-\sqrt{1+b^2F^2/2}\right) \nonumber \\&\qquad -\frac{2F_{\mu \rho }F_{\nu }{}^{\rho }}{\sqrt{1+b^2F^2/2}}\nonumber \\&\quad =-8\pi GT_{\mu \nu }^{(ex)}, \end{aligned}$$
(14)
$$\begin{aligned}&\qquad \nabla _{\mu }\left( \frac{F^{\mu \nu }}{\sqrt{1+b^2F^2/2}}\right) =-8\pi GJ^{\nu }_{(ex)}. \end{aligned}$$
(15)

Here we keep the cosmological constant \(\Lambda \) and the Newton’s constant G temporarily in the above equations. Then, the corresponding source \(T_{\mu \nu }\) and \(J^{\nu }\) can be solved as

$$\begin{aligned} T_{\mu \nu }^{(ex)}&=\frac{d-1}{z^{1-d}}\Bigg [{\dot{m}}(v) \nonumber \\&\quad -\frac{2}{z^{2-d}}{}_2F_1\left[ \frac{d-2}{2d-2};\frac{1}{2};\frac{3d-4}{2d-2};\frac{(d-2)(d-2)q(v)^2}{-2b^{-2}z^{2-2d}}\right] \nonumber \\&\quad \times q(v){\dot{q}}(v)\Bigg ]\delta _\mu ^v\delta _\nu ^v, \end{aligned}$$
(16)
$$\begin{aligned} J^{\nu }_{(ex)}&=\sqrt{\frac{(d-1)(d-2)}{8}}z^{d+1}{\dot{q}}(v)\delta ^{\nu v}, \end{aligned}$$
(17)

where we denote the dot as \(\partial _v\) and reset \(16\pi G=1\) as well as the AdS radius.

2.2 Holographic description of entanglement and complexity for a strip

In this subsection we analytically derive the integral expressions of holographic entanglement entropy and complexity for a \((d-1)\)-dimensional strip \({\mathcal {A}}\) on the boundary. The strip can be parameterized by the boundary coordinates \((x,y_{1},...,y_{d-2})\). We further assume that it has a width of l along x direction such that \(x\in [-l/2,l/2]\), while it has infinite length along the directions of \(y_i\) such that \(y_{i}\in (-\infty ,\infty )\), where \(i=1,...,d-2\). We will figure out the HRT surface \(\gamma _{{\mathcal {A}}}\) at first, and then locate the codimension-one extremal surface \(\Gamma _{{\mathcal {A}}}\) such that the evolution of the holographic subregion complexity can be evaluated by subregion CV conjecture.

2.2.1 Holographic entanglement entropy

Given a strip, the corresponding HRT surface can be parameterized by z(x) and v(x),with the boundary conditions

$$\begin{aligned} z(-l/2)=z(l/2)=\epsilon , v(-l/2)=v(l/2)=t-\epsilon , \end{aligned}$$
(18)

where \(\epsilon \) is a cut-off constant. At the tip of the HRT surface we have

$$\begin{aligned} z'(0)=v'(0)=0, z(0)=z_{t}, v(0)=v_{t}, \end{aligned}$$
(19)

where \((z_{t}\), \(v_{t})\) label the location of the tip and also characterize the HRT surface at boundary time t. As shown in [62], the induced metric on the HRT surface has the form as

$$\begin{aligned} ds^{2}=\frac{1}{z^{2}}\left[ -f(v,z)v'^{2}-2z'v'+1\right] dx^{2}+\frac{1}{z^{2}}\sum _{i=1}^{d-2}dy_{i}^{2}.\nonumber \\ \end{aligned}$$
(20)

The area of the HRT surface \(\gamma _{{\mathcal {A}}}\) is

$$\begin{aligned} A_{t}(\gamma _{{\mathcal {A}}})=L^{d-2}\int _{-l/2}^{l/2}\frac{\sqrt{1-f(v,z)v'^{2}-2z'v'}}{z^{d-1}}dx, \end{aligned}$$
(21)

where t denotes the HRT surface which is anchored on a boundary time slice with time t and \(L^{d-2}\) is the infinite area related to directions \(y_{i}\). Treating the area functional \(A_{t}(\gamma _{{\mathcal {A}}})\) as an action we can read the Lagrangian and the corresponding Hamiltonian as

$$\begin{aligned} {\mathcal {L}}_{S}&=\frac{\sqrt{1-f(v,z)v'^{2}-2z'v'}}{z^{d-1}}, \end{aligned}$$
(22)
$$\begin{aligned} {\mathcal {H}}_{S}&=\frac{1}{z^{d-1}\sqrt{1-f(v,z)v'^{2}-2z'v'}}. \end{aligned}$$
(23)

Since the Hamiltonian is conserved along the direction x, we have

$$\begin{aligned} 1-f(v,z)v'^{2}-2z'v'=\frac{z_{t}^{2d-2}}{z^{2d-2}}. \end{aligned}$$
(24)

Then we take the derivative of (24) and substitute it into the equations of motion (E.O.M) of z(x) and v(x) respectively, leading to

$$\begin{aligned} 0&= -2(d-1)+2zv''\nonumber \\&\quad +v'\left[ 2(d-1)f(v,z)v'+4(d-1)z'-zv'\partial _{z}f(v,z)\right] , \end{aligned}$$
(25)
$$\begin{aligned} 0&= 2(d-1)f(v,z)^{2}v'^{2}\nonumber \\&\quad +f(v,z)\left[ -2(d-1)+4(d-1)v'z'-zv'^{2}\partial _{z}f(v,z)\right] \nonumber \\&\quad -z\left[ 2z''+v'\left( 2z'\partial _{z}f(v,z)+v'\partial _{v}f(v,z)\right) \right] . \end{aligned}$$
(26)

We numerically solve above equations for the HRT surface \(\gamma _{{\mathcal {A}}}\) and denote the solutions as \(({\tilde{v}}(x),{\tilde{z}}(x))\), then the equation in (21) becomes

$$\begin{aligned} A_{t}(\gamma _{{\mathcal {A}}})=2L^{d-2}\int _{0}^{l/2}\frac{z_{t}^{d-1}}{{\tilde{z}}(x)^{2d-2}}dx. \end{aligned}$$
(27)

It corresponds to the holographic entanglement entropy of the strip on the boundary. Next we need to work out the solution of the codimension-one extremal surface \(\Gamma _{{\mathcal {A}}}\) at various boundary time t to study the evolution behavior of the holographic subregion complexity.

2.2.2 Holographic subregion complexity

Recall that the codimension-one extremal surface \(\Gamma _{{\mathcal {A}}}\) is bounded by \({\mathcal {A}}\) on the boundary and the HRT surface \(\gamma _{{\mathcal {A}}}\) in the bulk. As suggested in [62], \(\Gamma _{{\mathcal {A}}}\) can be parameterized by z(v, x) in general. For this model thanks to the translational invariance, the extremal surface \(\Gamma _{{\mathcal {A}}}\) is independent of x, so the parameterization can simply be written as

$$\begin{aligned} z=z(v). \end{aligned}$$
(28)

As a result, the induced metric on the extremal surface \(\Gamma _{{\mathcal {A}}}\) is

$$\begin{aligned} ds^{2}=\frac{1}{z^{2}}\left[ -\left( f(v,z)+2\frac{\partial z}{\partial v}\right) dv^{2}+dx^{2}+\sum _{i=1}^{d-2}dy_{i}^{2}\right] ,\nonumber \\ \end{aligned}$$
(29)

and the volume of \(\Gamma _{{\mathcal {A}}}\) is given by

$$\begin{aligned} V_{t}(\Gamma _{{\mathcal {A}}})= & {} 2L^{d-2}\int _{v_{t}}^{{\tilde{v}}(l/2)}dv\nonumber \\&\times \int _{0}^{{\tilde{x}}(v)}dx\left[ -f(v,z)-2\frac{\partial z}{\partial v}\right] ^{1/2}z^{-d}, \end{aligned}$$
(30)

where \({\tilde{x}}(v)\) is the x coordinate on the HRT surface \(\gamma _{{\mathcal {A}}}\). Then we can write down the Lagrangian

$$\begin{aligned} {\mathcal {L}}_{V}=\left[ -f(v,z)-2\frac{\partial z}{\partial v}\right] ^{1/2}z^{-d}, \end{aligned}$$
(31)

and the corresponding E.O.M ofFootnote 1 z(v)

$$\begin{aligned} 0&=\left[ 2df(v,z)^{2}+4dz'(v)^{2}-3z(v)z'(v)\partial _{z}f(v,z)\right. \nonumber \\&\quad +f(v,z)(6dz'(v)-z(v)\partial _{z}f(v,z))\nonumber \\&\quad -z(v)(2z''(v)+\partial _{v}f(v,z))]/[z(v)^{1+d}(-f(v,z)\nonumber \\&\qquad \left. -2z'(v))^{3/2}\right] . \end{aligned}$$
(32)

In principle, one should solve E.O.M (32) for z(v), with boundary conditions determined by \(\gamma _{{\mathcal {A}}}\) and \({\mathcal {A}}\). However as proved in [62], the relation \({\tilde{z}}({\tilde{v}})\) (where \({\tilde{z}}\) and \({\tilde{v}}\) are the solutions for the HRT surface \(\gamma _{{\mathcal {A}}}\)) is just the solution of the E.O.M (32). Thus the equation in (30) becomes

$$\begin{aligned} V_{t}(\Gamma _{{\mathcal {A}}})= & {} 2L^{d-2}\int _{v_{t}}^{{\tilde{v}}(l/2)}dv\nonumber \\&\times \left[ -f(v,z(v))-2\frac{\partial z}{\partial v}\right] ^{1/2}z(v)^{-d}{\tilde{x}}(v). \end{aligned}$$
(33)

So far, for a given strip on the boundary, we have figured out the integral expressions of the HRT surface \(\gamma _{{\mathcal {A}}}\) and the codimension-one extremal surface \(\Gamma _{{\mathcal {A}}}\) at some boundary time t. In next section we will explore the evolution behavior of holographic entanglement entropy and the subregion complexity in numerical manner.

3 Holographic subregion complexity in Einstein-Born-Infeld theory

The quench in CFT could be described holographically by the evolution of the bulk geometry in Einstein-Born-Infeld theory, whose initial state corresponds to the pure AdS and final state corresponds to the BI-AdS black brane. In this section we first work out the evolution of the holographic entanglement entropy, and then explore the evolution of the subregion complexity numerically after the global quench. Afterwards, we study the effect of the charge Q and the parameter b on the evolution of the subregion complexity.

Fig. 1
figure 1

Two distinct patterns of the evolution of HEE and subregion complexity. The figures on the top display a continuous pattern with \(l=1\), while the figures at the bottom display a discontinuous pattern with \(l=5\). The dashed lines denote the critical time for the transition \(t_{c}=3.7434\)

Full size image

3.1 Numeric setup

For numerical analysis we need to fix all free parameters and get rid of the UV divergence. Here we take the UV cut-off \(z_{\epsilon }\) to be \(\frac{1}{20}\), which turns out to be good enough for us to obtain the cut-off independent data. The thickness of the shell \(v_0\) is set to be \(\frac{1}{100}\), the boundary dimension d to be 3 if without notice(which means we mainly focus on \(AdS_{4}/CFT_{3}\)) and the mass M of the final black brane to be 1. With this setup Eqs. (10) and (11) reduce to

$$\begin{aligned} T = \frac{1}{4\pi r_h}\left[ (2b^{-2}+3)r_h^2-2b^{-1}\sqrt{b^{-2}r_h^{4}+Q^2}\right] \end{aligned}$$
(34)

and

$$\begin{aligned} Q_{ext}= \sqrt{3\left( 1+\frac{3b^2}{4}\right) r_h^{4}}. \end{aligned}$$
(35)

Given the value of parameter b, we can set the charge \(Q\in [0,Q_{ext}]\) to explore the evolution of the holographic entanglement entropy as well as subregion complexity.

Next we will solve E.O.M (26) and (25) for \(({\tilde{v}}(x),{\tilde{z}}(x))\) with the boundary conditions

$$\begin{aligned} v'(0)=z'(0)=0,\quad \ z(0)=z_{t},\quad v(0)=v_{t}, \end{aligned}$$
(36)

by the shooting method.

3.2 The evolution of subregion complexity

Once we figure out the HRT surface, the corresponding HEE can be obtained from Eq. (21). Since we are only concerned with the change of the HEE during the quench, we may subtract the vacuum HEE and define a finite quantity for HEE as

$$\begin{aligned} S=\frac{A_{t}(\gamma _{{\mathcal {A}}})-A_{AdS}(\gamma _{{\mathcal {A}}})}{2L^{d-2}}. \end{aligned}$$
(37)

Furthermore, the holographic subregion complexity can be obtained by computing the volume of the codimension-one surface \(\Gamma _{{\mathcal {A}}}\) from Eq. (30). In parallel, we define a normalized expression for the subregion complexity as

$$\begin{aligned} C=\frac{V_{t}(\Gamma _{{\mathcal {A}}})-V_{AdS}(\Gamma _{{\mathcal {A}}})}{2L^{d-2}}. \end{aligned}$$
(38)

Next we present our numerical results for the time evolution of these two quantities during the course of the quench. In Fig. 1 we demonstrate two typical patterns of evolution: the continuous pattern and the discontinuous pattern. We choose the same charge \(Q=0.65\) (which is less than the extremal charge) and the same parameter \(b=2\) but different width \(l=1\) and \(l=5\) respectively. First of all, from Fig. 1a and Fig. 1d we learn that the tip \(z_t\) of the HRT surface \(\gamma _{{\mathcal {A}}}\) is decreasing with the time and finally reaches a constant. In comparison, we notice that the HRT surface with large l takes longer time to get stable than the HRT surface with smaller l. This phenomenon can be intuitively understood based on the previous work in [83] and [84]. During the entanglement tsunami, the infalling thin shell divides the spacetime into two parts, namely the AdS-Schwarzschild and the pure AdS. The former region is swept by the tsunami while the latter region has not been affected by the tsunami yet. As a result, the HRT surface is also divided into two parts. The part in the AdS region is located on a time slice just like the static case, while the other part in the Schwarzschild region is not. Because the tip of the HRT surfaces with large l stretches deeper into the bulk, the infalling shell need take longer time to reach this location. Therefore, the location of HRT surfaces with larger l will take longer time to get stable.

Fig. 2
figure 2

The left plot is for the evolution of HEE with various values of b, where the blue, yellow, green and red lines correspond to \(b=0\), \(\frac{1}{2}\), 1, 2, respectively. The charge and the width of the strip are fixed as \(Q=0.65\), \(l=5\). While the right plot is for the evolution of HEE with various values of Q, where the blue, yellow and green lines correspond to \(Q=0.2\), 0.4, 0.65, respectively

Full size image
Fig. 3
figure 3

The dependence of the holographic subregion complexity on the parameter b with \(l=5\) (the left plot) and \(l=1\) (the right plot). The blue, yellow, green and red lines correspond to \(b=0\), \(\frac{1}{2}\), 1, and 2 respectively, with a fixed charge \(Q=0.65\)

Full size image

Secondly, we notice that when l is large (\(l=5\)), the HEE evolution will display a swallow tail before getting stable, which is marked by the gray line. This phenomenon has previously been observed in [85] as well. It indicates that at some given boundary time t, there exist multi solutions for the surface \(\gamma _{{\mathcal {A}}}\). We only keep the solutions with minimum area as the HEE.

In addition, the growth rate of HEE depends on the charge Q and the parameter b, as shown in Fig. 2. Fig. 2a demonstrates the evolution of HEE with different values of b. It is noticed that the larger the parameter b is, the sooner the curve saturates and the larger the maximal value is. While Fig. 2b shows the growth curves with various values of Q. We find that the larger the charge Q is, the later the curve saturates and the smaller the maximal value is.

Next we turn to the evolution of the subregion complexity. In general, we observe that it increases in the early stage of the boundary time and then decreases after meeting a maximum. Finally it reaches a constant at the late time (Fig. 1). This phenomenon is different from the evolution of entanglement entropy, which never decreases during the whole stage of the evolution. Moreover, the width of the strip also effects the evolution of the complexity. When the strip is narrow, the complexity evolves continuously while when the strip becomes wider, it evolves discontinuously at some moment (see Fig. 1c, f respectively). This discontinuity can be understood as following: The gray line in Fig. 1f corresponds to the swallow tail in Fig. 1e. Since we only keep the solutions with minimum area, the system does not undergo the evolution along the gray line but just dropping down vertically, as shown in Fig. 1f.

Our above result is in agreement with the previous one obtained in the Vaidya-AdS spacetime [62]. As argued in [5], the growth of the complexity is measured by the growth of the region inside the black hole. For a quench, we notice that during the evolution the extremal surface \(\Gamma _{{\mathcal {A}}}\) stretches into the interior of the black brane at first and then be squeezed out. Thus we tend to interpret the above results as: during the evolution the growth of the subregion complexity results from the fact that the extremal surface \(\Gamma _{{\mathcal {A}}}\) starts to probe the interior of the black brane, while finally its dropping down at later times reflects the fact that the surface \(\Gamma _{{\mathcal {A}}}\) is being squeezed out of the black brane.

In next subsection we will investigate the dependence of the subregion complexity on the charge Q and the parameter b, and its distinct behavior from that of HEE will be addressed.

Fig. 4
figure 4

The dependence of the holographic subregion complexity on the parameter b with \(Q=0.4\) (the left plot) and \(Q=0.2\) (the right plot). The blue, yellow, green and red lines correspond to \(b=0\), \(\frac{1}{2}\), 1, and 2 respectively, with a fixed width \(l=5\)

Full size image

3.2.1 Dependence on parameter b

In Fig. 3 we illustrate the evolution behavior of subregion complexity with different values of parameter b, while the charge Q and the width of the strip l are fixed. As we can see, at the early stage the growth rates of the complexity are almost the same for different b. However, at later time the effect of b becomes important. The smaller the parameter b is, the longer the subregion complexity grows and the larger the stable value is. That is to say, the nonlinear feature of the bulk theory prevents the subregion complexity from growing in its dual CFT.

Fig. 5
figure 5

The dependence of the holographic subregion complexity on the parameter Q with \(l=5\). The blue, yellow, green lines correspond to \(Q=0.2\), \(Q=0.4\) and \(Q=0.65\), respectively. The parameter b is fixed as \(b=2\), 1, 1 / 2 and 0 in subfigure (a) to (d), respectively

Full size image

Another novel feature of complexity observed here is that its maximal value increases with the decrease of the parameter b, which is in contrast to the behavior of the entanglement entropy. As demonstrated in (Fig. 2a), while decreasing b, the maximal value of HEE decreases.

Finally we remark that the discrepancy of the curves in four colors becomes more evident in the background with large charge Q as shown in Fig. 4. This is reasonable since the parameter b characterizes the nonlinearity of electromagnetical field. When the value of charge Q is small, the contribution of electromagnetical field becomes less important.

3.2.2 Dependence on the charge Q

Fig. 6
figure 6

The dependence of the holographic subregion complexity on the parameter Q with \(l=1\). The blue, yellow, green lines correspond to \(Q=0.2\), \(Q=0.4\) and \(Q=0.65\), respectively. The parameter b is fixed as \(b=0\)

Full size image
Fig. 7
figure 7

The impact of the charge Q on the evolution of subregion complexity in three dimensional RN-AdS background (\(b=0\)). In Fig. 7b, the green dashed line represents the linear growth stage at later time when l is large enough

Full size image

In this subsection, we study the impact of the charge Q on the evolution of subregion complexity when the parameter b is fixed. The relevant results are plotted in Figs. 5 and 6. At the early stage, the growth rate of complexity is almost the same for different values of charge Q, while at later time the effect of charge Q becomes more significant. We find the smaller the charge Q is, the sooner the subregion complexity drops down and the smaller the maximum complexity is. We remark that this result is in contrast to the evolution of entanglement entropy as well, where the maximum of entanglement entropy increases when decreasing the charge Q, as shown in Fig. 2b.

In both Figs. 5 and 6, the stable values increase with the charge Q. But in the 3-dimensional case as shown in Fig. 7, the stable values decrease with the charge Q.

In the 3-dimensional case when the charge Q is sufficiently large, the final constant value of the holographic subregion complexity is always less than its initial value regardless the width l, as illustrated in Fig. 7. But in the 4-dimensional case, only when the width l and the charge Q are both very small, the final stable value could be less than the initial value. Actually, the appearence of negative stable value is quite common while investigating quench process (see [62] and [86]). This fact can be interpreted as follows: Complexity measures the “difference” between two states. Therefore, negative stable value means that the “difference” between the finial state and some reference state is less than the “difference” between the initial state and the reference state. In holographic scenario, since the reference state is still unclear, the appearance of negative value is acceptable.

It is interesting to compare the impacts of charge Q and parameter b on the stable value. On the one hand, we notice the effects of the charge Q is always evident, regardless the value of parameter b and width l, as illustrated in Figs. 5 and 6. On the other hand, in Fig. 3 we notice that only when the width l is large and the value of charge Q is close enough to its extremal value, then the effect of b becomes obvious.

In the remainder of this section we focus on the effects on charge Q on the evolution pattern of the complexity. As found in [62], the evolution of complexity density (which means the complexity in the unit of width l) in 4-dimensional Vaidya-AdS spacetime shows a transition from a pattern of continuous growth into a pattern of discontinuous growth. But in 3-dimensional case, the evolution always exhibits a continuous growth pattern. In addition, when the width l is large enough, the growth exhibits two distinct stages: the first rapid growth and the second linear growth as shown in Fig. 7b. The above results are obtained in the neutral case [62]. Now when the black brane is charged, the Vaidya-RN-AdS metric in 3-dimensional spacetime can be given as [78]

$$\begin{aligned}&ds^{2}=\frac{1}{z^{2}}(-f(z,v)dv^{2}-2dvdz+dx^{2}) \nonumber \\&f(z,v)=1-m(v)z^{2}+q(v)^{2}z^{2}log(z), \end{aligned}$$
(39)

where m(v) and q(v) are shown in Eq. (12).

It is quite straightforward to obtain the complexity for charged black branes, as plotted in Fig. 7a, b. Interestingly enough, we find the charge Q can not only change the growth behavior, but also change the pattern of evolution. When the charge Q is large enough, the evolution of complexity changes the pattern from continuous to discontinuous (Fig. 7). Moreover, the sufficiently large charge Q will wash out two different growth stages. This result can be read from Fig. 7b, where the blue line represents the case of AdS-Schwarzschild background and we can see two distinct growth stage clearly. That is to say, with sufficiently large charge Q the evolution of complexity shows a transition from the continuous pattern into the discontinuous pattern and forgets about its later linear growth stage (Fig. 7a, b).

4 Conclusions and discussions

In this paper we have investigated the evolution of the subregion complexity during a quench in Einstein-Born-Infeld theory. The subregion \({\mathcal {A}}\) we consider here is an infinite strip on a time slice of the boundary. Holographically the subregion complexity can be described by a codimension-one extremal hypersurface \(\Gamma _{{\mathcal {A}}}\) in the bulk. We have numerically analyzed the evolution behavior of holographic entanglement entropy and the subregion complexity, which geometrically reflect the evolution of the HRT surface and the codimension-one extremal hypersurface during the course of the quench. The increasing and decreasing behavior of the subregion complexity are related to the part which is stretched into the black brane. we have also investigated the effect of varying the charge Q and the parameter b on the evolution of the complexity. It turns out that the maximum of the complexity drops down when we decrease the charge Q or increase the parameter b. Moreover, when the charge Q is large enough, it washes out the second stage featured by linear growth. But under the limit of \(l\rightarrow \infty \), we tend to interpret this effect as retarding the occurrence of the second stage of linear growth rather than washing out it directly. One should be cautious to extend this result to the limit of \(l\rightarrow \infty \), since the width of the strip l in numerical simulation perhaps is not large enough to probe the whole region due to the numerical limitation. When the charge Q is sufficiently large, whether the linearly growing stage would appear should be tested analytically with the strategy as proposed in [83]. And more detail of these results should be explored in an analytical way too. In addition, these results should be helpful for us to further disclose the role of subregion complexity in the direction of understanding the holographic nature of space time.

It should be interesting to explore the evolution of complexity analytically under the subregion CV or CA conjecture. It is also desirable to investigate the min flow-max cut theorem in the Vaidya-type spacetime to build the quantum gates in the bulk. Further, we should note that the features which can be probed by the holographic subregion complexity is also sensitive to the HEE in this paper, as shown in Fig. 1. It is quite intriguing to investigate the evolution behavior of the complexity in the circumstance that is insensitive to the HEE in future.