Abstract
We point out that the recently increased value of the angle \(\gamma \) in the unitarity triangle (UT), determined in tree-level decays to be \(\gamma =(74.0^{+5.0}_{-5.8})^\circ \) by the LHCb collaboration, combined with the most recent value of \(|V_{cb}|\) implies an enhancement of \(\Delta M_{d}\) over the data in the ballpark of \(30\%\). This is larger by roughly a factor of two than the enhancement of \(\Delta M_{s}\) that is independent of \(\gamma \). This disparity of enhancements is problematic for models with constrained minimal flavour violation (CMFV) and also for \(U(2)^3\) models. In view of the prospects of measuring \(\gamma \) with the precision of \(\pm 1^\circ \) by Belle II and LHCb in the coming years, we propose to use the angles \(\gamma \) and \(\beta \) together with \(|V_{cb}|\) and \(|V_{us}|\) as the fundamental parameters of the CKM matrix until \(|V_{ub}|\) from tree-level decays will be known precisely. Displaying \(\Delta M_{s,d}\) as functions of \(\gamma \) clearly demonstrates the tension between the value of \(\gamma \) from tree-level decays, free from new physics (NP) contributions, and \(\Delta M_{s,d}\) calculated in CMFV and \(U(2)^3\) models and thus exhibits the presence of NP contributions to \(\Delta M_{s,d}\) beyond these frameworks. We calculate the values of \(|V_{ub}|\) and \(|V_{td}|\) as functions of \(\gamma \) and \(|V_{cb}|\) and discuss the implications of our results for \(\varepsilon _K\) and rare K and B decays. We also briefly discuss a future strategy in which \(\beta \), possibly affected by NP, is replaced by \(|V_{ub}|\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The \(\Delta F=2\) transitions in the down-quark sector, that is \(B^0_{s,d}-{\bar{B}}^0_{s,d}\) and \(K^0-{\bar{K}}^0\) mixings, have been vital in constraining the standard model (SM) and in the search for new physics (NP) for several decades [1, 2]. However, theoretical uncertainties related to the hadronic matrix elements entering these transitions and their large sensitivity to the CKM parameters made clear cut conclusions about the presence of NP impossible. As we demonstrate in this paper, this could change in the near future.
Among the most important flavour observables we have at our disposal are
with \(\Delta M_{s,d}\) being the mass differences in \(B^0_{s,d}-{\bar{B}}^0_{s,d}\) mixings and \(S_{\psi K_S}\) and \(S_{\psi \phi }\) the corresponding mixing induced CP-asymmetries. \(\varepsilon _K\) describes the magnitude of indirect CP-violation in \(K^0-{\bar{K}}^0\) mixing. \(\Delta M_{s,d}\) and \(\varepsilon _K\) are already known experimentally with impressive precision. The asymmetries \(S_{\psi K_S}\) and \(S_{\psi \phi }\) are less precisely measured but have the advantage of being subject to only very small hadronic uncertainties.
On the other hand the CKM parameters of particular interest are
with the first three being the moduli of the most intensively studied elements of the CKM matrix, and \(\gamma \) and \(\beta \) being two angles in the unitarity triangle (UT). The angle \(\gamma \) is to an excellent approximation equal to the sole complex phase in the standard parametrization of the CKM matrix.
Now, as elaborated in [3], there are many ways to construct the rescaled UT. They all involve only two inputs, but as quantified in the latter paper, some pairs are particularly suited for the determination of the apex (\({\bar{\rho }},{\bar{\eta }}\)) of this triangle, as only moderate precision on them is required to obtain a satisfactory determination of \({\bar{\rho }}\) and \({\bar{\eta }}\). The clear winners from this study are the pairs
with \(R_b\) being the length of one side in the UT related to the ratio \(|V_{ub}|/|V_{cb}|\).
Ideally, one would like to use the second pair which allows to construct the so-called reference unitarity triangle (RUT) [4] that is supposed to be free of NP contributions. Unfortunately, the persistent discrepancy between inclusive and exclusive determinations of \(|V_{ub}|\) from tree-level decays precludes a satisfactory determination of the RUT at present.
On the other hand the tree-level determination of the angle \(\gamma \) has significantly been improved in the last years by various measurements of the LHCb collaboration, with the latest average being [5]Footnote 1
Moreover, the prospects of LHCb and Belle II [7, 8] to decrease the error down to \(\pm 1^\circ \) are promising. In view of this situation and significant recent progress in the determination of \(|V_{cb}|\), giving [9]
we will choose as the four fundamental CKM parameters
Within the SM and CMFV models [10,11,12], the hadronic uncertainties in \(\Delta M_{s,d}\) reside within a good approximation in the parameters
Fortunately, during the last years their uncertainties decreased significantly. In particular, an impressive progress has been made by the Fermilab Lattice and MILC Collaborations (Fermilab-MILC) that find [13]
with uncertainties of \(3\%\) and \(4\%\), respectively. An even higher precision is achieved for the ratio
Based on the results in (8) and (9) we have performed in [14] a detailed analysis of \(\Delta F=2\) processes in CMFV models, finding a significant tension between \(\Delta M_{s,d}\) and \(\varepsilon _K\) in these models with the pattern of the tension strongly dependent on the value of \(|V_{cb}|\). Moreover, constructing the universal unitarity triangle (UUT) [10] via \(R_t\) and \(\beta \) we could predict, independently of \(|V_{cb}|\), the value of \(\gamma \) to be
significantly below the value in (4). This number has not changed with respect to our 2016 analysis, and now displays a \(1.8\sigma \) tension with the improved tree level measurement in (4).Footnote 2 As we have discussed in [14] this problem arises not only in the SM and more generally in CMFV models but also in minimally broken \(U(2)^3\) models, where NP contributions in the \(B_d\) and \(B_s\) systems are universal and hence cancel in the ratio.
As the present paper deals again with the tensions between \(\Delta F=2\) observables in CMFV models, it is mandatory for us to state what is new in our paper:
-
In [14], we have considered two strategies. One in which \(\varepsilon _K\) has been used to determine \(|V_{cb}|\), implying a value consistent with the inclusive determination as well as \(\Delta M_{s,d}\) values well above the data. In the second strategy, \(|V_{cb}|\) has been determined from \(\Delta M_s\) resulting in a low value of \(|V_{cb}|\) consistent with the exclusive determination at that time. The predicted \(\varepsilon _K\) then turned out to be well below its experimental value. The recent improvements in the determinations of \(|V_{cb}|\) [16, 17] disfavours the second strategy and also the recent claim in [18] that there is a \(4\sigma \) anomaly in \(\varepsilon _K\).
-
More importantly, in view of the improved value of \(\gamma \), we decided to use it as an input in the present analysis, instead of the usual determination of the UT in CMFV models through \(S_{\psi K_S}~(\beta )\) and the side \(R_t\) of the UT determined from the ratio \(\Delta M_{d}/\Delta M_{s}\) and \(\xi \) in (9).
-
The most recent discussions, see in particular [19, 20], dealt exclusively with the implications of the enhanced value of \(\Delta M_s\) and not \(\Delta M_d\), for which in addition to the increased value of \(|V_{cb}|\) also the increased value of \(\gamma \) matters.
In the context of the second item we remark that the \((R_t,\beta )\) strategy for the determination of the UT has been found in [3] to be less powerful than the \((\beta ,\gamma )\) strategy used here. Moreover, as NP now is expected in \(\Delta M_{s,d}\), it appears as a better strategy to replace their ratio by the angle \(\gamma \) and instead treat \(\Delta M_{s,d}\) as outputs being functions of \(\gamma \), \(\beta \) and \(|V_{cb}|\).
One could wonder why the emerging \(\Delta M_d\) anomaly pointed out by us has not been noticed in the global fits performed by the CKMfitter and UTfit collaborations. In our view such global fits, involving simultaneously many quantities, are likely to miss NP effects present in only a subset of observables, in particular when the significance has not reached the discovery level. We are optimistic that the findings of this paper pointing towards NP in the \(B_d\) system will motivate both theorists and experimentalists to intensify the search for NP in \(b\rightarrow d\) transitions, after the last five years being dominated by the study of \(b\rightarrow s\) and \(b\rightarrow c\) transitions.
Our paper is organized as follows. In Sect. 2 we present the determination of the UT and of the CKM matrix using the \((\beta ,\gamma )\) strategy. In Sect. 3 we evaluate \(\Delta M_{d}\) and \(\Delta M_{s}\) as functions of \(\gamma \), finding their values to disagree with the data. The new result relative to [14] and other recent papers [19, 20] is the disagreement of \(\Delta M_{d}\) and the ratio \(\Delta M_{d}/\Delta M_{s}\) with the data, a direct consequence of the increased value of \(\gamma \). On the other hand \(\varepsilon _K\) agrees well with the data. We therefore provide the SM predictions for the branching ratios of \(K^+\rightarrow \pi ^+\nu {\bar{\nu }}\) and \(K_{L}\rightarrow \pi ^0\nu {\bar{\nu }}\) for different values of \(\gamma \), \(\beta \) and \(|V_{cb}|\). In Sect. 4 we have a look at the \((R_b,\gamma )\) strategy, which could become favourable in the next decade, once the tree-level determination of \(|V_{ub}|\) is settled. In Sect. 5 we briefly investigate what kind of NP could be responsible for the \(\Delta M_{s,d}\) anomalies found in Sect. 3 and what are the implications for NP in \(\Delta F =1\) transitions. We conclude in Sect. 6.
2 Deriving the UT and the CKM matrix
Our determination of the UT and of the CKM matrix proceeds in two steps:
Step 1:
We use as input parameters
with \(\beta \) obtained from
This allows us to determine the two sides \(R_b\) and \(R_t\) of the UT shown in Fig. 1, that are given in terms of \(\beta \) and \(\gamma \) as follows [3]
The angles \(\beta \) and \(\gamma \) of the unitarity triangle are directly related to the complex phases of the CKM-elements \(V_{td}\) and \(V_{ub}\), respectively, through
Step 2:
Including \(\lambda \equiv |V_{us}|\) and \(|V_{cb}|\) as the remaining input parameters we determine \(|V_{td}|\) and \(|V_{ts}|\) through
with
where we have used \(\beta \) in (11). \(\Delta M_{d,s}\) are taken from experiment as given in Table 1 but using our \(|V_{cb}|\) and \(\gamma \) dependent values would change the result by less than \(1\%\).
Finally, we find
Left: \(|V_{td}|\) as function of \(\gamma \), for different values of \(|V_{cb}|\). Right: \(|V_{ub}|\) as function of \(\beta \), for different values of \(|V_{cb}|\). The colours correspond to: \(|V_{cb}|=39 \times 10^{-3}\) (red, bottom), \(40 \times 10^{-3}\) (green), \(41 \times 10^{-3}\) (blue), \(42 \times 10^{-3}\) (purple), \(43 \times 10^{-3}\) (turquoise, top)
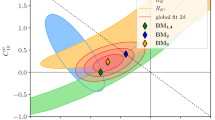
In Fig. 2 we show the constraints on the UT from the tree-level measurement of \(\gamma \), from \(\beta \) extracted from \(S_{\psi K_S}\), and \(R_t\) from \(\Delta M_d/\Delta M_s\). The advantage of the \((\gamma ,\beta )\) strategy over the \((R_t,\beta )\) strategy is not seen yet because of a significant error in \(\gamma \). With the future uncertainty on \(\gamma \) of \(\pm 1^\circ \) represented by the black area, the power of the \((\gamma ,\beta )\) strategy in determining the UT is clearly visible. However, already now we observe that the apex of the UT obtained from the \((\gamma ,\beta )\) strategy disagrees with the one from the \((R_t,\beta )\) one. This tension indicates the presence of some NP contributions.
In Fig. 3 we show \(|V_{td}|\) as a function of \(\gamma \) and \(|V_{ub}|\) as a function of \(\beta \) for different values of \(|V_{cb}|\). The dependences of \(|V_{td}|\) on \(\beta \) and of \(|V_{ub}|\) on \(\gamma \) are very small. These plots will allow to monitor the values of \(|V_{td}|\) and \(|V_{ub}|\) that enter various observables as the uncertainties of \(\gamma \), \(\beta \) and \(|V_{cb}|\) will shrink with time.
3 Calculating observables
For the mass differences in the \(B^0_{s,d}-{\bar{B}}^0_{s,d}\) systems we have the very accurate expressions [14]
Here S(v) is the box-function in CMFV models with v denoting parameters of a given model including \(x_t=m_t^2/M_W^2\). The value 2.322 in the normalization of S(v) is its SM value for \(m_t(m_t)=163.5\, \mathrm{GeV}\) obtained from
and \(\eta _B\) is the perturbative QCD correction [21]. Our input parameters, equal to the ones used in [13], are collected in Table 1. We find
which differ from the experimental values by \(1.9\sigma \) and \(1.4\sigma \), respectively. As the correlation matrix of the relevant lattice parameters entering these predictions is unknown to us, we do not attempt to derive a global significance for the anomaly in \(B_{d,s}-{\bar{B}}_{d,s}\) mixing.
Now, the overall factors in (18) and (19) are the central experimental values, and in CMFV models S(v) is bounded from below by its SM value [28]
Consequently, with the values of \(|V_{td}|\) found in the previous section, that are significantly larger than its nominal value in (18), it is evident that CMFV models have difficulties in describing the data for \(\Delta M_d\). In addition, with the value of \(|V_{cb}|\) in (5) also \(|V_{ts}|\) is significantly larger than its nominal value in (19). Therefore \(\Delta M_s\) in CMFV models is enhanced over its experimental value as already pointed out in [13, 14] and recently analysed in [19, 20]. Yet the latter enhancement is not as large as for \(\Delta M_d\) because \(\Delta M_s\) does not depend on \(\gamma \).
In Fig. 4 we show in the left panel \(\Delta M_d\) and \(\Delta M_s\) normalized to their experimental values. Evidently, for central values of all parameters, \(\Delta M_d\) differs by roughly \(30\%\) from the data while in the case of \(\Delta M_s\) the corresponding difference amounts only to \(12\%\). But the uncertainties in other parameters like \(|V_{cb}|\) and the hadronic parameters in (8) are still significant. However, we expect that in the coming years these uncertainties will significantly be reduced.
In the right panel of Fig. 4 we show the ratio \(\Delta M_s/\Delta M_d\) as a function of \(\gamma \). The dependence on \(|V_{cb}|\) cancels in this ratio and the error on \(\xi \) in (9) is much smaller than the errors in (8). Consequently the disagreement of the ratio in question with the data, shown as a horizontal line at 35.1, is clearly visible and expresses the problem of CMFV models and those based on the \(U(2)^3\) symmetry.
Of interest is also the ratio
with \(\Delta M_{s,d}\) predicted here to be compared with
with \(\Delta M_{s,d}\) taken from experiment. In CMFV models and those with \(U(2)^3\) symmetry this ratio depends only on the angle \(\gamma \). We show this in Fig. 5. A significant enhancement of \(|V_{td}|/|V_{ts}|\) over the value in (24) is observed.
As far as \(\varepsilon _K\) is concerned, using the standard expression as given e.g. in [2] and all input parameters collected in Table 1, we find the SM value of \(\varepsilon _K\) to be fully consistent with the data:
with higher values for the remaining CMFV models due to the bound in (22).
Despite the fact that the SM fails to describe the data for \(\Delta M_{s,d}\), having determined the CKM parameters, the agreement of the SM with the experimental value for \(\varepsilon _K\) invites us to calculate the branching ratios for \(K^+\rightarrow \pi ^+\nu {\bar{\nu }}\) and \(K_{L}\rightarrow \pi ^0\nu {\bar{\nu }}\) in the SM. This is of interest in view of the NA62 and KOTO experiments that should provide results for these decays in the coming years. Using the parametric formulae of [29] we find the central values of \({\mathcal {B}}(K^+\rightarrow \pi ^+\nu {\bar{\nu }})\) and \({\mathcal {B}}(K_{L}\rightarrow \pi ^0\nu {\bar{\nu }})\) given in Table 2 for different values of \(\gamma \), \(\beta \) and \(|V_{cb}|\).
4 \((R_b,\gamma )\) strategy
It is likely that in the next decade the \((\beta ,\gamma )\) strategy will be replaced by the \((R_b,\gamma )\) strategy. This could turn out to be even necessary if the value of \(|V_{ub}|\) determined from tree-level processes turned out to be very different from the one determined in the previous section. Therefore for completeness we want to give the relevant formulae for this strategy.
Knowing \(|V_{ub}|\) determined in tree-level decays, one finds \(R_b\) using
Together with \(\gamma \), this result allows to determine \(R_t\) and \(\beta \) by means of
so that the RUT is completely fixed.
If the resulting value of \(\beta \) differs from the one in (11), then the expression in (12) will have to be replaced by
with \(\varphi _{\mathrm{new}}\) being a new CP-violating phase. For instance for \(|V_{ub}|=4.0 \times 10^{-3}\) we find
5 Going beyond CMFV
Our analysis signals the violation of flavour universality in the function S(v), characteristic for CMFV models. It hints for the presence of new sources of flavour and CP-violation and/or new operators contributing to \(\Delta F=2\) transitions beyond the SM \((V-A)\otimes (V-A)\) ones.Footnote 3 For simplicity we restrict first our discussion of NP scenarios to the ones in which only SM operators are present.
A fully general and very convenient solution in this case is just to consider instead of the flavour universal function S(v) three functions
with \(\Delta S_i\) being real and positive definite quantities, and the minus sign required to suppress \(\Delta M_{d,s}\) below their SM values. It is evident that with two free parameters in each meson system it is always possible to obtain an agreement with the data on \(\Delta F=2\) observables. Our analysis indicates the following pattern of these parameters:
-
A clear breakdown of the universality of S(v) with
$$\begin{aligned} \Delta S_s < \Delta S_d . \end{aligned}$$(31) -
The new phases
$$\begin{aligned} \delta _s\approx \delta _d\approx 0 \end{aligned}$$(32)in order not to spoil the good agreement of the SM with the experimental values of \(S_{\psi K_S}\) and \(S_{\psi \phi }\).
-
In the case of \(K^0-{\bar{K}}^0\) mixing, the good agreement of \(\varepsilon _K\) with its measured value implies a small imaginary part of the NP contribution. This can either be achieved by a small value of \(\Delta S_K\), or by an appropriately chosen value of the new phase \(\delta _K\).
Note that the fate of \(\delta _d\) and to a lesser extend of \(\delta _K\) will depend on the future value of \(|V_{ub}|\) as remarked in connection with (28).
This pattern cannot be explained in models with a minimally broken \(U(2)^3\) flavour symmetry [31,32,33] in which the equality \(\Delta S_s =\Delta S_d\) is predicted, although the near equality of \(\delta _s\) and \(\delta _d\) is a property of these models. This could change if for instance \(|V_{ub}|\) was found significantly different from the value followed from our strategy, as shown in Fig. 6. But as these models fail anyway we will not consider them further.
The simplest models beyond the CMFV and \(U(2)^3\) frameworks one could consider are models with tree-level \(Z^\prime \) and Z exchanges. While in [34,35,36,37] general studies of such scenarios have been considered, specific examples are models with vector-like quarks [38] and 331 models [39]. These models have sufficient numbers of parameters to obtain an agreement with the data for \(\Delta F=2\) processes. This is explicitly shown for the case of 331 models in [39].
The minus sign in (30) has been introduced by us by hand. Strictly speaking, as already discussed in the context of \(\Delta M_s\) in [19], in the presence of only left-handed currents the minus sign in (30) truly requires the NP phases to be \(\pi +\delta _{d,s}\). Following the reasoning in [40], this implies the CP-violating phases in the corresponding \(\Delta F =1 \) \(b\rightarrow d,s\) transitions to be close to \(\pi /2\), i.e. maximal. We hence conclude that, within models with only left-handed currents, the observed suppression of \(\Delta M_{d}\) and to a lesser extent \(\Delta M_s\) implies significant deviations from the SM in CP-asymmetries of radiative and rare \(b\rightarrow d\) and \(b\rightarrow s\) decays. As quantitative predictions for these observables are model-dependent, we leave their thorough analysis for future work.
In the presence of both left- and right-handed couplings, on the other hand, the suppression of \(\Delta M_d\) is much easier to achieve without introducing large CP-violating phases. In this context probably most interesting are models in which the SMEFT operator \({\mathcal {O}}_{Hd}\) involving right-handed flavour violating couplings to down-quarks is generated at the NP scale. As demonstrated in [37], the renormalisation group evolution to low-energy scales involving also left-handed currents present already within the SM generates left-right \(\Delta F=2\) operators representing FCNCs mediated by the Z boson. At NLO this effect has also been discussed in [36]. An explicit realization of such a NP scenario is provided by models with vector-like quarks with an additional U(1) gauge symmetry so that both tree-level Z and \(Z^\prime \) exchanges are present, and in some models of this type also box diagram contributions with vector-like quarks, Higgs and other scalar and pseudoscalar exchanges are important [38]. The test of these scenarios is then mainly offered through the correlations of \(\Delta M_{d,s}\) with \(\Delta F=1\) processes, that is rare K or \(B_{s,d}\) decays, the ratio \(\varepsilon '/\varepsilon \) and other observables. This is evident from the analyses in [37, 38] and once the data on \(\gamma \), \(|V_{cb}|\) and \(|V_{ub}|\) improve, could be an arena for further investigation of the implications of the \(\Delta M_d\) anomaly pointed out here.
6 Summary
The main message of our paper is the emerging \(\Delta M_d\) anomaly which is significantly larger than the \(\Delta M_s\) one discussed in [14, 19, 20]. Its fate will depend strongly on the improved values of \(\gamma \) and \(|V_{cb}|\) from tree-level decays and, to a lesser extent, on \(|V_{ub}|\), which is more relevant for the prediction of \(\sin 2\beta \) in the SM. This anomaly, if confirmed, will have implications for observables sensitive to \(b\rightarrow d\) transitions like \(b\rightarrow d \ell ^+\ell ^-\) and \(b\rightarrow d \nu {\bar{\nu }}\) which will be explored by Belle II. It will open a new oasis of NP, analogous to the one related to the recent anomalies in \(b\rightarrow s \ell ^+\ell ^-\) and their implications for \(b\rightarrow s \nu {\bar{\nu }}\) transitions. Depending on the NP flavour structure, it could also have implications for \(K^+\rightarrow \pi ^+\nu {\bar{\nu }}\) and \(K_{L}\rightarrow \pi ^0\nu {\bar{\nu }}\).
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: There is no data associated with this article.]
Notes
References
G. Isidori, Y. Nir, G. Perez, Flavor physics constraints for physics beyond the standard model. Ann. Rev. Nucl. Part. Sci. 60, 355 (2010). arXiv:1002.0900
A.J. Buras, J. Girrbach, Towards the identification of new physics through quark flavour violating processes. Rept. Prog. Phys. 77, 086201 (2014). arXiv:1306.3775
A.J. Buras, F. Parodi, A. Stocchi, The CKM matrix and the unitarity triangle: another look. JHEP 0301, 029 (2003). arXiv:hep-ph/0207101
T. Goto, N. Kitazawa, Y. Okada, M. Tanaka, Model independent analysis of \(B {\bar{B}}\) mixing and CP violation in \(B\) decays. Phys. Rev. D 53, 6662 (1996). arXiv:hep-ph/9506311
LHCb Collaboration collaboration, M.W. Kenzie, M.P. Whitehead, Update of the LHCb combination of the CKM angle \(\gamma \), Tech. Rep. LHCb-CONF-2018-002. CERN-LHCb-CONF-2018-002, CERN, Geneva (2018)
HFLAV collaboration, Y. Amhis et al., Averages of \(b\)-hadron, \(c\)-hadron, and \(\tau \)-lepton properties as of summer 2016, Eur. Phys. J. C77, 895 (2017) arXiv:1612.07233
Belle II collaboration, E. Kou et al., The Belle II Physics Book. arXiv:1808.10567
P. Krishnan, Precision measurements of the CKM parameters (mainly \(\gamma /\phi _{3}\) measurements), in 16th Conference on Flavor Physics and CP Violation (FPCP 2018) Hyderabad, India, July 14–18, 2018 (2018) arXiv:1810.00841
P. Gambino, K.J. Healey, S. Turczyk, Taming the higher power corrections in semileptonic B decays. Phys. Lett. B 763, 60 (2016). arXiv:1606.06174
A.J. Buras, P. Gambino, M. Gorbahn, S. Jager, L. Silvestrini, Universal unitarity triangle and physics beyond the standard model. Phys. Lett. B 500, 161 (2001). arXiv:hep-ph/0007085
A.J. Buras, Minimal flavor violation. Acta Phys. Polon. B 34, 5615 (2003). arXiv:hep-ph/0310208
M. Blanke, A.J. Buras, D. Guadagnoli, C. Tarantino, Minimal flavour violation waiting for precise measurements of \(\Delta M_s\), \(S_{\psi \phi }\), \(A^s_\text{ SL }\), \(|V_{ub}|\), \(\gamma \) and \(B^0_{s, d} \rightarrow \mu ^+ \mu ^-\). JHEP 10, 003 (2006). arXiv:hep-ph/0604057
A. Bazavov et al., \(B^0_{(s)}\)-mixing matrix elements from lattice QCD for the Standard Model and beyond. arXiv:1602.03560
M. Blanke, A.J. Buras, Universal unitarity triangle 2016 and the tension between \(\Delta M_{s, d}\) and \(\varepsilon _K\) in CMFV models. Eur. Phys. J. C 76, 197 (2016). arXiv:1602.04020
RBC/UKQCD collaboration, P.A. Boyle, L. Del Debbio, N. Garron, A. Juttner, A. Soni, J.T. Tsang et al., SU(3)-breaking ratios for \(D_{(s)}\) and \(B_{(s)}\) mesons. arXiv:1812.08791
D. Bigi, P. Gambino, S. Schacht, A fresh look at the determination of \(|V_{cb}|\) from \(B\rightarrow D^{*} \ell \nu \). Phys. Lett. B 769, 441 (2017). arXiv:1703.06124
D. Bigi, P. Gambino, S. Schacht, \(R(D^*)\), \(|V_{cb}|\), and the Heavy Quark Symmetry relations between form factors. JHEP 11, 061 (2017). arXiv:1707.09509
J.A. Bailey, S. Lee, W. Lee, J. Leem, S. Park, \(4\sigma \) tension in \(\varepsilon _K\) obtained with lattice QCD inputs. arXiv:1808.09657
L. Di Luzio, M. Kirk, A. Lenz, Updated \(B_s\)-mixing constraints on new physics models for \(b\rightarrow s\ell ^+\ell ^-\) anomalies. Phys. Rev. D 97, 095035 (2018). arXiv:1712.06572
L. Di Luzio, M. Kirk, A. Lenz, \(B_s\)-\({\bar{B}}_s\) mixing interplay with \(B\) anomalies. In: 10th International Workshop on the CKM Unitarity Triangle (CKM 2018) Heidelberg, Germany, September 17–21, 2018. arXiv:1811.12884 (2018)
A.J. Buras, M. Jamin, P.H. Weisz, Leading and next-to-leading QCD corrections to \(\varepsilon \) parameter and \(B^0-\bar{B}^0\) mixing in the presence of a heavy top quark. Nucl. Phys. B 347, 491 (1990)
Particle Data Group collaboration, K. Olive et al., Review of particle physics. Chin. Phys. C38, 090001 (2014)
J.L. Rosner, S. Stone, R.S. Van de Water, Leptonic decays of charged pseudoscalar mesons. arXiv:1509.02220 (2015)
J. Brod, M. Gorbahn, Next-to-Next-to-leading-order charm-quark contribution to the CP violation parameter \(\varepsilon _K\) and \(\Delta M_K\). Phys. Rev. Lett. 108, 121801 (2012). arXiv:1108.2036
J. Brod, M. Gorbahn, \(\epsilon _K\) at next-to-next-to-leading order: the charm-top-quark contribution. Phys. Rev. D 82, 094026 (2010). arXiv:1007.0684
J. Urban, F. Krauss, U. Jentschura, G. Soff, Next-to-leading order QCD corrections for the \(B^0 - {\bar{B}}^0\) mixing with an extended Higgs sector. Nucl. Phys. B 523, 40 (1998). arXiv:hep-ph/9710245
A.J. Buras, D. Guadagnoli, G. Isidori, On \(\epsilon _K\) beyond lowest order in the operator product expansion. Phys. Lett. B 688, 309 (2010). arXiv:1002.3612
M. Blanke, A.J. Buras, Lower bounds on \(\Delta M_{s, d}\) from constrained minimal flavour violation. JHEP 0705, 061 (2007). arXiv:hep-ph/0610037
A.J. Buras, D. Buttazzo, J. Girrbach-Noe, R. Knegjens, \( {K}^{+}\rightarrow {\pi }^{+}\nu {\overline{\nu }} \) and \( {K}_L\rightarrow {\pi }^0\nu {\overline{\nu }} \) in the standard model: status and perspectives. JHEP 11, 033 (2015). arXiv:1503.02693
G. D’Ambrosio, G.F. Giudice, G. Isidori, A. Strumia, Minimal flavour violation: an effective field theory approach. Nucl. Phys. B 645, 155 (2002). arXiv:hep-ph/0207036
A.L. Kagan, G. Perez, T. Volansky, J. Zupan, General minimal flavor violation. Phys. Rev. D 80, 076002 (2009). arXiv:0903.1794
R. Barbieri, G. Isidori, J. Jones-Perez, P. Lodone, D.M. Straub, U(2) and minimal flavour violation in supersymmetry. Eur. Phys. J. C 71, 1725 (2011). arXiv:1105.2296
R. Barbieri, D. Buttazzo, F. Sala, D.M. Straub, Flavour physics from an approximate \(U(2)^3\) symmetry. JHEP 1207, 181 (2012). arXiv:1203.4218
A.J. Buras, F. De Fazio, J. Girrbach, The anatomy of Z’ and Z with flavour changing neutral currents in the flavour precision era. JHEP 1302, 116 (2013). arXiv:1211.1896
A.J. Buras, New physics patterns in \(\varepsilon ^\prime /\varepsilon \) and \(\varepsilon _K\) with implications for rare kaon decays and \(\Delta M_K\). JHEP 04, 071 (2016). arXiv:1601.00005
M. Endo, T. Kitahara, S. Mishima, K. Yamamoto, Revisiting Kaon physics in general \(Z\) scenario. Phys. Lett. B 771, 37 (2017). arXiv:1612.08839
C. Bobeth, A.J. Buras, A. Celis, M. Jung, Yukawa enhancement of \(Z\)-mediated new physics in \(\Delta S = 2\) and \(\Delta B = 2\) processes. JHEP 07, 124 (2017). arXiv:1703.04753
C. Bobeth, A.J. Buras, A. Celis, M. Jung, Patterns of flavour violation in models with vector-like quarks. JHEP 04, 079 (2017). arXiv:1609.04783
A.J. Buras, F. De Fazio, 331 models facing the tensions in \(\Delta F=2\) processes with the impact on \(\varepsilon ^\prime /\varepsilon \), \(B_s\rightarrow \mu ^+\mu ^-\) and \(B\rightarrow K^*\mu ^+\mu ^-\). arXiv:1604.02344
M. Blanke, Insights from the interplay of \(K \rightarrow \pi \nu {\bar{\nu }}\) and \(\varepsilon _K\) on the new physics flavour structure. Acta Phys. Polon. B 41, 127 (2010). arXiv:0904.2528
Acknowledgements
The research of AJB was fully supported by the DFG cluster of excellence “Origin and Structure of the Universe”.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Blanke, M., Buras, A.J. Emerging \(\Delta M_{d}\)-anomaly from tree-level determinations of \(|V_{cb}|\) and the angle \(\gamma \). Eur. Phys. J. C 79, 159 (2019). https://doi.org/10.1140/epjc/s10052-019-6667-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-6667-x