Low-redshift constraints on the Hubble constant from the baryon acoustic oscillation “standard rulers” and the gravitational wave “standard sirens”

Abstract

The multi-messenger observations of GW170817 indicated a new independent measurement of the Hubble constant ($H_0$). We obtain the low-redshift cosmological constraints on $H_0$ by combining this gravitational wave measurement with the observations of distance scales in baryon acoustic oscillations. Using Fisher information matrix, we estimate the projected constraints on $H_0$ from Einstein Telescope. Simulating $10^3$ gravitational-wave standard sirens from binary neutron star coalescences, we find that Einstein Telescope alone can constrain $H_0$ almost as tightly as Planck final data release in the cosmological constant plus cold dark matter model. This constraint can be further improved by combining Einstein Telescope with Dark Energy Spectroscopic Instrument. The Hubble constant tension can thus be checked by observing the standard sirens with Einstein Telescope in the future.

1 Introduction

The recent observations of GW170817 [1] in both gravitational waves (GWs) and electromagnetic waves provide us a gravitational-wave “standard siren” measurement of the Hubble constant [2]. Advanced Laser Interferometer Gravitational-Wave Observatory (aLIGO) and Virgo can estimate the luminosity distance of GW170817 directly, and does not require any form of cosmic “distance ladder”. In other words, the GW standard sirens are self-calibrated. Therefore, this is an independent measurement totally different from observations of the luminosity distance of Cepheids [3] and the cosmic microwave background (CMB) [4]. On the other hand, the electromagnetic wave analysis can infer the Hubble constant by measuring the recession velocity [2]. The Hubble’s law says that the recession velocity is a product of $H_0$ and the proper distance. Therefore, the Hubble constant derived in this way is $H_0=70.0_{-8.0}^{+12.0}~\text {km s}^{-1}~\text {Mpc}^{-1}$ at $68\%$ confidence level (CL) [2]. A recent work in Ref. [5] found a precise distance to the host galaxy of GW170817 and then shown $H_0=71.9\pm 7.1 ~\text {km s}^{-1}~\text {Mpc}^{-1}$. Ref. [6] obtained $H_0=69.9^{+4.7}_{-4.8}~\text {km s}^{-1}~\text {Mpc}^{-1}$ by combining the GW170817 and its electromagnetic (EM) counterpart GRB170817A with its radio counterpart.

The GW170817 constraints on $H_0$ are significantly less stringent than the pre-existing typical constraints, even though they are compatible with the latters. A local measurement of $H_0$, derived from the luminosity distances of Cepheids, shows $H_0=73.24\pm 1.74~\text {km s}^{-1}~\text {Mpc}^{-1}$ at $68\%$ CL [3]. The CMB constraint on $H_0$, obtained from a global fitting of the CMB data released by Planck 2015, gives $H_0=67.8\pm 0.9~\text {km s}^{-1}~\text {Mpc}^{-1}$ at $68\%$ CL [4]. Both constraints are much tighter than the GW constraint on $H_0$. However, the local measurement of $H_0$ is obviously in tension with the CMB constraint by more than $3\sigma$. The former may be affected by residual systematics [7]. The latter relies on the assumption of cosmological models, for example, the spatially-flat base $\varLambda$ Cold Dark Matter model ($\varLambda$CDM) model. Unfortunately, it is beyond the scope of the recent GW standard siren measurement to distinguish them from each other.

The GW170817 constraint on $H_0$ in Ref. [2] may bring underlying influences on the cosmological parameter inferences. It can be viewed as a prior of $H_0$ in cosmological global fittings. A recent work in Ref. [8] combined it with the Planck 2015 observations of the CMB to explore a twelve-parameter extended $\varLambda$CDM scenario, and found that an inclusion of the recent GW prior of $H_0$ can significantly reduce the allowed parameter space.

As standard rulers, the distance scales measured in the baryon acoustic oscillation (BAO) can also be able to constrain $H_0$. In the $\varLambda$CDM model, for example, Ref. [9] determined $H_0$ with a $1.3\%$ uncertainty using several BAO distance scales. Ref. [10] determined $H_0$ with a $3.38\%$ uncertainty using several BAO distance scales including the recent anisotropic BAO measurements at nine effective redshift bins. Ref. [11] obtained $H_0=67.87^{+1.21}_{-1.86}~\text {km s}^{-1}~\text {Mpc}^{-1}$ by combining several BAO distance scales with the Alcock–Paczynski test.

In this work, we will study the constraints on the Hubble constant as well as other cosmological parameters by combining the GW170817 measurement of $H_0$ [2] with the measurements of distance scales in the BAO [12,13,14,15]. Both observations have relatively lower redshifts than the CMB. Beside the Hubble constant, we focus on the spatial curvature and the equation of state of the dark energy. Extending the parameter space can more or less reduce the dependence on cosmological models. We wonder if an inclusion of the recent GW standard siren measurement can significantly improve the constraints on these cosmological parameters. In addition, we will estimate the projected constraints on the cosmological parameters by combining the Einstein Telescope (ET) [16] with the Dark Energy Spectroscopic Instrument (DESI) project [17]. The technique of Fisher information matrix will be utilized for our estimation in this work. We expect that the two low-redshift cosmological observations can provide tighter constraints on the Hubble constant as well as other cosmological parameters in the future.

The rest of this paper is arranged as follows. Section 2 introduces the cosmological models and the data compilations. Section 3 presents the results of our parameter inferences. Section 4 demonstrates to what extent the luminosity distance can be measured by the ET. Section 5 shows the projected constraints on cosmological parameters from the ET and the DESI project. The conclusions and discussions are given in Sect. 6.

2 Cosmological models and data compilations

The Hubble constant is correlated with the spatial curvature and the equation of state of the dark energy. For a given value of the angular diameter distance to the last scattering surface, one can always adjust the values of the two parameters to compensate the variation of $H_0$ in principle. Using both BAO and GW data sets, we explore several extended cosmological models taking into account of the spatial curvature, or the equation of state of the dark energy, or both of them.

In the Friedmann–Lemaitre–Robertson–Walker Universe, the angular diameter distance $D_A(z)$ to an astrophysical object at redshift z is defined as

$$\begin{aligned} D_A(z)=\frac{1}{1+z}S_k\left( \int _0^z\frac{dz^\prime }{H(z')}\right) \ , \end{aligned}$$

(1)

where the function $S_k(x)$ is defined as

$$\begin{aligned} S_k(x)= {\left\{ \begin{array}{ll} \frac{\sinh (H_0\sqrt{\varOmega _k}x)}{H_0\sqrt{\varOmega _k}}\quad (\varOmega _k>0),\\ x\quad (\varOmega _k=0),\\ \frac{\sin (H_0\sqrt{-\varOmega _k}x)}{H_0\sqrt{-\varOmega _k}}\quad (\varOmega _k<0), \end{array}\right. } \end{aligned}$$

(2)

and the Hubble parameter H(z) is given by

$$\begin{aligned} H^2(z)/H_0^2= & {} \varOmega _r(1+z)^4+\varOmega _m(1+z)^3+\varOmega _k(1+z)^2\nonumber \\&+(1-\varOmega _r-\varOmega _m-\varOmega _k)f(z)\ , \end{aligned}$$

(3)

$$\begin{aligned}&f(z)=\exp \left( \int _0^z 3(1+w(z^\prime ))\frac{dz^\prime }{1+z^\prime }\right) , \end{aligned}$$

(4)

where w(z) denotes the equation of state of the dark energy. The parameters $\varOmega _r$, $\varOmega _m$, and $\varOmega _k$ denote nowadays energy-density fractions of radiations, non-relativistic matter, and spatial curvature, respectively. To calculate the radiation density today, we refer to the formula $\varOmega _r=\varOmega _\gamma (1+0.2271N_{\mathrm {eff}})$. We use the Planck best-fitting results, namely, the nowadays energy-density fraction of photons $\varOmega _\gamma =2.469\times 10^{-5}h_0^{-2}$, and the relativistic degrees of freedom $N_{\mathrm {eff}}=3.046$ [18, 19]. Here we parameterize the Hubble constant as $H_0=100h_0~\text {km s}^{-1}~\text {Mpc}^{-1}$.

The sound horizon at the redshift $z_d$ (the moment when the baryons decoupled from the Compton drag of the photons) can be calculated by using the Eisenstein and Hu formula [20]. It is given by

$$\begin{aligned} r_s(z_d)=\frac{1}{\sqrt{3}H_0}\int _0^{\frac{1}{1+z_d}}\frac{da}{a^2E(a)\sqrt{1+\frac{3\varOmega _b}{4\varOmega _\gamma }a}}\ , \end{aligned}$$

(5)

where $z_d$ is given by a fitting formula, i.e. ,

$$\begin{aligned} z_d= & {} \frac{1291(\varOmega _m h_0^2)^{0.251}}{1+0.659(\varOmega _m h_0^2)^{0.828}}\left( 1+b_1(\varOmega _b h_0^2)^{b_2}\right) \ , \end{aligned}$$

(6)

$$\begin{aligned} b_1= & {} 0.313(\varOmega _m h_0^2)^{-0.419}\left( 1+0.607(\varOmega _m h_0^2)^{0.674}\right) \ , \end{aligned}$$

(7)

$$\begin{aligned} b_2= & {} 0.238(\varOmega _m h_0^2)^{0.223} \ . \end{aligned}$$

(8)

Here $a=1/(1+z)$ denotes the scale factor of the Universe at redshift z. In this paper, we fix $\varOmega _b h_0^2$ to its best-fit value obtained from Planck 2015 data release [4], namely, $\varOmega _b h_0^2=0.02222\pm 0.00023$. The variations of $\varOmega _b h_0^2$ within its error bar do not significantly shift our results.

The independent parameters which will be explored in this paper are composed of $H_0$, $\varOmega _m$, $\varOmega _k$, and the parameters in w(z) parameterizations. To study the constraints on $H_0$, we introduce a single parameter to parameterize w(z), and investigate the following models. First, we explore the parameter space $\{H_0,~\varOmega _m\}$ of the $\varLambda$CDM model. Second, we discuss the $\varOmega _k\varLambda$CDM model with parameter space $\{H_0,~\varOmega _m,~\varOmega _k\}$. Third, we study the generic dark energy model, i.e., $w(z)=w$, which is a constant. This is called the wCDM model, and the parameter space is spanned by $\{H_0,~\varOmega _m,~w\}$. Lastly, we consider the $\varOmega _k w$CDM model, and the parameter space is $\{H_0,~\varOmega _m,~\varOmega _k,~w\}$. We set priors as follows: $h_0\in [0.4,1]$, $\varOmega _m\in [0.1,0.9]$, $\varOmega _k\in [-\,\,0.9,0.9]$, and $w\in [-\,\,3.5,-\,\,0.5]$. All priors are uniform. To estimate the projected constraints on $H_0$ from future observations, we further consider the Chevallier–Polarski–Linder (CPL) parameterization [21, 22]. In the CPL model, one assumes $w(z)=w_0+w_a(1-a)$. Here $w_0$ and $w_a$ are constants. Therefore, the parameter space is spanned by $\{H_0,~\varOmega _m,~w_0,~w_a\}$. If the parameter space is enlarged as $\{H_0,~\varOmega _m,~\varOmega _k,~w_0,~w_a\}$, the model is denoted as $\varOmega _k$CPL instead.

To explore the parameter space, we adopt the Cosmological Mente Carlo (CosmoMC) package [23], which is a publicly available Markov-Chain Monte-Carlo (MCMC) sampler for cosmological parameter inferences. We combine the GW170817 measurement of the Hubble constant [2] with the measurements of distance scales in the BAO [12,13,14,15]. Therefore, the adopted datasets include: the “BAO” which only includes the BAO measurements, and the “BAO+GW” which combines the BAO measurements and the GW170817 constraint on $H_0$.

For the measurements of distance scales in the BAO, we adopt the 6-degree Field Galaxy Survey [12], the Sloan Digital Sky Survey (SDSS) DR7 Main Galaxy Sample [13], the tomographic BAO analysis of the SDSS III Baryon Oscillation Spectroscopic Survey (BOSS) DR12 combined sample [14], and the SDSS IV extended Baryon Oscillation Spectroscopic Survey (eBOSS) DR14 quasar sample [15]. For the BOSS DR12 data, we use the tomographic nine effective redshift bins. For each bin, the anisotropic BAO estimators are given by $\frac{D_A(z)}{r_s(z_d)}$ and $H(z)r_s(z_d)$. For the other three data points, we refer to the isotropic BAO estimator which is defined as the volume-averaged effective distance, namely, $D_V(z)=(1+z)^{2/3}D^{2/3}_A(z){z}^{1/3}{H(z)}^{-1/3}$.

For the GW170817 constraint on $H_0$ [2], we introduce a new likelihood of this data point into the CosmoMC package. Due to a highly non-Gaussian probability distribution function (PDF) of $H_0$ in GW170817, we explicitly utilize the PDF of $H_0$ shown in Fig. 1 of Ref. [2] as a $H_0$ prior in the CosmoMC.

3 The $H_0$ constraints from the GW170817 standard siren and the BAO standard rulers

For the four cosmological models, we list the $68\%$ CL constraints on the independent parameters and the best-fit $\chi ^2$ in the Tables 1, 2, 3 and 4. We depict the one dimensional (1D) PDFs of the independent parameters and the two dimensional (2D) $68\%$ and $95\%$ CL contours of any two independent parameters in Figs. 1, 2, 3 and 4.

Table 1 The $68\%$ CL constraints on the independent parameters of the $\varLambda$CDM model

Table 2 The $68\%$ CL constraints on the independent parameters of the $\varOmega _k \varLambda$CDM model

For the $\varLambda$CDM model, the $68\%$ CL constraints on $H_0$ and $\varOmega _m$ are shown in Table 1, and the 1D PDFs and the 2D contours are depicted in Fig. 1. As expected, the BAO only dataset reproduces the $H_0$ constraint in Ref. [10]. After the GW data is added, we do not find significant improvements to this constraint. Therefore, the BAO measurements dominate the constraints on cosmological parameters in the $\varLambda$CDM model.

Table 3 The $68\%$ CL constraints on the independent parameters of the wCDM model

Table 4 The $68\%$ CL constraints on the independent parameters of the $\varOmega _k w$CDM model

Fig. 1

The 1D PDFs and the 2D contours for the independent parameters in the $\varLambda$CDM model

Fig. 2

The 1D PDFs and the 2D contours for the independent parameters in the $\varOmega _k \varLambda$CDM model

For the $\varOmega _k\varLambda$CDM model, the $68\%$ CL constraints on $H_0$, $\varOmega _m$ and $\varOmega _k$ are shown in Table 2, and the 1D PDFs and the 2D contours are depicted in Fig. 2. Compared with the $\varLambda$CDM model, our cosmological constraints become not as tight as before due to an additional independent parameter $\varOmega _k$. The BAO data constrains the Hubble constant as $71^{+9}_{-20}~\text {km s}^{-1}~\text {Mpc}^{-1}$, while the BAO+GW data constrains the Hubble constant as $73.1^{+5.2}_{-10.0}~\text {km s}^{-1}~\text {Mpc}^{-1}$. The uncertainties on $H_0$ are reduced by around a half by adding the GW170817 data. We obtain similar results for the other two parameters. Therefore, the GW measurement, combining with the BAO distance measures, can significantly improve the constraints on cosmological parameters in the $\varOmega _k\varLambda$CDM model. In addition, the value of $\varOmega _k$ is consistent with 0 within $68\%$ CL.

Fig. 3

The 1D PDFs and the 2D contours for the independent parameters in the wCDM model

For the wCDM model, the constraints on $H_0$, $\varOmega _m$ and w are shown in Table 3, and the 1D PDFs and the 2D contours are depicted in Fig. 3. Compared with the $\varLambda$CDM model, the uncertainties become larger by around $30\%$ for $\varOmega _m$, and by several times for $H_0$. The Hubble constant is constrained to be $82^{+20}_{-7} ~\text {km s}^{-1}~\text {Mpc}^{-1}$ using the BAO data. After adding the GW data, it is improved to be $77.4^{+6.5}_{-11.0}~\text {km s}^{-1}~\text {Mpc}^{-1}$. The constraint on $H_0$ is thus dominated by the GW data. The constraints on two other parameters are also improved by adding the GW data. Therefore, the GW measurement, combining with the BAO distance measures, can significantly improve the cosmological constraints on the wCDM model. In addition, w is well consistent with the cosmological constant which takes $w=-1$.

Fig. 4

The 1D PDFs and the 2D contours for the independent parameters in the $\varOmega _k w$CDM model

For the $\varOmega _k w$CDM model, the $68\%$ CL constraints on $H_0$, $\varOmega _m$ and w are shown in Table 4, and the 1D PDFs and the 2D contours are depicted in Fig. 4. The cosmological constraints become significantly looser than those in the former three models. The Hubble constant is constrained to be $71^{+10}_{-20} ~\text {km s}^{-1}~\text {Mpc}^{-1}$ using the BAO data, while to be $73.1^{+5.2}_{-10.0}~\text {km s}^{-1}~\text {Mpc}^{-1}$ using the BAO+GW data. The uncertainty is reduced by a half by adding the GW170817 data. For three other parameters, the constraints also become tighter after adding the GW170817 data. Therefore, the GW measurement, combining with the BAO distance measures, can significantly improve the constraints on cosmological parameters in the $\varOmega _k w$CDM model. In addition, the value of $\varOmega _k$ is well consistent with 0, and w is well consistent with $-1$.

In summary, the GW170817 measurement introduces little influence on the $\varLambda$CDM model. However, it dominates the cosmological constraints on $H_0$ and improves the constraints on other parameters for the three extended cosmological models which introduce the spatial curvature, or the generic dark energy, or both. In principle, we can also extend our studies to the CPL parameterization of dark energy. However, we find that the present data combinations can not provide tight constraints on $w_a$. In the following sections, we will show the projected constraints on $w_a$ from future low-redshift observations. Our predictions will answer why we can not constrain $w_a$ using the present data combinations.

4 Luminosity distance measured by Einstein Telescope

There is only a single GW standard siren which has been detected by the aLIGO and Virgo detectors. The $H_0$ constraint in Ref. [2] is expected to be improved if more and more GW standard sirens were captured in the future. A work shown that $\varDelta H_0/ H_0 \sim 0.042$ will be achieved after the third observational run of aLIGO and Virgo [24]. The ET [16], a third-generation ground-based GW detector, is designed with higher sensitivity than the second-generation aLIGO and Virgo. More GW standard sirens from binary neutron star coalescences are expected to be detected by the ET. In this section, we will demonstrate to what extent the luminosity distance of the GW sources can be measured by the ET in the future.

For a coalescence of a neutron binary, the waveform of GW in an inspiral stage can be written as a 3.5 post-Newtonian (PN) (i.e., at order $(v/c)^7$ beyond Newtonian gravity) formalism [25,26,27,28,29,30,31,32,33]. This formula includes the effect of gravitational radiation reaction. Over a single period, the change of orbital frequency is negligible. Therefore, the stationary phase approximation (SPA) can be employed to compute the waveform of GWs [34]. In the frequency domain, the waveform of GWs in the source frame is given by

$$\begin{aligned} \mathcal {H}(f) = \mathcal {A}f^{-7/6} \exp [i(2\pi f t_c + \pi /4 + \psi (f)-\varphi _{(2,0)})]\ ,\nonumber \\ \end{aligned}$$

(9)

where one takes the following expressions

$$\begin{aligned}&\mathcal {A}= \sqrt{\frac{5}{96}}\frac{\mathcal {M}_c^{5/6}}{\pi ^{2/3}d_L} \sqrt{[\mathcal {F}_+(1+\cos ^2(\iota ))]^2 + [\mathcal {F}_\times 2 \cos (\iota )]^2}\ , \end{aligned}$$

(10)

$$\begin{aligned}&\psi (f) = \psi _c+\frac{3}{128\eta }\sum _{k=0}^7\psi _k(\pi Mf)^{(k-5)/3}\ , \end{aligned}$$

(11)

$$\begin{aligned}&\varphi _{(2,0)}= \tan ^{-1}\left( -\frac{2\cos (\iota )\mathcal {F}_\times }{(1+\cos ^2(\iota ))\mathcal {F}_{+}}\right) \ . \end{aligned}$$

(12)

Here f is the GW frequency, $d_{\mathrm {L}}$ is a luminosity distance to the binary, $t_c$ is a coalescence time, $\psi _c$ is an orbital coalescence phase, and $\iota$ is an inclination angle between the line of sight and the orbital angular momentum of the binary. $d_{\mathrm {L}}$ can be written as

$$\begin{aligned} d_{\mathrm {L}}=(1+z)^2D_{\mathrm {A}}\ . \end{aligned}$$

(13)

A description of parameters $\psi _k$ can be found in Ref. [35]. Conventionally, one represents the component masses $m_1$ and $m_2$ as a symmetric mass ratio $\eta =m_1m_2/(m_1+m_2)^2$ and a chirp mass $\mathcal {M}_c=(m_1+m_2)\eta ^{3/5}$. The total mass is thus given by $M=\mathcal {M}_{c}\eta ^{-3/5}$. One should notice that the above formulae in Eqs. (9)–(12) are established in the source frame. However, the GWs would be detected in the observer frame. To transform to the observer frame, one should substitute $m_i$ ($i=1,2$) in the above formulae with $m_i(1+z)$, where z is a cosmological redshift of the GW source.

The antenna pattern functions $\mathcal {F}_{+,\times }$ in Eq. (10) describe the responses of an interferometer to a GW signal propagating from a polar angle $\theta$ and an azimuthal angle $\phi$ with a polarization angle $\psi$. As a possible design, the ET has three interferometers with opening angles of ${\pi }/{3}$ and $10~\mathrm {km}$ length arms. Its antenna pattern functions are given by

$$\begin{aligned} \mathcal {F}_{+}^{(1)}(\theta ,\phi ,\psi )&= \frac{\sqrt{3}}{2}\left[ \frac{1}{2}(1+\cos ^2(\theta ))\cos (2\phi )\cos (2\psi )\right. \nonumber \\&\quad \left. -\cos (\theta )\sin (2\phi )\sin (2\psi )\right] \ , \end{aligned}$$

(14)

$$\begin{aligned} \mathcal {F}_\times ^{(1)}(\theta ,\phi ,\psi )&= \frac{\sqrt{3}}{2}\left[ \frac{1}{2}(1+\cos ^2(\theta ))\cos (2\phi )\sin (2\psi )\right. \nonumber \\&\quad \left. +\cos (\theta )\sin (2\phi )\cos (2\psi )\right] \ , \end{aligned}$$

(15)

$$\begin{aligned} \mathcal {F}_{+,\times }^{(2)}(\theta ,\phi ,\psi )&=\mathcal {F}_{+,\times }^{(1)}(\theta ,\phi +2\pi /3,\psi ), \end{aligned}$$

(16)

$$\begin{aligned} \mathcal {F}_{+,\times }^{(3)}(\theta ,\phi ,\psi )&=\mathcal {F}_{+,\times }^{(1)}(\theta ,\phi +4\pi /3,\psi ), \end{aligned}$$

(17)

where the superscript $^{(a)}$ indicates the ath interferometer. The coefficient $\sqrt{3}/2$ arises from the $\pi /3$ opening angle of the ET [36, 37].

In the frequency domain, the parameter space of the waveform is spanned by a set of nine independent parameters, namely, $\{\mathcal {M}_c,~\eta ,~t_c,~\psi _c,~\iota ,~\psi ,~d_L,~\theta ,~\phi \}$. However, the incident direction ($\theta$, $\phi$) of a GW standard siren can be exactly gotten by observing its electromagnetic counterpart. Therefore, a set of only seven independent parameters are left here. For the sake of simplicity, we denote them with $p_i=\{\ln \mathcal {M}_c,~\ln \eta ,~t_c,~\psi _c,~\iota ,~\psi ,~\ln d_L\}$, where $i = 1,2,3,\ldots ,7$.

The capability of a GW detector to measure a GW signal is determined by its noise power spectral density (PSD). For all the three interferometers of the ET, we use the same PSD which is called ETB [38]. This PSD is expressed as

$$\begin{aligned} S_n(f)= & {} 10^{-50} \times (2.39\times 10^{-27} x^{-15.64}+0.349x^{-2.145}\nonumber \\&+1.76x^{-0.12}+0.409x^{1.10})^2\text {Hz}^{-1}\ . \end{aligned}$$

(18)

where we define a dimensionless quantity $x=f/(100\text {Hz})$.

The Fisher information matrix [34, 39, 40] is performed to estimate the projected constraints on cosmological parameters from future GW observations. For the a-th interferometer, the Fisher matrix is defined as

$$\begin{aligned} F^{(a)}_{i j} = \bigg \langle \frac{\partial \mathcal {H}^{(a)}(f)}{\partial p_i},\frac{\partial \mathcal {H}^{(a)}(f)}{\partial p_j}\bigg \rangle \ . \end{aligned}$$

(19)

In the above definition, the angle bracket $\langle \rangle$ denotes a scalar product, i.e.

$$\begin{aligned} \langle h_1,h_2\rangle \equiv 4\int _{f_\text {lower}}^{f_\text {upper}}\frac{h_1(f)h_2^*(f)+ h_1^*(f)h_2(f)}{2 S_n(f)}\text {d}f\ , \end{aligned}$$

(20)

where a superscript $^*$ denotes a conjugation. For the ET, we choose $f_{\text {lower}}=1\text {Hz}$, and $S_n$ is essentially large for $f<1\text {Hz}$. Following Ref. [36], we assume that the end of an inspiral regime occurs when its radiation frequency reaches $f_\text {upper}=2f_{\text {LSO}}$, where $f_{\text {LSO}}=1/(6^{3/2}2\pi M_\text {obs})$. Here $M_\text {obs}=M(1+z)$ is the total mass in the observer frame. For multiple interferometers, the Fisher matrix is defined as follows

$$\begin{aligned} F = \sum _{a}F^{(a)}=F^{(1)}+F^{(2)}+F^{(3)}\ , \end{aligned}$$

(21)

which is a summation of all the Fisher matrices for single interferometers. For the ET, the sum runs from 1 to 3 due to there being three interferometers in total. Therefore, we get the second equality in last equation.

We focus on the GW events which are generated by the mergers of the neutron star binaries. The short gamma-ray bursts will also be generated as the electromagnetic counterparts. They are believed to be highly beamed, since the gamma rays are emitted into a narrow cone which is almost perpendicular to the orbital plane of the inspiral. The inclination angle $\iota$ is thus narrow [41]. We assume it to satisfy a bimodal normal distribution within the range $[0^\circ ,180^\circ ]$, namely,

$$\begin{aligned} P(\iota )= \frac{1}{\sqrt{2\pi }\sigma }\times {\left\{ \begin{array}{ll} \mathrm {exp}\left( {-\frac{\left( \iota -\iota _0\right) ^2}{2\sigma ^2}}\right) \ \\ \mathrm {exp}\left( {-\frac{\left( \iota -\iota _\pi \right) ^2}{2\sigma ^2}}\right) \ \end{array}\right. }\ , \end{aligned}$$

(22)

where we take $\iota _0=0^\circ$, $\iota _\pi =180^\circ$ and $\sigma =20^\circ$. This prior distribution of $\iota$ can be taken into account by adding an extra term to the Fisher matrix.¹ Therefore, we obtain the following transformation:

$$\begin{aligned} F_{i j} \longrightarrow F_{i j} + \frac{\delta _{i k}\delta _{j k}}{\sigma ^2}\ , \end{aligned}$$

(23)

where we take $k=5$ due to $\iota =p_5$. Without such a prior, the uncertainties on $d_L$ and $\iota$ will be badly constrained because of a high degeneracy between them.

The root-mean-square (rms) uncertainty on the a-th parameter $p_a$ is given by the a-th diagonal component of the covariance matrix C, i.e. $\varDelta p_a = \sqrt{C_{aa}}$. The Cramer–Rao bound indicates an inequality of the form $C\ge F^{-1}$, where F is called Fisher matrix and $F^{-1}$ means an inverse of F. Similar to a previous work [42], we employ the Cholesky decomposition to get the inverse matrix here. Therefore, a lower bound on the rms uncertainty of the i-th parameter is given by

$$\begin{aligned} \sigma _{p_i}= \sqrt{(F^{-1})_{ii}}\ . \end{aligned}$$

(24)

Therefore, the projected constraints on any $p_i$ can be inferred by calculating the Fisher matrix. In addition, a non-diagonal element of $(F^{-1})_{ij}$ describes a correlation between $p_i$ and $p_j$. Besides, we need to consider the effect of weak lensing on the luminosity distance. Similar to Ref. [43], we assume that the uncertainty due to weak lensing satisfies

$$\begin{aligned} \sigma _l=0.05z\ . \end{aligned}$$

(25)

Therefore, the total uncertainty on the luminosity distance is given by

$$\begin{aligned} \varDelta \ln d_L=\sqrt{\sigma _o^2+\sigma _l^2}, \end{aligned}$$

(26)

where $\sigma _o$ is given by $\sigma _7$ in Eq. (24) due to $\ln d_{L}=p_7$. The above discussion is available for a single GW event from the merger of neutron star binaries. In the next section, we will simulate multiple standard sirens to infer the constraints on the cosmological parameters.

5 Projected constraints on $H_0$ from ET and DESI

In this section, we will estimate the projected constraints on $H_0$ from future GW and BAO observations. As mentioned in last section, the ET has higher sensitivity than aLIGO and Virgo, and is expected to observe more standard sirens. On the other hand, the BAO distance measures are expected to be improved by the next-generation instruments of dark energy measurement, e.g. the DESI project [17]. Combining ET with DESI, we wonder if the constraint on $H_0$ can be improved significantly in the future. In this section, we explore six cosmological models, i.e. $\varLambda$CDM, $\varOmega _k \varLambda$CDM, wCDM, $\varOmega _k w$CDM, CPL, and $\varOmega _k$CPL. Note that the parameter w in ($\varOmega _k$)wCDM is also written as $w_0$ here.

5.1 Constraints on $H_0$ from the ET

As mentioned in Sect. 1, the GW standard sirens are self-calibrated, implying that the luminosity distance can be measured without the necessity of any distance ladders. Meanwhile, their redshifts can be measured by observing the electromagnetic counterparts. Therefore, one can utilize the $d_L-z$ relation to infer the cosmological parameters. As mentioned in Sect. 2, we focus on the parameters $h_0,~\varOmega _m,~\varOmega _k,~w_0,~w_a$. Based on Planck 2015 data release [4], we set $h_0 = 0.673, ~\varOmega _m = 0.313, ~\varOmega _k = 0, ~w_0 =-1, ~w_a =0$ as the fiducial model.

We utilize the Fisher information matrix to predict the uncertainties on $H_0$ and other cosmological parameters. For a set of multiple standard sirens, the Fisher matrix is defined as follows

$$\begin{aligned} F_{i j} = \sum _k \frac{\partial _i (\ln d_L(k))\partial _j(\ln d_L(k))}{(\varDelta \ln d_L(k))^2}, \end{aligned}$$

(27)

where both i and j run from 1 to 5, denoting the five independent parameters {$w_0, ~w_a, ~\varOmega _m, ~\varOmega _k, ~h_0$} in order, and k denotes the k-th GW event located at {$z_k,~\hat{\gamma _k}$}. Here $z_{k}$ denotes the redshift of k-th event, and $\hat{\gamma }_{k}$ stands for a set of four angle parameters $\{\theta , ~\phi , ~\psi , ~\iota \}_{k}$. Not all of the binary neutron star coalescences are associated with electromagnetic counterparts. For the sources with $\iota < 20^\circ$ and $\iota >160^\circ$, in this paper, we assume there being $10^3$ GW standard sirens up to the redshift $z=2$, at which the angle-averaged signal-to-noise ratio approximately reaches the value 8 [43].

Due to $d_L$ being independent of $\hat{\gamma }$ and the event number being large, one can replace the sum over GW events in the above equation with an integral. Therefore, the following equation can be obtained [36]

$$\begin{aligned} F_{i j}^{GW} = \int _{0}^{2} \partial _i (\ln d_L)\partial _j(\ln d_L) f(z) A(z) dz\ , \end{aligned}$$

(28)

where f(z) denotes the number distribution function of the GW standard sirens with respect to the redshift z, and A(z) denotes an average of $(\varDelta \ln d_{L})^{-2}$ over a set of angle parameters $\{\theta , ~\phi , ~\psi , ~\iota \}$.

One can express the number distribution function of GW standard sirens as follows

$$\begin{aligned} f(z)=\frac{4\pi \mathcal {N}r(z) d_C^2(z)}{H(z)(1+z)}\ , \end{aligned}$$

(29)

where $d_C=(1+z)D_A$ denotes a comoving distance, r(z) is a source distribution function, and $\mathcal {N}$ is a constant ensuring the total number of the binary neutron star coalescences. Following Ref. [36], we consider a uniform distribution of r(z), i.e. $r(z)=1$, and a nonuniform distribution of it, i.e. $r(z)=1+2z$ for $z\le 1$, $r(z)=(15-3z)/4$ for $1<z<5$, and $r(z)=0$ for otherwise. The nonuniform one is an approximation to the evolution of source rate suggested by Ref. [44]. In this work, the constant $\mathcal {N}$ is determined by requiring a relation of $\int _0^2f(z)dz=10^3$.

Fig. 5

The fitting formula $A^{-1/2}(z)$ as a function of redshift z. The red dots arise from the Monte Carlo simulation, while the blue solid curve denotes a fitting formula in Eq. (30)

Table 5 The ET GW Fisher matrix for the uniform distribution of GW sources

Table 6 The ET GW Fisher matrix for the nonuniform distribution of GW sources

Table 7 Projected constraints on cosmological parameters from the ET GWs for the uniform distribution of GW sources

The Monte Carlo sampling method is utilized to obtain an expression for A(z). We divide the redshift from 0 to 2 into 20 bins with a step 0.1. For each a bin, we generate $10^4$ samples of $\{\theta ,\phi ,\psi ,\iota \}$. Note that $\iota$ distributes following Eq. (22), while the three others are uniform. The mass of a neutrino star is set as $m_{\mathrm {NS}}=1.4M_\odot$. Averaging $(\varDelta \ln d_{L})^{-2}$ over $10^4$ samples of $\{\theta ,\phi ,\psi ,\iota \}$ for each redshift bin, we show our results with red dots in Fig. 5. We also fit our results with the following formula:

$$\begin{aligned} A^{-1/2}(z)=0.009295z^3-0.04530 z^2+0.1398 z+0.01941, \end{aligned}$$

(30)

which is shown with blue solid curve in Fig. 5. In addition, we have checked our method by reproducing the results of Ref. [45] with the code developed by us. Finally, we substitute Eq. (30) into Eq. (28) to calculate the Fisher matrix of cosmological parameters. Our detailed results will be shown in the following.

Table 8 Projected constraints on cosmological parameters from the ET GWs for the nonuniform distribution of GW sources

For the five parameters explored here, their GW Fisher matrices are shown as $5\times 5$ matrices in Tables 5 and 6 for the cases with uniform and nonuniform distributions, respectively. There is a specific set of cosmological parameters for a given cosmological model. To obtain the $1\sigma$ uncertainties on these parameters, one can construct a Fisher matrix associated with these parameters by marginalizing the original Fisher matrix over other remaining parameters. For example, if the $\varLambda$CDM model is considered, one should construct a Fisher matrix associated with $\varOmega _m$ and $h_0$ by marginalizing the $5\times 5$ Fisher matrix over $w_0$, $w_a$ and $\varOmega _k$. In other words, one removes the 1st, 2nd, and 4th columns and rows from the two matrices in Tables 5 and 6, respectively, and the remaining items thus form the required Fisher matrices for the $\varLambda$CDM model. A similar approach works for other cosmological models.

Once the Fisher matrix is gotten for a given cosmological model, as mentioned in last section, one can infer the $1\sigma$ uncertainties on the corresponding cosmological parameters by finding its inverse matrix. For the cases of uniform and nonuniform distributions, our results are shown in Tables 7 and 8, respectively. The constraints on $H_0$ and other parameters are a little tighter for the uniform distribution than those for the nonuniform distribution. The reason is that the GW sources are more concentrated at $z=1$ in the nonuniform distribution, and thus there are less sources at both higher and lower redshifts. Comparing with the uniform distribution, therefore, it is difficult for the nonuniform distribution to trace the evolution of the dark energy.

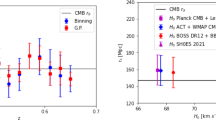
For the $\varLambda$CDM model, the $1 \sigma$ uncertainties on the independent parameters $\varOmega _m$ and $h_0$ are listed in the first rows of Tables 7 and 8. For the cases of uniform and nonuniform distributions, we find that the ET alone can achieve sensitivities of $\varDelta H_0 = 0.5953\,\hbox {km s}^{-1}\,\hbox {Mpc}^{-1}$ and $\varDelta H_0 = 0.7245\,\hbox {km s}^{-1}\,\hbox {Mpc}^{-1}$, respectively. Both constraints are tighter than the one from Planck 2015 data release. Our results show that the ET GW observations may provide new insights to checking the tension between the local measurement of $H_0$ and the global fitting of Planck CMB.

For the $\varOmega _k\varLambda$CDM model, the $1 \sigma$ uncertainties on $\varOmega _m$, $\varOmega _k$ and $h_0$ are listed in the second rows of Tables 7 and 8. For the cases of uniform and nonuniform distributions, we find that the ET can achieve sensitivities of $\varDelta H_0 = 0.7654~\text {km s}^{-1}~\text {Mpc}^{-1}$ and $\varDelta H_0 = 0.9609~\text {km s}^{-1}~\text {Mpc}^{-1}$, respectively. Comparing with Planck 2015 results, we find that the ET can still get tighter constraints on $H_0$ even in the $\varOmega _k\varLambda$CDM model when the GW sources distribute uniformly.

For the wCDM model, the $1 \sigma$ uncertainties on $\varOmega _m$, w and $h_0$ are listed in the third rows of Tables 7 and 8. For the cases of uniform and nonuniform distributions, we find that the ET can achieve sensitivities of $\varDelta H_0 = 1.233~\text {km s}^{-1}~\text {Mpc}^{-1}$ and $\varDelta H_0 = 1.596 ~\text {km s}^{-1}~\text {Mpc}^{-1}$, respectively. Both constraints are not as tight as Planck 2015 results. However, they are still tighter than the local measurement of $H_0$ derived from the luminosity distances of Cepheids.

In the $\varOmega _k w$CDM model, the $1\sigma$ uncertainties on $\varOmega _m$, $\varOmega _k$, w and $h_0$ are listed in the forth rows of Tables 7 and 8. For the cases of uniform and nonuniform distributions, we find that the ET can achieve sensitivities of $\varDelta H_0 = 1.642~\text {km s}^{-1}~\text {Mpc}^{-1}$ and $\varDelta H_0 = 2.180 ~\text {km s}^{-1}~\text {Mpc}^{-1}$, respectively. The former is almost comparable to the local measurement of $H_0$, while the latter is less stringent.

For other cosmological models, i.e. CPL and $\varOmega _k \text {CPL}$, we show our predicted constraints on $H_0$ in the last three rows of Tables 7 and 8, respectively. The $1\sigma$ uncertainties on $H_0$ are obviously larger than that of the local measurement of $H_0$. The reason is that there is an extra dependent parameter in the equation of state of the dark energy. In addition, for the CPL model, we find $\varDelta w_a=3.637$ and $\varDelta w_a=4.258$ for the cases of uniform and nonuniform distributions, respectively. For the $\varOmega _k$CPL model, we find both uncertainties being about three times larger. These are reasons why we do not use the existing datasets to constrain $w_a$ in Sect. 3.

Fig. 6

The 2D contours between $h_0$ and $w_0$, $w_a$, $\varOmega _m$, $\varOmega _k$ at $68\%$ CL. The upper/lower panels denote the uniform/nonuniform distribution of GW sources. The black and blue curves refer to the ET, while the green and red ones refer to the combinations of ET and DESI

Furthermore, we can obtain the correlations among the five cosmological parameters by using the non-diagonal elements of the inverse of Fisher matrix. For example, the $68\%$ CL correlations between $H_0$ and other parameters are depicted as the two-dimensional contours in Fig. 6. Here the black curves denote the uniform distribution of GW sources, while the blue curves denote the nonuniform source distribution of GW sources. We find that $H_0$ is anti-correlated with four other parameters.

5.2 Combine ET with the DESI project

As mentioned in Sect. 2, the BAO standard rulers depend on the angular diameter distance $D_{A}(z)$ and the Hubble parameter H(z), both of which rely on the five parameters $\{h_0,~\varOmega _m,\varOmega _k,~w_0,~w_a\}$. The property of the dark energy can be determined by measuring these two quantities at different redshift bins. To explore the detection ability of the BAO method, we employ the Fisher matrix to analyze the sensitivity of a typical experiment, e.g. the DESI project.

For the BAO method, the Fisher information matrix is constructed as follows [46]

$$\begin{aligned} F_{i j}^{BAO}= & {} \sum _z \frac{\partial _i (\ln D_A(z))\partial _j(\ln D_A(z))}{(\varDelta \ln D_A(z))^2} \nonumber \\&+ \sum _z \frac{\partial _i (\ln H(z))\partial _j(\ln H(z))}{(\varDelta \ln H(z))^2}\, \end{aligned}$$

(31)

where the sum runs over all of the redshift bins z. Here $\varDelta \ln D_A(z)\text { and } \varDelta \ln H(z)$ denote the $1 \sigma$ uncertainties on $\ln D_A(z)$ and $\ln H(z)$, respectively. For DESI, which covers a redshift range from 0.6 to 1.9 with an area of 14,000 $\text {deg}^{2}$, they can be found in Table 2.3 of Ref. [17].²

Table 9 The DESI BAO Fisher matrix

Table 10 Projected constraints on cosmological parameters from the DESI BAOs

Calculating the above formula numerically, we obtain all the elements of the DESI BAO Fisher matrix, which are listed in Table 9. Similar to what we did in the last subsection, we can obtain the projected constraints on all the six cosmological models from the DESI BAOs only. We list our results in Table 10. For any cosmological model considered here, the $1\sigma$ uncertainty on $H_0$ is smaller than the one in Planck 2015 results.

Table 11 Projected constraints on cosmological parameters from the combination of DESI BAOs and ET GWs for the uniform distribution of GW sources

Table 12 Projected constraints on cosmological parameters from the combination of DESI BAOs and ET GWs for the nonuniform distribution of GW sources

To obtain a joint constraint on $H_0$ from DESI and ET, we can obtain a joint Fisher matrix by adding together the DESI BAO Fisher matrix and the ET GW Fisher matrix. For the cases of uniform and nonuniform distributions, respectively, we can obtain the joint Fisher matrices by using Tables 5, 9 and Tables 6, 9. Then we obtain Tables 11 and 12 for the projected constraints on all the six cosmological models. Similar to what we did in last subsection, we can infer the projected constraints on the six cosmological models using the two Fisher matrices. We will demonstrate our detailed results in the following.

For the $\varLambda$CDM model, the $1 \sigma$ uncertainties on the independent parameters $\varOmega _m$ and $h_0$ are listed in the first rows of Tables 11 and 12. For the cases of uniform and nonuniform distributions, we find that the ET alone can achieve sensitivities of $\varDelta H_0 = 0.3468~\text {km s}^{-1}~\text {Mpc}^{-1}$ and $\varDelta H_0 = 0.3727~\text {km s}^{-1}~\text {Mpc}^{-1}$, respectively. Both constraints are tighter than the one from Planck 2015 data release. Our results show that the ET GW observations combining with BAO observations can provide new insights to checking the Hubble constant tension.

For the $\varOmega _k\varLambda$CDM model, the $1 \sigma$ uncertainties on $\varOmega _m$, $\varOmega _k$ and $h_0$ are listed in the second rows of Tables 11 and 12, For the cases of uniform and nonuniform distributions, we find that the ET can achieve sensitivities of $\varDelta H_0 = 0.3538~\text {km s}^{-1}~\text {Mpc}^{-1}$ and $\varDelta H_0 = 0.3790~\text {km s}^{-1}~\text {Mpc}^{-1}$, respectively. Comparing with Planck 2015 results, we find that the ET and BAO can get tighter constraints on $H_0$.

For the wCDM model, the $1 \sigma$ uncertainties on $\varOmega _m$, w and $h_0$ are listed in the third rows of Tables 11 and 12. For the cases of uniform and nonuniform distributions, we find that the ET can achieve sensitivities of $\varDelta H_0 = 0.8388~\text {km s}^{-1}~\text {Mpc}^{-1}$ and $\varDelta H_0 = 1.003 ~\text {km s}^{-1}~\text {Mpc}^{-1}$, respectively. Both constraints are almost as tight as Planck 2015 results.

In the $\varOmega _k w$CDM model, the $1\sigma$ uncertainties on $\varOmega _m$, $\varOmega _k$, w and $h_0$ are listed in the forth rows of Tables 11 and 12. For the cases of uniform and nonuniform distributions, we find that the ET can achieve sensitivities of $\varDelta H_0 = 0.8394~\text {km s}^{-1}~\text {Mpc}^{-1}$ and $\varDelta H_0 = 1.003 ~\text {km s}^{-1}~\text {Mpc}^{-1}$, respectively. The former is almost comparable to the local measurement of $H_0$, while the latter is less stringent.

For other cosmological models, i.e. CPL and $\varOmega _k \text {CPL}$, we show our predicted constraints on $H_0$ in the last three rows of Tables 11 and 12, respectively. For the uniform distribution of GW sources, the $1\sigma$ uncertainty on $H_0$ is obviously smaller than that of the local measurement of $H_0$, while for the nonuniform one it is obviously lager. In addition, for the CPL model, we find $\varDelta w_a=1.362$ and $\varDelta w_a=1.581$ for the uniform and nonuniform distributions of GW sources, respectively. For the $\varOmega _k$CPL model, they become $\varDelta w_a=1.364$ and $\varDelta w_a=1.584$, respectively. Therefore, we may be able to tightly constrain $H_0$ in dark energy models by combining ET with DESI in the future.

For the joint analysis of ET and DESI, the $68\%$ CL correlations between $H_0$ and other parameters are also depicted as the two-dimensional contours in Fig. 6. Here the green curves denote the uniform distribution of GW sources, while the red curves denote the nonuniform source distribution of GW sources. We find that $H_0$ is still anti-correlated with four other parameters.

6 Conclusion and discussion

In this work, we obtained low-redshift cosmological constraints on the Hubble constant by combining the GW170817 standard siren with several BAO standard rulers. We found that the GW170817 brings little influence on the $H_0$ constraint in the $\varLambda$CDM model, while it is significant when additional cosmological parameters, i.e. $\varOmega _k$ and w, are considered. The present data combinations can not be used to test the Hubble constant tension, due to significantly large uncertainties on $H_0$. The uncertainty on $H_0$ is expected to be reduced by observing more GW standard sirens.

Using Fisher information matrix, we estimated the projected constraints on $H_0$ from the ET by simulating $10^3$ GW standard sirens from the binary neutron star coalescences. In the $\varLambda$CDM model, we found that the ET alone can constrain $H_0$ tighter than the Planck 2015 results. The Hubble constant tension can thus be checked by the ET in the future. However, this constraint was significantly weakened if other cosmological parameters, i.e. $\varOmega _k$, $w_0$ and $w_a$, were included. Combining DESI BAOs with ET GWs together can significantly reduce the uncertainties on $H_0$, even in dark energy models.

After the writing of this paper, we notice that Planck Collaboration makes public its final data release [47]. The updated constraint on the Hubble constant is shown as $H_0=67.4\pm 0.5~\text {km s}^{-1}~\text {Mpc}^{-1}$ at $68\%$ CL. Assuming $10^3$ GW standard sirens from the binary neutron star coalescences, therefore, we can use the ET to obtain slightly less stringent constraints on $H_0$ than that of Planck final data release. Therefore, more than $\simeq 10^3$ GW standard sirens are of necessity for the ET to obtain a $H_0$ constraint as tight as Planck final data release. However, we can still obtain more stringent constraints on $H_0$ by combining the DESI BAO distance measures with the ET’s $10^3$ GW standard sirens.