1 Introduction

Data analysis in Particle Physics is based on observation of a set of numbers that can be represented by a (vector) random variable, here denoted as \(\mathbf{y }\). The probability of \(\mathbf{y }\) (or probability density for continuous variables) can in general be written \(P(\mathbf{y } | {\varvec{\mu }}, {\varvec{\theta }})\), where \({\varvec{\mu }}\) represents parameters of interest and \({\varvec{\theta }}\) are nuisance parameters needed for the correctness of the model but not of interest to the analyst.

The goal of the analysis is to carry out inference related to the parameters of interest. A procedure for doing this in the framework of frequentist statistics using the profile likelihood function is described in Sect. 2. This involves using control measurements with given standard deviations to provide information on the nuisance parameters. Here we will take the term “systematic error” to mean the standard deviation of a control measurement itself. The word “error” is used in the sense defined here and not to mean, e.g., the unknown difference between an inferred and true value. The systematic errors defined in this way should also not be confused with corresponding systematic uncertainty in the estimate of the parameter of interest.

Often the values assigned to the systematic errors are themselves uncertain. This can be incorporated into the model by treating their values as adjustable parameters and their estimates as random variables. A model is proposed in which the estimates of systematic variances are treated as following a gamma distribution, whose mean and width are set by the analyst to reflect the desired nominal value and its relative uncertainty.

The confidence intervals that result from this type of model are found to have interesting and useful properties. For example, when averaging measurements to estimate their mean, the size of the confidence interval increases with decreasing goodness-of-fit, and averages have reduced sensitivity to outliers. The basic properties of the model are presented and several types of examples relevant for Particle Physics are explored.

The approach followed here is that of frequentist statistics, as this is widely used in Particle Physics. Models with elements similar to the one proposed have been discussed in the statistics literature, e.g., Refs. [1, 2]. Analogous Bayesian procedures have been investigated in Particle Physics [3,4,5] and found to produce results with qualitatively similar properties.

After reviewing parameter inference using the profile likelihood with known systematic errors in Sect. 2, the model with adjustable error parameters is presented in Sect. 3 and its use in determining confidence intervals is discussed in Sect. 4. In this paper two areas where such a model can be applied are explored: a single Gaussian distribution measurement in Sect. 5 and the method of least squares in Sect. 6. The issue of correlated systematic uncertainties is discussed in Sect. 7 and conclusions are given in Sect. 8.

2 Parameter inference using the profile likelihood and the case of known systematic errors

Inference about a model’s parameters is based on the likelihood function \(L({\varvec{\mu }}, {\varvec{\theta }}) = P(\mathbf{y } | {\varvec{\mu }}, {\varvec{\theta }})\). More specifically one can construct a frequentist test of values of the parameters of interest \({\varvec{\mu }}\) by using the profile likelihood ratio (see, e.g., Ref. [6]),

$$\begin{aligned} \lambda ({\varvec{\mu }}) = \frac{L({\varvec{\mu }}, \hat{\hat{{\varvec{\theta }}}})}{L(\hat{{\varvec{\mu }}}, \hat{{\varvec{\theta }}})}. \end{aligned}$$
(1)

Here in the denominator, \(\hat{{\varvec{\mu }}}\) and \(\hat{{\varvec{\theta }}}\) represent the maximum-likelihood (ML) estimators of \({\varvec{\mu }}\) and \({\varvec{\theta }}\), and \(\hat{\hat{{\varvec{\theta }}}}\) are the profiled values of \({\varvec{\theta }}\), i.e., the values of \({\varvec{\theta }}\) that maximize the likelihood for a given value of \({\varvec{\mu }}\).

Often the nuisance parameters are introduced to account for a systematic uncertainty in the model. Their presence parameterizes the systematic uncertainty such that for some point in the enlarged parameter space the model should be closer to the truth. Because of correlations between the estimators of the parameters, however, the nuisance parameters result in a decrease in sensitivity to the parameters of interest. To counteract this unwanted effect, one often includes into the set of observed quantities additional measurements that provide information on the nuisance parameters.

A simple and often used form of such control measurements involves treating the best available estimates of the nuisance parameters \({\varvec{\theta }} = (\theta _1, \ldots , \theta _N)\) as independent Gaussian distributed values \(\mathbf{u } = (u_1, \ldots , u_N)\) with standard deviations \({\varvec{\sigma }}_{\mathbf{u }} = (\sigma _{u_1}, \ldots , \sigma _{u_N})\). In this way the full likelihood becomes

$$\begin{aligned} L({\varvec{\mu }}, {\varvec{\theta }})= & {} P(\mathbf{y }, \mathbf{u } | {\varvec{\mu }}, {\varvec{\theta }}) = P(\mathbf{y } | {\varvec{\mu }}, {\varvec{\theta }}) P(\mathbf{u } | {\varvec{\theta }}) \nonumber \\= & {} P(\mathbf{y } | {\varvec{\mu }}, {\varvec{\theta }}) \, \prod _{i=1}^N \frac{1}{\sqrt{2 \pi } \sigma _{u_i}} e^{-(u_i - \theta _i)^2 / 2 \sigma _{u_i}^2 }, \end{aligned}$$
(2)

or equivalently the log-likelihood is

$$\begin{aligned} \ln L({\varvec{\mu }}, {\varvec{\theta }}) = \ln P(\mathbf{y } | {\varvec{\mu }}, {\varvec{\theta }}) - \frac{1}{2} \sum _{i=1}^N \frac{(u_i - \theta _i)^2}{\sigma _{u_i}^2 } + C, \end{aligned}$$
(3)

where C represents terms that do not depend on the adjustable parameters of the problem and therefore can be dropped; in the following such constant terms will usually not be written explicitly.

The log-likelihood in Eq. (3) represents one of the most widely used methods for taking account of systematic uncertainties in Particle Physics analyses. First nuisance parameters are introduced into the model to parameterize the systematic uncertainty, and then these parameters are constrained by means of control measurements. The quadratic constraint terms in Eq. (3) correspond to the case where the estimate \(u_i\) of the parameter \(\theta _i\) is modeled as a Gaussian distributed variable of known standard deviation \(\sigma _{u_i}\).

In some problems one may have parameters \(\eta _i\) that are intrinsically positive with estimates \(t_i\) modeled as following a log-normal distribution. The Gaussian model covers this case as well by defining \(\theta _i = \ln \eta _i\) and \(u_i = \ln t_i\), so that \(u_i\) is the corresponding Gaussian distributed estimator for \(\theta _i\).

Often the estimates \(u_i\) are the outcome of real control measurements, and so the standard deviations \(\sigma _{u_i}\) are related to the corresponding sample size. The control measurement itself could, however, involve a number of uncertainties or arbitrary model choices, and as a result the values of the \(\sigma _{u_i}\) may themselves be uncertain.

Gaussian modelling of the \(u_i\) can be used even if the measurement exists only in an idealized sense. For example, the parameter \(\theta _i\) could represent a not-yet computed coefficient in a perturbation series, and \(u_i\) is one’s best guess of its value (e.g., zero). In this case one may try to estimate an appropriate \(\sigma _{u_i}\) by means of some recipe, e.g., by varying some aspects of the approximation technique used to arrive at \(u_i\). For example, in the case of prediction based on perturbation theory one may try varying the renormalization scale in some reasonable range. In such a case the estimate of \(\sigma _{u_i}\) results from fairly arbitrary choices, and values that may differ by 50% or even a factor of two might not be unreasonable.

3 Gamma model for estimated variances

One can extend the model expressed by Eq. (2) to account for the uncertainty in the systematic errors by treating the \(\sigma _{u_i}\) as adjustable parameters. The best estimates \(s_i\) for the \(\sigma _{u_i}\) are regarded as measurements to be included in the likelihood model. The width of the distribution of the \(s_i\) is set by the analyst to reflect the appropriate uncertainty in the \(\sigma _{u_i}\).

The characterization of the “error on the error” is described in Sect. 3.1. In Sect. 3.2 the full mathematical model is defined and the corresponding likelihood profiled over the \(\sigma _{u_i}\) is derived. This is shown in Sect. 3.3 to be equivalent to a model in which the estimates \(u_i\) follow a Student’s t distribution.

Fig. 1
figure 1

Plots of a the gamma distribution of the estimated variance v and b the Nakagami distribution for the estimated standard deviation \(s = \sqrt{v}\) for several values of the parameter r (see text)

Full size image

3.1 The relative error on the error

In the model proposed here it is convenient to regard the variances \({\varvec{\sigma }}^2_{\mathbf{u }}\) as the parameters, and to take values \(v_i = s_i^2\) as their estimates. There is a special case in which the estimated variances \(v_i\) will follow a chi-squared distribution, namely, when \(v_i\) is the sample variance of n independent observations of \(u_i\), i.e.,

$$\begin{aligned} v_i = \frac{1}{n-1} \sum _{j=1}^n (u_{i,j} - \overline{u}_i)^2, \end{aligned}$$
(4)

where \(u_{i,j}\) is the jth observation of \(u_i\) and \(\overline{u}_i = {\frac{1}{n}}\sum _{j=1}^n u_{i,j}\). If the \(u_{i,j}\) are Gaussian distributed with standard deviations \(\sigma _{u_i}\), then one finds (see, e.g., Ref. [7]) that the statistic \((n-1) v_i / \sigma _{u_i}^2\) follows a chi-squared distribution for \(n-1\) degrees of freedom. Furthermore, the chi-squared distribution for n degrees of freedom is a special case of the gamma distribution,

$$\begin{aligned} f(v ; \alpha , \beta ) = \frac{\beta ^{\alpha }}{\varGamma (\alpha )} v^{\alpha - 1} e^{- \beta v} \,, \quad \quad v \ge 0, \end{aligned}$$
(5)

for parameter values \(\alpha = n/2\) and \(\beta = 1/2\). The mean and variance are related to the parameters \(\alpha \) and \(\beta \) by \(E[v] = \alpha / \beta \) and \(V[v] = \alpha /\beta ^2\). Therefore if \((n-1)v_i/\sigma _{u_i}^2\) follows a chi-square distribution with \(n-1\) degrees of freedom, then \(v_i\) follows a gamma distribution with

$$\begin{aligned} \alpha _i= & {} \frac{n-1}{2}, \end{aligned}$$
(6)
$$\begin{aligned} \beta _i= & {} \frac{n-1}{2\sigma _{u_i}^2}. \end{aligned}$$
(7)

In general the analyst will not base the estimate \(v_i\) on n observations of \(u_i\) but rather on different types of information, such as related control measurements or approximate theoretical predictions. The analyst must then set the width of the distribution of \(v_i\) to reflect the appropriate level of uncertainty in the estimate of \(\sigma _{u_i}^2\).

For \(v_i = s_i^2\), using error propagation gives to first order

$$\begin{aligned} \frac{\sigma _{v_i}}{E[v_i]} \approx 2 \frac{\sigma _{s_i}}{E[s_i]}. \end{aligned}$$
(8)

To characterize the width of the gamma distribution we define

$$\begin{aligned} r_i \equiv \frac{1}{2} \frac{\sigma _{v_i}}{E[v_i]} = \frac{1}{2} \frac{\sigma _{v_i}}{\sigma _{u_i}^2}. \end{aligned}$$
(9)

From Eq. (8) one sees that to first approximation \(r_i \approx \sigma _{s_i} / E[s_i]\) and thus we can think of these factors as representing the relative uncertainty in the estimate of the systematic error. The parameters \(r_i\) will be referred to as the “error on the error”. A more accurate relation between \(r_i\) as defined here and the quantity \(\sigma _{s_i} / E[s_i]\) is given in Appendix A.

Using the expectation value of the gamma distribution \(E[v_i] = \alpha _i / \beta _i\) and its variance \(V[v_i] = \alpha _i / \beta _i^2\), we can relate the values \(r_i\) supplied by the analyst and the \(\sigma _{u_i}\) to \(\alpha _i\) and \(\beta _i\) by

$$\begin{aligned} \alpha _i= & {} \frac{1}{4r_i^2}, \end{aligned}$$
(10)
$$\begin{aligned} \beta _i= & {} \frac{1}{4 r_i^2 \sigma _{u_i}^2}. \end{aligned}$$
(11)

Figure 1a shows the gamma distribution for \(\sigma _u = 1\) and several values of r and Fig. 1b shows the corresponding distribution of \(s = \sqrt{v}\). More details on the distribution of s and its properties are given in Appendix A. The assumption of a gamma distribution is not unique but represents nevertheless a reasonable and flexible expression of uncertainty in the \(\sigma _{u_i}\). Moreover it will be shown that by using the gamma distribution one finds a very simple procedure for incorporating uncertain systematic errors into the model.

Using Eq. (6) to connect the relative uncertainty \(r_i\) to the effective number of measurements n gives \(n = 1 + 1/2r_i^2\). A relevant special case is \(n=2\), sometimes called the problem of “two-point systematics”, where one has two estimates \(u_{i,1}\) and \(u_{i,2}\) of a parameter \(\theta _i\). This gives

$$\begin{aligned} \hat{\theta }_i= & {} \overline{u}_i = {\frac{1}{2}}(u_{i,1} + u_{i,2}), \end{aligned}$$
(12)
$$\begin{aligned} s_i= & {} \frac{| u_{i,1} - u_{i,2} |}{\sqrt{2}}, \end{aligned}$$
(13)
$$\begin{aligned} r_i= & {} 1 / \sqrt{2}. \end{aligned}$$
(14)

It will be assumed in this paper that the analyst is able to assign meaningful values for the error-on-the-error parameters \(r_i\). The procedure for doing this will involve elicitation of expert knowledge from those who assigned the systematic errors and will in general vary depending on the experiment. One may want to regard a subset of the measurements as having a certain common r which could be fitted from the data, but we do not investigate this possibility further here.

The proposed model thus makes two important assumptions. First, the control measurements are taken to be independent and Gaussian distributed. As mentioned in Sect. 2, the Gaussian \(u_i\) can be extended to an alternative distribution if it can be related to a Gaussian by a transformation. Second, the estimates of the variances of the \(u_i\) are gamma distributed. Both assumptions are reasonable but neither is a perfect description in practice, and thus the resulting inference could be subject to corresponding systematic uncertainties. Nevertheless the proposed model will in general be an improvement over the widely used Gaussian assumption for \(u_i\) with fixed variances. In addition, the choice of the gamma distribution leads to important simplifications in mathematical expressions needed for inference, as shown in Sect. 3.2 below.

3.2 Likelihood for the gamma model

By treating the estimated variances \(\mathbf{v } = (v_1, \ldots , v_N)\) as independent gamma distributed random variables, the full likelihood function becomes

$$\begin{aligned}&L({\varvec{\mu }}, {\varvec{\theta }}, {\varvec{\sigma }}_{\mathbf{u }}^2) = P(\mathbf{y } | {\varvec{\mu }}, {\varvec{\theta }}) \nonumber \\&\quad \times \prod _{i=1}^N \frac{1}{\sqrt{2 \pi } \sigma _{u_i}} e^{-(u_i - \theta _i)^2 / 2 \sigma _{u_i}^2 } \, \frac{\beta _{i}^{\alpha _i}}{\varGamma (\alpha _i)} v_i^{\alpha _i - 1} e^{-\beta _i v_i}. \end{aligned}$$
(15)

By using Eqs. (10) and (11) to relate the parameters \(\alpha _i\) and \(\beta _i\) to \(\sigma _{u_i}^2\) and \(r_i\) one finds, up to additive terms that are independent of the parameters, the log-likelihood

$$\begin{aligned}&\ln L({\varvec{\mu }}, {\varvec{\theta }}, {\varvec{\sigma }}_{\mathbf{u }}^2) = \ln P(\mathbf{y } | {\varvec{\mu }}, {\varvec{\theta }}) \nonumber \\&\quad - \frac{1}{2} \sum _{i=1}^N \left[ \frac{(u_i - \theta _i)^2}{\sigma _{u_i}^2} + \left( 1 + \frac{1}{2 r_i^2} \right) \ln \sigma _{u_i}^2 + \frac{v_i}{2 r_i^2 \sigma _{u_i}^2} \right] .\nonumber \\ \end{aligned}$$
(16)

By setting the derivatives of \(\ln L\) with respect to the \(\sigma _{u_i}^2\) to zero for fixed \({\varvec{\theta }}\) and \({\varvec{\mu }}\) one finds the profiled values

$$\begin{aligned} \widehat{\widehat{\sigma ^2}}_{u_i} = \frac{v_i + 2 r_i^2 (u_i - \theta _i)^2}{1 + 2 r_i^2}. \end{aligned}$$
(17)

Using these for the \(\sigma _{u_i}^2\) gives the profile likelihood with respect to the systematic variances, but which still depends on \({\varvec{\theta }}\) as well as the parameters of interest \({\varvec{\mu }}\). After some manipulation it can be written up to constant terms as

$$\begin{aligned}&\ln L^{\prime }({\varvec{\mu }}, {\varvec{\theta }}) = \ln L (\mu , {\varvec{\theta }}, \widehat{\widehat{{\varvec{\sigma }}^2}}_{\mathbf{u }}) \nonumber \\&\quad = \ln P(\mathbf{y } | {\varvec{\mu }}, {\varvec{\theta }}) \nonumber \\&\qquad - \frac{1}{2} \sum _{i=1}^N \left( 1 + \frac{1}{2 r_i^2} \right) \ln \left[ 1 + 2 r_i^2 \frac{(u_i - \theta _i)^2}{v_i} \right] . \end{aligned}$$
(18)

Some intermediate steps in the derivation of Eq. (18) are given in Appendix B. In the limit where all of the \(r_i\) are small, the estimates \(v_i\) are very close to their expectation values \(\sigma _{u_i}^2\). Making this replacement and expanding the logarithmic terms to first order one recovers the quadratic terms as in Eq. (3).

3.3 Derivation of profile likelihood from Student’s t distribution

An equivalent derivation of the profile likelihood (18) can be obtained by first defining

$$\begin{aligned} z_i \equiv \frac{u_i - \theta _i}{\sqrt{v_i}} \,. \end{aligned}$$
(19)

As \(u_i\) follows a Gaussian with mean \(\theta _i\) and standard deviation \(\sigma _{u_i}\), and \(v_i\) follows a gamma distribution with mean \(\sigma _{u_i}^2\) and standard deviation \(\sigma _{v_i} = 2 r_i^2 \sigma _{u_i}^2\), one can show (see, e.g., Ref. [7]) that \(z_i\) follows a Student’s t distribution,

$$\begin{aligned} f(z_i | \nu _i) = \frac{\varGamma \left( \frac{\nu _i + 1}{2} \right) }{\sqrt{\nu _i \pi } \varGamma (\nu _i/2)} \left( 1 + \frac{z_i^2}{\nu _i} \right) ^{- \frac{\nu _i + 1}{2}}, \end{aligned}$$
(20)

with a number of degrees of freedom

$$\begin{aligned} \nu _i = \frac{1}{2 r_i^2}. \end{aligned}$$
(21)

By constructing the likelihood \(L({\varvec{\mu }}, {\varvec{\theta }})\) as the product of \(P(\mathbf{y } | {\varvec{\mu }}, {\varvec{\theta }})\) and Student’s t distributions,

$$\begin{aligned} L({\varvec{\mu }}, {\varvec{\theta }}) = P(\mathbf{y } | {\varvec{\mu }}, {\varvec{\theta }}) \, \prod _{i=1}^N \frac{\varGamma \left( \frac{\nu _i + 1}{2} \right) }{\sqrt{\nu _i \pi } \varGamma (\nu _i/2)} \left( 1 + \frac{z_i^2}{\nu _i} \right) ^{- \frac{\nu _i + 1}{2}}, \end{aligned}$$
(22)

one obtains the same log-likelihood as given by \(\ln L^{\prime }\) from Eq. (18). That is, the same model results if one replaces the estimates \(v_i\) by constants \(\sigma _{u_i}^2\), but still takes the \(z_i\) to follow a Student’s t distribution, with \(u_i = \theta _i + \sigma _{u_i} z_i\). Thus in the following we can drop the prime in the profile log-likelihood (18) and regard this equivalently as the log-likelihood resulting from a model where the control measurements are distributed according to a Student’s t. In the limit where \(r_i \rightarrow 0\) and thus the number of degrees of freedom \(\nu _i \rightarrow \infty \), the Student’s t distribution becomes a Gaussian (see, e.g., Ref. [7]), and the corresponding term in the log-likelihood becomes quadratic in \(u_i - \theta _i\), as in Eq. (3).

4 Estimators and confidence regions from profile likelihood

The ML estimators are found by maximizing the full \(\ln ~L({\varvec{\mu }}, {\varvec{\theta }}, {\varvec{\sigma }}^2_{\mathbf{u }})\) with respect to all of the parameters, which is equivalent to maximizing the profile likelihood with respect to \({\varvec{\mu }}\) and \({\varvec{\theta }}\). In this way the statistical uncertainties due to both the estimated biases \(u_i\) as well as their estimated variances \(v_i\) are incorporated into the variances of the estimators for the parameters of interest \(\hat{{\varvec{\mu }}}\).

Consider for example the case of a single continuous parameter of interest \(\mu \). Having found the estimator \(\hat{\mu }\), one could quantify its statistical precision by using the standard deviation \(\sigma _{\hat{\mu }}\). The covariance matrix for all of the estimated parameters can to first approximation be found from the inverse of the matrix of second derivatives of \(\ln L\) (see, e.g., Refs. [8, 9]). From this we extract the variance of the estimator of the parameter of interest \(\mu \), i.e., \(V[\hat{\mu }] = \sigma ^2_{\hat{\mu }}\). The presence of the nuisance parameters in the model will in general inflate \(\sigma _{\hat{\mu }}\), which reflects the corresponding systematic uncertainties.

But \(\sigma _{\hat{\mu }}\) is by construction a property of the model and not of a particular data set. One may want, however, to report a measure of uncertainty along with the estimate \(\hat{\mu }\) that reflects the extent to which the data values are consistent with the hypothesized model, and therefore \(\sigma _{\hat{\mu }}\) is not suitable for this purpose. We will show below, however, that a confidence region can be constructed that has this desired property.

In general to find a confidence region (or for a single parameter a confidence interval) one tests all values of \({\varvec{\mu }}\) with a test of size \(\alpha \) for some fixed probability \(\alpha \). Those values of \({\varvec{\mu }}\) that are not rejected by the test constitute a confidence region with confidence level \(1 - \alpha \). To determine the critical region of the test of a given \({\varvec{\mu }}\) one can use a test statistic based on the profile likelihood ratio

$$\begin{aligned} t_{{\varvec{\mu }}} = - 2 \ln \lambda ({\varvec{\mu }}) = -2 \ln \frac{L({\varvec{\mu }}, \hat{\hat{{\varvec{\theta }}}})}{L(\hat{{\varvec{\mu }}}, \hat{{\varvec{\theta }}})}. \end{aligned}$$
(23)

The critical region of a test of \({\varvec{\mu }}\) corresponds to the region of data space having probability content \(\alpha \) with maximal \(t_{{\varvec{\mu }}}\). Equivalently, provided \(t_{{\varvec{\mu }}}\) can be treated as continuous, the p-value of a hypothesized point in parameter space \({\varvec{\mu }}\) is

$$\begin{aligned} p_{{\varvec{\mu }}} = \int _{t_{{\varvec{\mu }},\mathrm{obs}}}^{\infty } f(t_{{\varvec{\mu }}} | {\varvec{\mu }}, {\varvec{\theta }}, {\varvec{\sigma }}^2_{\mathbf{u }}) \, dt_{{\varvec{\mu }}} = 1 - F(t_{{\varvec{\mu }},\mathrm{obs}}), \end{aligned}$$
(24)

where \(t_{{\varvec{\mu }},\mathrm{obs}}\) is the observed value of \(t_{{\varvec{\mu }}}\) and F is the cumulative distribution of \(t_{{\varvec{\mu }}}\). That is, we define the region of data space even less compatible with the hypothesis than what was observed to correspond to \(t_{{\varvec{\mu }}} > t_{{\varvec{\mu }},\mathrm{obs}}\).

The boundary of the confidence region corresponds to the values of \({\varvec{\mu }}\) where \(p_{{\varvec{\mu }}} = \alpha \). Solving Eq. (24) for the test statistic gives

$$\begin{aligned} t_{{\varvec{\mu }}} = F^{-1}(1 - p_{{\varvec{\mu }}}), \end{aligned}$$
(25)

where here \(t_{{\varvec{\mu }}}\) refers to the value observed, and \(F^{-1}\) is the quantile of \(t_{{\varvec{\mu }}}\). The statistic \(t_{{\varvec{\mu }}}\) is also defined in terms of the likelihood through Eqs. (1) and (23), and by using \(p_{{\varvec{\mu }}} = \alpha \) one finds that the boundary of the confidence region is given by

$$\begin{aligned} \ln L({\varvec{\mu }}, \hat{\hat{{\varvec{\theta }}}}) = \ln L(\hat{{\varvec{\mu }}}, \hat{{\varvec{\theta }}}) - \frac{1}{2} F^{-1}(1 - \alpha ). \end{aligned}$$
(26)

To find the p-values and thus determine the boundary of the confidence region one needs the distribution \(f(t_{{\varvec{\mu }}} | {\varvec{\mu }}, {\varvec{\theta }}, {\varvec{\sigma }}_{\mathbf{u }}^2)\). According to Wilks’ theorem [10], for M parameters of interest \({\varvec{\mu }} = (\mu _1, \ldots , \mu _M)\) the statistic \(t_{{\varvec{\mu }}}\) should follow a chi-squared distribution for M degrees of freedom in the asymptotic limit, which here corresponds to the case where the distributions of all ML estimators are Gaussian. To the extent that this approximation holds we may identify the quantile \(F^{-1}\) in Eq. (26) with \(F_{\chi ^2_M}^{-1}\), the chi-squared quantile for M degrees of freedom.

If it is further assumed that the log-likelihood can be well approximated by a quadratic function about its maximum, then one finds asymptotically (see, e.g., Ref. [11]) that

$$\begin{aligned} \ln L({\varvec{\mu }}, \hat{\hat{{\varvec{\theta }}}}) = \ln L(\hat{{\varvec{\mu }}}, \hat{{\varvec{\theta }}}) - \frac{1}{2} ({\varvec{\mu }} - \hat{{\varvec{\mu }}})^T V^{-1} ({\varvec{\mu }} - \hat{{\varvec{\mu }}}), \end{aligned}$$
(27)

where \(V_{ij} = \text{ cov }[\hat{\mu }_i, \hat{\mu }_j]\) is the covariance matrix for the parameters of interest. This equation says that the confidence region is a hyper-ellipsoid of fixed size centred about \(\hat{{\varvec{\mu }}}\). For example, for a single parameter \(\mu \) one finds that the endpoints

$$\begin{aligned} \mu _{\pm } = \hat{\mu } \pm \sigma _{\hat{\mu }} \left[ F_{\chi ^2_1}^{-1}(1 - \alpha ) \right] ^{1/2} \end{aligned}$$
(28)

give the central confidence interval with confidence level \(1 - \alpha \). For a probability content corresponding to plus or minus one standard deviation about the centre of a Gaussian, i.e., \(1 - \alpha \) = 68.3%, one has \(F_{\chi ^2_1}^{-1}(1 - \alpha ) = 1\), which gives the well-known result that the interval of plus or minus one standard deviation about the estimate is asymptotically a 68.3% CL central confidence interval.

The relations (27) and (28) depend, however, on a quadratic approximation of the log-likelihood. In the model where the \({\varvec{\sigma }}_{\mathbf{u }}\) are treated as adjustable, the profile log-likelihood is given by Eq. (18), which contains terms that are logarithmic in \((u_i - \theta _i)^2\), and not just the quadratic terms that appear in Eq. (3). As a result the relation (27) is only a good approximation in the limit of small \(r_i\), which is not always valid in the present problem.

We can nevertheless use Eq. (26) assuming a chi-squared distribution for \(t_{{\varvec{\mu }}}\) as a first approximation for confidence regions. We will see in the examples below that these have interesting properties that already capture the most important features of the model. If higher accuracy is required then Monte Carlo methods can be used to determine the distribution of \(t_{{\varvec{\mu }}}\). Alternatively we can modify the statistic so that its distribution is closer to the asymptotic form; this is explored further in Sect. 5.1.

5 Single-measurement model

To investigate the asymptotic properties of the profile likelihood ratio it is useful to examine a simple model with a single measured value y following a Gaussian with mean \(\mu \) and standard deviation \(\sigma \). The parameter of interest is \(\mu \) and we treat the variance \(\sigma ^2\) as a nuisance parameter, which is constrained by an independent gamma-distributed estimate v. Thus the likelihood is given by

$$\begin{aligned} L(\mu , \sigma ^2)= & {} f(y, v | \mu , \sigma ^2) \nonumber \\= & {} \frac{1}{\sqrt{2 \pi \sigma ^2}} e^{- (y - \mu )^2/2 \sigma ^2} \, \frac{\beta ^{\alpha }}{\varGamma (\alpha )} v^{\alpha - 1} e^{ - \beta v}. \end{aligned}$$
(29)

As before we set the parameters \(\alpha \) and \(\beta \) of the gamma distribution so that \(E[v] = \sigma ^2\) and so that from Eq. (9) the standard deviation of v is \(\sigma _v = 2 r \sigma ^2\), where r characterizes the relative error on the error. This gives

$$\begin{aligned} \alpha= & {} \frac{1}{4r^2}, \end{aligned}$$
(30)
$$\begin{aligned} \beta= & {} \frac{1}{4 r^2 \sigma ^2}. \end{aligned}$$
(31)

The goal is to construct a confidence interval for \(\mu \) by using the profile likelihood ratio

$$\begin{aligned} \lambda (\mu ) = \frac{L(\mu , \widehat{\widehat{\sigma ^2}}(\mu ))}{L(\hat{\mu }, \widehat{\sigma ^2})}. \end{aligned}$$
(32)

The log-likelihood is

$$\begin{aligned} \ln L(\mu , \sigma ^2) = - \frac{1}{2} \frac{(y - \mu )^2}{\sigma ^2} - \left( \frac{1}{2} + \frac{1}{4 r^2} \right) \ln \sigma ^2 - \frac{v}{4 r^2 \sigma ^2} + C, \end{aligned}$$
(33)

where C represents constants that do not depend on \(\mu \) or \(\sigma ^2\). From this we find the required estimators

$$\begin{aligned} \hat{\mu }= & {} y, \end{aligned}$$
(34)
$$\begin{aligned} \widehat{\sigma ^2}= & {} \frac{v}{1 + 2 r^2}, \end{aligned}$$
(35)
$$\begin{aligned} \widehat{\widehat{\sigma ^2}}(\mu )= & {} \frac{v + 2 r^2 (y - \mu )^2}{1 + 2 r^2}. \end{aligned}$$
(36)

With these ingredients we find the following simple expression for the statistic \(t_{\mu } = - 2 \ln \lambda (\mu )\),

$$\begin{aligned} t_{\mu } = \left( 1 + \frac{1}{2 r^2} \right) \ln \left[ 1 + 2 r^2 \frac{(y - \mu )^2}{v} \right] . \end{aligned}$$
(37)

According to Wilks’ theorem [10], the distribution \(f(t_{\mu } | \mu )\) should, in the large-sample limit, be chi-squared for one degree of freedom. The large-sample limit corresponds to the situation where estimators for the parameters become Gaussian, which in this case means \(r \ll 1\).

The behaviour of the distribution of \(t_{\mu }\) for nonzero r is illustrated in Fig. 2, which shows the distributions from data generated according to a Gaussian of mean \(\mu = 0\), standard deviation \(\sigma = 1\) and values of \(r = 0.01\), 0.2, 0.4 and 0.6. The case of \(r = 0.01\) approximates the situation where the relative uncertainty on \(\sigma \) is negligibly small. One can see that greater values of r lead to an increasing departure of the distribution from the asymptotic form.

Fig. 2
figure 2

Distributions of the test variable \(t_{\mu }\) for a single Gaussian distributed measurement with relative error-on-error r

Full size image

Depending on the size of the test being carried out or equivalently the confidence level of the interval, one may find that the asymptotic approximation is inadequate. In such a case one may wish to use the Monte Carlo simulation to determine the distribution of the test statistic. Alternatively one can modify the statistic so that its distribution is better approximated by the asymptotic form, as described in the following section.

5.1 Bartlett correction for profile likelihood-ratio statistic

The likelihood-ratio statistic can be modified so as to follow more closely a chi-square distribution using a type of correction due to Bartlett [12,13,14]. This method has received some limited notice in Particle Physics [15] but has not been widely used in that field. The basic idea is to determine the mean value \(E[t_{\mu }]\) of the original statistic. In the asymptotic limit, this should be equal to the number of degrees of freedom \(n_\mathrm{d}\) of the chi-square distribution, which in this example is \(n_\mathrm{d} = 1\). One then defines a modified statistic

$$\begin{aligned} t_{\mu }^{\prime } = \frac{n_\mathrm{d}}{E[t_{\mu }]} t_{\mu }, \end{aligned}$$
(38)

so that by construction \(E[t^{\prime }_{\mu }] = n_\mathrm{d}\). It was shown by Lawley [16] that the modified statistic approaches the reference chi-squared distribution with a difference of order \(n^{-3/2}\), where here the effective sample size n is related to the parameter r by \(n = 1 + 1/2r^2\) (cf. Eqs. (6) and (10)).

One could in principle find the expectation value \(E[t_{\mu }]\) by the Monte Carlo method. But for the method to be convenient to use one would like to determine the Bartlett correction without resorting to simulation. By expanding the expectation value

$$\begin{aligned} E[t_{\mu }] = \int \int t_{\mu }(y, v) \, f(y,v | \mu , \sigma ^2) \, dy \, dv \end{aligned}$$
(39)

as a Taylor series in r one finds

$$\begin{aligned} E[t_{\mu }] = 1 + 3 r^2 + c r^4, \end{aligned}$$
(40)

where the coefficient of the \(r^4\) term is found numerically to be \(c \approx 2\) with an accuracy of around 10%. Dividing \(t_{\mu }/n_\mathrm{d}\) (here with \(n_\mathrm{d} = 1\)) from Eq. (23) by \(E[t_{\mu }]\) to obtain the Bartlett-corrected statistic therefore gives

$$\begin{aligned} t^{\prime }_{\mu } = \frac{1 + 2 r^2}{2r^2(1 + 3r^2 + 2r^4)} \ln \left[ 1 + \frac{2r^2}{v} (y - \mu )^2 \right] . \end{aligned}$$
(41)

In more complex problems one may not have a simple expression for the expectation value needed in the Bartlett correction and calculation by Monte Carlo may be necessary.

Distributions of \(t^{\prime }_{\mu }\) are shown in Fig. 3 along with Monte Carlo distributions. As can be seen by comparing the uncorrected distributions from Figs. 2 to those in Fig. 3, the Bartlett correction is clearly very effective, as is needed when the parameter r is large.

Fig. 3
figure 3

Distributions of the Bartlett-corrected test variable \(t_{\mu }^{\prime }\) for a single Gaussian distributed measurement with relative error-on-error r

Full size image

5.2 Confidence intervals for the single-measurement model

In the simple model explored in this section one can use the measured values of y and v to construct a confidence interval for the parameter of interest \(\mu \). The probability that the interval includes the true value of \(\mu \) (the coverage probability) can then be studied as a function of the relative error on the error r. What emerges is that the interval based on the chi-squared distribution of \(t_{\mu }\) has a coverage probability substantially less than the nominal confidence level, but that this can be greatly improved by use of the Bartlett-corrected interval.

To derive exact confidence intervals for \(\mu \) we can use the fact that

$$\begin{aligned} z = \frac{y - \mu }{\sqrt{v}} \end{aligned}$$
(42)

follows a Student’s t distribution for \(\nu = 1/2r^2\) degrees of freedom (see, e.g., Ref. [7]). From the distribution of z one can find the corresponding pdf of

$$\begin{aligned} t_{\mu } = (1 + \nu ) \ln \left[ 1 + \frac{z^2}{\nu } \right] , \end{aligned}$$
(43)

but in fact this is not directly needed. Rather we can use the pdf of z to find confidence intervals for \(\mu \) from the fact that a critical region defined by \(t_{\mu } > t_\mathrm{c}\) is equivalent to the corresponding region of z given by \(z < -z_\mathrm{c}\) and \(z > z_\mathrm{c}\) where the boundaries of the critical regions in the two variables are related by Eq. (43). Equivalently one can say that the p-value of a hypothesized value of \(\mu \) is the probability, assuming \(\mu \), to find z further from zero than what was observed, i.e.,

$$\begin{aligned} p_{\mu } = 1 - \int _{-z_\mathrm{obs}}^{z_\mathrm{obs}} f(z) \, dz = 2 \left( 1 - F\left( \frac{y - \mu }{\sqrt{v}};\nu \right) \right) , \end{aligned}$$
(44)

where \(F(z;\nu )\) is the cumulative Student’s t distribution for \(\nu = 1/2r^2\) degrees of freedom.

Fig. 4
figure 4

Plots of a the interval half-width in units of the estimated standard deviation \(\sqrt{v}\) and b coverage probability of the 68.3% CL confidence intervals for \(\mu \)

Full size image

The boundaries of the confidence interval at confidence level \(\text{ CL } = 1 - \alpha \) (here \(\alpha \) refers to the size of the statistical test, not the parameter \(\alpha \) in the gamma distribution) are found by setting \(p_{\mu } = \alpha \) and solving for \(\mu \), which gives the upper and lower limits

$$\begin{aligned} \mu _{\pm } = y \pm \sqrt{v} z_{\alpha /2}. \end{aligned}$$
(45)

Here \(z_{\alpha /2}\) is the \(\alpha /2\) upper quantile of the Student’s t distribution, i.e., the value of \(z_\mathrm{obs}\) needed in Eq. (44) to have \(p_{\mu } = \alpha \).

If one were to assume that the statistic \(t_{\mu }\) follows the asymptotic chi-squared distribution, then \(z_{\alpha /2}\) is replaced by

$$\begin{aligned} z_\mathrm{a} = \frac{1}{\sqrt{2} r} \left[ \exp \left( \frac{2 r^2 Q_{\alpha } }{1 + 2 r^2} \right) - 1 \right] ^{1/2}. \end{aligned}$$
(46)

Here \(Q_{\alpha } = F^{-1}_{\chi ^2_1}(1 - \alpha )\) is obtained from the quantile of the chi-squared distribution for one degree of freedom. And if the Bartlett-corrected statistic \(t^{\prime }_{\mu }\) is used to construct the interval, then the \(Q_{\alpha }\) in Eq. (46) is replaced by \(Q_{\alpha } E[t_{\mu }]\), where \(E[t_{\mu }] = 1 + 3r^2 + 2r^4\) is the expectation value of \(t_{\mu }\) from Eq. (40). The half-width of the interval measured in units of the estimated standard deviation \(\sqrt{v}\), i.e., \(z_{\alpha /2}\) or \(z_\mathrm{a}\), are shown in Fig. 4a as a function of the r parameter.

The probability \(P_\mathrm{c}\) for the confidence interval to cover the true value of \(\mu \) is by construction equal to \(1 - \alpha \) for the exact confidence interval. For the interval based on the asymptotic distribution of the test statistic this is

$$\begin{aligned} P_\mathrm{c} = \int _{-z_\mathrm{a}}^{z_\mathrm{a}} f_{\chi ^2_1}(z) \, dz = 2 F_{\chi ^2_1}(z_\mathrm{a}) - 1, \end{aligned}$$
(47)

where \(F_{\chi ^2_1}\) is the cumulative chi-squared distribution for one degree of freedom and \(z_\mathrm{a}\) is given by Eq. (46), with \(Q_{\alpha }\) replaced by \(Q_{\alpha } E[t_{\mu }]\) for the Bartlett-corrected case.

The interval half-widths and coverage probabilities based on \(t_{\mu }\) and \(t^{\prime }_{\mu }\) are shown in Fig. 4. As can be seen, the interval based on the Bartlett-corrected statistic is very close to the exact one, and its coverage is close to the nominal \(1-\alpha \) for relevant values of r.

As seen from the distributions in Figs. 2 and 3 for the single-measurement model, the agreement with the asymptotic form worsens for increasing values of the test statistic. For \(Z = \sqrt{t_{\mu }}\) of 4 (a four standard-deviation significance; see, e.g., Ref. [6]), the Bartlett-corrected statistic is close to the asymptotic form for \(r = 0.2\), with a small but visible departure for \(r = 0.4\). In contrast, for a 68.3% confidence level (corresponding to \(\sqrt{t_{\mu }} = 1\)), one sees from Fig. 4a that the Bartlett corrected interval is in satisfactory agreement with the exact interval out to \(r \approx 1\). For a more complicated analysis with multiple measurements having different \(r_i\) parameters one would need to check the validity of asymptotic distributions with Monte Carlo.

6 Least-squares fitting and averaging measurements

An important application of the model described in Sect. 3 is the least-squares fit of a curve, or as a special case of this, the average of a set of measurements. Suppose the data consist of N independent Gaussian distributed values \(y_i\), with mean and variance

$$\begin{aligned} E[y_i]= & {} \varphi (x_i; {\varvec{\mu }}) + \theta _i, \end{aligned}$$
(48)
$$\begin{aligned} V[y_i]= & {} \sigma ^2_{y_i}. \end{aligned}$$
(49)

Here the nuisance parameters \(\theta _i\) represent a potential bias or offset. The function \(\varphi (x_i;{\varvec{\mu }})\) plus the bias \(\theta _i\) gives the mean of \(y_i\) as a function of a control variable x, and it depends on a set of M parameters of interest \({\varvec{\mu }} = (\mu _1, \ldots , \mu _M)\). That is, the probability \(P(\mathbf{y } | {\varvec{\varphi }}, {\varvec{\theta }})\) in Eq. (2) becomes

$$\begin{aligned} P(\mathbf{y } | {\varvec{\mu }}, {\varvec{\theta }}) = \prod _{i=1}^N \frac{1}{\sqrt{2 \pi } \sigma _{y_i}} e^{-(y_i - \varphi (x_i; {\varvec{\mu }}) - \theta _i)^2 / 2 \sigma _{y_i}^2}. \end{aligned}$$
(50)

As before suppose the nuisance parameters \(\theta _i\) are constrained by N corresponding independent Gaussian measurements \(u_i\), with mean and variance

$$\begin{aligned} E[u_i]= & {} \theta _i, \end{aligned}$$
(51)
$$\begin{aligned} V[u_i]= & {} \sigma ^2_{u_i}. \end{aligned}$$
(52)

Often the best estimates of a potential bias \(\theta _i\) will be \(u_i = 0\) for the actual measurement, but formally the \(u_i\) are treated as random variables that would fluctuate upon repetition of the experiment. Therefore the full log-likelihood or equivalently \(- 2 \ln L({\varvec{\mu }}, {\varvec{\theta }})\) is up to an additive constant given by

$$\begin{aligned} -2 \ln L({\varvec{\mu }}, {\varvec{\theta }}) = \sum _{i=1}^N \left[ \frac{(y_i - \varphi (x_i; {\varvec{\mu }}) - \theta _i)^2}{\sigma _{y_i}^2} + \frac{(u_i - \theta _i)^2}{\sigma _{u_i}^2} \right] . \end{aligned}$$
(53)

That is, if we consider the \(\sigma _{u_i}\) as known, then maximum-likelihood estimators are obtained by the minimum of the sum of squares (53) which is the usual formulation of the method of least squares.

The next step will be to treat the \(\sigma _{u_i}\) as adjustable parameters but before doing this is it interesting to note that by profiling over the nuisance parameters \(\theta _i\), one finds the profile likelihood

$$\begin{aligned} -2 \ln L^{\prime }({\varvec{\mu }}) = \sum _{i=1}^N \frac{(y_i - \varphi (x_i; {\varvec{\mu }}) - u_i)^2}{\sigma _{y_i}^2 + \sigma _{u_i}^2} \equiv \chi ^2({\varvec{\mu }}). \end{aligned}$$
(54)

That is, the same result is obtained by using the usual method of least squares with statistical and systematic uncertainties added in quadrature. This procedure gives the best linear unbiased estimator (BLUE), which is widely used in Particle Physics, particularly for the problem of averaging a set of measurements as described in Refs. [17,18,19,20].

Returning to the full dependence on \({\varvec{\mu }}\) and \({\varvec{\theta }}\) and following the model of Sect. 3 we now regard the systematic variances \(\sigma _{u_i}^2\) as free parameters for which we have independent gamma distributed estimates \(v_i\), with parameters \(\alpha _i\) and \(\beta _i\) set by \(\sigma _{u_i}^2\) and \(r_i\) according to Eqs. (10) and (11). The log-likelihood profiled over the \(\sigma _{u_i}^2\) is (cf. Eq. (18)),

$$\begin{aligned} -2 \ln L^{\prime }({\varvec{\mu }}, {\varvec{\theta }})= & {} \sum _{i=1}^N \left[ \frac{(y_i - \varphi (x_i; {\varvec{\mu }}) - \theta _i)^2}{\sigma _{y_i}^2} \right. \nonumber \\&+ \left. \left( 1 + \frac{1}{2 r_i^2} \right) \ln \left( 1 + 2 r_i^2 \frac{(u_i - \theta _i)^2}{v_i} \right) \right] .\nonumber \\ \end{aligned}$$
(55)

To find the required estimators we need to solve the system of equations

$$\begin{aligned} \frac{\partial \ln L^{\prime }}{\partial \mu _i}= & {} 0 \quad i = 1, \ldots ,M \,, \end{aligned}$$
(56)
$$\begin{aligned} \frac{\partial \ln L^{\prime }}{\partial \theta _i}= & {} 0, \quad i = 1,\ldots ,N . \end{aligned}$$
(57)

Equation (57) results in

$$\begin{aligned}&\theta _i^3 + \left[ - 2 u_i - y_i + \varphi _i \right] \theta _i^2 \nonumber \\&\quad + \left[ \frac{v_i + (1 + 2 r_i^2) \sigma _{y_i}^2}{2 r_i^2} + 2 u_i (y_i - \varphi _i) + u_i^2 \right] \theta _i \nonumber \\&\quad + \left[ (\varphi _i - y_i) \left( \frac{v_i}{2 r_i^2} + u_i^2 \right) - \frac{(1 + 2 r_i^2) \sigma _{y_i}^2 u_i}{2 r_i^2} \right] = 0 \,, \nonumber \\&\quad i = 1, \ldots , N, \end{aligned}$$
(58)

where here \(\varphi _i = \varphi (x_i; {\varvec{\mu }})\). Simultaneously solving all \(M+N\) equations for \({\varvec{\mu }}\) and the \({\varvec{\theta }}\) gives their ML estimators. Solving for the \(\theta _i\) for fixed \({\varvec{\mu }}\), i.e., fixed \(\varphi _i\), gives the profiled values \(\hat{\hat{\theta }}_i\). Equation (58) are cubic in \(\theta _i\) and so can be solved in closed form giving either one or three real roots. In the case of three roots, the one is chosen that maximizes \(\ln L^{\prime }\).

Using the profile log-likelihood from Eq. (55) one can use, for example, the test statistic \(t_{\mu }\) defined in Eq. (23) to find confidence regions for \({\varvec{\mu }}\) following the general procedure outlined in Sect. 4. Examples of this will be shown in Sect. 6.2.

6.1 Goodness of fit

In the usual method of least squares, the minimized sum of squares \(\chi ^2_\mathrm{min} = \chi ^2(\hat{{\varvec{\mu }}})\) based on Eq. (54) is often used to quantify the goodness-of-fit. Because it is constructed as a sum of squares of Gaussian distributed quantities, one can show (see, e.g., Ref. [11]) that its sampling distribution is chi-squared for \(N-M\) degrees of freedom, and the p-value of the hypothesis that the true model lies somewhere in the parameter space of \({\varvec{\mu }}\) is thus

$$\begin{aligned} p = \int _{\chi ^2_\mathrm{min}}^{\infty } f_{\chi ^2_{N-M}} (x) \, dx. \end{aligned}$$
(59)
Fig. 5
figure 5

Distributions of the test variable q for averages of \(N=2\) and 5 values using \(r = 0.2\) and \(r=0.4\)

Full size image

When using the gamma error model presented above, the quantity \(-2\ln L^{\prime }({\varvec{\mu }}, {\varvec{\theta }})\) is no longer a simple sum of squares. Nevertheless one can construct the statistic that will play the same role as the minimized \(\chi ^2({\varvec{\mu }})\) by considering the model in which the means \(\varphi (x_i, {\varvec{\mu }})\), which depend on the M parameters of interest \({\varvec{\mu }}\), are replaced by a vector of N independent mean values, one for each of the measurements: \({\varvec{\varphi }} = (\varphi _1, \ldots , \varphi _N)\). By requiring that the \(\varphi _i\) are given by \(\varphi (x_i, {\varvec{\mu }})\) one imposes \(N-M\) constraints and restricts the more general hypothesis to an M-dimensional subspace. One can then construct the likelihood ratio statistic

$$\begin{aligned} q = - 2 \ln \frac{L^{\prime }(\hat{{\varvec{\mu }}}, \hat{\hat{{\varvec{\theta }}}})}{L^{\prime }(\hat{{\varvec{\varphi }}}, \hat{{\varvec{\theta }}})}, \end{aligned}$$
(60)

where the numerator contains the M fitted parameters of interest \(\hat{{\varvec{\mu }}}\), and in the denominator one fits all N of the \(\varphi _i\).

When fitting separate values of \(\varphi _i\) and \(\theta _i\) for each measurement (the “saturated model”), one can see from inspection that the maximized value of \(\ln L^{\prime }({\varvec{\varphi }}, {\varvec{\theta }})\) is zero, and therefore the statistic q becomes

$$\begin{aligned} q= & {} \min _{{\varvec{\mu }}, {\varvec{\theta }}} \; \sum _{i=1}^N \left[ \frac{(y_i - \varphi (x_i; {\varvec{\mu }}) - \theta _i)^2}{\sigma _{y_i}^2} \right. \nonumber \\&+ \left. \left( 1 + \frac{1}{2 r_i^2} \right) \ln \left( 1 + 2 r_i^2 \frac{(u_i - \theta _i)^2}{v_i} \right) \right] . \end{aligned}$$
(61)

According to Wilks’ theorem [10], in the limit where the estimators \(\hat{{\varvec{\mu }}}\) and \(\hat{{\varvec{\theta }}}\) are Gaussian distributed, q will follow a chi-squared pdf for \(N-M\) degrees of freedom. The statistic q thus plays the same role as the minimized sum of squares \(\chi ^2_\mathrm{min}\) in the usual method of least squares. In the case of Eq. (61), however, the chi-squared approximation is not exact. One can see this from the fact that the \(v_i\) are gamma rather than Gaussian distributed; the Gaussian approximation holds only in the limit where the \(r_i\) are sufficiently small.

If all \(r_i \rightarrow 0\), i.e., there is no uncertainty in the reported systematic errors, then the statistic q reduces to the minimized sum of squares from the method of least squares or BLUE, namely,

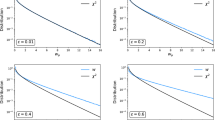
$$\begin{aligned} q = \sum _{i=1}^N \frac{(y_i - \mu (\hat{{\varvec{\varphi }}}))^2}{\sigma _{y_i}^2 + \sigma _{u_i}^2}. \end{aligned}$$
(62)

One can check in an example that the sampling distribution of q follows a chi-squared distribution by generating measured values \(y_i\), \(u_i\), and \(s_i\) according to the model described in Sect. 2 using the following parameter values: \(\varphi _i = \mu = 10\), \(\sigma _{y_i} = 1\), \(\sigma _{u_i} = 1\) for all \(i = 1, \ldots , N\). That is, the measurements are assumed to have the same mean \(\mu \) and the goal is to fit this parameter. The resulting distributions of q are shown in Fig. 5a, b for \(N=2\) and \(N=5\) using \(r_i = 0.2\) for all measurements. Overlayed on the histograms is the chi-squared pdf for \(N-1\) degrees of freedom. Although the agreement is reasonably good there is still a noticeable departure from the asymptotic distribution in the tails. The same set of curves is shown in Fig. 5c, d for \(r_i = 0.4\), for which one sees an even greater discrepancy between the true (i.e., simulated) and asymptotic distributions.

One might need a p-value with an accuracy such that assumption of the asymptotic distribution of q is not adequate. In such a case one can use Monte Carlo to determine the correct sampling distribution of q. Alternatively, following the procedure of Sect. 5.1 one can define a Bartlett-corrected statistic \(q^{\prime }\) as

$$\begin{aligned} q^{\prime } = \frac{N-M}{E[q]} q, \end{aligned}$$
(63)

so that by construction \(E[q^{\prime }] = N-M\) (in the example above for a single fitted parameter \(M = 1\)). Distributions of \(q^{\prime }\) corresponding to Fig. 5 are shown in Fig. 6, where the mean value E[q] was itself found from Monte Carlo simulation. While one sees that the distributions of \(q^{\prime }\) are in better agreement with the Monte Carlo, visible discrepancies remain. And since here simulation was required to determine the Bartlett correction, one could use it as well to find the p-value directly. The Bartlett correction is nevertheless useful in such a situation because the number of simulated values of q required to estimate accurately E[q] may be much less than what one needs to find the upper tail area for a very high observed value of the test statistic.

Fig. 6
figure 6

Distributions of the Bartlett-corrected test variable \(q^{\prime }\) for averages of \(N=2\) and 5 values using \(r = 0.2\) and \(r=0.4\)

Full size image

6.2 Averaging measurements

An important special case of a least-squares fit is the average of N independent measurements, \(y_1, \ldots , y_N\), of the same quantity, i.e., the fit function \(\varphi (x; \mu ) = \mu \) is in effect a horizontal line and the control variable x does not enter. The expectation values of the measurements are thus

$$\begin{aligned} E[y_i] = \mu + \theta _i \,, \quad \quad i = 1,\ldots ,N, \end{aligned}$$
(64)

where the parameter of interest \(\mu \) represents the desired mean value and as before \(\theta _i\) are the bias parameters. As there is one parameter of interest, the statistic q follows asymptotically a chi-squared distribution for N degrees of freedom, although as we have seen above this approximation breaks down as the \(r_i\) increase.

As an example, consider the average of two independent measurements, nominally reported as \(y_i \pm \sigma _{y_i} \pm s_i\) for \(i = 1, 2\), in which the \(\sigma _{y_i}\) represent the statistical uncertainties and \(s_i\) are the estimated systematic errors. Suppose here these are \(\sigma _{y_i} = 1\) and \(s_i = 1\) for both measurements, and that the analyst reports values \(r_i\) representing the relative accuracy of the estimates of the systematic errors, which in this example we will take to be equal to a common value r. Furthermore suppose that the observed values of \(y_1\) and \(y_2\) are \(10 + \delta \) and \(10 - \delta \), respectively, and we will allow \(\delta \) to vary. For the values of \(\sigma _{y_i}\) and \(s_i\) chosen in this example, the value of \(\delta \) corresponds to the significance of the discrepancy between \(y_1\) and \(y_2\) in standard deviations under assumption of \(r=0\).

Using the input values described above, the mean \(\mu \), bias parameters \(\theta _i\), and systematic errors \(\sigma _{u_i}\) are adjusted to maximize the log-likelihood from Eq. (16). Figure 7 show the half-width of the 68.3% confidence interval for \(\mu \) as a function of the parameter r for different levels of \(\delta \). This interval corresponds to the standard deviation \(\sigma _{\hat{\mu }}\) when the \(r_i\) are all small, where the problem is the same as in least squares or BLUE.

In Fig. 7a, the interval is based on Eq. (26), i.e., it is determined by the point where the profile log-likelihood drops by a fixed amount from its maximum (in Particle Physics often referred to as the “MINOS” interval [21]). In Fig. 7b, the interval is found by solving for the value of \(\mu \) where its p-value is \(p_{\mu } = \alpha \), and here \(\alpha = 1 - 0.683 = 0.317\). The p-value depends, however, on the assumed values of the nuisance parameters. Here we use the values of \(\theta _i\) and \(\sigma ^2_{u_i}\) profiled at the value of \(\mu \) tested. This technique is often called “profile construction” in Particle Physics [22], where it is widely used, and elsewhere called “hybrid resampling” [23, 24]. The resulting confidence interval will have the correct coverage probability of \(1 - \alpha \) if the nuisance parameters are equal to their profiled values; elsewhere the interval could under- or over-cover. Although the intervals from profile construction differ somewhat from those found directly on the log-likelihood, they have the same qualitative behaviour.

Fig. 7
figure 7

Plots of the half-length of the 1-\(\sigma \) (68.3%) central confidence interval for the parameter \(\mu \) as a function of the relative uncertainty on the systematic errors r for different levels of discrepancy \(\delta \) between two averaged measurements. Intervals are derived a from the log-likelihood and b using “profile construction” (see text)

Full size image

From Fig. 7 one can extract several interesting features. First, if r is small, that is, the systematic errors \(\sigma _{u_i}\) are very close to their estimated values \(s_i\), then the interval’s half-length is very close to the standard deviation of the estimator, \(\sigma _{\hat{\mu }} = 1\), regardless of the level of discrepancy between the two measured values.

Further, the effect of larger values of r is seen to depend very much on the level of discrepancy between the measured values. If \(y_1\) or \(y_2\) are very close (e.g., \(\delta = 0\) or 1), then the length of the confidence interval can even be reduced relative to the case of \(r=0\). If the measurements are in agreement at a level that is better than expected, given the reported statistical and systematic uncertainties, then one finds that the likelihood is maximized for values of the systematic errors \(\sigma _{u_i}\) that are smaller than the initially estimated \(s_i\). And as a consequence, the confidence interval for \(\mu \) shrinks.

Finally, one can see that if the data are increasingly inconsistent, e.g., in Fig. 7 for \(\delta \ge 4\), then the effect of allowing higher r is to increase the length of the interval. This is also a natural consequence of the assumed model, whereby an observed level of heterogeneity greater than what was initially estimated results in maximizing the likelihood for larger values of \(\sigma _{u_i}\) and consequently an increased confidence interval size.

The coverage properties of the intervals for the average of two measurements example are investigated by generating data values \(y_i\) for \(i = 1,2\) according to a Gaussian with a common mean \(\mu \) (here 10) and the standard deviations both \(\sigma _{y_i} = 1\), and the \(u_i\) are generated according to a Gaussian distributed with mean of \(\theta _i = 0\) and standard deviation \(\sigma _{u_i} = 1\). The values \(v_i\) are gamma distributed with parameters \(\alpha _i\) and \(\beta _i\) given by Eqs. (10) and (11) so as to correspond \(\sigma _{u_i} = 1\) and for different values of the parameters \(r_i\), taken here to be the same for both measurements.

Figure 8 shows the coverage probability for the interval with nominal confidence level 68.3% based on the log-likelihood (the MINOS interval) and also using profile construction (hybrid resampling), as a function of the r parameter. As seen in the figure, the coverage probability approximates the nominal value reasonably well out to \(r = 0.5\), where one finds \(P_\mathrm{cov} = 0.631\) and 0.667 for MINOS and profile construction respectively; at \(r = 1\), the corresponding values are 0.564 and 0.617 (the Monte Carlo statistical errors for all values is around 0.005). Thus reasonable agreement is found with both methods but one should be aware that the coverage probability may depart from the nominal value for large values of r.

Fig. 8
figure 8

The coverage probability of the intervals based on the likelihood (MINOS method) and on profile construction (hybrid resampling) as a function of the parameter r (see text)

Full size image
Fig. 9
figure 9

Result of averaging five quantities: a no outlier, \(r_i = 0.01\); b with outlier, \(r_i = 0.01\); c no outlier, \(r_i = 0.2\); d with outlier, \(r_i = 0.2\). Also indicated on the plots are the values of the Bartlett-corrected goodness-of-fit statistic \(q^{\prime }\) and the corresponding p value

Full size image

6.3 Sensitivity to outliers

One of the important properties of the error model used in this paper is that curves fitted to data become less sensitive to points that depart significantly from the fitted curve (outliers) as the \(r_i\) parameters of the measurements are increased. This is a well-known feature of models based on the Student’s t distribution (see, e.g., Ref. [2]).

The reduced sensitivity to outliers is illustrated in Fig. 9 for the case of averaging five measurements of the same quantity (i.e., the fit of a horizontal line). All measured values are assigned \(\sigma _{y_i}\) and \(s_i\) equal to 1.0, and in Fig. 9a, c they are all fairly close to the central value of 10. In Fig. 9b, d the middle point is at 20. In the top two plots, the \(r_i\) parameters for all measurements are taken to be \(r_i = 0.01\), which is very close to what would be obtained with an ordinary least-squares fit. In (a) the average is 10; in (b) the outlier causes the fitted mean to move to 12.00. In both cases the half-width of the confidence interval is 0.63.

In the lower two plots, (c) and (d), all of the points are assigned \(r_i = 0.2\), i.e., a 20% relative uncertainty on the systematic error. In the case with no outlier, (c), the estimated mean stays at 10.00, and the half-width of the confidence interval only increases a small amount to 0.65. With the outlier in (d), the fitted mean is 10.75 with an interval half-width of 0.78. That is, the amount by which the outlier pulls the estimated mean away from the value preferred by the other points (10.00) is substantially less than with \(r_i = 0.01\), (fitted mean 12.00). Furthermore, the lower compatibility between the measurements results in a confidence interval that is larger than without the outlier (half-width 0.78 rather than 0.65). When the \(r_i\) are small, however, the interval size is independent of the goodness of fit. Both the increase in the size of the confidence interval and the decrease in sensitivity to the outlier represent important improvements in the inference. It is important to note that the above-mentioned properties pertain to the case where each measurement has its own bias parameter \(\theta _i\) with its own \(r_i\).

It might appear that one would obtain a result roughly equivalent to that of the proposed model by using the ordinary least-squares approach, i.e., the log-likelihood of Eq. (53), and simply making the replacement \(\sigma _{u_i} \rightarrow \sigma _{u_i}(1 + r_i)\). In the example shown above with all \(r_i = 0.2\), however, the result is \(\hat{\mu } = 10.00 \pm 0.70\) without the outlier (middle data point at 10) and \(\hat{\mu } = 12.00 \pm 0.70\) if the middle point is moved to 20. So by inflating the systematic errors but still using least squares, one increases the size of the confidence interval by an amount that does not depend on the goodness of fit and the sensitivity to outliers is not improved.

7 Treatment of correlated uncertainties

The phrase “correlated systematic uncertainties” is often taken to mean the situation where a nuisance parameter affects multiple measurements in a coherent way. Suppose, for example, that the expectation values \(E[y_i]\) of measured quantities \(y_i\) with \(i = 1, \ldots , L\) are functions \(\varphi _i({\varvec{\mu }}, {\varvec{\theta }})\) of parameters of interest \({\varvec{\mu }} = (\mu _1, \ldots , \mu _M)\) and nuisance parameters \({\varvec{\theta }} = (\theta _1, \ldots , \theta _N)\). Suppose further that the nuisance parameters are defined such that for \({\varvec{\theta }} = 0\) the \(y_i\) are unbiased measurements of the nominal model \(\varphi _i({\varvec{\mu }})\). Expanding \(\varphi _i\) to first order in \({\varvec{\theta }}\) therefore gives

$$\begin{aligned} E[y_i] = \varphi _i({\varvec{\mu }}, {\varvec{\theta }}) \approx \varphi _i({\varvec{\mu }}) + \sum _{j=1}^N R_{ij} \theta _j, \end{aligned}$$
(65)

where the factors \(R_{ij} = \left. \partial \varphi _i/\partial \theta _j \right| _{{\varvec{\theta }} = 0}\) determine how much \(\theta _j\) biases the measurement \(y_i\).

Suppose that the \(R_{ij}\) are known, either from symmetry (e.g., a particular \(\theta _j\) could be known to contribute equally to all of the \(y_i\)) or they are determined using a Monte Carlo simulation. As before suppose one has a set of independent Gaussian-distributed control measurements \(u_j\) used to constrain the nuisance parameters, with mean values \(\theta _j\) and standard deviations \(\sigma _{u_j}\). One can define the total bias of measurement \(y_i\) as

$$\begin{aligned} b_i = \sum _{j=1}^N R_{ij} \theta _j. \end{aligned}$$
(66)

and an estimator for \(b_i\) is

$$\begin{aligned} \hat{b}_i = \sum _{j=1}^N R_{ij} u_j. \end{aligned}$$
(67)

These estimators of the biases are correlated. As the control measurements are assumed independent, and therefore \(\text{ cov }[u_k, u_l] = V[u_k] \delta _{kl}\), the covariance of the bias estimators is

$$\begin{aligned} U_{ij} = \text{ cov }[\hat{b}_i, \hat{b}_j] = \sum _{k=1}^N R_{ik} R_{jk} V[u_k]. \end{aligned}$$
(68)

It is in the sense described here that the proposed model is capable of treating correlated systematic uncertainties. That is, although the control measurements \(u_i\) are independent they result in a nondiagonal covariance for the estimated biases of the measurements.

The matrix \(U_{ij}\) is shown here only to illustrate how correlated bias estimates can be related to independent control measurements and it is not explicitly needed in the type of the analysis described here. The full likelihood can be constructed from the measurements \(y_i\) together with their expectation values given by Eq. (65), where the \(R_{ij}\) are assumed known. That is, in the log-likelihood of Eqs. (53) or (55) the terms \(y_i - \varphi (x_i; {\varvec{\mu }}) - \theta _i\) are replaced by \(y_i - \varphi _i({\varvec{\mu }}) - \sum _{j=1}^N R_{ij} \theta _j\). If the variances \(\sigma ^2_{u_i}\) of the control measurements \(u_i\) are themselves uncertain then they are treated as adjustable parameters with independent gamma-distributed estimates.

8 Discussion and conclusions

The statistical model proposed here can be applied in a wide variety of analyses where the standard deviations of Gaussian measurements are deemed to have a given relative uncertainty, reflected by the parameters \(r_i\) defined in Eq. (9). The quadratic constraint terms connecting control measurements to their corresponding nuisance parameters that appear in the log-likelihood are replaced by logarithmic terms [cf. Eqs. (3) and (18)]. The resulting model is equivalent to taking a Student’s t distribution for the control measurements, with the number of degrees of freedom given by \(\nu = 1/2r^2\).

It is not uncommon for systematic errors, especially those related to theoretical uncertainties, to be uncertain themselves to several tens of percent. The model presented here allows such uncertainties to be taken into account and it has been shown that this has interesting and useful consequences for the resulting inference. Confidence intervals are found to increase in size if the goodness of fit is poor and can decrease slightly if the data are more internally consistent than expected, given the level of statistical fluctuation assumed in the model. Averages and fitted curves become less sensitive to outliers.

If the relative uncertainty on the systematic errors is large enough (r greater than around 0.2 in the examples studied), then the sampling distribution of likelihood-ratio test statistics starts to depart from the asymptotic chi-squared form. Thus one cannot in general apply asymptotic results for p values and confidence intervals without taking some care to ensure their validity. In some cases Bartlett-corrected statistics can be used; alternatively one may need to determine the relevant distributions by Monte Carlo simulation.

In reporting results that use the procedure presented here it is important to communicate all of the \(r_i\) parameters. To allow for combinations with other measurements one should ideally report the full likelihood, including the \(r_i\) values, to permit a consistent treatment of uncertainties common to several of the measurements.

The point of view taken here has been that the analyst must determine reasonable values for the relative uncertainties in the systematic errors. One should not, for example, decide to use the proposed model only if the goodness of fit is found to be poor. Rather, the \(r_i\) parameters should reflect the accuracy with which the systematic variances have been estimated and the resulting inference about the parameters of interest then incorporates this knowledge in a manner that is valid for any data outcome.

An alternative mentioned here as a possibility would be to fit a common relative uncertainty to all systematic errors (a global r), e.g., when averaging a set of numbers for which no r values have been reported. This is analogous to the scale-factor procedure used by the Particle Data Group [9] or the method of DerSimonian and Laird [27] widely used in meta-analysis. Note, however, that in arriving at the log-likelihood (18), a number of terms dependent on the \(r_i\) were dropped, as they were considered fixed constants. If the \(r_i\) are adjustable parameters then these terms, given in Appendix B, must be retained in the log-likelihood.