Abstract
We discuss the inclusion of next-to–next-to leading order electromagnetic and of next-to leading order electroweak corrections to the leptonic decays of weak gauge and Higgs bosons in the Sherpa event generator. To this end, we modify the Yennie– Frautschi–Suura scheme for the resummation of soft photon corrections and its systematic improvement with fixed-order calculations, to also include the effect of virtual corrections due to the exchange of weak gauge bosons. We detail relevant technical aspects of our implementation and present numerical results for observables relevant for high-precision Drell–Yan and Higgs boson production and decay simulations at the LHC.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The experiments at the LHC are stress-testing the Standard Model (SM) of particle physics at unprecedented levels of precision. In particular, leptonic standard-candle signatures like charged- and neutral-current Drell–Yan production offer large cross sections together with very small experimental uncertainties, often at or even below the percent level. This allows to extract fundamental parameters in the electroweak (EW) sector of the SM at levels of precision surpassing the LEP heritage. Measurements of the W-boson mass, a key EW precision observable, are already reaching the 20 MeV level [1] based on 7 TeV data alone, with theory uncertainties being one of the leading systematics. Another example for the impressive achievements on the experimental side, challenging currently available theoretical precision, is the recent measurement of the triple differential cross section in neutral current Drell–Yan production based on 8 TeV data [2], the first of its kind at a hadron collider. Furthermore, precision measurements of the Z transverse momentum spectrum [3, 4] have been used to constrain parton distribution functions (PDFs) [5]. In order to fully harness available and future experimental datasets excellent theoretical control of various very subtle effects of higher-order QCD and EW origin is required. For recent reviews and studies on these issues, see e.g. [6,7,8]. With this paper we contribute to this effort by investigating higher-order QED/EW effects in the modelling of soft-photon radiation off vector-boson decays.
The demand for (sub-)percent precision in Drell–Yan production has led to formidable achievements in the theoretical description of corresponding collider observables, often pushing boundaries of technical limitations. The pioneering next-to-next-to-leading (NNLO) QCD corrections for differential Drell–Yan production [9,10,11] are available as public computer codes [12,13,14] and have recently been matched to QCD parton showers, using the \(\mathrm {UN}^2\mathrm {LOPS}\) framework within Sherpa [15, 16], and via a reweighting of a MiNLO improved calculation in Dynnlops [17]. Since recently also NNLO corrections to Drell–Yan production at finite transverse momentum are available [18,19,20,21,22,23,24,25]. Higher-order EW corrections at the NLO level for inclusive Drell–Yan production are available for quite some time [26, 27] and are implemented in a large number of public codes, including Wzgrad [28,29,30], Sanc [31], Rady [32, 33], Horace [34, 35] and Fewz [36]. At finite transverse momentum they have been calculated in [37,38,39,40]. The combination of higher-order QCD and EW effects is available within the Powheg framework [8, 41,42,43,44] matched to parton-showers, and also in [45]. Efforts to calculate the fixed-order NNLO mixed QCD and EW corrections explicitly are underway [46,47,48,49]. Their effect has been studied in the pole approximation [50, 51].
At the desired level of precision QED effects impacting in particular the leptonic final state have to be considered and understood in detail. In this case, soft and collinear photon radiation provides the major contributions. These can be resummed to all orders, and also improved order by order in perturbation theory. Implementations of such calculations have been performed via a QED parton shower matching in Horace [52, 53] and in the Powheg framework, in the structure function approach in Rady, and through a YFS-type exponentiation for particle decays in Photos [54], Winhac [55], the Herwig module Sophty [56] and the Sherpa module Photons [57]. In this paper, we present an extension of the Sherpa module Photons, which provides a simulation of QED radiation in (uncoloured) particle decays. Photons implements the approach of Yennie, Frautschi and Suura (YFS) [58] for the calculation of higher order QED corrections. In the YFS approach, leading soft logarithms, which are largely independent of the actual hard process involved, are resummed to all orders. Beyond this, the method also allows for the systematic improvement of the description through the inclusion of full fixed-order matrix elements. The present implementation allows for the inclusion of a collinear approximation to the real matrix element using dipole splitting kernels [59, 60]. Furthermore, for several relevant processes, including the decays of electroweak bosons, \(\tau \) decays as well as generic decays of uncharged scalars, fermionic and vector hadrons, the full real and virtual NLO QED matrix elements are included. This module has also been used for the description of electroweak corrections in the semileptonic decays of B mesons [61]. The aim of this publication is to further enhance the level of precision in the case of the decay of electroweak gauge- and Higgs-bosons by implementing the full one-loop EW corrections, as well as NNLO QED corrections in the case of Z- and Higgs-decays. The electroweak virtual corrections to particle decays are known for a long time [62, 63] and our implementation will be based on these results. In the case of Z-boson decays, the double virtual corrections in the limit of small lepton masses are known for about 30 years [64], which we will rely on.
The paper is organized as follows. In Sect. 2, we review the YFS algorithm, motivating and investigating the procedure to include higher order corrections at a given perturbative order. In Sect. 3, we summarize the numerical results for the decays \(Z\rightarrow \ell ^+\ell ^-\), \(W\rightarrow \ell \nu \) in Drell–Yan production. There we also present results for \(H\rightarrow \ell ^+\ell ^-\) decays in hadronic Higgs production. The measurement of the latter is highly challenging due to small leptonic Higgs couplings but potentially achievable at the HL-LHC. We discuss and conclude in Sect. 4.
2 Implementation
2.1 The YFS formalism
In this section, we will briefly recapitulate the YFS formalism in a form appropriate for the approximate description of photon radiation in particle decays, using the exponentiation of the universal soft limit of matrix elements for real and/or virtual photons and its systematic improvement through exact fixed-order calculations. The decay rate of a decaying particle with mass m and momentum q into a set of decay products with momenta \(p_f\), fully inclusive with respect to the number of real and virtual photons \(n_R\) and \(n_V\) reads,
Compared to the original, Born-level matrix element \(\mathcal {M}_0^0\) describing the decay, the matrix elements \(\mathcal {M}_{i}^j\) include i real photons at the overall order j in the electromagnetic coupling \(\alpha \). This equation for the decay rate describes an unrealistic situation, where we are able to calculate all matrix elements, to all orders, and where we can integrate them over their respective full phase space, while in reality at most the first few orders in perturbation theory can be calculated. The YFS algorithm addresses this by dressing the lowest order matrix elements with exponentiated eikonal factors that capture the leading logarithmic behaviour of the amplitude, thus providing an all-order description of QED radiation correct in this limit. The full result is restored, order by order in perturbation theory, by including the subleading process-dependent parts of the amplitude.
Encapsulating the leading soft behaviour of a single virtual photon in a process-independent factor \(\alpha B\), the full one-loop matrix element can be written as
where \(M_0^1\) is an infrared subtracted matrix element including a virtual photon. Note that throughout this paper we assume all charged particles to be massive; consequently the matrix elements do not exhibit collinear singularities. YFS showed that the simple structure at first order extends also to all further virtual photon corrections. Including the appropriate symmetrisation prefactors this generalises to
Summing over all numbers of virtual photons \(n_V\), we find that the soft behaviour exponentiates,
In QED, this argument generalises to matrix elements also containing any number \(n_R\) of real photons, i.e.,
where the \(M_{n_R}^{n_V+\frac{1}{2}n_R}\) are free of virtual soft singularities, but will still contain the soft divergences due to real photons.
In contrast to the virtual amplitudes, the factorization for real photons occurs at the level of the squared matrix elements. For a single photon emission it reads
where the eikonal factor \(\tilde{S}\left( k\right) \) contains the real soft divergence. We denote the complete infrared finite squared real matrix element as \(\tilde{\beta }_{n_R}^{n_V+n_R}\) and employ the abbreviation
to write the squared matrix element for the emission of \(n_R\) real photons, summed over all numbers \(n_V\) of virtual photons as
This expression contains all possible divergences due to real photon emission in the eikonal factors. The first term describes the leading logarithmic behaviour, and contains all virtual insertions to the matrix element without any real photon emission through \(\tilde{\beta }_0\). The second term corrects the approximate expression in the \(\tilde{S}\) for the real emission of one additional photon to the exact result, and so on. Expanding the \(\tilde{\beta }_i\) in the electromagnetic coupling constant \(\alpha \) we can get a systematic, perturbative expansion. Demanding agreement with the exact results up to \(\mathcal {O}\left( \alpha ^2\right) \) results in
effectively making explicit the terms related to virtual photon corrections.Footnote 1
Completing the exponentiation of the leading logarithmic behaviour in both real and virtual photon corrections and correcting the result to the exact first order expression we arrive at
In this expression, all virtual infrared singularities are contained in B while all real infrared singularities are contained in the integral over \(\tilde{S}(k)\). There, terms diverging in the limit \(k\rightarrow 0\) can easily be isolated by defining a small soft region \(\Omega \) that contains the limit \(k\rightarrow 0\) such that \(\Theta (k,\Omega ) = 1\) if \(k \notin \Omega \):
The two functions \(\tilde{B}(\Omega )\) and \(D(\Omega )\) are given by
where the former contains the infrared singularities and the latter is infrared regular. This separation allows the re-expansion of the exponentiated integral and the re-instating of explicit momentum conservation through \(\delta \)-functions, arriving at the master formula for the decay rate in the YFS approach:
In the equation above we made the dependence on momenta explicit: the Born-level momenta of the process before QED radiation are denoted by \(q_i\), while the momenta of the full final state including radiation are labelled \(p_i\). The mapping between both sets of momenta is detailed below. The individual terms are
-
the YFS form factor
$$\begin{aligned} Y(\Omega ) = \sum _{i<j} Y_{ij}(\Omega ) = 2\alpha \left( B_{ij}+\tilde{B}_{ij}(\Omega )\right) , \end{aligned}$$(2.14)with the sum running over all pairs of charged particles and the soft factors given by
$$\begin{aligned} B_{ij} =&-\frac{i}{8\pi ^3}Z_iZ_j\theta _i\theta _j\int \mathrm {d}^4k \frac{1}{k^2}\nonumber \\&\times \left( \frac{2q_i\theta _i-k}{k^2-2\left( k\cdot q_i\right) \theta _i} {+} \frac{2q_j\theta _j+k}{k^2+2\left( k\cdot q_j\right) \theta _j}\right) ^2, \end{aligned}$$(2.15)$$\begin{aligned} \tilde{B}_{ij}\left( \Omega \right) =&\, \frac{1}{4\pi ^2}Z_iZ_j\theta _i\theta _j\int \mathrm {d}^4k\ \delta \left( k^2\right) \nonumber \\&\times \left( \phantom {\frac{1}{2}}1-\Theta \left( k,\Omega \right) \right) \left( \frac{q_i}{q_i\cdot k} - \frac{q_j}{q_j\cdot k}\right) ^2. \end{aligned}$$(2.16)These two terms contain all infrared virtual and real divergences which cancel due to the Kinoshita-Lee-Nauenberg theorem [65, 66], guaranteeing the finiteness of \(Y(\Omega )\) and of the decay width. \(Z_i\) and \(Z_j\) are the charges of the particles i and j, and the factors \(\theta = \pm 1\) for particles in the final or initial state, respectively. We provide expressions for \(B_{ij}\) in final-final and initial-final dipoles in terms of scalar master integrals in Appendix C. The calculation of the full form factor can be found in [57];
-
the eikonal factor \(\tilde{S}\left( k\right) \)
$$\begin{aligned} \tilde{S}\left( k\right)= & {} \sum _{i<j} \tilde{S}_{ij}\left( k\right) \nonumber \\= & {} \frac{\alpha }{4\pi ^2}\sum _{i<j}Z_iZ_j\theta _i\theta _j \left( \frac{q_i}{q_i\cdot k} - \frac{q_j}{q_j\cdot k}\right) ^2 \end{aligned}$$(2.17)describing the soft emission of a photon off a collection of charged particles;
-
the lowest order matrix element \(\tilde{\beta _0^0}\);
-
a correction factor \(\mathcal {C}\) to the full matrix element, given by
$$\begin{aligned} \mathcal {C}= & {} 1 + \frac{1}{\tilde{\beta }_0^0} \left( \tilde{\beta }_0^1 + \sum _{i=1}^{n_\gamma } \frac{\tilde{\beta _1^1}\left( k_i\right) }{\tilde{S}\left( k_i\right) }\right) \nonumber \\&+ \frac{1}{\tilde{\beta }_0^0}\left( \tilde{\beta }_0^2 + \sum _{i=1}^{n_\gamma } \frac{\tilde{\beta _1^2}\left( k_i\right) }{\tilde{S}\left( k_i\right) } + \sum _{\begin{array}{c} i,j=1 \\ i\ne j \end{array}}^{n_\gamma } \frac{\tilde{\beta }_2^2\left( k_i,k_j\right) }{\tilde{S}\left( k_i\right) \tilde{S}\left( k_j\right) }\right) \nonumber \\&+ \frac{1}{\tilde{\beta }_0^0} \mathcal {O}\left( \alpha ^3\right) . \end{aligned}$$(2.18)The terms in the first bracket describe the next-to-leading order (NLO), i.e. the \(\mathcal {O}\left( \alpha \right) \) term of the expansion, and the terms in the second bracket describe the next-to–next-to-leading order (NNLO), i.e. the \(\mathcal {O}\left( \alpha ^2\right) \) term of the expansion. In this publication, we will primarily be concerned with this correction factor, in particular with the virtual corrections at NLO, the term \(\tilde{\beta }_0^1\), which we extend to an expression at full NLO in the electroweak theory for the decays of the weak bosons, as well as the complete NNLO bracket which we will be calculating for the neutral weak bosons;
-
and the Jacobean \(\mathcal {J}\) capturing the effect of the momenta mapping.
The mappings relevant for particle decays of both uncharged and charged initial particles have been outlined in section 3.3 of [57], but we repeat them in Appendix A for the benefit of the interested reader.
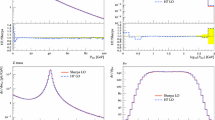
The invariant mass \(m_{\ell \ell }\) of the two leptons in Z-boson decays on the left and the invariant mass \(m_{\ell \nu }\) of the charged lepton and the neutrino in W-boson decays on the right are shown for the processes \(pp \rightarrow Z\rightarrow e^+ e^-\) and \(pp \rightarrow W^+\rightarrow e^+ \nu _e\) respectively. Different levels of fixed order accuracy are compared. The electrons in both cases are dressed with collinear photons within \(\Delta R=0.1\)
2.2 Motivation for higher order corrections
The previous subsection introduced the YFS procedure for dressing the lowest order matrix element with soft radiation to all orders. This basic procedure, in which \(\mathcal {C} = 1\), yields photon distributions that are correct in the limit of soft radiation. For the remainder of this paper, we will call this the soft approximation. Away from the strict soft limit, exact matrix elements are necessary to describe observables at the required accuracy, and we described the procedure for their systematic incorporation. Hard photon radiation occurs predominantly collinear to the emitter and more frequently in processes with large energy-to-mass ratios of the involved particles. With this in mind, generic collinear corrections for the real matrix element, based on the splitting functions developed in [59, 60], were employed in [57] to account for hard QED radiation in the soft-collinear approximation. While this approximation correctly describes radiation in the limits of soft and collinear radiation, it does neither account for interference effects nor hard wide-angle radiation. In order to capture these effects correctly, full matrix elements for real and virtual photon radiation have to be added, some of which have already been included in [57].
For illustration, in Fig. 1 (left) we compare the soft-collinear, the NLO QED-correct and the NNLO QED-correct results for the invariant mass \(m_{\ell \ell }\) of the electrons produced in Z-boson decays. To guide the eye we also show the leading-order result. The NLO QED result represents the maximal accuracy of the implementation in Photons as described in [57]. Figure 1 (left) clearly shows the necessity to include photon radiation in the first place. Photon radiation causes a significant shape difference, shifting events from large to lower \(m_{\ell \ell }\). This effect is a lot more striking in the decay into the lighter leptons, such as for the electrons exhibited here, which are much more likely to radiate photons. We can also appreciate that while the soft-collinear approximation does a good job of describing the distribution near the peak, it predicts a harder spectrum at lower values of \(m_{\ell \ell }\). The peak region corresponds to the limit of soft photon radiation, while the latter region corresponds to hard photon radiation. This observation thus suggests that in order to capture the behaviour of the distribution over its entirety, we need to employ full matrix elements. It is then natural to ask whether higher order corrections beyond the NLO in QED are required as well. The impact of NNLO QED corrections is already illustrated in Fig. 1 (left) and the description of these and of full NLO EW corrections will be the focus of the next two sections.
2.3 NLO electroweak corrections
The discussion in Sect. 2.1 was restricted to QED corrections only. Since the exponentiation relies on the universal behaviour of the amplitudes in the soft limit only, additional fixed-order corrections can easily be added, as long as they are not divergent in the soft limit and thus do not spoil the soft-photon exponentiation. This is, in fact, the case for the weak part of the corrections in the full electroweak theory, where the masses of the weak bosons regulate the soft divergence that is plaguing the massless photon. In this work, we are concerned with the decays of weak bosons; consequently, there is no phase space available for the emission of a real, massive weak boson, and the additional electroweak corrections contribute only to the virtual corrections \(\tilde{\beta }_0^{n_V}\).
The known one-loop virtual corrections for the decays of the electroweak bosons [62, 67] have been implemented in a number of programs dedicated to electroweak precision calculations already mentioned in the introduction. They can be calculated analytically with programs such as FeynCalc [68, 69], FormCalc [70] or Package-X [71], and numerically with programs such as GoSam [72, 73], MadGraph5 [74, 75], OpenLoops [76, 77] or Recola [78, 79]. The two-loop virtual electroweak corrections are not fully known yet, with only partial results for particular observables available, see for example [80, 81].
We implemented the electroweak corrections for the decays \(Z\rightarrow \ell ^+\ell ^-\), \(H\rightarrow \ell ^+\ell ^-\) and \(W\rightarrow \ell \nu \) in the YFS correction factor \(\mathcal {C}\). In doing so, we also re-implemented and re-validated the QED corrections in a more straightforward way. In our calculation we retain the full dependence on the lepton masses in the decay \(H\rightarrow \ell ^+\ell ^-\). In the two other decays we keep them only in the QED corrections, where they are required to regularize the collinear singularities, while we neglect them in the other contributions. To this end we used the vertex form factors found in [63] to describe the virtual corrections to the vertices. We renormalize the theory using the on-shell renormalization scheme, following the treatment described in [62]. We have validated the amplitudes on a point-by-point level against an implementation in OpenLoops [76, 77], all in the case of massless leptons for Z- and W-boson decays, and for the case of a Higgs decay into massive fermions. In addition, we also validated the values of the scalar integrals including masses against Collier [82,83,84,85] and QCDLoop [86], as well as individual renormalization constants for massive leptons against OpenLoops. Real corrections due to the emission of an additional photon are calculated in the helicity formalism [87,88,89] using building blocks available within Sherpa [90]. We validated these corrections explicitly, against Wzgrad [28,29,30] and by internal comparison with Amegic [90] and Comix [91]. These comparisons have yielded maximal relative deviations between our implementation and these references of at most \(10^{-10}\) in \(\mathcal {O}(100)\) randomly generated phase space points. We also validated full cross sections against Wzgrad [28,29,30] (containing only FSR corrections) and found very good agreement.
For the decays of Z- and Higgs-bosons, we further implement an option including only QED corrections. In the decay of neutral bosons, this choice forms a gauge–invariant subset of the full electroweak corrections and can thus be considered independently. Practically, this amounts to turning off the purely weak vertex form factors as well as turning off those parts of the renormalization constants that are of weak origin. This option is not available in the case of a W-boson decay as the W itself couples to the photon. We list the relevant form factors, renormalization constants and the necessary modifications in the pure QED case in Appendix B.
As an illustration in Fig. 1 (right) we compare the LO, the soft-collinear and the full NLO-correct results for the invariant mass of the charged electron and the neutrino in W-boson decays. As for the Z decay, the inclusion of the exact fixed-order corrections is mandatory for a reliable prescription below the resonance peak.
2.4 NNLO QED corrections
We will now turn to the discussion of NNLO QED corrections to Z- and Higgs-boson decays. They comprise double-virtual, real-virtual and real-real contributions. The NNLO QED corrections can be combined with the full NLO EW corrections, and we will label this combination as “NNLO QED \(\oplus \) NLO EW”. As illustrated in Fig. 1 (left) the NNLO corrections yield very small corrections beyond NLO - at least in observables defined at LO. However, their inclusion ensures precision at the sub-percent level required for future Drell–Yan measurements.
2.4.1 Double virtual corrections
The two-loop pure QED corrections to the form factor for the Z-boson decay have been known in the limit of small lepton masses since the LEP era [64, 92]. Including full mass dependence, currently the two-loop QED form factor is only known for the decay of a virtual photon [93].
To the best of our knowledge, no QED two-loop form-factors are available for the decay of Higgs bosons. In principle they could be obtained from corresponding QCD results [94,95,96,97,98] However, for simplicity here we rely on the leading logarithmic behaviour only, \(\tilde{\beta }_0^2 = \frac{1}{2} \log ^2\left( \frac{s}{m^2}\right) \). We find that for the decays into bare muons, this is a sufficient approximation. Appreciable effects due to this approximation might only be noticeable in Higgs decays into \(\tau \)-leptons.
For the decay of Z-bosons, we use the results in Eqs. (2.15) and (2.22) of [64], together with the subtraction term B expanded in the limit \(s \gg m^2\). The results for the form factors given in [64] are sufficient as we only require the squared contribution \(\mathrm {Re}({M_0^2M_0^{0 *}})\). In fact, here the two-loop amplitude \(M_0^2\) factorizes into a simple factor multiplying the leading order matrix element.
The double virtual corrections can be decomposed, following the procedure described in Sect. 2.1, as
such that the infrared subtracted matrix element reads
using the decomposition \(M_0^1 = \mathcal {M}_0^1 -\alpha B M_0^0\). Employing the results of [64] and the form of the subtraction term given in Eq. (C.2), we obtain
where \(\zeta (n)\) is the Riemann Zeta function, with \(\zeta (3) \approx 1.202056903159594\) and \(L = \log (s/m^2)\).
The final correction term \(\tilde{\beta }_0^2\) yields:
2.4.2 Real-virtual corrections
The real-virtual corrections correspond the virtual corrections to the process \(X\rightarrow f\bar{f}^{(')}\gamma \), with one real, hard photon. We can write the infrared subtracted, squared real-virtual matrix elements as
where \(k_1\) denotes the momentum of the hard photon, and the sum in the first term runs over the spins \(s_i\) of the leptons and the polarizations \(\lambda _j\) of the vector bosons. The factor \(\tilde{S}\left( k_1\right) \) is calculated using the momenta mapped to the single photon final state taking \(k_1\) as the hard photon momentum. For consistency, \(\tilde{\beta }_0^1\) contains only the one-loop QED corrections. Using FeynCalc [68, 69] we rewrite the amplitudes in terms of standard matrix elements multiplied by expressions involving scalar master integrals. We have encoded the neccessary master integrals using [62, 63, 99]. We also use the algorithm proposed in [100] for the evaluation of the complex dilogarithm occuring in the master integrals. We have confirmed the analytical cancellation of the UV divergences upon including the renormalization terms as well as the cancellation of the virtual IR divergences upon inclusion of the infrared subtraction term. However, the very nature of the expressions involved increases the likelihood of numerical instabilities in the evaluation of particular phase space points: while strictly finite, separate terms in the expression may suffer from numerical instabilities, causing incomplete cancellations between different terms. The reasons are twofold, and connected with the collinear regime of the emissions:
-
The YFS formalism relies on fermion masses to regularize the collinear singularities, which in the case of small fermion masses may amount to the evaluation of expressions very close to logarithmic singularities, of the type \(\log (s_{ij}/m^2)\), where \(s_{ij} = (p_i+p_j)^2\) is the invariant mass of two momenta. We find that in our implementation the amplitudes for the decays into electrons and to some extent also into muons are affected by numerical instabilities while the amplitudes for the decays into \(\tau \)’s are well-behaved.
-
In addition, the employed Passarino-Veltmann reduction may lead to the appearance of small Gram determinants in denominators. One way to circumvent this issue is by employing an expansion in the Gram determinant for the problematic tensor integrals rather than the full reduction, as implemented for example in Collier [85]. Since this requires the implementation of a significant number of expressions for different combinations of arguments in the tensor integrals and thus amounts to a large overhead, this is not pursued in this work.
To cure both problems, we instead use the following algorithm: We call a phase space point “collinear” when \(s_{ik} < a\cdot m_i^2\), where \(s_{ik}\) is the invariant mass between the photon and one of the fermions in the process and a is some predefined cutoff. Such a phase space point will not be evaluated using the full matrix element but rather using the quasi-collinear limit of the amplitude. Using this limit, the calculational complexity of the amplitude is significantly reduced and numerical instabilities are avoided. As an additional rescue system, in case a bad phase space point should still pass to be evaluated using the full matrix element, we also check the scaling behaviour of the amplitude under a rescaling of all dimensionful quantities. The expressions for the coefficients of the master integrals can be rewritten using reduced quantities, i.e. all dimensionful quantities are divided by the centre of mass energy of the decay. In this way, dimensionful quantities only survive in the master integrals themselves as well as in a single factor multiplying the master integral. The mass dimension of a four point function in four dimensions is 0, such that upon rescaling by a common factor \(\xi \ne 1\), the full expression should remain unchanged, \(\mathcal {M}(\xi ) = \mathcal {M}(1)\). Different terms in the matrix elements scale differently due to the different scaling behaviours of the master integrals, so a deviation from the expected scaling behaviour indicates numerical instabilities in the expression. For \(\left| \mathcal {M}(1)/\mathcal {M}(\xi ) - 1 \right| > c\), with c some predefined cutoff, we set the real-virtual matrix element to 0. We varified that all results remain unchanged varying the technical parameters a, c.
2.4.3 Real-real corrections
The real-real corrections stem from the emission of two hard photons. For the implementation, we choose the same strategy as in the case of single real corrections, by using helicity amplitudes and building blocks already present in Sherpa. After setting up the amplitude like this, we can calculate the infrared subtracted matrix element squared that enters into the correction factor \(\mathcal {C}\):
In this formula, the \(k_1\) and \(k_2\) denote the momenta of the two hard photons, the sum in the first term runs over the spins \(s_i\) of the leptons and the polarizations \(\lambda _j\) of the vector bosons. The \(\tilde{S}\left( k_i\right) \) are calculated using the momenta in the mapped \((n+2)\)-dimensional phase space, using the pair \(k_1,k_2\) as the hard photons, see Appendix A.
3 Results
3.1 Setup
In this section we present the numerical effects induced by the NLO EW and NNLO QED corrections presented in the previous section, focussing on the decays \(Z\rightarrow \ell ^+\ell ^-\), \(W\rightarrow \ell \nu \) and \(H\rightarrow \ell ^+\ell ^-\) with \(\ell =\{e,\mu ,\tau \}\) following hadronic neutral-current and charged-current Drell–Yan and Higgs production respectively.
The results presented here are based on an implementation in the Photons module [57] of the Sherpa Monte Carlo framework (release version 2.2.4) [15]. We consider hadronic collisions at the LHC at 13 TeV for the production of Z-, W- and Higgs-bosons and their subsequent decays. In the neutral-current Drell–Yan case we require \(65\,\mathrm {GeV}< m_{\ell \ell } < 115\,\mathrm {GeV}\), while for the other modes no generation cuts are applied. Since we aim to purely focus on the effects of photon radiation in the decays, we turn off the QCD shower, fragmentation and underlying event simulation. We use Rivet 2.5.4 [101] for the analysis. For the case of electrons in the final state, we perform the analysis either using bare leptons or using dressed leptons with a radius parameter \(\Delta R = 0.1\) or \(\Delta R = 0.2\). For the case of muon and \(\tau \) final states only bare results are shown. We focus our results on a few key distributions and always normalize to the respective inclusive cross section. Overall, we choose to focus on ratios between different predictions, in order to highlight small subtle differences relevant for precision Drell–Yan and Higgs physics.
Input parameters for the numerical results are chosen as listed in Table 1. The weak coupling \(\alpha \) is defined in the on-shell \(\alpha (0)\) scheme. This choice is sensible as we are explicitly also investigating distributions in resolved final-state photons. At the same time, the YFS formalism is strictly only defined in the limit of soft photon emissions. In this input scheme, the sine of the weak mixing angle is a derived quantity \(s_W^2 =1- \frac{M_W^2}{M_Z^2}\). Gauge- and Higgs-boson widths are taken into account in a fixed-width scheme.
In the decays of W and Z bosons, we apply an IR technical cutoff in the YFS formalism of \(E_{\gamma , \text {cut}} = 0.1 \,\mathrm {GeV}\), while in the Higgs-decay we reduce this value to \(E_{\gamma , \text {cut}} = 0.01 \,\mathrm {GeV}\) in order to improve the resolution near the resonance.Footnote 2 In both cases, we keep an analysis cut of \(E_{\gamma } > 0.1 \,\mathrm {GeV}\) for observables involving photons.
3.2 Neutral-current Drell–Yan production
On the left the invariant mass of the two leptons, \(m_{\ell \ell }\), and on the right the invariant mass of the system of the two decay leptons and the closest photon, \(m_{\ell \ell \gamma }\), is shown for \(pp \rightarrow Z\rightarrow \ell ^+ \ell ^-\) production. Nominal predictions are shown for \(pp \rightarrow Z\rightarrow e^+ e^-\) at LO, in soft-collinear NLO approximation, at NLO QED and at NNLO QED \(\oplus \) NLO EW, where electrons are always dressed with collinear photons within \(\Delta R=0.1\). The ratio plots highlight the effect of the considered higher-order corrections and the effect due to different photon dressing or lepton identity. See text for details
In Figs. 2, 3 and 4 we present several key observables in neutral-current Drell–Yan production including higher-order QED corrections up to NNLO and EW corrections up to NLO. All distributions are normalized and the effects of the higher-order corrections typically manifest themselves as very subtle shape distortions in the considered observables. All figures are identically structured and we show nominal predictions for dressed di-electron production, i.e. collinear photon–electron pairs with \(\Delta R<0.1\) are combined, at LO (black), considering soft-collinear QED corrections (blue), NLO QED corrections (green), and our best predictions at NNLO QED \(\oplus \) NLO EW (red). In the first two ratio plots we compare the predictions at NLO QED against the soft and soft-collinear approximations and against the NLO EW and NNLO QED \(\oplus \) NLO EW predictions respectively. In the third ratio plot we investigate different dressing prescriptions of the electrons, considering \(\Delta R=0.2\) and undressed bare electrons. Finally, in the last ratio plot we compare predictions for dressed electron with corresponding ones for bare muons and \(\tau \)’s. In the latter two ratios plots all predictions correspond to the most accurate level, i.e. NNLO QED \(\oplus \) NLO EW.
Plots of the transverse momentum of the leptons, \(p_{\perp ,\ell }\), on the left and the transverse momentum of the system of the two decay leptons, \(p_{\perp ,\ell }\), on the right. Predictions and labels as in Fig. 2
Plots of the sum of the photon energies in the decay rest frame, \(\sum _{n_{\gamma }} E_{\gamma }\), on the left and the \(\phi _{\eta }^{*}\) variable on the right. Predictions and labels as in Fig. 2
In Fig. 2, we present the distributions of the invariant mass of the two leptons (left) and of the invariant mass of the system made up of the decay leptons and the photon closest to either of them (right). Already from the plots in Sect. 2.2, it is clear that the inclusion of photon radiation is crucial for a reliable description of the dilepton invariant mass. All higher-order corrections significantly differ from the LO prediction, which fails to describe the lineshape below the peak. At the NLO QED level corrections beyond the soft and soft-collinear approximations induce distortions up to the 1% level. In fact, the soft approximation does not generate enough hard radiation, while the soft-collinear approximation produces about 1% too many events at low \(m_{\ell \ell }\), i.e. it seems to generate too much hard photon radiation. In this observable both the NLO EW and NNLO QED corrections provide only a marginal effect on the order of permille, and neither of these corrections provides a significant shift of the peak of the distribution. Clearly, the dressing of the electrons has a significant effect on this distribution, reflecting the sensitivity to QED radiation. Bare electrons show a significant shape difference compared to dressed electrons. The results based on different dressing parameters however differ by at most a few %, suggesting that much of the photon radiation occurs close to the electron. Comparing different lepton species, we see that muons, in comparison to the dressed electrons, radiate significantly more, yielding up to 25% more events at low \(m_{\ell \ell }\). In contrast, the heavier \(\tau \)’s radiate less in comparison, resulting in differences with respect to dressed electrons of only a few %.
A very similar behaviour can be found in the invariant mass of the dilepton system combined with the closest photon. As this observable requires the emission of at least one photon, the NLO QED curve corresponds effectively to a LO prediction. However, also the soft and soft-collinear approximations describe this observable reasonably well and higher order NNLO QED or NLO EW corrections are negligible. Comparing the dressing parameters, we find much smaller differences here: bare electrons only differing by about 15% from the dressed versions. There is barely a difference between the two dressings. In the same manner, the difference between lepton species is subdued as well: muons differing up to 2% at most from dressed electrons.
In Fig. 3, we present the distribution of the transverse momentum of the lepton, \(p_{\perp ,\ell }\), alongside the transverse momentum of the system of the two leptons, \(p_{\perp ,\ell \ell }\). The transverse momentum of the leptons, \(p_{\perp ,\ell }\), receives small corrections from the inclusion of higher order corrections beyond NLO QED into the YFS formalism. Only the phenomenologically irrelevant region of very low \(p_{\perp ,\ell }\) receives corrections at the permille level at NLO EW. Both the soft and soft-collinear approximations agree at the permill level with NLO QED for \(p_{\perp ,\ell }>20\) GeV. Correspondingly, also the dressing of the electrons has a small effect on this distribution, with bare electrons carrying significantly less transverse momentum than the dressed versions. The difference between lepton species is marginal, up to about 5% at very low \(p_{\perp ,\ell }\) and above the Jacobi peak.
In contrast, the transverse momentum of the system of leptons, \(p_{\perp ,\ell \ell }\), shows significantly larger effects. Of course this distribution is not defined at LO and correspondingly it is very sensitive to the modelling of photon radiation. This can be appreciated when comparing the NLO QED prediction with the soft and soft-collinear approximations. Only at small \(p_{\perp ,\ell \ell }\) the approximations agree. In this observable also the inclusion of NLO EW effects shows a significant impact, with differences reaching up to 5%. The NNLO QED effects provide a competing effect to the NLO EW corrections, lifting the distributions by about 2% across the entire distribution. The effects of the dressing on the distribution is unsurprisingly very large as well. Bare electrons show significantly more events at non-vanishing values of \(p_{\perp ,\ell \ell }\), while a different dressing parameter leads to an almost flat decrease across the spectrum. The comparison of the different lepton species shows that the muons again radiate a lot more, with up to 75% more events at medium \(p_{\perp ,\ell \ell }\). \(\tau \)’s in comparison show a reduction in the number of events at large \(p_{\perp ,\ell \ell }\) of up to 50%.
Finally, in Fig. 4, we show the distribution of the sum of the photon energies in the decay rest frame, \(\sum _{n_{\gamma }} E_{\gamma }\), and the distribution of the so-called \(\phi _{\eta }^{*}\)-variable. The sum of the photon energies is largely correlated with the \(p_{\perp ,\ell \ell }\), as discussed before. This distribution shows a distinct edge at about half the Z-boson mass, which is being washed out by multiple radiation. The kinematics of the decay restrict the energy of a single radiated photon to be smaller than \(E_{\gamma , \mathrm {max}}^1 = \frac{\hat{s}-4m_\ell ^2}{2\sqrt{\hat{s}}}\), which is roughly equal to half the boson mass near the resonance. For an event to have a total photon energy beyond this edge, two hard photons need to recoil at least partly against each other. The region above the kinematical edge is then only described approximately, as long as no NNLO corrections are considered. The NLO EW prediction mildly increases the number of events without photon radiation, leading to a decrease at the kinematic edge of about 3%. The NNLO QED corrections again provide a competing effect, leading to a difference of about 1% to the NLO QED predictions near the edge. Beyond it, the NNLO QED corrections show a significant departure from the shape of the previous predictions as this region is for the first time described correctly at fixed-order. The behaviour of different dressings and lepton species is very similar to the case of the \(p_{\perp ,\ell \ell }\). The bare electrons show a significantly larger number of hard photons, while another dressing only leads to an approximately flat decrease. Muonic decays contain a larger number of events with hard photons, while \(\tau \)’s radiate significantly less.
The \(\phi _{\eta }^{*}\)-variable [102] can be seen as an alternative to \(p_{\perp ,\ell \ell }\), with the aim of being easier measurable. It is defined purely in terms of lepton directions as:
where the acoplanarity angle \(\phi _{\mathrm {acop}}\) is defined in terms of the difference in azimuthal angles \(\Delta \phi \) between the two leptons as \(\phi _{\mathrm {acop}} = \pi - \Delta \phi \), and \(\theta _{\eta }^{*} = \tanh \left( \frac{\eta ^- - \eta ^+}{2}\right) \) in terms of the lepton pseudorapidities \(\eta ^i\). In this observable, the soft region corresponds to the region of low \(\phi _{\eta }^{*}\). In comparison to the NLO QED predictions, the soft approximation predicts too many events with low \(\phi _{\eta }^{*}\), the difference quickly reaches beyond 10%. The soft-collinear approximation shows the opposite behaviour, predicting too many events with large \(\phi _{\eta }^{*}\). The NLO EW prediction provide corrections of a few percent, while the NNLO QED corrections compensate the NLO EW corrections almost completely. The dressing shows effects of up to 25% at medium value of \(\phi _{\eta }^{*}\).
Transverse mass of the lepton-neutrino system \(M^{\perp }_{\ell \nu }\) (left) and the invariant mass of the system of the charged lepton and the nearest photon, \(m_{\ell \gamma }\) (right) in \(pp \rightarrow W^+ \rightarrow \ell ^+ \nu _\ell \). Nominal predictions are shown for \(pp \rightarrow W^+\rightarrow e^+ v_e\) at LO, in soft-collinear NLO approximation and at NLO EW, where electrons are always dressed with collinear photons within \(\Delta R=0.1\). The ratio plots highlight the effect of the considered higher-order corrections and the effect due to different photon dressing or lepton identity. See text for details
3.3 Charged Drell–Yan lepton-neutrino pair production
In Figs. 5, 6 and 7, observables crucial for the study of charged-current Drell–Yan dilepton production are investigated. We present results for the decay \(W^+ \rightarrow \ell ^+\nu _\ell \), as the charge conjugate case behaves practically identically. All figures are similar to the neutral-current case presented in Sect. 3.2. However, here the best prediction is of NLO EW, as pure QED corrections cannot be defined in a gauge-invariant way. As before all nominal predictions correspond to dressed electrons.
Plots of the transverse momentum of the charged leptons, \(p_{\perp ,\ell }\), on the left and the missing transverse E, \(E_{\perp }^{\mathrm {miss}}\), on the right. Predictions and labels as in Fig. 5
Plots of the sum of the photon energies in the decay rest frame, \(\sum _{n_{\gamma }} E_{\gamma }\), on the left and the number of photons with \(E_{\gamma } > 0.1 \,\mathrm {GeV}\), \(n_{\gamma }\), on the right. Predictions and labels as in Fig. 5
In Fig. 5, we start with the transverse mass of the lepton neutrino system, \(M^{\perp }_{\ell \nu }\), and the invariant mass of the charged lepton and the nearest photon, \(m_{\ell \gamma }\). The \(M^{\perp }_{\ell \nu }\) observable is barely affected by the NLO EW corrections. In fact the soft-collinear approximation agrees with NLO EW at the permill level. The dressing of the electrons has a rather large impact, with differences with respect to a bare treatment reaching up to 10% at the edge. A slight shift of the edge is observed when comparing different lepton species with one another, affecting the distribution to up to a few %.
The invariant mass of the charged lepton and the closest photon, \(m_{\ell \gamma }\) shows significantly larger corrections. Compared to the NLO EW corrections, the soft approximation predicts a spectrum that is too soft, while the soft-collinear approximation produces up to 5% more events with large \(m_{\ell \gamma }\). Bare electrons have a lot more events at low \(m_{\ell \gamma }\) coming from those photons that have not been clustered in comparison to the dressed cases. On the other hand, those electrons dressed with \(\Delta R = 0.2\) have a reduced number of events at low \(m_{\ell \gamma }\). The comparison between lepton species shows significant differences close to low \(m_{\ell \gamma }\), illustrating the differing size of the dead cone.
In Fig. 6, we show the transverse momentum of the charged lepton, \(p_{\perp ,\ell }\), alongside the missing transverse energy, \(E_{\perp }^{\mathrm {miss}}\). The latter corresponds in our simple setup to the transverse energy that the neutrino carries away. Both distributions are related and indeed they behave very similarly. As in the neutral-current case, the transverse momentum of the charged lepton is barely affected by NLO EW corrections, with corrections only becoming appreciable for very low values of \(p_{\perp ,\ell }\). The dressing affects the distributions by up to about 10% in the peak region, while different lepton species differ by up to 4% in the peak region and at low \(p_{\perp ,\ell }\).
In Fig. 7, we present the sum of photon energies in the decay rest frame, \(\sum _{n_{\gamma }} E_{\gamma }\), and the number of photons with energy \(E_{\gamma } > 0.1 \,\mathrm {GeV}\), \(n_{\gamma }\). The sum of photon energies shows a kinematic edge just as in the neutral current case. While the soft approximation predicts too soft a spectrum of photon energies, the soft-collinear approximation does a much better job in W-decays as the effects coming from NLO EW corrections reach at most 5% at the kinematic edge. The reason for this behaviour can be read from the distribution of the \(n_{\gamma }\). The soft approximation is shown to produce too few photons, while the soft-collinear approximation predicts more events with 1–3 photons. Analyses using bare electrons show a significantly larger number of photons, with already 4 times more events with 1 photon. At the same time, for \(\Delta R = 0.2\) electrons, the number of photons is suppressed significantly. A similar picture presents itself when comparing lepton species. Muonic decays contain significantly more photons, while decays into \(\tau \)’s end up with a lot less events with at least one photon.
As a noteworthy observation we want to point out a difference between neutral-current and charged-current processes: the soft-collinear approximation is more reliable in the charged-current case. This can be understood from the fact that here collinear radiation predominantly originates from just one particle, the lepton, rather than two competing particles as in the Z-boson case. In the latter case the effect of the error due to missing interference contributions in the soft-collinear approximation is thus enhanced.
3.4 Leptonic Higgs-boson decays
Plots of the invariant mass of the two decay leptons, \(m_{\ell \ell }\), on the left and the transverse momentum of the system of the two leptons, \(p_{\perp ,\ell \ell }\), on the right in the process \(pp\rightarrow H \rightarrow \ell ^+\ell ^-\). Nominal predictions are shown for \(pp \rightarrow H\rightarrow \mu ^+ \mu ^-\) at LO, in soft-collinear NLO approximation, at NLO QED and at NNLO QED \(\oplus \) NLO EW. The ratio plots highlight the effect of the considered higher-order corrections and lepton identity. See text for details
Finally we highlight the effect of higher-order corrections in photon radiation off leptonic Higgs decays. Numerical results are shown in Fig. 8, where the nominal distribution corresponds to \(H\rightarrow \mu ^+ \mu ^-\) with bare muons. Here we focus on the dilepton invariant mass \(m_{\ell \ell }\) and \(p_{\perp ,\ell \ell }\) recoil. As for neutral-current Drell–Yan we consider higher-order corrections at the level of soft and soft-collinear approximations, full NLO QED, NLO EW and also combining NLO EW with NNLO QED. The LO prediction clearly fails to describe the invariant mass distribution. Yet, the soft and soft-collinear approximations provide a quite reliable description with corrections smaller than 1–2% with respect to full NLO QED. The weak corrections are slightly larger compared to the neutral-current Drell–Yan case, still they alter the invariant mass distribution only at the permille level and are overcompensated by NNLO QED effects of the same order. As mentioned in Sect. 3.1 we are unable to resolve the sharp mass peak of the Higgs-boson with the lowest energy photons we generate. However, investigating the low energy tail of the invariant mass distribution, we observe that the NLO QED corrections provide a mostly flat contribution in the peak region. Comparing decays into bare muons with decays into bare \(\tau \)’s, we can appreciate a significantly smaller sensitivity of the \(\tau \) distribution to QED radiation.
The distribution of the transverse momentum of the di-lepton system shows similar effects as in the case of the Z-boson decay. The soft approximation predicts a distribution that is far too soft, while the soft-collinear approximation predicts too many events with large \(p_{\perp ,\ell \ell }\). The NLO EW corrections increase the number of events by about a permille at low \(p_{\perp ,\ell \ell }\), and decrease them at high values up to about 5%. The NNLO QED corrections in this case do not provide a large competing effect, and the NNLO QED \(\oplus \) NLO EW prediction agrees with the NLO EW one at the permille level. Decays into \(\tau \)’s show about 40% less events with non-vanishing \(p_{\perp ,\ell \ell }\), the effect being close to constant across the entire distribution.
4 Conclusions and outlook
In this paper, we have presented an implementation of NLO EW and NNLO QED corrections to the decays of weak gauge and Higgs bosons within the YFS formalism. For this purpose, we extended Sherpa ’s module Photons to include the relevant matrix elements, renormalized in the on-shell scheme, and subtractions needed within this formalism. In our numerical results we find that observables relating only to the leptons in the process are only marginally affected by the corrections, up to the level of a few permil. In particular, the peak of the invariant mass distributions is practically not affected. Distributions that relate to the energies of the generated photons themselves, or can be related to them, such as the transverse momentum of the pair of the leptons \(p_{\perp ,\ell \ell }\), naturally receive larger corrections. The electroweak corrections increase the likelihood of hard photon radiation by up to 2-3% for very hard radiation. The NNLO QED corrections compete with these corrections by reducing the likelihood of hard radiation, albeit to a smaller extent. At the same time, some regions of phase space are only described at leading order in \(\alpha \) upon the inclusion of the double real radiation, such that in these regions the corrections can be significantly larger. Examples for such regions are those where the sum of the photon energies exceeds half the boson mass or regions of large \(\phi ^{*}\). Angular distributions of the photons are not affected by higher order contributions confirming the general radiation pattern of QED radiation. The results give us confidence that the inclusion of the full EW corrections to particle decays within the YFS formalism in Sherpa are sufficient to achieve precise results for most leptonic observables. Beyond the corrections investigated in this work, it will be interesting to consider the YFS formalism also including initial state effects and the matching to NLO EW corrections to the hard production process, see [103].
The implemented NNLO QED and NLO EW corrections provide high precision also in extreme phase space regions and can be seamlessly added to standard precision QCD simulations. This provides an important theoretical input to future precision determinations of fundamental parameters of the EW theory at hadron colliders and beyond.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical study. Used simulation tools will be made publicly available. No experimental data has been listed.]
Notes
For an agreement correct up to order \(\mathcal {O}\left( \alpha \right) \), we would need to remove \(\tilde{\beta }_0^2\), \(\tilde{\beta }_1^2\) and \(\tilde{\beta }_2^2\). By far and large this has already been implemented in [57].
It should of course be noted that the SM Higgs has a resonance width of only \(\sim 4 \,\mathrm {MeV}\), which is smaller than this photon cut, suggesting that we still do not resolve the resonance well with this cut. However, we find that a cut of the order \(10 \,\mathrm {MeV}\) is necessary in order to guarantee a good performance of the method in both decay channels. In any case, this smaller choice of the cutoff still allows a closer investigation of the regions close to the resonance in plots generated from the lepton momenta, as long as the binning is not chosen too fine. In particular the regions that will be populated through the radiation of photons from leptons in the resonance region will be included in this description.
References
ATLAS collaboration, Measurement of the \(W\)-boson mass in pp collisions at \(\sqrt{s}=7\) TeV with the ATLAS detector. Eur. Phys. J. C 78, 110 (2018). arXiv:1701.07240
ATLAS collaboration, Measurement of the Drell-Yan triple-differential cross section in \(pp\) collisions at \(\sqrt{s} = 8\) TeV. JHEP 12, 059 (2017). arXiv:1710.05167
CMS collaboration, Measurement of the Z boson differential cross section in transverse momentum and rapidity in protonproton collisions at 8 TeV. Phys. Lett. B 749, 187 (2015). arXiv:1504.03511
ATLAS collaboration, Measurement of the transverse momentum and \(\phi ^*_{\eta }\) distributions of DrellYan lepton pairs in protonproton collisions at \(\sqrt{s}=8\) TeV with the ATLAS detector. Eur. Phys. J. C 76, 291 (2016). arXiv:1512.02192
R. Boughezal, A. Guffanti, F. Petriello, M. Ubiali, The impact of the LHC Z-boson transverse momentum data on PDF determinations, JHEP 07, 130 (2017). arXiv:1705.00343
J.R. Andersen, et al., Les Houches 2015: Physics at TeV Colliders Standard Model Working Group Report. In 9th Les Houches Workshop on Physics at TeV Colliders (PhysTeV 2015) Les Houches, France, June 1-19, 2015 (2016). arXiv:1605.04692. http://lss.fnal.gov/archive/2016/conf/fermilab-conf-16-175-ppd-t.pdf
S. Alioli et al., Precision studies of observables in \(p p \rightarrow W \rightarrow l\nu _l\) and \( pp \rightarrow \gamma, Z \rightarrow l^+ l^-\) processes at the LHC. Eur. Phys. J. C 77, 280 (2017). arXiv:1606.02330
C.M. Carloni Calame, M. Chiesa, H. Martinez, G. Montagna, O. Nicrosini, F. Piccinini et al., Precision measurement of the W-Boson mass: theoretical contributions and uncertainties. Phys. Rev. D96, 093005 (2017). arXiv:1612.02841
C. Anastasiou, L.J. Dixon, K. Melnikov, F. Petriello, High precision QCD at hadron colliders: Electroweak gauge boson rapidity distributions at NNLO. Phys. Rev. D 69, 094008 (2004). arxiv:hep-ph/0312266
C. Anastasiou, L.J. Dixon, K. Melnikov, F. Petriello, Dilepton rapidity distribution in the Drell-Yan process at NNLO in QCD. Phys. Rev. Lett. 91, 182002 (2003). arXiv:hep-ph/0306192
K. Melnikov, F. Petriello, Electroweak gauge boson production at hadron colliders through O(alpha(s)**2). Phys. Rev. D 74, 114017 (2006). arXiv:hep-ph/0609070
S. Catani, L. Cieri, G. Ferrera, D. de Florian, M. Grazzini, Vector boson production at hadron colliders: a fully exclusive QCD calculation at NNLO. Phys. Rev. Lett. 103, 082001 (2009). arXiv:0903.2120
R. Gavin, Y. Li, F. Petriello, S. Quackenbush, FEWZ 2.0: A code for hadronic Z production at next-to-next-to-leading order. Comput. Phys. Commun. 182, 2388 (2011). arXiv:1011.3540
M. Grazzini, S. Kallweit, M. Wiesemann, Fully differential NNLO computations with MATRIX. Eur. Phys. J. C 78, 537 (2018). arXiv:1711.06631
T. Gleisberg, S. Höche, F. Krauss, M. Schönherr, S. Schumann, F. Siegert, Event generation with Sherpa 1.1. JHEP 02, 007 (2009). arXiv:0811.4622
S. Höche, Y. Li, S. Prestel, Drell-Yan lepton pair production at NNLO QCD with parton showers. Phys. Rev. D 91, 074015 (2015). arXiv:1405.3607
A. Karlberg, E. Re, G. Zanderighi, NNLOPS accurate Drell–Yan production. JHEP 09, 134 (2014). arXiv:1407.2940
A. Gehrmann-De Ridder, T. Gehrmann, E.W.N. Glover, A. Huss, T.A. Morgan, Precise QCD predictions for the production of a Z boson in association with a hadronic jet. Phys. Rev. Lett. 117, 022001 (2016). arXiv:1507.02850
A. Gehrmann-De Ridder, T. Gehrmann, E.W.N. Glover, A. Huss, T.A. Morgan, The NNLO QCD corrections to Z boson production at large transverse momentum. JHEP 07, 133 (2016). arXiv:1605.04295
A. Gehrmann-De Ridder, T. Gehrmann, E.W.N. Glover, A. Huss, T.A. Morgan, NNLO QCD corrections for Drell-Yan \(p_T^Z\) and \(\phi ^*\) observables at the LHC. JHEP 11, 094 (2016). arXiv:1610.01843
A. Gehrmann-De Ridder, T. Gehrmann, E.W.N. Glover, A. Huss, D.M. Walker, Next-to-Next-to-Leading-Order QCD Corrections to the Transverse Momentum Distribution of Weak Gauge Bosons. Phys. Rev. Lett. 120, 122001 (2018). arXiv:1712.07543
R. Boughezal, J.M. Campbell, R.K. Ellis, C. Focke, W.T. Giele, X. Liu, Z-boson production in association with a jet at next-to-next-to-leading order in perturbative QCD. Phys. Rev. Lett. 116, 152001 (2016). rXiv:1512.01291
R. Boughezal, X. Liu, F. Petriello, Phenomenology of the Z-boson plus jet process at NNLO. Phys. Rev. D 94, 074015 (2016). arXiv:1602.08140
R. Boughezal, C. Focke, X. Liu, F. Petriello, \(W\)-boson production in association with a jet at next-to-next-to-leading order in perturbative QCD. Phys. Rev. Lett. 115, 062002 (2015). arXiv:1504.02131
R. Boughezal, X. Liu, F. Petriello, W-boson plus jet differential distributions at NNLO in QCD. Phys. Rev. D 94, 113009 (2016). arXiv:1602.06965
D. Wackeroth, W. Hollik, Electroweak radiative corrections to resonant charged gauge boson production. Phys. Rev. D 55, 6788 (1997). arXiv:hep-ph/9606398
U. Baur, S. Keller, W.K. Sakumoto, QED radiative corrections to \(Z\) boson production and the forward backward asymmetry at hadron colliders. Phys. Rev. D 57, 199 (1998). arXiv:hep-ph/9707301
U. Baur, S. Keller, D. Wackeroth, Electroweak radiative corrections to \(W\) boson production in hadronic collisions. Phys. Rev. D 59, 013002 (1999). arXiv:hep-ph/9807417
U. Baur, O. Brein, W. Hollik, C. Schappacher, D. Wackeroth, Electroweak radiative corrections to neutral current Drell-Yan processes at hadron colliders. Phys. Rev. D 65, 033007 (2002). arXiv:hep-ph/0108274
U. Baur, D. Wackeroth, Electroweak radiative corrections to \(p \bar{p} \rightarrow W^\pm \rightarrow \ell ^\pm \nu \) beyond the pole approximation. Phys. Rev. D 70, 073015 (2004). arXiv:hep-ph/0405191
A. Andonov, A. Arbuzov, D. Bardin, S. Bondarenko, P. Christova, L. Kalinovskaya, SANCscope - v.1.00. Comput. Phys. Commun. 174, 481 (2006). arXiv:hep-ph/0411186
S. Dittmaier, M. Krämer, Electroweak radiative corrections to W boson production at hadron colliders. Phys. Rev. D 65, 073007 (2002). arXiv:hep-ph/0109062
S. Dittmaier, M. Huber, Radiative corrections to the neutral-current Drell-Yan process in the Standard Model and its minimal supersymmetric extension. JHEP 01, 060 (2010). arXiv:0911.2329
C.M. Carloni Calame, G. Montagna, O. Nicrosini, A. Vicini, Precision electroweak calculation of the charged current Drell–Yan process. JHEP 12, 016 (2006). arXiv:hep-ph/0609170
C.M. Carloni Calame, G. Montagna, O. Nicrosini, A. Vicini, Precision electroweak calculation of the production of a high transverse-momentum lepton pair at hadron colliders. JHEP 10, 109 (2007). arXiv:0710.1722
Y. Li, F. Petriello, Combining QCD and electroweak corrections to dilepton production in FEWZ. Phys. Rev. D 86, 094034 (2012). arXiv:1208.5967
A. Denner, S. Dittmaier, T. Kasprzik, A. Mück, Electroweak corrections to W+jet hadroproduction including leptonic W-boson decays. JHEP 08, 075 (2009). arXiv:0906.1656
A. Denner, S. Dittmaier, T. Kasprzik, A. Mück, Electroweak corrections to dilepton + jet production at hadron colliders. JHEP 06, 069 (2011). arXiv:1103.0914
A. Denner, S. Dittmaier, T. Kasprzik, A. Mück, Electroweak corrections to monojet production at the LHC. Eur. Phys. J. C 73, 2297 (2013). arXiv:1211.5078
S. Kallweit, J.M. Lindert, P. Maierhöfer, S. Pozzorini, M. Schönherr, NLO QCD+EW predictions for V + jets including off-shell vector-boson decays and multijet merging. JHEP 04, 021 (2016). arXiv:1511.08692
S. Alioli, P. Nason, C. Oleari, E. Re, NLO vector-boson production matched with shower in POWHEG. JHEP 07, 060 (2008). arXiv:0805.4802
C. Bernaciak, D. Wackeroth, Combining NLO QCD and electroweak radiative corrections to W boson production at hadron colliders in the POWHEG framework. Phys. Rev. D 85, 093003 (2012). arXiv:1201.4804
L. Barze, G. Montagna, P. Nason, O. Nicrosini, F. Piccinini, Implementation of electroweak corrections in the POWHEG BOX: single W production. JHEP 04, 037 (2012). arXiv:1202.0465
L. Barze, G. Montagna, P. Nason, O. Nicrosini, F. Piccinini, A. Vicini, Neutral current Drell-Yan with combined QCD and electroweak corrections in the POWHEG BOX. Eur. Phys. J. C 73, 2474 (2013). arXiv:1302.4606
A. Mück, L. Oymanns, Resonace-improved parton-shower matching for the Drell-Yan process including electroweak corrections. JHEP 05, 090 (2017). arXiv:1612.04292
R. Bonciani, F. Buccioni, R. Mondini, A. Vicini, Double-real corrections at \(\cal{O}(\alpha \alpha _s)\) to single gauge boson production. Eur. Phys. J. C 77, 187 (2017). arXiv:1611.00645
R. Bonciani, S. Di Vita, P. Mastrolia, U. Schubert, Two-Loop Master Integrals for the mixed EW-QCD virtual corrections to Drell–Yan scattering. JHEP 09, 091 (2016). arXiv:1604.08581
A. von Manteuffel, R.M. Schabinger, Numerical Multi-Loop Calculations via Finite Integrals and One-Mass EW-QCD Drell–Yan Master Integrals. JHEP 04, 129 (2017). arXiv:1701.06583
D. de Florian, M. Der, I. Fabre, QCD\(\oplus \)QED NNLO corrections to Drell Yan production. arXiv:1805.12214
S. Dittmaier, A. Huss, C. Schwinn, Mixed QCD-electroweak \(O(\alpha _s\alpha )\) corrections to Drell-Yan processes in the resonance region: pole approximation and non-factorizable corrections. Nucl. Phys. B 885, 318 (2014). arXiv:1403.3216
S. Dittmaier, A. Huss, C. Schwinn, Dominant mixed QCD-electroweak O(\(\alpha _s \alpha \)) corrections to Drell–Yan processes in the resonance region. Nucl. Phys. B 904, 216 (2016). arXiv:1511.08016
C. Carloni Calame, G. Montagna, O. Nicrosini, M. Treccani, Higher order QED corrections to W boson mass determination at hadron colliders. Phys. Rev. D69, 037301 (2004). arXiv:hep-ph/0303102
C.M. Carloni Calame, G. Montagna, O. Nicrosini, M. Treccani, Multiple photon corrections to the neutral-current Drell–Yan process. JHEP 05, 019 (2005). arXiv:hep-ph/0502218
E. Barberio, Z. Wa̧s, PHOTOS—a universal monte carlo for QED radiative corrections: version 2.0. Comput. Phys. Commun. 79, 291 (1994)
W. Placzek, S. Jadach, Multiphoton radiation in leptonic W boson decays. Eur. Phys. J. C 29, 325 (2003). arXiv:hep-ph/0302065
K. Hamilton, P. Richardson, Simulation of QED radiation in particle decays using the YFS formalism. JHEP 07, 010 (2006). arXiv:hep-ph/0603034
M. Schönherr, F. Krauss, Soft photon radiation in particle decays in sherpa. JHEP 12, 018 (2008). arXiv:0810.5071
D.R. Yennie, S.C. Frautschi, H. Suura, The infrared divergence phenomena and high-energy processes. Ann. Phys. 13, 379 (1961)
S. Dittmaier, A general approach to photon radiation off fermions. Nucl. Phys. B 565, 69 (2000). arXiv:hep-ph/9904440
M. Schönherr, An automated subtraction of NLO EW infrared divergences. arXiv:1712.07975
F.U. Bernlochner, M. Schönherr, Comparing different ansatzes to describe electroweak radiative corrections to exclusive semileptonic B meson decays into (pseudo)scalar final state mesons using Monte-Carlo techniques. arXiv:1010.5997
A. Denner, Techniques for calculation of electroweak radiative corrections at the one loop level and results for W physics at LEP-200. Fortsch. Phys. 41, 307 (1993). arXiv:0709.1075
D. Yu. Bardin, G. Passarino, The Standard Model in the Making: Precision Study of the Electroweak Interactions (Clarendon, Oxford, 1999)
F.A. Berends, W.L. van Neerven, G.J.H. Burgers, Higher order radiative corrections at LEP energies. Nucl. Phys. B 297, 429 (1988)
T. Kinoshita, Mass singularities of Feynman amplitudes. J. Math. Phys. 3, 650 (1962)
T. Lee, M. Nauenberg, Degenerate systems and mass singularities. Phys. Rev. 133, B1549 (1964)
W.F.L. Hollik, Radiative corrections in the standard model and their role for precision tests of the electroweak theory. Fortsch. Phys. 38, 165 (1990)
R. Mertig, M. Bohm, A. Denner, FEYN CALC: computer algebraic calculation of Feynman amplitudes. Comput. Phys. Commun. 64, 345 (1991)
V. Shtabovenko, R. Mertig, F. Orellana, New developments in FeynCalc 9.0. Comput. Phys. Commun. 207, 432 (2016). arXiv:1601.01167
T. Hahn, M. Perez-Victoria, Automatized one loop calculations in four-dimensions and D-dimensions. Comput. Phys. Commun. 118, 153 (1999). arXiv:hep-ph/9807565
H.H. Patel, Package-X: A Mathematica package for the analytic calculation of one-loop integrals. Comput. Phys. Commun. 197, 276 (2015). arXiv:1503.01469
M. Chiesa, N. Greiner, F. Tramontano, Automation of electroweak corrections for LHC processes. J. Phys. G43, 013002 (2016). arXiv:1507.08579
M. Chiesa, N. Greiner, M. Schnherr, F. Tramontano, Electroweak corrections to diphoton plus jets. JHEP 10, 181 (2017). arXiv:1706.09022
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer, The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP 07, 079 (2014). arXiv:1405.0301
R. Frederix, S. Frixione, V. Hirschi, D. Pagani, H.S. Shao, M. Zaro, The automation of next-to-leading order electroweak calculations. JHEP 07, 185 (2018). arXiv:1804.10017
F. Cascioli, P. Maierhöfer, S. Pozzorini, Scattering amplitudes with open loops. Phys. Rev. Lett. 108, 111601 (2012). arXiv:1111.5206
S. Kallweit, J. M. Lindert, P. Maierhöfer, S. Pozzorini, M. Schönherr, NLO electroweak automation and precise predictions for W+multijet production at the LHC. arXiv:1412.5157
S. Actis, A. Denner, L. Hofer, A. Scharf, S. Uccirati, Recursive generation of one-loop amplitudes in the standard model. JHEP 1304, 037 (2013). arXiv:1211.6316
S. Actis, A. Denner, L. Hofer, J.-N. Lang, A. Scharf, S. Uccirati, RECOLA: REcursive computation of one-loop amplitudes. Comput. Phys. Commun. 214, 140 (2017). arXiv:1605.01090
I. Dubovyk, A. Freitas, J. Gluza, T. Riemann, J. Usovitsch, The two-loop electroweak bosonic corrections to \(\sin ^2\theta ^{\rm b}_{\rm eff}\). Phys. Lett. B 762, 184 (2016). arXiv:1607.08375
I. Dubovyk, A. Freitas, J. Gluza, T. Riemann, J. Usovitsch, Complete electroweak two-loop corrections to Z boson production and decay. Phys. Lett. B 783, 86 (2018). arXiv:1804.10236
A. Denner, S. Dittmaier, Reduction of one loop tensor five point integrals. Nucl. Phys. B 658, 175 (2003). arXiv:hep-ph/0212259
A. Denner, S. Dittmaier, Reduction schemes for one-loop tensor integrals. Nucl. Phys. B 734, 62 (2006). arXiv:hep-ph/0509141
A. Denner, S. Dittmaier, Scalar one-loop 4-point integrals. Nucl. Phys. B 844, 199 (2011). arXiv:1005.2076
A. Denner, S. Dittmaier, L. Hofer, Collier: a fortran-based complex one-loop library in extended regularizations. Comput. Phys. Commun. 212, 220 (2017). arXiv:1604.06792
S. Carrazza, R.K. Ellis, G. Zanderighi, QCDLoop: a comprehensive framework for one-loop scalar integrals. Comput. Phys. Commun. 209, 134 (2016). arXiv:1605.03181
R. Kleiss, W.J. Stirling, Spinor techniques for calculating p anti-p - W+- / Z0 + Jets. Nucl. Phys. B 262, 235 (1985)
A. Ballestrero, E. Maina, S. Moretti, Heavy quarks and leptons at \(e^+e^-\) colliders. Nucl. Phys. B 415, 265 (1994). arXiv:hep-ph/9212246
A. Ballestrero, E. Maina, A new method for helicity calculations. Phys. Lett. B 350, 225 (1995). arXiv:hep-ph/9403244
F. Krauss, R. Kuhn, G. Soff, AMEGIC++ 1.0: a matrix element generator in C++. JHEP 02, 044 (2002). arXiv:hep-ph/0109036
T. Gleisberg, S. Höche, Comix, a new matrix element generator. JHEP 12, 039 (2008). arXiv:0808.3674
G.J.H. Burgers, On the two loop QED vertex correction in the high-energy limit. Phys. Lett. 164B, 167 (1985)
R. Bonciani, P. Mastrolia, E. Remiddi, QED vertex form-factors at two loops. Nucl. Phys. B 676, 399 (2004). arXiv:hep-ph/0307295
W. Bernreuther, R. Bonciani, T. Gehrmann, R. Heinesch, T. Leineweber, P. Mastrolia, Two-loop QCD corrections to the heavy quark form-factors: the vector contributions. Nucl. Phys. B 706, 245 (2005). arXiv:hep-ph/0406046
W. Bernreuther, R. Bonciani, T. Gehrmann, R. Heinesch, T. Leineweber, P. Mastrolia, Two-loop QCD corrections to the heavy quark form-factors: axial vector contributions. Nucl. Phys. B 712, 229 (2005). arXiv:hep-ph/0412259
W. Bernreuther, R. Bonciani, T. Gehrmann, R. Heinesch, T. Leineweber, E. Remiddi, Two-loop QCD corrections to the heavy quark form-factors: anomaly contributions. Nucl. Phys. B 723, 91 (2005). arXiv:hep-ph/0504190
W. Bernreuther, R. Bonciani, T. Gehrmann, R. Heinesch, P. Mastrolia, E. Remiddi, Decays of scalar and pseudoscalar Higgs bosons into fermions: two-loop QCD corrections to the Higgs-quark-antiquark amplitude. Phys. Rev. D 72, 096002 (2005). arXiv:hep-ph/0508254
J. Ablinger, A. Behring, J. Blümlein, G. Falcioni, A. De Freitas, P. Marquard, Heavy quark form factors at two loops. Phys. Rev. D 97, 094022 (2018). arXiv:1712.09889
R.K. Ellis, G. Zanderighi, Scalar one-loop integrals for QCD. JHEP 0802, 002 (2008). arXiv:0712.1851
H. Frellesvig, D. Tommasini, C. Wever, On the reduction of generalized polylogarithms to \(\text{ Li }_n\) and \(\text{ Li }_{2,2}\) and on the evaluation thereof. JHEP 03, 189 (2016). arXiv:1601.02649
A. Buckley, J. Butterworth, L. Lönnblad, D. Grellscheid, H. Hoeth, Rivet user manual. Comput. Phys. Commun. 184, 2803 (2013). arXiv:1003.0694
A. Banfi, S. Redford, M. Vesterinen, P. Waller, T.R. Wyatt, Optimisation of variables for studying dilepton transverse momentum distributions at hadron colliders. Eur. Phys. J. C 71, 1600 (2011). arXiv:1009.1580
S. Kallweit, J.M. Lindert, S. Pozzorini, M. Schönherr, NLO QCD+EW predictions for \(2\ell 2\nu \) diboson signatures at the LHC. JHEP 11, 120 (2017). arXiv:1705.00598
G. Passarino, M.J.G. Veltman, One loop corrections for e+ e- annihilation Into mu+ mu- in the Weinberg model. Nucl. Phys. B 160, 151 (1979)
Acknowledgements
We would like to thank our colleagues from the Sherpa and OpenLoops collaborations for discussions. We are indebted to D. Wackeroth and A. Vicini for support with Wzgrad and for clarification of sometimes subtle issues in the calculational framework. This work was financially supported by the European Commission under Grant Agreements PITN-GA-2012-315877 (MCnet) and PITN-GA-2012-316704 (HiggsTools), and by the ERC Advanced Grant 340983 (MC@NNLO).
Author information
Authors and Affiliations
Corresponding author
Appendices
Momentum mappings
For the purposes of event generation, we need to define the momenta that are used in the master formula Eq. (2.13). We will refer to the momenta used in the leading order matrix element, \(\tilde{\beta }_0^0\), as the “undressed” momenta, i.e. the momenta before the event is dressed with photons. The undressed momenta are labelled through \(q_i^{\mu }\), and we define as
the sums of the final state neutral and charged momenta. After the generation of the additional photon momenta, the undressed momenta have to be mapped to a set of “dressed” momenta to account for momentum conservation. The dressed momenta are labelled through \(p_i^{\mu }\) and we define the sums of the neutral and charged final state particles in the same way as for the undressed momenta:
In a similar manner, we define the sum of the photon momenta as
The mappings relevant for particle decays of both uncharged and charged initial particles have been outlined in section 3.3 of [57], but we will repeat them here for the benefit of the interested reader. The only condition the mapping has to meet is that in the limit of \(K\rightarrow 0\), the underlying momenta of the undressed n-parton phase space have to be recovered exactly. QED provides no guiding principle which particle should be taken to balance the momenta of the generated photons. It is therefore sensible to treat all the final state momenta fully democratically and let them all take the recoil. Considering all particles in the rest frame of the multipole responsible for the radiation, this can be achieved by scaling the three-momenta of all final state particles by a common factor u, distributing the photon momenta across, and finally enforcing momentum conservation and on-shell conditions.
1.1 Neutral initial states
For a neutral particle of mass m decaying into charged particles, such as is the case of a Z- or a Higgs-boson, the above procedure fixes the mapping to a rescaling of all final state momenta, balancing the photonic momentum by moving the frame of the multipole.
We start with the undressed momenta in the multipole rest frame
The outlined procedure maps these momenta onto the final state momenta \(P_C\) and \(P_N\):
We can rewrite the three momentum of the initial state as \(u\vec {Q}_N+\vec {K} = u\vec {q}+\vec {K}\) showing that the two vectors q and \(q'\) are the same vector in different frames. All momenta now reside in the rest frame of the dressed multipole. We can then determine the scaling parameter u from energy conservation:
1.2 Charged initial states
For a charged particle of mass m decaying into a charged particle and a number of neutral particles, such as is the case of a W-boson, we require a different approach. In order to remain in the rest frame of the dressed multipole, we cannot accomodate the photon momenta purely in the initial state.
Again, we start with the undressed momenta in the multipole rest frame:
In the most democratic approach, the photon momenta are accomodated equally by all particles in the final state and the undressed momenta will be mapped onto:
All momenta now reside in the rest frame of the dressed multipole. The \(n_C\) and \(n_N\) denote the number of charged and neutral final state particles, and \(\vec {\kappa }\) is defined as:
One can however also choose to let only the charged particles or only the neutral particles in the process accomodate the photon momenta, in which case \(\vec {\kappa } = \vec {K}/(2n_C)\) or \(\vec {\kappa } = \vec {K}/(n_N)\), respectively, and corresponding terms in the mapping vanish. The default option in Photons, and the one that we employ for the results presented this paper, is the choice of letting only the neutral particles take the recoil.
Again, the scaling parameter u can be determined from energy conservation:
1.3 Momenta in higher order corrections
Having discussed the momentum mappings necessary to map from undressed to dressed momenta, it is worth briefly discussing which set of momenta is to be used in each component of Eq. (2.13).
Every part of this formula apart from the correction factor, \(\mathcal {C}\), is calculated using the undressed momenta \(q_i\), with the Jacobean \(\mathcal {J}\) accounting for the mapping from undressed to dressed momenta. This in particular includes the factors \(\tilde{S}\) that implement the soft approximation to the real matrix elements.
The correction factor \(\mathcal {C}\) amounts to a reweighting of the YFS approximation to the required perturbative order. Practically, for the real matrix element corrections, the eikonal factors \(\tilde{S}\) have to be cancelled out. Thus, the eikonals in the denominators in Eq. (2.18) have to be calculated using the undressed momenta.
All matrix elements containing no additional photon, \(\tilde{\beta }_0^i\), are calculated in the n-particle Born phase space, i.e. using the undressed momenta. The terms describing real matrix element corrections are then calculated in the phase space appropriate to the number of photons they contain: In the \(n+1\)-particle phase space for the single real matrix elements \(\tilde{\beta }_1^i\), in an \(n+2\)-particle phase space for double real matrix elements, \(\tilde{\beta }_2^i\), and so on. In order to define the momenta in these phase spaces, we repeat the mapping procedure described previously, but now only taking into account the photons that are taken to be hard in the matrix element correction. This procedure is repeated for every photon or set of photons that have been created. For the single real matrix elements, this means there are in total \(n_{\gamma }\) calls to the mapping and the matrix elements, while for the double real matrix elements, there are \(n_{\gamma }(n_{\gamma }-1)/2\) calls to the mapping and the matrix element.
NLO EW form factors and counterterms
For completeness in this section we collect the electroweak vertex form factors and counterterms required for setting up the NLO electroweak corrections to \(\tilde{\beta }_0^1\). We use the vertex form factors found in [63] and the counterterms in the on-shell renormalization scheme from [62]. The vertex form factors retain the full dependence on the lepton masses only in the QED corrections, while the purely weak contributions are calculated in the massless limit. In order to find the pure NLO QED corrections, out of the form factors we need to only include the QED form factors. In the counterterms, we only need to include the photonic corrections to the wavefunction renormalization. The tree-level couplings are formally purely weak couplings and do not need to be renormalized in this case. This procedure amounts to the full separation of the U(1)- from the SU(2)-theory. Such a procedure is only possible for the decays of electroweak particles that do not couple to the photon, in our case the Z- and Higgs bosons. For the charged W-boson, such a separation does not yield a gauge-invariant subset of contributions and we can only calculate matrix elements in the full electroweak theory. Here we note, that shifts due to a different metric signature in Sherpa and [62] versus [63] have been considered. All results presented here are in Feynman gauge. We call the left- and right-handed tree-level couplings \(c_L\) and \(c_R\) and introduce \(g_L = c_L \frac{s_Wc_W}{ie}\), \(g_R = c_R \frac{s_Wc_W}{ie}\) for convenience. We further use the vector coupling \(v_f = (g_L+g_R)\) and the axial coupling \(a_f = (g_L-g_R)\). Any quantity denoted as \(x_{f'}\) refers to the iso-spin partner of the fermion f.
1.1 \(Z\rightarrow f\bar{f}\)
The QED corrections to this vertex are given by:
In the massless limit, only the structure proportional to \(\gamma _{\mu }\left( c_L P_L+c_RP_R\right) \) contributes. The form factor \(F_{Aa}(s)\) is given by:
The other form factors are all proportional to the fermion mass and read
The effect of abelian Z- and \(\phi ^0\)-exchanges is given by:
where
For the diagrams involving W bosons (and the associated ghosts), we introduce:
The effect of abelian W- and \(\phi \)-exchanges, i. e. all diagrams not involving a three-boson vertex, is described by:
Note that this is purely a contribution to the left-handed part of the amplitude. The necessary auxilliary functions are given by:
The effect of non-abelian W- and \(\phi \)-exchanges, i.e. all the diagrams containing a three-boson vertex, is described by:
Note that this is again purely a contribution to the left-handed part of the amplitude. The necessary auxilliary functions are given by:
The counterterms for this vertex read:
where the left- and right-handed, tree-level couplings \(c_R\), \(c_L\) and their counterterms \(\delta c_R\), \(\delta c_L\) are given by:
1.2 \(W^-\rightarrow \ell ^-\bar{\nu }_\ell \) and \(W^+\rightarrow \nu _\ell \bar{\ell }^+\)
The decay of W-bosons will only be applied to \(\ell \nu \) final states within the YFS framework, whereas \(q\bar{q}'\) final states will be treated within the parton shower to allow for consistent matching with the dominant QCD corrections. In the case of \(\ell \nu \) final states, there is no diagram for photon exchange between the final state particles. All the corrections to this decay are purely corrections to the left-handed coupling (since fermion masses are neglected in these subamplitudes). The effect of non-abelian photon exchange is given by:
The form factor is given by:
The effect of abelian Z-exchange is described by:
with the function \(F_{Za}(s)\) as in the decay \(Z\rightarrow f\bar{f}\) (Eq. (B.7)).
The effect of non-abelian Z-exchange is given by:
The form factor reads:
The counterterms for this process read:
Here, the conjugated wavefunction counterterm is chosen for the antiparticle, with the usual unchanged counterterm chosen for the particle in the process. The tree level couplings are:
1.3 \(H\rightarrow f\bar{f}\)
The vertex corrections to the Higgs decay into fermions are more complex than the previously considered examples as all masses have to be retained. The amplitude will only be used for \(H\rightarrow \ell ^+\ell ^-\)-decays, while the colourful decays are treated via the parton shower.
The QED corrections to this vertex read:
The QED form factor is given by:
The complete weak result reads:
The form factor reads:
The coefficients are given by the following expressions:
where we used the following shorthands:
Note that the corrections as written do not completely agree with Eqs. (5.546)–(5.548) of [63]. Ref. [63] provides expressions both with all masses included in Eqs. (5.546)-(5.548), and with terms \(\sim m_f^2\) neglected in Eqs. (5.619), (5.621), (5.625). This is an appropriate approximation for the decay \(H\rightarrow b\bar{b}\) for which \(m_f = m_b\), \(m_{f'} = m_t\) and \(m_b \ll m_t\). For our purposes, we require the exact opposite case, with \(m_f = m_\ell \), \(m_{f'} = 0\). Nonetheless, the two forms can be used to cross-check terms. In comparison to the expressions including the full mass dependence, there is a factor of 2 in the overall vertex in the approximated form. The latter form appears to be correct as it reproduces the correct divergences. Secondly, the coefficients \(f_2\) and \(f_6\) differ. In \(f_6\), the last term should read \(\frac{1}{2c_W^2}\) instead of \(\frac{2}{c_W^2}\) in agreement with the limiting expression in Eq. (5.623). Similarly, \(f_2\) has been adapted to match the limiting expression. In particular, the second to last term is multiplied by a factor of \(\frac{4}{c_W^2}\), and the last term by \(w_f\). The second to last term can then be cast into a form \(\sim \sigma ^{(2)}\) as in Eq. (5.623) by adding and subtracting \(a_f^2\). Performing these changes we find perfect agreement with OpenLoops.
Infrared form factors
To complete the calculation of the infrared subtracted matrix elements, we need the expression of the infrared factor \(B_{ij}\). This factor, and its real counterpart \(\tilde{B}_{ij}(\Omega )\) are defined in Eqs. (2.15) and (2.16) respectively, have been calculated in [57], where it has also been shown that their sum leads to a finite result as expected from the Kinoshita-Lee-Nauenberg theorem. In that calculation, the expressions were split up to give a number of separate integrals which were calculated. Here, we are going to use a different approach to also match more closely with the way the vertex form factors are expressed. We will thus express the factor in terms of scalar master integrals.
The virtual infrared form factor B can be rewritten in the following form, which will be more useful in expressing it in terms of master integrals:
The prefactor depends on whether the particles i and j are in the initial or final state. For the purpose of this publication, we have to consider final-final and initial-final dipole combinations. In both cases, the factor \(Z_i Z_j \theta _i \theta _j = -1\) so that the prefactor before the integral becomes \(\frac{i}{8\pi ^3}\). Note that the \(p_i\) used are the momenta of the external particles. To translate these into the momenta \(q_i\) running in the loop, we use \(p_1 = q_1\), \(p_2 = -q_2\) for the final state particles and \(p_3 = -p_1-p_2 = (q_2-q_1)\) for the initial state particle.
In the following we list the explicit expressions for the form factors in terms of standard scalar integrals [104].
1.1 Final-final
For the double virtual corrections in the decay of the Z-boson in Sect. 2.4.1, we need the infrared factor B in the limit of \(s \gg m_i^2\), regulated with a small photon mass \(\lambda \). In this case, we have \(m_1 = m_2 \equiv m\) and the factor reads:
1.2 Initial-final
Real corrections
We will describe here the way we implement the real corrections. We will describe the procedure for the decays of the vector bosons and define the shorthand \(\Gamma ^{\mu } \equiv \gamma ^{\mu }\left( c_LP_L+c_RP_R\right) \), with the couplings \(c_{L/R}\) given in Appendix B. For the decays of a scalar boson, this reduces instead to \(\Gamma = \left( c_LP_L+c_RP_R\right) \) and we remove the polarization vector of the decaying vector boson.
The real matrix element for the process \(Z\rightarrow f\bar{f}\gamma \) reads:

We can express the fermion propagator as a sum over spins of an intermediate particle:

where u[v](p, s) are [anti-]spinors of a fictitious fermion with mass \(m = \sqrt{p^2}\).
In the following, we will make use of a function called X, which is defined as:

where the u may be particle or anti-particle spinors. The latter case will be denoted through a bar over the spin index \(s_i\). Similarly, we can define another function Y:
which would be used in the decay of a Higgs boson, when there is no structure \(\Gamma ^{\mu }\) in the real matrix element. The calculation of these functions has been outlined in [57, 90], and are based on the work in [87,88,89].
Using these functions, we can write the full amplitude as:
with
For the double real matrix elements, to reduce the size of the expressions, we only write the spin labels, the intermediate momenta and the respective internal vector, so that \(X(p_i,s_i;\epsilon _j;p_k,s_k;c_{L'},c_{R'}) \equiv X(\{p_i,\}s_i,\epsilon _j,\{p_k,\}s_k)\). For the external leptons, it is understood that the spin label \(s_i\), \(i\in \{1,2\}\), corresponds to the momentum \(p_i\) and we leave the momentum out. It is further understood, that the left- and right-handed couplings are 1, 1 when contracted with a photon polarization and \(c_L,c_R\) when contracted with the Z-polarization.
For the process \(Z\rightarrow f\bar{f}\gamma \gamma \), the matrix element reads:

We can repeat the procedure used for the single real matrix element, replacing each propagator by a spin sum, ending with a large expression which we will not reproduce here.
For the decay of a W boson, we have the following real matrix element:

where we introduced the triple boson vertex \(V_{\tau \rho \nu } = g_{\tau \rho }\left( p_2-p_1\right) _{\nu } + g_{\rho \nu }\left( p_3-p_2\right) _{\tau } + g_{\nu \tau }\left( p_1-p_3\right) _{\rho }\). The first term in this matrix element can be treated like the terms in the process \(Z\rightarrow f\bar{f}\gamma \). For the second term, we first contract the triple boson vertex, the W-propagator and the polarization vectors. What remains is a structure as in the definition of the X-function, so we can directly write down the result.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Krauss, F., Lindert, J.M., Linten, R. et al. Accurate simulation of W, Z, and Higgs boson decays in Sherpa. Eur. Phys. J. C 79, 143 (2019). https://doi.org/10.1140/epjc/s10052-019-6614-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-6614-x