Charged anisotropic strange stars in general relativity

Abstract

The present paper provides a new exact and analytic solution of the Einstein–Maxwell field equations describing compact anisotropic charged stars satisfying the MIT bag model equation of state for quark matter. The model is obtained by assuming the Tolman–Kuchowicz spacetime geometry (Tolman, in Phys Rev 55:364, 1939; Kuchowicz, in Acta Phys Pol 33:541, 1968). Our stellar model is free from central singularity and obeys all the conditions for a realistic stellar object. The solution is smoothly matched with the exterior Reissner–Nordstrom spacetime in order to obtain the physical parameters of the system. An interesting phenomenon which arises in this model is the fact that the force due to the pressure anisotropy initially dominates the Coulomb repulsive force, nevertheless as the radius increases the electric force dominates the anisotropic one. This may be an additional mechanism required for stability and equilibrium against the gravitational collapse of the stellar object. Detailed analyses of the obtained model are also given with the help of graphical representations.

1 Introduction

At present, it remain a great challenge to obtain analytic solutions to Einstein field equations describing compact configurations e.g neutron stars, strange stars, white dwarfs and black holes, all of them representing the final stages of a star’s evolution. However, last decades the theoretical studies modeling these kind of objects have improved considerably. Specifically the development of fluid sphere models containing anisotropic matter distributions i.e. unequal radial and tangential pressure: $p_{r}\ne p_{t}$. Of course, from the astrophysical point of view it represents a more realistic and intriguing scenario. The pioneering work by Bowers and Liang [3] about anisotropic spheres with uniform energy density suggested that anisotropy could also play an important role in describing the high redshift objects like quasars and could has a significantly affect on the physical parameters like maximum compactness, mass and radius of star. Later on it was shown that the inclusion of anisotropies within the stellar configuration play an important role in the stability and equilibrium. Heintzmann and Hillebrandt [4] studied fully relativistic anisotropic neutron star models at high densities and have shown that for arbitrary large anisotropy there is no limiting mass for neutron star. Moreover, Herrera and Santos [5] studied local anisotropy in self-gravitating systems supposing that an anisotropic model can be stable. On the other hand the studies by Gokhroo and Mehra [6] suggested that stability is improved for a positive anisotropy factor i.e. ${\varDelta }\equiv p_{t}-p_{r}>0$, in distinction with the isotropic case, allowing it the construction of more massive and compact objects. Another way to enhance the stability of the system was analyzed by K. Dev and M. Gleiser submitting the object under small radial adiabatic oscillation when anisotropy is present [7], also they explain that for many compact stars with surface redshift $Z_{s}>2$ can be described by assuming anisotropic matter distributions at the interior [8]. There is an abundant literature devoted to the study of the effect of local anisotropy on the global properties of relativistic compact objects [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72] (and references contained therein).

Bonnor’s [73] investigations on charged isotropic solutions and subsequent studies by Ivanov [74] showed that singularities can be avoided during the gravitational collapse, consequently the presence of a net electric charge improves the balance and stability of the system. It is worth mentioning that some solutions which do not meet the admissibility physical criteria become relevant after the inclusion of charge in them [75, 76]. Over the years several works available in the literature have been addressed the study of models including both anisotropy and electric charge [77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92]. In fact, as was pointed out early the presence of anisotropy and electric charge improve the stability and equilibrium of the configuration. The first one introduces a repulsive force (in the case ${\varDelta }> 0$) that counteracts the gravitational gradient, while the second one does it due to the Coulomb force.

On the other hand, as mentioned earlier, it is not an easy task to solve Einstein’s equations analytically. In the case of isotropic uncharged fluid solutions, one has four unknown functions i.e. $\{\rho ,p,e^{\nu },e^{\lambda }\}$ and in the case of anisotropic uncharged solutions one has five unknown functions that is $\{\rho ,p_{r},p_{t}, e^{\nu },e^{\lambda }\}$ and three equations. However, in the case of Einstein–Maxwell equations one has six unknown functions i.e. $\{\rho ,p_{r},p_{t},e^{\nu },e^{\lambda },E\}$ and four equations. Therefore, in order to solve this system it is necessary to give additional information. For example, assume a suitable form for the metric potentials and impose an adequate equation of state (EoS) e.g. $p_{r}=f(\rho )$. Within this framework several authors have been considered the well known linear equation of state based on the MIT bag model [6, 14, 36, 44, 79,80,81,82,83, 85, 92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128]. From the theoretical point of view, the quark matter hypothesis put forward by Witten [129], has driven the study of an entirely new class of compact astrophysical objects composed of strange quark matter called strange stars. According to Alford [130], in the dense core of a neutron star there is sufficiently high density and corresponding low temperature to crush the hadrons into quark matter. In the MIT bag model [131] for strange stars, the quark confinement has been assumed to be caused by a universal pressure $B_{g}$, called the bag constant. The studies by Farhi and Jafee [132] and Alcock et al [133] had shown that for a stable strange quark matter the value of the bag constant should be $B_{g}\sim$55–75 MeV/fm$^{3}$. Besides the studies by Chamel et al. [134] on nucleonic EOSs BSk 19, BSk 20 and BSk 21, used the values of effective bag constant to be 78.6, 65.5 and 56.7 Mev/fm$^{3}$, respectively. However, the datasets of CERN-SPS and RHIC22 [135] show that a wide range of bag constant are permissible.

Following the above spirit the main motivation of this article is to develop some new analytical relativistic stellar models by obtaining closed-form solutions of Einstein–Maxwell field equations. So, the outline of this work is: Sect. 2 presents the Einstein–Maxwell equations for anisotropic fluid spheres, regarding the MIT bag model EoS, Sect. 3 is devoted to the physical and mathematical analysis on the constant parameters in order to obtain a well behaved solution. In Sect. 4 we match the solution with the Reissner–Nordstrom spacetime, Sect. 5 we study the equilibrium, stability and energy conditions. Finally, Sect. 6 concludes the work.

2 The Einstein–Maxwell field equations

We begin with the space–time describing the interior of a spherically symmetric star with zero angular momentum in the form:

$$\begin{aligned} ds^{2}=e^{\nu (r)}dt^{2}-e^{\lambda (r)}dr^{2}-r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2} \right) , \end{aligned}$$

(1)

where

$$\begin{aligned} \lambda (r)=\ln (1+a\,r^2+b\,r^4), \quad \text{ and } \quad \nu =2h\,r^2+lnC, \end{aligned}$$

(2)

being a, b, h and C constants parameters and the above metric potentials describe as a Tolman–Kuchowicz (TK) metric [1, 2, 67]. However, these constants will be fixed by physical requirements of the solution.

The Einstein–Maxwell equations for a static charged fluid can be given in terms of density $\rho (r)$, radial pressure $p_r$, tangential pressure $p_t$, electric field E(r) and proper charge density $\sigma (r)$ as,

$$\begin{aligned} 8\pi \,p_r-E^2= & {} -\frac{1}{r^2}+e^{-\lambda }\,\left[ \frac{1}{r^2}+\frac{\nu '}{r}\right] , \end{aligned}$$

(3)

$$\begin{aligned} 8\pi \,p_t+E^2= & {} \frac{e^{-\lambda }}{4}\,\left[ 2\nu ''+\nu '^2-\lambda '\,\nu '+\frac{2(\nu '-\lambda ')}{r}\right] \end{aligned}$$

(4)

$$\begin{aligned} 8\pi \,\rho +E^2= & {} \frac{1}{r^2}-e^{-\lambda }\,\left[ \frac{1}{r^2}-\frac{\lambda '}{r}\right] , \end{aligned}$$

(5)

$$\begin{aligned} E(r)= & {} \frac{1}{r^2}\,\int _0^r\,{4\,\pi \,r^2\,\sigma \,e^{\lambda /2}}=\frac{q(r)}{r^2} \end{aligned}$$

(6)

where q(r) is the total charge within a sphere of radius r. To solve the system of equations, we take the following EOS for a strange matter,

$$\begin{aligned} p_r=\frac{1}{3}\,(\rho - 4\,B_g) \end{aligned}$$

(7)

The above EOS represents MIT bag model equation of state where $B_g$ is a Bag constant. To solve the system of equations for above EOS, we have four unknowns namely, $p_r$, $p_t$, $\rho$ and $\sigma$. By substituting the metric potentials $\lambda (r)=\ln (1+a\,r^2+b\,r^4)$ and $\nu =2\,h\,r^2+\ln C$ in Eqs. (3–6), we obtain

$$\begin{aligned}&\rho = \frac{3\,[a^2\,B\, r^4+B\,f^2+4\,(h\,f+b\,r^2)+2\,a\,(1+2\,h\,r^2+B \,r^2\,f)]}{32\,\pi \,(1+a\,r^2+b\,r^4)^2}, \nonumber \\\end{aligned}$$

(8)

$$\begin{aligned}&p_r=\frac{-3\,a^2\,B\, r^4-3\,B\,f^2+4\,(h\,f+b\,r^2)+a\,(2+4\,h\,r^2-6B \,r^2\,f)]}{32\,\pi \,(1+a\,r^2+b\,r^4)^2}, \nonumber \\\end{aligned}$$

(9)

$$\begin{aligned}&p_t=\frac{a^2\,r^2\,(3\,B \, r^2-4)+3\,B\,f^2+2\,a\,[-5+10\,h\,r^2-4\,b\,r^4+{\varPhi }(r)]}{32\,\pi \,(1+a\,r^2+b\,r^4)^2}, \nonumber \\\end{aligned}$$

(10)

$$\begin{aligned}&E^2=\frac{a^2\,r^2\,(4-3\,B\,r^2)-3B\,f^2+4\,[-3\,h\,f+b\,r^2\,(2+b\,r^4)]-E_1(r)}{4\,(1+a\, r^2+b\,r^4)^2}, \nonumber \\\end{aligned}$$

(11)

$$\begin{aligned}&{\varDelta }=\frac{a^2r^2(-2+3\,B\,r^2)+3B\,f^2+a\,[-2-4f+8hr^2(1+hr^2)]+{\varDelta }_1(r)}{16\,\pi \, (1+a r^2+b r^4)^2}.\nonumber \\ \end{aligned}$$

(12)

where,

$$\begin{aligned} f= & {} (1+b\,r^4),~~~~~~~B=\frac{32\,\pi \,B_g}{3} \\ {\varPhi }(r)= & {} 8\,h^2\,r^4+3\,B\,r^2\,f \\&\quad +4[-br^2\,(4+br^4)+h\,(7+3b\,r^4)+4\,h^2r^2\,f], \\ E_1(r)= & {} 2\,a\,(-3+ 6\,h\,r^2-4\,b\,r^4+3\,\beta \,r^2\,f) \\ {\varDelta }_1(r)= & {} 6B\,r^2\,f \\&\quad +2\,[2\,h\,(3 + b r^4)-b\,r^2\,(5 + b\, r^4)+4\,h^2\,r^2\,f] \end{aligned}$$

Moreover, the gradients of density and pressures can be written as,

$$\begin{aligned}&\frac{d\rho }{dr}=-3r\,\nonumber \\&\frac{[a^2\, (1+h r^2)+a (h+3 b r^2+3 b h r^4)-b (1-3 b r^4-2 h r^2\,f)]}{4\,\pi \, (1+a r^2+b r^4)^3} \end{aligned}$$

(13)

$$\begin{aligned}&\frac{dp_r}{dr}=- r\nonumber \\&\frac{[a^2 (1+h\,r^2)+a (h+3 b r^2+3 b h r^4)-b (1-3 b r^4-2 h\, r^2\,f)]}{4\,\pi \, (1+a r^2+b r^4)^3} \end{aligned}$$

(14)

$$\begin{aligned}&\frac{dp_t}{dr}=r\,\nonumber \\&\frac{\left[ 4h^2+a^3 r^2+b^3 r^8-2b (2+11hr^2)+a^2 (1+3f-5 h r^2)+p_{t11}\right] }{4\,\pi \,(1+a r^2+b r^4)^3}\nonumber \\ \end{aligned}$$

(15)

where,

$$\begin{aligned} p_{t11}= & {} b^2\,r^4\,(9 - 6\,h\,r^2 -4\,h^2\,r^4) + a\,[b\,r^2\,(3f+7) \nonumber \\&- 3\,h\,(5\,f-2) +4\,h^2\,r^2\,(1-b\,r^4)] \end{aligned}$$

(16)

3 Bounds on the physical parameters

3.1 Regularity at centre ($r=0$)

One of the most important features in the study of compact configurations in general relativity, correspond to the study of the existence of physical and geometric singularities within the star. To check the presence of singularities, one needs to analyze the behaviour of both metric potentials $e^{\nu (r)}$ and $e^{\lambda (r)}$ at the center $r=0$ and also study the behaviour of the energy density $\rho$, radial $p_{r}$ and tangential $p_{t}$ pressures. For the metric potentials at the center, it is expected: $e^{\lambda (r)}|_{r=0}=1$ ans $e^{\nu (r)}|_{r=0}>0$. So, from Eq. (2) we get

$$\begin{aligned} e^{\lambda (r)}|_{r=0}=(1+ar^{2}+br^{4})|_{r=0}=1, \end{aligned}$$

(17)

$$\begin{aligned} e^{\nu (r)}|_{r=0}=Ce^{2hr^{2}}|_{r=0}=C. \end{aligned}$$

(18)

Of course, Eq. (18) demands $C>0$. Figure 1 shows the monotonically increasing behavior with increasing r for both metric potentials. On the other hand, Eqs. (8), (9) and (10) yield to

$$\begin{aligned} p_r(r)|_{r=0}= & {} \frac{2a - 3B + 4h}{32\pi }, \end{aligned}$$

(19)

$$\begin{aligned} p_t(r)|_{r=0}= & {} \frac{-10 a + 3B + 28 h}{32\pi }, \end{aligned}$$

(20)

$$\begin{aligned} \rho (r)|_{r=0}= & {} \frac{3(2 a +B +4 h)}{32\pi }. \end{aligned}$$

(21)

Besides, the radial and tangential pressures must be equal at the center of the configuration. So, equating (19) and (20) we obtaining the following constrain for the constant B (related with the bag model constant $B_{g}$)

$$\begin{aligned} p_{r}(0)=p_{t}(0)>0 \Rightarrow B=2a-4h. \end{aligned}$$

(22)

Since pressure anisotropy factor ${\varDelta }$ and electric field intensity E must be regular within the star, the above constraint over B ensures,

$$\begin{aligned} {\varDelta }(r)|_{r=0}=0 \quad \text{ and } \quad E(r)|_{r=0}=0. \end{aligned}$$

(23)

On the other hand, for any realistic strange star models the pressure must be positive at centre, then using Eqs. (19) and (22) we get,

$$\begin{aligned} h>\frac{a}{4}. \end{aligned}$$

(24)

Fig. 1

Behavior of gravitational potentials ($e^{\lambda }$ and $e^{\nu }$) versus radial coordinates r / R. For plotting of this figure, the corresponding values of arbitrary constants or parameters are displayed in Table 1

Fig. 2

Behavior of pressures (radial pressure ($p_r$) and tangential pressure ($p_t$)) versus radial coordinates r / R. For plotting of this figure, the corresponding values of arbitrary constants or parameters are displayed in Table 1

Because all the thermodynamic observables must be monotone decreasing functions of the radial coordinate r, we check the second derivative evaluated at the center of the configuration,

$$\begin{aligned} \left( \frac{d^2\rho }{dr^2}\right) |_{r=0}= & {} -2\,\left( \frac{3\,a^2 - 3\,b +3\, a\, h)}{8\,\pi }\right) \end{aligned}$$

(25)

$$\begin{aligned} \left( \frac{d^2p_r}{dr^2}\right) |_{r=0}= & {} -2\,\left( \frac{a^2 - b + a\, h}{8\,\pi }\right) \end{aligned}$$

(26)

$$\begin{aligned} \left( \frac{d^2p_t}{dr^2}\right) |_{r=0}= & {} 2\,\left( \frac{4 \,a^2 - 4 \,b - 9\, a\, h + 4\, h^2}{8\,\pi }\right) , \end{aligned}$$

(27)

which give

$$\begin{aligned} h > \frac{b-a^2}{a} \quad \text{ and } \quad 4a^2-4b-9ah+4h^2 <0. \end{aligned}$$

(28)

Figures 2 and 3 (upper panel) expose the thermodynamic variables within the configuration, that is the radial pressure $p_{r}$, the tangential pressure $p_{t}$ and the density $\rho$, respectively. It can be seen that all of them have their maximum values at the center of the star, are monotone decreasing functions of the radial coordinate, finite and positive definite everywhere inside of the compact object. Moreover, Fig. 3 (lower panel) shows the anisotropy factor behaviour. It is remarkable that the anisotropy factor is ${\varDelta }=0$ at the center of the star which is in complete agreement with the statement $p_{r}(0)=p_{t}(0)$, additionally it is positive in all points inside the star, implying $p_{t}>p_{r}$. This fact, as was pointed out by Gokhroo and Mehra [6] allows the construction of more massive and compact object. Furthermore, a positive anisotropy factor, introduces a repulsive force that counteracts the gravitational gradient.

Fig. 3

Behavior of density ($\rho$) and anisotropy factor (${\varDelta }$) versus radial coordinates r / R. For plotting of this figure, the corresponding values of arbitrary constants or parameters are displayed in Table 1

4 Junction conditions

Besides the above, the charged fluid balls are expected to join smoothly with the Reissner–Nordstrom exterior solution at the pressure free boundary ${\varSigma }$ (defined by $r=R$)

$$\begin{aligned} ds^{2}= & {} \left( 1-\frac{2M}{r}+\frac{q^2}{r^2}\right) \, dt^{2} -\left( 1-\frac{2M}{r}+\frac{q^2}{r^2} \right) ^{-1} dr^{2} \nonumber \\&-r^{2} (d\theta ^{2} +\sin ^{2} \theta \, d\phi ^{2} ) \end{aligned}$$

(29)

where M is a constant representing the total mass of the charged compact star and q is representing the total charge of the ball. For this purpose we employ the Israel–Darmois junction conditions [136, 137]. So, the continuity of $e^{\lambda }$, $e^{\nu }$ and q across the boundary, is known as the first fundamental form $[ds^{2}]_{{\varSigma }}=0$, yielding to

$$\begin{aligned} e^{-\lambda (R)}= & {} 1-\frac{2{M}}{R}+\frac{Q^{2}}{R^{2}} \end{aligned}$$

(30)

$$\begin{aligned} e^{\nu (R)}= & {} 1-\frac{2{M}}{R}+\frac{Q^{2}}{R^{2}} \end{aligned}$$

(31)

$$\begin{aligned} q(R)= & {} Q. \end{aligned}$$

(32)

On the other hand the radial pressure (8) vanishes at the surface star $(r=R)$, consequently

$$\begin{aligned} {p}_{r}|_{r=R}=0. \end{aligned}$$

(33)

The above expression corresponds to the second fundamental form $[G_{\mu \nu }x^{\nu }]_{{\varSigma }}=0$, where $x^{\nu }$ is a unit vector projected in the radial direction. Therefore, we obtain the following expression for the constant h (using $B=2a-4h$)

Table 1 The predicted radius for the strange star of Mass $M=2.1\left( M_\odot \right)$ in Tolman–Kuchowicz space time via. MIT bag equation of state

Table 2 The central density ($\rho _0$), surface density ($\rho _s$), central pressure ($p_0$), surface redshift ($z_s$) and bag constant ($B_g$) for Strange star candidates

$$\begin{aligned} h= \frac{-2bR^2+3a^3R^4+6a^2R^2 (1+bR^2)+a (3b^2R^4+6bR^2+2)}{2 (1+a R^2+b R^4)\,(4+3aR^2+3bR^4)}\nonumber \\ \end{aligned}$$

(34)

The constant C can be determined by using the condition $e^{\nu (R)}=e^{-\lambda (R)}$, which yields:

$$\begin{aligned} C=\frac{e^{-hR^2}}{1+aR^2+bR^4} \end{aligned}$$

(35)

The condition (30) gives the total mass of the charged compact star as

$$\begin{aligned}&\frac{M}{R}=\frac{R^2\,[2a^2R^2(1-3F+3hR^2)+2bR^2 (1+2F+3hR^2 F)+{\varPsi }(R)]}{4\,(1+a R^2+b R^4)^2} \nonumber \\ \end{aligned}$$

(36)

where,

$$\begin{aligned} F= & {} 1+b\,R^4, \nonumber \\ {\varPsi }(R)= & {} -3a^3R^4+ a[2F -3b^2R^4 +6hR^2(2F-1)].\nonumber \\ \end{aligned}$$

(37)

In Table 1 are displayed the values obtained for the mass M, the radius R, the bag constant $B_{g}$ and all the constant parameters. Moreover, in Table 2 the corresponding values of the central density $\rho _{0}$, surface density $\rho _{s}$ and central pressure $p_{0}$ are shown and the bag constant $B_{g}$ is expressed in energy units Mev/fm$^{3}$. At this stage we observe that the values of the bag constant $B_{g}$ are larger than those claimed in the literature for stable compact objects that include anisotropic matter distributions formed by quarks [133]. From the perspective of a mathematically self-consistent model, it appears that a wide range of values of the bag constant are possible which is consistent with the CERN-SPS and RHIC data [135]. The possibility of large values of the bag constant are also claimed by Rahaman et al. [114].

5 Some silent features of strange star models

5.1 Equilibrium under four different forces

It is interesting to study the equilibrium conditions under the different forces, namely, gravitational $F_{g}$, hydrostatic $F_{h}$, anisotropic $F_{a}$ and electric $F_{e}$ forces, respectively. In the case of isotropic uncharged fluid spheres this study can be performed using the well known Tolman–Oppenheimer–Volkov (TOV) equation [138, 139]. Nevertheless, in this opportunity we are in presence of an anisotropic charged fluid sphere, then the TOV equation should be modified in order to analyze the equilibrium of the configuration. So, the modified TOV equation is given by

$$\begin{aligned} \underbrace{\frac{dp_r}{dr}}_{F_{h}} = \underbrace{- \frac{\nu ^{\prime }(\lambda ^{\prime }+\nu ^{\prime })}{2re^{\lambda }}}_{F_{g}}+\underbrace{\frac{q}{4\pi r^4} \frac{dq}{dr}}_{F_{e}} + \underbrace{\frac{2{\varDelta }}{r}}_{F_{a}}, \end{aligned}$$

(38)

where the effective gravitational mass $M_G(r)$ inside the fluid sphere of radius ‘r’ is given by :

$$\begin{aligned} M_G(r)=4\pi \int _0^r \Big (T_0^0-T_1^1-T_2^2-T_3^3 \Big )~r^2 e^{(\nu +\lambda )/2} dr, \nonumber \\ \end{aligned}$$

(39)

and, for notational convenience, the factors may be written as

$$\begin{aligned} M_G(r)=\frac{1}{2}r^{2}\nu '~e^{(\nu -\lambda )/2}. \end{aligned}$$

(40)

The explicit form of the above forces are

$$\begin{aligned}&F_g=-\,h\,r\,\frac{\,[a+2\,a\,h\,r^2 + 2\,(h+b\, r^2+b \,h\, r^4)]}{2\,\pi \,(1+a\,r^2+b\,r^4)^2} \end{aligned}$$

(41)

$$\begin{aligned}&F_h=r\,\frac{[a^2\, (1+h\, r^2)+a (h+3 b\, r^2+3 b\, h \,r^4)-b (1-3\, b \,r^4-2 h \,r^2\,f)]}{4\,\pi \, (1+a\, r^2+b\, r^4)^3} \end{aligned}$$

(42)

$$\begin{aligned}&F_e=r\,\frac{[F_{e1} -3\,a^4\,r^4-8\,a^3\,r^2 +F_{e2}+ F_{e3}]}{4\,\pi \,(1+a\, r^2+b\, r^4)^3} \end{aligned}$$

(43)

$$\begin{aligned}&F_a=r\,\frac{4 h^2 + 3 a^3 r^2 - b^2 r^4 (1 + 6 h r^2) + a^2 (5 - 6 h r^2 + 6 b r^4)+F_{a1}}{4\,\pi \, (1+a\, r^2+b\, r^4)^2} \end{aligned}$$

(44)

where,

$$\begin{aligned} F_{e1}= & {} a^3 r^2 (6 h r^2 - 9 b r^4)-3 a^2 \\&[2 + 5 b r^4 + 3 b^2 r^8 - h r^2 (5 + 6 b r^4)], \\ F_{e2}= & {} b [6 + 3 b r^4 + b^2 r^8 \\&+ 6 h r^2 (2 + 3 b r^4 + b^2 r^8)], \\ F_{e3}= & {} a\,[-b r^2 (2 + 6 b r^4 + 3 b^2 r^8) \\&+ 3 h (3 + 11 b r^4 + 6 b^2 r^8)], \\ F_{a1}= & {} b (4 h^2 r^4-5 - 10 h r^2 ) \\&+ a [4 h^2 r^2 - 4 h (2 + 3 b r^4) + b r^2 (4 + 3 b r^4)] \end{aligned}$$

Fig. 4

Behavior of different forces versus radial coordinates r / R. For plotting of this figure, the corresponding values of arbitrary constants or parameters are displayed in Table 1

It is observed from Fig. 4 that the system is in complete equilibrium under the foregoing mentioned forces. Inspection of the upper panel (corresponding to the star I) and the lower panel (corresponding to star II) shows that the force due to anisotropy initially dominates the electromagnetic force, nevertheless as the fractional radius r / R increases the electromagnetic force dominates the anisotropic force (it phenomenon occurs approximately at $r/R=0.5$). This change between these forces can be explained by the presence of a high electric field (approximately at $r/R=0.5$) of the compact object.

5.2 Energy condition

In the study of compact configurations describing charged anisotropic matter distributions, is necessary to check if the energy-momentum tensor is well behaved i.e. positive defined everywhere within the star. To check it, the following energy conditions must satisfy simultaneously [140]

$$\begin{aligned}&\mathbf NEC: ~ \rho (r)+\frac{E^2}{8\,\pi } \ge 0, \end{aligned}$$

(45)

$$\begin{aligned}&\mathbf WEC: ~ \rho (r)+p_r(r) \ge 0~~, \rho (r)+p_t(r)+\frac{E^2}{4\,\pi } \ge 0, \end{aligned}$$

(46)

$$\begin{aligned}&\mathbf SEC: ~ ~\rho +p_r(r)+2p_t(r)+\frac{E^2}{4\,\pi } \ge 0. \end{aligned}$$

(47)

The above inequalities correspond to the null energy condition (NEC), the weak energy condition (WEC) and the strong energy condition (SEC). In Fig. 5 it is shown that all the above inequalities are satisfied inside the star. Then the energy-momentum tensor associated with this model is positive defined.

Fig. 5

Behavior of energy conditions versus radial coordinates r / R. For plotting of this figure, the corresponding values of arbitrary constants or parameters are displayed in Table 1

5.3 Stability via subliminal sound speeds

It is well known that for physically acceptable anisotropic charged models, the radial and transverse subliminal speed of sound should lie between 0 and 1, i.e. $0\le v_{r}<1$ and $0\le v_{t}<1$. It is observed from these inequalities that the parameters also should satisfy the inequalities $0\le v^{2}_{r}<1$ and $0\le v^{2}_{t}<1$. From Fig. 6, we conclude that the square of the radial and transverse speeds of sound are within the range everywhere inside the stars. Therefore causality condition is preserved. Moreover, from Fig. 7 we observe that $0\le |v^{2}_{t}-v^{2}_{r}|<1$, which means that the system is stable where the radial speed of sound is greater than the transverse speed of sound. This implies that there is no change in sign of $v^{2}_{t}-v^{2}_{r}$ and $v^{2}_{r}-v^{2}_{t}$ [32].

Fig. 6

Behavior of radial velocity ($v^2_r$) and tangential velocity ($v^2_t$) versus radial coordinates r / R. For plotting of this figure, the corresponding values of arbitrary constants or parameters are displayed in Table 1

Fig. 7

Behavior of $v^2_r-v^2_t$ and $v^2_t - v^2_r$ versus radial coordinates r / R. For plotting of this figure, the corresponding values of arbitrary constants or parameters are displayed in Table 1

5.4 Effective mass–radius relation

Regarding the mass–radius ratio of a compact object, in the case of a perfect fluid spheres (uncharged) it is well known that this is given by the Buchdhal’s limit i.e. $2M/R\le 8/9$ [141]. In the case of uncharged anisotropic fluid spheres this limit is more general [142], notwithstanding it can be obtained from the effective mass [27]. However, in the case of anisotropic charged spheres this limit is still quite general respect to the previous cases. The lower limit was given by Andreasson [143] and the upper bound was given by Bohmer and Harko [144]. This constraint on the mass–radius ratio for anisotropic charged spheres explicitly reads

$$\begin{aligned}&\frac{Q^{2}\left( 18R^{2}+Q^{2}\right) }{2R^{2}\left( 12R^{2}+Q^{2}\right) } \nonumber \\&\quad \le \frac{M}{R}\le \frac{4R^{2}+3Q^{2}+2R\sqrt{R^{2}+3Q^{2}}}{9R^{2}}. \end{aligned}$$

(48)

In Table 3 we can see the values for the mass–radius ratio and its lower and upper bounds for both strange star candidates considered in this study. Of course, due to the presence of anisotropies and electric charge in the matter distribution, the corresponding values for the mass–radius ratio are greater that the corresponding ones for the isotropic uncharged matter configurations. Furthermore, the mass–radius ratio (the compactness parameter u) can be expresses in terms of the effective mass $M_{eff}$ which for charged matter distribution is given by

$$\begin{aligned} M_{eff}=4\pi \int _{0}^{R}\left( {\rho }+\frac{E^{2}}{8\pi }\right) r^{2}dr=\frac{R}{2}\left[ 1-e^{-\lambda (R)}\right] , \end{aligned}$$

(49)

explicitly

$$\begin{aligned} M_{eff}=\frac{R}{2}\left[ \frac{aR^{2}+bR^{4}}{1+aR^{2}+bR^{4}}\right] , \end{aligned}$$

(50)

so, the compactness parameter of the star is therefore

$$\begin{aligned} u(R)=\frac{M_{eff}}{R}=\frac{1}{2}\left[ 1-e^{-\lambda (R)}\right] , \end{aligned}$$

(51)

$$\begin{aligned} u(R)=\frac{1}{2}\left[ \frac{aR^{2}+bR^{4}}{1+aR^{2}+bR^{4}}\right] . \end{aligned}$$

(52)

On the other hand, an important quantity related with the above compactness factor u is the gravitational surface redshift $Z_{s}$. It can be calculated as

$$\begin{aligned} Z_{s}=\left( 1-2u\right) ^{-1/2}-1. \end{aligned}$$

(53)

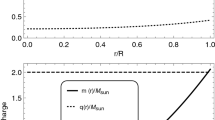
As was pointed out by Bowers and Liang [3], anisotropic matter distribution can affects the value of the surface redshift. In the case of isotropic matter distribution the maximum value that $Z_{s}$ can reaches is $Z_{s}=2$, which is in complete agreement with the Buchdahl’s limit $u=M/R\le 4/9$. Then from Eq. (53), we observed that the surface redshift of star cannot be arbitrary large due to Buchdahl’s limit. However, Bowers and Liang considered an hypothetical model containing a constant density $\rho =\rho _{0}$ (incompressible fluid) and a specific form of the anisotropy factor ${\varDelta }$. They concluded that when the anisotropy factor is null i.e. ${\varDelta }=0 \Rightarrow p_{r}=p_{t}$ the maximum value for the surface redshift corresponds to $Z_{s}=4.77$, and in the case of a positive anisotropy factor ${\varDelta }>0 \Rightarrow p_{t}>p_{r}$ the above value can be exceed (otherwise if ${\varDelta }<0$). Moreover, if the anisotropy factor is extremely large then the surface redshift will be too. On the other hand, Ivanov [74] shown that for a realistic anisotropic star models the $Z_{s}$ can not exceed the value $Z_{s}\le 5.211$ (this value corresponds to a model without cosmological constant). We can see in Fig. 8 the monotonically increasing behaviour of the surface redshift $Z_{s}$ within the compact configuration and in Table 2 the maximum values reached by the considered strange star candidates I and II. So, based on the above discussion we therefore conclude that for an anisotropic star without cosmological constant the values for our model are in good agreement.

On the other hand, as we said before the electric charge has an incidence on the mass–radius relation. We note from Table 3 that charged stars have large mass and radius as we should expect due to the effect of the repulsive Coulomb force with the M / R ratio increasing with charge [29].

Table 3 The lower and upper bounds for the mass–radius ratio and the mass–radius relation for Strange star candidates

5.5 Electric charge

The electric charge on the surface in Coulomb unit: $4.04378\times 10^{19}$ [C] for the I star whose radius is 8 km and $1.638631\times 10^{20}$ [C] for the II star whose radius is 7.1 km, these values are in accordance with the upper limits reported in previous studies [34, 146,147,148]. As was argued by Thirukkanesh et al. [145] on the study reported by Madsen [149], electron-positron pair creation in supercritical electric fields limits the net charge Q of a static, spherically symmetric strange star consisting of quark matter to $Q<7\times 10^{33}$ (units in fm scale), which is self-bound due to strong interactions in addition to gravity. Then we can conclude that our model is in agreement with the established values for the electric charge in the literature. On the other hand we can see from Fig. 9 the behaviour of the electric field intensity $E^{2}$. As we expect it is vanishes at center and completely regular everywhere inside the star.

Fig. 8

Behavior of surface redshift function ($z_s$) versus radial coordinates r / R. For plotting of this figure, the corresponding values of arbitrary constants or parameters are displayed in Table 1

Fig. 9

Behavior of electric field ($E^2$) versus radial coordinates r / R. For plotting of this figure, the corresponding values of arbitrary constants or parameters are displayed in Table 1

6 Concluding remarks

We have presented an exact static model of the Einstein–Maxwell equations which describes a spherically symmetric charged body arising from the requirement that the internal geometry is given by the Tolman–Kuchowicz spacetime and assuming the MIT bag model EoS. We have studied different features of a strange star presenting interesting physical characteristics and featured the variation of different physical parameters with the fractional radial coordinate graphically. One of the most remarkable result obtained in this work were the predicted exact values for the bag constant $B_{g}$ which are incomplete accordance with other model reported in the literature [115, 128]. It shown that the bag constant values are not restricted to be $B_{g}\sim$55–75 MeV/fm$^{3}$ [133] and as was shown by Burgios [135] a wide range of the bag constant value are permissible. Moreover, the value of the bag constant increases with the increasing values of the density of the stellar systems as can be seen in Table 2. On the other hand, we find in the same table that the central and surface density of both stars are much higher than the normal nuclear density $\rho \sim 2\times 10^{14}$ g/cm$^{3}$ and such high density confirms the presence of quark matter inside the discussed stars. The another salient features of the present study can be summarized as follow:

• It is observed from Figs. 1, 2 and 3 that the model is free from physical and geometrical singularities. Of course, both metric potentials are finite, positive and well behaved at the center of the star i.e. $e^{\lambda (r)}|_{r=0}=1$ and $e^{\nu (r)}|_{r=0}=C>0$ and are monotone increasing functions with increasing radial coordinate r towards the surface within the compact configuration. Furthermore, all the thermodynamic observables $\rho$, $p_{r}$ and $p_{t}$ are monotonically decreasing functions with increasing radius, positive and well behaved everywhere inside the system.

• Through out the stellar distribution the anisotropy factor is positive (i.e. ${\varDelta }>0 \Rightarrow p_{t} > p_{r}$), it helps to construct a more massive and compact stellar structure.

• The model satisfied simultaneously the standard point wise energy conditions that are required by normal matter, i.e. the NEC, WEC and SEC. Therefore, the energy-momentum tensor is well defined everywhere inside the star, it can be corroborated in Fig. 5. The graphical representation of TOV equation (Fig. 4) shows that the stellar structure is in equilibrium under gravitational, ani- sotropic, electric and hydrostatic forces. Where initially the aniso- tropic force dominates the electric one, however as the radial coordinate grows the electric force finally dominates the anisotropic force. This implies that the surface layers are more stable (larger repulsive forces here) than the inner core layers. Therefore, the equilibrium of the compact object is enhanced.

• For our model, causality condition is satisfied and stability through Abreu et al. criterion hold, representing a stable configuration.

• The influence over the surface redshift $Z_{s}$ and the mass–radius ratio u due to the presence of anisotropies and electric charge in the system are shown in Tables 2 and 3 respectively. The obtained values obtained here are in correspondence with the expected values for compact objects including charged anisotropic matter distribution. Additionally, Fig. 8 shows the trend of the surface redshift inside the star. As we can see it can not be arbitrary large due to the value of compactness ($u=M/R$) of the stars.

• The values for the surface electric charge found in this model, are within the range of the values reported in previous studies [34, 146,147,148]. These values may be interpreted to represent the strangelet charge of strange stars made of color superconducting strange matter [145]. Furthermore, the electric field intensity $E^{2}$ is well behaved in all points inside the configuration and it is vanishes at center as is expected. This can be seen in Fig. 9.

At this stage it is noteworthy to mention that the experimental support given by the LIGO and Virgo observatories in the detection of the GW170817 signal in 2017 from the merging of a binary neutron star system, has made possible to investigate and study the properties of matter in the extreme conditions found inside these stars [150]. A few months ago Abbott et al. [151] based on the observational data provided by LIGO and Virgo in the detection of gravitational waves and using the equation-of-state-insensitive relations between various macroscopic properties of the neutron stars, presented a study on the size of such stars. Determining that the heaviest component had a radius $R_{1}= 10.8^{+2.0}_{-1.7}$ km while the lightest had a radius $R_{2}=10.7^{+2.1}_{-1.5}$ km, both results with $90\%$ reliability. On the other hand the use of an efficient parametrization of the defining function $p(\rho )$ of the equation of state supports neutron stars with masses larger than $1.97 M_{\odot }$ as required from electromagnetic observations, constraining $R_{1}= 11.9^{+1.4}_{-1.4}$ km and $R_{2}= 11.9^{+1.4}_{-1.4}$ km at the $90\%$ confidence level. They also predicted that at twice the nuclear saturation density the pressure should be $3.5^{+2.7}_{1.7}\times 10^{34}$ dyne/cm$^{2}$. In comparison with the obtained model whe- re the star I with a mass $2.1M_{\odot }$ and radii $R_{I}=8$ km has a central pressure $p_{0}=9.072097\times 10^{35}$ dyne/cm$^{2}$ and the star II with $2.1M_{\odot }$ and radii $R_{ II}=7.1$ km with a central pressure value $p_{0}=1.582416\times 10^{36}$ dyne/cm$^{2}$, it can be highlighted that the strange stars having more dense and smaller in size compared to the neutron stars. On the other hand, this results can be matched within the range of the data as predicted by Abbott et al. [151].

Finally, it can be concluded that an analytic solution to the Einstein–Maxwell field equations has been obtained, which meets all the requirements to be a physically and mathematically admissible solution representing a static, spherically symmetric spacetime described by a charged anisotropic en- ergy-momentum tensor.