1 Introduction

Deflection of light ray in weak gravitational field was the first experimental proof of the theory of general relativity for the Schwarzschild spacetime since 1919 [1]. Now it is serving as one of the important tool of probing a number of interesting phenomena in astronomy and cosmology. It is widely used for investigating the astrophysical objects, e.g., black holes, wormholes, super-dense neutron stars, naked singularity etc. This phenomenon has also been considered to study exoplanet detection from the dark energy, dark matter, and Hubble parameter measurements. Moreover, the gravitational lensing (GL) provides an alternative approach towards mass measurement that leads to measure the mass of the white dwarf Stein 2051 B by using the Hubble space telescope [2]. Earlier works focused on the weak field theory of gravitational lensing which is based on the first order expansion of the small deflection angle [3]. Although the main disadvantage is when the lens is a very compact object (e.g. black hole), in this case the weak field approximation is no longer valid. The weak field approximation can not able to distinguish between various different solutions that are asymptotically flat. Therefore, after the pioneering work of Darwin [4], the strong gravitational lensing has received much attentions. Note that in the case of strong lensing, the effect of lensing is strong, which means multiple imaging or strong deformation of the image. On the other hand, in case of weak lensing, the effect is weak, and the lensing images are characterized by weak distortions and small magnifications. In this case the fact of lensing cannot be identified by using an individual source, but can be revealed by statistical analysis of many objects. In addition, we can distinguish situations of lensing on the basis of the magnitude of the deflection angle: weak deflection of photons (with small deflection angles, sometimes referred as weak field situation) and strong deflection of photons (deflection angles are not small, sometimes referred as strong field situation), correspondingly. However, the crucial thing is that all observational areas of GL (strong, weak and micro) are based on using only weak deflection approximation meaning that, the deflection angle remains to be small. Strong deflection case on the other hand, is used for another problems: for example, for investigations of so-called relativistic images. To this end, we wish to point out the strong gravitational lensing for the Schwarzschild black hole [5, 6], then extended to the Reissner–Nordström black hole [7, 8], regular black holes [9], and wormholes [10,11,12,13], while the investigations of so-called relativistic images see also Refs. [14,15,16,17,18,19,20].

An interesting method has immersed for computing the angle of light deflection by Gibbons and Werner [21, 22]. They considered the source and the receiver are located at an asymptotic region and then they applied the Gauss–Bonnet theorem (GBT) to the optical metric of a lens which allows us to describes a light ray as a spatial curve. Later on Werner [23] extended this approach to the stationary spacetime and computed the deflection angle for the Kerr black hole. This method has also been applied in the weak limit approximation to compute the deflection of light for global monopole and rotating cosmic string spacetime [24, 25]. Note that the deflection angle of conical singularities has been pointed out in the old paper [26] . Nowadays the scientific community is discussing this phenomenon with great interest. Along this line of thinking, Ishihara et al. [27] obtained the bending angle of light by using the GBT for finite distance from a lens object to a light source and a receiver. Further, this approach was extended by considering the stationary, axisymmetric and asymptotically flat spacetimes [28]. Jusufi and Övgün [29] studied the effect of the cosmological constant on the deflection angle by a rotating cosmic string. For the influence of cosmological constant on the light deflection see the recent review by Lebedev and Lake [30]. On the other hand the GBT method has been considered for the several wormholes [31,32,33] and black holes [34,35,36] solutions.

It is worth noticing that in the gravitational field the bending trajectories not only found for light or massless particles but also for massive particles. For a review on massive particles whose trajectories can go through a bending process, we refer the reader to [37,38,39], in particular the deflection angle for massive particles in weak deflection case is calculated in Ref. [40], and for strong deflection case see [41, 42]. Thus the important fact is trajectory bending due to the strong gravity near the black holes and the large velocity of the hypervelocity stars needs a full relativistic treatment, which will differ from the calculations made using only Newtonian gravity. In recent years, the existence of strong gravitationally lensed supernovae has long been predicted [43,44,45,46]. Thus it is natural to expect that the neutrinos and cosmic rays emitted by these supernova and AGN are also lensed. Neutrino gravitational lensing by astrophysical objects has already been done in [47]. Besides their positions, they also estimated the depletion of the neutrino flux after crossing a massive object [47]. At the same time, Eiroa and Romero [48] have studied gravitational lensing of neutrinos by Schwarzschild black holes.

Recently, Crisnejo and Gallo [49] showed that how one can successfully study the GBT theorem in a plasma medium for a static and spherically symmetric gravitational field. The gravitational deflection in plasma medium was considered in details before, see [50, 51]. Even in the GBT method, they computed the deflection of massive particles with the same symmetries. On the other hand, Jusufi [52] introduced a new method based on GBT to compute the deflection angle for massive particles in a rotating spacetime geometry such as the Kerr black hole [53] and Teo wormhole [54]. In doing so, he used an isotropic type metrics for a linearized rotating gravitational field where the refractive index of the corresponding optical media can be obtained. Motivated by the works we study the gravitational deflection of massive particles by Janis–Newman–Winicour (JNW) spacetimes [55] (also known as a rotating source with a surface-like naked singularity), and a rotating Kerr-like wormholes [56]. Along this line of thought, recently different aspects of naked singularities and Kerr-like wormholes have been studied, including the iron line spectroscopy [57], accretion disc properties [58], spin precession of a test gyroscope [59, 60], echoes of Kerr-like wormholes [56], shadow images [61] the strong and the weak deflection of light by Kerr-like wormholes [62, 63]. In the present article, we study the deflection of massive particles by assuming the propagating particles as a de Broglie wave packets introduced in [64].

The paper is organized as follows. In Sect. 2, we use a coordinate transformation to recover an isotropic metric form for the rotating naked singularities, then derive the refractive index of the corresponding optical media. In Sect. 3, we consider the problem of the gravitational deflection of massive particles by Kerr-like wormholes. We present a detailed analyses of the deflection of massive particles by using the Hamilton–Jacobi approach in Sect. 4. We conclude our results in Sect. 5. We use the geometrized unit \(G=c=\hbar = 1\) throughout this paper.

2 Deflection of massive particles by rotating naked singularities

In this section, we calculate the deflection angle of rotating naked singularities thereby we consider Janis–Newman–Winicour (JNW) spacetime. It is a solution of the Einstein equation described with the assumption of spherical symmetry, asymptotic flatness with the static massless scalar field \(\Phi \). The action associated with this spacetime [55, 57] is

$$\begin{aligned} S=\int d^4x \sqrt{-g} \left[ R+g^{\mu \nu } (\partial _{\mu } \Phi ) (\partial _{\nu } \Phi ) \right] , \end{aligned}$$
(1)

the variation of action turns out the following field equations

$$\begin{aligned} R_{\mu \nu }= 8 \,(\partial _{\mu } \Phi ) (\partial _{\nu } \Phi ) , \quad \Box \Phi =0, \end{aligned}$$
(2)

where the scalar field is given by

$$\begin{aligned} \Phi =\frac{\sqrt{1-\gamma ^2}}{4} \ln \left( 1-\frac{2 mr }{\Sigma }\right) . \end{aligned}$$
(3)

The corresponding rotating spacetime metric [57] has the form

$$\begin{aligned} ds^2= & {} \left( 1-\frac{2 m r}{\Sigma }\right) ^{\gamma }(dt-\omega d\phi )^2 +2 \omega (dt-\omega d\phi ) d\phi \nonumber \\&- \left( 1 -\frac{2mr}{ \Sigma }\right) ^{1-\gamma } \Sigma \left( \frac{dr^2}{\Delta } +d\theta ^2 +\sin ^2 \theta d\phi ^2\right) , \end{aligned}$$
(4)

where \(m=M/\gamma \), M is the Arnowitt–Deser–Misner (ADM) mass, and

$$\begin{aligned} \Sigma&= r^2+a^2 \cos ^2\theta , \quad \omega = a \sin ^2 \theta , \quad \Delta = r^2 +a^2-2mr, ~~\nonumber \\&\quad \gamma = \frac{M}{\sqrt{M^2+q^2}}. \end{aligned}$$
(5)

Note that \(a =J/M\), where J is the spin angular momentum of the source. For an instant if we set \(\gamma =1\) and \(q=0\), one can recover the Kerr black hole solution and the larger root of \(\Delta = 0\) provides the radius of the event horizon, \(r_{h}=M+\sqrt{M^2-a^2}\). It can be easily checked that for \(0< \gamma <1\), and \(q \ne 0\), the metric (4) describes rotating naked singularities with a scalar curvature [57]

$$\begin{aligned} R= & {} \frac{2(\gamma ^2-1)m^2}{\Sigma ^5}\left( 1-\frac{2m r}{\Sigma }\right) ^{\gamma -3}\nonumber \\&\times \left[ \Delta (r^2- a^2 \cos ^2 \theta )^2+(r a^2 \sin ^2 (2 \theta ))^2\right] , \end{aligned}$$
(6)

and diverges on the surface

$$\begin{aligned} r_{\star }= m+\sqrt{m^2-a^2 cos^2\theta }, \end{aligned}$$
(7)

\(r_{\star }\) is the surface-like singularity, where curvature invariants diverge and the spacetime is geodetically incomplete as well. In addition, the scalar curvature diverges where \(g_{tt}=0\) and represent the presence of a curvature singularity at

$$\begin{aligned} r_{\text {cs}}= \frac{1}{\gamma }\left[ m+\sqrt{m^2-\gamma ^2 a^2 cos^2\theta } \right] , \end{aligned}$$
(8)

as the domain of variation of \(\theta \) depends on the ratio \(\gamma ^2 a^2/m^2\). Also, it follows that in the transition from a black hole (\(\gamma = 1\)) to a naked singularity (\(\gamma < 1\)), the singularity is indeed naked, not the event horizon.

2.1 Deflection angle

Since, we are mainly interested in the weak limit, we shall simplify the problem by considering the deflection of particles in the equatorial plane (\(\theta =\pi /2\)) with a linearized metric in a, which results in

$$\begin{aligned} ds^2= & {} \left[ \left( 1-\frac{2 m }{r}\right) ^{\gamma }+2a \frac{d \phi }{dt} \left( 1-\left( 1-\frac{2m}{r}\right) ^{\gamma }\right) \right] dt^2\nonumber \\&-\left( 1-\frac{2m}{ r}\right) ^{1-\gamma }\left( \frac{dr^2}{1-\frac{2m}{ r}}+r^2 d\phi ^2\right) . \end{aligned}$$
(9)

Now introducing a coordinate transformation via

$$\begin{aligned} r=\rho \left( 1+\frac{m}{2 \,\rho }\right) ^2, \end{aligned}$$
(10)

we deduce an isotropic metric with the line element given by

$$\begin{aligned}&ds^2=\mathcal {F}^2(\rho ) dt^2-\left( 1+\frac{m}{2 \rho }\right) ^4 \left( \frac{2 \rho -m}{2 \rho +m}\right) ^{2(1-\gamma )}\nonumber \\&\quad \left( d\rho ^2+\rho ^2 d\varphi ^2\right) , \end{aligned}$$
(11)

where \(\mathcal {F}^2(\rho )\) is

$$\begin{aligned} \mathcal {F}^2(\rho )=\left( \frac{2 \rho -m}{2 \rho +m}\right) ^{2\gamma }+2a \frac{d \phi }{dt} \left( 1-\left( \frac{2 \rho -m}{2 \rho +m}\right) ^{2\gamma }\right) . \end{aligned}$$
(12)

The velocity of light in this particular optical media can be found by setting \(ds^2=0\), and using the definition \(v=|d\mathbf {\rho }|/dt\), where \(|d\mathbf {\rho }|^2=d\rho ^2+\rho ^2 d\varphi ^2 \). With this information in hand, we can find the effective refractive index of the optical media by using \(n(\rho )=c/v(\rho )\) and \(c=1\), yielding

$$\begin{aligned} n(\rho )=\frac{\left( \frac{2 \rho +m}{2 \rho }\right) ^2 \left( \frac{2 \rho -m}{2 \rho +m}\right) ^{1-\gamma }}{\sqrt{\left( \frac{2 \rho -m}{2 \rho +m}\right) ^{2\gamma }-2 a \left( \frac{2 \rho -m}{2 \rho +m}\right) ^{2\gamma }\frac{d \varphi }{dt}+2 a \frac{d \varphi }{dt}}}. \end{aligned}$$
(13)

We can, therefore, write down the optical metric in terms of the refractive index as follows

$$\begin{aligned} dt^2=n(\rho )^2 d\rho ^2+\rho ^2 n(\rho )^2 d\varphi ^2. \end{aligned}$$
(14)

By inverting the coordinate transformation (10), we obtain

$$\begin{aligned} \rho = \frac{r-m+\sqrt{r^2-2m r}}{2}, \end{aligned}$$
(15)

which shows leading terms in \(\rho \simeq r - m\). The above relations holds for the deflection of light. However, we are interested in studying the deflection of massive particles. One way to incorporate this is to consider the propagating massive particles as the de Broglie wave packets. In particular, following [52, 64], we can argue that by using \(p=\hbar k\) and \(H=E=\hbar \omega \), (note that we have temporarily introduced \(\hbar \)) results

$$\begin{aligned} \lambda =\frac{h}{n H \sqrt{1-\frac{\mu ^2 \mathcal {F}^2 }{H^2}}}, \end{aligned}$$
(16)

where \(\mu \) is the rest mass of the particle. We rearrange this equation to obtain a constant quantity of the given optical media

$$\begin{aligned} \lambda n \sqrt{1-\frac{\mu ^2 \mathcal {F}^2 }{H^2}}=\frac{h}{ H }=const. \end{aligned}$$
(17)

In other words, this equation is a generalization of well-known result in wave-optics. For massive particles, in a given isotropic metric, the expression should be constant everywhere in the optical medium, i.e., \(\lambda N=const\). Thus the refractive index relation for massive particles is given by

$$\begin{aligned} n(\rho )_{mass. \,particles} \rightarrow N(\rho )=n(\rho )\sqrt{1-\frac{\mu ^2}{E^2}\mathcal {F}^2(\rho )}, \end{aligned}$$
(18)

modifying the optical metric

$$\begin{aligned} \mathrm {d}\sigma ^2_{mass. particles}=N(\rho )^2 \mathrm {d}\rho ^2+\rho ^2 N(\rho )^2 \mathrm {d}\varphi ^2. \end{aligned}$$
(19)

Furthermore, the energy of the particles measured at infinity is given by

$$\begin{aligned} E =\frac{\mu }{\left( 1-w^2\right) ^{1/2}}, \end{aligned}$$
(20)

where w represents the relativistic velocity. The angular momentum can be written as

$$\begin{aligned} J=\frac{\mu w b}{\left( 1-w^2\right) ^{1/2}}, \end{aligned}$$
(21)

where b is the impact parameter. Following the definition of the impact parameter, we can write

$$\begin{aligned} \frac{J}{E }=w\,b, \end{aligned}$$
(22)

which reduces to b in the case of light \(w=c=1\). Therefore, the quantity \(\mathrm {d} \varphi /\mathrm {d}t\), in case of massive particles is modified as follow

$$\begin{aligned} \frac{\mathrm {d} \varphi }{\mathrm {d}t}=\frac{a+\left( 1-\frac{2m}{ r}\right) ^{\gamma } b w-(1-\frac{2m}{ r})^{\gamma }a}{\left( 1-\frac{2m}{ r}\right) ^{1-\gamma }r^2+\left( 1-\frac{2m}{ r}\right) ^{\gamma } a b w}, \end{aligned}$$
(23)

yielding

$$\begin{aligned} N(r)= & {} w+\frac{\gamma m (r^2w^2-2 ab w+r^2)}{w r^3} \nonumber \\&+\mathcal {O}(m^2,a^2). \end{aligned}$$
(24)

This result clearly indicates that the refractive index is modified due to the angular momentum parameter a.

Let us continue to calculate the Gaussian optical curvature using metric (19). Rewriting the optical metric (19), in terms of a new coordinates,

$$\begin{aligned} \mathrm {d}r^{\star }=N(\rho )\, \mathrm {d}\rho ,\,\,\,f(r^{\star })=N(\rho )\, \rho , \end{aligned}$$
(25)

thus the optical metric reads

$$\begin{aligned} \mathrm {d}\sigma ^{2}=\tilde{g}_{ab}\,\mathrm {d}x^{a}\mathrm {d}x^{b}= \mathrm {d}{r^{\star }}^{2}+f^{2}(r^{\star })\mathrm {d}\varphi ^{2}. \end{aligned}$$
(26)

In terms of these coordinates, the Gaussian optical curvature \(\mathcal {K}\) can be expressed as:

$$\begin{aligned} \mathcal {K}= & {} - \frac{1}{f (r^{\star })} \frac{\mathrm {d}^2 f (r^{\star })}{\mathrm {d} r^{\star 2}} \nonumber \\= & {} - \frac{1}{f (r^{\star })} \left[ \frac{\mathrm {d} \rho }{\mathrm {d} r^{\star }} \frac{\mathrm {d}}{\mathrm {d} \rho } \left( \frac{\mathrm {d} \rho }{\mathrm {d} r^{\star }} \right) \frac{\mathrm {d} f}{\mathrm {d} \rho } + \left( \frac{\mathrm {d} \rho }{\mathrm {d} r^{\star }} \right) ^2 \frac{\mathrm {d}^2 f}{\mathrm {d} \rho ^2} \right] . \end{aligned}$$
(27)

We can, therefore, express the Gaussian optical curvature for massive particles in terms of the modified refractive index as

$$\begin{aligned} \mathcal {K} =&-\frac{N(\rho ) N''(\rho ) \rho -(N'(\rho ))^2\rho +N(\rho ) N'(\rho )}{N^4(\rho ) \rho }. \end{aligned}$$
(28)

In particular, by using (15) we can rewrite the last equation, in terms of the old coordinate r, which in leading order terms results with

$$\begin{aligned} \mathcal {K} \simeq - \frac{m \gamma (1+w^2)}{r^3 w^4}+\frac{18 m \gamma b a}{r^5 w^3}+\mathcal {O}(m^2,a^2). \end{aligned}$$
(29)

With these results in hand, we can chose a non-singular region \(\mathcal {D}_{R}\) with boundary \(\partial \mathcal {D}_{R}=\gamma _{\tilde{g}}\cup C_{R}\). The GBT provides a connection between geometry (in a sense of optical curvature) and topology (in a sense of Euler characteristic number) stated as follow

$$\begin{aligned} \iint \limits _{\mathcal {D}_{R}}\mathcal {K}\,\mathrm {d}S+\oint \limits _{\partial \mathcal { D}_{R}}\kappa \,\mathrm {d}\sigma +\sum _{i} \theta _{i}=2\pi \chi (\mathcal {D}_{R}), \end{aligned}$$
(30)

with \(\kappa \) is the geodesic curvature, and \(\mathcal {K}\) is the Gaussian optical curvature. Now we can choose a non-singular domain with Euler characteristic number \(\chi (\mathcal {D}_{R})=1\). The geodesic curvature \(\kappa \), in the case of massive particles is defined by the relation

$$\begin{aligned} \kappa =\tilde{g}\,\left( \nabla _{\dot{\gamma }}\dot{\gamma },\ddot{\gamma }\right) , \end{aligned}$$
(31)

but also keeping in mind an additional unit speed condition \(\tilde{g}(\dot{\gamma },\dot{ \gamma })=1\), with \(\ddot{\gamma }\) being the unit acceleration vector. The two corresponding jump angles in the limit \(R\rightarrow \infty \), reads \(\theta _{ O }+\theta _{ S }\rightarrow \pi \). Therefore the GBT now is simplified as follow

$$\begin{aligned} \lim _{R\rightarrow \infty }\int _{0}^{\pi +\hat{\alpha }}\left[ \kappa \frac{\mathrm {d} \sigma }{\mathrm {d} \varphi }\right] _{C_R} \mathrm {d} \varphi =\pi -\lim _{R\rightarrow \infty }\iint \limits _{\mathcal {D}_{R}}\mathcal {K}\,\mathrm {d}S. \end{aligned}$$
(32)

By construction, there is a zero contribution from the geodesics i.e. \(\kappa (\gamma _{\tilde{g}})=0\), therefore, we end up with a contribution only for the the curve \(C_{R}\), thus we can write

$$\begin{aligned} \kappa (C_{R})=|\nabla _{\dot{C}_{R}}\dot{C}_{R}|. \end{aligned}$$
(33)

To evaluate the above expression one can express the curve in terms of the radial coordinate \(C_{R}:=r(\varphi )=R=\text {const}\), resulting with a nonzero contribution for the radial component

$$\begin{aligned} \left( \nabla _{\dot{C}_{R}}\dot{C}_{R}\right) ^{r}=\dot{C}_{R}^{\varphi }\,\left( \partial _{\varphi }\dot{C}_{R}^{r}\right) +\tilde{\Gamma } _{\varphi \varphi }^{r}\left( \dot{C}_{R}^{\varphi }\right) ^{2}. \end{aligned}$$
(34)

The first term vanishes, however, using the unit speed condition and the optical metric, we find the final result

$$\begin{aligned} \lim _{R\rightarrow \infty }\kappa (C_{R})= & {} \lim _{R\rightarrow \infty }\left| \nabla _{\dot{C}_{R}}\dot{C}_{R}\right| , \nonumber \\\rightarrow & {} \frac{1}{w R}. \end{aligned}$$
(35)

We see that the final result of the geodesic curvature is slightly modified, letting \(w=1\), we recover \(\kappa (C_{R}) \rightarrow R^{-1}\), as expected. For an observer located at the coordinate R, we find

$$\begin{aligned} \lim _{R\rightarrow \infty } d \sigma\rightarrow & {} w R \, d\varphi . \end{aligned}$$
(36)

Putting together these results, from the GBT, we find the following expression for the deflection angle

$$\begin{aligned} \hat{\alpha }=-\int \limits _{0}^{\pi }\int \limits _{\frac{b}{\sin \varphi }}^{\infty }\left( - \frac{m \gamma (1+w^2)}{r^3 w^4}+\frac{18 m \gamma b a}{r^5 w^3}\right) dS, \end{aligned}$$
(37)

where the surface element is given by \(dS=\sqrt{\tilde{g}} \,dr^{\star } d\varphi \simeq N^2(r) r dr d\varphi \). In addition to that, from Eq. (24) the following approximation holds \(N(r)^2 \simeq w^2\). This integral can easily be evaluated,

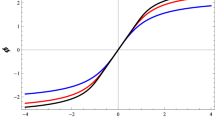
$$\begin{aligned} \hat{\alpha }\simeq \frac{2 m \gamma }{b w^2}(1+w^2) \pm \frac{4 m a \gamma }{b^2 w}, \end{aligned}$$
(38)

where the plus and minus sign refers to the retrograde and prograde light rays, respectively. That being said, it is clear that the deflection angle is bigger in the case of retrograde orbit, and smaller in the case of prograde orbit. Now we can consider three special cases in the last equation: (i) If \(\gamma =1\), we find the deflection angle of massive particles in Kerr black hole geometry. (ii) If \(w=1\), then the deflection angle of light by a JNW spacetime is recovered. (iii) Finally, letting \(\gamma =w=1\), we recover the deflection of light in a Kerr geometry. Our result for the deflection angle is consistent with previous studies [65,66,67,68,69,70,71,72,73]. It is important to realize that our method applies only for relativistic particles, i.e. \(0<w \le 1\), in other words, there is an apparent singularity in the deflection angle in the limit \(w \rightarrow 0\). Of course, this apparent singularity can be removed but a more general setup is needed (Fig. 1).

Fig. 1
figure 1

In the left panel we have plotted the deflection angle as a function of b and \(\gamma \) when \(w=0.5\), \(m=a=1\), and in the right panel same thing plotted as a function of b and w for \(\gamma =0.5\), \(m=a=1\)

Full size image

3 Deflection of massive particles by Kerr-like wormholes

We consider a Kerr-like wormhole spacetime, recently proposed in [56]. The spacetime metric can be written, in Boyer–Lindquist coordinates (\(t, r, \theta , \phi \)) as

$$\begin{aligned} ds^2= & {} \left( 1-\frac{2Mr}{\Sigma }\right) dt^2 +\frac{4Mar\sin ^2 \theta }{\Sigma } dt d\phi -\frac{\Sigma }{\hat{\Delta }}dr^2 \nonumber \\&- \Sigma d \theta ^2 - \left( r^2+ a^2 +\frac{2Ma^2r \sin ^2 \theta }{\Sigma } \right) \sin ^2 \theta d\phi ^2,\nonumber \\ \end{aligned}$$
(39)

where \(\Sigma \) and \(\hat{\Delta }\) are expressed by

$$\begin{aligned} \Sigma = r^2 + a^2 \cos ^2\theta , \quad \hat{\Delta }=r^2 + a^2 - 2 M(1+\lambda ^2)r. \end{aligned}$$
(40)

It contains a family of parameters where a and M corresponds to the spin and the mass of wormhole, and \(\lambda ^2\) is the deformation parameter. A non vanishing \(\lambda ^2\) differs this metric from Kerr metric, we can recover the Kerr metric when \(\lambda ^2 =0\). Although the throat of the wormhole can be easily obtained by equating the \(\hat{\Delta }\) to zero,

$$\begin{aligned} r_{+} = (1+\lambda ^2) M + \sqrt{M^2(1+\lambda ^2)^2 -a^2}, \end{aligned}$$
(41)

which represents a special region that connects two different asymptotically flat regions. To simplify the problem, we can consider the deflection in the equatorial plane in a linearized Kerr-like wormhole metric in spin a. Such a metric can also describe the gravitational field around the rotating star or planet given by

$$\begin{aligned} ds^2\simeq & {} \left( 1-\frac{2M}{r}+\frac{4Ma }{r} \frac{d\varphi }{dt}\right) dt^2 \nonumber \\&- \left( 1-\frac{2M(1+\lambda ^2)}{r}\right) ^{-1} dr^2 -r^2d\varphi ^2. \end{aligned}$$
(42)

3.1 Deflection angle

We follow the same GBT approach to calculate the deflection angle of Kerr-like wormhole as discussed in previous section. Here we use the following coordinate transformation

$$\begin{aligned} r=\rho \left( 1+\frac{M(1+\lambda ^2)}{2 \rho }\right) ^2, \end{aligned}$$
(43)

after substitution the metric takes the following form

$$\begin{aligned} ds^2= & {} \frac{\left( 1+\frac{M(1+\lambda ^2)}{2\rho }\right) ^2-\frac{2M}{\rho }+ \frac{4Ma}{\rho }\frac{d\varphi }{dt}}{\left( 1+\frac{M (1+\lambda ^2)}{2\rho }\right) ^2}dt^2\nonumber \\&-\left( 1+\frac{M (1+\lambda ^2)}{2\rho }\right) ^4\left( d\rho ^2+\rho ^2 d\varphi ^2\right) . \end{aligned}$$
(44)

The last equation represents an isotropic metric, so that the line element can be written in the form

$$\begin{aligned} ds^2=\mathcal {F}^2(\rho ) dt^2-\mathcal {G}^2(\rho ) |d\mathbf {\rho }|^2. \end{aligned}$$
(45)

The isotropic coordinate speed of light \(v(\rho )\) can be found from the relation

$$\begin{aligned} v(\rho )=|\frac{d\mathbf {\rho }}{dt}|=\frac{\left[ \left( 1+\frac{M(1+\lambda ^2)}{2\rho }\right) ^2-\frac{2M}{\rho }+\frac{4Ma}{\rho }\frac{d\varphi }{dt} \right] ^{1/2}}{\left( 1+\frac{M(1+\lambda ^2)}{2\rho }\right) ^3}. \end{aligned}$$
(46)

Using \(n(\rho )=c/v(\rho )\) and \(c=1\), the last equation yields the effective refractive index for light in the Kerr gravitational field

$$\begin{aligned} n(\rho )=\frac{\left( 1+\frac{M(1+\lambda ^2)}{2\rho }\right) ^3}{\left[ \left( 1+\frac{M(1+\lambda ^2)}{2\rho }\right) ^2-\frac{2M}{\rho }+ \frac{4Ma}{\rho }\frac{d\varphi }{dt}\right] ^{1/2}}, \end{aligned}$$
(47)

In this way the optical metric reads

$$\begin{aligned} dt^2=n(\rho )^2 d\rho ^2+\rho ^2 n(\rho )^2 d\varphi ^2. \end{aligned}$$
(48)

By inverting the coordinate relation (43), we find

$$\begin{aligned} \rho = \frac{1}{2}\left[ r-M(1+\lambda ^2)\pm \sqrt{r^2-2Mr(1+\lambda ^2)}\right] , \end{aligned}$$
(49)

which suggests that in leading order terms \(\rho \simeq r -M(1+\lambda ^2)\). The refractive index relation for massive particles in that case reads

$$\begin{aligned} N(r)=n(r)\sqrt{1-\frac{m^2}{E^2}\mathcal {F}^2(r)}. \end{aligned}$$
(50)

We can apply this expression to our Kerr optical media which results with

$$\begin{aligned} \mathcal {F}^2(r)=\frac{\left( 1+\frac{M(1+\lambda ^2)}{2 r}\right) ^2-\frac{2M}{r} +\frac{4Ma}{r}\frac{d\varphi }{dt}}{\left( 1+\frac{M (1+\lambda ^2)}{2r}\right) ^2}, \end{aligned}$$
(51)

in which Eq. (43) has been used. Therefore, the quantity \(d \varphi /dt\), in the case of massive particles is modified as follow

$$\begin{aligned} \frac{d \varphi }{dt}=\frac{2M a+(r-2M) w b}{r^3-2Ma w b}, \end{aligned}$$
(52)

yielding

$$\begin{aligned} N(r)=w+\frac{w \left( r^2 \lambda ^2 w^2+r^2 w^2-2 a b w+r^2 \right) M}{r^3 w^2}+\mathcal {O}(M^2,a^2). \end{aligned}$$
(53)

This result clearly indicates that the refractive index is modified due to the angular momentum parameter a. In particular, in leading order terms, we find

$$\begin{aligned} \mathcal {K} \simeq - \frac{\left( w^2 r^2-18 ab w+r^2\right) M}{w^4 r^5} -\frac{\lambda ^2 M}{r^3 w^3 }+\mathcal {O}(M^2,a^2). \end{aligned}$$
(54)

Going through the same procedure we find

$$\begin{aligned} \lim _{R\rightarrow \infty }\kappa (C_{R})= & {} \lim _{R\rightarrow \infty }\left| \nabla _{\dot{C}_{R}}\dot{C}_{R}\right| , \nonumber \\\rightarrow & {} \frac{1}{w R}. \end{aligned}$$
(55)

From the optical metric is quite easy to see that at a very large distance

$$\begin{aligned} \lim _{R\rightarrow \infty } d\sigma\rightarrow & {} w R \, d\varphi . \end{aligned}$$
(56)

Now from the GBT we find the following expression for the deflection angle

$$\begin{aligned} \hat{\alpha }=-\int \limits _{0}^{\pi }\int \limits _{\frac{b}{\sin \varphi }}^{\infty }\left( - \frac{\left( w^2 r^2-18 ab w+r^2\right) M}{w^4 r^5}-\frac{\lambda ^2 M}{r^3 w^3 }\right) w^2 r dr d\varphi . \end{aligned}$$
(57)

This integral can easily be evaluated, yielding

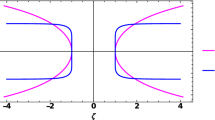
$$\begin{aligned} \hat{\alpha }\simeq \frac{2M}{b}\left( 1+\lambda ^2+\frac{1}{w^2}\right) \pm \frac{4Ma}{b^2}\frac{1}{w}. \end{aligned}$$
(58)

Note that the plus and minus signs refers to the retrograde and prograde light ray, respectively. Setting \(w=1\), in the last equation we recover the deflection angle of light (Fig. 2).

Fig. 2
figure 2

The deflection angle has been plotted as a function of b and \(\lambda \) when \(w=0.8\), \(M=a=1\) in the left panel, whereas for a function of b and w when \(\lambda =0.1\), \(M=a=1\) in the right panel

Full size image

4 Geodesics approach

In this section, we will derive the equations of motion of an uncharged test particle of mass \(\mu \) and then we will calculate the deflection angle of the particle moving in the rotating naked singularity or the Kerr-like wormhole spacetime, given by (4) and (39), respectively. The geodesic equations may be derived using Hamilton–Jacobi approach, as we look for a function of the coordinates and the geodesic affine parameter \(\sigma \),

$$\begin{aligned} S=S(x^{\mu },\sigma ), \end{aligned}$$
(59)

which is a solution of the Hamilton–Jacobi equation

$$\begin{aligned} \mathcal {H}\left( x^{\mu },\frac{\partial S}{\partial x^{\mu }}\right) +\frac{\partial S}{\partial \sigma }=0. \end{aligned}$$
(60)

In general, the solution S of the Hamiltonian–Jacobi equation depends on four integration constants and satisfy the relations for the conjugate momenta

$$\begin{aligned} \frac{\partial S}{\partial x^{\mu }}=p_{\mu }(\sigma ), \end{aligned}$$
(61)

which can be defined by the Lagrangian of the system \(\mathcal {L}=\frac{1}{2}g_{\mu \nu }\dot{x}^{\mu }\dot{x}^{\nu }\) through the equations \(p_{\mu }-\partial \mathcal {L}/\partial \dot{x}^{\mu }=0\). Here, the dot represents differentiation with respect to the geodesic affine parameter \(\sigma \). In order to involve the mass of the test particle, \(\sigma \) must be related to the proper time by \(\tau =\mu \sigma \), which turns the conjugate momenta into

$$\begin{aligned} p_{\mu }(\tau )=\mu g_{\mu \nu }u^{\nu }, \end{aligned}$$
(62)

where \(u^{\mu }\equiv d x^{\mu }/d\sigma \) stands for the four-velocity of the particle with normalization condition \(g_{\sigma \rho }u^{\sigma }u^{\rho }=1\). Therefore, one can obtain the Hamiltonian

$$\begin{aligned} \mathcal {H}=\frac{1}{2}g^{\mu \nu }p_{\mu }p_{\nu }=\frac{1}{2}\mu ^2, \end{aligned}$$
(63)

which does not depend explicitly on geodesic affine parameter \(\sigma \) and is a constant of motion. By taking zero or positive values of \(\mu ^2\), the Hamiltonian (63) can be used to give null or timelike geodesics, respectively. The corresponding Hamilton–Jacobi equation is

$$\begin{aligned} -\frac{\partial S}{\partial \sigma }=\frac{1}{2}g^{\mu \nu }\frac{\partial S}{\partial x^{\mu }} \frac{\partial S}{\partial x^{\nu }}, \end{aligned}$$
(64)

where S is the Jacobi function (59). From the symmetries one can obtain two constants of motion corresponding to conservation of energy, E, and angular momentum with respect to the rotational symmetry axis of the naked singularity or Kerr-like wormhole, J. Therefore, we have

$$\begin{aligned} \begin{aligned} p_{t}&=g_{tt}\dot{t}+g_{t\phi }\dot{\phi }=E, \\ p_{\phi }&=g_{\phi \phi }\dot{\phi }+g_{\phi t}\dot{t}=-J. \end{aligned} \end{aligned}$$
(65)

It follows that for the time and azimuthal coordinates we obtain the equations

$$\begin{aligned} \begin{aligned} \dot{t}&=-\frac{g_{\phi \phi }\,E+g_{t\phi }\,J}{g_{t\phi }^2-g_{tt} g_{\phi \phi }},\\ \dot{\phi }&=\frac{g_{t\phi }\,E+g_{tt}\,J}{g_{t\phi }^2-g_{tt}g_{\phi \phi }}. \end{aligned} \end{aligned}$$
(66)

In addition, we have the constant of motion given by Eq. (63), corresponding to the conservation of the rest mass of the particle. The energy E and the angular momentum of the particle J can be expressed by relativistic velocity w and impact parameter b at infinity, where the spacetime is asymptotically flat, as it is shown by Eqs. (20) and (21).

Hereafter, we will consider only a light ray laying on \(\theta =\pi /2\) hypersurface of the considered rotating naked singularity or wormhole geometry expecting the largest ray deviation. Therefore, we shall seek a solution of the Hamilton–Jacobi equation of the form

$$\begin{aligned} S=-\frac{1}{2}\mu ^2 \sigma +E\,t -J\,\phi +S_{r}(r,E,J). \end{aligned}$$
(67)

Taking into account the relationship between a metric tensor and its inverse, thus the nonzero contravariant metric coefficients are

$$\begin{aligned} \begin{aligned} g^{tt}&=\frac{g_{\phi \phi }}{g_{tt}g_{\phi \phi }-g_{t\phi }^2}, \quad g^{rr}=\frac{1}{g_{rr}}, \quad g^{\theta \theta }=\frac{1}{g_{\theta \theta }}, \\ g^{\phi \phi }&=\frac{g_{tt}}{g_{tt}g_{\phi \phi }-g_{t\phi }^2}, \quad g^{t\phi }=g^{\phi t}=-\frac{g_{t\phi }}{g_{tt}g_{\phi \phi }-g_{t\phi }^2}. \end{aligned} \end{aligned}$$
(68)

The Hamilton–Jacobi equation than takes the form

$$\begin{aligned} \frac{1}{g_{rr}}\left( \frac{d S_{r}(r)}{d r}\right) ^2+\frac{g_{\phi \phi }E^2+2g_{t\phi }EJ+g_{tt}J^2}{g_{tt}g_{\phi \phi }-g_{t\phi }^2}=\mu ^2. \end{aligned}$$
(69)

Using the relation \(p_{r}=g_{rr}\dot{r}=\partial S/\partial r=dS_{r}/dr\), it may be related directly to the radial equation of motion of a particle with rest mass \(\mu \)

$$\begin{aligned} \begin{aligned} \left( \frac{dr}{d\sigma }\right) ^2&=\frac{g_{\phi \phi }E^2+2g_{t\phi }EJ+g_{tt} J^2}{g_{rr}(g_{t\phi }^2-g_{tt}g_{\phi \phi })}+\frac{\mu ^2}{g_{rr}}\\&=\frac{g_{\phi \phi }(E-V_{+})(E-V_{-})}{g_{rr}(g_{t\phi }^2-g_{tt} g_{\phi \phi })}+\frac{\mu ^2}{g_{rr}}, \end{aligned} \end{aligned}$$
(70)

where the solutions of the equation in E

$$\begin{aligned} g_{\phi \phi }E^2+2g_{t\phi }EJ+g_{tt}J^2=0 \end{aligned}$$
(71)

represent the effective potentials

$$\begin{aligned} V_{\pm }(r)=\frac{J}{g_{\phi \phi }}\bigg (-g_{t\phi }\pm \sqrt{g_{t\phi }^2 -g_{tt}g_{\phi \phi }}\bigg ). \end{aligned}$$
(72)

Evaluating the Hamiltonian at the minimum distance of approach of the particle, where \(\dot{r}\) = 0, we find the precise relation between the impact parameter \(\xi =J/E=wb\) and the closest approach distance \(r_{0}\)

$$\begin{aligned} \xi (r_0)=\frac{-g_{t\phi }+\sqrt{(g_{t\phi }^2-g_{tt}g_{\phi \phi })[1 -g_{tt}(1-w^2)]}}{g_{tt}}\Big |_{r_{0}}, \end{aligned}$$
(73)

which reduces to expected photon impact parameter b for stationary axially symmetric metrics, when \(w=c=1\) [74]. The sign in front of the square root is chosen to be positive when the orbital motion of the particle and rotation of the compact object are in the same direction.

The orbital equation of the particle in terms of azimuthal \(\phi \) and radial r coordinates can be obtained by using the fact that the partial derivative of the Jacobi function with respect to the constant of motion J is a constant

$$\begin{aligned} \frac{\partial S}{\partial J}=\phi -\frac{\partial S_{r}(r,E,J)}{\partial J}=const. \end{aligned}$$
(74)

Solving Eq. (69) or taking into account Eq. (70), we obtain the azimuthal shift function of the particle by Eq. (74)

$$\begin{aligned} \begin{aligned}&\phi (r)-\phi (r_{0}) =\frac{\partial S_{r}(r,E,J)}{\partial J} \\&\quad =\quad \int _{r_{0}}^{r}g_{rr}\frac{\partial }{\partial J}\left( \frac{dr}{d\sigma }\right) dr \\&\quad =\pm \int _{r_{0}}^{r}\frac{(g_{t\phi }E+g_{tt}J)}{(g_{t\phi }^2-g_{tt} g_{\phi \phi })} \\&\qquad \times \left[ \frac{g_{\phi \phi }(E-V_{+})(E-V_{-})}{g_{rr} (g_{t\phi }^2-g_{tt}g_{\phi \phi })}+\frac{\mu ^2}{g_{rr}}\right] ^{-1/2}dr\\&\quad =\pm \int _{r_{0}}^{r}\frac{(g_{t\phi }+\xi g_{tt})}{(g_{t\phi }^2-g_{tt}g_{\phi \phi })} \\&\qquad \times \left[ \frac{g_{\phi \phi }(1-\mathcal {V}_{+})(1-\mathcal {V}_{-})}{g_{rr}(g_{t\phi }^2-g_{tt}g_{\phi \phi })}+\frac{1-w^2}{g_{rr}}\right] ^{-1/2} dr, \end{aligned} \end{aligned}$$
(75)

where the sign in front of the integral is changing when the particle passes thought a turning point \(r_{0}\) of the orbital motion. \(\mathcal {V}_{\pm }(r,\xi )\equiv V_{\pm }(r,J)/E\) stand for the effective potentials per unit of the energy and depend directly on the impact parameter \(\xi \). It can be verified that an Eq. (75) is consistent with Eqs. (66) and (70).

Having the azimuthal shift of the photon as a function of the coordinate distance r, we can calculate the deflection angle of the test-particle as we assume that the source \(r_{S}\) and observer \(r_{O}\) are placed in the asymptotically flat region of the spacetime, so that \(r_{S}\rightarrow \infty \) and \(r_{O}\rightarrow \infty \). Then, after calculating the total azimuthal angle according to the orbital equation (75), the deflection angle is

$$\begin{aligned} \hat{\alpha }= & {} \phi (r_{S})-\phi (r_{O})-\pi \end{aligned}$$
(76)
$$\begin{aligned}= & {} 2|\phi (r_{\infty })-\phi (r_{0})|-\pi . \end{aligned}$$
(77)

4.1 Deflection angle by rotating naked singularities

In order to calculate the deflection angle of a test-particle in the spacetime of rotating naked singularities, firstly we will calculate the impact parameter of the test-particle \(\xi =wb\) as a function of the distance of closest approach \(r_{0}\). According to Eq. (73) the equatorial impact parameter of a particle with relativistic velocity w is given by

$$\begin{aligned} \xi (r_{0})=\frac{a\left( 1-\frac{2m}{r_{0}}\right) ^{\gamma }+a+ \sqrt{(r_{0}^2+a^2-2mr_{0})\left[ \left( 1-\frac{2m}{r_{0}}\right) ^{\gamma } (w^2-1)+1\right] }}{\left( 1-\frac{2m}{r_{0}}\right) ^{\gamma }} \end{aligned}$$
(78)

The impact parameter (78) reduces to that for photons, obtained in [75], letting \(w = 1\). For \(a > 0\) the naked singularity rotates counterclockwise, while for \(a < 0\) the naked singularity and the particles rotate in converse direction.

Expecting small deviations in the orbital motion of the test-particles, we will assume that the distance of closest approach \(r_{0}\) is of the same order as the impact parameter b due to the validity of inequalities, \(b\gg m\) and \(b\gg a\). Therefore, considering Eq. (70) in the framework of the assumptions adopted, we suggest the following solution

$$\begin{aligned} r_{0}\simeq b \left\{ 1+\sum \limits _{i,j=1}^{2} c_{m,a}\,\epsilon _{m}^{i}\epsilon _{a}^{j}+\mathcal {O}(\epsilon ^3)\right\} , \end{aligned}$$
(79)

where we are introducing two independent expansion parameters, as the former is in term of metric parameter m related to the ADM mass M and scalar charge q, while the latter is in term of specific angular momentum a of the rotating naked singularity

$$\begin{aligned} \epsilon _{m}=\frac{m}{b}, \quad \epsilon _{a}=\frac{a}{b}. \end{aligned}$$
(80)

Here the coefficients \(c_{m,a}\) are real numbers, and the summation is over all possible combinations of epsilon powers i, j up to and including second order terms.

Applying the procedure to the equation \(\dot{r}(r_{0})=0\) as discussed above, we acquire the following result

$$\begin{aligned} \begin{aligned}&r_{0}\simeq b \left\{ 1+\frac{[w^2-\gamma (1+w^2)]m}{b w^2} \right. \\&\quad + \frac{[w^4+\gamma ^2(1-4w^2-w^4)]m^2}{2w^4b^2}\\&\quad \left. -\frac{a^2}{2b^2}+\frac{2\gamma ma}{w b^2}+\mathcal {O}(\epsilon ^3) \right\} . \end{aligned} \end{aligned}$$
(81)

The calculation of the deflection angle of massive particles in the spacetime of rotating naked singularities requires integration of the first derivative of the azimuthal shift function \(d\phi /dr\), as follows from Eq. (75). Since, we are expecting small deviation in the orbital motion of the particle, we will consider only terms with the most significant contribution, for simplicity. Introducing new small enough parameters \(\varepsilon _{m}=m/r_{0}\) and \(\varepsilon _{a}=a/r_{0}\), we will perform power series expansion of \(d\phi /dr\), in the spacetime under consideration (3), up to and including second order terms of \(\varepsilon _{m}\) and \(\varepsilon _{a}\). After the convenient change of variables \(r=r_{0}/u\), we obtain

$$\begin{aligned} \begin{aligned} \frac{d\phi }{du}&\simeq \frac{1}{\sqrt{1-u^2}} +\left[ \frac{\gamma +w^2\left( u^2+u+\gamma -1\right) }{ w^2(1+u)\sqrt{1-u^2}}\right] \varepsilon _{m} \\&\quad +\frac{1}{2}\left[ \frac{\mathcal {P}_{4}(u\,|\,\gamma ,w)}{w^4(1+u)^2 \sqrt{1-u^2}}\right] \varepsilon _{m}^2\\&\quad \pm \left[ \frac{2 \gamma }{w(1+u) \sqrt{1-u^2}}\right] \varepsilon _{m}\varepsilon _{a} \\&\quad + \frac{1}{2}\left[ \frac{1-2u^2}{\sqrt{1-u^2}}\right] \varepsilon _{a}^2 +\mathcal {O}(\varepsilon ^3), \end{aligned} \end{aligned}$$
(82)

where we are introducing the quartic polynomial in powers of u

$$\begin{aligned} \begin{aligned} \mathcal {P}_{4}(u\,|\,\gamma ,w) =&\, 3w^4u^4+6w^4u^3+(w^4+2w^4\gamma ^2+6w^2\gamma ^2)u^2 \\&- [6w^4-6w^2(w^2+1)\gamma -(4w^2-4)\gamma ^2]u \\&+(w^4+4w^2-1)\gamma ^2-w^4. \end{aligned} \end{aligned}$$

Completing the integration of (82) from the minimal distance of closest approach \(r_{0}\) to observer and source positioned at infinite distance with respect to the center of the compact object, we obtain the following approximate expression for the deflection angle of a massive particle, according to Eq. (76)

$$\begin{aligned} \hat{\alpha }(r_{0})&\simeq \frac{2m\gamma }{r_{0}w^{2}}(1+w^2)\pm \frac{4ma\gamma }{r_{0}^{2}w} \nonumber \\&\quad + \frac{m^2}{4 r_{0}^2 w^4}\Big (\pi w^2 \left[ 4\left( 3+w^2\right) \gamma ^2-w^2\right] \nonumber \\&\quad +8 \gamma \left( 1+w^2\right) \left[ w^2(1-\gamma )-\gamma \right] \Big )+\mathcal {O}(\varepsilon ^3). \end{aligned}$$
(83)

The most significant contribution to the deflection angle of massive particles is given by massive term proportional to \(\mathcal {O}(\varepsilon _{m})\), while the order proportional to angular momentum \(\mathcal {O}(\varepsilon _{a})\) is vanishing. The next second order terms proportional to the mass \(\mathcal {O}(\varepsilon _{m}^2)\) and to the mass and angular momentum \(\mathcal {O} (\varepsilon _{m}\varepsilon _{a})\) give also a contribution, as opposed to the second order term proportional to the square of the angular momentum \(\mathcal {O}(\varepsilon _{a}^2)\), which is missing. Moreover, taking into account the power series (81), we can represent the deflection angle of the relativistic particles in terms of the impact parameter b up to and including the second powers of the small parameters \(\epsilon _{m}\) and \(\epsilon _{a}\). After performing the calculations, we get the following invariant representation of the deflection for a given relativistic velocity w of the massive particle

$$\begin{aligned} \hat{\alpha }(b)&\simeq \frac{2m\gamma }{b w^{2}}(1+w^2) + \frac{m^2\gamma ^2}{b^2}\left( 1+\frac{3}{w^2}-\frac{1}{4\gamma ^2} \right) \pi \nonumber \\&\quad \pm \frac{4ma\gamma }{b^{2}w}+\mathcal {O}(\epsilon ^3). \end{aligned}$$
(84)

By comparison of the calculated approximate expression for the deflection angle of massive particles (84) via geodesic approach with the result (38) found by GBT it appears that up to the second formal order in the expansion parameters the both angles coincide. Letting \(w=1\), we recover the light deflection angle

$$\begin{aligned} \hat{\alpha }(b) \simeq \frac{4m\gamma }{b}+\frac{4m^2\gamma ^2}{b^2} \left( 1-\frac{1}{16\gamma ^2}\right) \pi \pm \frac{4ma\gamma }{b^2}+ \mathcal {O}(\epsilon ^3), \end{aligned}$$
(85)

presented in the static case in [5, 75, 76]. Similarly, the plus (minus) sign represents the retrograde (prograde) light ray, respectively.

4.2 Deflection angle by Kerr-like wormholes

In the case of the Kerr-like wormhole (39) the impact parameter of the massive particles \(\xi =wb\) with relativistic velocity w and the minimal distance of closest approach \(r_{0}\) obey the following relation

$$\begin{aligned} \xi (r_{0})=\frac{-2Ma+\sqrt{r_{0}(r_{0}^2+a^2-2Mr_{0}) \big [r_{0}-(r_{0}-2M)(1-w^2)\big ]}}{r_{0}-2M} \end{aligned}$$
(86)

Since, we are considering propagation of massive particles in the asymptotically flat spacetime regions with geometrical curvature, causing small deflection angles of trajectories, then \(r_{0}\) is expected to be of the same order as the impact parameter b. Therefore, under assumptions \(b\gg M\) and \(b\gg a\), we are taking advantage of the two small enough expansion parameters

$$\begin{aligned} \epsilon _{M}=\frac{M}{b}, \quad \epsilon _{a}=\frac{a}{b}, \end{aligned}$$
(87)

where M and a are the mass and spin of the Kerr-like wormhole, respectively. Hence, we could find an approximate solution of the radial Eq. (70), as for itself we suggest the ansatz

$$\begin{aligned} r_{0}\simeq b \left\{ 1+\sum \limits _{i,j=1}^{2} c_{M,a}\,\epsilon _{M}^{i}\epsilon _{a}^{j}+\mathcal {O}(\epsilon ^3)\right\} , \end{aligned}$$
(88)

Here the coefficients \(c_{M,a}\) are real numbers.

Solving the equation \(\dot{r}(r_{0})=0\), for the closest approach distance we obtain the following power series expansion

$$\begin{aligned} \begin{aligned} r_{0}\simeq b \left\{ 1 -\frac{M}{b w^2}+\frac{(1-4w^2)M^2}{2w^4b^2}-\frac{a^2}{2b^2}+\frac{2Ma}{b^2 w} +\mathcal {O}(\epsilon ^3) \right\} . \end{aligned} \end{aligned}$$
(89)

Now, we can proceed ahead toward finding of the perturbative expansion of the deflection angle of a massive particle moving in the spacetime of the Kerr-Like wormhole. Since, we are interested in the weak deflection limit, we will perform power series expansion of the derivative \(d\phi /dr\), adopting the new small parameters \(\varepsilon _{M}=M/r_{0}\) and \(\varepsilon _{a}=a/r_{0}\) up to and including second order terms. In order to perform the integration afterwards more easily, we introduce a new variable \(u=r_{0}/r\) in terms of which we obtain

$$\begin{aligned} \begin{aligned} \frac{d\phi }{du}&\simeq \frac{1}{\sqrt{1-u^2}} +\left[ \frac{1+w^2 (1+\lambda ^2)(1+u)u}{w^2(1+u)\sqrt{1-u^2}}\right] \varepsilon _{m} \\&\quad +\frac{1}{2}\left[ \frac{\mathcal {P}_{4}(u\,|\,\lambda ,w)}{w^4(1+u)^2 \sqrt{1-u^2}}\right] \varepsilon _{m}^2 \\&\quad \pm \left[ \frac{2}{w(1+u)\sqrt{1-u^2}}\right] \varepsilon _{m} \varepsilon _{a} \\&\quad + \frac{1}{2}\left[ \frac{1-2u^2}{\sqrt{1-u^2}}\right] \varepsilon _{a}^2 +\mathcal {O}(\varepsilon ^3), \end{aligned} \end{aligned}$$
(90)

where it is introduced the fourth degree polynomial in variable u

$$\begin{aligned} \begin{aligned} \mathcal {P}_{4}(u\,|\,\lambda ,w) = \;&3w^4(1+\lambda ^2)^2u^4+6w^4(1+\lambda ^2)^2u^3 \\&+w^2[3w^2(1+\lambda ^2)^2+2(3+\lambda ^2)]u^2 \\&+2[w^2(5+\lambda ^2)-2]u + 4w^2-1. \end{aligned} \end{aligned}$$

Therefore, the bending angle of the light ray, defined by Eq. (76), up to and including the second orders of the expansion parameters \(\varepsilon _{M}\) and \(\varepsilon _{a}\) is given by

$$\begin{aligned} \hat{\alpha }(r_{0})&\simeq \frac{2M}{r_{0}}\left( 1+\lambda ^2+\frac{1}{w^2} \right) \pm \frac{4Ma}{r_{0}^{2}}\frac{1}{w}\nonumber \\&\quad + \frac{M^2}{4 r_{0}^2 w^4}\Big (3\pi w^4(1+\lambda ^2)^2+4w^2 [3\pi \nonumber \\&\quad -2+(\pi -2)\lambda ^2]-8\Big )+\mathcal {O}(\varepsilon ^3). \end{aligned}$$
(91)

Taking advantage of the power series (89) we can represent the deflection angle of the relativistic particles in terms of the impact parameter b, up to and including second order terms of the small parameters \(\epsilon _{M}\) and \(\epsilon _{a}\). Therefore, the deviation of trajectories of the massive particles by the Kerr-like wormhole leads to the following components of the deflection angle

$$\begin{aligned} \hat{\alpha }(b)&\simeq \frac{2M}{b}\left( 1+\lambda ^2+\frac{1}{w^2}\right) +\frac{M^2}{b^2}\left[ \frac{3(1+\lambda ^2)^2}{4}+\frac{3+\lambda ^2}{w^2} \right] \pi \nonumber \\&\quad \pm \frac{4Ma}{b^2}\frac{1}{w} +\mathcal {O}\left( \epsilon ^3\right) . \end{aligned}$$
(92)

As in the previous case of the rotating naked singularities, here as well the most significant contribution to the deflection angle is given by the massive term proportional to \(\mathcal {O} (\epsilon _{M})\). The second order terms proportional to the mass \(\mathcal {O}(\epsilon _{M}^2)\) and to the mass and angular momentum of the wormhole \(\mathcal {O}(\epsilon _{M}\epsilon _{a})\) give a contribution to the deflection angle of the relativistic massive particles. The first and second order terms based on the wormhole’s angular momentum, \(\mathcal {O}(\epsilon _{a})\) and \(\mathcal {O}(\epsilon _{a}^2)\) respectively, do not contribute in the perturbative analysis. In the special case \(w=c=1\), from expression (92) the deflection angle of light is recovered [63]

$$\begin{aligned} \hat{\alpha }(b)&\simeq \frac{2M}{b}\left( 2+\lambda ^2\right) +\frac{M^2}{b^2}\left[ \frac{3(1+\lambda ^2)^2}{4}+\lambda ^2+3\right] \pi \nonumber \\&\quad \pm \frac{4Ma}{b^2} +\mathcal {O}\left( \epsilon ^3\right) . \end{aligned}$$
(93)

Comparing between the obtained results for the deflection angles (58) and (92) via the GBT and geodesic approach respectively, shows coincidence of the perturbative expressions up to the leading terms proportional to \(\mathcal {O}(\epsilon _{M}^2)\) and \(\mathcal {O}(\epsilon _{M}\epsilon _{a})\).

Fig. 3
figure 3

The deflection angle as a function of b. We chose \(\lambda =0.1\), \(w=0.8\),\(\gamma =0.6\), \(m=M=a=1\)

Full size image

5 Conclusions

We studied the gravitational deflection of massive/massless particles in a rotating naked singularities and Kerr-Like wormholes backgrounds. In the first part of this paper, we used a recent geometric approach to compute the gravitational deflection angle using the refractive index of the optical media and by utilizing the GBT applied to the optical metric. In order to incorporate the effect of relativistic speed on the deflection angle, we have assumed the propagating massive particles as a de Broglie wave packets yielding a modification of the refractive index N, and a constant quantity of a given optical media, \(\lambda N=const\). In particular, we have shown that the refractive index and the Gaussian optical curvature are affected by the mass M, angular momentum parameter a, naked singularity parameter \(\gamma \), the deformation parameter \(\lambda \), and the relativistic velocity of the particle w. Although the geodesic curvature \(\kappa (C_R)\) is slightly modified due the velocity of the particle, i.e. \(\kappa (C_R) \rightarrow w R^{-1}\), we have shown that the expression for the deflection angle reads

$$\begin{aligned} \hat{\alpha }=-\int \limits _{0}^{\pi }\int \limits _{r_{\gamma }}^{\infty }\, \mathcal {K}\,dS. \end{aligned}$$

In other words we have found exactly the same expression as in the case of deflection of light, which suggests that the above result can be viewed as a form-invariant quantity for asymptotically flat spacetimes. Again, the total deflection angle is found by integrating over a domain outside the light ray described by \(r_{\gamma }\), hence the global effects are important. Note that in our setup we have simplified the problem by considering a linearized spacetime metrics and we have also assumed that the source and the observer are located at infinity. Applying then the GBT to the isotropic metrics we have found two interesting results for the deflection angles, namely

$$\begin{aligned} \hat{\alpha }_{Naked\, sing.}\simeq \frac{2 m \gamma }{b w^2}(1+w^2) \pm \frac{4 m a \gamma }{b^2 w} \end{aligned}$$

in the case of rotating naked singularity, and

$$\begin{aligned} \hat{\alpha }_{Kerr-like \,wormhole}\simeq \frac{2M}{b}\left( 1+\lambda ^2+\frac{1}{w^2}\right) \pm \frac{4Ma}{b^2}\frac{1}{w} \end{aligned}$$

in the case of Kerr-like wormholes. From the last two equations we see that an apparent singularity appears when \(w\rightarrow 0\), therefore an additional constraint should be imposed, namely \(0 < w \le 1\). Now we specialize further the case of \(\lambda =0\) and \(\gamma =1\), in that case both results coincide with the Kerr deflection angle for massive particles reported recently in [52], but also in [77, 78]. Note that our approach works perfectly well for relativistic particles, in this sense the apparent singularity is not problematic. Furthermore, we did a careful analyses by studying the problem of deflection of particles using the Hamilton–Jacobi equation and we find agreement of results in leading order terms. Our results show that, while the deflection angle decreases with \(\gamma \) in the case of JNW spacetime, contrary to this, the deflection angle increases with the deformation parameter \(\lambda ^2\) in the case of Kerr-like wormholes as can be seen from Fig. 3. Our results are not important only from conceptual point of view, namely the difference between deflection angels may shed light from observational point of view in order to distinguish the two spacetimes. Finally, we plan in the near future to extend these results by including finite distance corrections on the deflection angle, in other words by assuming that the distance between the source and the observer is finite.