1 Introduction

The phenomenon of gravitational collapse has become a widely investigated subject due to its many interesting applications in astrophysics. The first solution for the non-adiabatic collapse of a spherically symmetric matter distribution in the form of a dust cloud and having a Schwarzschild exterior was produced by Oppenheimer and Snyder [1]. Taking into consideration that a radiating collapsing mass distribution has outgoing energy, its exterior spacetime is no longer a vacuum but contains null radiation. In this regard, Vaidya [2] obtained an exact solution to the Einstein field equations which describe the exterior field of a radiating spherically symmetric fluid. Santos [3] derived the junction conditions for a collapsing spherically symmetric shear-free non-adiabatic fluid with heat flow. This pioneering work allowed for the matching of the interior and exterior spacetimes of a collapsing star, and paved the way for the study of dissipative gravitational collapse. For some interesting developments on the subject of dissipative collapse, refer to [4,5,6,7,8,9,10].

When a system initially in static equilibrium experiences a disturbance or a perturbation, the stability of that system is affected. Dynamical stability is the property of a system to retain its stable state under a perturbation. The problem of stability is an important one in the study of self-gravitating objects because a static stellar model is of little significance if it proves to be highly unstable under collapse. Also, depending on the extent of instability of a system in collapse, the resulting patterns of evolution will vary. Hence the stability problem has become a subject of much investigation.

Chandrasekhar [11] was the first to examine the dynamical instability of a spherically symmetric mass with isotropic pressure. With the aid of the adiabatic index \(\varGamma \), he showed that for a system to remain stable under collapse, \(\varGamma \) must be greater than \(\frac{4}{3}\). Following this, much has been written in the literature about dynamical instability. Herrera et al. [12] studied the instability range for a non-adiabatic sphere and showed that relativistic corrections as a result of heat flow decreases the unstable range of \(\varGamma \) and renders the fluid less unstable. Chan et al. [13] investigated the stability criteria by deviating from the perfect fluid condition in two ways : they considered radiation in the free-streaming approximation, and they assumed local anisotropy of the fluid. Herrera et al. [14] also examined the dynamical instability of expansion-free, locally anisotropic spherical stellar bodies.

In this work, we consider a spherically symmetric static configuration undergoing radiative collapse. We assume shear-free and isotropic conditions. We impose a linear equation of state of the form \(p_r = \gamma \mu \) on the perturbed radial pressure and energy density, and we obtain the complete gravitational behaviour of the collapsing star. The stability ranges have been explored through the adiabatic index \(\varGamma \) for the Newtonian and post-Newtonian regimes.

The structure of this paper is as follows: In Sect. 2 we introduce the field equations describing the geometry and matter content for a star undergoing shear-free gravitational collapse. In Sect. 3 we present the exterior spacetime and the junction conditions necessary for the smooth matching of the interior spacetime with Vaidya’s exterior solution across the boundary. In Sect. 4 the perturbative scheme is described and the field equations for the static and perturbed configurations are given. In Sect. 5 we present the temporal equation employed in the perturbative scheme that begins with an initially static star that is perturbed so that the perturbations decay exponentially with time. Sect. 6 presents respectively a radiating and a static model . In Sect. 7 we discuss dissipative collapse, express the perturbed quantities in terms of two unspecified quantities and introduce an equation of state which allows us to present the perturbed quantities in terms of r only . We explore the stability of our collapsing model in the Newtonian and post-Newtonian approximations in Sect. 8, and our results are discussed in Sect. 9.

2 Interior spacetime

The line element for the interior of a spherically symmetric, shear-free spacetime in simultaneously comoving and isotropic coordinates is

$$\begin{aligned} ds^2 = -A^2dt^2 + B^2\left[ dr^2 + r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2)\right] \end{aligned}$$
(1)

where \(A = A(t,r)\) and \(B = B(t,r)\) are the metric functions. The interior matter content is that of a spherical fluid undergoing dissipation in the form of a radial heat flow and producing pure radiation. The energy-momentum tensor for the interior matter distribution is given by

$$\begin{aligned} T_{ab}= & {} (\mu + p_t)w_a w_b + p_tg_{ab} \nonumber \\&+ (p_r - p_t)X_aX_b + q_aw_b + q_b w_a , \end{aligned}$$
(2)

where \(\mu \) is the energy density, \(p_r\) the radial pressure, \(p_t\) the tangential pressure and \(q_a\) the heat flux. \(w_a\) is the four-velocity of the fluid and \(X_a\) is a unit four-vector along the radial direction. These quantities must satisfy the conditions \(w_aw^a = -1\), \(w_aq^a = 0\), \(X_aX^a = 1\) and \(X_aw^a = 0\).

Furthermore, in comoving coordinates we have

$$\begin{aligned} w^a= & {} A^{-1}\delta ^a_0 \end{aligned}$$
(3)
$$\begin{aligned} q^a= & {} q\delta ^a_1 \end{aligned}$$
(4)

and

$$\begin{aligned} X^a = B^{-1}\delta ^a_1 \end{aligned}$$
(5)

The nonzero components of the Einstein field equations for the line element (1) and the energy momentum (2) are

$$\begin{aligned}&\mu = - \frac{1}{B^2}\left[ 2\frac{B^{\prime \prime }}{B} - \left( \frac{B^{\prime }}{B}\right) ^2 +\frac{4}{r}\frac{B^{\prime }}{B}\right] +\frac{3}{A^2}\left( \frac{{\dot{B}}}{B}\right) ^2, \end{aligned}$$
(6)
$$\begin{aligned}&p_r = \frac{1}{B^2}\left[ \left( \frac{B^{\prime }}{B}\right) ^2 + \frac{2}{r}\left( \frac{A^{\prime }}{A}+ \frac{B^{\prime }}{B}\right) + 2\frac{A^{\prime }}{A}\frac{B^{\prime }}{B}\right] \nonumber \\ \nonumber \\&\qquad \,\,+ \frac{1}{A^2}\left[ -2\frac{{\ddot{B}}}{B} - \left( \frac{\dot{B}}{B}\right) ^2 + 2\frac{\dot{A}}{A}\frac{\dot{B}}{B}\right] \end{aligned}$$
(7)
$$\begin{aligned}&p_t = \frac{1}{A^2}\left[ -2\frac{{\ddot{B}}}{B} -\left( \frac{\dot{B}}{B}\right) ^2 +2 \frac{\dot{A}}{A}\frac{\dot{B}}{B}\right] \nonumber \\&\qquad \,\, + \frac{1}{B^2}\left[ \frac{B^{\prime \prime }}{B} -\left( \frac{B^{\prime }}{B}\right) ^2+\frac{1}{r} \left( \frac{A^{\prime }}{A}+\frac{B^{\prime }}{B}\right) +\frac{A^{\prime \prime }}{A}\right] \end{aligned}$$
(8)
$$\begin{aligned}&q = \frac{2}{AB^2}\left[ \frac{{\dot{B}}^{\prime }}{B}-\frac{\dot{B}}{B}\left( \frac{B^{\prime }}{B}+\frac{A^{\prime }}{A}\right) \right] \end{aligned}$$
(9)

where the dots and primes represent partial derivatives with respect to t and r respectively.

3 Exterior spacetime and junction conditions

Spacetime is divided by the boundary of a star into two distinct regions, the interior spacetime described by the metric (1) and the exterior spacetime. Since the collapsing star is radiating energy, the exterior spacetime is not a vacuum and is therefore described by Vaidya’s metric

$$\begin{aligned} ds^2_+ = -\left[ 1 - \frac{2m(v)}{r}\right] dv^2 - 2dvdr + r^2 d\theta ^2 + r^2\sin ^2\theta d\phi ^2 \end{aligned}$$
(10)

where m(v) represents the Newtonian mass of the gravitating body as measured by an observer at infinity.

The junction conditions to be satisfied across the boundary of the star are

$$\begin{aligned} \left( K^+_{ij} - K^-_{ij}\right) _{\varSigma } = 0 \end{aligned}$$
(11)

and

$$\begin{aligned} \left( ds^2_+ - ds^2_-\right) _{\varSigma } =0 \end{aligned}$$
(12)

where \(K_{ij}\) is the extrinsic curvature on the two sides of the boundary.

Following similar calculations as in de Oliveira et al. [15] we obtain

$$\begin{aligned}&\left( p_r\right) _{\varSigma } = \left( qB\right) _{\varSigma } \end{aligned}$$
(13)
$$\begin{aligned}&\left( qB\right) _{\varSigma } = -\left( \frac{2}{r^2}{{\dot{v}}^2}\frac{dm}{dv}\right) _{\varSigma } \end{aligned}$$
(14)
$$\begin{aligned}&\left( rB\right) _{\varSigma } = r_{\varSigma } \end{aligned}$$
(15)
$$\begin{aligned}&m(v) = \left( \frac{r^3B{\dot{B}}^2}{2A^2} - r^2{B^{\prime }} - \frac{r^3{{B^{\prime }}^2}}{2B}\right) _{\varSigma } \end{aligned}$$
(16)

and

$$\begin{aligned} \left( A dt\right) _{\varSigma } = \left( 1 - \frac{2m}{r} + 2\frac{dr}{dv}\right) ^{1/2}_{\varSigma } dv \end{aligned}$$
(17)

Equations (13)–(17) represent respectively the following conditions at the time-like hypersurface \(\varSigma \) : conservation of momentum flux, conservation of radiation flux, radius of \(\varSigma \) in both coordinate systems, total energy inside \(\varSigma \) and the relationship between the two times t and v.

The total energy entrapped within a radius \(r = r_\varSigma \) is given by

$$\begin{aligned} m(r,t) = \frac{r^3B{\dot{B}}^2}{2A^2} - r^2{B^{\prime }} - \frac{r^3{{B^{\prime }}^2}}{2B} \end{aligned}$$
(18)

4 The perturbed equations

We assume that the fluid is initially in static equilibrium, hence the fluid is described by quantities that are not time-dependent, ie they are expressed in terms of the radial coordinate only. We then assert that the static system is perturbed, undergoing slow shear-free collapse and producing pure radiation. We denote the quantities such as energy density, radial pressure and tangential pressure of the static system by a zero subscript and those of the perturbed fluid by an overhead bar. We further assume that the metric functions A(r, t) and B(r, t) have the same time dependence in their perturbations. This assumption would imply that the perturbed material functions also have the same time dependence.

Therefore the metric functions and the material functions are given by

$$\begin{aligned}&A(r,t) = A_0(r) + \epsilon a(r)T(t) \end{aligned}$$
(19)
$$\begin{aligned}&B(r,t) = B_0(r) + \epsilon b(r)T(t) \end{aligned}$$
(20)
$$\begin{aligned}&\mu (r,t)= \mu _0(r) + \epsilon {\bar{\mu }}(r,t) \end{aligned}$$
(21)
$$\begin{aligned}&p_r(r,t) = p_{r0}(r) + \epsilon {{\bar{p}}}_r(r,t) \end{aligned}$$
(22)
$$\begin{aligned}&p_t(r,t) = p_{t0}(r) + \epsilon {{\bar{p}}}_t(r,t) \end{aligned}$$
(23)
$$\begin{aligned}&m(r,t) = m_0(r) + \epsilon {\bar{m}}(r,t) \end{aligned}$$
(24)

where we assume that \(0 < \epsilon \ll 1\)

Einstein’s field equations for the static configuration are

$$\begin{aligned}&\mu _0 = - \frac{1}{B_0^2}\left[ 2\frac{B_0^{\prime \prime }}{B_0} - \left( \frac{B_0)^{\prime }}{B_0}\right) ^2 +\frac{4}{r}\frac{B_0^{\prime }}{B_0}\right] \end{aligned}$$
(25)
$$\begin{aligned}&p_{r0} \frac{1}{B_0^2}\left[ \left( \frac{B_0^{\prime }}{B_0}\right) ^2 + \frac{2}{r}\left( \frac{A_0^{\prime }}{A_0}+ \frac{B_0^{\prime }}{B_0}\right) + 2\frac{A_0^{\prime }}{A_0}\frac{B_0^{\prime }}{B_0}\right] \end{aligned}$$
(26)
$$\begin{aligned}&p_{t0} = \frac{1}{B_0^2}\left[ \frac{B_0^{\prime \prime }}{B_0}-\left( \frac{B_0^{\prime }}{B_0}\right) ^2+\frac{1}{r}\left( \frac{A_0^{\prime }}{A_0}+\frac{B_0^{\prime }}{B_0}\right) +\frac{A_0^{\prime \prime }}{A_0}\right] \end{aligned}$$
(27)

The perturbed field equations up to first order in \(\epsilon \) can be written as

$$\begin{aligned}&{\bar{\mu }} = -3\mu _0\frac{b}{B_0}T + \frac{1}{B_0^3} \nonumber \\&\qquad \,\,\times \left[ -\left( \frac{B_0^{\prime }}{B_0}\right) ^2 b + 2\left( \frac{B_0^{\prime }}{B_0} - \frac{2}{r}\right) b^{\prime } - 2b^{\prime \prime }\right] T \end{aligned}$$
(28)
$$\begin{aligned}&{\bar{p}}_r = -2p_{r0}\frac{b}{B_0}T + \frac{2}{B_0^2}\left[ \left( \frac{B_0^{\prime }}{B_0} + \frac{1}{r} + \frac{A_0^{\prime }}{A_0}\right) \left( \frac{b}{B_0}\right) ^{\prime }\right. \nonumber \\&\qquad \,\,\left. + \left( \frac{B_0^{\prime }}{B_0}+ \frac{1}{r}\right) \left( \frac{a}{A_0}\right) ^{\prime }\right] T- 2\frac{b}{{A_0^2}B_0}{{\ddot{T}}} \end{aligned}$$
(29)
$$\begin{aligned}&{\bar{p}}_t = -2p_{t0}\frac{b}{B_0}T \nonumber \\&\qquad \,\,+ \frac{1}{B_0^2}\left[ \left( \frac{b}{B_0}\right) ^{\prime \prime } + \frac{1}{r}\left( \frac{b}{B_0}\right) ^{\prime } + 2\frac{A_0^{\prime }}{A_0}\left( \frac{a}{A_0}\right) ^{\prime } \right. \nonumber \\&\qquad \,\,\left. +\left( \frac{a}{A_0}\right) ^{\prime \prime }+ \frac{1}{r}\left( \frac{a}{A_0}\right) ^{\prime }\right] T - 2\frac{b}{{A_0^2}B_0}{{\ddot{T}}} \end{aligned}$$
(30)
$$\begin{aligned}&qB = \frac{2}{B_0}\left( \frac{b}{A_0 B_0}\right) ^{\prime }{\dot{T}} \end{aligned}$$
(31)

The total energy entrapped up to radius r inside \(\varSigma \) for the static and perturbed configurations are respectively given by

$$\begin{aligned}&m_0(r_{\varSigma }) = -\left( r^2{B_0^{\prime }} + \frac{r^3{{B_0^{\prime }}^2}}{2B_0}\right) _{\varSigma } \end{aligned}$$
(32)
$$\begin{aligned}&{\bar{m}}(r_{\varSigma },t) = -\left( \left[ {r^2}b^{\prime } + \frac{r^3{{B_0^{\prime }}^2}}{2B_0} \left( 2\frac{b^{\prime }}{B_0^{\prime }}-\frac{b}{B_0}\right) \right] T(t)\right) _{\varSigma }\nonumber \\ \end{aligned}$$
(33)

The smooth matching of the interior spacetime to the Vaidya exterior is facilitated by using the junction conditions derived by Santos [3], and we may rewrite Eqs. (29) and (31) as

$$\begin{aligned} {\bar{p}}_r = -2p_{r0}\frac{b}{B_0}T +\frac{2b}{{A_0^2}B_0}\left( {\alpha }T - {{\ddot{T}}}\right) \end{aligned}$$
(34)

and

$$\begin{aligned} qB = \frac{4b}{{A_0^2}B_0}{\beta }{\dot{T}} \end{aligned}$$
(35)

where

$$\begin{aligned} \alpha (r)= & {} \frac{A_0^2}{B_0 b}\left[ \left( \frac{B_0^{\prime }}{B_0} + \frac{1}{r} + \frac{A_0^{\prime }}{A_0}\right) \left( \frac{b}{B_0}\right) ^{\prime } \right. \nonumber \\&\left. + \left( \frac{B_0^{\prime }}{B_0}+ \frac{1}{r}\right) \left( \frac{a}{A_0}\right) ^{\prime }\right] \end{aligned}$$
(36)

and

$$\begin{aligned} \beta (r) = \frac{A_0^2}{2b}\left( \frac{b}{A_0B_0}\right) ^{\prime } \end{aligned}$$
(37)

5 The temporal equation of the perturbations

We make use of the junction condition \(\left( {\bar{p}}_r\right) _{\varSigma } = \left( qB\right) _{\varSigma }\) together with the fact that \(\left( p_{r0}\right) _{\varSigma } = 0\) to obtain

$$\begin{aligned} \alpha _{\varSigma }T - {{\ddot{T}}} = 2 {\beta }_{\varSigma }{\dot{T}} \end{aligned}$$
(38)

which has a particular solution

$$\begin{aligned} T(t) = -\exp \left[ \left( -\beta _{\varSigma }+\sqrt{\alpha _{\varSigma }+\beta ^2_{\varSigma }}\right) t\right] \end{aligned}$$
(39)

where we have assumed that \(\alpha _{\varSigma } > 0\) and \(\beta _{\varSigma } < 0\). This solution represents a system in static equilibrium that starts to collapse at \(t = -\infty \) and continues to collapse as t increases. The solution (39) has been used by many authors investigating gravitational collapse. This solution formed the basis of the work of Chan et al. [13] in which they investigated the dynamical instability for radiating anisotropic collapse. More recently, Govender et al. [16] used the solution in their investigation on the role of shear in dissipative collapse.

6 A radiating model

In order to provide an analysis of the collapse process, we select a particular model in which the following quantities are specified:

$$\begin{aligned}&A_0(r) = c_1 - \frac{c_2\left( 1-r^2\right) }{1+r^2} \end{aligned}$$
(40)
$$\begin{aligned}&B_0(r) = \frac{2R}{1+r^2} \end{aligned}$$
(41)
$$\begin{aligned}&T(t) = - e^{\lambda t} \end{aligned}$$
(42)

where \(c_1\) , \(c_2\) and R are constants and \(\lambda = -\beta _{\varSigma } + \sqrt{\alpha _{\varSigma }+\beta ^2_{\varSigma }}\). Then (25) and (26) can be written as

$$\begin{aligned}&\mu _0 = \frac{3}{R^2} \end{aligned}$$
(43)
$$\begin{aligned}&p_{r0} = -\frac{c_1 - 3c_2 + r^2\left( c_1 + 3c_2\right) }{R^2\left( c_1 -c_2 +r^2\left( c_1 + c_2\right) \right) } \end{aligned}$$
(44)

which is the Schwarzschild constant density sphere.

7 Dissipative collapse

Using (19)–(24) together with (40)–(42) we obtain the perturbative quantities as follows :

$$\begin{aligned} {\bar{\mu }}= & {} \frac{e^{\lambda t}\left( r^2 +1\right) }{4rR^3}\left[ 2r\left( r^2 +9\right) b(r)\right. \nonumber \\&\left. +\left( 4r^4 +6r^2 +2\right) b^{\prime }(r) +r\left( r^2 + 1\right) ^2 b^{\prime \prime }(r)\right] \nonumber \\ \end{aligned}$$
(45)
$$\begin{aligned} {\bar{p}}_r= & {} -\frac{1}{R^3 r\left( r^2+1\right) \left( c_1 - c_2 +r^2\left( c_1+c_2\right) \right) ^2} \nonumber \\&\times \left[ 16c_2 e^{\lambda t}R^3 r \left( r^2-1\right) a(r)\right. \nonumber \\&\left. + \left( r^2+1\right) \left\{ 2r\left( r^2+1\right) \right. \right. \nonumber \\&\times \left. \left. \langle c_1^2\left( r^2+1\right) ^2\left( r^2+2e^{\lambda t}-1\right) \right. \right. \nonumber \\&\left. \left. +c_2^2\left( r^2-1\right) \left( r^4-6r^2+1+6e^{\lambda t}\left( r^2-1\right) \right) \right. \right. \nonumber \\&\left. \left. +2c_1c_2\left( r^6+1+4e^{\lambda t}\left( r^4-1\right) -3r^2\left( r^2+1\right) \right) \right. \right. \nonumber \\&\left. \left. -2e^{\lambda t}R^2{\lambda ^2}\left( r^2+1\right) ^2\rangle b(r)\right. \right. \nonumber \\&\left. \left. +\left( c_1-2c_2+r^2\left( c_1+c_2\right) \right) \right. \right. \nonumber \\&\times \left. \left. \left( -4e^{\lambda t}R^3\left( r^2-1\right) a^{\prime }(r) +\left( r^2+1\right) ^2\right. \right. \right. \nonumber \\&\times \left. \left. \left. \left( -c_1+c_2-6c_2r^2+r^4\left( c_1+c_2\right) \right) b^{\prime }(r)\right) \right\} \right] \nonumber \\ \end{aligned}$$
(46)
$$\begin{aligned} {\bar{p}}_t= & {} -\frac{e^{\lambda t}\left( r^2+1\right) }{8R^3r\left( c_1-c_2+r^2\left( c_1+c_2\right) \right) ^2} \nonumber \\&\times \left[ 16c_2Rr\left( r^2-1\right) a(r)\right. \nonumber \\&\left. +\left\{ 4r\langle c_1^2\left( r^2+1\right) ^2\left( r^2+3\right) \right. \right. \nonumber \\&\left. \left. +c_2^2\left( r^4-2r^2+1\right) \left( r^2+7\right) \right. \right. \nonumber \\&\left. \left. +2c_1c_2\left( r^6+5r^4-r^2-5\right) -2R^2{\lambda ^2}\left( r^2+1\right) ^2\rangle b(r)\right. \right. \nonumber \\&\left. \left. +\left( r^2+1\right) \left( c_1-c_2+r^2\left( c_1+c_2\right) \right) \left\langle 2R\left( r^2+1\right) a^{\prime }(r)\right. \right. \right. \nonumber \\&\left. \left. \left. +\left( 5r^2+1\right) \left( c_1-c_2+r^2\left( c_1+c_2\right) \right) b^{\prime }(r)\right. \right. \right. \nonumber \\&\left. \left. \left. +2Rr\left( r^2+1\right) a^{\prime \prime }(r)\right. \right. \right. \nonumber \\&\left. \left. \left. +\left( \left( r^3+r\right) \left( c_1-c_2+r^2\left( c_1+c_2\right) \right) \right) b^{\prime \prime }(r)\right\rangle \right\} \right] \nonumber \\ \end{aligned}$$
(47)
$$\begin{aligned} Q= & {} -\frac{{\lambda }e^{\lambda t}\left( r^2+1\right) ^2}{2R^2\left( c_1-c_2+r^2\left( c_1+c_2\right) \right) ^2} \nonumber \\&\times \left[ 2r\left( c_1-3c_2+r^2\left( c_1+c_2\right) \right) b(r)\right. \nonumber \\&\left. +\left( r^2+1\right) \left( c_1-c_2+r^2\left( c_1+c_2\right) \right) b^{\prime }(r)\right] \end{aligned}$$
(48)

where we have written \(Q = qB\). We note that (45)–(48) contain two unspecified quantities, namely a(r) and b(r). Following Chan et al. [13] we adopt the following form for b(r)

$$\begin{aligned} b(r) = \left( 1+\xi f(r)\right) A_0B_0 \end{aligned}$$
(49)

where we choose \(f(r)=r^2\). Then Eq. (31) together with (49) can be expressed as

$$\begin{aligned} qB = \frac{2}{B_0}{\xi }{ f^{\prime }}{\dot{T}}. \end{aligned}$$
(50)

Note that, for our choice of f(r), \(f^{\prime }(r) = 2r > 0\). Furthermore, \({\dot{T}} < 0\) since the fluid is collapsing. The heat flow is positive so it follows that \(\xi < 0\). For dissipative collapse \(\xi \ne 0\). We observe that for \(\xi = 0\) the heat flow vanishes.

In order to determine a(r) we impose an equation of state of the form

$$\begin{aligned} {\bar{p}}_r = \gamma {\bar{\mu }} \end{aligned}$$
(51)

which yields

$$\begin{aligned} 0= & {} \frac{1}{Rr\left( r^2+1\right) \left( c_1-c_2+r^2\left( c_1+c_2\right) \right) } \nonumber \\&\times \left[ -4c_2r\left( r^2-1\right) \left( \left( r^2+1\right) ^3\right) a(r)\right. \nonumber \\&\left. + \left( c_1-c_2+r^2\left( c_1+c_2\right) \right) \right. \nonumber \\&\times \left. \Bigg \{2r\langle \left( 2R^2{\lambda ^2}\left( \left( 1+r^2\right) ^3\right) \left( 1+r^2{\xi }\right) \right) \right. \nonumber \\&\left. +2c_1c_2\left( 1+r^2\right) \left[ \left( 3+9{\gamma }+6R{\gamma }\left( -2+{\xi }\right) +{\xi }\right) \right. \right. \nonumber \\&\left. \left. +r^8\xi - r^6\left( 5+\left( 9+2R\right) \gamma \right) \xi \right. \right. \nonumber \\&\left. \left. - r^4\left( 3+6\xi +\left( 9+2R\xi \right) \gamma \right) \right. \right. \nonumber \\&\left. \left. + r^2\left( 6R\gamma \left( 2 - 3\xi \right) +\xi +9\gamma \xi \right) \right] +c_1^2\left( \left( r^2+1\right) ^2\right) \right. \nonumber \\&\times \left. \left[ -2- \xi + r^6\xi - r^4\left( 1+\left( 9+2R\right) \gamma \right) \xi - r^2(2+3\xi \right. \right. \nonumber \\&\left. \left. +\left( 9+9\xi +2R\xi \right) \gamma )+\left( -9+6R-6R\xi \right) \gamma \right] \right. \nonumber \\&\left. +c_2^2\left[ -4-\xi +r^10\xi - r^8\left( 9+9\gamma +2R\gamma \right) \xi \right. \right. \nonumber \\&\left. \left. - r^6\left( 4+10\xi +\left( 9-9\xi +2R\xi \right) \gamma \right) \right. \right. \nonumber \\&\left. \left. +r^4\left( -4+2\xi +\left( 9+18R+9\xi -28R\xi \right) \gamma \right) \right. \right. \nonumber \\&\left. \left. +r^2\left( -4+\xi +\left( 9-36R-9\xi +38R\xi \right) \gamma \right) \right] \rangle \right. \nonumber \\&\left. +\left( r^2-1\right) \left( \left( r^2+1\right) ^4\right) a^{\prime }(r)\Bigg \}\right] \end{aligned}$$
(52)

The above Eq. (52) is a first order linear differential equation in a(r) which has the solution

$$\begin{aligned} a(r)= & {} \frac{1}{2\left( r^2+1\right) }\left( c_1-c_2+r^2\left( c_1+c_2\right) \right) \nonumber \\&\times \left[ -\frac{18c^2R\gamma \left( \xi -1\right) }{\left( r^2+1\right) ^2} -\left( 2\left( c_1+c_2\right) \left( r^2-1\right) \xi \right) \right. \nonumber \\&\left. +\frac{1}{r^2+1}\left\{ 6c_1R\gamma \left( \xi -1\right) \right. \right. \nonumber \\&\left. \left. +2c_2\left( -2-9\gamma +\left( 2+\left( 9+6R\right) \gamma \right) \xi \right) \right\} +2c_1\right. \nonumber \\&\left. +\frac{1}{c_1}\left\{ 4c_1c_2\left( 1+2R\gamma \right) \xi \right. \right. \nonumber \\&\left. \left. +2\left( c_2-R\lambda \right) \left( c_2+R\lambda \right) \left( 1-\xi \right) \right. \right. \nonumber \\&\left. \left. +c_1^2\left( 2\left( 1+\xi \right) +\left( 9-3R+9\xi +5R\xi \right) \gamma \right) \right\} \right. \nonumber \\&\times \left. \log \left( r^2-1\right) -\left\{ c_1\left( 4+\gamma \left( 9-3R+R\xi -9\xi \right) -4\xi \right) \right. \right. \nonumber \\&\left. \left. +2c_2\left( -6+\left( -9+2R\right) \gamma \right) \xi \right\} \log \left( r^2+1\right) \right. \nonumber \\&\left. -\frac{1}{c_1\left( c_1+c_2\right) }\left\{ 2\left( c_1^2-c_2^2+R^2{\lambda ^2}\right) \right. \right. \nonumber \\&\times \left. \left. \left( c_1\left( \xi -1\right) -c_2\left( \xi +1\right) \right) \right. \right. \nonumber \\&\left. \left. \log \left( c_1-c_2+r^2\left( c_1+2\right) \right) \right\} \right] \end{aligned}$$
(53)

This completes the gravitational behaviour of our model.

We can now recast the thermodynamical quantities as

$$\begin{aligned} {\bar{\mu }}= & {} \frac{e^{\lambda t}}{R^2}\left[ 6c_1+\left\{ 3c_1-3c_2+10r^2\left( c_1+c_2\right) \right. \right. \nonumber \\&\left. \left. + r^4\left( c_1+c_2\right) \right\} \xi \right] \end{aligned}$$
(54)
$$\begin{aligned} {\bar{p}}_r= & {} \frac{1}{R^2\left( r^2+1\right) ^4\left( c_1 - c_2+ r^2\left( c_1+c_2\right) \right) } \nonumber \\&\times \left[ \left\{ 2e^{\lambda t}\left( \left( r^2+1\right) ^3\right) \left( r^2\xi +1\right) R^2\right. \right. \nonumber \\&\times \left. \left. \left( -2R^2k_1 - 4R^2k_2^2\right. \right. \right. \nonumber \\&\left. \left. \left. + 4R^2k_2\sqrt{k_1 +k_2^2} +{\lambda ^2}\left( r^2+1\right) ^2\right) \right\} \right. \nonumber \\&\left. -2c_1c_2\left( r^2+1\right) \left\{ \left( r^2+1\right) ^3\right. \right. \nonumber \\&\times \left. \left. \left( -1+\xi +r^2+\left( r^4-2r^2-4\right) r^2\xi \right) \right. \right. \nonumber \\&\left. \left. +2e^{\lambda t}\left\langle -2+3R^2+3R^2\left( 3-4R+2R\xi \right) \gamma +R^2\xi \right. \right. \right. \nonumber \\&\left. \left. \left. +2r^{10}\xi +r^8\left( 2+4\xi +R^2\xi \right) \right. \right. \right. \nonumber \\&\left. \left. \left. +r^6\left( 4-5R^2\xi -R^2\xi \left( 9+2R\right) \gamma \right) \right. \right. \right. \nonumber \\&\left. \left. \left. - r^4\left( 4\xi +3R^2+6R^2\xi + R^2\left( 9+2R\xi \right) \gamma \right) \right. \right. \right. \nonumber \\&\left. \left. \left. +r^2\left( -4-2\xi +6R^3\left( 2-3\xi \right) \gamma \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. +R^2\xi +9R^2\gamma \xi \right) \right\rangle \right\} \right. \nonumber \\&\left. -c_1^2\left( r^2+1\right) ^2\left\{ \left( r^2-1\right) \left( r^2+1\right) ^4\xi \right. \right. \nonumber \\&\left. \left. +2e^{\lambda t}\left\langle -1-2R^2-R^2\xi -R^2\left( 9-6R+6R\xi \right) \gamma \right. \right. \right. \nonumber \\&\left. \left. \left. +r^8\xi +r^6\left( 1+3\xi +R^2\xi \right) \right. \right. \right. \nonumber \\&\left. \left. \left. +r^4\left( 3+3\xi -R^2\xi -r^2\xi \left( 9+2R\right) \gamma \right) \right. \right. \right. \nonumber \\&\left. \left. \left. +r^2\left( 3+\xi -2R^2-3R^2\xi \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. -r^2\left( 9+9\xi +2r\xi \right) \gamma \right) \right\rangle \right\} \right. \nonumber \\&\left. +c_2^2\left\{ -\left( r^2+1\right) ^3\left( r^4-6r^2+1\right) \right. \right. \nonumber \\&\times \left. \left. \left( 2+\left( r^4+2r^2-1\right) \xi \right) \right. \right. \nonumber \\&\left. \left. \left. -2e^{\lambda t}\langle 3-4R^2-3R^2\left( 3-6R+2R\xi \right) \gamma -R^2\xi \right. \right. \right. \nonumber \\&\left. \left. \left. +3r^{12}\xi +r^{10}\left( 3+3\xi +R^2\xi \right) \right. \right. \right. \nonumber \\&\left. \left. \left. -r^8\left( -3+6\xi +R^2\xi \left( 9+9\gamma +2R\gamma \right) \right) \right. \right. \right. \nonumber \\&\left. \left. \left. - r^6\left( 6+6\xi +4R^2+9R^2\gamma \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. +R^2\xi \left( 10-9\gamma +2R\gamma \right) \right) \right. \right. \right. \nonumber \\&\left. \left. \left. +r^4\left( 3\xi -6+2R^2\xi -4R^2\right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. +R^2\left( 9+18R+9\xi -28R\xi \right) \gamma \right) \right. \right. \right. \nonumber \\&\left. \left. \left. +r^2\left( 3+3\xi -4R^2+R^2\xi \ \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. +R^2\left( 9-36R-9\xi +38R\xi \right) \gamma \right) \right\rangle \right\} \right] \end{aligned}$$
(55)
$$\begin{aligned} {\bar{p}}_t= & {} -\frac{e^{\lambda t}}{R^2\left( r^4-1\right) \left( c_1-c_2+r^2\left( c_1+c_2\right) \right) ^2} \nonumber \\&\times \left[ c_1^2c_2\left( r^2+1\right) ^2\left\{ 3\gamma \left( r^2-1\right) ^2\left( 9-9r^4\right. \right. \right. \nonumber \\&\left. \left. \left. -10R+20r^2R\right) \right. \right. \nonumber \\&\left. \left. +2r^2\xi \left( 3r^8-10r^4-8r^2-1\right) \right. \right. \nonumber \\&\left. \left. +2\gamma \xi \left( 27r^2\left( r^2-1\right) ^2\left( r^2+1\right) \right) \right. \right. \nonumber \\&\left. \left. +2R\gamma \xi \left( 4r^8-48r^6+61r^4-58r^2+9\right) \right\} \right. \nonumber \\&\left. -c_2\left( r^2-1\right) ^2\left\{ 2R^2{\lambda ^2}\left( r^2-1\right) \left( r^2+1\right) ^3\right. \right. \nonumber \\&\left. \left. +9c_2^2\gamma \left( r^2-1\right) \left( 1-2R-5r^2-5r^4\right. \right. \right. \nonumber \\&\left. \left. \left. +r^6-4Rr^4+14Rr^2\right) \right. \right. \nonumber \\&\left. \left. -2c_2^2\xi \left\langle \left( r^3+r\right) ^2\left( r^4+10r^2-3\right) \right. \right. \right. \nonumber \\&\left. \left. \left. +3R\gamma + r^8\gamma \left( 4R+27\right) - 3r^6\gamma \left( 8R+3\right) \right. \right. \right. \nonumber \\&\left. \left. \left. +9r^4\gamma \left( 11R-3\right) +r^2\gamma \left( -50R+9\right) \right\rangle \right. \right. \nonumber \\&\left. \left. +2r^2R^2{\lambda ^2}\left( r^2-1\right) \left( r^2+1\right) ^3\right. \right. \nonumber \\&\left. \left. +R^2\left( r^2+1\right) ^3\left( 1-r^2+2r^2\xi \right) \right. \right. \nonumber \\&\times \left. \left. \left\langle 2k_1+4k_2^2-4k_2\sqrt{k_1+k_2^2}\right\rangle \right\} \right. \nonumber \\&\left. +c_1^3\left( r^2+1\right) ^3\left\{ -3\gamma \left( 3-2R+2R\xi \right) +2r^8\xi \right. \right. \nonumber \\&\left. \left. -r^6\left( 9\gamma +6\xi \right) \right. \right. \nonumber \\&\left. \left. -r^4\left( 4+6\xi +\gamma \left( 9+18\xi -12R+16R\xi \right) \right) \right. \right. \nonumber \\&\left. \left. +r^2\left( -4-9\gamma -6R\gamma -2\xi +2\gamma \xi \left( R-9\right) \right) \right\} \right. \nonumber \\&\left. +c_1\left( r^2+1\right) \left\{ -2R^2\left( r^2+1\right) ^3\right. \right. \nonumber \\&\times \left. \left. \left\langle {\lambda ^2}\left( r^2-1\right) ^2\left( r^2\xi +1\right) \right. \right. \right. \nonumber \\&\left. \left. \left. + \left( r^4+2r^2\xi +1\right) \left( -k_1-k_2^2\right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. +2k_2\sqrt{k_1+k_2^2}\right) \right\rangle \right. \right. \nonumber \\&\left. \left. +c_2^2\left\langle -3\gamma \left( 9-14R+6R\xi \right) +6r^{12}\xi \right. \right. \right. \nonumber \\&\left. \left. \left. +r^{10}\left( 22\xi -27\gamma +4\gamma \xi \left( 4R+27\right) \right) \right. \right. \right. \nonumber \\&\left. \left. \left. +r^8\left( 4-24\xi +135\gamma +84R\gamma \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. -18\gamma \xi \left( 8R+9\right) \right) \right. \right. \right. \nonumber \\&\left. \left. \left. 2r^6\left( -10+24\xi -54\gamma -27\gamma \xi \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. +R\gamma \left( -189+215\xi \right) \right) \right. \right. \right. \nonumber \\&\left. \left. \left. +2r^4\left( -10+\xi \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. +3\gamma \left( -18+91R+27\xi -85R\xi \right) \right) \right. \right. \right. \nonumber \\&\left. \left. \left. +r^2\left( 4+10\xi \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. +\gamma \left( 135-294R-54\xi +226R\xi \right) \right) \right\rangle \right\} \right] \end{aligned}$$
(56)
$$\begin{aligned} Q= & {} -\frac{2e^{\lambda t} r\left( r^2+1\right) \lambda \xi }{R} \end{aligned}$$
(57)
Fig. 1
figure 1

\(\varGamma \) as a function of the radial coordinate, r for the Newtonian limit. Blue: \(\gamma =-1\), Brown: \(\gamma =-1/3\), Orange: \(\gamma =0\), Green: \(\gamma =1/3\), Red: \(\gamma =1\)

Full size image

8 Stability

The stability of a star undergoing dissipative collapse has been studied by several authors over the past three decades. The role of pressure anisotropy and the presence of radiation within the stellar core affects the stability factor, \(\varGamma \). It was shown that a change in sign in the anisotropy parameter can render the core unstable as can be deduced from the Newtonian limit

$$\begin{aligned} \varGamma < \frac{4}{3}+\left[ -\frac{4}{3}\frac{\left( p_{r0}-p_{t0}\right) }{|p_{r0}^{\prime }|r} +\frac{2}{3}\alpha _{\varSigma }\xi \frac{|f^{\prime }|}{|p_{r0}^{\prime }|}\right] _{max}. \end{aligned}$$
(58)

However, we have elected to base this work on an isotropic static model in order to determine the link between the stability index \(\varGamma \) and the equation of state parameter \(\gamma \). Relativistic contributions from the energy density predicts a stability factor different from its Newtonian counterpart.

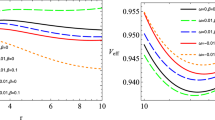
$$\begin{aligned} \varGamma< & {} \frac{4}{3}+\left[ -\frac{4}{3}\frac{\left( p_{r0}-p_{t0}\right) }{|p_{r0}^{\prime }|r} +\frac{1}{3}\frac{\mu _0 p_{r0}}{|p_{r0}^{\prime }|}r \right. \nonumber \\&\left. +\frac{2}{3}\alpha _{\varSigma }\xi \frac{|f^{\prime }|}{|p_{r0}^{\prime }|} -\frac{1}{3}\mu _0\frac{\xi |f^{\prime }|}{|p_{r0}^{\prime }|}\right] _{max}. \end{aligned}$$
(59)

Figure 1 shows the stability factor in the Newtonian regime, when the star is close to hydrostatic equilibrium. During this stage the energy emission from the core is small and we expect the star to be stable from the centre outwards towards its surface. Figure 1 shows us that the different matter configurations all possess \(\varGamma > \frac{4}{3}\) indicating that the core is stable. It is interesting to note that there is a deviation for different EoS parameter (\(\gamma \)) as one approaches the surface of the star. The so-called ’dark’ stars corresponding to the blue and brown curves are more stable than the stars composed of baryonic matter. We also observe that the surface layers are more stable than the inner core region of the star. We expect this as the outer layers are cooler than the central regions. Figure 2 displays the stability factor for the Post-Newtonian limit. This epoch corresponds to late stage collapse of the star. During this period we expect the core to be dynamically unstable. It is clear from Fig. 2 that different configurations (varying \(\gamma \)) are unstable at the centre with the baryonic matter configurations having \(\varGamma _{centre} < 4/3\) and dark star models having \(\varGamma _{centre} = 4/3\). As we move away from the central regions of the star the stability index increases to above the critical value of 4/3. Again, we observe that the collapse with the loss of energy in the form of a radial heat flux drives the dark energy stars to increased stability as compared to their baryonic counterparts. Our analysis of the stability factor clearly indicates the strong connection between the equation of state parameter \((\gamma )\) and the stability of the stellar configuration.

It has been shown that the scalar function [17]

$$\begin{aligned} {{{\mathscr {Y}}}}_{TF} = 16\pi \eta \sigma + \frac{4\pi }{R^3}\int _0^R{R^3\left( D_R{\mu } - 3{q}\frac{U}{RE}\right) dR} \end{aligned}$$
(60)

where \(\sigma \) is the shear scalar, \(D_R = \frac{1}{R^{\prime }}\frac{\partial }{\partial {r}}\) is the proper radial derivative, \(D_T = \frac{1}{A}\frac{\partial }{\partial {t}}\) is the proper time derivative, \(U = D_TR < 0\) and

$$\begin{aligned} E = \left( 1 + U^2 - \frac{2m}{R}\right) ^{1/2} \end{aligned}$$

is the mass function measures the stability of the shear-free condition. We note that \({{\mathscr {Y}}}_{TF}\) is a combination of shear viscosity, pressure anisotropy, inhomogeneities in the density and the heat flux. The presence of the dissipative flux, anisotropy and inhomogeneity can lead to deviation from the shear-free profile as the collapse proceeds. From observation of the various terms in (60) it is clear that even in the absence of shear viscosity (the vanishing of the internal friction between the adjacent fluid layers of the collapsing fluid) there can be an increase in the absolute value of the shear scalar due to the presence of density inhomogeneity and heat flux. On the otherhand, it is possible that all the factors contributing to \({{\mathscr {Y}}}_{TF}\) may cancel each other during some epoch thus leading to a stable shear-free profile. This scenario would require very fine-tuning of the various parameters involved and is unlikely to occur during a realistic collapse process. Since shear-free profiles are unstable in the presence of dissipation, anisotropy and inhomogeneity, the invoking of the shear-free condition may be valid for a limited timescale during the collapse process.

Fig. 2
figure 2

\(\varGamma \) as a function of the radial coordinate, r for the post-Newtonian limit. Blue \(\gamma =-1\), Brown: \(\gamma =-1/3\), Orange: \(\gamma =0\), Green: \(\gamma =1/3\), Red: \(\gamma =1\)

Full size image

9 Discussion

In this work we investigated the effect of an equation of state on the dynamical stability or instability of a spherically symmetric star undergoing dissipative collapse. We adopted a perturbative approach in which the star starts collapsing from an initial static configuration in the infinite past \((t = - \infty )\). The radial perturbation in the gravitational potential was determined by specifying a linear equation of state of the form \(p_r = \gamma \mu \). The temporal evolution of the model was determined from the junction conditions. We showed that the temporal behaviour of the model is intrinsically linked to the equation of state parameter, \(\gamma \). We studied the stability of our model by investigating the stability index and its dependence on \(\gamma \). We were in a position to clearly show the variation of the stability index with the equation of state parameter throughout the stellar fluid. More importantly, our investigation revealed that the stability depends on the nature of the matter making up the stellar interior. Our results are new and contribute to recent findings by Naidu et al. [18] and Bogadi et al. [19] in which they found that the equation of state affects the end state of collapse and temperature profiles of the radiating body.