Surrounded Bonnor–Vaidya solution by cosmological fields

Abstract

In the present work, we generalize our previous work (Heydarzade and Darabi in arXiv:1710.04485, 2018 on the surrounded Vaidya solution by cosmological fields to the case of Bonnor–Vaidya charged solution. In this regard, we construct a solution for the classical description of the evaporating-accreting charged Bonnor–Vaidya black holes in the generic dynamical backgrounds. We address some interesting features of these solutions and classify them according to their behaviors under imposing the positive energy condition. Also, we analyze the timelike geodesics associated with the obtained solutions and show that some new correction terms arise in comparison to the case of standard Schwarzschild black hole. Then, we explore all these features for each of the cosmological backgrounds of dust, radiation, quintessence and cosmological constant-like fields in more detail.

1 Introduction

In 1951, Vaidya introduced a new non-static solution, describing a spherical symmetric object possessing an outgoing null radiation, for the Einstein field equations [1, 2]. This solution is characterized by a dynamical mass function, depending on the retarded time coordinate. Based on its dynamical nature, the Vaidya solution has been used for studying the process of spherical symmetric gravitational collapse and as a testing ground for the cosmic censorship conjecture [3,4,5,6,7], and as a dynamical generalisation of the Schwarzschild solution representing a spherically symmetric evaporating black hole, as well as studying the Hawking radiation [8,9,10,11,12,13,14,15]. This solution was generalized by Bonnor and Vaidya to the charged case, well known as the Bonnor–Vaidya solution [16]. This solution and its interesting features and applications are studied in [17,18,19,20] as instances. Further generalization of the original Vaidya solution were introduced in [21] by Husain for a null fluid with a particular equation of state, and in [22] by wang and Wu using the fact that any linear superposition of particular solutions is also a solution to the Einstein field equations. Using this approach, one can find other general solutions such as the Vaidya–de Sitter [23], Bonnor–Vaidya–de Sitter [18, 24,25,26,27] and radiating dyon solutions [28]. The Vaidya solution and its generalizations are also studied in the context of modified theories of gravity, see for examples [4, 29,30,31,32,33].

Black holes have such an strong gravitational attraction that their nearby matter, even light, cannot escape from their gravitational field. Although, the black holes cannot be observed directly but there are some different ways to detect them in the binary systems as well as at the centers of their host galaxies. The most promising way for this detection is the accretion process. In the language of astrophysics, the accretion is defined as the inward flow of captured matter fields by a gravitating object towards its centre which leads to an increase of the mass and angular momentum of the accreting body. The observation of supermassive black holes at the center of galaxies represents that such massive black holes could have been gradually developed through the appropriate accretion processes. However, the accretion processes do not always increase the mass of the accreting bodies but they can also decrease their mass and lead them to shrink. It is shown that the accretion of phantom energy can decrease the black hole area [34,35,36,37,38,39]. For instance, in [34], it is shown that black holes will gradually vanish as the universe approaches to a cosmological big rip state. The shrink of the black hole area during the accretion of a potentially surrounding field is an interesting phenomena in the sense that it can be considered as an alternative for the black hole evaporation through the Hawking radiation or even as an auxiliary for speeding up the evaporation process. One physical explanation for diminishing the black hole mass through the accretion process is that the accreting particles of a phantom scalar field have a total negative energy [40]. Similar particles with negative energies are created through the Hawking radiation process as well as in the process of energy extraction from a black hole by the Penrose mechanism. Thus, the accretion process into the black holes is one of the most interesting research fields in relativistic astrophysics to answer how black holes affect their cosmological surrounding fields and what are the consequences or what are the influences of these surrounding fields on the features, dynamical behaviors and abundance of black holes [41,42,43,44,45,46,47,48,49]. See also [50] for the accretion of dark energy into black holes, and [38, 39, 51, 52] for the accretion into the charged black holes.

In the present work, following the approach of [53, 54] and [55, 56], we construct a dynamical solution for the classical description of the evaporating-accreting Bonnor–Vaidya black holes in generic dynamical backgrounds. The organization of the paper is as follows. In Sect. 2, the surrounded Bonnor–Vaidya black hole solution and some of its general features are introduced. In Sects. 2.1–2.4, the special classes of this solution named as the Bonnor–Vaidya black hole surrounded by the dust, radiation, quintessence and cosmological constant fields, as well as their properties are studied in detail. Finally, the Sect. 3 is devoted to the summary and concluding remarks.

2 Surrounded evaporating-accreting Bonnor–Vaidya black hole solution

In this section, we generalize our previous solution [55, 56] to the surrounded charged Bonnor–Vaidya black hole solution by following the approach of [53, 54]. There are two main motivations for us for doing this generalization. The first one is that the existence of the charge can drastically change the global structure of the original spacetime [57]. For instance, we know the Reissner–Nordström black hole has a very distinct causal structure relative to the Schwarzschild case such that it predicts infinite series of parallel universes. The second reason is that a charged black hole possesses a spacetime structure almost similar to a rotating one, the Kerr black hole. Regarding that the existing spherical symmetry in the charged case makes it more easily analyzable, then understanding the structure of a charged black hole may be a suitable ground to better understanding the structure of a more realistic rotating one.

We consider the general spherical symmetric spacetime metric

$$\begin{aligned} ds^{2}=- \ f(u,r)du^2+2\epsilon dudr+r^2d\Omega ^2,\quad \epsilon =\pm 1, \end{aligned}$$

(1)

where $d\Omega ^2=d\theta ^2+sin^2\theta d\phi ^2$ is the metric of two dimensional unit sphere and f(u, r) is a generic metric function depending on both of the the radial coordinate r and advanced/retarded time coordinate u. The cases $\epsilon =\pm \ 1$ associated with the possible outgoing-ingoing flows corresponding to the effectively evaporating-accreting Bonnor–Vaidya black hole. For the metric (1), the nonvanishing components of the Einstein tensor are given by

$$\begin{aligned}&{G^{0}}_{0}={G^{1}}_{1}=\epsilon G_{01}=\epsilon G_{10}=\frac{1}{r^2} (f^{\prime }r-1+f ),\nonumber \\&{G^{1}}_{0}=G_{00}+fG_{01}=-\frac{{\dot{f}}}{r},\nonumber \\&{G^{2}}_{2}=\frac{1}{r^2}G_{22}=\frac{1}{r^2}\left( rf^{\prime }+\frac{1}{2}r^2 f^{\prime \prime }\right) ,\nonumber \\&{G^{3}}_{3}=\frac{1}{r^2 sin^2 \theta }G_{33}=\frac{1}{r^2}\left( rf^{\prime }+\frac{1}{2}r^2 f^{\prime \prime }\right) , \end{aligned}$$

(2)

where dot and prime signs denote the derivatives with respect to the time coordinate u and the radial coordinate r, respectively. Thus, one can find that the total energy–momentum tensor supporting this spacetime must have the following non-diagonal form

$$\begin{aligned} {T^{\mu }}_{\nu }= \begin{pmatrix}{T^{0}}_{0} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {T^{1}}_{0} &{}\quad {T^{1}}_{1} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {T^{2}}_{2} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad {T^{3}}_{3}\\ \end{pmatrix}, \end{aligned}$$

(3)

which must possess the same symmetries in the Einstein tensor ${G^{\mu }}_{\nu }$. Then, regarding the equations in (2), the equalities ${G^{0}}_{0}={G^{1}}_{1}$ and ${G^{2}}_{2}={G^{3}}_{3}$ in the Einstein tensor components demand the equalities ${T^{0}}_{0}={T^{1}}_{1}$ and ${T^{2}}_{2}={T^{3}}_{3}$ for the energy–momentum tensor components, respectively. Then, one may introduce an energy–momentum tensor obeying these properties as in our previous work giving the surrounded Vaidya black hole [55, 56]. One possible generalization to [55, 56] can be obtained by including the Maxwell electromagnetic energy–momentum tensor. In the following, we prove that the resulting total energy–momentum tensor obeys all the symmetries in ${G^{\mu }}_{\nu }$. Then, we show that this provides the possibility of finding the charged Bonnor–Vaidya black hole solutions [16] in a general dynamical background in the context of the Einstein–Maxwell theory. Thus, we consider the Einstein field equations, corresponding to the components of the Einstein tensor (2), with the total energy–momentum tensor ${T^{\mu }}_{\nu }$ given by

$$\begin{aligned} {T^{\mu }}_{\nu }={\tau ^{\mu }}_{\nu }+{E^{\mu }}_{\nu }+{\mathcal {T}^{\mu }}_{\nu }, \end{aligned}$$

(4)

where ${\tau ^{\mu }}_\nu$ is the energy–momentum tensor associated to the Bonnor–Vaidya null radiation-accretion as

$$\begin{aligned} {\tau ^{\mu }}_{\nu }=\sigma k^{\mu }k_{\nu }, \end{aligned}$$

(5)

such that $\sigma =\sigma (u,r)$ is the density of the “outgoing radiation-infalling accretion” flow and $k_\mu ={\delta ^{0}}_{\mu }$ is a null vector field and ${E^{\mu }}_{\nu }$ is the trace-free Maxwell tensor given by

$$\begin{aligned} E_{\mu \nu }=2\left( F_{\mu \alpha }{F_{\nu }}^{\alpha }- \frac{1}{4}g_{\mu \nu }F^{\alpha \beta }F_{\alpha \beta }\right) , \end{aligned}$$

(6)

where $F_{\mu \nu }$ is the antisymmetric Faraday tensor satisfying the vacuum Maxwell equations

$$\begin{aligned}&{F^{\mu \nu }}_{;\mu }=J^{\nu },\nonumber \\&\partial _{[\sigma } F_{\mu \nu ]}=0. \end{aligned}$$

(7)

The spherical symmetry in the spacetime metric (1) dictates the only non-zero components of $F^{\mu \nu }$ tensor to be $F^{01}=-F^{10}$. Then, from the Eq. (7), one obtains

$$\begin{aligned} F^{01}=\frac{Q(u)}{r^2}, \end{aligned}$$

(8)

where Q(u) is the dynamical electric charge and its associated null current is

$$\begin{aligned} J^{\mu }=\frac{{\dot{Q}}(u)}{r^2} {\delta ^{\mu }}_r, \end{aligned}$$

(9)

where ${\dot{Q}}(u)=\frac{dQ(u)}{du}$. Using the Eqs. (1), (6) and (8), the only non-vanishing components of Maxwell tensor ${E^{\mu }}_{\nu }$ will be

$$\begin{aligned} {E^{\mu }}_{\nu }=\frac{Q^2(u)}{ r^4}~diag(-\ 1,-\ 1,1,1). \end{aligned}$$

(10)

Finally, ${\mathcal {T}^{\mu }}_{\nu }$ in (4) is the energy–momentum tensor of the surrounding perfect fluid defined as in [53]

$$\begin{aligned}&{\mathcal {T}^{0}}_{0}=-\ \rho _s(u,r),\nonumber \\&{\mathcal {T}^{i}}_{j}=-\ \rho _{s}(u,r)\alpha \left[ -(1+3\beta )\frac{r^i r_j}{r^n r_n}+\beta {\delta ^{i}}_{j}\right] . \end{aligned}$$

(11)

Here, the subscript $``s''$ stands for the surrounding field which generally can be a dust, radiation, quintessence and cosmological constant or even any complex field constructed by the combination of these fields. From (11), it is seen that the spatial profile of the surrounding energy–momentum tensor is proportional to its time component, representing the dynamical energy density $\rho _s(u,r)$, with the arbitrary parameters $\alpha$ and $\beta$ which depend on the internal structure of the corresponding surrounding fields. The isotropic averaging over the angles results in [53]

$$\begin{aligned} \langle {\mathcal {T}^{i}}_{j}\rangle =\frac{\alpha }{3}\rho _{s}{\delta ^{i}}_{j}=p_{s}{\delta ^{i}}_{j}. \end{aligned}$$

(12)

The last equality follows from the fact that $\langle r^{i}r_{j}\rangle =\frac{1}{3}{\delta ^{i}}_{j}r_n r^n$ which results in the barotropic equation of state for the surrounding field as

$$\begin{aligned} p_s(u,r)=\omega _s \rho _s(u,r), \quad \omega _s=\frac{1}{3}\alpha , \end{aligned}$$

(13)

where $p_s(u,r)$ and $\omega _s$ are the dynamical pressure and the constant equation of state parameter, respectively. Then, regarding the Einstein tensor components in (2) and the total energy–momentum tensor given by the Eqs. (3)–(5) and (11), we find that ${\mathcal {T}^{0}}_{0}={\mathcal {T}^{1}}_{1}$ and ${\mathcal {T}^{2}}_{2}={\mathcal {T}^{3}}_{3}$. These exactly provide us the principle of additivity and linearity condition proposed in [53] for determining the free $\beta$ parameter in the energy momentum-tensor (11) as

$$\begin{aligned} \beta =-\frac{1+3\omega _s}{6\omega _s}. \end{aligned}$$

(14)

Now, by substituting $\alpha$ and $\beta$ parameters given in (13) and (14) into (11), one obtains the non-vanishing components of the surrounding energy–momentum ${\mathcal {T}^{\mu }}_{\nu }$ in the following forms

$$\begin{aligned}&{\mathcal {T}^{0}}_{0}={\mathcal {T}^{1}}_{1}=- \ \rho _s(u,r),\nonumber \\&{\mathcal {T}^{2}}_{2}={\mathcal {T}^{3}}_{3}=\frac{1}{2}\left( 1+3\omega _s\right) \rho _s(u,r). \end{aligned}$$

(15)

Then, having the Einstein tensor components (2) and the corresponding general energy–momentum tensor ${T^{\mu }}_{\nu }$ in (4), we have the corresponding field equations. The ${G^{0}}_{0}={T^{0}}_{0}$ and ${G^{1}}_{1}={T^{1}}_{1}$ components of the Einstein–Maxwell field equations give

$$\begin{aligned} \frac{1}{r^2}\left( f^{\prime }r-1+f \right) =-\ \rho _s-\frac{Q^2}{ r^4}. \end{aligned}$$

(16)

Similarly, from ${G^{1}}_{0}={T^{1}}_{0}$ we have

$$\begin{aligned} -\frac{{\dot{f}}}{r}=\epsilon \sigma , \end{aligned}$$

(17)

and ${G^{2}}_{2}={T^{2}}_{2}$ and ${G^{3}}_{3}={T^{3}}_{3}$ components lead to

$$\begin{aligned} \frac{1}{r^2}\left( rf^{\prime }+\frac{1}{2}r^2 f^{\prime \prime }\right) =\frac{1}{2}(1+3\omega )\rho _{s}+\frac{Q^2}{ r^4}. \end{aligned}$$

(18)

By simultaneous solving the differential equations (16) and (18), one can find the following general solution for the metric function

$$\begin{aligned} f(u,r)=1-\frac{2M(u)}{r}+\frac{Q^2(u)}{r^2}-\frac{N_s(u)}{{r}^{{3\omega _s +1}}}, \end{aligned}$$

(19)

with the energy density of the surrounding filed in the form of

$$\begin{aligned} \rho _s (u,r)=- \frac{3\omega _s N_s(u)}{{r}^{{3(\omega _s +1)}}}, \end{aligned}$$

(20)

in which M(u), Q(u) and $N_s(u)$ are integration coefficients representing the black hole dynamical mass and charge and dynamical surrounding field structure parameter, respectively. The weak energy condition on the energy density (20) of the surrounding field, i.e $\rho _s\ge 0$, requires

$$\begin{aligned} \omega _s N_{s}(u)\le 0, \end{aligned}$$

(21)

implying that for the surrounding fields with $\omega _s\ge 0$, it is needed to have $N_{s}(u)\le 0$ and conversely for $\omega _s\le 0$ we have $N_{s}(u)\ge 0$.

Regarding (19), the metric (1) takes the form of

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M(u)}{r}+\frac{Q^2(u)}{r^2}-\frac{N_s(u)}{{r}^{{3\omega _s +1}} }\right) du^2\nonumber \\&+ \ 2\epsilon dudr+r^2d\Omega ^2, \end{aligned}$$

(22)

representing an effectively evaporating-accreting charged black hole in a dynamical background.

Here, it is worth to discuss about the stability of this black hole. The stability is achieved if the metric solution (22) be time independent, namely $\partial _u g_{ab}=0$ or

$$\begin{aligned} \left( -\frac{2{\dot{M}}(u)}{r}+\frac{2Q(u){\dot{Q}}(u)}{r^2}-\frac{{\dot{N}}_s(u)}{{r}^{{3\omega _s +1}} }\right) =0. \end{aligned}$$

(23)

However, because of different powers of r which yields an r-dependent differential equation, one cannot obtain a global stability condition. In other words, this metric solution cannot be stabilized unless in a local way. It seems this is the case for any other metric solution, studied throughout this paper, for which the corresponding differential equation of stability condition is r-dependent.

Regarding (22), one may realize the following two distinct subclasses for this general solution for the field equations (16) and (18).

• The solution by setting $f=f(u,r)$ and $\rho _s=\rho _s(r)$

  These considerations lead to $M=M(u)$, $Q=Q(u)$ and $N_s=constant$ in the metric function f(u, r) and $\sigma (u,r)\ne 0$ for the energy density. Then, there is no dynamics in the surrounding field and consequently the accretion of the surrounding field by the black hole cannot happen. Indeed, this case represents an evaporating charged black hole solution in a static background. The radiating charged black holes in an empty background $(\rho _s=0)$ known as the original Bonnor–Vaidya solution [16], and in (anti)-de Sitter space $(\rho _s = \rho _{\Lambda }=constant)$ are special subclasses of this solution [18, 58]. Some interesting features of these black holes can be found in [15, 19, 20, 59].

• The solution by setting $f=f(r)$ and $\rho _s=\rho _s(r)$

  These considerations lead to $M=constant$, $Q=constant$ and $N_s=constant$ in the metric function f(u, r) and consequently $\sigma (u,r)= 0$ for the radiation-accretion density. This case represents a static charged back hole in a static background and consequently, there is no radiation-accretion. The Reissner–Nordström black hole as well as its generalization to (anti)-de Sitter background are special subclasses of this solution. For a general background, not just the (anti)-de Sitter background, it is interesting that for a constant mass and charge black hole in a static non-empty background, using the coordinate transformation

  $$\begin{aligned} du=dt+\frac{\epsilon dr}{1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{N_s}{{r}^{{3\omega _s +1}} }}, \end{aligned}$$

  (24)

  one arrives at the solution of the Reissner–Nordström black hole surrounded by a surrounding field as

  $$\begin{aligned} ds^2= & {} -\left( 1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{N_{s}}{{r}^{{3\omega _s +1}} } \right) dt^2\nonumber \\&+\frac{dr^2}{1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{N_{s}}{{r}^{{3\omega _s +1}} }}+r^2 d\Omega ^2. \end{aligned}$$

  (25)

  This solution is a generalization of the Kiselev solution [53] to the charged case and its interesting properties are studied in [60,61,62,63]. Then, the generalized Kiselev solution is a subclass of our general dynamical solution (22) in the stationary limit.

Substituting f(u, r) given by (19) in (17) gives the radiation-accretion density of the effectively evaporating-accreting Bonnor–Vaidya black hole as

$$\begin{aligned} \sigma (u,r)=\epsilon \left( \frac{2{\dot{M}}(u)}{r^{2}} -\frac{2Q(u){\dot{Q}}(u)}{r^3} +\frac{{\dot{N}}_s(u)}{{r}^{{3\omega _s +2}} }\right) . \end{aligned}$$

(26)

Then, we observe that the radiation-accretion density is resulted not only from the change in the black hole mass ($\sigma _M$) and surrounding field ($\sigma _{N_s}$) but also from the change in the charge of the black hole ($\sigma _Q$), representing the electromagnetic energy. In this case, the black hole may have just the outgoing charged null radiation. Turning off the surrounding field dynamics, i.e ${\dot{N}}_s(u)=0$, we recover the energy flux associated to the mass and charge changes of the central black hole corresponding to the Bonnor–Vaidya solution [16]. It is seen that if ${\dot{M}}(u)$, $Q(u){\dot{Q}}(u)$ and ${\dot{N}}_s(u)$ have a same order of magnitude, the following distinct physical situations can be realized.

• For $\omega _s<0$, the charge contribution is dominant near the black hole. For the far distances ($r\gg$), the black hole charge contribution falls down faster than the black hole mass and the surrounding field contributions, respectively, i.e $|\sigma _Q|<|\sigma _M|<|\sigma _{N_s}|$. Then, at large distances the surrounding field contribution is dominant.

• For $0<\omega _s<1/3$, the charge contribution is dominant near the black hole. For the far distances ($r\gg$), the charge contributions falls down faster than the surrounding field and mass contributions, respectively, i.e $|\sigma _Q|<|\sigma _{N_s}|<|\sigma _M|$. Then, at large distances the black hole mass contribution is dominant.

• For $\omega _s>1/3$, the surrounding field contribution is dominant near the black hole. For the far distances ($r\gg$), the the surrounding field contributions falls down faster than the charge and mass contributions, respectively, i.e $|\sigma _{N_s}|<|\sigma _Q|<|\sigma _M|$. Then, at large distances the black hole mass contribution is dominant again.

Considering the positive energy density condition on the total radiation-accretion density $\sigma (u,r)$ requires

$$\begin{aligned} \epsilon \left( \frac{2{\dot{M}}(u)}{r^{2}}-\frac{2Q(u){\dot{Q}}(u)}{r^3}+\frac{{\dot{N}}_{s}(u)}{{r}^{{3\omega _s +2}} }\right) \ge 0. \end{aligned}$$

(27)

This inequality confines the dynamical behaviours of the charged Bonnor–Vaidya black hole and its background at arbitrary time and distance (u, r). In the case of a static background and neutral black hole, as in the Vaidya’s original solution, it is required that $\epsilon$ and ${\dot{M}}(u)$ have the same signs. In the presence of the black hole charge and background field dynamics, it is not mandatory that $\epsilon$ and ${\dot{M}}(u)$ take the same signs, and the satisfaction of the positive energy density condition can be achieved even by their opposite signs depending on the dynamics of the black hole charge (${\dot{Q}}(u)$) and surrounding field parameters (${\dot{N}}_{s}(u)$ and $\omega _{s}$). Then, the dynamical behaviour of the surrounding field is governed by

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{N}}_{s}(u)\le 2 {r}^{{3\omega _s -1}}\left( Q(u){\dot{Q}}(u)- r{\dot{M}}(u)\right) , &{} \epsilon =-\ 1, \\ {\dot{N}}_{s}(u)\ge 2 {r}^{{3\omega _s -1}}\left( Q(u){\dot{Q}}(u)- r{\dot{M}}(u)\right) , &{}\epsilon =+ \ 1. \end{array}\right. } \end{aligned}$$

(28)

Then, at an arbitrary distance r from the black hole, the surrounding field must obey the above conditions. Interestingly, for the special case of ${\dot{N}}_{s}(u)=2 {r}^{{3\omega _s -1}} (Q(u){\dot{Q}}(u)- r{\dot{M}}(u) )$, there is no pure radiation-accretion density, i.e $\sigma (u,r)=0$. This case is associated with two possible physical situations. The first one corresponds to the situation where for any particular distance $r_0$, the background field ${\dot{N}}_s(u)$ and black hole with ${\dot{M}}(u)$ and ${\dot{Q}}(u)$ behave such that their contributions cancel out each others, leading to $\sigma (u,r_0)=0$. The second situation corresponds to the case where for the given dynamical behaviors of the black hole and its background, one can find the particular distance $r_{*}(u)=Roots ~of [2{\dot{M}}(u)r^{3\omega _s}-2Q(u){\dot{Q}}(u)r^{3\omega _s -1}+{\dot{N}}_s(u) ]$, which is generally dynamical, possessing zero energy density $\sigma (u,r_{*}(u))$. Generally, to have a particular distance at which the density $\sigma (u,r_{*})$ is zero, the reality and positivity of $r_*$ also requires that ${\dot{M}}(u)$, ${\dot{Q}}(u)$ and ${\dot{N}}_{s}(u)$ obey some specific conditions. Here, due to the fact that finding the location of $r_*(u)$ in its general form is very complicated, in comparison to our previous solution [55, 56], we discuss in this regard by considering some specific surrounding fields through the following subsections.

However, before we study the features of obtained solution for some specific cosmological surrounding fields, we would like to investigate the timelike geodesics corresponding to the metric (22) in its general form. Due to the spherical symmetry, the geodesics for this metric lie on a plane, in which one may choose $\theta =\pi /2$ for the sake of simplicity. Considering the action

$$\begin{aligned} I=\int \mathcal {L}d\tau =\frac{1}{2}\int \left( -\ f(u,r)\overset{*}{u}^2+2\epsilon \overset{*}{u} \overset{*}{r}+r^2 \overset{*}{\varphi }^2 \right) d\tau , \end{aligned}$$

(29)

where the star sign denotes the derivative with respect to the proper time $\tau$, and using the variation, we arrive at the following equations for the $\varphi , r$ and u variables, respectively, as

$$\begin{aligned} \overset{*}{\varphi }=\frac{L}{r^2}, \end{aligned}$$

(30)

and

$$\begin{aligned} -\frac{1}{2}f^{\prime }\overset{*}{u}^2 +r\overset{*}{\varphi }^2 -\epsilon \overset{**}{u}=0, \end{aligned}$$

(31)

and

$$\begin{aligned} \epsilon \overset{**}{r}=\frac{1}{2}{\dot{f}} \overset{*}{u}^2+f\overset{**}{u}+f^{\prime }\overset{*}{u}\overset{*}{r}, \end{aligned}$$

(32)

where L is the conserved angular momentum per unit mass and dot and prime signs denote the derivative with respect to u and r coordinates, respectively. Substituting (30) in (31), we have

$$\begin{aligned} f\overset{**}{u}=\epsilon f\frac{L^2}{r^3}-\frac{1}{2}\epsilon f f^\prime \overset{*}{u}^2. \end{aligned}$$

(33)

Moreover, using the timelike geodesics condition, i.e $g_{\mu \nu }{\dot{x}}^{\mu }{\dot{x}}^{\nu }=-1$, we obtain

$$\begin{aligned} f^\prime \overset{*}{r} \overset{*}{u}=-\frac{1}{2}\epsilon f^\prime +\frac{1}{2}\epsilon ff^\prime -\frac{1}{2}\epsilon f^\prime \frac{L^2}{r^2} \overset{*}{u}^2, \end{aligned}$$

(34)

where we have used also the Eq. (30). Now, substituting (33) and (34) in (32), we arrive at the following general equation of motion

$$\begin{aligned} \overset{**}{r}=\frac{1}{2}\epsilon {\dot{f}}\overset{*}{u}^2-\frac{1}{2}f^\prime -\frac{1}{2}f^\prime \frac{L^2}{r^2}+f\frac{L^2}{r^3}. \end{aligned}$$

(35)

for the radial coordinate r. Substituting our metric function (19), our equation of motion (35) takes the form of

$$\begin{aligned} \overset{**}{r}= & {} -\frac{M(u)}{r^2}+\frac{L^2}{r^3}-\frac{3M(u)L^{2}}{r^4}\nonumber \\&+\frac{Q^2(u)}{r^3}+\frac{2Q^2(u)L^{2}}{r^5} \nonumber \\&-\frac{(3\omega _s+1)N_{s}(u)}{2r^{3\omega _s+2}}-\frac{3(\omega _s+1)N_{s}(u)L^{2}}{2r^{3\omega _s+4}}\nonumber \\&+\frac{1}{2}\epsilon {\dot{f}}\overset{*}{u}^2. \end{aligned}$$

(36)

Consequently, we realize the following interesting points.

• The terms in the first line are exactly the same as that of the standard Schwarzschild black hole solution except the time dependance in the mass of the black hole. Here, the terms represent the Newtonian gravitational force, the repulsive centrifugal force and the relativistic correction of general relativity (which accounts for the perihelion advance of planets), respectively.

• The terms in the second line are new correction terms, in comparison to the standard Schwarzschild case, due to the charge of the central object. Here, the first term represents the Coulomb force while the second one represents a relativistic-like correction of GR through the coupling between the charge Q(u) and L angular momentum. These new correction terms may be small in general in comparison to their Schwarzschild counterparts. However, one can show that there are possibilities that these terms can be comparable or equal to them. Then, for finding the situations where these forces are comparable to the Newtonian gravitational force and the GR correction term in (36), we define the distances $D_{q_{1}}$ and $D_{q_{2}}$ corresponding to $\big |\frac{a_{q_1}}{a_{N}}\big |\simeq 1$ and $\big |\frac{a_{q_2}}{a_{L}}\big |\simeq 1$, respectively, in which $a_N$, $a_L$ are the Newtonian and the relativistic correction accelerations, respectively, and $a_{q_1}$ and $a_{q_2}$ are defined as

  $$\begin{aligned} a_{q_1}=\frac{Q^2(u)}{r^3},\quad a_{q_2}=\frac{2Q^2(u)L^{2}}{r^5}. \end{aligned}$$

  (37)

  Accordingly, we obtain the distances $D_{q_{1}}$ and $D_{q_{2}}$ corresponding to $\big |\frac{a_{q_1}}{a_{N}}\big |\simeq 1$ and $\big |\frac{a_{q_2}}{a_{L}}\big |\simeq 1$, respectively, as

  $$\begin{aligned} D_{q_{1}}=\frac{Q^2(u)}{M(u)},\quad D_{q_{2}}=\sqrt{\frac{2Q^2(u)}{3M(u)}}. \end{aligned}$$

  (38)

• In the third line, we have two new correction terms due to the presence of the surrounding field. Here, the first term is similar to that of Newtonian gravitational term and the second term is similar to the relativistic correction of GR through the coupling between the background filed parameter $N_s(u)$ and angular momentum L. Then, we see that for the more realistic non-empty backgrounds, the geodesic equation of any object depends strictly not only on the mass of the central object of the system and the conserved angular momentum of the orbiting body, but also on the background field nature. Similar to the previous case, one can show that there are possibilities that the background correction terms can be comparable to their Schwarzschild counterparts. Thus, for this case, we define the distances $D_{s_{1}}$ and $D_{s_{2}}$ which correspond to $\big |\frac{a_{s_1}}{a_{N}}\big |\simeq 1$ and $\big |\frac{a_{s_2}}{a_{L}}\big |\simeq 1$, respectively, in which $a_{s_1}$ and $a_{s_2}$ are

  $$\begin{aligned} a_{s_1}=\frac{(3\omega _s+1)N(u)}{2r^{3\omega _s+2}},\quad a_{s_2}=\frac{3(\omega _s+1)N(u)L^{2}}{2r^{3\omega _s+4}}. \end{aligned}$$

  (39)

  Then, we obtain the distances $D_{s_{1}}$ and $D_{s_{2}}$ as

  $$\begin{aligned} D_{s_{1}}\simeq & {} \left( \frac{|(3\omega _s +1)N_s(u)|}{2M(u)}\right) ^{\frac{1}{3\omega _s}},\nonumber \\ D_{s_{2}}\simeq & {} \left( \frac{|(\omega _s +1)N_s(u)|}{2M(u)}\right) ^{\frac{1}{3\omega _s}}. \end{aligned}$$

  (40)

• The term in the fourth line is also a new non-Newtonian correction resulting from the dynamics of black hole and its surrounding field. It is associated with the radiation-accretion power of the black hole and its surrounding field.¹ Calling this acceleration as the induced acceleration $a_{i}$ by the dynamics, where the subscript i stands for “induced”, we have

  $$\begin{aligned} a_{i}=\frac{1}{2}\epsilon {\dot{f}}\overset{*}{u}^{2} =- \ \epsilon \left( \frac{{\dot{M}}(u)}{r}-\frac{Q(u){\dot{Q}}(u)}{r^{2}} +\frac{{\dot{N}}(u)}{2r^{3\omega _s+1}}\right) \overset{*}{u}^{2}, \end{aligned}$$

  (41)

  in which, following Lindquist, Schwartz and Misner [64], we define the generalized “total apparent flux” as $\mathcal {A}_{F}=\epsilon \left( {\dot{M}}(u)- \frac{Q(u){\dot{Q}}(u)}{r}+\frac{{\dot{N}}(u)}{2r^{3\omega _s}}\right) {\overset{*}{u}}^{2}={\mathfrak {L}}-\frac{\mathcal {Q}}{r}+\frac{\mathfrak {N}}{2r^{3\omega _{s}}}$ where $\mathfrak {L}, \mathcal {Q}$ and $\mathfrak {N}$ are the apparent fluxes associated to the black hole mass, charge and its surrounding field, respectively. Using these definitions, we can rewrite (41) as

  $$\begin{aligned} a_{i}=-\frac{\mathfrak {L}}{r}+\frac{\mathcal {Q}}{r^{2}}-\frac{\mathfrak {N}}{2r^{3\omega _s+1}}. \end{aligned}$$

  (42)

  This new correction term may also be small in general in comparison to the Newtonian term [64]. However, one can show that there are also possibilities that these two terms can be comparable. Then, we define the distance $D_i$ which satisfies $a_i\simeq a_N$, and it will be given by the solutions of the following equation for different values of M, $\omega _s$ and apparent fluxes $\mathfrak {L}, \mathcal {Q}$ and $\mathfrak {N}$ as

  $$\begin{aligned} \mathfrak {L}D_i^{3\omega _s}-\mathcal {Q}D_i^{3\omega -1} +\frac{1}{2}\mathfrak {N}\simeq MD_i^{3\omega _s-1}. \end{aligned}$$

  (43)

  It is hard to find the general solutions to this equation in terms of its generic parameters $\mathfrak {L}, \mathcal {Q}, \mathfrak {N}, M$ and $\omega _s$. However, we will show that there are possible solutions for the various backgrounds of dust, radiation, quintessence and cosmological constant-like fields for some particular ranges of the parameters.

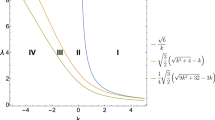
As we see from (38), the distances $D_{q_{1}}$ and $D_{q_{1}}$ depend only on the parameters of the black hole, and not on the background parameters, while $D_{s_{1}}, D_{s_{2}}$ and $D_{i}$ depend on both the black hole and its background parameters. Then, in the following we give some plots denoting the possibility of having $D_{q_{1}}$ and $D_{q_{1}}$ representing $\big |\frac{a_{q_1}}{a_{N}}\big |\simeq 1$ and $\big |\frac{a_{q_2}}{a_{L}}\big |\simeq 1$, respectively, and postpone the studying of the remaining cases ($D_{s_{1}}, D_{s_{2}}$ and $D_{i}$) till the following subsections. In Fig. 1, the possibility of having $\big |\frac{a_{q_1}}{a_{N}}\big |\simeq 1$ and $\big |\frac{a_{q_2}}{a_{L}}\big |\simeq 1$, for some typical values of M(u) and Q(u) parameters are shown. Then, one can realize that there are possibilities for the phase space of our parameters such that the charge contributions can be comparable to their Schwarzschild counterparts.

Fig. 1

$D_{q1}$ and $D_{q2}$ for some typical values of M(u) and Q(u) representing the possibility of $\big |\frac{a_{q_1}}{a_{N}}\big |\simeq 1$ and $\big |\frac{a_{q_2}}{a_{L}}\big |\simeq 1$, respectively

In the following subsections, we consider the cosmological surrounding fields of dust, radiation, quintessence and cosmological constant-like fields as the special classes of the obtained general solution (22), and we will investigate some of their interesting features in more detail.

2.1 Evaporating-accreting Bonnor–Vaidya black hole surrounded by the dust field

For the dust surrounding field, we set $\omega _d=0$ [53, 65]. Then, the metric (22) appears in the following form

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M(u)+N_d(u)}{r}+\frac{Q^2(u)}{r^2}\right) du^2\nonumber \\&+ \ 2\epsilon dudr+r^2d\Omega ^2. \end{aligned}$$

(44)

It is seen that a charged black hole in the dust background appears as an effectively evaporating-accreting charged black hole with an effective mass $2M_{eff}=2M(u)+N_d(u)$. Then, the presence of effective mass term changes the thermodynamics, causal structure and Penrose diagrams of the original Bonnor–Vaidya black hole up to a mass re-scaling.

The total radiation-accretion density in the dust background is given by

$$\begin{aligned} \sigma (u,r)=\epsilon \left( \frac{2{\dot{M}}(u)+{\dot{N}}_{d}(u)}{r^{2}} -\frac{2Q(u){\dot{Q}}(u)}{r^3}\right) , \end{aligned}$$

(45)

and consequently dynamical behaviour of the background dust field at (u, r) is governed by

$$\begin{aligned} {\left\{ \begin{array}{ll}{\dot{N}}_{d}(u)\le \frac{2}{r} \left( Q(u){\dot{Q}}(u)-r{\dot{M}}(u)\right) , &{} \epsilon =- \ 1, \\ {\dot{N}}_{d}(u)\ge \frac{2}{r} \left( Q(u){\dot{Q}}(u)-r{\dot{M}}(u)\right) , &{}\epsilon =+ \ 1. \end{array}\right. } \end{aligned}$$

(46)

Then, at an arbitrary distance r from the black hole, the background dust field must obey the above conditions. Interestingly, for the special case of ${\dot{N}}_{d}(u)=\frac{2}{r} (Q(u){\dot{Q}}(u)-r{\dot{M}}(u) )$, there is no pure radiation-accretion density, i.e $\sigma (u,r)=0$, and then the total energy–momentum tensor (4) will be diagonalized. The case $\sigma (u,r)=0$ corresponds to two possible physical situations. The first one is related to the situation where for any particular distance $r_0$, the background dust field (${\dot{N}}_d(u)$) and black hole (${\dot{M}}(u)$ and ${\dot{Q}}(u)$) behave such that their contributions cancel out each others, leading to $\sigma (u,r_0)=0$. The second situation is associated with the case where for the given dynamical behaviors of the Bonnor–Vaidya black hole and its surrounding dust field, one can find the particular distance

$$\begin{aligned} r_{*}(u)=\frac{2Q(u){\dot{Q}} (u)}{2{\dot{M}}(u)+{\dot{N}}_d(u)}, \end{aligned}$$

(47)

possessing zero energy density, i.e $\sigma \left( u,r_{*}(u)\right) =0$. Then, regarding (45)–(47), the following points can be realized for a Bonnor–Vaidya black hole surrounded by the dust field.

• Regarding (45), for ${\dot{N}}_d(u)\ne \frac{2}{r} (Q(u){\dot{Q}}(u)-r{\dot{M}}(u) )$, we find that the radiation-accretion density vanishes only for $r_*\rightarrow \infty$. This means that for the emission case, the outgoing charged radiation can penetrate through the dust background so far from the black hole horizon and for the accretion case by the black hole, the black hole affects the so far surrounding dust field.

• Regarding (47), for the case of constant rate for ${\dot{N}}_{d}(u)$, ${\dot{M}}(u)$ and ${\dot{Q}}(u)$, the distance $r_{*}$ is fixed to a particular value. In general case where ${\dot{N}}_{d}(u)$ and ${\dot{M}}(u)$ and ${\dot{Q}}(u)$ have no constant rates, the $r_*$ is a dynamical position with respect to the time coordinate u, i.e $r_*=r_*(u)$.

• Regarding (47), to have a particular distance at which the energy density $\sigma (u,r_{*})$ is zero, the positivity of $r_*(u)$ also requires that $Q(u){\dot{Q}}(u)$ and $2{\dot{M}}_{eff}=2{\dot{M}}(u)+{\dot{N}}_d(u)$ have the same signs. For the cases in which $r_*(u)$ is not positive, the lack of a positive value radial coordinate is interpreted as follows: the total radiation-accretion density $\sigma (u,r)$ never and nowhere vanishes.

• Regarding (47), demanding that ${\dot{Q}}(u)$ and ${\dot{M}}(u)$ have the same signs for both of the radiation and accretion processes, the positivity condition of $r_*(u)$ requires the condition $|2{\dot{M}}(u)|\ge |\,{\dot{N}}_d(u)|$ when ${\dot{N}}_d (u)$ takes opposite sign.

• In the case of $r_*(u)$ being the positive radial distance, for the given radiation-accretion behaviors of the black hole and its surrounding dust field, i.e ${\dot{M}}(u)$, ${\dot{Q}}(u)$ and ${\dot{N}}_{d}(u)$, it is possible to find a distance at which we have no any radiation-accretion energy density contribution. In other words, it turns out that the rate of outgoing radiation energy density of the black hole is exactly balanced by the rate of ingoing absorption rate of surrounding field at the distance $r_{*}$ and vice versa.

• Regarding (47), for the case of $|Q(u){\dot{Q}}(u)| \ll |{\dot{M}}_{eff} |$, we have $r_*\rightarrow \infty$. Considering the unit charge gauge, for the extremal case ${\dot{Q}}(u)\approx {\dot{M}}(u)$, for $r_*\rightarrow \infty$, we find that black hole evolves very slow relative to its background. Then, by satisfaction of these dynamical conditions to have $r_*\rightarrow \infty$, the positive energy density condition is respected everywhere in the spacetime. In other cases, the positive energy density is respected in some regions while it is violated beyond those regions.

• Another interesting situation happens when ${\dot{M}}_{eff}=0$, i.e $2{\dot{M}}(u)=-\ {\dot{N}}_d(u)$. In this case, regarding (45) and (47), the radiation-accretion density is only resulting from the charge contribution in the form of $\sigma (u,r)=- \ \epsilon \frac{2Q(u){\dot{Q}}(u)}{r^3}$ and consequently $r_*\rightarrow \infty$. Also, in order to respect to the positive energy condition here, it is required that $\epsilon$ and $Q(u){\dot{Q}}(u)$ have opposite signs.

• Regarding (45), for both of the cases of neutral black hole ($Q(u)=0$) and black hole with static charge (${\dot{Q}}(u)=0$), if ${\dot{M}}_{eff}\ne 0$, we have $r_*\rightarrow \infty$.

In the following, we demonstrate the various general situations which can be realized for the Bonnor–Vaidya black hole surrounded by a dust field in the Tables 1 and 2. Here, we assume that the radiation case corresponds to ${\dot{M}}(u)<0$, ${\dot{Q}}(u)\le 0$ and the accretion case corresponds to ${\dot{M}}(u)>0$, ${\dot{Q}}(u)\ge 0$.

Table 1 General Bonnor–Vaidya BH and its dust SF parameters for $\epsilon =- \ 1$. ECM denotes external charged matter which may contribute to the accretion

Table 2 General Bonnor–Vaidya BH and its dust SF parameters for $\epsilon =+ \ 1$

Regarding Table 1, we see that for the cases I, II, VII and VIII, there are regions in spacetime that the positive energy condition is respected, while beyond these regions it is violated. The cases IV, V, VIIII and XII are not physical in the sense that the positive energy condition is violated in the whole spacetime. The cases III, VI and XI as well as X represent the situations that the positive energy condition is respected in the whole spacetime with and without a priory condition on the black hole and its surrounding dust field dynamics, respectively.

Regarding Table 2, we see that for the cases I, II, VII and VIII, there are regions in spacetime that the positive energy condition is respected, while beyond these regions it is violated. The cases III, VI, X and XI are not physical in the sense that the positive energy condition is violated in the whole spacetime. The cases IV as well as V, VIIII and XII represent the situations that the positive energy condition is respected in the whole spacetime without and with a priory condition on black hole and its surrounding dust filed dynamics, respectively.

Regrading the conditions in the Tables 1 and 2 for $\epsilon =- \ 1$ and $\epsilon =+\ 1$, the behaviour of radiation-accretion density $\sigma (u,r)$ in (45) is plotted for some typical values of ${\dot{M}}(u)$, ${\dot{Q}}(u)$ and ${\dot{N}}_{d}(u)$ in the Figs. 2 and 3, respectively. Using these plots, one can compare the radiation-accretion density values for the various situations.

Fig. 2

Radiation-accretion density $\sigma$ versus the distance r for some typical constant ${\dot{M}}$, ${\dot{Q}}$ and ${\dot{N}}_{d}$ values for $\epsilon =-\ 1$ in the dust background. Here, we have set $Q=1$ for simplicity

Fig. 3

Radiation-accretion density $\sigma$ versus the distance r for some typical constant ${\dot{M}}$, ${\dot{Q}}$ and ${\dot{N}}_{d}$ values for $\epsilon =+\ 1$ in the dust background. Here, we have set $Q=1$ for simplicity

Fig. 4

The variation of $D_{s_1}$ and $D_{s_2}$ versus typical values of the M(u) and $N_d(u)$ parameters for the dust background

Fig. 5

The variation of $D_{i}$ versus typical values of the $\mathfrak {L}, \mathcal {Q}$ and $\mathfrak {N}$ parameters in (48) for the dust background. We have set $M=1$ without loss of generality in all these plots. The plots a–c represent the cases of $\mathcal {Q}=-1, 0$ and $+1$, respectively. The plots d–f represents the case of $\mathfrak {L}=-1, 0$ and $+1$. The plots g–i represent of $\mathfrak {N}=-\ 1, 0$ and $+ \ 1$

Finally, considering the timelike geodesic equations, for this case, we have $D_{s_1}=D_{s_2}$ and both the situations of $\big |\frac{a_{s_1}}{a_{N}}\big |\simeq 1$ and $\big |\frac{a_{s_2}}{a_{L}}\big |\simeq 1$ can be met for $M(u)=\frac{|N_d(u)|}{2}$ in the whole spacetime. In the Fig. 4, we have plotted the possibility of being these particular situations for some typical ranges of M(u) and $N_d(u)$ parameters. Then, regarding this figure, we realize the possibility of the equality of the Newtonian force as well as GR correction terms to the corresponding contributions of the dust background.

Also, the Eq. (43) associated with $a_i\simeq a_N$ takes the form of

$$\begin{aligned} D_i\mathfrak {L} -\mathcal {Q}+\frac{1}{2}D_i\mathfrak {N}\simeq M, \end{aligned}$$

(48)

which has the solution

$$\begin{aligned} D_{i}\simeq \frac{2(M+\mathcal {Q})}{2\mathfrak {L}+\mathfrak {N}}. \end{aligned}$$

(49)

Then, we see that how this particular distance depends on the parameters $\mathfrak {L}, \mathcal {Q}, \mathfrak {N}$ and M. In Fig. 5, we have plotted the solutions of (48) for some typical ranges of $\mathfrak {L}, \mathcal {Q}$ and $\mathfrak {N}$ parameters. This figure indicates that in the dust background, and depending the values of our parameters, there are locations where the induced force resulting from the radiation-accretion phenomena can be equal to the Newtonian force.

2.2 Evaporating-accreting Bonnor–Vaidya black hole surrounded by the radiation field

For the radiation surrounding field, we set $\omega _r=\frac{1}{3}$ [53, 65]. Then, the metric (22) appears in the following form

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M(u)}{r}+\frac{Q^2(u)-N_{r}(u)}{r^2}\right) du^2\nonumber \\&+ \ 2\epsilon dudr+r^2d\Omega ^2. \end{aligned}$$

(50)

The positive energy condition on the surrounding radiation field, represented by the relation (21), requires $N_r(u)\leqslant 0$. By defining the positive structure parameter $\mathcal {N}_r(u)=- \ N_r(u)$, the metric (50) reads as

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M(u)}{r}+\frac{Q^2(u)+\mathcal {N}_{r}(u)}{r^2}\right) du^2\nonumber \\&+ \ 2\epsilon dudr+r^2d\Omega ^2. \end{aligned}$$

(51)

This metric is the metric of a charged Bonnor–Vaidya black hole with the effective dynamical charge of $Q_{eff}(u)=\sqrt{Q^{2}(u)+\mathcal {N}_r(u)}$. This result can be interpreted as the positive contribution of the characteristic feature of the surrounding radiation field to the effective charge of the black hole. As the consequence of arising the effective charge, the causal structure and Penrose diagrams for this black hole solution differs from the original Bonnor–Vaidya black hole up to a charge re-scaling.

The total radiation-accretion density is given by

$$\begin{aligned} \sigma (u,r)=\epsilon \left( \frac{2{\dot{M}}(u)}{r^{2}}-\frac{2Q(u){\dot{Q}}(u) +{\mathcal {{\dot{N}}}}_{r}(u)}{r^3}\right) , \end{aligned}$$

(52)

and consequently, the dynamical behaviour of the background radiation field is governed by the following conditions

$$\begin{aligned} {\left\{ \begin{array}{ll}\mathcal {{\dot{N}}}_{r}(u)\ge 2 \left( r{\dot{M}}(u)-Q(u){\dot{Q}}(u)\right) , &{} \epsilon =- \ 1, \\ \mathcal {{\dot{N}}}_{r}(u)\le 2 \left( r{\dot{M}}(u-Q(u){\dot{Q}}(u)\right) , &{}\epsilon =+ \ 1. \end{array}\right. } \end{aligned}$$

(53)

Then, at an arbitrary distance r from the black hole, the background field must obey the above conditions regarding the $\epsilon$ values. Interestingly, for the specific case of $\mathcal {{\dot{N}}}_{r}(u)=2\left( r{\dot{M}}(u) - Q(u){\dot{Q}}(u)\right)$, there is no pure radiation-accretion density, i.e $\sigma (u,r)=0$, and the energy–momentum tensor (4) will be diagonalized. The case of zero energy density corresponds to two possible physical situations. The first one is related to the situation where the observer can be located at any distance $r_0$ such that the background radiation field ($\mathcal {{\dot{N}}}_{r}(u)$), and black hole (${\dot{M}}(u)$ and ${\dot{Q}}(u)$) contributions cancel out each others, leading to $\sigma (u,r_0)=0$ for a moment or even a period of time. The second situation is associated with the case where for the given dynamical behaviors of the charged black hole and its background, one can find the particular distance

$$\begin{aligned} r_{*}(u)=\left( \frac{2Q{\dot{Q}} (u)+ \mathcal {{\dot{N}}}_r(u)}{2{\dot{M}}(u)}\right) , \end{aligned}$$

(54)

possessing zero energy density, i.e $\sigma (u,r_*(u))=0$. Then, regarding (52)–(54), the following points can be realized for a Bonnor–Vaidya black hole surrounded by the radiation field.

• Regarding (52), for $\mathcal {{\dot{N}}}_{r}(u)\ne 2 ( r{\dot{M}}(u)-Q(u){\dot{Q}}(u) )$, we find that the radiation-accretion density vanishes only for $r_*\rightarrow \infty$. This means that for the emission case, the outgoing charged radiation can penetrate through the radiation background so far from the black hole horizon and for the accretion case by the black hole, the black hole affects the so far surrounding radiation.

• Regarding (54), for the case of constant rate for $\mathcal {{\dot{N}}}_{r}(u)$, ${\dot{M}}(u)$ and ${\dot{Q}}(u),$ the distance $r_{*}$ is fixed to a particular value. In general case where $\mathcal {{\dot{N}}}_{r}(u)$ and ${\dot{M}}(u)$ and ${\dot{Q}}(u)$ have no constant rates, the $r_*$ is a dynamical position with respect to the time coordinate u, i.e $r_*=r_*(u)$.

• Regarding (54), for having a particular distance at which the density $\sigma (u,r_{*})$ is zero, the positivity of $r_*$ also requires that ${\dot{M}}(u)$ and $2Q_{eff}(u){\dot{Q}}_{eff}(u)=2Q{\dot{Q}} (u)+ \mathcal {{\dot{N}}}_r(u)$ have the same signs. For the cases in which $r_*$ is not positive, the lack of a positive value radial coordinate is interpreted as follows: the radiation-accretion density $\sigma (u,r)$ never and nowhere vanishes.

• Regarding (54), demanding that ${\dot{Q}}(u)$ and ${\dot{M}}(u)$ have the same signs for both of the radiation and accretion processes, the positivity condition of $r_*(u)$ requires the condition $|2Q(u){\dot{Q}}(u)|\ge |\mathcal {{\dot{N}}}_r(u)|$ when $\mathcal {{\dot{N}}}_r(u)$ takes opposite sign.

• In the case of $r_*$ being the positive radial distance, for the given radiation-accretion behaviors of the black hole and its surrounding field, i.e ${\dot{M}}(u)$, ${\dot{Q}}(u)$ and $\mathcal {{\dot{N}}}_r(u)$, it is possible to find a distance at which we have no any radiation-accretion energy density contribution. In other words, it turns out that the rate of outgoing radiation energy density of the black hole is exactly balanced by the rate of ingoing absorption rate of surrounding field at the distance $r_{*}$ and vice versa.

• Regarding (54), for the case of $|{\dot{M}}(u)| \ll |Q_{eff}(u){\dot{Q}}_{eff}(u)|$, we have $r_*\rightarrow \infty$. Considering the unit charge gauge, for the extremal case ${\dot{Q}}(u)\approx {\dot{M}}(u)$, we find that black hole evolves very slow relative to its radiation background. Then, by satisfaction of these dynamical conditions to have $r_*\rightarrow \infty$, the positive energy density is respected everywhere in the spacetime. In other cases, the positive energy density will be respected in some regions, while it is violated beyond those regions.

• Another interesting situation happens for two different cases as $Q_{eff}(u)=0$ and ${\dot{Q}}_{eff}(u)=0$ corresponding to $Q=\mathcal {N}_{r}=0$ and $2Q(u){\dot{Q}}(u)=-\mathcal {{\dot{N}}}_r(u)$, respectively. In these cases, regarding (52) and (54), the radiation-accretion density is only resulting from the black hole mass contribution in the form of $\sigma (u,r)=\epsilon \frac{2{\dot{M}}(u)}{r^2}$ and consequently $\epsilon$ must have the same sign as ${\dot{M}}(u)$ to have a positive energy density. In this case, the radiation-accretion density looks like the original neutral Vaidya solution in an empty space, while the black hole and its background here is completely different, and vanishes as $r_*\rightarrow \infty$.

• Regarding (52), for both of the cases of neutral black hole ($Q(u)=0$) and black hole with static charge (${\dot{Q}}(u)=0$), we have

  $$\begin{aligned} r_{*}(u)=\frac{\mathcal {{\dot{N}}}_{r}(u)}{2{\dot{M}}(u)}. \end{aligned}$$

  (55)

  Then, the positivity of $r_*$ demands that $\mathcal {{\dot{N}}}_{r}(u)$ and ${\dot{M}}(u)$ have same signs, and for $|2{\dot{M}}(u)|\ll |\mathcal {{\dot{N}}}_{r}(u)|$, we have $r_*\rightarrow \infty$.

In the following, we demonstrate the various general situations which can be realized for the Bonnor–Vaidya black hole surrounded by the radiation field in the Tables 3 and 4.

Table 3 General Bonnor–Vaidya BH and its radiation SF parameters for $\epsilon =- \ 1$

Table 4 General Bonnor–Vaidya BH and its radiation SF parameters for $\epsilon =+\ 1$

Fig. 6

Radiation-accretion density $\sigma$ versus the distance r for some typical constant ${\dot{M}}$, ${\dot{Q}}$ and $\mathcal {{\dot{N}}}_r$ values for $\epsilon =-\ 1$ in the dust background. Here, we have set $Q=1$ for simplicity

Fig. 7

Radiation-accretion density $\sigma$ versus the distance r for some typical constant ${\dot{M}}$, ${\dot{Q}}$ and $\mathcal {{\dot{N}}}_r$ values for $\epsilon =+\ 1$ in the dust background. Here, we have set $Q=1$ for simplicity

Fig. 8

The variation of $D_{s_1}$ (green plot) and $D_{s_2}$ (yellow plot) versus typical values of the M(u) and $N_r(u)$ parameters for the radiation background

Fig. 9

The variation of $D_{i}$ versus typical values of the $\mathfrak {L}, \mathcal {Q}$ and $\mathfrak {N}$ parameters in (48) for the radiation background. We have set $M=1$ without loss of generality in all the plots. The plots a–c represent the cases of $\mathcal {Q}=-\ 1, 0$ and $+1$, respectively. The plots d, e represents the case of $\mathfrak {L}=-1, 0$ and $+1$. The plots f–h represent of $\mathfrak {N}=-\ 1, 0$ and $+\ 1$

Regarding Table 1, we see that for the cases I, II, IV, VI, VII and VIIII, there are regions in spacetime where the positive energy condition is respected, while beyond these regions it is violated. The cases IV, V, VIIII and XII are not physical in the sense that the positive energy condition is violated in the whole spacetime. The cases VIII and X represent the situations where the positive energy condition is respected in the whole spacetime with and without a priory condition on the black hole and its surrounding radiation field dynamics, respectively.

Regarding Table 2, we see that for the cases I, II, IV, VI, VII and VIIII, there are regions in spacetime where the positive energy condition is respected, while beyond these regions it is violated. The cases VIII, X are not physical in the sense that the positive energy condition is violated in the whole spacetime. The cases IIII as well as V represent the situations where the positive energy condition is respected in the whole spacetime with and without a priory condition on the black hole and its surrounding radiation filed dynamics, respectively.

Regrading the conditions in the Tables 3 and 4 for $\epsilon =-\ 1$ and $\epsilon =+\ 1$, the behaviour of radiation-accretion density $\sigma (u,r)$ in (52) is plotted for some typical values of ${\dot{M}}(u)$, ${\dot{Q}}(u)$ and ${\dot{N}}_{d}(u)$ in the Figs. 6 and 7, respectively. Using these plots, one can compare the radiation-accretion density values for the various situations.

Finally, considering the timelike geodesics, for this case, the distances $D_{s_{1}}$ and $D_{s_{2}}$ corresponding to $\big |\frac{a_{s_1}}{a_{N}}\big |\simeq 1$ and $\big |\frac{a_{s_2}}{a_{L}}\big |\simeq 1$, respectively, are given by

$$\begin{aligned} D_{s_{1}}=\frac{|N_r(u)|}{M(u)},\quad D_{s_{2}}=\frac{2|N_r(u)|}{3M(u)}. \end{aligned}$$

(56)

In Fig. 8, the particular distances $D_{s_{1}}$ and $D_{s_{2}}$ versus some typical ranges of M(u) and $N_r(u)$ parameters are plotted. Then, we see that the possibility of the equality of Newtonian force and GR correction terms to the corresponding radiation background field contributions are provided.

Also, the Eq. (55) associated with $a_i\simeq a_N$ takes the following form

$$\begin{aligned} \mathfrak {L} D_{i}-\mathcal {Q}+\frac{1}{2}\mathfrak {N}\simeq M. \end{aligned}$$

(57)

Then, it admits the following solution

$$\begin{aligned} D_{i}\simeq \frac{2M-\mathfrak {N}+2\mathcal {Q}}{2\mathfrak {L}}. \end{aligned}$$

(58)

We see that how this particular distance depends on the values of parameters $\mathfrak {L}, \mathcal {Q}, \mathfrak {N}$ and M. In Fig. 9, we have plotted the solutions of (57) for some typical ranges of $\mathfrak {L}, \mathcal {Q}$ and $\mathfrak {N}$ parameters. According to this figure, depending the parameter values, there are locations where the induced force, resulting from the radiation-accretion phenomena in the radiation background, can be equal to the Newtonian force.

2.3 Evaporating-accreting Bonnor–Vaidya black hole surrounded by the quintessence field

In the context of cosmology, the quintessence filed is known as the simplest scalar field dark energy model free of the theoretical problems such as Laplacian instabilities or ghosts. The energy density and the pressure profile of the quintessence field are generally supposed as time varying quantities and depend on the scalar field and its associated potential given by $\rho = \frac{1}{2}{{\dot{\phi }}}^2 + V(\phi )$ and $p = \frac{1}{2}{\dot{\phi }}^2 -V(\phi )$, respectively. Thus, the corresponding quintessence equation of state parameter lies in the range $-\ 1<\omega _q<-\ \frac{1}{3}$. The static Schwarzschild black hole solution surrounded by a quintessence field was first introduced by Kiselev [53]. Then, this solution was generalized to the Reissner–Nordström case and investigated in [60,61,62].

For the quintessence surrounding field, we set $\omega _q=-\frac{2}{3}$ [53, 65]. Then, the metric (1) takes the following form

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M(u)}{r}+\frac{Q^2(u)}{r^2}-N_{q}(u)r\right) du^2\nonumber \\&+\ 2\epsilon dudr+r^2d\Omega ^2. \end{aligned}$$

(59)

This result is interpreted as the non-trivial contribution of the characteristic feature of the surrounding quintessence field to the metric of the Bonnor–Vaidya black hole. The presence of the background quintessence filed changes the causal structure and Penrose diagrams of this black hole solution in comparison to the charged Vaidya black hole in an empty background. A rather similar effect happens when one immerses an static Schwarzschild in a (anti)-de Sitter background with the difference that here the spacetime tends asymptotically to quintessence rather than (anti)-de Sitter asymptotic state.

Table 5 General Bonnor–Vaidya BH and its quintessence SF parameters for $\epsilon =- \ 1$

Table 6 General Bonnor–Vaidya BH and its quintessence SF parameters for $\epsilon =+ \ 1$

Fig. 10

Radiation-accretion density $\sigma$ versus the distance r for some typical constant ${\dot{M}}$, ${\dot{Q}}$ and ${\dot{N}}_q$ values for $\epsilon =- \ 1$ in the dust background. Here, we have set $Q=1$ for simplicity

Regarding the positive energy density condition for this case, represented by the relation (21), it is required that $N_q(u)\geqslant 0$. In this case, the radiation density is given by

$$\begin{aligned} \sigma (u,r)=\epsilon \left( \frac{2{\dot{M}}(u)}{r^{2}} -\frac{2Q(u){\dot{Q}}(u)}{r^3}+{\dot{N}}_{q}(u)\right) . \end{aligned}$$

(60)

Based on this relation, the dynamical behaviour of the surrounding quintessence field is governed by

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{N}}_{q}(u)\le \frac{2}{{r}^{{3}}}\left( Q(u){\dot{Q}}(u)- r{\dot{M}}(u)\right) , &{} \epsilon =- \ 1, \\ \\ {\dot{N}}_{q}(u)\ge \frac{2}{{r}^{{3}}}\left( Q(u){\dot{Q}}(u)- r{\dot{M}}(u)\right) , &{}\epsilon =+\ 1. \end{array}\right. } \end{aligned}$$

(61)

Then, at an arbitrary distance r from the black hole, the surrounding quintessence field must obey the above conditions. Interestingly, for the special case of ${\dot{N}}_{q}(u)= \frac{2}{{r}^{{3}}} (Q(u){\dot{Q}}(u)- r{\dot{M}}(u) )$, there is no pure radiation-accretion density, i.e $\sigma (u,r)=0$, and the total energy–momentum tensor (4) will be diagonalized. This means that the black hole and its surrounding quintessence field completely cancel out the effects of each others. This case corresponds to two possible physical situations. The first one is related to the situation where the observer can be located at any distance $r_0$ such that the background ${\dot{N}}_{q}(u)$, and black hole ${\dot{M}}(u)$ and ${\dot{Q}}(u)$ contributions cancel out each others, leading to $\sigma (u,r_0)=0$ for a moment or even a period of time. The second situation is related to the case where for the given dynamical behaviors of the charged black hole and its quintessence background, one can find the particular distance

$$\begin{aligned} r_{*}(u)=\frac{3Q(u) {\dot{Q}}(u)}{2{\dot{M}}(u)}, \end{aligned}$$

(62)

possessing zero energy density ($\sigma (u,r_*(u))=0$), see the Appendix A for more details. Then, regarding (60)–(62), the following points can be realized for a Bonnor–Vaidya black hole surrounded by the quintessence field.

• Regarding (60), for ${\dot{N}}_{q}(u)\ne \frac{2}{{r}^{{3}}} (Q(u){\dot{Q}}(u)- r{\dot{M}}(u) )$, we find that in contrast to the cases of the Bonnor–Vaidya black hole surrounded by the dust and radiation fields, here the radiation-accretion density does not vanish at $r_*\rightarrow \infty$. This is due to the fact that the spacetime here has the quintessence asymptotic rather than an empty Minkowski.

• Regarding (62), for the case of constant rates for ${\dot{N}}_{q}(u)$, ${\dot{M}}(u)$ and ${\dot{Q}}(u)$, the distance $r_{*}$ is fixed to a particular value. In general case which ${\dot{N}}_{q}(u)$ and ${\dot{M}}(u)$ and ${\dot{Q}}(u)$ have no constant rates, the $r_*$ has a dynamical position with respect to the time coordinate u, i.e $r_*=r_*(u)$.

• Regarding (62), to have a particular distance at which the density $\sigma (u,r_{*})$ is zero, the positivity of $r_*$ also requires that ${\dot{N}}_q (u)$ takes an opposite sign of ${\dot{M}}(u)$ (and ${\dot{Q}}(u)$), see (78). This is in agreement with our primary consideration for the signs of dynamical parameters (${\dot{N}}_q (u)$, ${\dot{M}}(u)$ and ${\dot{Q}}(u)$) for the radiation and accretion processes in the previous sections. For the cases in which $r_*$ is not positive, the lack of a positive value radial coordinate is interpreted as follows: the radiation-accretion density $\sigma (u,r)$ never and nowhere vanishes.

• In the case of $r_*$ being the positive radial distance, for the given radiation-accretion behaviors of the black hole and its surrounding field, i.e ${\dot{M}}(u)$, ${\dot{Q}}(u)$ and ${\dot{N}}_q(u)$, it is possible to find a distance at which we have no any radiation-accretion energy density contribution. In other words, it turns out that the rate of outgoing radiation energy density of the black hole is exactly balanced by the rate of ingoing absorption rate of surrounding field at the distance $r_{*}$ and vice versa.

• Regarding (62) and (78), for both of the black holes with $|{\dot{M}}(u)|\ll |Q(u){\dot{Q}}(u)|$ and ${\dot{M}}(u)\rightarrow 0$, we have $r_*\rightarrow \infty$ and ${\dot{N}}_q(u)\rightarrow 0$. This means that for a black which is almost active only due to its dynamical charge, one can find that (i) there is a non-zero radiation density even at far distance from the black hole and (ii) positive energy condition is respected everywhere.

• Regarding (62) and (78), working in the unit charge gauge, for the extremal case ${\dot{Q}}(u)\approx {\dot{M}}(u)$, we find

  $$\begin{aligned} r_*\rightarrow \frac{3}{2},\quad {\dot{N}}_q(u)\rightarrow -\frac{8}{27} {\dot{M}}(u). \end{aligned}$$

  (63)

• Regarding (60), for both of the cases of neutral black hole ($Q(u)=0$) and black hole with static charge (${\dot{Q}}(u)=0$), we have

  $$\begin{aligned} r_{*}(u)=\left( -\frac{2{\dot{M}}(u)}{{\dot{N}}_{q}(u)}\right) ^{\frac{1}{2}}. \end{aligned}$$

  (64)

  Then, for $|{\dot{N}}_{q}(u)| \ll |2{\dot{M}}(u)|$, we have $r_*\rightarrow \infty$. This means that for an almost static background (the background with negligible dynamics relative to the black hole mass), the zero of the radiation-accretion density lies at infinity and the positive energy density is respected everywhere in the spacetime. In other cases, one can find a finite value for $r_*$ representing the zero radiation-accretion density in which the positive energy density will be respected in some regions while it is violated beyond those regions, see our previous work on the neutral black hole case for more details [55, 56].

• Regarding both the solutions (62) and (64), the signs of ${\dot{M}}(u)$ and ${\dot{N}}_q (u)$ should be opposite to have a zero radiation-accretion density for both of the radiation-accretion processes.

In the following, regarding the obtained solutions and the above discussions, we demonstrate the various situations which can be realized for the Bonnor–Vaidya black hole surrounded by the quintessence field in the Tables 5 and 6.

Regarding Table 5, we see that for the cases III and V, there are regions is spacetime that the positive energy condition is respected, while beyond these regions it is violated. The case II is not physical in the sense that the positive energy condition is violated in the whole spacetime. The case IV is also not physical in the sense that the positive energy condition is violated in whole spacetime except at the zero density point. The cases I and VI represent the situations that the positive energy condition is respected in the whole spacetime without a priory condition on the black hole and its surrounding quintessence filed dynamics.

Regarding Table 6, we see that for the cases III and V, there are regions in spacetime that the positive energy condition is respected, while beyond these regions it is violated. The cases I and VI are not physical in the sense that the positive energy condition is violated in whole spacetime. The cases II and IV represent the situations that the positive energy condition is respected in the whole spacetime without a priory condition on the black hole and its surrounding quintessence filed dynamics. Regrading the conditions in the Tables 5 and 6 for $\epsilon =-1$ and $\epsilon =+1$, respectively, the behaviour of radiation-accretion density $\sigma (u,r)$ in (60) is plotted for some typical values of ${\dot{M}}(u)$, ${\dot{Q}}(u)$ and ${\dot{N}}_{q}(u)$ in the Figs. 10 and 11, respectively. Using these plots, one can compare the radiation-accretion density values for the various situations.

Fig. 11

Radiation-accretion density $\sigma$ versus the distance r for some typical constant ${\dot{M}}$, ${\dot{Q}}$ and ${\dot{N}}_q$ values for $\epsilon =-\ 1$ in the quintessence background. Here, we have set $Q=1$ for simplicity

Considering the timelike geodesics for this case, the distances $D_{s_{1}}$ and $D_{s_{2}}$ associated with $\big |\frac{a_{s_1}}{a_{N}}\big |\simeq 1$ and $\big |\frac{a_{s_2}}{a_{L}}\big |\simeq 1$, respectively, are given as

$$\begin{aligned} D_{s_{1}}^2=\frac{2M(u)}{|-N_q(u)|},\quad D_{s_{2}}^2=\frac{6M(u)}{|N_q(u)|}. \end{aligned}$$

(65)

In Fig. 12, we have plotted the location of these particular distances versus some typical ranges of the black hole mass M(u) and background quintessence field $N_q(u)$ parameters. Then, one finds that there are possibilities for the equality of the Newtonian force and GR correction terms to the corresponding quintessence background field contributions.

Also, the Eq. (43) associated with $a_{i}\simeq {a_{N}}$ for this case takes the following form

$$\begin{aligned} {\mathfrak {L} D{_i}-\mathcal {Q}+\frac{1}{2}\mathfrak {N}D_{i}^3\simeq M.} \end{aligned}$$

(66)

The solutions to (66) in general are complicated and are given in the Appendix B. However, we can demonstrate those solutions in Fig. 13 for some typical values of our $\mathfrak {L}, \mathcal {Q}, \mathfrak {N}$ and M parameters. This figure represents that depending on the values of our parameter, we can find locations where the induced force, resulting from the radiation-accretion phenomena in the quintessence background, can be equal to the Newtonian force.

Fig. 12

The variation of $D_{s_1}$ (green plot) and $D_{s_2}$ (yellow plot) versus typical values of the M(u) and $N_r(u)$ parameters for the quintessence background

Fig. 13

The variation of $D_{i}$ versus typical values of the $\mathfrak {L}, \mathcal {Q}$ and $\mathfrak {N}$ parameters in (48) for the quintessence background. We have set $M=1$ without loss of generality in all the plots. The plots a–c represent the cases of $\mathcal {Q}=- \ 1, 0$ and $+ \ 1$, respectively. The plots d–f represents the case of $\mathfrak {L}=- \ 1, 0$ and $+ \ 1$. The plots g–i represent of $\mathfrak {N}=-\ 1, 0$ and $+\ 1$

2.4 Evaporating-accreting Bonnor–Vaidya black hole surrounded by the cosmological field

For the cosmological surrounding field, we set $\omega _c=- \ 1$ [53, 65]. Then, the metric (1) takes the following form

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M(u)}{r}+\frac{Q^2(u)}{r^2}-N_c(u)r^2\right) du^2\nonumber \\&+ \ 2\epsilon dudr+r^2d\Omega ^2. \end{aligned}$$

(67)

This result is interpreted as the non-trivial contribution of the characteristic feature of the surrounding cosmological field to the metric of the charged Bonnor–Vaidya black hole. The presence of the background cosmological filed changes the causal structure and Penrose diagrams of this black hole solution in comparison to the black hole in an empty background. The similar effect happens when one immerse an static Schwarzschild black hole in a (anti)-de Sitter background.

The positive energy density condition on the surrounding cosmological field, represented by the relation (21), requires $N_c(u)\geqslant 0$. Then, in this case, $N_{c}(u)$ plays the role of a positive dynamical cosmological field. This case may represents the dynamical black holes in more general cosmological models proposing a time varying cosmological term. The main purpose of these cosmological scenarios is to provide an explanation for the recent observed accelerating expansion of the universe, see [66,67,68,69,70,71,72] as some instances. For the case of $N_c=constant=\Lambda >0$, we recover the Bonnor–Vaidya black hole embedded in a de Sitter space obtained by Patino and Rago [18]. The solution in [18] was generalized to the case of the rotating radiating charged black hole in a static de Sitter space in [25]. In [73], the causal structure of the solution obtained in [25] is studied.

In this case, the total radiation-accretion density is given by

$$\begin{aligned} \sigma (u,r)=\epsilon \left( \frac{2{\dot{M}}(u)}{r^{2}}-\frac{2Q(u){\dot{Q}}(u)}{r^3}+{\dot{N}}_{c}(u)r\right) . \end{aligned}$$

(68)

Then, the dynamical behaviour of the surrounding cosmological field is governed by the following conditions

$$\begin{aligned} {\left\{ \begin{array}{ll}{\dot{N}}_{c}(u)\le \frac{2}{{r}^{{4}}}\left( Q(u){\dot{Q}}(u)- r{\dot{M}}(u)\right) ,&{} \epsilon =-1, \\ \\ {\dot{N}}_{c}(u)\ge \frac{2}{{r}^{{4}}}\left( Q(u){\dot{Q}}(u)- r{\dot{M}}(u)\right) , &{}\epsilon =+1. \end{array}\right. } \end{aligned}$$

(69)

This represents that at an arbitrary distance r from the black hole, the surrounding cosmological field must obey the above conditions. Interestingly, for the special case of ${\dot{N}}_{c}(u)= \frac{2}{{r}^{{4}}} (Q(u){\dot{Q}}(u)- r{\dot{M}}(u) )$, there is no pure radiation-accretion density, i.e $\sigma (u,r)=0,$ and the total energy–momentum tensor (4) will be diagonalized. This case corresponds to two possible physical situations. The first one is associated with the situation where the observer can be located at any distance $r_0$ such that the background cosmological field (${\dot{N}}_{c}(u)$), and the black hole (${\dot{M}}(u)$ and ${\dot{Q}}(u)$) contributions cancel out each others leading to $\sigma (u,r_0)=0$ for a moment or even a period of time. The second situation is related to the case that for the given dynamical behaviors of the charged black hole and its cosmological background, one can find the particular distance

$$\begin{aligned} r_{*}(u)=\frac{4Q(u) {\dot{Q}}(u)}{3{\dot{M}}(u)}, \end{aligned}$$

(70)

possessing zero energy density, i.e $\sigma (u,r_*(u))=0$, see the Appendix C for more details. Then, regarding (68)–(70), the following points can be realized for a Bonnor–Vaidya black hole surrounded by the cosmological field.

• Regarding (68), for ${\dot{N}}_{c}(u)\ne \frac{2}{{r}^{{4}}} (Q(u){\dot{Q}}(u)- r{\dot{M}}(u) )$, we find that in contrast to the cases of Bonnor–Vaidya black hole surrounded by dust and radiation fields, the radiation-accretion density does not vanish for $r_*\rightarrow \infty$. This is due to the fact that here the spacetime has the de Sitter asymptotic rather than an empty Minkowski.

• Regarding (70), for the case of constant rates for ${\dot{N}}_{c}(u)$, ${\dot{M}}(u)$ and ${\dot{Q}}(u)$, the distance $r_{*}$ is fixed to a particular value. In general case which ${\dot{N}}_{c}(u)$ and ${\dot{M}}(u)$ and ${\dot{Q}}(u)$ have no constant rates, the $r_*$ has a dynamical position with respect to the time coordinate u, i.e $r_*=r_*(u)$.

• Regarding (70) and (84), to have a particular distance at which the density $\sigma (u,r_{*})$ is zero, the positivity of $r_*$ also requires that ${\dot{N}}_c(u)$ takes an opposite sign of $Q{\dot{Q}} (u)$ (and ${\dot{M}}(u)$). This is in agreement with our primary consideration for the signs of dynamical parameters (${\dot{N}}_c (u)$, ${\dot{M}}(u)$ and ${\dot{Q}}(u)$) for the radiation and accretion processes in the previous sections. Similarly, for the cases in which $r_*$ is not positive, the lack of a positive value radial coordinate is interpreted as follows: the radiation-accretion density $\sigma (u,r)$ never and nowhere vanishes.

• In the case of $r_*$ being a real and positive radial distance, for the given radiation-accretion behaviors of the black hole and its surrounding field, i.e ${\dot{M}}(u)$, ${\dot{Q}}(u)$ and ${\dot{N}}_c(u)$, it is possible to find a distance at which we have no any radiation-accretion energy density contribution. In other words, it turns out that the rate of outgoing radiation energy density of the black hole is exactly balanced by the rate of ingoing absorption rate of surrounding cosmological field at the distance $r_{*}$ and vice versa.

• Regarding (70) and (84), for both of the black holes with $|{\dot{M}}(u)|\ll |Q(u){\dot{Q}}(u)|$ and ${\dot{M}}(u)\rightarrow 0$, we have $r_*\rightarrow \infty$ and ${\dot{N}}_c(u)\rightarrow 0$. This means that for a black which is almost active only due to its dynamical charge, one can find (i) a non-zero radiation density even at far distance from the black hole and (ii) the respected positive energy condition at everywhere.

• Regarding (70) and (84), working in the unit charge gauge, for the extremal case ${\dot{Q}}(u)\approx {\dot{M}}(u)$, we find

  $$\begin{aligned} r_*\rightarrow \frac{4}{3},\quad {\dot{N}}_c(u)\rightarrow -\frac{27}{128} {\dot{M}}(u). \end{aligned}$$

  (71)

  Then, regarding (63) and (71), comparing the quintessence and cosmological background fields for the extremal case, we have

  $$\begin{aligned} r_{*c}<r_{*q},\quad |{\dot{N}}_c(u)|<|{\dot{N}}_q(u)|. \end{aligned}$$

  (72)

• Regarding (68), for both of the cases of neutral black hole ($Q(u) = 0$) and black hole with static charge (${\dot{Q}}(u) = 0$), we have

  $$\begin{aligned} r_{*}(u)=\left( -\frac{2{\dot{M}}(u)}{{\dot{N}}_{c}(u)}\right) ^{\frac{1}{3}}. \end{aligned}$$

  (73)

  Then, for $|{\dot{N}}_{c}(u)| \ll |2{\dot{M}}(u)|$, we have $r_*\rightarrow \infty$. This means that for an almost static background (the background with negligible dynamics relative to the black hole), the zero of the radiation-accretion density lies at infinity and the positive energy density is respected everywhere in the spacetime. In other cases, one can find a finite value for $r_*$ representing the total zero accretion density in which the positive energy density will be respected in some regions while violated beyond those regions, see our previous work on the neutral black hole case for more details [55, 56].

• Regarding both the solutions (70) and (73), the signs of ${\dot{M}}(u)$ and ${\dot{N}}_c (u)$ should be opposite to have a zero radiation-accretion density for both of the radiation-accretion processes.

• Regarding (64) and (73), in the case that the quintessence and cosmological backgrounds have a same behavior ($|{\dot{N}}_{q}(u)|=|{\dot{N}}_{c}(u)|$), for $|{\dot{N}}_{c,q}(u)| < |2{\dot{M}}(u)|$, we have $r_{*c}(u)<r_{*q}(u)$ while for $|{\dot{N}}_{c,q}(u)| >|2{\dot{M}}(u)|$, we have $r_{*c}(u)>r_{*q}(u)$.

• Regarding (64) and (73) for both of the cases of neutral black hole ($Q(u) = 0$) and black hole with static charge (${\dot{Q}}(u) = 0$), when ${\dot{M}}(u)$ and ${\dot{N}}_q(u)$ as well as ${\dot{N}}_c(u)$ have the same signs, $r_*(u)$ is imaginary and negative for the quintessence and cosmological fields, respectively. Then, for these cases, the radiation-accretion density never be zero and the positive energy condition is respected or violated in the whole spacetime.

In the following, regarding the obtained solutions and the above discussions, we demonstrate the various situations which can be realized for the Bonnor–Vaidya black hole surrounded by the cosmological field in the Tables 7 and 8.

Table 7 General Bonnor–Vaidya BH and its cosmological SF parameters for $\epsilon =- \ 1$

Table 8 General Bonnor–Vaidya BH and its cosmological SF parameters for $\epsilon =+ \ 1$

Regarding Table 7, we see that for the cases III and V, there are regions in spacetime that the positive energy condition is respected, while beyond these regions it is violated. The case II is not physical in the sense that the positive energy condition is violated in the whole spacetime. The case IV is also not physical in the sense that the positive energy condition is violated in the whole spacetime except at the zero density point. The cases I and VI represent the situations that the positive energy condition is respected in the whole spacetime without a priory condition on the black hole and its surrounding cosmological filed dynamics.

Regarding Table 8, we see that for the cases III and V, there are regions in spacetime that the positive energy condition is respected, while beyond these regions it is violated. The cases I and VI are not physical in the sense that the positive energy condition is violated in the whole spacetime. The cases II and IV represent the situations that the positive energy condition is respected in the whole spacetime without a priory condition on the black hole and its surrounding cosmological filed dynamics.

Regrading the conditions in the Tables 7 and 8 for $\epsilon =- \ 1$ and $\epsilon =+ \ 1$, the behaviour of radiation-accretion density $\sigma (u,r)$ in (68) is plotted for some typical values of ${\dot{M}}$, ${\dot{Q}}$ and ${\dot{N}}_{c}$ in the Figs. 14 and 15, respectively. Using these plots, one can compare the radiation-accretion density values for the various situations.

Fig. 14

Radiation-accretion density $\sigma$ versus the distance r for some typical constant ${\dot{M}}$, ${\dot{Q}}$ and ${\dot{N}}_c$ values for $\epsilon =- \ 1$ in the dust background. Here, we have set $Q=1$ for simplicity

Fig. 15

Radiation-accretion density $\sigma$ versus the distance r for some typical constant ${\dot{M}}$, ${\dot{Q}}$ and ${\dot{N}}_c$ values for $\epsilon =- \ 1$ in the quintessence background. Here, we have set $Q=1$ for simplicity

Concerning the timelike geodesics, the distances $D_{s_{1}}$ and $D_{s_{2}}$ associated with $\big |\frac{a_{s_1}}{a_{N}}\big |\simeq 1$ and $\big |\frac{a_{s_2}}{a_{L}}\big |\simeq 1$, respectively, read as

$$\begin{aligned} D_{s_{1}}^3=\frac{M(u)}{|-N_c(u)|},\quad D_{s_{2}}\rightarrow \infty . \end{aligned}$$

(74)

According to (37), the case of $D_{s_2}\rightarrow \infty$ is resulting from the fact that, in contrast to black hole itself, the cosmological constant-like field does not couple to angular momentum L, see $a_{s_2}$. Then, there is no similar effect to the GR correction term for the cosmological constant-like field. The location of the particular distance $D_{s_1}$ for some typical ranges of the black hole mass M(u) and background cosmological constant-like field $N_c(u)$ parameters is plotted in Fig. 16. Thus, we realize that the possibilities for the equality of the Newtonian force to the corresponding cosmological constant-like background field contributions are provided

Moreover, the Eq. (55) associated with $a_i\simeq a_N$ takes the form of

$$\begin{aligned} \mathfrak {L} D{_i}-\mathcal {Q}+\frac{1}{2}\mathfrak {N}D_{i}^4\simeq M. \end{aligned}$$

(75)

Fig. 16

The variation of $D_{s_1}$ versus typical values of the M(u) and $N_c(u)$ parameters for the cosmological background

The solutions to (75) in general are complicated and are given in the Appendix D. However, we can demonstrate those solutions in Fig. 17 for some typical values of our $\mathfrak {L}, \mathcal {Q}, \mathfrak {N}$ and M parameters. From this figure, we see that, depending on the values of our parameter, we can find locations where the induced force of the radiation-accretion phenomena in the cosmological background can be equal to the Newtonian one.

Fig. 17

The variation of $D_{i}$ versus typical values of the $\mathfrak {L}, \mathcal {Q}$ and $\mathfrak {N}$ parameters in (48) for the cosmological constant-like background. We have set $M=1$ without loss of generality in all the plots. The plots a–c represent the cases of $\mathcal {Q}=- \ 1, 0$ and $+\ 1$, respectively. The plots d–f represents the case of $\mathfrak {L}=- \ 1, 0$ and $+ \ 1$. The plots g–i represent of $\mathfrak {N}=-\ 1, 0$ and $+ \ 1$, respectively

3 Summary and concluding remarks

By generalizing our previous work [55, 56], we have constructed a general solution for the classical description of the evaporating-accreting charged black holes in the generic dynamical backgrounds of dust, radiation, quintessence and cosmological constant, namely as the surrounded Bonnor–Vaidya black holes. We have shown that (i) the original Bonnor–Vaidya solution can be recovered by turning off the background field, and (ii) the charged Kiselev static solution can be obtained as another subclass of our general solution in the stationary limit. Regarding the obtained total radiation-accretion density for these solutions, if ${\dot{M}}(u)$, ${\dot{Q}}(u)$ and ${\dot{N}}_s(u)$ have a same order of magnitude, the following distinct physical situations can be realized for the various backgrounds with the equation of state parameter $\omega _s$.

• For $\omega _s<0$, the charge contribution is dominant near the black hole while for the far distances, we have $|\sigma _Q|<|\sigma _M|<|\sigma _{N_s}|$, meaning that the surrounding field contribution is dominant at large distances.

• For $0<\omega _s<1/3$, the charge contribution is dominant near the black hole while for the far distances, we have $|\sigma _Q|<|\sigma _{N_s}|<|\sigma _M|$, meaning that the black hole mass contribution is dominant at large distances.

• For $\omega _s>1/3$, the surrounding field contribution is dominant near the black hole while for the far distances, we have $|\sigma _{N_s}|<|\sigma _Q|<|\sigma _M|$ meaning that the black hole mass contribution is dominant again at large distances.

We have addressed some interesting features of these solutions and classified them according to their behaviors under imposing the positive energy condition. We have discussed that this condition gives some severe restrictions on the black hole and its background field dynamics. Using this condition, we have found a particular distance possessing zero effective radiation-accretion density. For all the Bonnor–Vaidya black holes surrounded by the dust, radiation, quintessence and cosmological constant fields, we have found a corresponding particular distance $r_*(u)$ possessing zero effective radiation-accretion density, i.e $\sigma (u,r_{*})=0$. This distance has a dynamical location in general, except for the case of constant rates for the black hole and its surrounding field parameters, i.e ${\dot{M}}(u)$, ${\dot{Q}}(u)$ and ${\dot{N}}_{s}(u)$. For the cases in which there is no real and positive $r_*(u)$, the interpretation is that the total radiation-accretion density $\sigma (u,r)$ never and nowhere vanishes. Also, we have studied the timelike geodesics for the obtained solutions and have found that three new correction terms arise relative to the case of the standard Schwarzschild black hole. The first kind of corrections is due to the charge of the central black hole which includes two terms in which its first term is rather similar to the term of Newtonian gravitational force, while its second term is similar to the relativistic correction of GR due to the coupling of charge and angular momentum. The second kind of our correction terms is resulting from the presence of the background fields which surround the black hole. This corrections also include two terms in which the first term looks like to Newtonian gravitational term, while the second term is similar to the relativistic correction of GR due to the coupling of background field parameter to the angular momentum. We have discussed that for the various background fields, there are possibilities for the equality of Newtonian and GR correction terms to the corresponding charge and background field contributions. We have given some plots denoting these possibilities for each case. The third type of new corrections, as a non-Newtonian correction, is resulting from the dynamics of the central black hole and its surrounding field. For this case also, it is shown that depending on the dynamical features of black hole and its background, one can find possibilities that this new dynamical correction can be compared with the Newtonian case. We have given some plots denoting these particular situations. Accordingly, we realize that for more realistic cases which are non-static and possess non-empty backgrounds in nature, the geodesic equation of any object depends strictly not only on the (i) mass of the central object of the system, (ii) the angular momentum of the orbiting body, but also on (iii) background field features and (iv) black hole-background field dynamics. We have summarized our obtained results for the various surrounding fields as follows.

• For the dust background, we have the Bonnor–Vaidya black hole with the effective dynamical mass $2M_{eff}= 2M(u)+N_d(u)$. To have a particular distance $r_*$ at which $\sigma (u,r_{*})=0$, the condition $|2{\dot{M}}(u)|\ge |\,{\dot{N}}_d(u)|$ is required. For the case of $|Q(u){\dot{Q}}(u)| \ll |{\dot{M}}_{eff} |$, we have $r_*\rightarrow \infty$. In the unit charge gauge, for the extremal case (${\dot{Q}}(u)\approx {\dot{M}}(u)$), for $r_*\rightarrow \infty$, we find that black hole evolves very slow relative to its dust background. Then, by satisfaction of these dynamical conditions to have $r_*\rightarrow \infty$, the positive energy density condition is respected everywhere in the spacetime. In other cases, the positive energy density is respected in some regions while it is violated beyond those regions. Another interesting situation happens when ${\dot{M}}_{eff}=0$. In this case, the radiation-accretion density is only resulting from the charge contribution with $r_*\rightarrow \infty$.

• For the radiation background, we have the Bonnor–Vaidya black hole with the effective dynamical charge $Q_{eff}(u)=\sqrt{Q^{2}(u)+\mathcal {N}_r(u)}$. To have a particular distance $r_*$ at which $\sigma (u,r_{*})=0$, the condition $|2Q(u){\dot{Q}}(u)|\ge |\mathcal {{\dot{N}}}_r(u)|$ is required. For the case of $|{\dot{M}}(u)| \ll |Q_{eff}(u){\dot{Q}}_{eff}(u)|$, we have $r_*\rightarrow \infty$. In the unit charge gauge, for the extremal case (${\dot{Q}}(u)\approx {\dot{M}}(u)$), we find that black hole evolves very slow relative to its radiation background. Then, by satisfaction of these dynamical conditions to have $r_*\rightarrow \infty$, the positive energy density is respected everywhere in the spacetime. In other cases, the positive energy density will be respected in some regions, while it is violated beyond those regions. Another interesting situation happens for two different cases as $Q_{eff}(u)=0$ and ${\dot{Q}}_{eff}(u)=0$ corresponding to $Q=\mathcal {N}_{r}=0$ and $2Q(u){\dot{Q}}(u)=- \ \mathcal {{\dot{N}}}_r(u)$, respectively. In these cases, the radiation-accretion density is only resulting from the black hole mass contribution. For both of the cases of neutral black hole ($Q(u)=0$) and black hole with static charge (${\dot{Q}}(u)=0$), for $|2{\dot{M}}(u)| \ll |\mathcal {{\dot{N}}}_{r}(u)|$, we have $r_*\rightarrow \infty$.

• For the quintessence background, the positive energy density condition demands $N_q(u)\geqslant 0$. To have a particular distance $r_*$ at which $\sigma (u,r_{*})=0$, the positivity of $r_*$ requires that ${\dot{N}}_q (u)$ takes an opposite sign of ${\dot{M}}(u)$ (and ${\dot{Q}}(u)$). For both of the black holes with $|{\dot{M}}(u)|\ll |Q(u){\dot{Q}}(u)|$ and ${\dot{M}}(u)\rightarrow 0$, we have $r_*\rightarrow \infty$ and ${\dot{N}}_q(u)\rightarrow 0$. This means that for a black which is almost active only due to its dynamical charge, one can find that (i) there is a non-zero radiation density even at far distance from the black hole and (ii) positive energy condition is respected everywhere. Here, in the unit charge gauge, for the extremal case (${\dot{Q}}(u)\approx {\dot{M}}(u)$), we find $r_*\rightarrow \frac{3}{2}$ and ${\dot{N}}_q(u)\rightarrow -\frac{8}{27} {\dot{M}}(u)$. For both of the cases of neutral black hole ($Q(u)=0$) and black hole with static charge (${\dot{Q}}(u)=0$), for $|{\dot{N}}_{q}(u)| \ll |2{\dot{M}}(u)|$, we have $r_*\rightarrow \infty$. This means that for an almost static background (the background with negligible dynamics relative to the black hole mass), the zero of the radiation-accretion density lies at infinity and the positive energy density is respected everywhere in the spacetime.

• For the cosmological background, the positive energy density condition demands $N_c(u)\geqslant 0$ representing (dynamical) de Sitter space. To have a particular distance $r_*$ at which $\sigma (u,r_{*})=0$, the positivity of $r_*$ requires that ${\dot{N}}_c(u)$ with respect to $Q{\dot{Q}} (u)$ (and ${\dot{M}}(u)$) takes an opposite sign. For both of the black holes with $|{\dot{M}}(u)|\ll |Q(u){\dot{Q}}(u)|$ and ${\dot{M}}(u)\rightarrow 0$, we have $r_*\rightarrow \infty$ and ${\dot{N}}_c(u)\rightarrow 0$. This means that for a black which is almost active only due to its dynamical charge, one can find (i) a non-zero radiation density even at far distance from the black hole and (ii) the respected positive energy condition at everywhere. In the unit charge gauge, for the extremal case (${\dot{Q}}(u)\approx {\dot{M}}(u)$), we find $r_*\rightarrow \frac{4}{3}$ and ${\dot{N}}_c(u)\rightarrow -\frac{27}{128} {\dot{M}}(u)$. Then, comparing the quintessence and cosmological background fields for the extremal case, we have $r_{*c}<r_{*q}$ and $|{\dot{N}}_c(u)|<|{\dot{N}}_q(u)|$. Also, for both of the cases of neutral black hole ($Q(u) = 0$) and black hole with static charge (${\dot{Q}}(u) = 0$), for $|{\dot{N}}_{c}(u)| \ll |2{\dot{M}}(u)|$, we have $r_*\rightarrow \infty$. This means that for an almost static background (the background with negligible dynamics relative to the black hole), the zero of the radiation-accretion density lies at infinity and the positive energy density is respected everywhere in the spacetime. In the case that the quintessence and cosmological backgrounds have a same behavior ($|{\dot{N}}_{q}(u)|=|{\dot{N}}_{c}(u)|$), for $|{\dot{N}}_{c,q}(u)| < |2{\dot{M}}(u)|$, we have $r_{*c}(u)<r_{*q}(u)$ while for $|{\dot{N}}_{c,q}(u)| >|2{\dot{M}}(u)|$, we have $r_{*c}(u)>r_{*q}(u)$. Finally, for both of the cases of neutral black hole ($Q(u) = 0$) and black hole with static charge (${\dot{Q}}(u) = 0$), when ${\dot{M}}(u)$ and ${\dot{N}}_q(u)$ as well as ${\dot{N}}_c(u)$ have the same signs, $r_*(u)$ is imaginary and negative for the quintessence and cosmological fields, respectively. Then, for these cases, the radiation-accretion density never be zero and the positive energy condition is respected or violated in the whole spacetime.

For all of the mentioned surrounding fields, by classifying the possible situations in Tables 1, 2, 3, 4, 5, 6, 7 and 8, we find that (i) there are situations possessing regions in spacetime that the positive energy condition is respected, while beyond these regions it is violated. (ii) there are some other situations that are not physical in the sense that the positive energy condition is violated in the whole spacetime, and (iii) there are also possible situations such that the positive energy condition is respected in the whole spacetime with or without a priory condition on black hole and its surrounding filed dynamics. To depict these situations, we have given some plots (Figs. 2 and 3 for dust, 6 and 7 for radiation, 10 and 11 for quintessence as well as 14 and 15 for the cosmological constant-like background) for the radiation-accretion density versus the distance r for some typical values of ${\dot{N}}_{s}(u)$, ${\dot{M}}(u)$ and ${\dot{Q}}(u)$ in the different backgrounds. Also, considering the timelike geodesics, the possibility of (i) the equality of the Newtonian force as well as GR correction terms to the corresponding contributions of various backgrounds, and (ii) the equality of the induced force resulting from the radiation-accretion phenomena to the Newtonian force are shown in the Figs. 4 and 5 for the dust background, in 8 and 9 for the radiation background, in 12 and 13 for the quintessence background, and in 16 and 17 for the cosmological constant-like background.

In our next work, we aim to report elsewhere on the causal structures, horizon and thermodynamical properties of our obtained solutions.

Appendices

Appendix A

For the Bonnor–Vaidya black hole in the quintessence background, we have the following solutions

$$\begin{aligned} r_{1}(u)= & {} -\frac{2{\dot{M}}(u)}{3^{\frac{1}{3}}x^\frac{1}{3}(u)}+\frac{x^\frac{1}{3}(u)}{3^\frac{2}{3}{\dot{N}}_q(u)},\nonumber \\ r_{2}(u)= & {} \frac{(1+i\sqrt{3}){\dot{M}}(u)}{3^{\frac{1}{3}}x^\frac{1}{3}(u)}-\frac{(1-i\sqrt{3})x^\frac{1}{3}(u)}{2\times 3^\frac{2}{3}{\dot{N}}_q(u)},\nonumber \\ r_{3}(u)= & {} \frac{(1-i\sqrt{3}){\dot{M}}(u)}{3^{\frac{1}{3}}x^\frac{1}{3}(u)}-\frac{(1+i\sqrt{3})x^\frac{1}{3}(u)}{2\times 3^\frac{2}{3}{\dot{N}}_q(u)}, \end{aligned}$$

(76)

where

$$\begin{aligned} x(u)= & {} 9{{\dot{N}}_q(u)}^2 Q(u){\dot{Q}}(u) \nonumber \\&+ \sqrt{3} \sqrt{8{\dot{M}}^3(u) {\dot{N}}_q^3(u) +27{\dot{N}}_q^4(u) Q^2(u) {\dot{Q}}^2(u)},\nonumber \\ \end{aligned}$$

(77)

for $\sigma (u,r)=0$ where $\sigma (u,r)$ is given by (60). Due to the complexity of these solutions, one may consider the special case of

$$\begin{aligned} {\dot{N}}_q(u) =-\frac{8{\dot{M}}^3(u) }{27Q^2 (u){\dot{Q}}^2 (u)}. \end{aligned}$$

(78)

Then, Eq. (77) simplifies to

$$\begin{aligned} x(u)=9{{\dot{N}}_q(u)}^2 Q(u){\dot{Q}}(u) , \end{aligned}$$

(79)

and the solutions (76) reduce to

$$\begin{aligned}&r_1(u)=-\frac{3{\dot{Q}}(u) Q(u)}{{\dot{M}}(u)},\nonumber \\&r_2(u)=r_3(u)= \frac{3{\dot{Q}}(u) Q(u)}{2{\dot{M}}(u)}. \end{aligned}$$

(80)

Finally, regarding the fact that ${\dot{Q}}(u)$ and ${\dot{M}}(u)$ have the same signs in both of the radiation and accretion processes, the only positive solution representing a zero radiation-accretion energy density will be $r_*(u)=r_2(u)=r_3(u)$. Note that here, the presence of negative solution $r_1(u)$ does not change the total physical properties of the solution, because there is a positive solution $r_*(u)=r_2(u)=r_3(u)$ for radial distance which possesses zero energy density.

Appendix B

The solutions to the Eq. (66) are as follows.

$$\begin{aligned}&D_{i1}\simeq - \frac{2^{\frac{4}{3}}\mathfrak {L}}{\left( 54M+54\mathfrak {N}+\sqrt{864\mathfrak {L}^{3} +(54M+54 \mathcal {Q})^2} \right) ^{\frac{1}{3}}}\nonumber \\&\quad + \frac{\left( 54M+54\mathfrak {N}+\sqrt{864\mathfrak {L}^{3} +(54M+54 \mathcal {Q})^2 }\right) ^{\frac{1}{3}}}{3\times 2^{\frac{1}{3}}},\nonumber \\&D_{i2}\simeq \frac{2^{\frac{1}{3}}(1+i\sqrt{3})\mathfrak {L}}{\left( 54M+54\mathfrak {N}+\sqrt{864\mathfrak {L}^{3} +(54M+54 \mathcal {Q})^2} \right) ^{\frac{1}{3}}}\nonumber \\&\quad - \frac{(1-i\sqrt{3})\left( 54M+54\mathfrak {N}+\sqrt{864\mathfrak {L}^{3} +(54M+54 \mathcal {Q})^2 }\right) ^{\frac{1}{3}}}{6\times 2^{\frac{1}{3}}},\nonumber \\&D_{i3}\simeq \frac{2^{\frac{1}{3}}(1-i\sqrt{3})\mathfrak {L}}{\left( 54M+54\mathfrak {N}+\sqrt{864\mathfrak {L}^{3} +(54M+54 \mathcal {Q})^2} \right) ^{\frac{1}{3}}}\nonumber \\&\quad - \frac{(1+i\sqrt{3})\left( 54M+54\mathfrak {N}+\sqrt{864\mathfrak {L}^{3} +(54M+54 \mathcal {Q})^2 }\right) ^{\frac{1}{3}}}{6\times 2^{\frac{1}{3}}}\nonumber \\ \end{aligned}$$

(81)

Appendix C

For the Bonnor–Vaidya black hole in the cosmological field background, we have the following solutions

$$\begin{aligned} r_1(u)= & {} \frac{1}{2}\sqrt{ x(u)} -\frac{1}{2} \sqrt{-x(u)-\frac{4{\dot{M}}(u)}{{\dot{N}}_c(u)\sqrt{ x(u)}}},\nonumber \\ r_2(u)= & {} \frac{1}{2}\sqrt{ x(u)} +\frac{1}{2} \sqrt{-x(u)-\frac{4{\dot{M}}(u)}{{\dot{N}}_c(u)\sqrt{ x(u)}}},\nonumber \\ r_3(u)= & {} -\frac{1}{2}\sqrt{ x(u)} -\frac{1}{2} \sqrt{-x(u)+\frac{4{\dot{M}}(u)}{{\dot{N}}_c(u)\sqrt{ x(u)}}},\nonumber \\ r_4(u)= & {} -\frac{1}{2}\sqrt{ x(u)} +\frac{1}{2} \sqrt{-x(u)+\frac{4{\dot{M}}(u)}{{\dot{N}}_c(u)\sqrt{ x(u)}}}, \end{aligned}$$

(82)

where

$$\begin{aligned} x(u)= & {} -\frac{2^{\frac{8}{3}}Q(u){\dot{Q}}(u) }{3^{\frac{1}{3}}{\dot{N}}_c(u)\left( \frac{9{\dot{M}}^2(u)}{{\dot{N}}^2_c(u)} +\frac{\sqrt{3} \sqrt{27 {\dot{M}}^4(u) + 128 {\dot{N}}_c(u) Q^3(u) {\dot{Q}}^3(u)} }{{\dot{N}}_c^2(u)}\right) ^{\frac{1}{3}}}\nonumber \\&+\frac{2^{\frac{1}{3}}\left( \frac{9{\dot{M}}^2(u)}{{\dot{N}}^2_c(u)} +\frac{\sqrt{3} \sqrt{27 {\dot{M}}^4(u) + 128 {\dot{N}}_c(u) Q^3(u) {\dot{Q}}^3(u)} }{{\dot{N}}_c^2(u)}\right) ^{\frac{1}{3}}}{3^{\frac{2}{3}}},\nonumber \\ \end{aligned}$$

(83)

for $\sigma (u,r)=0$ where $\sigma (u,r)$ is given by (68). Due to the complexity of these solutions, one may consider the special case of

$$\begin{aligned} {\dot{N}}_c(u) =-\frac{27{\dot{M}}^4(u) }{128 Q^3(u) {\dot{Q}}^3(u) }. \end{aligned}$$

(84)

Then, Eq. (83) simplifies to

$$\begin{aligned} x(u)=\left( \frac{8Q(u){\dot{Q}}(u)}{3{\dot{M}}(u)}\right) ^2, \end{aligned}$$

(85)

and the solutions (82) reduce to

$$\begin{aligned}&r_1(u)=r_{2}(u)=\frac{4{\dot{Q}}(u) Q(u)}{3{\dot{M}}(u)},\nonumber \\&r_3(u)= -\frac{4 i \left( \sqrt{2} Q(u) {\dot{Q}}(u)-i Q(u) {\dot{Q}}(u)\right) }{3 {\dot{M}}(u)},\nonumber \\&r_4(u)= \frac{4 i \left( \sqrt{2} Q(u) {\dot{Q}}(u)+i Q(u) {\dot{Q}}(u)\right) }{3 {\dot{M}}(u)}. \end{aligned}$$

(86)

Finally, regarding the fact that ${\dot{Q}}(u)$ and ${\dot{M}}(u)$ have the same signs in both of the radiation and accretion processes, the only positive solution representing a zero radiation-accretion energy density will be $r_*(u)=r_1(u)=r_2(u)$. Note that here, the presence of complex solutions $r_3(u)$ and $r_4(u)$ do not change the total physical properties of the solution, because there is a positive solution $r_*(u)=r_1(u)=r_2(u)$ for radial distance which possesses zero energy density.

Appendix D

The solutions to (75) are

$$\begin{aligned} D_{i1}= & {} \frac{1}{2}\sqrt{ E} -\frac{1}{2} \sqrt{-E-\frac{4\mathfrak {L}}{\mathfrak N\sqrt{ E}}},\nonumber \\ D_{i2}= & {} \frac{1}{2}\sqrt{ E} +\frac{1}{2} \sqrt{-E-\frac{4\mathfrak {L}}{\mathfrak N\sqrt{ E}}},\nonumber \\ D_{i3}= & {} -\frac{1}{2}\sqrt{ E} -\frac{1}{2} \sqrt{-E-\frac{4\mathfrak {L}}{\mathfrak N\sqrt{ E}}},\nonumber \\ D_{i4}= & {} -\frac{1}{2}\sqrt{ E} +\frac{1}{2} \sqrt{-E-\frac{4\mathfrak {L}}{\mathfrak N\sqrt{ E}}}, \end{aligned}$$

(87)

where

$$\begin{aligned} E= & {} -\frac{8\times 2^{\frac{1}{3}} (M+\mathcal {Q}) }{\left( 108\mathfrak {L}^{2}\mathfrak {N}+{\sqrt{11664 \mathfrak {L}^4 \mathfrak {N}^2+55296 \mathfrak {N}^3 (M+\mathcal {Q})^3} }\right) ^{\frac{1}{3}}} \nonumber \\&+\frac{\left( 108\mathfrak {L}^{2}\mathfrak {N}+{\sqrt{11664 \mathfrak {L}^4 \mathfrak {N}^2+55296 \mathfrak {N}^3 (M+\mathcal {Q})^3} }\right) ^{\frac{1}{3}}}{3\times 2^{\frac{2}{3}}\mathfrak {N}}.\nonumber \\ \end{aligned}$$

(88)