1 Introduction

In the context of AdS/CFT duality a thermal system on field theory could be expressed by a gravity model in AdS spacetime. By considering various models of black hole solution in the bulk we can explore field theory behaviors which may be complicated when they are studied in a quantum field theory. One of the important aspects of field theory is the computational complexity. This is number of qubit gates in the smallest quantum circuit [1, 2] or in the another definition is the minimal depth of a quantum circuit [3]. Actually computational complexity regarding AdS/CFT duality could explain something about the inside of black hole and corresponding geometry. There are two conjectures that relate complexity on the boundary to the geometry of bulk: (I) At the first and older one, complexity is supposed to be equal to the maximal volume in the spacelike slice into the bulk [4], or CV as

$$\begin{aligned} {\mathcal {C}}(t_L,t_R)\sim \frac{V}{L}, \end{aligned}$$
(1.1)

where G is the Newton‘s coupling constant, L is a length scale of the system which is given by the AdS radius for large black holes and the horizon radius for small black holes. V is the volume of spacelike slice or the Einstein–Rosen bridge (ER) with connected points \(t_L\) and \(t_R\) corresponding to the left and the right boundaries, respectively. (II) At the newer conjecture, quantum complexity is proportional to classical action in the bulk which is defined in “Wheeler-DeWitt”’ (WD) patch, or CA [5, 6]. The privilege of this conjecture rather than the older one is needlessness to any length scale chosen by hand, such as “L” or the event horizon radius,

$$\begin{aligned} {\mathcal {C}}(\Sigma )=\frac{{\mathcal {A}}_{WDW}}{\pi \hbar }, \end{aligned}$$
(1.2)

in which \(\Sigma \) is a time slice equals to the intersection of asymptotical boundary and Cauchy surface in the bulk [5, 6]. Action for WDW patch is given by the summation of the action and all boundary terms of this patch which is defined between the times \(t_L\) and \(t_R\) on the boundaries and at late time approximation could be restricted by the Lloyd bound [7] as follows:

$$\begin{aligned} \frac{d({\mathcal {A}}_{bulk}+{\mathcal {A}}_{boundary})}{dt}\le 2E, \end{aligned}$$
(1.3)

in which E is the excited energy of the boundary quantum state. It is now understood that satisfying the Lloyd bound in holographic theories are due to the orthogonality of quantum states and so in general does not need to be hold [8, 9]. To obtain the growth rate of complexity on the boundary we must calculate the time derivative of this action on the boundary by attention to conjecture of “CA” given by (1.2) as

$$\begin{aligned} \frac{d{\mathcal {C}}}{dt}\le \frac{2E}{\pi \hbar }. \end{aligned}$$
(1.4)

We can see the action growth rate by considering CA conjecture for the WDW patch at late time approximation in AdS black holes is bounded as follows [5, 6]:

$$\begin{aligned} \frac{d{\mathcal {A}}}{dt}= & {} 2M,\nonumber \\ \frac{d{\mathcal {A}}}{dt}\le & {} 2[(M-\mu Q)-(M-\mu Q)_{gs}],\nonumber \\ \frac{d{\mathcal {A}}}{dt}\le & {} 2[(M-\Omega J)-(M-\Omega J)_{gs}], \end{aligned}$$
(1.5)

where \(``gs''\) stands for ground state and the first equation satisfies for neutral black hole and second and third ones happens for charged and rotating black holes, separately. For a charged black hole solution this bound depends on the size of the black hole [5, 6] and can violate the Lloyd‘s bound by assuming that it holds. The argument in the original paper [5] involved the weak gravity conjecture. It is found in [10] that all size of charged black hole violate the original bound (1.4). The authors corrected the bound by investigating some other AdS black holes like Kerr-AdS black hole and charged Gauss–Bonnet-AdS black hole and summarized the final result as following bound:

$$\begin{aligned} \frac{d{\mathcal {A}}}{dt}\le (M-\Omega J-\mu Q)_+-(M-\Omega J-\mu Q)_-, \end{aligned}$$
(1.6)
Fig. 1
figure 1

Penrose diagram for a neutral two sided black hole and WDW patch in a initial and b late time regimes

Full size image

at which \(+\) and − stand for the states of the most outer and inner horizon, respectively. Equality satisfies for stationary AdS black holes in Einstein gravity and charged AdS black hole in Gauss–Bonnet gravity. In general non-stationary cases inequality would be expected. In the other words the work [10] shows that there is a universal formula for the action growth of stationary black holes for which the Lloyd bound is independent of the charged black hole size and so would be satisfied for any arbitrary size of charged black hole.

In this work we use non-rotating case of this universal form of the action growth and seek relation between this bound and the non-abelian charges. To do so we choose the Yang–Mills (YM) field given in the Maxwell-power-Yang–Mills theory propagating in AdS spacetime. There are two important motivations which encourage us to consider YM field in our study: at first we can find YM equations in the low energy limit of some string theory models which leads to certain revisions of the no-hair theory of black hole physics. Secondly, the unification of general relativity and quantum mechanics in high energy regime of the most of string theory models is possible when it predicts a non-abelian gauge field.

In the other side, considering YM fields let us study small range effects inside the nuclei which are neglected in the long range effects of Maxwell field. Actually, these short-range effects are due to some length scales arisen by confinement in YM theory. Indeed, a confining YM theory undergoes a confinement-deconfinement phase transition in CFT side at a such given scale which leads to these short range effects. In the AdS/CFT dictionary, it is interesting we seek operators in the field theory side because they correspond to other quantities given in the gravity side. Actually in a top-down approach we can specify dual field of the used gravity model which is included both Maxwell and YM fields. It would be an interesting subject to find familiar results from CFT side which come from the string theory solutions. This can be considered as a future work which we will study. Another important aspect of thermal systems is chaos which could be described with its corresponding dual in the bulk as the shock waves near the horizon of AdS black holes [11,12,13]. Actually a perturbation disturbs the geometry of the black hole and then grows by time due to the backreaction effects. During the chaos behaviors, the similar initial orthogonal quantum states are changed to some totally different states. An interesting point that makes the study of shock wave geometry important, is the reflection of complexity on the boundary as the existence of a firewall. When the perturbation on the boundary depends on transverse coordinates then corresponding complexity is closely connected to the speed of the perturbation spreading (butterfly velocity) in spatial directions. This butterfly velocity is studied by out-of-time order four-point function between pairs of local operators \(V(t=0)\) and W(t) which are separated in spatial coordinates such that [14]

$$\begin{aligned} \langle V(0,x)W(t,y)V(0,x)W(t,y)\rangle _\beta , \end{aligned}$$
(1.7)

in which \(\beta \) or the inverse of the temperature stands for thermal expectation value. After the scrambling time \(t_*\) the butterfly effects could be seen by a sudden decay as follows [15].

$$\begin{aligned} \frac{\langle V(0,x)W(t,y)V(0,x)W(t,y)\rangle _\beta }{\langle V(0,x)V(0,x)\rangle _\beta \langle W(t,y)W(t,y)\rangle _\beta }\sim 1- e^{\lambda _L\left( t-t_*+\frac{|x-y|}{v_B} \right) }, \end{aligned}$$
(1.8)

where \(\lambda _L=2\pi /\beta \) stands for the Lyapunov exponent and \(v_B\) is the butterfly velocity. There is a wide variety of works has been devoted to the calculation of butterfly velocity for gravity theories in the bulk such as [16] for planar black hole in the Einsteins general theory of relativity framework, [15] for the topologically massive gravity (TMG) and the new massive gravity (NMG), [17] for the Einstein–Gauss–Bonnet gravity and other works [11, 12, 18, 19]. The action growth could be affected in the shock wave geometry by attention to the characteristics of gravity models. Authors of the references [20, 21] used particular gravity models and showed that the butterfly velocity is depended to change of the source fields due to the alteration of the action growth. However there is no fundamental connection in quantum information between the growth of complexity and quantum chaos and the relations found in [20, 21] are just merely circumstantial and do not hold in general. In this paper we devotes our work to the black hole solution including both Maxwell and YM fields in the Einstein–Maxwell-power-Yang–Mills gravity. We seek the constraints and circumstances on the parameter of YM theory when the Lloyd bound is applied on the complexity growth rate. The outline of this work is as follows: in Sect. 2 we obtain the evolution of complexity growth at the late time approximation and check the Lloyd bound in presence of the YM field and find a constraint condition on the parameters of the gravity theory. In Sect. 3 we focus on the effects of a disturbance on the boundary and the spreading of shock wave in the used gravity model. We also discuss the effects of the parameters of this theory on the butterfly velocity. Last section denotes to summarize of the results and the conclusion.

2 The complexity growth

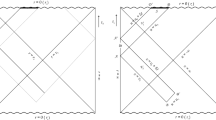
As we know from [5, 6] the growth rate of the action of a WDW patch of the two-sided black hole at the late time, i.e. \(t_L+t_R>> \beta \), corresponds to the increasing rate of complexity of the boundary state. At the late time and without any shock wave the contribution of the region behind the past horizon goes to zero exponentially. By adding any kind of conserved charges WDW patch terminates slower than neutral case and Lloyd bound must be generalized due to changing of average energy of the quantum state related to the ground state. In Fig. 1 we can see the general Penrose diagram and WDW patch for a neutral two sided black hole for initial times and late times approximations. In Fig. 1a which is indicated initial times the patch intersects both the future and past singularities at \(r=0\), but in late time indicated by Fig. 1b only intersects the future one. In this section we are about to consider a Maxwell–Yang–Mills theory for the black hole inside the bulk and study action growth rate for the late time approximation. Also we study the Lloyd bound in presence of the conserved charges of this model. The action for the Einstein–Maxwell-power-Yang–Mills gravity with a negative cosmological constant in 4-dimension is given by [22, 23]:

$$\begin{aligned} {\mathcal {A}}= & {} \frac{1}{16\pi G}\int d^4x\sqrt{-g} \nonumber \\&\quad \times \left( {\mathcal {R}}+ \frac{6}{\ell ^2}-F_{\mu \nu }F^{\mu \nu }- \left[ {{\mathbf {T}}}{{\mathbf {r}}}\left( F_ {\mu \nu }^{(a)}F^{(a)\mu \nu } \right) \right] ^\gamma \right) \nonumber \\&\quad +\,\frac{1}{8\pi G}\int _{\partial {\mathcal {M}}} d^3x\sqrt{-h}{\mathcal {K}}, \end{aligned}$$
(2.1)

in which the first integral equation represents the action in the bulk and the second integral equation is the boundary part of WDW patch (WDW patch located in our two sided black hole is indicated in Fig. 2 in which only dark blue region contributes to the complexity growth at late time approximation.). Radius of AdS spacetime is indicated by \(\ell \) and \({\mathcal {R}}\) stands for Ricci scalar. \(\gamma \) is a real positive parameter and the Yang–Mills tensor fields \(F_{\mu \nu }^{(a)}\) are defined as follows.

$$\begin{aligned} F_{\mu \nu }^{(a)}=\partial _\mu A_\nu ^{(a)}-\partial _\nu A_\mu ^{(a)}+\frac{1}{2\sigma }C^{(a)}_{(b)(c)}A^b_\mu A^c_\nu , \end{aligned}$$
(2.2)

in which \(\sigma \) is a coupling constant and \(C^{(a)}_{(b)(c)}\) are the structure constants of \((d-1)(d-2)/2\) parameter Lie group G in general d-dimensional theory and \(A_\mu ^{(a)}\) is the \(SO(d-1)\) gauge group Yang–Mills potentials. According to Wu-Yang ansatz the YM invariant \({\mathcal {F}}\) reduces to the following form [23].

$$\begin{aligned} {\mathcal {F}}_{YM}={{\mathbf {T}}}{{\mathbf {r}}}\left( F_{\mu \nu }^{(a)}F^{(a)\mu \nu }\right) =-\frac{2q_{YM}^2}{r^4}. \end{aligned}$$
(2.3)

The electromagnetic tensor field is defined by the usual Maxwell potential \(A_\mu \) such that

$$\begin{aligned} F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu , \end{aligned}$$
(2.4)

for which the gauge invariant counterpart \({\mathcal {F}}_{EM}\) is

$$\begin{aligned} {\mathcal {F}}_{EM}=F_{\mu \nu }F^{\mu \nu }=-\frac{2q_{E}^2}{r^4}. \end{aligned}$$
(2.5)
Fig. 2
figure 2

Penrose diagram for a charged two sided black hole with multiple horizons and WDW patch in late time approximation. \(r_1\) is the most internal horizon and \(r_0\) is the null spatial infinity. The wavy lines indicate the singularities at \(r=0\), and \(r_\infty \) stands for \(r=-\infty \)

Full size image

For a spherically symmetric 4 dimensional static space time metric equation defined in a Schwarzschild frame is given by

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{dr^2}{f(r)}+r^2{d\Omega _2}^2, \end{aligned}$$
(2.6)

which by substituting it into the Einstein metric equation obtained from (2.1) one can infer that there is a black hole solution [24] as

$$\begin{aligned} f(r)=1-\frac{2M}{r}+\frac{r^2}{\ell ^2}+\frac{q_E^2}{r^2}+\frac{Q}{r^{4\gamma -2}},~~~ Q=\frac{2^{\gamma -1}}{4\gamma -3}q_{YM}^{2\gamma }. \end{aligned}$$
(2.7)

for \(\gamma \ne \frac{3}{4}\) and

$$\begin{aligned} f(r)=1-\frac{2M}{r}+\frac{r^2}{\ell ^2}+\frac{q_E^2}{r^2}-\frac{Q_0lnr}{r},~~~ Q_0=2^{-\frac{1}{4}}q_{YM}^{\frac{3}{2}}. \end{aligned}$$
(2.8)

for \(\gamma =\frac{3}{4}\) where \(q_{EM}\) and \(q_{YM}\) correspond to the electric and Yang–Mills charges respectively. Writing f(r) like an equipotential surface \(f(r)=constant\) the first law of the black hole thermodynamics could be derived for which

$$\begin{aligned}&df(S,M,P,q_E,q_{YM})=0\nonumber \\&\quad =\frac{\partial f}{\partial S}dS+\frac{\partial f}{\partial M}dM+\frac{\partial f}{\partial P}dP \nonumber \\&\quad +\frac{\partial f}{\partial q_E}dq_E+\frac{\partial f}{\partial q_{YM}}dq_{YM}, \end{aligned}$$
(2.9)

where \(S=\pi r^2\) is the entropy of the black hole and \(P=\frac{3}{8\pi \ell ^2}\) is the pressure of AdS spacetime. Applying the above relation we can obtain

$$\begin{aligned} dM=TdS+VdP+\phi _Edq_E+\phi _{YM}dq_{YM}, \end{aligned}$$
(2.10)

where \(T=\frac{1}{2r}\partial _Sf\) is the temperature, \(V=4\pi r^3/3\) is the thermodynamic volume, \(\phi _E=q_E/r\) stands for electric potential and the Yang–Mills potential reads.

$$\begin{aligned} \phi _{YM}= \left( \frac{\gamma }{4\gamma -3} \right) \frac{2^{\gamma -1}q_{YM}^{2\gamma -1}}{r^{4\gamma -3}}, \quad \textit{for}~\gamma \ne \frac{3}{4}\nonumber \\ \phi _{YM}=-3\times 2^{-\frac{9}{4}}q_{YM}^{\frac{1}{2}}lnr,\quad \textit{for}~\gamma =\frac{3}{4}. \end{aligned}$$
(2.11)

Regarding the above solution, Ricci scalar could be achieved as:

$$\begin{aligned} {\mathcal {R}}=-\frac{12}{\ell ^2}-\frac{4Q}{r^{4\gamma }}\left( 4\gamma ^2-7\gamma +3 \right) \quad \textit{for}~~\gamma \ne \frac{3}{4}, \end{aligned}$$
(2.12)

and

$$\begin{aligned} {\mathcal {R}}=-\frac{12}{\ell ^2}+\frac{Q_0}{r^3} \quad \textit{for}~~\gamma =\frac{3}{4}. \end{aligned}$$
(2.13)

Therefore, the growth rate of the bulk action given by first integral equation in (2.1), can be calculated at late time approximation as follows:

$$\begin{aligned}&\frac{d{\mathcal {A}}_{bk}}{dt}=\frac{1}{16\pi G}\int \int _{r_-}^{r_+}r^2 \quad \Bigg [-\frac{6}{\ell ^2}-\frac{4Q}{r^{4\gamma }} (4\gamma ^2 \nonumber \\&\quad -7\gamma +3)+\frac{2q_E^2}{r^4} +\frac{2^\gamma q_{YM}^{2\gamma }}{r^{4\gamma }}\Bigg ]drd\Omega _2 \nonumber \\&\quad =-\frac{1}{2\ell ^2} \left( r_+^3-r_-^3 \right) -\frac{q_E^2}{2} \left( \frac{1}{r_+}- \frac{1}{r_-} \right) \nonumber \\&\quad + \left( \frac{2\gamma -3}{4\gamma -3} \right) 2^{\gamma -2} q_{YM}^{2\gamma } \left( \frac{1}{r_+^{4\gamma -3}}-\frac{1}{r_-^{4\gamma -3}} \right) , \end{aligned}$$
(2.14)

for \(\gamma \ne \frac{3}{4}\) and

$$\begin{aligned} \frac{d{\mathcal {A}}_{bk}}{dt}&=\frac{1}{16\pi G}\int \int _{r_-}^{r_+}r^2 \left[ -\frac{6}{\ell ^2}+\frac{Q_0}{r^3} \right. \nonumber \\&\left. \quad +\,\frac{2q_E^2}{r^4} +\frac{2^{3/4} q_{YM}^{3/2}}{r^{3}} \right] drd\Omega _2\nonumber \\&=\frac{1}{2\ell ^2}(r_+^3-r_-^3)-\frac{q_E^2}{2}\left( \frac{1}{r_+}- \frac{1}{r_-}\right) \nonumber \\&\quad +\,3\times 2^{-9/4}q_{YM}^{3/2}ln \left( \frac{r_+}{r_-} \right) ,\nonumber \\ \end{aligned}$$
(2.15)

for \(\gamma =\frac{3}{4}\) respectively. In the above integral equations we put \(\Omega _2/4\pi G=1\). It must be noted that spatial integral is calculated between two horizons \(r_+\) and \(r_-\) which are the outer and inner horizons of the black hole. As we can see from (2.7) there are multiple horizons which are obtained from \(f(r)=0\) and its number depends on \(\gamma \). So for any values of \(\gamma \) we will have several horizons (see Eq. (2.8) as a special case), but \(r_-\) and \(r_+\) would be the most internal and outer horizons, respectively. Penrose diagram for a black hole solution depends on the number of horizons as it is shown for a black hole with multiple horizons in Ref. [25]. In our case for any values of \(\gamma \) we can have different real roots obtained from \(f(r)=0\), but in a general form the Penrose diagram looks like Fig. 2 in which \(r_1\) is the most internal horizon and so \(0<r_-\equiv r_1<r_2<r_3< \cdots <r_+\), also \(r_\infty \) stands for \(r=-\infty \) and \(r_0\) indicates spatial null infinity. One can see the position of singularities and multiple horizons in ref. [25]. As we mentioned earlier Fig. 2 deoicted WDW patch at late time approximation in our multiple horizon case. In the other side, the boundary part [second integral Eq. (2.1)] of the action growth rate at late time approximation is given by:

$$\begin{aligned} \frac{d{\mathcal {A}}_{bd}}{dt}= & {} \frac{1}{8\pi G}\int _{\partial {\mathcal {M}}} {d\Omega _2} \left( \sqrt{-h}{\mathcal {K}} \right) \nonumber \\= & {} \frac{1}{2} \left[ r^2\sqrt{f(r)} \left( \frac{2}{r}\sqrt{f(r)}+ \frac{f^{\prime }(r)}{2\sqrt{f(r)}}\right) \right] _{\partial {\mathcal {M}}},\nonumber \\ \end{aligned}$$
(2.16)

where the extrinsic curvature is defined by

$$\begin{aligned} {\mathcal {K}}=\frac{1}{r^2}\frac{\partial }{\partial r}\left( r^2\sqrt{f(r)}\right) =\frac{2}{r}\sqrt{f(r)}+\frac{f^{\prime }(r)}{2\sqrt{f(r)}}. \end{aligned}$$
(2.17)

One can see that the Eq. (2.16) only contains the Gibbons-Hawking term. However, for the computation of complexity one needs further boundary terms for the abelian and non-abelian fields as well as extra terms for the null boundaries and corners of the WDW patch. In fact these extra terms become negligible just at late time approximation which we considered here. So by attention to the metric solutions (2.7) and (2.8) we can obtain:

$$\begin{aligned} \frac{d{\mathcal {A}}_{bd}}{dt}= & {} (r_+-r_-)+\frac{3}{2\ell ^2}\left( r_+^3-r_-^3 \right) +\frac{q_E^2}{2}\left( \frac{1}{r_+} -\frac{1}{r_-}\right) \nonumber \\&+\,\frac{(3-2\gamma )Q}{2} \left( \frac{1}{r_+^{4\gamma -3}}-\frac{1}{r_-^{4\gamma -3}} \right) ,\nonumber \\ \end{aligned}$$
(2.18)

for \(\gamma \ne \frac{3}{4}\) and

$$\begin{aligned} \frac{d{\mathcal {A}}_{bd}}{dt}= & {} (r_+-r_-)+\frac{3}{2\ell ^2} \left( r_+^3-r_-^3 \right) + \frac{q_E^2}{2} \left( \frac{1}{r_+} -\frac{1}{r_-} \right) \nonumber \\&-3\times 2^{-9/4}q_{YM}^{3/2}ln \left( \frac{r_+}{r_-} \right) , \end{aligned}$$

for \(\gamma \ne \frac{3}{4}\). Hence the total growth rate of the action for all values of \(\gamma \) is achieved as follows.

$$\begin{aligned} \frac{d{\mathcal {A}}}{dt}=(r_+-r_-)+\frac{r_+^3-r_-^3}{\ell ^2}. \end{aligned}$$
(2.19)

It is useful to rewrite the total growth action equation with respect to the black hole characteristics like charges and mass. By using the horizon equations \(f(r_+)=f(r_-)=0,\) one can obtain the following relations for the electric charge and mass of the black hole.

$$\begin{aligned} q_E^2= & {} r_+r_-\left[ 1+\frac{1}{\ell ^2} \left( \frac{r_+^3-r_-^3}{r_+-r_-}\right) \right. \nonumber \\&\left. + \frac{2^{\gamma -1}}{4\gamma -3}q_{YM}^{2\gamma } \left( \frac{r_+^{-(4\gamma -3)}-r_-^{-(4\gamma -3)}}{r_+-r_-}\right) \right] , \end{aligned}$$
(2.20)

with

$$\begin{aligned} M= & {} \frac{1}{2}\left[ (r_++r_-)+\frac{1}{\ell ^2}\left( \frac{r_+^4-r_-^4}{r_+-r_-} \right) \right. \nonumber \\&\left. \quad +\frac{2^{\gamma -1}}{4\gamma -3}q_{YM}^{2\gamma } \left( \frac{r_+^{-4(\gamma -1)} -r_-^{-4(\gamma -1)}}{r_+-r_-} \right) \right] , \end{aligned}$$
(2.21)

for \(\gamma \ne \frac{3}{4}\) and,

$$\begin{aligned} q_E^2= & {} r_+r_- \left[ 1+\frac{1}{\ell ^2} \left( \frac{r_+^3-r_-^3}{r_+-r_-} \right) -2^{-1/4}q_{YM}^{3/2} \left( \frac{ln(\frac{r_+}{r_-})}{r_+-r_-} \right) \right] ,\nonumber \\ \end{aligned}$$
(2.22)

with

$$\begin{aligned} M= & {} \frac{1}{2}\left[ (r_++r_-)+\frac{1}{\ell ^2} \left( \frac{r_+^4-r_-^4}{r_+-r_-} \right) \right. \nonumber \\&\left. \quad +2^{-1/4}q_{YM}^{3/2} \left( \frac{r_+lnr_+-2r_+lnr_-+r_-lnr_-}{r_+-r_-} \right) \right] .\nonumber \\ \end{aligned}$$
(2.23)

for \(\gamma =\frac{3}{4}\) respectively. By attention to these definitions one could rewrite the total action growth rate for various values of \(\gamma \) as follows:

$$\begin{aligned} \frac{d{\mathcal {A}}}{dt}= & {} -q_E^2 \left( \frac{1}{r_+}-\frac{1}{r_-} \right) \nonumber \\&- \left( \frac{2^{\gamma -1}}{4\gamma -3} \right) q_{YM}^{2\gamma } \left( \frac{1}{r_+^{4\gamma -3}}-\frac{1}{r_-^{4\gamma -3}} \right) . \end{aligned}$$
(2.24)

for \(\gamma \ne \frac{3}{4}\) and

$$\begin{aligned} \frac{d{\mathcal {A}}}{dt}=-q_E^2 \left( \frac{1}{r_+}-\frac{1}{r_-} \right) +2^{-\frac{1}{4}}q_{YM}^{\frac{3}{2}}ln \left( \frac{r_+}{r_-} \right) . \end{aligned}$$
(2.25)

for \(\gamma =\frac{3}{4}\) respectively. So by attention to the conjugated potentials \((\phi _{E}, \phi _{YM})\) which are derived earlier in this section, the total action growth at the late time approximation would be:

$$\begin{aligned} \frac{d{\mathcal {A}}}{dt}= & {} \left( M-\phi _{E+}q_E-\frac{1}{\gamma }\phi _{YM+} q_{YM} \right) \nonumber \\&\quad - \left( M-\phi _{E-}q_E-\frac{1}{\gamma }\phi _{YM-}q_{YM} \right) , \end{aligned}$$
(2.26)

where \(\gamma \) can be take all real values. It is simple to check the Lloyd bound is satisfied for \(\gamma \ge 1\) [7] regarding to the Eq. (1.4) and so the case where \(\gamma =\frac{3}{4}\), however all situations where \(\gamma <1\) violate the Lloyd bound.

3 The complexity growth in a shock wave geometry

In this section we are about to study the above mentioned problem but in presence of a chaotic shock wave which makes perturbed the background geometry. Actually when a shock wave is sent into the bulk at time \(t_w\), a precursor operator W(t) acts on the boundary at the same time. It will be effective on the initial state of black hole which is a thermofield double state (TFD), so the old state changes to \(W(t_w)|TFD\rangle \). For a local shock wave this operator depends on transverse coordinates and localizes on the boundary at x. \(W(t_w,x)\) grows in this spatial direction vs the time which leads to the growth of action due to the perturbation on the boundary. In the other word action growth depends on the growth velocity of perturbation on the boundary in spatial direction which is called “butterfly velocity”. To see the evolution of action growth in the presence of a local shock wave it would be useful to study this perturbation in more details. Shock wave perturbs the black hole solution by injection of a small amount of energy from the boundary of AdS spacetime towards the horizon. This perturbation grows by raising the time due to the back reaction effects and so propagates on the horizon. By attention to the work presented by Dary and t‘Hooft [26], we study the problem in Kruskal null coordinates (u, v) as ,

$$\begin{aligned} uv=-\text {exp} \left[ \frac{4\pi }{\beta }r_* \right] ,~~~u/v=-\text {exp} \left[ -\frac{4\pi }{\beta }t \right] , \end{aligned}$$
(3.1)

in which \(\beta \) is proportional to the inverse of Hawking temperature and \(r_*\) is a function of r which is defined by \(dr_*=\frac{dr}{f(r)}\). The effect of shock wave geometry is considered as the effect of a massless particle at \(u=0\) which moves in the direction of v with the speed of light. So geometry for \(u<0\) stays unchanged like (2.6) and in Kruskal form will be [20] :

$$\begin{aligned} ds^2=-2A(u,v)dudv+B(u,v){d\mathbf {x}_2}^2, \end{aligned}$$
(3.2)

where

$$\begin{aligned} A(u,v)=-\frac{4}{uv}\frac{f(r)}{[f^{\prime }(r_h)]^2},~~~B(u,v)=r^2 \end{aligned}$$
(3.3)

while for \(u>0\) the particle moves in direction of shifted advance coordinate \(v\rightarrow v+\alpha (x)\), where \(\alpha (x)\) is the shift function. So in general for all values of u we can determine new coordinates system from the old ones by using the well known step function \(\theta (u)\) such as follows.

$$\begin{aligned} {\hat{u}}\equiv & {} u \nonumber \\ {\hat{v}}\equiv & {} v+\theta (u)\alpha (x)\nonumber \\ {\hat{x}}\equiv & {} x. \end{aligned}$$
(3.4)

By these transformations the metric and the energy momentum tensor are affected. If there are some stress tensor of matter fields then their non-zero components have changed to new form. This new geometry and new energy momentum tensor still satisfies the Einstein equation, \(\mathcal {{\hat{G}}}=\mathcal {{\hat{T}}}_{matter}\), in which \(\mathcal {{\hat{G}}}\) and \(\mathcal {{\hat{T}}}_{matter}\) are the Einstein tensor and the energy momentum tensor of all matter fields defined in the new coordinates system, respectively. After acting a scalar operator at \(t_w<0\) and producing the shock wave, this perturbation propagates along \({\hat{u}}=0\) and its stress-energy tensor will have only \({\hat{u}}{\hat{u}}\) component [6],

$$\begin{aligned} \mathcal {{\hat{T}}}_{\{shock\}{\hat{u}}{\hat{u}}}\sim \delta ({\hat{u}}) \exp \left[ \frac{2\pi |t_w|}{\beta } \right] . \end{aligned}$$
(3.5)

By adding this part of perturbation to the stress-energy tensor and solving the Einstein equation we find a relationship for shift function \(\alpha (x)\). If we consider this function independent of the transverse coordinates, \(\theta \) and \(\phi \) which are valid just for spherical shock waves, so it will be obtained as:

$$\begin{aligned} \alpha \sim e^{\lambda _L(|t_w|-t_*)}, \end{aligned}$$
(3.6)

in which \(\lambda _L=\frac{2\pi }{\beta }\) is the Lyapunov exponent and the scrambling time \(t_*=\frac{\beta }{2\pi }ln(S)\) is related to the entropy S and it is a delay time on the action growth due to the “switchback effect”. In other side when the shock wave is local, the shift function depends on the transverse coordinates. By solving the equations in this case we have an extra term in the above exponential part. If there is just one transverse coordinate, named x, so the shift function yields:

$$\begin{aligned} \alpha (x)\sim e^{\lambda _L \left( |t_w|-t_*-\frac{|x|}{v_B} \right) }, \end{aligned}$$
(3.7)

where

$$\begin{aligned} v_B=\sqrt{\frac{f^{\prime }(r_h)}{4r_h}}, \end{aligned}$$
(3.8)

is called the butterfly velocity and presents the speed of the local shock wave on the boundary. \(r_h\) is the outer horizon radius which is achieved by \(f(r_h)=0\).

The action behind the future horizon is \(A_{future}=2M\lambda _{L}\int \ln (u_0v_R)dx\) where \(v_R\) is the right boundary of the WDW patch, \(v_R=v_0+\alpha (x)\) (see [21]) which by substituting the shift function (3.7) reads

$$\begin{aligned} {\mathcal {A}}_{future}=\frac{2M}{L\lambda _L}\int \ln e^{\lambda _L \left( |t_w|-t_*+t_L-\frac{|x|}{v_B}\right) }dx \end{aligned}$$
(3.9)

where \(L=\int dx\) is the length of the transverse direction that goes to infinite for a planar black hole [20]. Similarly, substituting the expression of the shift Eq. (3.7) into the action behind the past horizon, we obtain

$$\begin{aligned} {\mathcal {A}}_{past}=\frac{2M}{L\lambda _L}\int \ln e^{\lambda _L \left( |t_w|-t_*-t_R-\frac{|x|}{v_B} \right) }dx \end{aligned}$$
(3.10)

where the upper limit of the integrals should be chosen as \(|x|=v_B(|t_w|-t_*-t_R)\) called as maximal transverse coordinate coming from “the large shift condition” at which shock wave could be effective and described through \(|t_w|-t_*-\frac{|x|}{v_B}\ge t_{R}\). Now we can obtain action of WDW patch by adding (3.9) and (3.10) as follows.

$$\begin{aligned} {\mathcal {A}}_{WDW}= & {} {\mathcal {A}}_{future}+ {\mathcal {A}}_{past}\nonumber \\= & {} 2M(t_L+t_R)+2Mv_B(|t_w|-t_*-t_R)^2. \end{aligned}$$
(3.11)

The first term denotes action of WDW patch for the case with no shock wave and the second term that depends on the butterfly velocity represents the effect of local shock wave. As we can see the second term only depends on \(t_R\) because the shock wave reaches the right side of our two sided black hole. By keeping one of boundary times fixed and varying it with respect to another time we can study the growth rate of boundary complexity. As we can see action growth with respect to \(t_L\) leads to the same result with no shock wave case, but it linearly depends on butterfly velocity when it is calculated with respect to \(t_R\) or \(t_w\). Therefore to study the action growth in the presence of a local shock wave it will be necessary computing butterfly velocity and knowing how it changes in various models of gravity. In the model under consideration with f(r) defined in (2.7) or (2.8) the butterfly velocity reads

$$\begin{aligned} v_B=\frac{1}{2}\sqrt{\frac{1}{r_h^2}+\frac{3}{\ell ^2}-\frac{q_E^2}{r_h^4}- \frac{1}{2} \left( \frac{2q_{YM}^2}{r_h^4} \right) ^\gamma }. \end{aligned}$$
(3.12)

As one can see the butterfly velocity in the presence of Yang–Mills fields takes an extra term which depends on the Yang–Mills charge \(q_{YM}\) and \(\gamma \). It should be useful to compare \(v_B (q_{YM}\ne 0)\) with \(v_B(q_{YM}=0)\). To do so we ignore the effect of Maxwell fields by setting \(q_E=0\) for simplicity. In the spacetime without the electric and Yang–Mills charge we have simply the Schwarzschild spacetime with its own single event horizon \({{\varvec{r}}}_h=2M\) and the butterfly velocity become simplified as

$$\begin{aligned} {{\varvec{v}}}_B=\frac{1}{2}\sqrt{\frac{1}{{{{\varvec{r}}}_h}^2}+ \frac{3}{\ell ^2}}. \end{aligned}$$
(3.13)

By attention to (2.7) and (2.8) for \(q_E=0\) with fixed mass we have \(f(r)>{{{\varvec{f}}}}~(r)\), in which \({{\varvec{f}}}~(r)\approx 1-\frac{2M}{r}\) corresponds to the Schwarzschild metric potential. This inequality is true for all radiuses such as the event horizon \(r_h\), so:

$$\begin{aligned} f(r_h)=0>{{{\varvec{f}}}}~(\textit{r}_h), \end{aligned}$$
(3.14)

hence \({{\varvec{f}}}~(\textit{r}_h)<0\) and since \({{\varvec{f}}}~({{\varvec{r}}}_h)=0\) as well, then we lead to the following statement.

$$\begin{aligned} {{\varvec{f}}}~(\textit{r}_h)<{{\varvec{f}}}~({{\varvec{r}}}_h)~ \Rightarrow ~\textit{r}_h<{{\varvec{r}}}_h. \end{aligned}$$
(3.15)

It is easy to check from the above statement that for the butterfly velocity in presence and absence of the YM fields one can infer

$$\begin{aligned} v_B>{{\varvec{v}}}_B. \end{aligned}$$
(3.16)

Also it is interesting to know that the value of butterfly velocity is decreased by increasing \(\gamma .\) Regarding to the results of these two sections we can conclude that the butterfly velocity has a same behaviour for all \(\gamma \) and decreases by the increasing of \(\gamma \), but the system violates the Lloyd’s bound for \(\gamma <1\) at late time approximations. We can see opposite situation in the gravity dual of a non-local theory in [28] in which the violation is correlated to some violation of the butterfly velocity studied in [29].

4 Conclusion and summary

In this work we used a black hole metric solution containing the electric and the Yang–Mills charges and calculate corresponding complexity growth rate by applying conjecture of “complexity=action” [5, 6]. We obtained that the Lloyd bound is saturated only for \(\gamma \ge 1\) in late time approximation, but not for values less than one. In the other side, when the boundary is disturbed by a small amount of energy and so the spacetime takes form of a shock wave geometry [4, 10], then the spreading of perturbation near the horizon affects on the complexity growth rate via the butterfly velocity. We show that the existence of the Yang–Mills field causes to increase the butterfly velocity and it decreases by raising the \(\gamma \) factor of the YM field. This is in an opposition direction of [29] at which the violation of Lloyd bound is correlated to the exceeding of butterfly velocity from the speed of light. It is shown that in large shift condition the action of WDW patch raises as linearly by increasing the butterfly velocity \(v_B\).