1 Introduction

There are various cosmological observations which indicate that our Universe is now experiencing an accelerated expansion phase [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. The origin of this accelerated phase is attributed to a mysterious matter which is called dark energy (DE). For reviews on the DE problem and the modified gravity theories, which is called geometric DE, to account for the late-time cosmic acceleration, see, e.g., [17,18,19,20,21,22,23,24,25,26]. In this regard, the holographic dark energy (HDE) is an interesting attempt which can address this bizarre problem in the framework of quantum gravity by using the holographic hypothesis [27,28,29]. This model is in agreement with various astronomical observations [30,31,32,33,34], and various scenarios of it can be found in [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60]. Horizon entropy is the backbone of the HDE models, and hence, any change of the horizon entropy affects the HDE model. Another important player in these models is the IR cutoff, and indeed, the various IR cutoffs lead to different HDE models [35, 36, 40, 41].

Since gravity is a long-range interaction, one can also use the generalized statistical mechanics to study the gravitational systems [61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78]. In this regard, due to the fact that the black hole entropy can be obtained by applying the Tsallis statistics to the system [61,62,63], three new HDE models with titles THDE, SMHDE and RHDE have recently been proposed [1, 64, 65]. Among these three models, in the absence of an interaction between the cosmos sectors, RHDE, based on the Renyi entropy and the first law of thermodynamics, shows more stability by itself [65]. In fact, in a noninteracting universe, while SMHDE is classically stable whenever SMHDE is dominant in the universe, THDE, built using the Tsallis generalized entropy [78], is never stable at the classical level [1, 64]. It is also worth mentioning that a THDE model whose IR cutoff is the future event horizon has been studied in a noninteracting universe showing satisfactory results [79].

On the other side, the cosmological observations admit an interaction between the two dark sectors of cosmos including DE and DM [80,81,82,83,84,85,86,87,88,89,90]. The existence of such mutual interaction may provide a solution for the coincidence problem [88,89,90,91,92,93,94,95,96]. In the present work, we are interested in studying the dynamics of a flat FRW universe filled with a pressureless source and THDE in both interacting and non-interacting cases. In order to build THDE, we shall employ various IR cutoffs, including the apparent and the particle horizons together with the GO and the Ricci cutoffs.

The organization of this paper is as follows. In the next section, we study the evolution of the Universe by considering an interaction between DM and THDE whose IR cutoff is the apparent horizon. Thereinafter, a new THDE is built by employing the particle horizon as the IR cutoff, and then, the cosmic evolution are investigated for both interacting and non-interacting universes in Sect. 3. The cases of the GO and Ricci cutoffs are studied in Sects. 4 and 5, respectively. The last section is devoted to a summary and concluding remarks.

2 Interacting THDE with Hubble cutoff

The energy density of THDE model is given by [78]

$$\begin{aligned} \rho _D=BL^{2\delta -4}, \end{aligned}$$
(1)

where B is an unknown parameter. We consider a homogeneous and isotropic flat Friedmann–Robertson–Walker (FRW) universe which is described by the line element

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}t^{2}+a^{2}\left( t\right) \left[ \mathrm{d}r^2 +r^{2}\mathrm{d}\Omega ^{2}\right] , \end{aligned}$$
(2)

where a(t) is the scale factor. The first Friedmann equation takes the form

$$\begin{aligned} H^{2}=\frac{1}{3m_{p}^{2}}\left( \rho _{D}+\rho _{m}\right) , \end{aligned}$$
(3)

where, \(\rho _m\) and \(\rho _D\) denote the energy density of dark matter (DM) and THDE, respectively. Defining, as usual, the dimensionless density parameters as

$$\begin{aligned} \Omega _{D}=\frac{\rho _{D}}{\rho _c}=\frac{B}{3m_{p}^{2}}H^{-2\delta +2}, \ \ \Omega _{m}=\frac{\rho _{m}}{\rho _c}, \end{aligned}$$
(4)

where \(\rho _c=3m_{p}^{2}H^{2}\) is called the critical energy density, we can easily rewrite the first Friedmann equation in the form

$$\begin{aligned} \Omega _{m}+\Omega _{D}=1. \end{aligned}$$
(5)

Moreover, we assume that DM and DE interact with each other meaning that the conservation law is decomposed as

$$\begin{aligned}&\dot{\rho }_m+3H\rho _m=Q, \end{aligned}$$
(6)
$$\begin{aligned}&\dot{\rho }_D+3H(1+\omega _D)\rho _D=-Q, \end{aligned}$$
(7)

in which \(\omega _D\equiv {p_D}/{\rho _D}\) is the equation of state (EoS) parameter of THDE and Q denotes the interaction term between DE and DM. Throughout this paper, \(Q=3b^2 H(\rho _m+\rho _D)\), where \(b^2\) is a coupling constant, is considered as the mutual interaction between the cosmos sectors [89, 90]. The ratio of the energy densities is also evaluated as

$$\begin{aligned} r=\frac{\Omega _m}{\Omega _D}=\frac{1-\Omega _D}{\Omega _D}. \end{aligned}$$
(8)

Taking the time derivative of Eq. (3), and by using Eqs. (6), (7) and (8), we can obtain

$$\begin{aligned} \frac{\dot{H}}{H^{2}}=-\frac{3}{2}(1+\omega _{D}+r)\Omega _{D}. \end{aligned}$$
(9)

In addition, by considering the Hubble horizon as the IR cutoff, \(L=H^{-1}\), the energy density (1) takes form

$$\begin{aligned} \rho _D=BH^{-2\delta +4}, \end{aligned}$$
(10)

The time derivative of above equation, combined with Eqs. (7) and (9), also leads to

$$\begin{aligned} \omega _{D}=\dfrac{\delta -1+\frac{b^2}{\Omega _D}}{(2-\delta )\Omega _{D}-1}. \end{aligned}$$
(11)

Simple calculations for the deceleration parameter, defined as

$$\begin{aligned} q=-1-\frac{\dot{H}}{H^{2}}, \end{aligned}$$
(12)

yield

$$\begin{aligned} q=\left[ \dfrac{(1-2\delta )\Omega _{D}+1-3b^2}{2(1-(2-\delta )\Omega _{D})}\right] , \end{aligned}$$
(13)

where we used Eqs. (11) and (9) to obtain this result. Combining the time derivative of Eq. (4) with Eqs. (9) and (11), and defining \(\Omega _{D}^{\prime }={d\Omega _D}/{d (\ln a)}\), we get

$$\begin{aligned} \Omega _{D}^{\prime }=3(\delta -1)\Omega _{D} \left( \dfrac{1-\Omega _{D}-b^2}{1-(2-\delta )\Omega _{D}}\right) , \end{aligned}$$
(14)

for the \(L=H^{-1}\) case.

Fig. 1
figure 1

The evolution of \(\Omega _D\) versus redshift parameter z for interacting THDE with Hubble horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\) and \(\delta =1.4\)

Full size image

For \(\delta =1.4\) case and the initial condition \(\Omega ^{0}_D=\Omega _D(z=0)=0.73\), the evolutions of \(\Omega _D\), \(\omega _D\) and q versus \((1+z)\) have been plotted in Figs. 1, 2 and 3. From these figures, one can see that \(\omega _D\) can cross the phantom line, and moreover, the value of the transition redshift is increased as a function of \(b^2\). Finally, we explore the stability of the THDE model as

$$\begin{aligned} v_{s}^{2}=\frac{dP_D}{d\rho _D}=\frac{\dot{P}_D}{\dot{\rho }_D}=\dfrac{\rho _{D}}{\dot{\rho }_{D}} \dot{\omega }_{D}+\omega _{D}, \end{aligned}$$
(15)
Fig. 2
figure 2

The evolution of \(\omega _D\) versus redshift parameter z for interacting THDE with Hubble horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\) and \(\delta =1.4\)

Full size image
Fig. 3
figure 3

The evolution of q versus redshift parameter z for interacting THDE with Hubble horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\) and \(\delta =1.4\)

Full size image

Combining time derivative of Eq. (10) with Eq. (9), we have

$$\begin{aligned} \dot{\rho }_{D}=3\rho _D(\delta -2)H(1+\Omega _D \omega _D), \end{aligned}$$
(16)

which finally leads to

$$\begin{aligned} v_{s}^{2}=\dfrac{(\delta -1)(\Omega _{D}-1)+b^2[\delta +\frac{1}{(\delta -2)\Omega _D}]}{\left[ 1-(2-\delta )\Omega _{D}\right] ^{2}}, \end{aligned}$$
(17)

where Eq. (15) and the time derivative of Eq. (11) have been employed to obtain the above result. It is also useful to note here that in the absence of interaction term \((b^2=0)\), Eqs. (11), (13), (14) and (17) are reduced to relations obtained in Ref. [1]. Figures 4 and 5 show that the interacting THDE with Hubble cutoff is stable neither for a fixed \(\delta \) nor for a fixed \(b^2\) meaning that the model is unstable, a result the same as that of the non-interacting case [1].

Fig. 4
figure 4

The evolution of \({v}^{2}_{s}\) versus redshift parameter z for interacting THDE with Hubble horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\) and \(\delta =1.4\)

Full size image
Fig. 5
figure 5

The evolution of \({v}^{2}_{s}\) versus redshift parameter z for interacting THDE with Hubble horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\) and \(b^2=0.1\)

Full size image

3 THDE with particle horizon cutoff

3.1 Non-interacting

It is well-known that HDE model with particle horizon as the IR cutoff cannot lead to an accelerated universe and it is impossible to obtain an accelerated expansion [35, 36]. Indeed, with this cutoff, one always arrives at \(\omega _D>-1/3\), which is in contradiction with recent cosmological observations [35, 36]. As we shall see in this section, for the THDE with particle horizon as the IR cutoff, it is quite possible to reproduce an accelerating universe which is one of the main advantages of THDE in comparison with the usual HDE model. The particle horizon is defined as [35, 36]

$$\begin{aligned} R_{p}=a(t)\int _{0}^{t}{\frac{\mathrm{d}t}{a(t)}}, \end{aligned}$$
(18)

which satisfies the following condition

$$\begin{aligned} \dot{R}_{p}=H R_p +1. \end{aligned}$$
(19)

Therefore, bearing Eq. (1) in mind, the energy density of THDE is obtained as

$$\begin{aligned} \rho _D=B R_{p}^{2\delta -4}, \end{aligned}$$
(20)

where its time derivative leads to

$$\begin{aligned} \dot{\rho }_{D}=\rho _D(2\delta -4)H(1+F), \end{aligned}$$
(21)

in which

$$\begin{aligned} F=\left( \frac{3\Omega _D H^{2\delta -2}}{B}\right) ^{{1}/{(4-2\delta )}}. \end{aligned}$$
(22)

By substituting Eq. (21) into the conservation law,

$$\begin{aligned} \dot{\rho }_D+3H(1+\omega _D)\rho _D=0, \end{aligned}$$
(23)

one finds the EoS parameter of THDE as

$$\begin{aligned} \omega _D=-1-\left( \frac{2\delta -4}{3}\right) (1+F). \end{aligned}$$
(24)

Additionally, if we combine the time derivative of \(\Omega _{D}={\rho _{D}}/{(3m_{p}^{2}H^{2})}\) with Eqs. (9), (21) and (24), then one may arrive at

$$\begin{aligned} \Omega _{D}^{\prime }=\Omega _D(\Omega _D-1)[1+2F(\delta -2)-2\delta ]. \end{aligned}$$
(25)

The deceleration parameter q and the squared speed of sound (defined in Eq. (15)), are also founded out as

$$\begin{aligned} q=\frac{[1+(1-2F(\delta -2)-2\delta )\Omega _D]}{2}. \end{aligned}$$
(26)

and

Fig. 6
figure 6

The evolution of \(\Omega _D\) versus redshift parameter z for non-interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(B=2.4\) and \(H(a=1)=67\)

Full size image
Fig. 7
figure 7

The evolution of \(\omega _D\) versus redshift parameter z for non-interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(\delta =2.4\) and \(H(a=1)=67\)

Full size image
Fig. 8
figure 8

The evolution of q versus redshift parameter z for non-interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(B=2.4\) and \(H(a=1)=67\)

Full size image
Fig. 9
figure 9

The evolution of \({v}^{2}_{s}\) versus redshift parameter z for non-interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(\delta =2.4\) and \(H(a=1)=67\)

Full size image
Fig. 10
figure 10

The evolution of \({v}^{2}_{s}\) and \(\omega _D\) versus redshift parameter z for non-interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(B=2.4\), \(\delta =2.4\) and \(H(a=1)=67\)

Full size image
Fig. 11
figure 11

The evolution of \({v}^{2}_{s}\) and \(\omega _D\) versus redshift parameter z for non-interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(B=2.4\), \(\delta =2.6\) and \(H(a=1)=67\)

Full size image
Fig. 12
figure 12

The evolution of \({v}^{2}_{s}\) and \(\omega _D\) versus redshift parameter z for non-interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(B=2.4\), \(\delta =2.8\) and \(H(a=1)=67\)

Full size image
$$\begin{aligned} v_{s}^{2}= & {} \frac{-2-9F-10F^{2}+4\delta (F+1)^{2}}{-6(F+1)} \nonumber \\&+\,\frac{F[-1+2F(-2+\delta )+2\delta ]\Omega _D}{6(F+1)}, \end{aligned}$$
(27)

respectively. Here, in order to obtain Eq. (26), we employed Eq. (24) in writing Eq. (9), and then we used relation (12). In Figs. 6, 7, 8, 9, 10, 11, 12, the system parameters have been plotted for some values of the system unknowns and the initial condition \(\Omega ^{0}_D=0.73\) and \(H(a=1)=67\). As it is apparent, although this cutoff leads to a model can provide acceptable behavior for \(\Omega _D\), q and \(\omega _D\), the model is not stable.

3.2 Interacting

Using Eq. (21) and \(Q=3b^2 H(\rho _m+\rho _D)\) in the conservation equation (7), the EoS parameter is found as

$$\begin{aligned} \omega _D=-1-\frac{b^2}{\Omega _D}-\left( \frac{2\delta -4}{3}\right) (1+F). \end{aligned}$$
(28)

For this choice of interaction, the evolution of density parameter, the deceleration parameter q and stability for the model are calculated as

$$\begin{aligned} \Omega _{D}^{\prime }=-3b^2 \Omega _D+\Omega _D(\Omega _D-1)[1+2F(\delta -2)-2\delta ],\nonumber \\ \end{aligned}$$
(29)
$$\begin{aligned} q=\frac{[1-3b^2+(1-2F(\delta -2)-2\delta )\Omega _D]}{2}, \end{aligned}$$
(30)

and

$$\begin{aligned} v_{s}^{2}= & {} \frac{9b^2(b^2-1)+\Omega _D[A-FB]}{-6(F+1)(\delta -2)\Omega _D},\nonumber \\ A= & {} (\delta -2)(-2-9F-10F^{2}+4(F+1)^{2}\delta )\nonumber \\&+\,b^2(-3-6F+6\delta +3F\delta ),\nonumber \\ B= & {} [-1+2F(-2+\delta )+2\delta ](\delta -2)\Omega _D, \end{aligned}$$
(31)

respectively. They are also plotted in Figs. 13, 14, 15, 16, 17 for some values of the model’s parameters. Figures 17 and 16 show that, unlike the noninteracting case, the model is stable for some values of z. In addition, comparing Figs. 13 and 6 with each other, we observe that the changes in the density parameter of interacting case is slower than the noninteracting case. Moreover, Figs. 14 and 15 indicate that the model behaves as the phantom source, and thus, the model eventually enters the accelerated phase with the EoS for the universe being less than \(-1\) (or equally \(q<-1\)).

Fig. 13
figure 13

The evolution of \(\Omega _D\) versus redshift parameter z for interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(B=2.4\), \(\delta =2.4\) and \(H(a=1)=67\)

Full size image
Fig. 14
figure 14

The evolution of \(\omega _D\) versus redshift parameter z for interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(B=2.4\), \(\delta =2.4\) and \(H(a=1)=67\)

Full size image
Fig. 15
figure 15

The evolution of q versus redshift parameter z for interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(B=2.4\), \(\delta =2.4\) and \(H(a=1)=67\)

Full size image
Fig. 16
figure 16

The evolution of \({v}^{2}_{s}\) versus redshift parameter z for interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(B=2.4\), \(\delta =2.4\) and \(H(a=1)=67\)

Full size image
Fig. 17
figure 17

The evolution of \({v}^{2}_{s}\) versus redshift parameter z for interacting THDE with particle horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(b^2=0.1\), \(B=2.4\) and \(H(a=1)=67\)

Full size image

4 THDE with GO horizon cutoff

4.1 Non-interacting

In order to solve the causality and coincidence problems, Granda and Oliveros (GO) [40, 41] suggested a new cutoff, usually known as GO cutoff in the literatures, which is defined as \(L=(\gamma H^2+\zeta \dot{H})^{-{1}/{2}}\). In this case the energy density of THDE becomes

$$\begin{aligned} \rho _D=(\alpha H^2+\beta \dot{H})^{-\delta +2}, \end{aligned}$$
(32)

which leads to

$$\begin{aligned} \frac{\dot{H}}{H^2}= \frac{1}{\beta }\left( \frac{{(3m_p^2 \Omega _D)}^{\frac{1}{2-\delta }}}{{H}^{\frac{2-2\delta }{2-\delta }}}-\alpha \right) . \end{aligned}$$
(33)

Simple calculations for the deceleration and density parameters yield

$$\begin{aligned} q=-1-\frac{1}{\beta }\left( \frac{{(3m_p^2 \Omega _D)}^{\frac{1}{2-\delta }}}{{H}^{\frac{2-2\delta }{2-\delta }}}-\alpha \right) , \end{aligned}$$
(34)

and

$$\begin{aligned} \dot{\Omega }_D=\frac{\dot{\rho }_D}{3M_p^2H^2}-2\Omega _D\frac{\dot{H}}{H}, \end{aligned}$$
(35)

respectively. For the \(Q=0\) case, inserting the time derivative of Eq. (3) into Eq. (6), we obtain

$$\begin{aligned} \frac{\dot{\rho }_D}{3m_p^2H^3}=\frac{2\dot{H}}{H^2}+3(1-\Omega _D). \end{aligned}$$
(36)

Combining with Eqs. (35) and (33), we obtain

$$\begin{aligned} {\Omega }^\prime _D=(1-\Omega _D) \left[ 3+\frac{2}{\beta }\left( \frac{{(3m_p^2 \Omega _D)}^{\frac{1}{2-\delta }}}{{H}^{\frac{2-2\delta }{2-\delta }}}-\alpha \right) \right] . \end{aligned}$$
(37)

In this manner, the EoS parameter of THDE is given by

$$\begin{aligned} \omega _D=-1-\frac{1}{3\Omega _D}\left[ \frac{2}{\beta } \left( \frac{{(3m_p^2 \Omega _D)}^{\frac{1}{2-\delta }}}{{H}^{\frac{2-2\delta }{2-\delta }}}-\alpha \right) +3(1-\Omega _D)\right] , \end{aligned}$$
(38)

where we have inserted \(\dot{\rho }_D\) from Eq. (36) in the energy conservation law (7). Finally by taking time derivative from Eq. (38), and using it in rewriting Eq. (15), one can easily find

$$\begin{aligned} v_{s}^{2}= & {} -1+\frac{2\alpha }{3\beta }+2\frac{3^{\frac{-1+\delta }{2-\delta }}~ {H}^{\frac{2-2\delta }{-2+\delta }} ~{\Omega _D}^{\frac{-1+\delta }{2-\delta }}}{\beta (-2+\delta )}\nonumber \\&-\,\frac{(2\alpha -3\beta ) ~{H}^{\frac{2\delta }{-2+\delta }}(-1+\Omega _D)}{-2*{3}^{\frac{1}{2-\delta }} ~{H}^{\frac{2}{-2+\delta }} ~{\Omega _D}^{\frac{1}{2-\delta }}+ {H}^{\frac{2 \delta }{-2+\delta }}[2\alpha -3\beta +3\beta \Omega _D]}, \end{aligned}$$
(39)
Fig. 18
figure 18

The evolution of \(\Omega _D\) versus redshift parameter z for noninteracting THDE with GO horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(\alpha =0.8\), \(\beta =0.5\) and \(H(a=1)=67\)

Full size image
Fig. 19
figure 19

The evolution of \(\omega _D\) versus redshift parameter z for noninteracting THDE with GO horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(\alpha =0.8\), \(\beta =0.5\) and \(H(a=1)=67\)

Full size image
Fig. 20
figure 20

The evolution of q versus redshift parameter z for noninteracting THDE with GO horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(\alpha =0.8\), \(\beta =0.5\) and \(H(a=1)=67\)

Full size image
Fig. 21
figure 21

The evolution of \({v}^{2}_{s}\) versus redshift parameter z for noninteracting HDE with GO horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(\alpha =0.8\), \(\beta =0.5\) and \(H(a=1)=67\)

Full size image

In Figs. 18, 19, 20, 21, the system parameters including \(\omega _D\), q, \(\Omega _D\) and \({v}^{2}_{s}\) are plotted for some values of \(\alpha \), \(\beta \) and \(\delta \) by considering the initial conditions \(\Omega ^{0}_D=0.73\) and \(H(a=1)=67\). It is interesting to note here that the model begin to show stability from itself whenever \(q\rightarrow \frac{1}{2}\). Moreover, the depicted curves are some of those which do not cross the phantom line for \(z\ge -1\).

4.2 Interacting

One can check that q and \(\omega _D\) have the same form as those of the non-interacting case meaning that the mutual interaction does not affect them. Thus, we only need the \({\Omega }^\prime _D\) and \(v_{s}^{2}\) parameters evaluated as

$$\begin{aligned} {\Omega }^\prime _D=-3b^2+(1-\Omega _D) \left[ 3+\frac{2}{\beta }\left( \frac{{(3m_p^2 \Omega _D)}^{\frac{1}{2-\delta }}}{{H}^{\frac{2-2\delta }{2-\delta }}}-\alpha \right) \right] , \end{aligned}$$
(40)

and

$$\begin{aligned} v_{s}^{2}= & {} -1+\frac{2\alpha }{3\beta }+2\frac{3^{\frac{-1+\delta }{2-\delta }}~{H}^{\frac{2-2\delta }{-2+\delta }} {\Omega _D}^{\frac{-1+\delta }{2-\delta }}}{\beta (-2+\delta )}\nonumber \\&-\,\frac{(2\alpha -3\beta ) ~{H}^{\frac{2\delta }{-2+\delta }}(-1+b^2+\Omega _D)}{-2{3}^{\frac{1}{2-\delta }} ~{H}^{\frac{2}{-2+\delta }} ~{\Omega _D}^{\frac{1}{2-\delta }}+ {H}^{\frac{2 \delta }{-2+\delta }}[2\alpha +3\beta (-1+b^2)+3\beta \Omega _D]}, \end{aligned}$$
(41)

respectively. These parameters are plotted in Figs. 22, 23 for some values of the system constants. As it is apparent, for \(q\rightarrow {1}/{2}\) the model shows stability from itself, a result in full agreement with the noninteracting case.

Fig. 22
figure 22

The evolution of \(\Omega _D\) versus redshift parameter z for interacting THDE with GO horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(\alpha =0.8\), \(\beta =0.5\), \(b^2=0.01\) and \(H(a=1)=67\)

Full size image
Fig. 23
figure 23

The evolution of \({v}^{2}_{s}\) versus redshift parameter z for interacting THDE with GO horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(\alpha =0.8\), \(\beta =0.5\), \(b^2=0.01\) and \(H(a=1)=67\)

Full size image

5 HDE with Ricci horizon cutoff

5.1 Non-interacting

The energy density of THDE with Ricci scalar as the IR cutoff is written as [98]

$$\begin{aligned} \rho _D=\lambda (2H^2+ \dot{H})^{-\delta +2}, \end{aligned}$$
(42)

where \(\lambda \) is an unknown HDE constant as usual [35, 36, 98]. This energy density is also obtainable by inserting \(\alpha =2\beta \) in Eq. (32) and defining new unknown constant \(\lambda \) as \(\lambda =\beta ^{2-\delta }\), a desired result. In order to find the deceleration parameter q, we rewrite Eq. (42) as

$$\begin{aligned} \frac{\dot{H}}{H^2}= \left( \frac{{(3 {\lambda }^{-1} m_p^2 \Omega _D)}^{\frac{1}{2-\delta }}}{{H}^{\frac{2-2\delta }{2-\delta }}}-2 \right) , \end{aligned}$$
(43)

and use Eq. (12) to obtain

$$\begin{aligned} q=-1-\left( \frac{{(3 {\lambda }^{-1} m_p^2 \Omega _D)}^{\frac{1}{2-\delta }}}{{H}^{\frac{2-2\delta }{2-\delta }}}-2 \right) . \end{aligned}$$
(44)

It is also a matter of calculation to combine Eqs. (35) and (36) with (43) to reach at

$$\begin{aligned} {\Omega }^\prime _D=(1-\Omega _D) \left[ 3+2\left( \frac{{(3 {\lambda }^{-1} m_p^2 \Omega _D)}^{\frac{1}{2-\delta }}}{{H}^{\frac{2-2\delta }{2-\delta }}}-2 \right) \right] . \end{aligned}$$
(45)

In this manner, we have

$$\begin{aligned} \omega _D=-1-\frac{1-\Omega _D}{\Omega _D}\left[ \frac{2}{3(1-\Omega _D)}\left( \frac{{(3 {\lambda }^{-1} m_p^2 \Omega _D)}^{\frac{1}{2-\delta }}}{{H}^{\frac{2-2\delta }{2-\delta }}}-2 \right) +1\right] , \end{aligned}$$
(46)

where Eqs. (36), (7) and (43) have been used to obtain the above result. Moreover, by taking time derivative from Eq. (46) we find

$$\begin{aligned} v_{s}^{2}= & {} \frac{1}{3}+2\frac{{3}^{\frac{-1+\delta }{2-\delta }}~ {H}^{\frac{2-2\delta }{-2+\delta }} ~{( {\lambda }^{-1} \Omega _D)}^{\frac{1}{2-\delta }}}{\Omega _D(-2+\delta )}\nonumber \\&+\,\frac{(-1+\Omega _D)}{-1-3\Omega _D+2\times {3}^{\frac{1}{2-\delta }} ~{H}^{\frac{2-2\delta }{-2+\delta }} ~{( {\lambda }^{-1}\Omega _D)}^{\frac{1}{2-\delta }}}. \end{aligned}$$
(47)
Fig. 24
figure 24

The evolution of \(\Omega _D\) versus redshift parameter z for non-interacting THDE with Ricci horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\) and \(H(a=1)=67\) and \(\delta =1\)

Full size image
Fig. 25
figure 25

The evolution of \(\omega _D\) versus redshift parameter z for non-interacting THDE with Ricci horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\) and \(H(a=1)=67\) and \(\delta =1\)

Full size image
Fig. 26
figure 26

The evolution of q versus redshift parameter z for non-interacting THDE with Ricci horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\) and \(H(a=1)=67\) and \(\delta =1\)

Full size image
Fig. 27
figure 27

The evolution of \({v}^{2}_{s}\) versus redshift parameter z for non-interacting THDE with Ricci horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\) and \(H(a=1)=67\) and \(\delta =1\)

Full size image

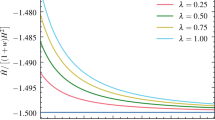
It can be seen from Figs. 24, 25, 26, 27 that the current accelerated universe can be achieved. The \(\lambda =1\) case is interesting, because unlike SMHDE [64], this model is stable (unstable) for \(q>0\) (\(q<0\)). Hence, since the Ricci horizon is a special case of the GO cutoff, the GO cutoff can also produce the same results if proper values for the system unknown constants have been chosen.

5.2 Interacting

Just the same as the GO cutoff, one can easily check that we only need to calculate the \(\Omega _D\) and \(v_{s}^{2}\) parameters in this case, a result due to the fact that the Ricci cutoff is a special case of the GO cutoff. The calculations lead to

$$\begin{aligned} {\Omega }^\prime _D=-3b^2+(1-\Omega _D)\left[ 3+2\left( \frac{{(3 {\lambda }^{-1} m_p^2 \Omega _D)}^{\frac{1}{2-\delta }}}{{H}^{\frac{2-2\delta }{2-\delta }}}-2\right) \right] , \end{aligned}$$
(48)

and

$$\begin{aligned} v_{s}^{2}= & {} \frac{1}{3}+\frac{2*{3}^{\frac{-1+\delta }{2-\delta }}~{H}^{\frac{2-2\delta }{-2+\delta }} ~{( {\lambda }^{-1} \Omega _D)}^{\frac{1}{2-\delta }}}{\Omega _D(-2+\delta )}\nonumber \\&+\,\frac{(-1+b^2+\Omega _D)}{-1-3b^2-3\Omega _D+2*{3}^{\frac{1}{2-\delta }} ~{H}^{\frac{2-2\delta }{-2+\delta }} ~{( {\lambda }^{-1}\Omega _D)}^{\frac{1}{2-\delta }}}, \end{aligned}$$
(49)

In Figs. 28, 29, 30, 31, the system parameters have been plotted versus z for some values of the unknown constants. It is obvious that the system parameters affected by the mutual interaction. It is also interesting to note that while \(v_{s}^{2}\) was not negative for \(\lambda =1.5\) in the non-interacting case, here, we always have it is not stable for all values of \(v_{s}^{2}<0\).

Fig. 28
figure 28

The evolution of \(\Omega _D\) versus redshift parameter z for interacting THDE with Ricci horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(H(a=1)=67\), \(b^2=0.01\) and \(\delta =1\)

Full size image
Fig. 29
figure 29

The evolution of \(\omega _D\) versus redshift parameter z for interacting THDE with Ricci horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\) and \(H(a=1)=67\), \(b^2=0.01\) and \(\delta =1\)

Full size image
Fig. 30
figure 30

The evolution of q versus redshift parameter z for interacting THDE with Ricci horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\) and \(H(a=1)=67\), \(b^2=0.01\) and \(\delta =1\)

Full size image
Fig. 31
figure 31

The evolution of \({v}^{2}_{s}\) versus redshift parameter z for interacting THDE with Ricci horizon as the IR cutoff. Here, we have taken \(\Omega ^{0}_D=0.73\), \(H(a=1)=67\), \(b^2=0.01\) and \(\delta =1\)

Full size image

6 Closing remarks

In the shadow of the holographic principle and based on the non-additive generalized Tsallis entropy expression [78], a new holographic dark energy model called THDE has recently been proposed [1]. In this paper, by considering various IR cutoffs, including the particle horizon, the Ricci horizon and the GO cutoff in the background of the FRW universe, we investigated the evolution of the THDE models and studied their cosmological consequences. We found out that when the particle horizon is considered as IR cutoff, then the THDE model can explain the current acceleration of the universe expansion. This is in contrast to the usual HDE model which cannot lead to an accelerated universe, if one consider the particle horizon as IR cutoff [35, 36]. We also explored the sound stability of the THDE models with various cutoffs. In this manner, the assumed mutual interaction between the cosmos sectors makes the model to be stable for some values of the redshift parameter z. For the GO and the Ricci horizon cutoffs, we found out that although acceptable behavior for some parameters of the system, including q, the density parameter and \(\omega _D\), are achievable, the model is not always stable. Finally, we have explored the effects of considering a mutual interaction between the two dark sectors of the universe on the behavior of the solutions.