1 Introduction

It is well known that the concept of dark energy (DE) was introduced in order to describe the accelerated expansion of the universe. Therefore, understanding the nature of DE is considered one of the most difficult and fundamental problems in cosmology. The introduction of a cosmological constant, \(\varLambda \) (\(\rho _{\varLambda }=\hbox {const}.\)), is perhaps the simplest form of DE which can be considered [1]. The outcome of this consideration is the concordance \(\varLambda \hbox {CDM}\) model, for which the \(\varLambda \) constant coexists with cold dark matter (CDM) and baryonic matter. In general, this model is a good description of the observed universe, since it is consistent with the cosmological data, namely Cosmic Microwave Background (CMB) [2,3,4,5], Baryon Acoustic Oscillation (BAO) [6,7,8,9,10,11] and Supernovae Type-Ia (SnIa)[12,13,14,15]. Despite the latter achievement \(\varLambda \hbox {CDM}\) suffers from the cosmological constant and the coincidence problems [16,17,18,19,20]. A third possible problem is related with the fact that the determination of the Hubble constant and the mass variance at \(8h^{-1}\hbox {Mpc}\) have indicated a tension between the values resulting by the analysis of Planck data and the results obtained by the late time observational data [21,22,23].

An alternative avenue to overcoming the above problems is to introduce a dynamical DE, wherein the density of DE is allowed to evolve with cosmic time [24,25,26,27,28,29,30]. The first choice is to consider a DE fluid where the equation of state parameter varies with redshift, w(z). Usually, in these kinds of studies the EoS parameter can be written either as a first-order Taylor expansion around \(a(z)=1\) [31, 32] or as a Padé parametrization [33,34,35,36], where the corresponding free parameters are fitted by the cosmological data [37,38,39,40,41,42,43,44]. Notice that for \(w>-1\) we are in the quintessence regime [20, 45], namely the corresponding scalar field has a canonical Lagrangian form. In the case of \(w<-1\) we are in the phantom region where the Lagrangian of the scalar field has a non-canonical form (K-essence) [45,46,47,48,49]. On the other hand, it is possible to reconstruct a DE model directly from observations. This approach is an excellent platform to study DE and indeed one may find several attempts in the literature. Specifically, one may use parametric criteria toward reconstructing directly the evolution of DE density \(\rho _\mathrm{de}(z)\) [50,51,52] and the potential of the scalar field [53].Footnote 1 Comparing the two methods, namely w(z) and \(\rho _\mathrm{de}(z)\) for the same observational data sets, it has been found that the latter method leads to tighter constraints on the free parameters than the former [50,51,52].

In this work we have decided to reconstruct the evolution of the DE density, using the well-known Padé approximation for which an unknown function [58, 59] is well approximated by the ratio of two polynomials. In contrast to the case where the Padé approximation is used to describe the DE EoS, our approach leads to an interesting parameterization which can be regarded as an expansion around the \(\varLambda \hbox {CDM}\). In Sect. 2 we introduce the concept of a Padé approximation in DE cosmologies. In Sect. 3 we briefly discuss the main features of the Bayesian analysis used in this work and we briefly present the observational data. In Sect. 4 we discuss the main results of our work; namely, we present the observational constraints on the fitted model parameters and we test whether a dynamical DE is allowed by the current data. Finally, in Sect. 5 we present our conclusions.

2 Reconstruction of dark energy using Padé approximation

2.1 Background evolution

Considering an isotropic and homogeneous universe, driven by radiation, non-relativistic matter and dark energy with equation of state, \(P_\mathrm{Q}=w(a)\rho _\mathrm{Q}<0\), the first Friedman equation is given by

$$\begin{aligned} H^{2}=\left( \frac{\dot{a}}{a} \right) ^{2}= \frac{8\pi G}{3}(\rho _{r}+\rho _{m}+\rho _\mathrm{Q})-\frac{k}{a^{2}} \end{aligned}$$
(1)

with \(k=-1, 0\) or 1 for an open, a flat and a closed universe, respectively. For the rest of the analysis we have set \(k=0\). Notice that a(t) is the scale factor, \(\rho _{r}=\rho _{r0} a^{-4}\) is the radiation density, \(\rho _{m}=\rho _\mathrm{m0} a^{-3}\) is the matter density and \(\rho _\mathrm{Q}=\rho _\mathrm{Q0} X(a)\) is the dark energy density, with

$$\begin{aligned} X(a)=\mathrm{exp}\left[ 3\int _{a}^{1} \left( \frac{1+w(u)}{u}\right) \mathrm{d}u \right] \end{aligned}$$
(2)

or

$$\begin{aligned} w(a)=-1 + \frac{1}{3}a\frac{X^{\prime }}{X},\; \end{aligned}$$
(3)

where the prime denotes the derivative with respect to the scale factor. Combining the above equations we easily obtain the normalized Hubble parameter, \(E(a)=H(a)/H_{0}\),

$$\begin{aligned} E(a)=\left[ \varOmega _{r0}a^{-4}+\varOmega _{m0}a^{-3}+ \varOmega _\mathrm{Q0 }X(a)\right] ^{1/2}, \end{aligned}$$
(4)

where \(\varOmega _{r0}= 8\pi G \rho _{r0}/3H_{0}^{2}\) (radiation density parameter), \(\varOmega _{m0}= 8\pi G \rho _{m0}/3H_{0}^{2}\) (matter density parameter), \(\varOmega _\mathrm{Q0}= 8\pi G \rho _\mathrm{Q0}/3H_{0}^{2}\) (DE density parameter) at the present time with \(\varOmega _{r0}+\varOmega _{m0}+\varOmega _\mathrm{Q0}=1\). Since the physics of DE is still an open issue the function X(a) encodes our ignorance concerning the underlying mechanism powering the late time cosmic acceleration. Of course, for \(X(a)=1\) we recover the concordance \(\varLambda \)CDM model, namely \(w=-1\).

In order to investigate possible deviations from the concordance \(\varLambda \) cosmology, we consider an expansion of the function X(a) using the so-called Padé approximation. In general, for an arbitrary function f(x) the Padé approximation of order (n, m) is given by [58, 59]

$$\begin{aligned} f(x)=\frac{b_0 + b_1x+b_2x^2+b_3x^3+\cdots +b_nx^n}{c_0 + c_1x+c_2x^2+c_3x^3+\cdots +c_mx^m},\; \end{aligned}$$
(5)

where the exponents are positive and the corresponding coefficients \((b_i,c_i)\) are constants. Obviously, in the case of \(c_i=0\) (\(i>0\)) the above expansion reduces to the usual Taylor expansion. One of the main advantages of such an approximation is that by considering the same order, for \(m=n\), the Padé approximation tends to finite values at both \(x\rightarrow \infty \) and \(x\rightarrow 0\).

Based on the above formulation the unknown X(a) function is approximated by

$$\begin{aligned} X(a)=\frac{b_0 + b_1(1-a)+b_2(1-a)^2+\cdots +b_n(1-a)^n}{b_0 + c_1(1-a)+c_2(1-a)^2+\cdots +c_m(1-a)^m},\; \end{aligned}$$
(6)

where we have set \(x=1-a\) and \(c_0=b_0\) as a result of \(X(a=1)=1\). In order to simplify further the calculation, we may cancel \(b_0\) from both the numerator and the denominator and rename the corresponding constants. Therefore, we have

$$\begin{aligned} X(a)=\frac{1+ b_1(1-a)+b_2(1-a)^2+\cdots +b_n(1-a)^n}{1 + c_1(1-a)+c_2(1-a)^2+\cdots +c_m(1-a)^m}.\; \end{aligned}$$
(7)

Using Eq. (7) and differentiating X(a) with respect to the scale factor, the EoS parameter (3) takes the following form:

$$\begin{aligned} w=-1-\frac{1}{3}a\left[ \frac{\sum _{i=1}^{n}ib_{i}(1-a)^{i-1}}{1+\sum _{i=1}^{n}b_{i}(1-a)^{i}}- \frac{\sum _{i=1}^{m} ic_{i}(1-a)^{i-1}}{1+\sum _{i=1}^{m}c_{i}(1-a)^{i}}\right] . \end{aligned}$$
(8)

Here we use the Padé approximation to model the energy density of DE rather than the EoS [36]. Our approach leads to a new and interesting parameterization which can be regarded as an expansion around the \(\varLambda \hbox {CDM}\).

Fig. 1
figure 1

The relative difference of the Hubble parameter using some typical values of the model parameters. \(\varDelta E\) becomes positive (negative) when \(b_1>c_1\) \((b_1<c_1)\)

Full size image

Inserting \(a=1\) into the latter equation we obtain the EoS parameter at the present time, namely

$$\begin{aligned} w_{0}\equiv w(a=1)=-1 + \frac{1}{3}(c_1-b_1)\; . \end{aligned}$$
(9)

Interestingly, in the case of \(b_1>c_1\) the current value of \(w_{0}\) can cross the phantom line \(w_{0}<-1\), while for \(b_1<c_1\) it remains in the quintessence regime \(w_{0}>-1\). Moreover, for \(b_{i}=c_{i}=0\) we recover the \(\varLambda \hbox {CDM}\) model, while for \(b_{i+1}<b_i\) and \(c_{i+1}<c_i\) the current family of Padé models can be seen as an expansion around the \(\varLambda \)CDM where the extra terms indicate a dynamical DE. Unlike most DE parametrizations (CPL and the like), here it is easy to show that the EoS parameter avoids the divergence in the far future, hence it is a well-behaved function in the range of \(a\in (0,+\infty )\). Keeping the leading terms \((b_{1},c_{1})\) in Eq. (8) we arrive at

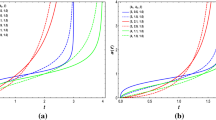
$$\begin{aligned} w(a) = -1 +a\frac{1}{3}\frac{c_1-b_1}{(1+c_1(1-a))(1+b_1(1-a))}. \end{aligned}$$
(10)

To visualize the differences of various Padé models with respect to the expectations of the usual \(\varLambda \hbox {CDM}\) model we plot in Fig. 1 the corresponding relative differences

$$\begin{aligned} \varDelta E(\%)=\frac{E(z)-E_{\varLambda }(z)}{E_{\varLambda }(z)}\times 100. \end{aligned}$$
(11)

For simplicity the matter density parameter is fixed to \(\varOmega _{m0}=0.3\). Using Eq. (11) and in the case of \(b_{1}>c_{1}\) we have \(\varDelta E>0\) and the present value of the EoS parameter is in the phantom regime (\(w<-1\)). Notice that the opposite holds for \(b_{1}<c_{1}\). Moreover, prior to \(z\sim 1\) we find \(\pm \, 6\%\) Hubble function differences, while \(\varDelta E\) tends to zero at high redshifts.

Lastly, we would like to illustrate how extra terms of X(a) affect the Hubble parameter. As an example, we introduce the quantity \((1-a)^{2}\) in Eq. (6), where the corresponding constants have been set either to \((b_{2},c_{2})=(0.1,-0.1)\) or \((b_{2},c_{2})=(-0.1,0.1)\). In Fig. 1 we present for the above set of \((b_{2},c_{2})\) parameters the evolution of \(\varDelta E\). It is obvious from the figure that the extra term \((1-a)^{2}\) in the function X(a) does not really affect the cosmic expansion.

Consequently, our model can be considered as an expansion around the \(\varLambda \hbox {CDM}\) in the sense that adding extra terms changes the Hubble parameter slightly.

2.2 Growth of perturbations

It is well known that DE not only affects the expansion rate of the universe but also has an impact on the growth rate of matter perturbations. In order to realize how different forms of Padé parametrizations affect the growth rate of fluctuations, we solve the perturbed equations and compare the solution with that of \(\varLambda \)CDM model. Assuming a homogeneous DE fluid, the evolution of matter perturbations in the linear regime is given by [60]

$$\begin{aligned}&\dot{\delta _m}+\frac{\theta _m}{a}=0,\; \end{aligned}$$
(12)
$$\begin{aligned}&\dot{\theta _m}+H\theta _m - \frac{k^2\phi }{a}=0,\; \end{aligned}$$
(13)

where the dot denotes the derivative with respect to cosmic time, \(\delta _m\) is the overdensity contrast and \(\theta _m\) is the velocity divergence. Combining the above set of equations with the Poisson equation,

$$\begin{aligned} -\frac{k^2\phi }{a^2}=\frac{3}{2}H^2\varOmega _m\delta _m,\; \end{aligned}$$
(14)

we find after some calculations

$$\begin{aligned} \delta _m^{\prime \prime }+\frac{1}{a}\left( 3+\frac{\dot{H}}{H^2}\right) \delta _m^{\prime }=\frac{3}{2}\varOmega _m\delta _m,\; \end{aligned}$$
(15)

where \(\varOmega _m=\frac{\varOmega _{m0} a^{-3}}{E^2(a)}\). Notice that the latter differential equation is written in terms of the scale factor; hence

$$\begin{aligned} \frac{\dot{H}}{H^2}=\frac{1}{2}a\frac{(E^2)^{\prime }}{E^2}.\; \end{aligned}$$
(16)

Therefore, for those cosmological models which are within GR the linear matter perturbations are only affected by E(a), while in the case of extended gravity models we need to modify the Poisson equation.

An important quantity as regards testing the performance of the DE models at the perturbation level is \(f\sigma _8(a)\), where \(f=a\frac{\delta _m^{\prime }}{\delta _m}\) is the growth rate of clustering and \(\sigma _8(a)\) is the mass variance inside a sphere of radius 8\(h^{-1}\)Mpc. The mass variance is written as \(\sigma _8(a)=\sigma _8\frac{\delta _m(a)}{\delta _m(a=1)}\), where \(\sigma _{8}\equiv \sigma _8(a=1)\) is the corresponding value at the present time. Notice that in our work we treat \(\sigma _8\) as a free parameter and thus it will be constrained by the available growth data.

In order to understand the differences between the \(\varLambda \hbox {CDM}\) and Padé models at the perturbation level in Fig. 2 we plot the relative fractional difference, namely

$$\begin{aligned} \varDelta f\sigma _8(\%)=\frac{f\sigma _8-(f\sigma _8)_{\varLambda }}{(f\sigma _8)_{\varLambda }}\times 100.\; \end{aligned}$$
(17)
Fig. 2
figure 2

The relative difference of growth rate as a function of redshift. The free parameters are the same as those of Fig. 1

Full size image

For better comparison, the free parameters used in this figure are the same as those of Fig. 1, where we have set \(\varOmega _{m0}=0.3\), \(h=0.7\) and \(\sigma _8=0.8\). Overall, for phantom Padé cosmologies (\(b_1>c_{1}\); see the red line) we find that the expected differences are small at low redshifts, but they become larger for \(z\simeq 0.5\), reaching variations of up to \(\sim -3\%\), while they turn positive at high redshifts. Notice that the opposite behavior holds in the case of quintessence Padé cosmologies (\(b_1<c_{1}\); see the blue line).

3 Bayesian evidence and data processing

Using Bayes’ theorem, it is possible to find the probability of a model in the light of given observational data. Given a data set (D) the probability of having a model (M) is

$$\begin{aligned} P(M|D)=\frac{P(M|D)P(M)}{P(D)}.\; \end{aligned}$$
(18)

The posterior probability of the free parameters (\(\theta \)) of the model is given by

$$\begin{aligned} P(\theta |D,M)=\frac{P(D|\theta ,M)P(\theta |M)}{P(D|M)},\; \end{aligned}$$
(19)

where \(P(D|\theta ,M)\) is the likelihood function of the model with its parameters and \(P(\theta |M)\) is the prior information on the free parameters. For parameter estimations, we only need the likelihood function and the prior, hence the denominator, which is a normalization constant that has no impact on the value of the free parameters. Practically, the denominator is the integral of the likelihood and prior product over the parameter space

$$\begin{aligned} {\mathscr {E}} = P(D|M)=\int d\theta P(D|\theta ,M)P(\theta |M).\; \end{aligned}$$
(20)

The latter quantity has been widely used in the literature [61,62,63,64], as regards selecting the best model from a given family of models.

With the aid of the Padé parametrization which can be seen as an expansion around \(\varLambda \hbox {CDM}\) (\(w=-1\)) our aim is to check whether the current observational data prefer a dynamical DE. First we consider a large body of Padé parametrizations (7) and then we test the statistical performance of each Padé model against the data.

Now, let us briefly present the observational data that we utilize in our analysis.

  • We use the JLA SnIa data of (full likelihood version) [15].

  • The Baryon Acoustic Oscillations (BAO) data from 6dF [65], SDSS [66] and WiggleZ [67] surveys. Notice that details of the data concerned with processing and likelihoods can be found in [44, 68].

  • The Hubble parameter measurements as a function of redshift. We utilize the H(z) data set as provided by [69].

  • The CMB shift parameters as measured by the Planck team [70]. Notice that we use the covariance matrix which is introduced in Table 4 of [70].

  • The Hubble constant from [22].

  • For the growth rate data, in addition to the “Gold” growth data set \(f\sigma _8(z)\) provided by [71], we also use five new data points as collected by [72]. These new data points provide a growth rate at relatively higher redshifts and there is no overlap between these data and the gold sample. These new data points and their references are presented in Table 1.

Table 1 New \(f\sigma _8\) data points which we use along with the Gold sample
Full size table

Concerning the estimation of the sound horizon, needed when we compute the CMB and BAO likelihoods, we follow the procedure of [76]. Using the aforementioned data sets, we first perform a MCMC analysis to find the best value of the parameters and their uncertainties and then we quantify the statistical ability of each model to fit the observational data. To do this we use the MULTINEST sampling algorithm [77] and the python implementation pymultinest [78]. The latter technique was initially proposed in order to select the best model of AGN X-ray spectra via a Bayesian approach.

4 Results and discussion

As we have already mentioned nowadays, testing the evolution of the DE EoS parameter is considered as one of the most fundamental problems in cosmology. We attempt to check such a possibility in the context of Padé parametrizations. Specifically, the family of Padé models and the corresponding free parameters used here are shown in Tables 2 and 3 respectively. Since, unlike the parameter estimation, the evidence strongly depends on the prior, we consider two different priors to show how the evidence changes due to different prior ranges. Here we select flat priors, which are often a standard choice. The upper panel in Table 3 shows a narrow range of priors while the lower panel presents a wider prior. The priors on the cosmological parameters (\(\varOmega _\mathrm{dm},\varOmega _\mathrm{ba},h,\sigma _8\)) are physically reasonable due to our understanding from observational data including SN Ia, CMB, BAO and growth rate of large scale structures. On the other hand, the range of priors in (\(\alpha ,\beta , M ,\varDelta M\)) comes from an analysis of the SN Ia data in [15, 79]. In contrast, we have no prior information regarding our free parameters in the Padé expansion (\(b_1,c_1,b_2,c_2,b_3,c_3,b_4,c_4\)). Therefore, we select priors on these parameters from the intuition that they should construct an expansion around the \(\varLambda { {CDM}}\) model. In this sense, we consider smaller prior ranges for parameters which are of higher order in the expansion. According to [61], one possibility in such a case is to consider a prior which maximizes the probability of the new model, given the data. In this case, if the evidence is not significantly larger than the simpler model, then we can say that the data does not support additional parameters. In addition to these two prior ranges, we have examined other prior ranges and our results did not change significantly.

In Table 3, \(\alpha ,\beta \) and M are nuisance parameters which are used to model the empirical distance modulus of each SN and \(\varDelta M\) is used to correct for the dependency of the absolute magnitude in the rest-frame B band on the host stellar mass. For more information regarding the definitions of these parameters we refer to [15]. Therefore, using the cosmological data we place constraints on the model parameters but also we present a visual way to discriminate cosmological models.

Table 2 Various models used in our analysis
Full size table
Table 3 Two ranges of the model parameters which we consider in this work. The upper panel (lower panel) indicates a narrow(broad) prior
Full size table

First, the best-fit parameters and their uncertainties for all of the models utilized in this analysis were obtained with the aid of the MCMC method and the results are listed in Table 4. For comparison we also present the results of the \(\varLambda \hbox {CDM}\) cosmological model, namely the Padé \(\hbox {M}_{1}\) parametrization. Notice that we use the getdist python packageFootnote 2 for the analysis of the MCMC samples. We find that the main cosmological parameters, namely \((\varOmega _{m0},h,\sigma _{8})\), are practically the same for all models. Concerning the DE parameters it seems that, although the best-fit values indicate \(w<-1\) at the present time, we cannot exclude the possibility of \(w>-1\) at \(1\sigma \) level. Moreover, for all Padé parametrizations we find that the best-fit values obey the inequalities \(b_{1}>c_{1}\) and \(b_{2}>c_{2}\).

Table 4 The best-fit values and the corresponding \(1\sigma \) uncertainties for the current Padé parametrizations. Notice that the \(\varLambda \hbox {CDM}\) model can be seen as a Padé \(M_{1}\) parametrization, namely \(b_{i}=c_{i}=0\)
Full size table
Table 5 The goodness-of-fit statistics \(\chi ^{2}_{min}\), \(\varDelta \)AIC, \(\varDelta \)BIC, \(\varDelta \mathrm{ln}{\mathscr {E}}\) for the narrow and broad ranges of priors (N (B) stands for narrow(broad) prior ranges) and the Bayesian complexity for our models
Full size table

Second we run the pymultinest code in order to check the statistical performance of the current Padé models in fitting the data and we compare them with that of \(\varLambda \hbox {CDM}\). The minimum \(\chi ^2_\mathrm{min}\), Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC) and the bayesian evidence (for two ranges of priors) of our models are summarized in Table 5. We remind the reader that the AIC [80] and BIC [81] estimators are given by

$$\begin{aligned} \mathrm{AIC} = \chi ^2_\mathrm{min} + 2n_\mathrm{fit},\quad \mathrm{BIC} = \chi ^2_\mathrm{min} + n_\mathrm{fit}\ln N, \; \end{aligned}$$
(21)

where \(n_\mathrm{fit}\) (N) is the number of fitted parameters (number of data points). Clearly, AIC identifies the statistical significance of our results, namely a smaller value of AIC implies a better model–data fit. On the other hand, the model pair difference \(\varDelta \mathrm{AIC}=\mathrm{AIC}_\mathrm{model}-\mathrm{AIC}_\mathrm{min}\) is the statistical performance of the different models in reproducing the observational data. Specifically, the condition \(4<\varDelta \mathrm{AIC} <7\) indicates a positive evidence against the model with higher value of \(\mathrm{AIC}\) [82, 83], while the inequality \(\varDelta \mathrm{AIC} \ge 10\) points to strong evidence thereof. Lastly, the restriction \(\varDelta \mathrm{AIC} \le 2\) leads to an indication of the consistency between the two comparison models.

Another way of testing the ability of the models to fit the data is via the Bayesian evidence \({\mathscr {E}}\); namely, a model with the higher evidence is favored. In this context, in order to measure the significant difference between two models \(M_{i}\) and \(M_{j}\) we can use the Jeffreys scale [84], which is given by \(\varDelta {\ln \mathscr {E}}={\ln \mathscr {E}}_{M_{i}}-{\ln \mathscr {E}}_{M_{j}}\). This model pair difference leads to the following situations: (1) \(0<\varDelta {\ln \mathscr {E}}<1.1\) suggests weak evidence against \(M_{j}\) model when compared with \(M_{i}\), (2) the restriction \(1.1<\varDelta \ln {\mathscr {E}}<3\) means that there is definite evidence against \(M_{j}\), while in the case of \(\varDelta \ln {\mathscr {E}}\ge 3\) such evidence becomes strong [85].

In order to realize that extra parameters in a given model can be constrained by the data in hand, one can compute the so-called Bayesian complexity which was introduced in [86]. The quantity measures the number of parameters that the data can support. Following [61], the Bayesian complexity is given by

$$\begin{aligned} C_b \equiv \overline{\chi ^2(\theta )}- \chi ^2(\hat{\theta }) \end{aligned}$$
(22)

where a bar indicates a mean taken over the posterior distribution and \(\hat{\theta }\) can be either the best or the mean value of the parameters. The Bayesian complexity is a quantity to measure the power of data to constrain the parameters comparing with the predictivity of the model which is given by the prior. Generally, the Bayesian complexity depends on both data and prior. But in our case, the sample of the free parameters is almost the same for the two prior ranges; the Bayesian complexity does not depend on the prior.

Our estimations of the Bayesian complexities are given in Table 5. Here we consider both cases for \(\hat{\theta }\), so \(\hat{\theta _b}\) (\(\hat{\theta _m}\)) indicates the best value (mean value) of the parameters.

Clearly, after considering the above statistical tests we find that the best model is the \(\varLambda \)CDM model, hence \(\mathrm{AIC}_\mathrm{min}\equiv \mathrm{AIC}_{M_{1}}\), \({\mathscr {E}}_{M_{j}}\equiv {\mathscr {E}}_{M_{1}}\). Using the model pair difference \(\varDelta \mathrm{AIC}\) we find strong evidence against models \(M_{4}\) and \(M_{5}\), namely \(\varDelta \mathrm{AIC} \gtrsim 10\). Also, in the case of the \(M_{3}\) model we have \(\varDelta \mathrm{AIC} \simeq 4.79\), which indicates positive evidence against that model, while for \(M_{2}\) model we obtain \(\varDelta \mathrm{AIC} \simeq 1.13\) and thus we cannot reject this model. In contrast to the AIC, BICs of our models indicate a “decisive” evidence against the \(M_2\), \(M_3\) \(M_4\) and \(M_5\) models. The main reason is that the BIC penalizes models with a high number of parameters more than AIC, specifically when there are large numbers of data points.

From the viewpoint of \(\varDelta {\ln \mathscr {E}}\)Footnote 3 we argue that there is a weak evidence in favor of all dynamical models when compared with \(M_{1}\) (\(\varLambda \)CDM). Note that we consider two different prior ranges to check the possible dependency of the evidence on the prior (see Table 3). In fact, the evidence of each model is different considering different priorsFootnote 4 but \(\varDelta {\ln \mathscr {E}}\) (in our case) does not change significantly. In Table 5 the results are presented for both narrow (\(\varDelta {\ln \mathscr {E}}_{N}\) ) and broad (\(\varDelta {\ln \mathscr {E}}_B\)) priors.

Of course, such results disagree with Occam’s razor, which simply penalizes models with a large number of free parameters. Models \(M_5, M_4\) and \(M_3\) have eight, six and four free parameters more than the \(\varLambda \hbox {CDM}\), but the Bayesian evidence does not show any significant difference between them. Similar conclusions can be found in the work of [85] in which one proved that a linear model \(M_{a}\) with 14 free parameters provides the same value of Bayesian evidence as another model, \(M_{b}\), which contains four free parameters. According to these authors, the latter can be explained if the extra 10 parameters of \(M_{b}\) do not really improve the statistical performance of the model in fitting the data. In our case we confirm the results of [85] for Padé cosmologies; namely, the extra parameters of the \(M_3\), \(M_4\) and \(M_5\) parametrizations do not improve the corresponding DE models.

Moreover, the Bayesian complexity is a diagnostic tool to break the degeneracy when two competing models have almost the same evidence. Since, from the evidence alone, it is not clear that the extra parameters are unmeasured or improve the quality of the fit just enough to offset the Occam’s razor penalty term, the Bayesian complexity can be used to break this degeneracy (for more information see [61]). Our results indicate a slightly larger Bayesian complexity when the two competing models are \(M_1\) and \(M_2\), which is consistent with our conclusion that current data slightly prefer a dynamical dark energy model. The Bayesian complexities for other models are more and less the same, which indicates that current data are not good enough to measure the additional parameters and extra parameters are not needed.

Combining the aforementioned results we argue that, although the \(\varLambda \hbox {CDM}\) model reproduces very well the cosmological data, the possibility of a dynamical DE in the form of the \(M_{2}\) Padé model cannot be excluded by the data.

5 Conclusion

In this article we attempt to check whether a dynamical dark energy is allowed by the current cosmological data. The evolution of dark energy is treated within the context of a Padé parameterization, which can be seen as an expansion around the usual \(\varLambda \hbox {CDM}\) cosmology. Unlike most DE parameterizations (CPL and the like), in the case of the Padé parametrization the equation of state parameter does not diverge in the far future (\(a\gg 1\)) and thus its evolution is smooth in the range of \(a\in (0,+\infty )\).

Using the latest cosmological data we place observational constraints on the viable Padé dark energy models, by implementing a joint statistical analysis involving the latest observational data, SNIa (JLA), BAOs, direct measurements of H(z), and CMB shift parameters from Planck and growth rate data. In particular, we consider four Padé parametrizations, each with several independent parameters and we find that practically the examined Padé models are in very good agreement with observations. In all of them the main cosmological parameters, namely \((\varOmega _{m0},h,\sigma _{8})\), are practically the same. Regarding the free parameters of Padé parametrtization we show that, although the best-fit values indicate \(w<-1\) at the present time, we cannot exclude the possibility of \(w>-1\) at \(1\sigma \) level.

Finally, for all Padé models we quantify their deviation from \(\varLambda \hbox {CDM}\) cosmology through the AIC and Jeffreys scale. We find that the corresponding \(\chi ^{2}_\mathrm{min}\) values are very close to that of \(\varLambda \hbox {CDM}\), which implies that the chi-square estimator cannot distinguish Padé models from \(\varLambda \hbox {CDM}\). Among the family of current Padé parametrizations, the model which contains two dark energy parameters is the one for which a small but non-zero deviation from \(\varLambda \)CDM cosmology is slightly allowed by the AIC test. On the other hand, based on Jeffreys’ scale we show that a deviation from \(\varLambda \hbox {CDM}\) cosmology is also allowed, hence the possibility of a dynamical DE in the form of Padé parametrization cannot be excluded.

Furthermore, we estimate the so-called Bayesian complexity to realize whether the current data can constrain the extra parameters in our models or not. The Bayesian complexity is a measure of the effective number of parameters, which can be measured, given the data, and our results show a slightly larger Bayesian complexity for the \(M_2\) model, which is consistent with our conclusion as regards possible dynamical DE models. In contrast, the Bayesian complexity does not change significantly by adding extra parameters in our other models, which indicates that the current data is not good enough to measure the extra parameters.