Abstract
We carry out an analysis of \(\pi \pi \) scattering in the \(IJ=00\), 11 and 20 channels in configuration space up to a maximal center-of-mass energy \(\sqrt{s}=1.4\) GeV. We separate the interaction into two regions marked by an elementarity radius of the system; namely, a long distance region above which pions can be assumed to interact as elementary particles and a short distance region where many physical effects cannot be disentangled. The long distance interaction is described by chiral dynamics, where a two-pion-exchange potential is identified, computed and compared to lattice calculations. The short distance piece corresponds to a coarse grained description exemplified by a superposition of delta-shell potentials sampling the interaction with the minimal wavelength. We show how the so constructed non-perturbative scattering amplitude complies with the proper analytic structure, allowing for an explicit N/D type decomposition in terms of the corresponding Jost functions and fulfilling dispersion relations without subtractions. We also address renormalization issues in coordinate space and investigate the role of crossing when fitting the scattering amplitudes above and below threshold to Roy-equation results. At higher energies, we show how inelasticities can be described by one single complex and energy dependent parameter. A successful description of the data can be achieved with a minimal number of fitting parameters, suggesting that coarse graining is a viable approach to analyze hadronic processes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hadronic interactions at low and intermediate energies are typically characterized by a combination of elementary and composite particle features. While at long distances hadrons behave as elementary particles and their interactions can be described in terms of purely color singlet degrees of freedom, at short distances their composite character becomes manifest in terms of quark and gluon fields in the fundamental and adjoint representations of the color group, respectively. The relevant scale separating between this dual description marks the onset of a confinement scale and we expect it to be of the order of the hadron size, which generally is found to be about 1 fm. While the hadronic dynamics can be organized quite often as a long distance perturbative hierarchy with an increasing number of exchanged particles, it is by itself incomplete; some further either ab initio or phenomenological information reflecting the underlying quark-gluon structure is needed to provide a full description of the scattering process.
The way how this separation is visualized in the complex energy plane is not completely straightforward. Traditionally, and within a genuinely hadronic picture, one appeals to Mandelstam analyticity [1], i.e. the assumption that a scattering amplitude can be expressed by double dispersive integrals in terms of double-spectral density functions, where the integration ranges extend over those regions in the Mandelstam plane where the corresponding double-spectral functions have non-vanishing support [2]. This viewpoint is ultimately grounded in the Mandelstam conjecture, which holds in lowest order in the coupling constant in quantum field theory [1, 3] or to all orders within a non-relativistic context in potential scattering [4], and, which, in the \(\pi \pi \) scattering case, has been rigorously proved in a finite domain [5, 6]. It is noteworthy that under this same assumption an equivalent local and energy dependent optical potential of non-relativistic form was derived many years ago by Cornwall and Ruderman [7, 8]. For a balanced review on these issues at the textbook level see, for e.g., [9, 10]. The existence of a finite analyticity domain suggests in turn the very existence of a finite cut-off on a purely hadronic basis but without an explicit reference to the underlying quark-gluon dynamics and in particular to the confinement scale, so that the cut-off may be determined phenomenologically from data.
Pion-pion scattering is the simplest reaction in QCD mediated by strong interactions involving the lightest hadrons. Tight theoretical constraints based on analyticity, crossing, unitarity, chiral symmetry and Regge behavior can be imposed (see for e.g. [11] for an early review). The machinery of effective field theories (EFT) [12] and in particular its implementation in Chiral Perturbation Theory (\(\chi \)PT) [13] has enabled as a consequence, the most precise theoretical extraction of the \(\pi \pi \) S-wave scattering lengths to date with about an order of magnitude more precision than the experiment [14,15,16,17,18,19,20,21,22], an unprecedented case in strong interactions, where invariably just the opposite situation happens. A historic overview is given in [23]. Along these lines, the most precise \(\pi \pi \)-scattering analyses to date have been obtained in [16, 18, 22]. The latter corresponds to a \(\pi \pi \) description up to \(\sqrt{s}=1.42\) GeV, obtained by fitting the available experimental data from \(\pi N \rightarrow \pi \pi N\) and \(K_{e4}\) decays while imposing as further constraints Roy and Roy-like equations, and with statistical uncertainties satisfying the necessary normality requirements of the residual distributions [24], (see for e.g. [25, 26] for reviews). We stress that despite all these tight mathematical constraints, most of its non-perturbative setup rests upon the validity of the Mandelstam conjecture [1, 3], a result which, as already mentioned, has not yet been rigorously proven since it was first proposed in 1958. This tacit assumption will also be made throughout our work.
In the present paper we invoke the equivalent local and energy dependent optical potential approach suggested long ago in [7, 8] to describe \(\pi \pi \) scattering in coordinate space. In order to do so, we consider a relativistic Schrödinger equation and define a potential to describe the \(\pi \pi \) interaction by matching the field theoretical result to an equivalent quantum mechanical problem in perturbation theory. Phenomenological precursors of \(\pi \pi \) scattering analyses in coordinate space were prompted in [27, 28] within the boundary condition model of strong interactions [29]. Equivalent coordinate space potentials using the Mandelstam representation or the Bethe–Salpeter equation as a starting point were also proposed to all orders in [30,31,32]. As it will become clear below, it is remarkable if not surprising that so little work on \(\pi \pi \) scattering has been conducted within this approach as compared to more popular momentum space methods. Our work fills this gap by implementing Wilsonian ideas inspired by recent developments in the NN case [33,34,35]. These NN investigations had as a consequence a selection of the largest np and pp database up to energies about pion production threshold of \(3 \sigma \) mutually consistent data. Our present investigation within \(\pi \pi \) is in a sense of exploratory character and it pretends also to provide some training playground with an eye put on the more compelling \(\pi N\) case, where the selection of the currently existing database is largely needed (see for e.g. [36,37,38] and references therein).
At short distances, where the interaction is non perturbative, we will assume a complete ignorance of the strong interaction behavior and consider a coarse graining of the interaction instead, very much in the spirit of the work done in [33,34,35] for the NN case. The basic idea is to separate the \(\pi \pi \) interaction into an inner and outer region at a given separation distance, \(r_c\), located at about some elementarity radius. This radius is defined so that at larger distances pions behave effectively as point-like particles. We will assume that in this long distance regime their interactions are ruled by chiral symmetry, and hence they become calculable within \(\chi \)PT. Thus, for \(r>r_c\), we will construct a chiral potential with the correct low-energy analytic properties by matching both quantum mechanical and field theoretical scattering amplitudes in perturbation theory.Footnote 1 On the contrary, the inner region, \(r<r_c\), is regarded as unknown and sampled with the minimal de Broglie wave length determined by the maximum energy we want to describe. This corresponds to a coarse graining of the short range piece and, in its simplest realization, the inner potential will be written as a superposition of equidistant delta-shell interactions. A key issue is to confidently determine the numerical value of the separation scale \(r_c\), since, as noted in [41, 42] and we will see below, the combination \(p r_c \), with p the CM momentum, will fix the total number of independent fitting parameters. The longest range interaction corresponds to a \(2\pi \)-exchange which is \({\mathscr {O}} ( e^{-2 m_\pi r}) \), so that a naive estimate suggests \(r_c \sim 2/(2\,m_\pi )\sim 1.4 \) fm,Footnote 2 a number which will be corroborated by our numerical analysis.
While the potential approach has been explained in great detail in previous works within the NN context (see for instance [42]), it is unconventional within the \(\pi \pi \) scattering folklore. Thus, we will assume no previous knowledge from the side of the reader and for the sake of completeness we will briefly go through all the important issues along the paper. Moreover, \(\pi \pi \) scattering is characterized because at resonance energies relativistic effects cannot be ignored. For instance, for the prominent case of the \(\rho \)-meson \(\sqrt{s}=m_\rho \gg 2 m_\pi \). Unlike the NN case, a new important aspect in the discussion is related to crossing symmetry, which actually intertwines the s, t and u channels.Footnote 3 In addition, the current extraordinary precision achieved theoretically in extracting the S-waves scattering lengths or the lightest \(\pi \pi \) resonance pole parameters [43,44,45,46] provides a great confidence on the theoretical ideas supporting these benchmarking extractions. The fact that the coarse graining approach works for NN scattering in a regime where relativistic and inelastic effects become important, such as pp scattering up to \( \sqrt{s}~\sim 2\) GeV [42], suggests extending the method to other hadronic reactions under similar operating conditions.Footnote 4
Finally, for the sake of completeness let us mention that lattice calculations are naturally formulated in coordinate space. These calculations attack the problem on the finite lattice spacing and the finite volume in two different fashions: either an (energy dependent) potential is determined and the Schrödinger equation is solved subsequently in the continuum or, alternatively, the energy level shifts are determined on the lattice and converted into phase-shifts by means of Lüscher’s formula [47]. Actually, in a pioneering work [48], the \(I=2\) \(\pi \pi \) S-wave scattering phase shifts from Lattice QCD have been determined. Later on, \(\pi \pi \) scattering has been studied from \(N_{\mathrm {f}} = 2+1\) and \(N_{\mathrm {f}} = 2+1+1\) flavors in [49] and [50], respectively. Connected and Disconnected Contractions have also been analyzed in [51]. In addition, the \(\pi \pi I=2\) channel has also been studied within the potential approach [52]. A comparison between potential and Lüscher’s approaches has been undertaken in [53] for the \(I=2\) case, with rather similar results. We remind that both methods have potential drawbacks. On the one hand, the potential method uses interpolating fields which may distort the physics at short distances, and we will explicitly show that in a chiral expansion such potential presents a short distance singularity, which evades the conventional solutions of the Schrödinger equation. On the other hand, the current applicability of this Lüscher’s method [47] requires the interaction to sharply vanish at the edges of the volume (in the relative coordinate), a fact that has been often ignored in momentum space treatments (see for e.g. [54, 55]) but needs to be established for the \(\pi \pi \) case. Our analysis below supports this assumption.
The paper is organized as follows. In Sect. 2, we provide a general and brief field theoretical overview of \(\pi \pi \) scattering to fix our notation in a way that our problem can be easily formulated. In Sect. 3, we show our choice for a quantum mechanical description in terms of a complex local and energy dependent optical potential. We analyze the long-range contributions within \(\chi \)PT in Sect. 4, where an expression for the potential is obtained from the discontinuities of the \(\pi \pi \) scattering amplitude in the t-channel. This requires introducing a short distance cut-off to handle the strong short distance power divergences of the chiral potential, an issue which we discuss at length in Sect. 5. In Sect. 6, we analyze the concept of effective elementarity in order to display in two examples how the elementarity radius depends on the particular process. In Sect. 7, we address the problem of coarse graining \(\pi \pi \) interactions with and without the long-range contributions. The analytical properties of the scattering amplitude and the relation of our approach with the N/D method is discussed in Sect. 8. The implementation of inelasticities within a coarse grained perspective is explained in Sect. 9. We also analyze some aspects concerning low energy constants and the number of parameters in Sect. 10. Finally, in Sect. 11 we summarize our main results and provide some outlook for future work.
2 Formalism for \(\pi \pi \) scattering
We start by summarizing the relevant formulae for \(\pi \pi \) scattering to fix our notation and to provide a proper perspective of our subsequent analysis. A comprehensive presentation at the textbook level can be seen in [11] and also in the lecture [56]. More recent upgrades can be consulted in [25, 26]
2.1 Kinematics
For a pion state \(\varphi _\alpha \) with \(\alpha =\{\pm ,0\}\), the \(\pi _ \alpha (p_1)+ \pi _\beta (p_2) \rightarrow \pi _ \gamma (p_1')+ \pi _ \delta (p_2') \) relativistically invariant scattering amplitude can be written as
with \(s=(p_1+p_2)^2\), \(t=(p_1-p_1')^2\) and \(u=(p_1-p_2')^2\) the standard choice of Mandelstam variables. If we take \(\varphi _{\pm } = ( \phi _1 \pm i \phi _2) /\sqrt{2} \) and \(\varphi _{0}= \phi _3\), with \(\phi _a \cdot \phi _b = \delta _{ab}\), in the Cartesian basis we obtain
where A(s, t, u) stands for the \(\pi ^+\pi ^-\rightarrow \pi ^0 \pi ^0\) amplitude. This amplitude is the only independent one thanks to isospin, crossing and Bose-Einstein symmetries, \(B(s,t,u)=A(t,s,u)\) and \(C(s,t,u)=A(u,t,s)\). Denoting \(T_{I}(s,t,u)\) as the isospin combination with well defined isospin I in the s-channel, one has
For the normalization, we will use here the conventions in [57,58,59]. The partial-wave decomposition in the s-channel becomes
where \(z = 1 + 2 t/(4m_\pi ^2 -s)\) is the s-channel scattering angle, \(m_\pi =139.57\) MeV the pion mass, \(P_J( \cos \theta )\) the Legendre polynomials and \(t_{IJ}(s)\) is the partial-wave projection of the \(\pi \pi \) scattering amplitude with isospin I and total angular momentum J. Thus, for waves fulfilling the relation \((-1)^{J+I}=1\) one has
with
the \(\pi \pi \) phase factor and \(\delta _{IJ}\) the scattering phase shift. The in-elasticity \(\eta _{IJ} (s)= 1 \) for \(s< 16 m_\pi ^2\) and the unitarity condition for the partial wave amplitude reads in the elastic region
Of course, for \(s> 16 m_\pi ^2\) one has absorption \(\eta _{IJ} (s) < 1 \) and inelastic processes such as \(2\pi \rightarrow n \pi \) take place at \(\sqrt{s}=0.56,\,0.84,\,1.12\) and 1.40 GeV for \(n=4,6,8\) and 10, respectively, as well as \(K \bar{K}\) and \(\eta \eta \) at \(\sqrt{s} \sim 1\,\mathrm{GeV}\), etc.
In our discussion we will also use the quantum mechanical amplitude \(f_{IJ}(p)\) defined by
with p the CM momentum. For elastic scattering one has \(f_{IJ}(s)^{-1}= p \cot \delta _{IJ} - i p\), so that at low energies one has the threshold expansion
with \(a_{IJ}\) and \(b_{IJ} \) the lowest threshold parameters. An equivalent way of representing the low energy behavior is
or by an effective range expansion
where \(\alpha _{IJ}=-a_{IJ}\) and \(r_{IJ}/2=-b_{IJ}/a_{IJ}^2 \) is the effective range, which is generally positive (see below). Usually, the expansion (9) works for small scattering lengths, such as \(\pi \pi \) whereas (10) works for large scattering lengths, such as NN (see, e.g., [60, 61] for a discussion).
2.2 Anatomy of the \(\pi \pi \) interaction
The purpose of the present paper is to coarse grain the unknown pieces of the \(\pi \pi \) interaction in configuration space. It is thus important to gather some features emerging from comprehensive studies over the last decades [14,15,16,17, 19,20,21,22]. According to these findings the partial wave expansion in (3) is decomposed into two contributions: the low energy contribution described by means of a partial wave (PW) expansion to finite order and the high energy contribution assumed to be given by the leading Regge trajectories,
which accounts for the long and short distance behavior of the scattering amplitude respectively.
A standard quantum mechanical argument based on the impact parameter provides in the semi-classical limit and for an interaction of finite range \(r_c\), the number of necessary partial waves.Footnote 5 The impact parameter is defined as \(b = L/p\) with p the CM momentum and L the orbital angular momentum, which in our case equals the total angular momentum J. The quantization condition for the angular moment yields \(L \approx \sqrt{J(J+1)} \sim (J+1/2)\) for \(J \gg 1\). For a finite range, the maximal impact parameter where scattering happens is \(b_\mathrm{max} \sim r_c\). Thus, for a maximum CM momentum \(p_\mathrm{max}\), the maximum angular momentum \(J_\mathrm{max}\) for which the phase shift is compatible with zero within uncertainties is
For a maximum energy \(s_\mathrm{max}=2\) GeV\(^2\), corresponding to \(p_\mathrm{max} \sim 0.7 \) GeV, it was found in [22] that waves beyond \(J_\mathrm{max}=4\) are vanishingly small for \(\pi \pi \) scattering. Therefore, one obtains from (12) a range \(r_c \sim 1.3\) fm. This simple estimate will be explicitly exploited below as an educated guess.
Low energies close to threshold are encoded by the threshold parameters, see (8) and (10). The S-wave scattering lengths are \(\alpha _{00}=-0.3\) fm and \(\alpha _{20}=0.03\) fm whereas for the P-wave we have \(\alpha _{11}= -(0.48\,\mathrm{fm})^3\) [22]. These are unnaturally small numbers compared with our above estimate of the range of the interaction, \(r_c \sim 1.3\,\mathrm{fm}\) and the elementarity radius, \(r_e \sim 1.2\,\mathrm{fm}\) (see the discussion in Sect. 6). While the behavior of the isotensor S-wave resembles a repulsive core, with positive effective range \(r_{20}=131.4\,\mathrm{fm}\), the effective range in the isoscalar S-wave and isovector P-wave are negative, \(r_{00}=-8.08\,\mathrm{fm}\) and \(r_{11}=-5.25\,\mathrm{fm}\), respectively. For S waves the Wigner causality bound [64] (see also [65]) restricts the maximum value of the effective range by the inequality
which for \(I=2\) implies \(r_c \ge 0.95\,\mathrm{fm}\). The positivity of the effective range is not implied by this condition, and is usually violated in the presence of resonances. This requires some unconventional shape for the S-wave potential as we will see.
2.3 Chiral Perturbation theory
The scattering amplitude can be computed perturbatively in Quantum Field Theory and in particular in \(\chi \)PT as a sum of Feynman diagrams in an expansion in 1 / f, with \(f \sim 86\,\mathrm{MeV}\) the pion weak decay constant in the chiral limit. In the partial waves basis the expansion can schematically be written as
where \(t_{IJ}^{(-2n)}={\mathscr {O}} (f^{-2n})\). To one loop order, they were first computed in [12, 13] and the relevant non-polynomial contributions are reproduced for completeness in appendix 1. Explicit analytical expressions for the corresponding partial wave amplitudes are displayed in [40]. They obey the perturbative unitarity relation
At lowest order (LO) in the chiral expansion the threshold parameters are unnaturally small, a fact naturally accommodated by \(\chi \)PT with pions coupled derivatively.
2.4 Unitarization vs Crossing
The requirement of crossing is a fundamental one which stems from the local character of Quantum Field Theories. Chiral Perturbation Theory implements this symmetry at any order in the chiral expansion. The problems with perturbation theory, however, are on the one hand the lack of exact unitarity given by (6) and on the other hand the impossibility of describing outstanding non-perturbative features such as the generation of resonances, which emerge as poles of the scattering amplitude on unphysical Riemann sheets. Within a \(\chi \)PT framework, many methods have been proposed (see for instance [40, 66, 67] and references therein) based on imposing exact unitarity while matching perturbation theory at low energies. Most of them are nothing but algebraic tricks or functional solutions to a set of a priori conditions. As such, unitarization methods are not unique but strongly driven by experimental information, which explains partly their success. The Bethe–Salpeter method discussed at length in [40] preserves an identification of Feynman diagrams but it is not free from field reparameterizations or off-shell ambiguities. In addition, they violate crossing symmetry, which, in general, is only fulfilled order by order, although these violations can be statistically not-significant [68].
In Sects. 4 and 7, we will propose yet a new method based on first defining an equivalent quantum mechanical problem and, more importantly, on coarse graining the interaction. Of course, above the inelastic threshold \(s \ge 16 m_\pi ^2\) one may wonder what condition should be imposed instead of just (6).Footnote 6 We will extend the coarse graining idea to the case with inelasticities.
3 Quantum mechanics Formalism
3.1 Relativistic equation
At the maximum CM energy we will be considering in this work \(s_\mathrm{max}=2\;\mathrm{GeV}^2\), relativity and inelasticities are crucial physical ingredients since firstly \(\sqrt{s_\mathrm{max}} \gg m_\pi \) and secondly we can produce up to \(n=(\sqrt{s_\mathrm{max}}-2 m_\pi )/m_\pi \sim 8\) pions as well as one \(K \bar{K} \) and \(\eta \eta \) pair in the final state. From a field theoretical point of view, this could be solved by using a multichannel Bethe–Salpeter equation for the several \(2\pi \), \(4\pi \), \(6\pi \), \(8 \pi \), \(K \bar{K}\) and \(\eta \eta \) coupled channels, but it would be an extremely difficult task, which has never been accomplished to our knowledge. Even in the simplest elastic case the off-shell ambiguities are present for calculations with a truncated kernel [39, 40]. In order to grasp the nature of the ambiguities, consider for instance the case of \(\pi ^0(p_1) \pi ^0(p_2) \rightarrow \pi ^0(k_1)\pi ^0(k_2)\) scattering, in the elastic regime. The Bethe–Salpeter (BS) equation reads,
where \(p=\frac{p_1-p_2}{2}\), \( k=\frac{k_1-k_2}{2}\), \(P=p_1+p_2\) and \( q_\pm = P/2 \pm q\). \(\Delta (q_\pm ) = 1/(q_\pm ^2-m_\pi ^2+i0^+)\) is the free pion propagator and \(V_P (p,k)\) and \(T_P (p,k)\) stand for the two-particle irreducible kernel or potential and the scattering amplitude, respectively. The factor 1 / 2 comes from the scattering of identical particles.
While the BS equation has been the subject of extensive research for a given potential, the main point of [39, 40] was the flexible interpretation of the BS equation within \(\chi \)PT or more generally within EFT. Indeed, while the potential \(V_P (p,k)\) can be organized as a power series \(V_P (p,k)=V_P^{(2)} (p,k)+V_P^{(4)}(p,k)+ \cdots \) with reference to the same expansion of the scattering amplitude \(T_P (p,k)=T_P^{(2)} (p,k)+T_P^{(4)} (p,k)+\cdots \), it can be done only in a on-shell mass scheme, i.e. for
Thus, there is an inherent ambiguity in the definition and form of the potential, which has no consequences perturbatively but becomes relevant in the solution of (16) where the off-shellness enters explicitly. This was mended in [39, 40] by invoking an on-shell scheme, namely considering only on shell intermediate states, i.e. \(q^2 = s/4-m_\pi ^2\) and \( P \cdot q=0 \), so that the on-shell amplitude T(s, t) depends only on the on-shell potential V(s, t). Unfortunately, it also gives rise to pathologies in the coupled channel case producing spurious singularities due to an improper treatment of the crossed-channel exchanges [69]. The present paper pretends to address crossed-channel exchanges without invoking the on-shell scheme.
3.2 Invariant mass and equivalent Schrödinger equation
We will follow here the invariant mass formulation [70],Footnote 7 already used for NN scattering with an optical potential [42, 71]. This is the simplest way of retaining relativity without solving a BS equation but with a phenomenological optical potential that we review here for completeness. The idea is to write the total squared mass operator as
where W represents the (invariant) interaction, which can be determined in the CM frame by matching in the non-relativistic limit to a non-relativistic potential \(V(\vec x)\). This yields for \(\pi \pi \) scattering after quantization \({\mathscr {\hat{M}}}^2 = 4(\hat{p}^2+m_\pi ^2) + 4 m_\pi V \), with \(\hat{p} = - i \nabla \). Thus, the relativistic equation can be written as \({\mathscr {\hat{M}}}^2 \Psi = 4 (p^2+m_\pi ^2) \Psi \), with p the CM momentum, i.e. as a non-relativistic Schrödinger equation
This corresponds to the simple rule that one may effectively implement relativity by just promoting the non-relativistic CM momentum to the relativistic CM momentum. This minimal relativity ansatz is as good as the more fundamental one based on the Bethe–Salpeter equation as long as we use scattering data to determine the corresponding potential rather than an ab initio determination (see Ref. [40] for an in-depth discussion).
To take into account the inelasticity within the mass-squared construction, we assume a local and energy-dependent phenomenological potential, \(V(\vec r,s)= {\mathrm{Re}}\, V(\vec r,s) + i\,{\mathrm{Im}}\,V(\vec r,s)\), which could be obtained by fitting inelastic scattering data. Due to causality, the optical potential in the s-channel satisfies a dispersion relation for each CM radial distance r of the form [7]

where \(\sqrt{s_0}= 4 m_\pi \) is the first \(4\pi \) inelastic threshold and V(r) is an energy independent component. The complete potential includes also the crossed u channel component.Footnote 8 The simple looking Eq. (19), together with the fixed-r dispersion relation (20), incorporates the necessary physical ingredients present in any theoretical approach: relativity and inelasticity consistent with analyticity.
3.3 Isospin and exchange potential
The incorporation of isospin into the game is straightforward. Rotational, isospin and particle exchange invariance requires the representation of the potential to be given by
where \(V_\mathrm{D}\) and \(V_\mathrm{X}\) stand for the direct and exchange potential pieces, respectively. \({\mathscr {P}}_{12}\) is the particle exchange operator, which implements the Bose-Einstein symmetry and that can be factorized as \({\mathscr {P}}_{12} = {\mathscr {P}}_{x}{\mathscr {P}}_{I}\). Moreover, for states with a well defined total isospin \(\vec I = \vec I_1+ \vec I_2\), we can use the relation \(\vec I_1 \cdot \vec I_2 = I(I+1)/2-2\) with \(I=0,1,2\), so that \( {\mathscr {P}}_{I} = (-1)^I\). In addition, for angular momentum eigenstates \({\mathscr {P}}_{x} = (-1)^J \), so that \({\mathscr {P}}_{12} = (-1)^{I+J}\). Therefore, in the isospin basis the potential can be decomposed as
where we have introduced the projection operators
fulfilling the orthogonality relations \(P_I P_{I'} = \delta _{II'}P_I\).
In the partial wave representation, the exchange symmetry of the potential is preserved by just solving the Schrödinger equation for the direct potential for the allowed IJ channels with \((-1)^{J+I}=1\). In addition, for a spherically symmetric potential we have the usual factorization of the wave function [72]
where \(Y_{l m_l} (\hat{x})\) are the spherical harmonics and \(u_l(r)\) is the reduced wave function, fulfilling the radial Schrödinger equation
where \(U_I (r)=U_I (\vec r)\) is the central potential with isospin I. This equation is indeed regular at the origin Footnote 9
and it satisfies the asymptotic scattering condition at infinity
Thus, the partial wave expansion for the quantum mechanical scattering amplitude with isospin I in the CM system is defined by:
3.4 Inverse scattering problem
Although we will be determining the potentials from fits to phase shifts, it is worth reminding that the inverse scattering problem allows one to determine a local and continuous potential directly from scattering data by solving for each partial wave either the Gelfand-Levitan or Marchenko equations (see for e.g. [73] for a review). It can be shown that for holomorphic S-matrix functions both methods yield the same local potential. While usually the discussion is conducted within a non-relativistic setup, according to our discussion above, the analysis can directly be overtaken and interpreted at the relativistic level.
This inverse scattering approach was adopted in [74], where a holomorphic S-matrix was used to parameterize the scattering data. In that work it was found that the S and P-wave potentials have a range around 0.25 fm with strengths between \(100-200\) GeV. Quite remarkably they also found a barrier in the isoscalar S-wave and a repulsive core in the isotensor S-wave. While this is a very insightful and mathematically rigorous approach, this method requires exact knowledge of the phase shifts at all energies. In practice, a meromorphic function is fitted up to a maximum energy corresponding to a maximum momentum \(p_\mathrm{max}\). As we will see below, this puts in practice a limitation to the resolution \(\Delta r \sim 1/p_\mathrm{max}\) with which the potential V(r) may be determined, so that a suitable coarse graining makes sense.
4 The Chiral \(\pi \pi \) local potential
In this section we outline the perturbative matching procedure between quantum mechanic (QM) and quantum field theory (QFT) calculations in order to determine the local and energy dependent chiral potential. The connection between the QFT and QM scattering amplitudes is given by
The potential appearing in this equation will be determined in perturbation theory. For the quantum mechanical problem we have the Born series
where \(r_{12}=\vert \vec r_1-\vec r_2\vert \), \(\vec p\) and \(\vec p'\) are the initial and final CM momenta, respectively, and \(\vec q=\vec p'-\vec p=2 \vec p\sin {(\theta /2)}\) is the momentum transfer. The potential U(r, s) is directly defined from the two-particle irreducible states included in the scattering amplitude. We will define the potential through the t-channel exchanges of the amplitude, so that crossing symmetry will be incorporated exactly when symmetrizing the partial wave expansion.Footnote 10 Moreover, in a coordinate space description, contact terms are irrelevant as long as the field theoretical potential is not extended to the origin \(r=0\) since
with \(\hat{P}(q^2)\) a generic polynomial in \(q^2\). Thus, any polynomial part of the scattering amplitude gives a vanishing contribution to the long-range piece of the potential. Therefore, we will analyze only the effect of pion loop contributions on the t-channel.
4.1 Leading order
We will first discuss the lowest non-trivial order since it provides just contact terms. In the Born approximation, i.e. taking the first term in (30), the scattering amplitude just becomes the Fourier transform of the potential [72]
This equation can be inverted to give
so in the Born approximation, the scattering amplitudes can be related to the potential by:
where \(T_I(s,t)\big \vert _{B}\) denotes the part of the amplitude containing contact terms and t-channel exchange. In the same way, the potential (defined in spatial coordinates) is defined from this part of the amplitude by:
Using the \(\chi \)PT lowest order amplitudes [13] we get
These algebraic manipulations are purely formal, and in fact is unspecified what is the meaning of solving the wave equation with these highly singular potentials. Already at this level, we can see the need of introducing a regularization.Footnote 11
4.2 Next-to-leading order
The NLO contribution becomes more cumbersome. Firstly, we take the potential to be expanded as
so we get the matching condition
Due to the Dirac delta functions in the LO potential (36), we have a divergence for the real part of \( e^{i p r_{12}}/r_{12} \), albeit it can be absorbed in the real part of the NLO potential \(U^{(4)}(r,s)\). Besides, the non-polynomial pieces in \(T^{(4)}\) amplitude corresponding to the t-channel exchange can generally be written as
where P(s, t) is a polynomial in both t and s, whose analytical expression can be read from (A3), and J(t) denotes the one-loop \(2\pi \) function. In order to integrate this amplitude, we will take advantage of the analytic structure of the loop function J(t), which is analytic in the whole complex plane but for a cut above \(4m_\pi ^2\) with a discontinuity, \(\mathrm{disc}\, J(t)=2\,i\,\mathrm{Im}\, J(t)=2\pi \,i\sigma (t)/16\pi \), with \(\sigma (t)\) the phase-space factor defined in (5). Thus, up to subtractions one finds the dispersion relation
where C.T. is a subtraction constant that can be fixed by setting the value of \(J(4m_\pi ^2) = 1/8\pi ^2 \). Likewise we have
where \(\overline{C.T.}\) is a new subtraction constant ensuring the convergence of the dispersion relation. Thus, taking into account the Yukawa integral
and the inversion of (38), the NLO potential becomes
where \(t=\mu ^2\) and the spectral function \(\rho _I(\mu ,s)\) is defined as
with \(P_I(s,\mu ^2)\) polynomials in s and \(\mu ^2\) of second degree (see Appendix 1) and C.T. map into contact terms, which are distributions at the origin and hence vanish elsewhere. All necessary integrals can be obtained from the general integral valid for \(r>0\),
with \(K_n(x)\) the modified Bessel function of order n and \(\Gamma (z)\) the Euler’s Gamma. Polynomials in \(\mu \) can be generated from derivation with respect to r. The chiral potentials obtained directly from the spectral representation (43), read then
From a more general point of view, these potentials play for the \(\pi \pi \)-system the role of relativistic van der Waals interactions (see [75] for a review in the atomic case) and hence display their characteristic features: they are attractive and diverge at short distances as \(\sim 1/( r^7 f^4 \sqrt{s}) \), i.e.
and have the expected exponentially suppressed long distance behavior \(\sim e^{-2 m_\pi r}\), namely
In Fig. 1 we show the threshold combination \(V_{I}(r, 4 m_\pi ^2) \equiv m_\pi U_{I}(r, 4 m_\pi ^2)\) and, as we can see, they are attractive at all distances. The energy dependence generates a repulsive effect for increasing values of s, i.e.
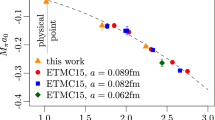
On the lattice, the energy dependence of the potential is generated from the Nambu-Bethe wave function [53]. As already stated in the introduction, the \(\pi \pi \) potential in the \(I=2\) channel has been computed on the lattice by the HAL QCD collaboration [53, 76] for \(a \approx 0.12\) fm on a \(163 \times 32 \) lattice and with a pion mass \(m_\pi \approx 870\) MeV. For these pion masses the value the chiral potentials in (46) become smaller than for the physical case depicted in Fig. 1. In addition, the HAL QCD lattice potential presents a repulsive core below 0.5 fm. This is a feature one can not obtain using the chiral potentials in (46) which display strong short distance singularities. This fact already suggests that they can not be used at arbitrary short distances. At this point it is worth stressing that both the lattice as well as the present approach based on chiral perturbation theory assume point-like sources, a unrealistic feature. In the next sections we analyze this topic in more detail.
5 Renormalization
The renormalization of non-perturbative amplitudes is a tricky matter, particularly with the highly power-divergent kernels deduced from \(\chi \)PT (see for e.g. [39, 40] for a discussion within the Bethe–Salpeter framework in momentum space). The chiral potential deduced in coordinate space by a perturbative matching procedure presents an energy dependence. In this section we show how the scattering amplitude stemming from the iteration of the two-pion exchange (TPE) chiral potentials in (46) can be renormalized from a coordinate space point of view if the energy dependence is ignored by taking, say, the threshold value \(\sqrt{s}=2 m_\pi \). Hence, we will implement as renormalization conditions the scattering amplitude at threshold. We will see that, while this is a mathematically viable approach, it fails phenomenologically. Furthermore, the consideration of energy dependence will prevent a sensible non-perturbative renormalization procedure. For large values of the coordinate space cut-off \(r_c \gtrsim 1.2\, \mathrm{fm}\), the results will not be affected by taking either \(U_I(s,r)\) or \(U_I(4 m_\pi ^2,r)\).
5.1 Discussion
One of the advantages of the energy dependent coordinate space representation of the potential is that off-shell and field reparameterization ambiguities manifest as contact interactions at the origin. Thus, they reflect the cut-structure of the amplitude, which is hence unambiguously defined. This is unlike their momentum space counterpart, where both polynomial and cut contributions are treated on equal footing [40].
On the other hand, a difficulty with the chiral \(\pi \pi \) potentials in the previous section is that they become singular at short distances. Hence, the solution of the Schrödinger equation is not well defined in a conventional sense, since the short distance behavior is not dominated by the centrifugal barrier and the regular solution given in (26) is not suitable. An early review on the subject can be found in [77]. Singular potentials are commonplace within EFT and finite solutions exist in a renormalization sense within well specified conditions, as discussed at length in the NN scattering case [78,79,80]. Applications for \(\alpha \alpha \)-scattering [81, 82] and atom-atom scattering [83, 84] are well documented by now (see e.g. [85] for a sucint and pedagogical presentation). While these renormalized solutions represent theoretically a viable solution to the problem, we will consider here a more phenomenological interpretation by introducing a short distance cut-off \(r_c\), whose value reflects short distance effects not taken into account in the derivation of the chiral \(\pi \pi \) potential.Footnote 12 This leaves undefined the short distance dynamics.
The energy dependence of the potential takes into account retardation effects. This can be seen as follows; if the potential is given as a function of the difference of two space-time causally related events \(K(x-x')\) then we have
explaining the \(1/\sqrt{s}\) factor in (46). In the case of “heavy pions” or very low energies \( p \ll m_\pi \), we can take \(\sqrt{s} \sim 2 m_\pi \) and work within a non-relativistic approximation. A compelling consequence of causality is the verification of dispersion relations in the complex energy plane. We will dedicate Sect. 8 to prove that the right analytical properties hold for the partial wave amplitudes.
The spectral representation (40) suggests the use of a spectral regularization consisting of introducing a cut-off \(\Lambda \) at a given value of \(\mu \), so that the potential at short distances becomes regular. We find that for \(\Lambda > 5 m_\pi \) the regularization quenches the potential for \(r < 1/m_\pi \). We explore this issue in more detail in Sect. 6.3.
5.2 The short distance cut-off and boundary condition regularization
Zero momentum integrated-in wave functions (solid) from large distances using the scattering length as input and the chiral \(2\pi \) exchange potentials \(V_{\pi \pi }\) at threshold \(\sqrt{s}= 2 m_\pi \) as a function of the distance for \(I=0\) (left), \(I=1\) (middle) and \(I=2\) (right). We also draw the asymptotic zero energy wave function (dashed) for comparison
One way to analyze the range of validity of the chiral potentials is to discuss the zero momentum scattering, \(p=0\). Thus, we solve the Schrödinger equation using the asymptotic solutions at zero momentum (we discard the isospin label here),
with \(\alpha _l \equiv - \lim _{p \rightarrow 0} \delta _l(p) /p^{2 l+1}\) and integrating inward. The result is illustrated in Fig. 2 where we see that the zero momentum wave function presents oscillations at short distances. This behavior can qualitatively be understood if we write the potential at short distances in the form
where \(R \propto 1/f \) is the van der Waals scale, which in our case and from (47) takes the values \(R = 0.94,\,0.68,\,0.79\) fm for \(I=0,1,2\), respectively. Actually, for \(r \ll R \) the centrifugal barrier, \(l(l+1)/r^2\) , can be neglected and a semi-classical approximation holds since \(\lambda '(r) \ll 1\), where \(\lambda (r)\) is the local wavelength, \(\lambda (r) \equiv 1/k(r)=1/\sqrt{-U(r)}\), with k(r) the local wavenumber. Thus, one finds \(\lambda '(r) = 7/2\,(r/R)^{5/2} \ll 1\) for (51). In this case, the WKB wave function reads [72]
where \(\varphi \) is an arbitrary phase, which is fixed by the long distance solution.
According to the oscillation theorem [72], the number of nodes of the wave function at zero momentum corresponds to the number of bound states. However, as we know, there are no bound states in the \(\pi \pi \) scattering case. Thus, if we want to avoid these spurious solutions, we cannot remove the cut-off completely, but it should be larger than the outmost right node of the wave functions depicted in Fig. 2, which are located at \(r\sim 0.5,\,0.4,\,0.4\) fm for \(I=0,1,2\), respectively. In practice, we will take a cut-off slightly above the van der Waals scale. Note that there is a priori no other reason to discard the chiral potential down to these scales. In fact, phase shifts in any partial wave \(\delta _l(p)\) are convergent when the short distance cut-off goes to zero, provided the scattering length \(\alpha _l \) is fixed. This corresponds to a renormalization program already developed in previous studies [78,79,80,81,82,83,84,85] that will not be pursued any further here. The upshot of these considerations in the \(\pi \pi \) case is that generally one needs a cut-off \(r_c > 0.5\) fm to prevent the appearance of unphysical bound states generated by the TPE potential. However, for these kind of short distance attractive singularity \(U(r) \propto -1/r^7\) finite \(r_c\) effects are minor in physical observables if the energy dependence of the potential is neglected. Take for instance the effective range defined in (10) and depicted in Fig. 3. As one can see, the chiral potential and the scattering length lead to a finite result at short distances, \(r < R\). Up to minor oscillations, it provides values which differ from the experimental ones. In Sect. 6, we will see that this turns out to be much smaller than the elementarity radius, \(r_e \sim 1.2\) fm. Moreover, there is no finite cut-off \(r_c\) which reproduces the experimental values \(r_{00}=-8.08\,\mathrm{fm}\) and \(r_{20}=131.4\,\mathrm{fm}\).
In the previous discussion the energy dependence of the potential was neglected. On the one hand, if we take the energy dependence into account, we see in Fig. 3 a quite different trend at short distances, namely the effective range is not convergent when the cut-off is removed, i.e. for \(r_c \rightarrow 0\). On the other hand, we also see that for \(r_c \gtrsim 1.2 \mathrm{fm}\) this energy dependence in the chiral potential becomes irrelevant.
Renormalized effective range for the integrated-in large-distance wave functions (solid), as a function of the distance for \(I=0\) (left) and \(I=2\) (right) It is obtained using the scattering length as input and the chiral \(2\pi \) exchange potentials \(V_{\pi \pi }\) at threshold \(\sqrt{s}= 2 m_\pi \). In addition, we also plot the energy dependence case (red-dashed), which leads to a divergent value at \(r \rightarrow 0\)
6 Effective elementarity
As we have seen, even at the perturbative level we must introduce a short distance cut-off, \(r_c\). In this section we elaborate on sensible choices of this cut-off on the light of the onset of effective elementarity and its corresponding radius \(r_e\). This is the scale above which particles interact as if they were pointlike. Thus, they can be taken as elementary, so that a hadronic field can be attached to the particle.
6.1 Hadron sizes and form factors
Hadrons have a finite size, which is usually characterized by their form factors and corresponding radii. Roughly speaking, we expect that for two hadrons of size \(r_1\) and \(r_2\) they will not overlap at relative separations above the mean average distance \((r_1+r_2)/2\), and their interaction will correspond to that of two elementary particles. However, hadronic sizes obtained from, say, electroweak form factors are specific on that particular process, as we will illustrate below. In fact, in order to describe \(\pi \pi \) interactions we are interested on the corresponding effective elementary size, \(r_e\), as seen by the interaction. Unfortunately, without a microscopic calculation, there is no way to know this size in the case of strong interactions. Nonetheless, for our discussion on the relevant scales it is important to estimate a priori the separation distance \(r_c\) between the inner and outer pieces of the potential, as this determination has an impact on the minimal number of fitting parameters. Quite generally, this separation distance should be larger than the elementarity radius, \(r_e \le r_c\), and the optimal choice would be to take both distances equal.
Since the pion size is around 1 fm, it is natural to expect that the inelastic non-perturbative description of the interaction will take place in the region below 2 fm.
In order to illustrate our point, let us consider the implications of elementarity for electric and gravitational interactions between pions. The electromagnetic pion form factor reads
whereas the gravitational form factors \(\Theta _1(q^2)\) and \(\Theta _2(q^2)\) are defined by
where \(q=p'-p\), \(P=p'+p\). In the Breit frame, where there is no energy transfer, form factors can be interpreted as the Fourier transform of a density [86]
so that the charge form factor determines the charge density. The gravitational form factor corresponds to the traceless spin 2 component. In the Breit frame the mass density of the pion is given by the 00 component of the energy momentum tensor in the pion state, since its integrated value yields the total mass of the state (see e.g. the discussion in Ref. [88] and the recent review [89]). We will work in the chiral limit so that the \(\Theta _2(q^2)\) contribution is neglected.
Quite generally, form factors are matrix elements of local operators between hadronic states. For the case of operators with well-defined \(J^{PC}\) quantum numbers, a generalized meson dominance is expected to work in harmony with the high energy behavior deduced from QCD counting rules (see for e.g. [87] for a thorough discussion and comparison with lattice QCD data). For example, in the electromagnetic case, it can be parameterized according to vector meson dominance as,
where we have kept only the \(\rho \) meson with \(m_\rho = 0.77\,\mathrm{GeV}\), as we are only interested in the long distance properties.
6.2 Point-like vs extended particles interactions
According to the previous discussion, the electrostatic potential can be written as
which is depicted in the left panel of Fig. 4 and reflects that for \(r>1.2\sim 1.5\) fm, pions start to interact as expected from point-like particles.Footnote 13 In the gravitational case, a good description is found with the tensor \(f_2(1270)\) meson [87] with the mass scale given by \(m_f = 1.2\,\mathrm{GeV}\), so that
In this case, right panel of Fig. 4, the interaction becomes elementary at \(r_e \sim 1\,\mathrm{fm}\), a shorter scale. The previous discussion illustrates our point, namely effective elementarity depends on the particular process.
Before proceeding further, it should be noted that within a more microscopic point of view, for instance a cluster quark model, these are not the only possible contributions to the interactions between pions (see e.g. [90,91,92]). Actually, in a Hartree-Fock approximation they would correspond to the direct interaction (Hartree) term. In addition, one also has the exchange (Fock) term where the quarks inside different pions are interchanged. These terms are genuinely non-local at short distances, so that they are exponentially suppressed at long distances. Therefore, they are expected to contribute below the elementarity radius, \(r_e\), and hence can be regarded as finite size effects.
Ratio of spectral regularized and unregularized TPE chiral potentials \(U_\Lambda ^I(r)/U^I(r) \) for spectral cut-offs of \(\Lambda =1.4\) GeV (solid, black), \(\Lambda =1.12\) GeV (dotted, red) \(\Lambda =0.84\) GeV (dashed, blue) at threshold \(\sqrt{s}= 2 m_\pi \) as a function of the distance for \(I=0\) (left), \(I=1\) (middle) and \(I=2\) (right) channels
6.3 Spectral regularization
While we might estimate the elementarity radius for the chiral potentials from the corresponding folding of “strong” densities, we prefer to analyze instead the effect of introducing a cut-off \(\Lambda \) in the spectral function in (43), i.e.
which corresponds to the two-pion invariant mass spectrum.
In Fig. 5 we show the ratio \(U_\Lambda ^I(r)/U^I(r) \) for spectral cut-offs of \(\Lambda =1.4,\,1.12,\,0.84\) GeV at threshold \(\sqrt{s}= 2 m_\pi \) as a function of the distance. This estimate yields a larger elementarity radius, which becomes \(r_e = 1.2\) fm for the largest spectral cut-off and a quenching of about a half for \(\Lambda \sim m_\rho \). This numerical exercise shows that the naive estimate \(r_e \sim 1/\Lambda \) is numerically rather inaccurate. Of course, one could consider \(\Lambda \) as a fitting parameter in the analysis of \(\pi \pi \) scattering. Nevertheless, in our view this has the disadvantage that a model dependence is introduced by the cut-off procedure above the elementarity radius.
Note also that the larger \(r_e\) the smaller the TPE potential, since \(U(r_e) = {\mathscr {O}} (e^{-2 m_\pi r_e})\), so that one may end up a the situation where a model independent treatment becomes only possible when the chiral contribution is actually vanishingly small. In the next section we will present a different strategy. Overall, our numerical results will confirm this pessimistic expectation.
6.4 Potential separation
The previous discussion suggests that we should decompose the potential for each isospin channel as
where \(U_\mathrm{Short} (r)\) is a short distance and \(U_\mathrm{Long} (r)\) stands for the long distance contribution. The natural choice is to take for the long-range part the unregularized chiral TPE potential
i.e. potential computed in \(\chi \)PT to a given order in the chiral expansion. As we have seen in the previous section, the lowest order effect in the chiral potential comes from the two pion exchange, which gives a contribution that at long distances is \(U_{\chi } (r) = {\mathscr {O}} (e^{- 2 m_\pi r} /f^4)\). For \(r_c \sim 1/m_\pi \) this contribution will in principle play a role. Of course, these most peripheral contributions to the interaction will contain perturbative corrections to all orders in \(m_\pi /f\), which are expected to modify slightly the tail of the potential. Therefore the question is what is the relative importance of the unknown short distance piece and the known long distance contribution. Finally, let us mention that while we will keep the energy dependence already present in the chiral potential we will assume for simplicity that the short distance potential is energy independent, as long as the inelasticity is negligible (see also Sect. 9).
Energy independent fits with the delta-shells potential given in (62) using \(\Delta r=0.3\) fm for the \(\pi \pi \) S0-, P- and S2-wave phase shifts. The uncertainties are those quoted in [22], whereas solid-black, green-dashed, red-dotted and blue dot-dashed lines stand for for the central results for \(r_c=\,0.9,\, 1.2,\, 1.5,\, 1.8\) fm, respectively
7 Coarse graining
The basic notion of coarse graining in the scattering problem was outlined by Avilés as early as 1972 in an insightful but forgotten paper [93] within the context of NN interactions. In this article the potential was effectively represented as a sum of delta-shell potentials. This form has important simplifications and a recent comprehensive mathematical study of this specific case has been carried out [94]. Here we extend the approach to account for the \(\chi \)PT potential tail at long distances (see also Refs. [33,34,35] for a parallel treatment of the NN case).
7.1 Short distance potential
The basic idea is as follows. If we want to describe the two-particle CM wave-functions limited to the range \(\Delta p\), only gross information can be determined in an interval \(\Delta r\), with \(\Delta r\Delta p\sim 1\). Thus, for a maximal \(s_\mathrm{{\max }}=2\) GeV\(^2\), we have \(\Delta p \sim \sqrt{s_\mathrm{{max}}/4-m_\pi ^2}\sim 0.70\) GeV and one obtains \(\Delta r \sim 0.3\) fm. This uncertainty suggests that for a limited energy range the potential only needs to be known in a limited number of points. With this in mind, we consider for \(r< r_c\) the \(\pi \pi \) potential as a sum of a subsequent number of \(\delta \) functions separated by about \(\Delta r\). Thus, up to \(r_c\), it requires to introduce \(N_\delta \) delta shellsFootnote 14
with \(r_n = n \Delta r\). Thus, we have two relevant scales in our setup: the separation distance \(r_c\) and the coarse graining scale \(\Delta r\). While one expects the results and main properties of the potential to be independent of the particular choices of \(r_c\) and \(\Delta r\), this can only happen when accurate information on the interaction is available at all energies. In our case \(\Delta r\) acts as an UV regulator whereas \(r_c\) works as an IR regulator.
We will analyze this problem for four different values of \(r_c\). For convenience, we will set \(r_c=0.9\), 1.2, 1.5 and 1.8 fm. The solution of (25) for the delta-shell potential in (62) is straightforward. One has
where \(\hat{j}_l(x) = x\,j_l(x)\) and \(\hat{y}_l(x) = x\,y_l(x)\) are the reduced Bessel functions of first and second kind, respectively, and \(\delta _{l,n}\) is the accumulated phase shift. The discontinuity in the logarithmic derivative at \(r=r_n\)
with \(r_n^+ \equiv r_n +0^+\) and \(r_n^- \equiv r_n +0^-\) leads after using the unit Wronskian condition \(\hat{j}_l'(x) \hat{y}_l (x)- \hat{y}_l'(x) \hat{j}_l (x)=-1 \) to the bilinear recursion relation for \(\tan \delta _{l,n}\)
with
with the initial and final conditions
As shown in [95], these equations can be interpreted as the discrete version of the variable phase equation of Calogero [96], corresponding to the limit \(\Delta r \rightarrow 0\). Of course, the previous equations define an integration method in this limit. We stress that the idea of coarse graining is that if U(r) is determined from data with a maximum CM momentum \(p_\mathrm{max}\), the natural resolution of the problem is \(\Delta r \sim 1/p_\mathrm{max}\), and \(U(r_n)\) are the natural fitting parameters.Footnote 15
7.2 Fitting procedures
In this section we present our numerical results based on standard \(\chi ^2\)-fits. Precise \(\pi \pi \)-scattering phase shifts have been obtained in [22, 24] using Roy equations up to \(\sqrt{s_\mathrm{{max}}}=1.42\) GeV and we will use their tabulated values to determine our fitting parameters. While the standard strategy in \(\pi \pi \) scattering studies has been to use the physical region \(\sqrt{s}> 2 m_\pi \), for reasons to be justified in Sect. 7.6 we also include in the S0 fit the subthreshold region, \(0 < \sqrt{s} \le 2m_\pi \) , also deduced in those Roy-equation analyses [22, 24].
In order to exemplify this formalism, we will focus just on the lowest \(\pi \pi \) partial-waves, namely the isoscalar and isotensor S waves S0 and S2, respectively, and the P wave. For any isospin channel we will take the potential
where \(\lambda _n = U(r_n) \Delta r \). For such a maximal energy this means \(\Delta r =0.3 \) fm. Thus, up to \(r_c=\{0.9,1.2,1.5,1.8\}\) fm, it requires to introduce \(N_\delta =\{3,4,5,6\}\) delta shells.
Anticipating the result, we will carry out the study, first without including the chiral tail, since as we will see in Sect. 7.7, it plays a minor role in the resulting fitting parameters \(\lambda _n\).
7.3 Energy independent coarse graining
To start with, we will assume on purpose sufficiently large separation distances so that the long-distance field theoretical contribution \({\mathscr {O}} (e^{-2 m_\pi r})\) can be safely neglected.
One of the main difficulties of the fitting procedure is that we do not have a priori any idea on what a reasonable values of the parameters \(\lambda _j\) are. To overcome this difficulty and in order to constrain as much as possible the delta-shell coefficient values \(\lambda _j\), we will introduce each delta-shell adiabatically, one by one. In addition, the starting fit values for the most internal delta-shell parameters, \(\lambda _0\) and \(\lambda _1\), will be extracted by fitting the \(\pi \pi \) scattering lengths and slope parameters when only one and two delta shells are considered, respectively. These values will change once the physical energy region is fitted. Nevertheless, this procedure will help us to asses the expected size of the inner delta-shell parameter values. The \(\pi \pi \) S0-, S2- and P-wave phase shift obtained in this way for the different values of \(r_c\) previously chosen are plotted in Fig. 6, whereas the value of the delta-shell parameters are given in Table 1. The statistical uncertainties are smaller than the quoted numbers and hence they are not included in Table 1. The maximum fitted energy \(\sqrt{s}\) for each partial waves is chosen as the largest one for which one finds a \(\chi ^2/d.o.f=1\pm \sqrt{2/d.o.f}\). This provides us an indication that we are not underfitting the data and hence that it defines an admissible boundary region. Note that for the S2 wave this condition is already satisfied for the minimum number of parameters and the maximum number of of data points. In addition, as we will discuss in Sect. 7.6, we also include for the S0 fit the subthreshold region \(m_\pi<s<2m_\pi \).
We can see from these results that with a few free parameters, from 3 to 6 depending on the particular choice of \(r_c\), this formalism already allows one to describe the \(\pi \pi \) scattering in the elastic region. In the case of the S2 wave, where the inelasticities are very small at low energies, it is possible to obtain a perfect description up to the maximum energy at \(s_\mathrm{{max}}=2\) GeV\(^2\). For the P wave one obtains a good description, up to energies around the \(\bar{K}K\) threshold at \(\sqrt{s}=1\) GeV, whereas for the S0-wave the description is limited to the region around 0.9 GeV, where the phase presents a huge rise due to the effect of the inelastic \(f_0(980)\) resonance.
Our results reproduce qualitatively features found in [74] using inverse scattering methods, where by construction the potential is a local and continuous function. In particular, for the S waves we find a short distance barrier in the isoscalar and a repulsive core in the isotensor. Of course, we only get a coarse grained version of those potentials, which befits our idea of a finite resolution sampling.
7.4 Threshold parameters
Our results for the threshold parameters defined by (8) are presented in Table 2. As expected from the quality of the fits, they agree within uncertainties with the results obtained in previous analyses [14,15,16,17, 19,20,21,22], which for completness are also given in Table 3.
7.5 Resonance poles
Resonances are determined by looking for poles in the second Riemann sheet, which is defined by the complex wavenumber \(k_R= k_r + i k_i \) with \(k_r \equiv \mathrm{Re}\,k_R > 0\) and \(k_i \equiv \mathrm{Im}\,k_R <0\). This can be achieved directly by substituting \(k \rightarrow k_R\) in the Schrödinger Eq. (19), or its coarse-grained delta-shell implementation (65) and (66).
Our numerical results are presented in Table 4. The numerical values are slightly different from those quoted in benchmarking studies based on Roy equations [16, 43, 44], which for completeness are also given in Table 5. This is not fully surprising since the analytic structure of our scattering amplitude are not the same as in the analyses based on the Roy equations, but only to leading order in the chiral expansion and hence the extension to the complex plane is not determined from the phase-shift analysis only. Nonetheless, we find that the result is encouraging and we expect to return in the future in order to implement higher orders to analyze the effect.
7.6 Crossing and comparison with Roy equations
As we have mentioned in the introduction, there are no direct \(\pi \pi \) scattering data. The closest thing to it are possibly the outcome of Roy equations, which incorporate by construction crossing, analyticity, unitarity and Regge behavior [16, 17, 22]. Moreover, a proper identification of the LECs requires by definition the satisfaction of crossing, particularly in the sub-threshold region. For definiteness, we show in Fig. 7 the real part of the amplitude starting at the edge of the left hand cut \(s=0\), covering the subthreshold region \(0 < \sqrt{s} \le 2 m_\pi \) (where the amplitude is purely real) and the physical elastic region, \(2 m_\pi<\sqrt{s}<2 m_K\), where the imaginary part of the amplitude is determined from unitarity and the corresponding real part. Note that we are neglecting possible inelasticities coming from multi-pion channels. In particular, one can clearly see the Adler zeros of the S0 and S2-wave amplitudes, a characteristic features of the subthreshold region and a distinct fingerprint of chiral symmetry [11].
The comparison in Fig. 7 supports the view that fits to phase shifts in the physical region, even to relatively high energies, do not constrain the subthreshold region. This has a large effect on the location of the \(\sigma \)-resonance and the implications will be discussed in more detail elsewhere. In addition, our fits have not imposed crossing correlations and the consideration or not of the subthreshold region in the S0 channel can be grasped by comparing the location of the corresponding resonance. If the subthreshold region \(m_\pi<s<2m_\pi \) is not imposed in the fit, one gets substantially smaller values for the real part. For instance, for \(r_c=0.9\) fm and \(N_\delta =3\) delta-shells one gets \(\sqrt{s_\sigma }= (324 - i\,194 )\) MeV, whereas the pole moves to \(\sqrt{s_\sigma }= (453 - i\,212 )\) MeV when the subthreshold region is also fitted. This large influence of the subthreshold region in the S0 wave is not surprising, since the pole is rather far from the real axis. In contrast, the location of the \(\rho \)-resonance pole proves rather insensitive to the subthreshold region in the P-wave. Although we are not fitting the subthreshold region in this channel, one gets for \(r_c=0.9\) fm and \(N_\delta =3\) delta-shells \(\sqrt{s_\rho }= (762 - i\,70)\) MeV, even when the subthreshold extrapolation of the fit, middle panel of Fig. 7, shows a significant discrepancy with the outcome of the Roy equations. Finally, we also report a discrepancy in the isotensor channel, where the phase shifts are compatible up to \(s_\mathrm{max}\). Actually, in all cases the amplitude has a zero at \(s=0\), due to the factor \(\sqrt{s}\) in the definition of \(t_{IJ}(s)\). Thus, the failure to satisfy the subthreshold behavior in the S2 wave is intrinsic.Footnote 16 We have checked that this does not improve by incorporating the TPE tail of the chiral potential (see also next subsection). The fact that the subthreshold region is quantitatively as relevant as the physical region, is another manifestation of the relevance of crossing in \(\pi \pi \) scattering, and calls for improvement when all relevant partial waves are considered.
7.7 Full potential: Inclusion of two pion exchange
Once the chiral tail has been defined, we can finally construct a full potential. At short distances (\(r< r_c\)), the non-perturbative regime of QCD is encoded by a sum of delta-shells separated by the minimum De Broglie wave-length considered in the analysis. At large distances (\(r> r_c\)), the chiral potential constructed in (46) with the correct analytical properties and left-hand cut contribution is included. Higher order corrections in the chiral expansion are \({\mathscr {O}} (f^{-6})\) and the determination of the corresponding potential requires going in the quantum mechanical picture to second order in the Born approximation. Their analysis is left for future research.
The resulting fits are reported in Table 6. As one can see, and with the exception of the S2 wave with three delta shells, we do not find a substantial improvement due to the explicit incorporation of the TPE potential. A similar trend is found for the corresponding low energy threshold and resonance parameters, see Tables 7 and 8. In any case, chiral effects due to explicit TPE are generally found to play a minor role.
In our analysis we have restricted to the lowest S- and P-waves. The implementation of higher partial waves is straightforward and requires introducing further short range contributions. Due to the centrifugal barrier term, we expect that the number of grid points will be reduced as the angular momentum increases.
8 Analytic properties and the N/D method
Traditionally, much of the discussion of \(\pi \pi \) scattering has been marked by analyticity and dispersion relations, which at the partial-wave level and in the unsubtracted case read
where \(0< s_n < 4 m_\pi ^2\) are the possible bound states, which we keep for generality, and \(\mathrm{Im}\,t_{IJ}(s) = \rho (s) |t_{IJ}(s)|^2\) for elastic scattering. In this section, we will discuss this issue within the context of our coordinate space framework and for the specific chiral potential derived in Sect. 4, but the results are general. Actually, we will see that the subtractions are not explicitly needed, although they are somewhat encoded into the short distance component of the potential. While many of the issues discussed here have been known for potential scattering since many years [97, 98] (see also [9, 10]), we feel it is necessary to review the main aspects for completeness.
The analytical properties of the scattering amplitude in the complex energy plane are determined by the long-distance behavior of the interaction. This is the basis for dispersion relations, which own their popularity to their link to axiomatic field theory and its straightforward implementation in terms of leading singularities. A frequent method, which has been used in these regard to implement known analytical properties, is the so-called N/D approach. In the N/D approach the partial wave amplitude is written in the form [99]
with \(N_{IJ}(s)\) having only left-hand cut singularities and \(D_{IJ}(s)\) having only right-hand cut singularities. This method has often been invoked in \(\pi \pi \) scattering and implemented in several approximations (see e.g. [100]).
8.1 Jost functions
The way of realizing the N/D representation in potential scattering is well-known. We will describe here the formalism within the coarse grained approach for completeness as well as to provide the \(N_l(k)\) and \(D_l(k)\) functions explicitly, (we drop the isospin index for simplicity). The discussion is naturally carried in terms of the quantum mechanical scattering amplitude defined in (7), \(f_l(k)= 2 t_{l} (s)/\sqrt{s}\), as a function of the CM momentum, k, with \(s=4 (k^2+m_\pi ^2)\). Note that s is invariant under \(k \rightarrow -k \) and hence two-valued. The discussion below entitles to take \(\mathrm{Im} k >0\) for the first Riemann sheet and \(\mathrm{Im} k <0\) for the second.
For a regular potential, the Jost functions, \(F_l(k)\), are defined by the regular solutions of the wave equation at short distances, i.e. \(u_l(r) \rightarrow \hat{j}_l ( kr)\) and subjected to the asymptotic condition at \(r \rightarrow \infty \) [72]
where \(\hat{h}_l^{(1,2)} (x) = \hat{j}_l(x) \pm i \hat{y}_l(x) \) are the reduced Hankel functions fulfilling \(\hat{h}_l^{(1)} (x)^* = \hat{h}_l^{(2)} (x) \) and \(\hat{h}_l^{(1)} (-x) = (-1)^{l+1} \hat{h}_l^{(2)}(x) \). Thus, the S-matrix is then defined as
so that the scattering amplitude becomes
The Jost functions fulfill the reflection conditions
for complex k. Furthermore, due to (74), it can be shown [9, 10] that the functions
fulfill the relations
which means that \(n_l(k)\) is purely real for \(\text {Im}\,\,k=0\). Moreover, \(\mathrm{Re}\, n_l(k)=\mathrm{Re}\,n_l(-k^*)\) and \( \mathrm{Im}\, n_l(k) = -\mathrm{Im}\, n_l(-k^*)\), so that \(n_l(k)\) is purely imaginary for \(\mathrm{Re}\,k=0\). In addition,
Thus, they have the desired properties for a potential constructed as a superposition of Yukawa potentials. A straightforward consequence of these properties is Levinson’s theorem. While the proofs of these statements have been known for a long time [97, 98], to our knowledge they have not been considered within the present context. We will review them adapted to our complete potential, which can be decomposed into two pieces: a cut-off potential and a Yukawa superposition. While they are discussed separately in the literature, our case at hand involves both cases at the same time. We will show next the pertinent steps.
8.2 Analytic properties
The scattering amplitude obtained perturbatively from \(\chi \)PT enjoys analytical properties deduced from the corresponding Feynman diagrams, i.e. particle exchange generated at the partial-wave level a left-hand cut, whose discontinuity has been used to reconstruct the chiral potential. A relevant question is whether our resulting full amplitudes obtained by solving the Schrödinger equation, share these properties beyond first order in perturbation theory, i.e. whether they satisfy, as expected, dispersion relations.
In order to check the analytical properties of the quantum mechanical amplitude, we note that our chiral potential is indeed a superposition of Yukawa potentials with the exception of the explicit s-dependence in the spectral function. It is convenient to write the potential as a superposition of exponentials in the form
where
and \(\rho _I\) was defined in (44). This is indeed our case for the TPE potential in \(\pi \pi \) scattering, as one can see comparing (43) and (78). Being a Laplace transformation, it corresponds to the so-called analytical potential in the complex-r plane for \(\mathrm{Re}\, r >0\) [101], which fulfills the relation \(\lim _{\rho \rightarrow 0}\,U_I( \rho e^{i \theta },s)=0\) for \(-\pi /2< \theta < \pi /2\), with \(r=\rho e^{i \theta }\).
As we will see below, while the exponential falloff of the potential at long distances suffices to prove the analyticity in the strip \( | \mathrm{Im}\,k | < m_\pi \), with \(k=\sqrt{s/4-m_\pi ^2}\), the spectral decomposition is indeed needed to establish the cut along the line \(\mathrm{Re}\,k=0\) and \( m_\pi < \mathrm{Im}\,k \) of the S-matrix. There are several versions of the proof. On the one hand, it can be proved by estimating a bound for the Jost function using directly the spectral representation. On the other hand, by profiting from the analytical character of the potential and deforming the integration in r into the complex plane so that \(k r >0 \). For completeness we will review next and in a sketchy fashion the second method, as it does not require a bounded spectral function or the use of an spectral regularization (see Sect. 6.3).
The determination of the analyticity domain of the quantum mechanical problem is based on the equivalent integral equation for the Jost Functions as follows
which is a Volterra type integral equation and the kernel is given by
Taking the large-r limit and comparing with (71), we get
This equation is the basis for the analytical continuation to the complex-k plane. Actually, in the limit \(r \rightarrow \infty \) one has from (71) that \( |h^{(1)}_l (kr) | = {\mathscr {O}} (e^{-\mathrm{Im}\,k\,r})\) for \(\mathrm{Im}\,k> 0\). Thus, even when \(|u_{k,l} (r)| ={\mathscr {O}} (e^{\mathrm{Im }\,k\,r})\), one has a finite integral provided that the potential goes to zero. As a consequence, \(F_l(k)\) is analytical for \(\mathrm{Im }\,k> 0\). On the contrary, for \(- m_\pi< \mathrm{Im}\,k< 0\) one has \(|h^{(1)}_l (k\,r)\,U(r,s)\,u_{k,l} (r) | = {\mathscr {O}} (e^{-2\mathrm{Im}\,k\, r- 2 m_\pi r} )\) which is convergent for \(\mathrm{Im k}> -m_\pi \). Therefore, \(F_l(k)\) is analytical for \(\mathrm{Im k}> -m_\pi \) and hence \(F_l(-k)\) is analytical for \(\mathrm{Im }\,k < m_\pi \). In conclusion, \(S_l(k)= F_l(-k)/F_l(k)\) is analytical in the strip \( | \mathrm{Im}\,k | < m_\pi \).
For \(k=|k| e^{i\theta }\), due to the analytical character of U(r, s), we can deform the contour to \(r=\rho e^{-i\theta }\), so that, for any term in the spectral integral over \(\mu \), one has a pole at \(k = -i \mu /2\). In the case of \(F_l(k) \) and \(F_l(-k) \), this pole becomes a cut after \(\mu \)-integration along the lines \(\mathrm{Re}\,k=0\) and \(-\infty< \mathrm{Im}\,k < -m_\pi \) and \( m_\pi< \mathrm{Im}\,k < \infty \), respectively. The fact that \(F_l(k)\) is analytical for \(\mathrm{Im}\,k>0\) and \(\lim _{k\rightarrow \infty } F_l(k) \rightarrow 1\) allows one to write a dispersion relation in the upper half-circle
where the antisymmetry of \(\mathrm{Im} F_l(-k)=-\mathrm{Im} F_l(-k)\) from (74) has been used. Thus, passing to the variable \(s=4(k^2+m_\pi ^2)\), which is one-valued in \(\mathrm{Im} k >0\), one can define the functionFootnote 17
so that we can identify \(D_l(s)=F_l(k)\) for \(\mathrm{Im} k > 0\)
where \( \mathrm{Im}\, D_l(s') = \mathrm{Im}\,F_l(s') \) has a right-hand cut in \(4 m_\pi ^2<s<\infty \) and is real for \(s<4 m_\pi ^2\). Furthermore, in the elastic approximation, using (6) we get
where
is real for \(s> 4 m_\pi ^2\). For real \(s <0\) we get that \(s+i0^+ \leftrightarrow 0^+ + i \kappa \) with \(\kappa > m_\pi \) and hence
Thus, the discontinuity is
where we have used that for \(\mathrm{Im} k>0\), \(F_l(k)\) is analytical and hence \(F_l(0^+ + i \kappa )=F_l(-0^+ + i \kappa )\). Finally, note that the s-dependence appearing in the spectral function does not spoil these analytic properties. This completes the proof that the scattering amplitude obtained by solving the Schrödinger equation for the potential in (60) has the correct analytical properties.
8.3 Coarse graining
In order to calculate the Jost functions, in practice we coarse grain the interaction using the delta-shells and we proceed as before. In the discretized version we define the accumulated Jost functions \(F_{l,n}(k) \) and \(F_{l,n}(-k)\) as
However, we keep track of both the continuity of the wave functions and the discontinuity of the derivative separately,
with \(r_n^+ \equiv r_n +0^+\) and \(r_n^- \equiv r_n +0^-\). Again we use the fact that the Wronskian \(2i ( \hat{h}_l^{(1)} (x) \hat{h}_l^{(2)\,\prime }(x)- \hat{h}_l^{(1)\,\prime } (x) \hat{h}_l^{(2)} (x))= 1\) so that
where we have introduced the coefficients,
and the initial conditions are
which corresponds to take the normalization \(u_{l,0}(r) = \hat{j}_l(k,r)\). The final values are
For illustration purposes, we plot in Fig. 8 the functions \(N_{IJ}(s)\) (which is real) and \(D_{IJ}(s)\) (which is complex) separately above the threshold for the five delta-shell case. Of course, these functions reproduce the phase shifts presented before. As expected, \(\mathrm{Im}\,D_{IJ} (4m_\pi ^2)=0\). In this representation the Breit-Wigner position of the resonance is given by computing the zeros of \(\mathrm{Re}\,D_{IJ}(s_R)=0\). While it is not shown in the pictures, the Jost functions display some oscillatory behavior at higher energies due to the explicit delta-shells. Nevertheless, they still go to the expected values \(D(\infty )=1\) and \(N(\infty )=0\).
9 Coarse graining inelasticities
9.1 Energy dependent coarse graining
As mentioned in the introduction, at sufficiently high energies particles are produced and elastic scattering happens in the presence of absorption, which one may view as a leak or hole in the probability. The inelastic region is characterized by the recombination of the two-pion internal configuration, which, of course, demands a complex energy-dependent potential. The complexification of the potential can be understood in terms of the loss of probability of the elastic channel. In order to have an idea of the size of the inelastic hole \(a_\mathrm{inel}\), we show in Fig. 9 the inelastic \(\pi \pi \) total cross sections in different isospin channels, defined as
If we take \(\sigma ^\mathrm{inel}_I = 4 \pi a_\mathrm{inel}^2\), the largest inelastic cross section in Fig. 9 is compatible with an inelastic hole of less than half a fm, i.e. \(a_\mathrm{inel} \lesssim 0.5\) fm. Of course, this corresponds according to (97) to the contribution of all partial waves.
As we have already seen, this loss of probability at the partial-wave level is parameterized in terms of a momentum-dependent inelasticity \(\eta _I^J(s)\), see (4). The imaginary part of the potential plays exactly the same role. At this point, we will assume that this complexification of the potential can be implemented just in the most inner layer of the potential. This assumption can be justified by analyzing the phenomenological inelasticities as a function of the impact parameter given by the relation \(b = (l+1/2)/p\), with l the angular momentum quantum number. In order to provide the range of the inelasticity, we show this dependence in Fig. 10. For the S waves it is found that only for the smallest value, \(b_\mathrm{min} = 1/(2 p_\mathrm{max}) \lesssim \Delta r \), the inelasticity is \(\eta \ll 1\). As we see, if we take \(\Delta r \sim 0.3 \) we may parameterize the inelasticity by one single energy dependent and complex parameter.Footnote 18
Hence, starting from our elastic previous description, we will assume \(\lambda _0\) in (62) to be a complex unknown function of the momentum and we will fit again the pseudo data given in [22] for the phase shift and inelasticity in [22] up to the maximum energy value provided \(\sqrt{s_\mathrm{max}}=1.42\) GeV. This procedure allows us to describe each partial wave (phase shift and inelasticities) exactly at each energy point. The results for the four \(r_c\)-values considered are plotted in Fig. 11, whereas the value of the real and imaginary part of the inner delta-shell layer is depicted in Fig. 12.
S0-, P- and S2-wave phase shifts (left panels) and inelasticities (right panels). The uncertainties are those quoted in [22], whereas solid-black, green-dashed, red-dotted and blue dot-dashed lines stand for the central results for \(r_c=0.9,\) 1.2, 1.5 and 1.8 fm, respectively. Nevertheless, the procedure described in the main text allows one to describe the input exactly at each energy point, so the four lines coincide exactly
Real and imaginary part of the inner delta-shell potential for the S0, P and S2 partial waves whereas solid-black, green-dashed, red-dotted and blue dot-dashed lines correspond to the results with \(r_c=0.9\), 1.2, 1.5 and 1.8 fm, respectively. The error bands have been computed using at each energy point a bootstrap with a uniformly distributed sample of 1000 points and taking the 68% of their distribution as the standard deviation
9.2 Traces of analyticity in the inelastic case
An interesting feature which can be appreciated in Fig 12 is the close resemblance of the real and imaginary parts of the inner delta-shell coefficient with the expected behavior from dispersion relations around a pole or a inelastic threshold. These two effects reflect in the S0 and P channels higher resonances or inelastic channels not explicitly included in the present optical potential analysis. Interestingly, Cornwall and Ruderman [7] found the fixed-r dispersion relation for the optical potential V(r, s) given in (20). The implementation of such a dispersion relation in our analysis would reduce the number of fitting parameters in the inelastic region but it would also require a clear understanding of the high energy behavior. We leave this interesting investigation for future research.
The results for the real and imaginary part of the energy-dependent inner delta-shell when the chiral tail is included differ from those without, plotted in Fig. 12, only at low energies. The comparison is depicted in Fig. 13 showing again the rather small effect introduced by chiral corrections in the inelasticity parameter.
Real part of the inner delta-shell potential for the S0, P and S2 partial waves when the chiral tail is included or excluded. The only differ at low energies. Gray (light-gray), green (light-green), red (orange) and blue (cyan) bands correspond to the results with (without) the chiral tail for \(r_c=0.9\), 1.2, 1.5 and 1.8 fm, respectively
Another interesting possibility which deserves some further investigation is the generalization to the coupled channel case, to account explicitly for the opening of the \(K \bar{K}\) and \(\eta \eta \) thresholds, while keeping multi-pion channels in the inelasticity factor.
10 Subtractions, low energy constants and the number of parameters
In our construction of the chiral \(\pi \pi \) potential the low energy constants (LECs) have been discarded as they do not contribute for \(r \ne 0 \). In fact, the spectral representation does provide the same coordinate dependent potential regardless on the number of subtractions.
This raises the problem of where is this counterterm information gone within the present approach. In this last section we want to address the relation among subtraction constants in dispersion relations, low energy constants and the number of independent parameters within our coarse graining approach. We warn the reader that we have not succeeded in finding a unambiguous relation, which may ultimately be traced to two aspects. Firstly, it has to do with known ambiguities in mapping different regularization methods, namely the one used in \(\chi \)PT and the coordinate space regularization used here. Secondly, there is a difficulty in separating the short distance parameters in perturbation theory, particularly if we use a non-perturbative resummation scheme to fit the parameters.
In order to elaborate on this issue and appreciate the difficulties, we proceed in perturbation theory and re-write the problem in terms of a Fredholm integral equation,
where \({\hat{j}}_{l}(x)=x j_{l}(x)\) is a reduced spherical Bessel function of the first kind and \(G_{k,l}(r,r')\) is the Green’s function satisfying
An analytic expression for the Green’s function \(G_{k,l}(r,r')\) can be written in terms of two function ansatz u(r) and v(r) as
Inserting this in (99), it follows that u(r) and v(r) are solutions of the homogeneous equation with a unit Wronskian, i.e.,
We choose one of the two solutions to be proportional to the regular one, \({\hat{j}}_{l} (kr)\). Then the other linearly independent solution with the desired Wronskian has to be proportional to \({\hat{y}}_{l}(kr)=kr\; y_{l}(kr)\), i.e. the reduced spherical Bessel function of the second kind. Therefore the Green’s function of the ordinary differential equation with the proper normalization can be written as
where \(r_<= \mathrm{min} \{ r,r'\}\) and \(r_>= \mathrm{max} \{ r,r'\}\).
For the normalization of (98) the scattering amplitude can be written as
which using the perturbative expansion inferred from reiteration of the integral equation gives
Actually, the singularity structure in coordinate space suggests introducing a short distance cut-off \(r_c\) and hence a short distance potential \(U_\mathrm{Short}(r)\).Footnote 19 That means that in order to identify numerically the counterterms in perturbation theory we may split the integrals as
so that we get
and apparently the matching to the one-loop result could be undertaken in a straightforward fashion. This is actually not so, since this implies disentangling the fitting parameters in a chiral expansion, namely
where we can arbitrarily shift \(\lambda _n^{(2)} \) and \( \lambda _n^{(4)} \) by equal but opposite constants keeping \(\lambda _n\) constant, say the values of Tables 1 or 6.
This situation is not exclusive to the present approach and in fact is common to all unitarization schemes. For instance in the IAM method the fitted LEC’s are different than those of \(\chi \)PT or the predicted unitarized amplitudes from \(\chi \)PT develop huge uncertainties [68].
The fact that this perturbative matching can ultimately provide a successful description and still fulfilling the condition \(\lambda _n^{(2)} \gg \lambda _n^{(4)} \) is expected. We note, however, that the small changes between the \(\lambda _n\) parameters corresponding to the case without TPE potential listed in 1 and the case with TPE listed in 6 suggest this hypothesis.
11 Conclusions
The optical potential in \(\pi \pi \) scattering is a meaningful object under the most common and general assumption of the validity of the Mandelstam double spectral representation. Therefore, it plays a relevant role in the analysis of such an interaction within a invariant mass formulation of the relativistic two-body problem. Contrary to the more employed Bethe–Salpeter equation, such an approach is free from well-documented spurious singularities, which are triggered by incomplete calculations embodying subsets of Feynman diagrams with particle exchange. In addition, it is a much simpler approach in the CM frame, as it effectively reduces to a Schrödinger equation for equal mass particles.
Within such a framework, in the present paper we have analyzed \(\pi \pi \) scattering from a coarse-grained point of view at distances smaller than the elementarity radius of the pion. This means sampling the interaction in coordinate space at a resolution of the order of the shortest de Broglie wavelength. In our case, where we choose a maximal CM energy of \(s_\mathrm{max}=2\) GeV\(^2\), the resolution turns out to be \(\Delta r \sim 0.3\) fm. As a result, we obtain successful fits in the S0, P and S2 partial waves with the expected number of parameters. We have also analyzed the role of inelasticities by an energy dependent coarse grained interaction. The implications from chiral symmetry have also been analyzed in terms of a long-distance potential featuring the two-pion-exchange mechanism. This potential has been determined for the first time.
A non-perturbative renormalization of the amplitude, based on boundary conditions in coordinate space, is precluded by the energy dependence of the chiral potential. For a finite short distance cut-off about 1.2–1.5 fm this energy dependence becomes irrelevant.
A somewhat surprising result of our analysis is that explicit chiral corrections play a minor role, since at the distances above 1.2–1.5 fm chiral potentials are almost negligible. A rewarding consequence in this regard concerns the extraction of phase-shifts from energy shifts calculated in a finite box in the relative distance by means of the Lüscher formula [47]; its applicability requires the interaction to vanish above a given size which provides a lower limit to the size of the box, L. While the mere \({\mathscr {O}} (e^{-m_\pi L})\) nominal estimate suggests \(L \gtrsim 2 \mathrm{fm}\), our analysis is compatible with taking \(L \sim 1-1.5 \mathrm{fm}\), a much smaller value.
We have also shown that the quantum mechanical re-interpretation of the problem does not spoil the proper analytical properties of the partial wave scattering amplitude, which are explicitly fulfilled by the Feynman diagrams. Thus, the conventional dispersion relations with both a left-hand cut due to particle exchange in the crossed channel and the right hand cut due to unitarity are fulfilled. The standard N/D decomposition of the amplitude is explicitly realized, albeit without subtractions. We expect subtractions to be encoded in the short distance components of the potential, but the explicit determination and identification of the subtraction constants in terms of the short-distance parameters remains to be accomplished.
An important advantage of the coarse graining perspective is that the number of independent parameters is determined a priori by the shortest wavelength and the available crossing constraints. These constraints become increasingly large as we increase the angular momentum of the partial wave. This point deserves further investigation and the determination of all partial waves with this minimal number of parameters is left for future research.
A traditional objection to the successful data-driven unitarity methods is based on their lack of a power counting scheme, reflecting field dependence and off-shell ambiguities absent in the conventional bona fide EFT framework. The present coarse graining approach to \(\pi \pi \) scattering makes no further assumptions than those usually made. Namely, it implements unitarity in the elastic regime and it matches \(\chi \)PT in perturbation theory above a given separation distance, which is estimated to be about 1.2–1.5 fm. In contrast, it does have the advantage that we can estimate the number of fitting parameters a priori. More demanding fits due to an increase in the number of (consistent) data should not require more fitting parameters, but rather determining short distance parameters more accurately. Besides, the method is quite simple as it parameterizes the unknown short distance behavior regardless of any power counting. This also allows a discussion a posteriori of the chiral contributions which turn out to be minor.
Notes
Details here are important. The extra factor 2 is to ensure that \(e^{-2 m_\pi r_c} = 1/e^2 \sim 0.13\) is really negligible. This is confirmed by our analysis below.
Crossing for NN relates the two-pion exchange interaction with the \(N \bar{N} \rightarrow 2 \pi \) production channel. This implies an exponentially suppressed effect in the NN potential\(\sim e^{-2 M_N r}\) and hence having little practical relevance.
We remind that within such a context the methods based in analyticity, dispersion relations and crossing are currently considered to be, besides QCD, the most rigorous framework. We stress again that such an approach is based on the validity of the double spectral representation of the four-point function conjectured by Mandelstam.
Usually the coupled channel unitarity condition is implemented instead. Typically analyses within such a setup leave out the “small” multiple production channels, \(2\pi \rightarrow n \pi \), see e.g. [69] and works cited therein.
These authors wondered if there was a way to promote non-relativistic fits of NN scattering to a relativistic formulation without refitting parameters. The answer is in the affirmative by just reinterpreting the CM momentum by its relativistic counterpart.
Eventually, subtractions might be needed depending on the large-s behavior of the amplitude. We will return to this point in Sect. 10.
We are assuming that at short distances the centrifugal barrier dominates, i.e. \(r^2 U(r) \rightarrow 0 \). Nevertheless, chiral potentials diverge as \(1/r^7\), as it is discussed below, and require special treatment if extended to the origin.
We have checked that one can work either in the particle or the isospin basis, the resulting potential is the same.
There is a conservation of difficulty principle here, one could stay in momentum space in which case the potential is well defined, but the scattering equation is UV divergent.
The renormalization procedure would correspond to take \(r_c \rightarrow 0\) while keeping scattering lengths fixed. This consistent choice assumes point-like hadrons.
The value at \(r=0\) corresponds to the electromagnetic mass difference between charged and neutral pions, \( V_{\pi \pi }^\mathrm{el}(0)=\Delta m_\pi |_\mathrm{EM} = m_{\pi ^+}-m_{\pi ^0} |_\mathrm{EM} = e^2 m_\rho /2= 2.8\,\mathrm{MeV}\), which provides a reasonable value.
The specific form of the potential is not essential, see for e.g. [42] for a detailed comparison. In our case, we take delta-shells for simplicity.
One may argue that the coarse grained potential is generally nonlocal. While this is certainly expected, our assumption is compatible with allocating the non-locality for scales smaller than the resolution scale \(\Delta r\).
This is in common with other unitarization methods, such as IAM where the unitarized amplitude \(t_{IJ}(s)= t_{IJ}^{(2)}(s) + t_{IJ}^{(4)}(s) + \cdots = \frac{[t_{IJ}^{(2)}(s)]^2 }{t_{IJ}^{(2)}(s) - t_{IJ}^{(4)}(s)} \) develops a double Adler zero instead of the expected single one (see e.g. Ref. [68]) and Fig. 7.
We use capital letters for the function \(n_l\) and \(d_l\) in (75) when referring to the \(t_{l}(s)\) amplitudes.
The fixed-r dispersion relation in (20) suggests that in fact this parameter is an analytical function of the energy. (see also the discussion below.)
Here we assume for simplicity a local form. More generally we may assume a nonlocal form of the type \( [U \psi ] (r) =\int \nolimits _0^{r_c} U(r,r') \psi (r') \text {d}r'\) with \(U(r,r') =0\) for \(r>r_c\). The coarse graining interpretation below reduces effectively this non locality to a local form within a sampling distance \(\Delta r\).
References
S. Mandelstam, Phys. Rev. 112, 1344 (1958)
M. Hoferichter et al., Phys. Rep. 625, 1 (2016). arXiv:1510.06039
S. Mandelstam, Phys. Rev. 115, 1741 (1959)
R. Blankenbecler et al., Ann. Phys. 10, 62 (1960)
A. Martin, Nuovo Cimento A 42, 930 (1965)
A. Martin, Nuovo Cimento A 44, 1219 (1966)
J.M. Cornwall, M.A. Ruderman, Phys. Rev. 128, 1474 (1962)
R. Omnes, Phys. Rev. 137, B653 (1965)
H.M. Nussenzveig, Causality and Dispersion Relations (Academic Press, New York, 1972)
M. Goldberger, K. Watson, Collision Theory (Dover Publications, Mineola, 2004)
B. Martin, D. Morgan, G. ShawPion, Pion Interactions in Particle Physics, vol. 101 (Academic Press, London, 1976)
S. Weinberg, Phys. A 96, 327 (1979)
J. Gasser, H. Leutwyler, Ann. Phys. 158, 142 (1984)
G. Colangelo, J. Gasser, H. Leutwyler, Phys. Lett. B 488, 261 (2000). arXiv:hep-ph/0007112
B. Ananthanarayan et al., Phys. Rep. 353, 207 (2001). arXiv:hep-ph/0005297
G. Colangelo, J. Gasser, H. Leutwyler, Nucl. Phys. B 603, 125 (2001). arXiv:hep-ph/0103088
I. Caprini et al., Phys. Rev. D 68, 074006 (2003). arXiv:hep-ph/0306122
I. Caprini, G. Colangelo, H. Leutwyler, Eur. Phys. J. C 72, 1860 (2012)
J.R. Pelaez, F.J. Yndurain, Phys. Rev. D 71, 074016 (2005). arXiv:hep-ph/0411334
R. Kaminski, J.R. Pelaez, F.J. Yndurain, Phys. Rev. D 74, 014001 (2006). arXiv:hep-ph/0603170, [Erratum: Phys. Rev. D74,079903(2006)]
R. Kaminski, J.R. Pelaez, F.J. Yndurain, Phys. Rev. D 77, 054015 (2008). arXiv:0710.1150
R. Garcia-Martin et al., Phys. Rev. D 83, 074004 (2011). arXiv:1102.2183
J. Gasser, PoS EFT 09, 029 (2009)
R. Navarro Pérez, E. Ruiz Arriola, J. Ruiz de Elvira, Phys. Rev. D 91, 074014 (2015). arXiv:1502.03361
J. Ruiz de Elvira, Study of the properties and nature of the lightest scalar mesons and their relation to spontaneous chiral symmetry breaking, PhD thesis, Madrid U., 2012-12-07
J.R. Pelaez, Phys. Rep. 658, 1 (2016). arXiv:1510.00653
W. Au, E. Lomon, Phys. Lett. 4, 327 (1963)
W. Au, E. Lomon, Il Nuovo Cimento (1955–1965) 31, 113 (1964)
H. Feshbach, E. Lomon, Ann. Phys. 29, 19 (1964)
L.A. Balázs, Phys. Rev. 137, B1510 (1965)
L.A. Balázs, Phys. Rev. 139, B1646 (1965)
L.A.P. Balazs, Phys. Rev. 176, 1769 (1968)
R. Navarro Perez, J.E. Amaro, E. Ruiz Arriola, Prog. Part. Nucl. Phys. 67, 359 (2012). arXiv:1111.4328
R. Navarro Pérez, J.E. Amaro, E. Ruiz Arriola, Phys. Rev. C 88, 064002 (2013). arXiv:1310.2536 [Erratum: Phys. Rev.C91,no.2,029901(2015)]
R. Navarro Pérez, J.E. Amaro, E. Ruiz Arriola, Phys. Rev. C 89, 024004 (2014). arXiv:1310.6972
E. Matsinos, G. Rasche, Int. J. Mod. Phys. E 26, 1750002 (2017). arXiv:1610.02921
J. Ruiz de Elvira, J. Phys. G 45, 024001 (2018). arXiv:1706.01465
E. Ruiz Arriola, J.E. Amaro, R. Navarro Pérez, PoS Hadron2017 134, (2018) arXiv:1711.11338
J. Nieves, E. Ruiz Arriola, Phys. Lett. B 455, 30 (1999). arXiv:nucl-th/9807035
J. Nieves, E. Ruiz Arriola, Nucl. Phys. A 679, 57 (2000). arXiv:hep-ph/9907469
R. Navarro Perez, J.E. Amaro, E. Ruiz Arriola, Few Body Syst. 55, 983 (2014). arXiv:1310.8167
P. Fernandez-Soler, E. Ruiz Arriola, Phys. Rev. C 96, 014004 (2017). arXiv:1705.06093
I. Caprini, G. Colangelo, H. Leutwyler, Phys. Rev. Lett. 96, 132001 (2006). arXiv:hep-ph/0512364
R. Garcia-Martin et al., Phys. Rev. Lett. 107, 072001 (2011). arXiv:1107.1635
P. Masjuan, J. Ruiz de Elvira, J.J. Sanz-Cillero, Phys. Rev. D 90, 097901 (2014). arXiv:1410.2397
I. Caprini, Phys. Rev. D 93, 076004 (2016). arXiv:1602.02062
M. Luscher, Nucl. Phys. B 354, 531 (1991)
NPLQCD, S.R. Beane et al., Phys. Rev. D85 034505, (2012) arXiv:1107.5023
J. Bulava, Nucl. Phys. B 910, 842 (2016). arXiv:1604.05593
ETM, C. Helmes et al., JHEP 09 109, (2015) arXiv:1506.00408
N.R. Acharya, Nucl. Phys. B 922, 480 (2017). arXiv:1704.06754
T. Yamazaki, PoS LATTICE2014 009, (2015) arXiv:1503.08671
T. Kurth et al., JHEP 12, 015 (2013). arXiv:1305.4462
M. Doring et al., Eur. Phys. J A 47, 139 (2011). arXiv:1107.3988
M. Doring et al., Eur. Phys. J A 48, 114 (2012). arXiv:1205.4838
F.J. Yndurain, (2002), arXiv:hep-ph/0212282
A. Gomez Nicola, J.R. Pelaez, J. Ruiz de Elvira, Phys. Rev. D 82, 074012 (2010). arXiv:1005.4370
J. Ruiz de Elvira, Phys. Rev. D 84, 096006 (2011). arXiv:1009.6204
A. Gomez Nicola, J.R. Pelaez, J. Ruiz de Elvira, Phys. Rev. D 87, 016001 (2013). arXiv:1210.7977
S.K. Adhikari, Phys. Lett. B 126, 489 (1983)
S.K. Adhikari, arXiv:1807.05208 (2018)
R. Omnes, Phys. Rev. 146, 1123 (1966)
M. Kugler, R. Roskies, Phys. Rev. 155, 1685 (1967)
E.P. Wigner, Phys. Rev. 98, 145 (1955)
D.R. Phillips, T.D. Cohen, Phys. Lett. B 390, 7 (1997). arXiv:nucl-th/9607048
Z.H. Guo, J.A. Oller, J. Ruiz de Elvira, Phys. Lett. B 712, 407 (2012). arXiv:1203.4381
Z.H. Guo, J.A. Oller, J. Ruiz de Elvira, Phys. Rev. D 86, 054006 (2012). arXiv:206.4163
J. Nieves, M. Pavon Valderrama, E. Ruiz Arriola, Phys. Rev. D 65, 036002 (2002). arXiv:hep-ph/0109077
T. Ledwig et al., Phys. Rev. D90, 114020 (2014). arXiv:1407.3750
T.W. Allen, G.L. Payne, W.N. Polyzou, Phys. Rev. C 62, 054002 (2000). arXiv:nucl-th/0005062
E. Ruiz Arriola, W. Broniowski, Few Body Syst. 57, 485 (2016). arXiv:1602.00288
A. Galindo, P. Pascual, Quantum Mechanics I and II (Springer, New York, 2012)
K. Chadan, P.C. Sabatier, Inverse Problems in Quantum Scattering Theory (Springer, New York, 1977)
M. Sander, H.V. von Geramb, Phys. Rev. C 56, 1218 (1997). arXiv:nucl-th/9703031
G. Feinberg, J. Sucher, C.K. Au, Phys. Rep. 180, 83 (1989)
D. Kawai et al., (2017) arXiv:1711.01883
W. Frank, D.J. Land, R.M. Spector, Rev. Mod. Phys. 43, 36 (1971)
M. Pavon Valderrama, E. Ruiz Arriola, Phys. Rev. C 72, 054002 (2005). arXiv:nucl-th/0504067
M. Pavon Valderrama, E. Ruiz Arriola, Phys. Rev. C 74, 054001 (2006). arXiv:nucl-th/0506047
M. Pavon Valderrama, E. Ruiz Arriola, Phys. Rev. C 74, 064004 (2006). arXiv:nucl-th/0507075 [Erratum: Phys. Rev.C75,059905(2007)]
E. Ruiz Arriola, (2007), arXiv:0709.4134
E. Ruiz Arriola, AIP Conf. Proc. 1030, 135 (2008). arXiv:0804.2199
A.C. Cordon, E. Ruiz Arriola, Phys. Rev. A 81, 044701 (2010). arXiv:0912.1714
E. Ruiz Arriola, A.C. Cordon, EPJ Web Conf. 3, 02005 (2010). arXiv:0912.2658
E. Ruiz Arriola, A. Calle Cordon, M. Pavon Valderrama, eConf C 070910, 161 (2007). arXiv:0710.2770
F.J. Ernst, R.G. Sachs, K.C. Wali, Phys. Rev. 119, 1105 (1960)
P. Masjuan, E. Ruiz Arriola, W. Broniowski, Phys. Rev. D 87, 014005 (2013). arXiv:1210.0760
J. Hudson, P. Schweitzer, Phys. Rev. D 96(11), 114013 (2017). arXiv:1712.05316 [hep-ph]
M. V. Polyakov, P. Schweitzer, arXiv:1805.06596 [hep-ph]
T. Barnes, E.S. Swanson, Phys. Rev. D 46, 131 (1992)
E.S. Swanson, Ann. Phys. 220, 73 (1992)
T. Barnes, N. Black, E.S. Swanson, Phys. Rev. C 63, 025204 (2001). arXiv:nucl-th/0007025
J.B. Aviles, Phys. Rev. C 6, 1467 (1972)
S. Albeverio et al., J. Math. Phys. 54, 052103 (2013)
D.R. Entem et al., Phys. Rev. C 77, 044006 (2008). arXiv:0709.2770
F. Calogero, Variable Phase Approach to Potential Scattering by F Calogero, vol. 35 (Elsevier, Amsterdam, 1967)
D.I. Fivel, A. Klein, J. Math. Phys. 1, 274 (1960)
R.G. Newton, J. Math. Phys. 1, 319 (1960)
G.F. Chew, S. Mandelstam, Phys. Rev. 119, 467 (1960)
J.A. Oller, E. Oset, Phys. Rev. D 60, 074023 (1999). arXiv:hep-ph/9809337 [165(1998)]
J.R. Taylor, Scattering Theory: A Quantum Theory on Nonrelavistic Collisions (Wiley, Hoboken, 1972)
Acknowledgements
We thank Jose Antonio Oller for a discussion and Jose Manuel Alarcón for reading the manuscript. E.R.A is very grateful to the AEC and the ITP in Bern for hospitality and financial support. Work partially supported by Spanish MINEICO and European FEDER funds (grants FIS2014-59386-P, FIS2017-85053-C2-1-P and FPA2015-64041-C2-1-P), Junta de Andalucía (grant FQM-225) and the Swiss National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Appendix A: Chiral \(\pi \pi \) amplitudes and potentials
Appendix A: Chiral \(\pi \pi \) amplitudes and potentials
1.1 1. \(\pi \pi \) scattering at one loop in \(\chi \)PT
At \({\mathscr {O}}(p^4)\) in \(\chi \)PT, the \(\pi \pi \) elastic scattering amplitudes can be written in the form [13]:
The lowest-order amplitude \(A_2 (s,t,u)\) is identical to the first term in (36) (pion contribution) and only depends on the pion mass and weak decay constant. The \({\mathscr {O}}(p^4)\) correction involves four SU(2) renormalization-scale-independent LECs: \({\bar{l}}_i\) (\(i=1,2,3,4\)). In addition, \(A_4 (s,t,u)\) includes one-loop chiral corrections, which are suppressed by one power of \(1/N_C\); they are parameterized through the loop function
We list here for completeness the non-polynomial contributions to the \(\pi \pi \) scattering amplitudes at one-loop order [13]
As said, only the piece containing the loop integral J(t) contributes to the potential, according to (31).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Ruiz de Elvira, J., Ruiz Arriola, E. Coarse graining \(\pi \pi \) scattering. Eur. Phys. J. C 78, 878 (2018). https://doi.org/10.1140/epjc/s10052-018-6342-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6342-7