Abstract
Using the first law of thermodynamics, we propose a relation between the system entropy (S) and its IR (L) and UV (\(\Lambda \)) cutoffs. In addition, applying this relation to the apparent horizon of flat FRW universe, whose entropy meets the Rényi entropy, a new holographic dark energy model is addressed. Thereinafter, the evolution of the flat FRW universe, filled by a pressureless source and the obtained dark energy candidate, is studied. In our model, there is no mutual interaction between the cosmos sectors. We find out that the obtained model is theoretically powerful to explain the current accelerated phase of the universe. This result emphasizes that the generalized entropy formalism is suitable for describing systems including the long-range interactions such as gravity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The nature of current accelerated universe [1,2,3,4,5,6,7,8,9,10,11,12], related to an unknown source called dark energy (DE), is one of the unsolved physical mysteries [13,14,15,16]. In order to solve it, modified theories of gravity have been proposed which describe it in terms of various geometrical effects [17]. On the other hand, introducing the new types of matter or diverse state equations constitutes some other theoretical attempts to solve the DE problem [18,19,20,21,22,23,24,25,26,27,28]. It has been also argued that there are deep connections between DE, the horizon entropy and the thermodynamics laws [29,30,31,32,33].
It seems that systems including the long-range interactions, such as gravity, are more in agreement with the generalized entropy formalisms based on the power-law distribution of probabilities [34,35,36,37,38,39,40,41,42,43,44]. Recently, two generalized entropies including the Rényi and Tsallis entropies [34,35,36,37,38,39,40,41], have been used in order to study various gravitational and cosmological phenomena [42,43,44,45,46,47,48,49,50,51,52,53,54]. It has been shown in various ways that the generalized entropy formulation can provide suitable descriptions for DE, also motivating us to consider generalized entropies as the horizon entropy instead of the Bekenstein entropy [42, 44, 47,48,49,50,51,52,53,54]. In fact, the Bekenstein entropy is also obtainable by applying the Tsallis statistics to the systems including gravity [42, 43, 46,47,48,49].
To reconcile the breakdown of quantum field theory in large scale with the success of effective field theory, Cohen et al, [55] proposed a new relation between the system entropy (S) together with the IR (L) and UV (\(\Lambda \)) cutoffs which finally lead to [56, 57]
where \(\rho _\Lambda \sim \Lambda ^4\) is the vacuum energy density. Applying this hypothesis to cosmological setup, authors got a model for DE called Holographic Dark Energy (HDE), in which \(\rho _\Lambda \) plays the role of the energy density of DE (\(\rho _d\)), [58,59,60]. One problem with the original model (OHDE) is that if one uses the Hubble radius as the IR cutoff, and considers the Bekenstein entropy, then both dark matter (DM) and OHDE are scaled with the same function of scale factor [60, 61]. Although this problem may be solved by introducing new cutoffs [60, 61], such cutoffs cannot always lead to stable models for DE whenever it is dominant in cosmos [62]. More studies on HDE and its various features can be found in Refs. [63,64,65].
Recently, using Eq. (1) and a generalized entropy, called the Sharma-Mittal measure [34], a new model of HDE has been proposed and studied [44]. In this new model (SMHDE), Hubble horizon is the IR cutoff, and there is no interaction between the cosmos components [44]. SMHDE is compatible with the universe expansion history, and it is stable whenever it is dominant in cosmos [44]. Hence, this model suffers from less weakness compared to the OHDE corrected by considering other cutoffs [44, 62]. The obtained behavior of SMHDE also motivates us to farther study the HDE hypothesis in other generalized entropy formalisms. Such analysis may help us to become more familiar with thermodynamics and the statistical aspects of spacetime and gravity [42, 44, 48].
It is also useful to remind here that the apparent horizon is a proper causal boundary for cosmos in agreement with the thermodynamics laws and thus the energy-momentum conservation law [66,67,68,69,70,71]. Moreover, in flat FRW universe, Friedmann equations indicate that whenever DE is dominant in cosmos, its energy density will scale with \(H^2\) [16]. Therefore, from a thermodynamic point of view, a HDE model in flat FRW universe, for which the Hubble radius and the radius of apparent horizon (1 / H) are the same, will be more compatible with the thermodynamics laws, if it can provide a proper description for the universe by using the Hubble radius as its IR cutoff. It is worthwhile mentioning that the first law of thermodynamics (FLT) helps us in relating the equation of state of HDE to that of black holes leading to a model for the current accelerated universe [72]. FLT is also employed in building HDE models based on energy density of vacuum entanglement [65, 73]. As a result, one can argue that we should use the thermodynamics laws in order to build a relation between \(\Lambda ^4\), the IR cutoff and the horizon entropy to get a model for HDE.
Here, considering FLT, a relation between the system entropy (S) together with the IR (L) and UV (\(\Lambda \)) cutoffs will be proposed. In addition, using the Hubble radius as the IR cutoff, and employing a Q-generalized entropy, proposed by Rényi [38], we are going to introduce a new HDE model in flat FRW universe. In order to achieve our goal, the paper is organized as follows. Our thermodynamic version of Eq. (1) has been introduced in the next section. In section (III), a brief review on the Rényi and Tsallis entropy is given, and then, we introduce our new model of HDE. The behavior of the model whenever there is no interaction between the cosmos sectors is studied in Sec. (\(IV \)). The last section is devoted to a summary and concluding remarks. We also work in the unit of \(c=\hbar =G=k_B=1\), where \(k_B\) denotes the Boltzmann constant.
2 A thermodynamic version for HDE
Bearing the Cai–Kim temperature (\(T=\frac{1}{2\pi L}\)) in mind [71], for a system with IR cutoff L, one can reach Eq. (1) by considering the \(E_d\sim \rho _d V\simeq E_T\propto TS\) assumption, in which \(\rho _d\equiv \rho _\Lambda \sim \Lambda ^4\), [56, 57]. In fact, since DE is dominant in the current cosmos, the \(E_d\sim \rho _d V\simeq E_T\propto TS\) assumption is acceptable. Here, \(V=\frac{4\pi L^3}{3}\) is the aerial volume of FRW spacetime, S is the horizon entropy (represents the total entropy of system), \(E_T\) also denotes the total energy content of cosmos [56, 57]. Moreover, \(E_d\) represents the energy content of the DE candidate (vacuum energy) [56, 57]. Recently, the above assumption has also been used in order to provide a thermodynamic description for HDE, and also a relation between holographic minimal information density and the de Broglie’s wavelength [74]. Although Eq. (1) is compatible with the dimensional analysis [60], but since only in flat FRW universe the aerial volume is the same as the actual volume (\(L=\frac{1}{H}\)), the above argument, and thus Eq. (1) are more reliable in the flat FRW universe [55, 75, 76]. Hence, since the non-flat FRW universe has not completely been rejected [16], it is better to modify the \(E_d\sim \rho _d V\simeq E_T\propto TS\) assumption in a more consistent way with the non-flat cases.
For the first time, using the \(dE_T\equiv d\mathcal {Q}\) assumption in order to find the energy flux (\(d\mathcal {Q}\)) seen by an accelerated observer inside horizon, and applying the Calusius relation to the horizon, Jacobson wrote the Einstein field equations in the static spacetimes as a thermodynamic equation of state [77]. The generalizations of his idea to the cosmological setups suggest that the \(dE_T=TdS\) relation can be considered as the first law of thermodynamics for the cosmological horizon [69, 78].
The above arguments motivate us to introduce \(dE_d=\rho _d dV\propto dE_T=TdS\) for building a thermodynamic consistent relation between the UV cutoff (\(\Lambda ^4\sim \rho _\Lambda \equiv \rho _d)\) and the IR cutoff. In order to check this assumption, consider a flat FRW universe for which \(S=\frac{\pi }{H^2}\), \(T=\frac{H}{2\pi }\) and \(V=\frac{4\pi }{3H^3}\), where H is the Hubble parameter. By using \(\rho _d dV\propto TdS\), we easily reach \(\rho _d\propto \frac{H^2}{4\pi }\) which is nothing but OHDE for which Hubble horizon is considered as the IR cutoff [58,59,60]. In fact, our thermodynamic reformulation of Eq. (1) claims that the changes in the energy (entropy) of system can not be more than that of the black hole of the same size. In other words, we have \(dE_d\le dE_T\) in every infinitesimal interval leading to \(E_d=\int dE_d\le E_T=\int dE_T\), a result in agreement with the HDE hypothesis [55,56,57,58,59,60,61,62,63]. Therefore, in our setup, the final amount of the system energy (entropy) can not also be more than that of its same size black hole.
3 Rényi entropy and HDE: general remarks
For a system consisting of W discrete states, Tsallis entropy is defined as [39]
in which \(P_i\) denotes the ordinary probability of accessing state i, and Q is a real parameter which may be originated from the non-extensive features of system such as the long range nature of gravity [37, 39, 42, 44]. In this formalism, two probabilistically independent systems obey the non-additive composition rule [39, 40]
where \(\delta \equiv 1-Q\). Thus, even for probabilistically independent systems, although it is a non-additive entropy, unless we have \(\delta =0\) [39], it is also not always non-extensive [37]. In fact, differences between non-additivity and non-extensivity are very delicate [35,36,37], and the concept of non-extensivity is much more complex than that of the non-additivity [37]. For example, the famous Bekenstein entropy is non-extensive and non-additive simultaneously [43, 46].
In addition, there is another Q-generalized entropy definition as
which returns to Rényi [38]. One can combine Eqs. (4) and (2) with each other to reach [47,48,49]
as the Rényi entropy content of system. Thus, based on Eq. (5), \(\mathcal {S}\) will remain additive as long as Eq. (3) is obtained by \(S_T\) [34, 36, 46]. The above Q-generalized entropies can be used whenever systems are described better by using the power law distributions \(P_i^Q\), also called Q-distribution, instead of the ordinary probability distribution \(P_i\) [36, 46]. Systems including long-range interactions, such as gravity, are primary candidates for using Q-distribution [34,35,36,37,38,39,40,41,42,43,44].
It is also useful to remind here that a Q-distribution-based description of the universe can theoretically describe the current accelerated universe [44, 47,48,49,50,51,52,53,54] which more motivates us to assign various Q-generalized entropies to the cosmological horizons. Recently, it has been argued that the Bekenstein entropy (\(S=\frac{A}{4}\)) is in fact a Tsallis entropy [40, 42, 43, 46,47,48,49] leading to
for the Rényi entropy content of system [43, 46,47,48,49].
3.1 Rényi holographic dark energy (RHDE)
Here, we only focus on the flat FRW universe indicated by the WMAP data [16]. In our model, the vacuum energy density plays the role of DE meaning that we have \(\Lambda ^4\sim \rho _\Lambda \equiv \rho _d\). Now, using the \(\rho _d dV\propto TdS\) assumption and Eq. (6), one can get RHDE as
where \(C^2\) is a numerical constant as usual. In order to obtain this equation, we also used the \(T=\frac{H}{2\pi }\) and \(A=\frac{4\pi }{H^2}=4\pi (\frac{3V}{4\pi })^{\frac{2}{3}}\) relations, valid in a flat FRW universe [71]. It is apparent that in the absence of \(\delta \), we have \(\rho _d=\frac{3C^2H^2}{8\pi }\) in full agreement with OHDE [58,59,60].
In order to obtain the corresponding pressure, we assume that RHDE obeys ordinary energy-momentum conservation law in the FRW universe with scale factor a, and thus
in which dot denotes derivative with respect to time. It finally leads to
where prime denotes derivative with respect to H, for the pressure of RHDE.
4 Universe evolution
For a flat FRW universe filled by a pressureless source with energy density \(\rho _m\) and RHDE, the Friedmann equations are written as
Let us define the density parameters corresponding to the \(\rho _m\) and \(\rho _d\) sources as \(\Gamma _m\equiv \frac{\rho _m}{\rho _c}\) and \(\Omega _D\equiv \frac{\rho _d}{\rho _c}\), respectively, where \(\rho _c(\equiv \frac{3H^2}{8\pi })\) is called critical density. Now, inserting these definitions in the first line of Eq. (10), one easily finds
Here, since DE candidate obeys Eq. (8), there is no interaction between matter source and RHDE meaning that we have
in which \(\rho _0\) is the integration constant equal to the current value of the energy density of pressureless component (\(\rho _m\)). Now, defining \(H(z)=E(z)H_0\), bearing the \(1+z=a^{-1}\) relation in mind, where z and \(H_0\) denote redshift and the current value of the Hubble parameter, respectively, and combining Eqs. (7) and (12) with either the first equation of (10) or Eq. (11), one easily finds that
where \(\Omega _m\equiv \Gamma _m(z=0)= \frac{\rho _0}{\frac{3H_0^2}{8\pi }}\) denotes the current value (\(z=0\)) of the density parameter of \(\rho _m\). In obtaining this equation, we assumed that for \(z=0\) we have \(E(z)=1\) leading to \(C^2=(1+\frac{\delta \pi }{H_0^2})(1-\Omega _m)\), which can finally be combined with Eq. (7) to get
for energy density. Deceleration parameter is also evaluated as
Moreover, if we characterize the total state equation of cosmos as \(w\equiv \frac{p_d}{\rho _d+\rho _m}\), then using Eqs. (10) and (15), we can find
Bearing the definitions of \(\Omega _D\) and \(\Gamma _m\) in mind, one can use Eq. (13) to reach at
for the density parameter of RHDE. In order to investigate the stability of RHDE, we need to study the evolution of square of the sound speed evaluated as
One can use the second Friedmann equation (10) to find \(\dot{H}=-4\pi p_d-\frac{3H^2}{2}\). Now, employing this result along with Eqs. (9) and (14), we reach at
This result together with Eq. (14) can be used to evaluate \(v_{s}^{2}\) as
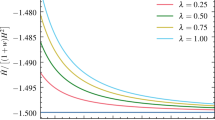
In Figs. 1 and 2, the system parameters, including q, w, \(\Omega _D\) and \(v_{s}^{2}\), have been plotted versus z for some values of \(\delta \), whenever \(\Omega _m=0\cdot 26\) and \(\Omega _m=0\cdot 23\), respectively. In general, even for \(z>z_t\), \(v_{s}^{2}\) can remain positive meaning that, unlike the OHDE and SMHDE [44, 62], RHDE can be stable in matter dominated era. Moreover, at the high redshift limit, we have \(q\rightarrow 1/2\) and \(w\rightarrow 0\), while at the \(z\rightarrow -1\) limit, \(q\rightarrow -1\) and \(w\rightarrow -1\). It is also worthwhile mentioning that, depending on the value of \(\delta \), the cosmos may cross the phantom line (\(q<-1\)) for \(z<-1\).
The transition redshift (\(z_t\)), at which \(q(z_t)=0\), versus \(\delta \) has also been plotted in Fig. 3 for some values of \(\Omega _m\) which lies within the \(0\cdot 2{\le }\Omega _m{\le }0\cdot 3\) range [1,2,3, 13,14,15]. We see that the model can give proper values for \(z_t\), and as an example, the model predicts that, depending on the value of \(\delta \), \(z_t\sim 0\cdot 5\) for \(\Omega _m=0\cdot 3\) [1,2,3, 13,14,15].
5 Conclusion
Recently, the notion of generalized entropy has been used to study various properties of spacetime, gravitational and cosmological phenomena. Here, by using FLT, we built a thermodynamic constraint on the relation between the system entropy (S) and the IR (L) and UV (\(\Lambda \)) cutoffs. Following this relation, using the Rényi entropy, and considering the Bekenstein entropy as the Tsallis entropy [40, 42, 43, 46,47,48,49], we finally proposed a new holographic model for dark energy (RHDE).
The model can generate acceptable values for the transition redshift. We also studied the evolution of the system parameters including q, w, \(v_{s}^{2}\) and \(\Omega _D\) which showed satisfactory behavior by themselves. It has also been obtained that RHDE shows more stability during the cosmic evolution compared to SMHDE [44] and OHDE [62].
References
P. Garnavich et al., Astrophys. J. 493, 53 (1998)
A.G. Riess et al., Astron. J. 116, 1009 (1998)
S. Perlmutter et al., Astrophys. J. 517, 565 (1999)
P. de Bernardis et al., Nature 404, 955 (2000)
S. Perlmutter et al., Astrophys. J. 598, 102 (2003)
M. Colless et al., Mon. Not. R. Astron. Soc. 328, 1039 (2001)
M. Tegmark et al., Phys. Rev. D 69, 103501 (2004)
S. Cole et al., Mon. Not. R. Astron. Soc. 362, 505 (2005)
V. Springel, C.S. Frenk, S.M.D. White, Nature (London) 440, 1137 (2006)
S. Hanany et al., Astrophys. J. Lett. 545, L5 (2000)
C.B. Netterfield et al., Astrophys. J. 571, 604 (2002)
D.N. Spergel et al., Astrophys. J. Suppl. 148, 175 (2003)
Carl L. Gardner, Nucl. Phys. B 707, 278 (2005)
J. Ponce de Leon, Gen. Relativ. Gravit. 38, 61 (2006)
J.V. Cunha, Phys. Rev. D 79, 047301 (2009)
M. Roos, Introduction to Cosmology (Wiley, New York, 2003)
S. Capozziello, V. Faraoni, Beyond Einstein Gravity (Springer, New York, 2011)
C. Wetterich, Nucl. Phys. B 302, 668 (1988)
R.R. Caldwell, M. Kamionkowski, N.N. Weinberg, Phys. Rev. Lett. 91, 071301 (2003)
C. Armendariz-Picon, V.F. Mukhanov, P.J. Steinhardt, Phys. Rev. Lett. 85, 4438 (2000)
R.G. Cai, Phys. Lett. B 657, 228 (2007)
H. Wei, R.G. Cai, Phys. Lett. B 660, 113 (2008)
S. Nojiri, Sergei D. Odintsov, Phys. Rev. D 72, 023003 (2005)
N. Ohta, Phys. Lett. B 695, 41 (2011)
H. Moradpour, A. Abri, H. Ebadi, Int. J. Mod. Phys. D 25, 1650014 (2016)
H. Moradpour, R.C. Nunes, E.M.C. Abreu, J.A. Neto, Mod. Phys. Lett. A 32, 1750078 (2017)
S. Nojiri, S.D. Odintsov, Phys. Lett. B 639, 144 (2006)
K. Bamba, S. Capozziello, S. Nojiri, S.D. Odintsov, Astrophys. Space Sci. 342, 155 (2012)
H. Moradpour, A. Sheykhi, N. Riazi, B. Wang, AHEP 2014, 718583 (2014)
H. Ebadi, H. Moradpour, Int. J. Mod. Phys. D 24, 1550098 (2015)
H. Moradpour, M.T. Mohammadi Sabet, Can. J. Phys 94, 1 (2016)
H. Moradpour, N. Riazi, Int. J. Theor. Phys. 55, 268 (2016)
J.P. Mimoso, D. Pavón, Phys. Rev. D 94, 103507 (2016)
M. Masi, Phys. Lett. A 338, 217 (2005)
H. Touchette, Phys. A 305, 84 (2002)
T.S. Biró, P. Ván, Phys. Rev. E 83, 061147 (2011)
C. Tsallis, Entropy 13, 1765 (2011)
A. Rényi, Probability Theory (North-Holland, Amsterdam, 1970)
C. Tsallis, J. Stat. Phys. 52, 479 (1988)
S. Abe, Phys. Rev. E 63, 061105 (2001)
S. Abe, Foundations of Nonextensive Statistical Mechanics, in Chaos, Nonlinearity, Complexity. Studies in Fuzziness and Soft Computing 206, ed. by A. Sengupta (Springer, Berlin, 2006)
A. Majhi, Phys. Lett. B 775, 32 (2017)
T.S. Biró, V.G. Czinner, Phys. Lett. B 726, 861 (2013)
A. Sayahian Jahromi et al., Phys. Lett. B 780, 21 (2018)
A. Bialas, W. Czyz, EPL 83, 60009 (2008)
V.G. Czinner, H. Iguchi, Phys. Lett. B 752, 306 (2016)
N. Komatsu, Eur. Phys. J. C 77, 229 (2017)
H. Moradpour, A. Bonilla, E.M.C. Abreu, J.A. Neto, Phys. Rev. D 96, 123504 (2017)
H. Moradpour, A. Sheykhi, C. Corda, I.G. Salako, Phys. Lett. B 783, 82 (2018)
H. Moradpour, Int. J. Theor. Phys. 55, 4176 (2016)
E.M.C. Abreu, J. Ananias Neto, A.C.R. Mendes, W. Oliveira, Phys. A 392, 5154 (2013)
E.M.C. Abreu, J. Ananias Neto. Phys. Lett. B 727, 524 (2013)
E.M. Barboza Jr., R.C. Nunes, E.M.C. Abreu, J.A. Neto, Phys. A Stat. Mech. Appl. 436, 301 (2015)
R.C. Nunes et al., JCAP 08, 051 (2016)
A.G. Cohen, D.B. Kaplan, A.E. Nelson, Phys. Rev. Lett. 82, 4971 (1999)
B. Guberina, R. Horvat, H. Nikolić, JCAP 01, 012 (2007)
S. Ghaffari, M.H. Dehghani, A. Sheykhi, Phys. Rev. D 89, 123009 (2014)
P. Horava, D. Minic, Phys. Rev. Lett. 85, 1610 (2000)
S. Thomas, Phys. Rev. Lett. 89, 081301 (2002)
S.D.H. Hsu, Phys. Lett. B 594, 13 (2004)
M. Li, Phys. Lett. B 603, 1 (2004)
Y.S. Myung, Phys. Lett. B 652, 223 (2007)
W. Hao, Commun. Theor. Phys. 52, 743 (2009)
B. Wang, E. Abdalla, F. Atrio-Barandela, D. Pavon, Rep. Prog. Phys. 79, 096901 (2016)
S. Wang, Y. Wang, M. Li, Phys. Rep. 696, 1 (2017)
S.A. Hayward, Class. Quantum Gravity 15, 3147 (1998)
S.A. Hayward, S. Mukohyana, M.C. Ashworth, Phys. Lett. A 256, 347 (1999)
D. Bak, S.J. Rey, Class. Quantum Gravity 17, 83 (2000)
R.G. Cai, S.P. Kim, J. High Energy Phys. 0502, 050 (2005)
M. Akbar, R.G. Cai, Phys. Rev. D 75, 084003 (2007)
R.G. Cai, L.M. Cao, Y.P. Hu, Class. Quantum Gravity 26, 155018 (2009)
Y.S. Myung, Phys. Lett. B 649, 247 (2007)
S. Capozziello, O. Luongo, Inter. J. Mod. Phy. D. 27(3), 1850029 (2018)
O. Luongo, AHEP, 2017, Article ID 1424503 (2017)
E. Chang-Young, D. Lee, JHEP 1404, 125 (2014)
M. Eune, W. Kim, Phys. Rev. D 88, 067303 (2013)
T. Jacobson, Phys. Rev. Lett. 75, 1260 (1995)
A.V. Frolov, L. Kofman, JCAP 0305, 009 (2003)
Acknowledgements
We are grateful to the anonymous reviewer for worthy hints and constructive comments. The work of H. Moradpour has been supported financially by Research Institute for Astronomy & Astrophysics of Maragha (RIAAM) under project No. 1/5237-5. JPMG and IPL are supported by CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Moradpour, H., Moosavi, S.A., Lobo, I.P. et al. Thermodynamic approach to holographic dark energy and the Rényi entropy. Eur. Phys. J. C 78, 829 (2018). https://doi.org/10.1140/epjc/s10052-018-6309-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6309-8