1 Introduction

Gravitational lensing is one of the first applications ever studied by general relativity [1]. It is formed by the deflection of light rays as photons pass closely to a compact and massive body, and the object causing a detectable deflection is usually named a gravitational lens. The study of strong gravitational lensing by black holes has received a boost due to the discovery of gravitational waves [2] which has proved the existence of black holes in the universe. It was first illuminated by Darwin in 1959 [3] that light rays have a large deviation when pass closely to an astrophysical object (such as black hole), even can wind several loops before escaping, which result in one infinite set of relativistic images on each side of the object. These relativistic images carry the information about the source stars and gravitational lens, and they could provide the profound verification of alternative theories of gravity [4,5,6,7,8,9,10,11,12,13,14]. Thus, strong gravitational lensing is regarded as a powerful indicator of the physical nature of the central celestial object, and has been studied extensively in various theories of gravity [15,16,17,18,19,20,21,22,23,24] in recent years.

As is known to all, strong gravitational lensing depends on the structure of background spacetime, the dynamical properties of the photon itself, and the interactions between light and other fields. At the same time, due to light is actually a kind of electromagnetic wave, the propagation of photon will be changed when the electromagnetic tensor coupled to curvature tensor, and this will lead to some particular phenomena on strong gravitational lensing. By considering the effects of one-loop vacuum polarization on the photons effective action for quantum electrodynamics, Drummond et al. [25] noted that the characteristics of propagation of the light are altered by the tidal gravitational forces, which could result in the superluminal phenomenon. For the reason that the equivalence principle does not hold for quantum electrodynamics in curved spacetime, this velocity shift does not imply an alteration in the causality structure of events. However, as a quantum phenomenon, the coupling constants are of the order of the square of the Compton wave length of the electron \(\lambda _e\) in this effective field theory. Recently, for physical motivation, the extended theoretical models with arbitrary coupling constants have been extensively discussed in Refs. [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. For instance, Ni [26, 27] puts forward a classical generalized electromagnetic model in which electromagnetic tensor is interacted with curvature tensor by adding some special coupled terms. And then, Ni’s model has been discussed widely in astrophysics [28,29,30,31] and black hole physics [32,33,34] basing on the consideration that, the coupling between electromagnetic tensor and curvature tensor presences reasonably in the region close to the compact and supermassive bodies at the center of galaxies due to their strong gravity and high mass density. Furthermore, Turner et al. [35,36,37,38,39,40,41,42,43] dug over Drummond’s model [25] with arbitrary coupling constants to interpret the large scale magnetic fields observed in clusters of galaxies and the power-law inflation in the early Universe. These studies show that the coupling between electromagnetic tensor and curvature tensor can exist in arbitrary coupling constants and arbitrary mass of spacetime.

It is feasible to couple electromagnetic tensor and curvature tensor through the Weyl tensor, since Weyl tensor is a function of the Riemann tensor \(R_{\mu \nu \rho \sigma }\), Ricci tensor \(R_{\mu \nu }\), and Ricci scalar R. The coupling effect has been investigated extensively in the cases of holographic conductivity and superconductors [44,45,46,47,48,49,50,51,52] and the dynamical evolution of electromagnetic field in the black hole spacetime [53,54,55,56,57]. Lots of works regarding to strong gravitational lensing have been done, i.e., the photons coupled to Weyl tensor in the background of a Schwarzschild black hole spacetime [58], and a Kerr black hole spacetime [59]. Furthermore, the time delay in strong gravitational field for photons coupled to Weyl tensor in a Schwarzschild black hole spacetime has been studied in Ref. [60].

Modern observational programs indicate that the Universe is going through a phase of accelerated expansion [61, 62] which is dominated by about \(30\%\) consists of baryonic and nonbaryonic visible and dark matter, while the remaining \(70\%\) by dark energy, characterized by negative values of the pressure to density ratio \(\omega \). If \(\omega >-\,1\), it is called as quintessence and \(\omega =-\,1\) corresponds to a cosmological constant while a phantom field if \(\omega <-\,1\). After that, phantom dark energy is an exotic kind of theoretical model with the negative kinetic energy to describe an increasing acceleration [63] and favorite by many recent precise observational data, i.e., according to the 7-year WMAP data, the value of \(\omega \) is \(-\,1.10\pm 0.14\) (\(1\sigma \)) [64], and according to the type Ia supernovae from the SNLS3 sample data, the value of \(\omega \) is \(-\,1.069^{+0.091}_{-0.092}\) [65]. If a phantom field, be it basic or effective, is part of the real field content of our Universe, it is natural to seek its manifestations in various fields of physics. In this background, regular black hole and wormhole phantom solutions with spherical symmetry were found in Ref. [66]. The stability of such a solution supported by a scalar field with a negative kinetic term has been investigated [67]. And the gravitational lensing of such kind of black holes with phantom hair has been discussed in Refs. [68,69,70]. In this paper, we are going to study the strong gravitational lensing for photons coupled to Weyl tensor in a regular phantom black hole spacetime and then probe the effects of the coupling on the deflection angle and observable.

This paper is arranged as follows. In Sect. 2, we derive the equation of motion for the photon coupled to Weyl tensor in a regular phantom black hole spacetime. In Sect. 3, we investigate the difference between the two polarizations by discussing how the coupling constant and phantom hair affect the difference of photon sphere radius, difference of minimum impact parameter and difference of deflection angle. In Sect. 4, by supposing that the gravitational field of the supermassive black hole at the centre of our Galaxy can be described by this solution, we obtain the numerical results for the difference of angular image position and the relative magnitudes of the first relativistic image between the two types of different polarized photons. Our conclusions and discussions are presented in the last section.

2 Equation of motion for photons coupled to Weyl tensor in a regular phantom black hole spacetime

We consider the action corresponding to Einstein gravity coupled to a phantom scalar field \(\Phi \)

$$\begin{aligned} S=\int \sqrt{-\,g}d^4x\left[ R-\frac{1}{2}g^{\mu \nu }\partial _{\mu } \Phi \partial _{\nu }\Phi +V\right] , \end{aligned}$$
(1)

where R is the Ricci scalar, and \( \Phi =\sqrt{2}\psi =\sqrt{2} \arctan \frac{r}{b},\) \( V=\frac{3M}{b^3}[(\frac{\pi }{2}-\psi )(3-2\cos ^2\psi )- 3\sin \psi \cos \psi ]. \) This action admits a solution describing the gravity of a regular and static spacetime with phantom scalar hair, whose metric can be written as [66]

$$\begin{aligned} ds^2=-A(r)dt^2+\frac{1}{A(r)}dr^2+C(r) (d\vartheta ^2+\sin ^2{\vartheta } d\phi ^2),\nonumber \\ \end{aligned}$$
(2)

with

$$\begin{aligned} A(r)= & {} 1-\frac{3M}{b} \left[ \left( \frac{\pi }{2}-\arctan \frac{r}{b}\right) \left( 1+\frac{r^2}{b^2} \right) -\frac{r}{b} \right] ,\nonumber \\ C(r)= & {} r^2+b^2, \end{aligned}$$
(3)

where M is the mass of black hole, and b is a positive constant related to the scalar charge of phantom field, also termed as phantom hair. When \(M<0\), we obtain a wormhole with an asymptotically anti-de Sitter region at \(r\rightarrow -\infty \) and an asymptotically flat region at \(r\rightarrow \infty \). When \(M=0\), this solution describes an Ellis wormhole, which connects two symmetric asymptotically flat regions. When \(M>0\), there is a Killing horizon \(r_{H}\) corresponding to the unique root of \(A(r)=0\). In its internal region \(r<r_{H}\), instead of a singularity, an expanding and asymptotically de Sitter–Kantowski–Sachs cosmology occurs [66, 71]. These regular black holes also receive the name of black universes. The presence of phantom hair brings richer properties for the spacetime (2). When \(0<b<\frac{3\pi M}{2}\), the event horizon \(r_{H}\) is in the range \(0<r_{H}<2M\). When \(b=\frac{3\pi M}{2}\), there does not exist any event horizon due to \(r_{H}=0\). When \(b>\frac{3\pi M}{2}\), we obtain \(r_{H}<0\), so a throat appears like a wormhole. In the limit \(b\rightarrow 0\), it is easy to find that the phantom scalar field \(\Phi \) becomes a constant \(\frac{\sqrt{2}}{2}\pi \), and the corresponding potential V approaches zero, which yields that the action turns to the usual action without any matter fields, and then the corresponding solution (2) reduces to the usual Schwarzschild black hole.

When photon coupled to the curvature of the spacetime, the Lagrangian density for the electromagnetic field can be written as [44]

$$\begin{aligned} \mathcal {L}=-\frac{1}{4}F_{\mu \nu }F^{\mu \nu }+ \hat{\alpha } C^{\mu \nu \rho \sigma }F_{\mu \nu }F_{\rho \sigma }, \end{aligned}$$
(4)

where \(F_{\mu \nu }=A_{\nu ;\mu }-A_{\mu ;\nu }\) is the electromagnetic tensor, \(\hat{\alpha }\) is a coupling constant with the dimension of length-squared, and \(C^{\mu \nu \rho \sigma }\) is the Weyl tensor. Varying the Lagrangian in Eq. (4) with respect to \(A_{\mu }\), one can easily obtain the corrected Maxwell equation

$$\begin{aligned} \nabla _{\mu }\left( F^{\mu \nu }-4\hat{\alpha } C^{\mu \nu \rho \sigma }F_{\rho \sigma }\right) =0, \end{aligned}$$
(5)

which means that the coupled to Weyl tensor will change propagation of photon in background spacetime. With the purpose of getting the equation of motion for photon from the above corrected Maxwell equation (5), we resort to the geometric optics approximation in which the photon wavelength \(\lambda _{p}\) is much smaller than a typical curvature scale \(\mathfrak {L}\), but larger than the electron Compton wavelength \(\lambda _{e}\), i.e., \(\lambda _{e}<\lambda _{p}<\mathfrak {L}\). This ensures that the changes of the background gravitational and electromagnetic field with the typical curvature scale can be neglected for the photon propagation [25, 72,73,74,75,76,77,78,79]. Under this approximation, the electromagnetic tensor can be written as

$$\begin{aligned} F_{\mu \nu }=f_{\mu \nu }e^{i\tilde{\theta }}, \end{aligned}$$
(6)

where \(f_{\mu \nu }\) is a slowly varying amplitude, so the derivative term \(f_{\mu \nu ;\lambda }\) can be neglected. Meanwhile, the quantity \(\tilde{\theta }\) is a rapidly varying phase, and the wave vector is defined as \(k_{\mu }=\partial _{\mu }\tilde{\theta }\), which can be treated as the coupled photon momentum in the usual theory of quantum particle. Based on the Bianchi identity, we note that the amplitude \(f_{\mu \nu }\) has a form \(f_{\mu \nu }=k_{\mu }a_{\nu }-k_{\nu }a_{\mu }\), here \(a_{\mu }\) is the polarization vector satisfying the condition \(k_{\mu }a^{\mu }=0\). Combining Eq. (5) with Eq. (6), we obtain the equation of motion for the photon coupled to Weyl tensor

$$\begin{aligned} k_{\mu }k^{\mu }a^{\nu }+8\hat{\alpha } C^{\mu \nu \rho \sigma }k_{\sigma }k_{\mu }a_{\rho }=0. \end{aligned}$$
(7)

The above equation shows that the wave vector for this model is not a null vector. In other words, the interactions between the electromagnetic field and the spacetime curvature lead to a dependence of the photons velocity on their polarization directions and curvature of the spacetime, so that in some cases photons travel at speeds greater or less than unity, and the birefringence takes place [73,74,75,76,77,78,79].

By taking the vierbeins fields as

$$\begin{aligned} e^a_{\mu }=diag\left( \sqrt{A(r)},\frac{1}{\sqrt{A(r)}},\sqrt{r^2+b^2},\sqrt{r^2+b^2}\sin \vartheta \right) ,\nonumber \\ \end{aligned}$$
(8)

and defining the antisymmetric combination of vierbeins as \( U^{ab}_{\mu \nu }=e^a_{\mu }e^b_{\nu }-e^a_{\nu }e^b_{\mu }, \) we can introduce three linear combinations of momentum components \(l_{\nu }=k^{\mu }U^{01}_{\mu \nu }, n_{\nu }=k^{\mu }U^{02}_{\mu \nu }, m_{\nu }=k^{\mu }U^{23}_{\mu \nu }\) [25, 77,78,79] to simplify the equation of motion for the coupled photon.

After tedious calculation, we find

$$\begin{aligned} \widetilde{g}^{00}k_0k_0+\widetilde{g}^{11}k_1k_1+\widetilde{g}^{22}k_2k_2+\widetilde{g}^{33}k_3k_3=0, \end{aligned}$$
(9)

with

$$\begin{aligned} \widetilde{g}^{00}= & {} g^{00},\\ \widetilde{g}^{11}= & {} g^{11},\\ \widetilde{g}^{22}= & {} W(r) g^{22},\\ \widetilde{g}^{33}= & {} W(r) g^{33}, \end{aligned}$$

where W(r) is

$$\begin{aligned} W(r)=\frac{3(r^2+b^2)^2+8\hat{\alpha } (b^2+3Mr)}{3(r^2+b^2)^2-16\hat{\alpha } (b^2+3Mr)}, \end{aligned}$$
(10)

for photons with the polarization along \(l_{\mu }\) (PPL), which corresponds to the case that the polarization vector \(a_{\mu }\) is proportional to \(l_{\mu }\), and

$$\begin{aligned} W(r)=\frac{3(r^2+b^2)^2-16\hat{\alpha } (b^2+3Mr)}{3(r^2+b^2)^2+8\hat{\alpha } (b^2+3Mr)}, \end{aligned}$$
(11)

for photons with the polarization along \(m_{\mu }\) (PPM), which means that the polarization vector \(a_{\mu }\) is proportional to \(m_{\mu }\).

From Eq. (9), we know that the light cone condition is not modified for the radially directed photons (i.e., \(k_{2}=k_{3}=0\)), but it is modified for the general orbital photons, and the velocities of the photons for the two polarizations are different, i.e., photons will travel at speeds greater or less than unity. Therefore, the phenomenon of gravitational birefringence takes place. Obviously, we notice that \(W(r)\rightarrow 1\) as \(\hat{\alpha }\rightarrow 0\), which implies that the photons travel at speed of unity and the phenomenon of gravitational birefringence disappears. We will study strong gravitational lensing for the PPL and PPM cases starting from Eq. (9).

Fig. 1
figure 1

Variation of the difference of photon sphere radius \(\Delta r_{ps}\) with phantom hair b (left) and coupling constant \(\widetilde{\alpha }\) (right) in the regular phantom black hole

Full size image

3 Deflection angle in strong gravitational lensing

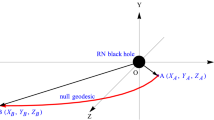
Now, we study the physical properties of strong gravitational lensing as photons coupled to Weyl tensor in the background of a regular phantom black hole, and probe the effects of coupling and polarization types on strong gravitational lensing. For the spherically symmetric black hole spacetime, the photons coming from infinite always move on a central planes of the black hole. Since any central planes can be transformed into the equatorial plane by coordinate transformation, we only consider that both the observer and the source lie in the equatorial plane (\(\vartheta =\frac{\pi }{2}\)), and the photon is confined on the same plane. It is well known that photons with different polarizations have different trajectories, so there are two sets of relativistic images on each side of the object. However, in our paper, we only consider the relativistic images on one side of the object due to the relativistic images on both sides of the object are symmetric when the angular source position is small.

From the symmetry of the static phantom black hole, we can define the energy and angular momentum as \( E=-\widetilde{g}_{00}\dot{x}^{0}=A(r)\dot{t}\) and \( L=\widetilde{g}_{33}\dot{x}^{3}=C(r)W(r)^{-1} \dot{\phi }, \) where a dot represents a derivative with respect to affine parameter \(\lambda \). Taking advantage of the relationship \(k_{\mu }=\widetilde{g}_{\mu \nu }\frac{dx^{\nu }}{d\lambda }\), we can express the equation of motion (9) for coupled photon as

$$\begin{aligned} \left( \frac{dr}{d\lambda } \right) ^2 =A(r) \left[ \frac{E^2}{A(r)}-W(r)\frac{L^2}{C(r)} \right] . \end{aligned}$$
(12)

It is useful for the calculation to follow the scaling symmetries in the forms

$$\begin{aligned}&\frac{r}{2M}\rightarrow r,\quad \frac{t}{2M}\rightarrow t,\quad \frac{b}{2M}\rightarrow b,\quad \frac{E}{2M}\rightarrow E,\nonumber \\&\frac{\hat{\alpha }}{(2M)^{2}}\rightarrow \hat{\alpha }, \quad \frac{C(r)}{(2M)^{2}}\rightarrow C(r),\quad \frac{L}{(2M)^{2}}\rightarrow L. \end{aligned}$$
(13)

After taking the scaling symmetries, the Eq. (12) still takes the same form as above. It is easy to find that \(\hat{\alpha }\) is a constant with the dimension of length-squared, and in order to be consistent with the observation, we have to constrain \(|\hat{\alpha }|\le 10^{13} m^{2}\) [80]. If we take the mass of the black hole in the Galactic center as \(4.4\times 10^{6}M_{\odot }\) [81], the dimensionless \(\hat{\alpha } \sim 10^{-7}\), then we denote \(\widetilde{\alpha }=\hat{\alpha }/10^{-7}\) for simplicity. By setting \(E=1\) and conservation of the angular momentum along the null geodesics, we can get the relation between the impact parameter u (projected distance of closest approach to the lens [82]) and the distance of the closest approach of the light ray \(r_{0}\) as

$$\begin{aligned} u=\frac{L}{E}=\sqrt{\frac{C(r_{0})}{A(r_{0})W(r_{0})}}. \end{aligned}$$
(14)

And then, the equation of the photon sphere can be expressed as

$$\begin{aligned}&W(r)[A'(r)C(r)-A(r)C'(r)]\nonumber \\&\quad +A(r)C(r)W'(r)=0, \end{aligned}$$
(15)

where the prime represents the derivative with respect to r.

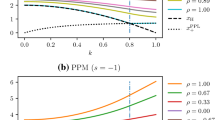
The photon sphere radius \(r_{ps}\) is defined as the biggest real root of Eq. (15). However, we have to resort to the numerical method because Eq. (15) is too complicated to solve analytically. After that, we get the photon sphere radius \(r_{ps}\) is about 1.5 whether for PPL case or PPM case. Furthermore, in this paper, we care more about the difference between PPL case and PPM case. Therefore, we define the difference of photon sphere radius \(\Delta r_{ps}\) as \(\Delta r_{ps}=r_{ps(PPL)}-r_{ps(PPM)}\), and then we plot the variation of \(\Delta r_{ps}\) in terms of phantom hair b and coupling parameter \(\widetilde{\alpha }\) in Fig. 1. We can find that \(|\Delta r_{ps}|\) increases with the increase of \(|\widetilde{\alpha }|\) for fixed b or with the decrease of b for fixed \(\widetilde{\alpha }\). It implies that it is easy to distinguish the PPL case from PPM case when the effect of \(\widetilde{\alpha }\) is enhanced or the effect of b is reduced. We can also find that \(\Delta r_{ps}<0\) which means \(r_{ps(PPL)}<r_{ps(PPM)}\) for \(\widetilde{\alpha }>0\) and \(\Delta r_{ps}>0\) which means \(r_{ps(PPL)}>r_{ps(PPM)}\) for \(\widetilde{\alpha }<0\), this will be analyzed in conjunction with the deflection angle later. It should be pointed out that the result recovers to the result of uncoupled case [68, 69] when \(\widetilde{\alpha }=0\), so there is no difference between PPL case and PPM case, i.e., \(\Delta r_{ps}=0\) which shows us that the green lines in the left panel in Fig. 1 couple to the axis, and all the lines in the right panel intersect at the origin. It is worthy to note that the presence of the couple between the photons and Weyl tensor brings richer behaviors for the photon sphere radius \(r_{ps}\), and \(r_{ps}\) has an impact on all of the physical quantities in strong gravitational lensing.

The deflection angle \(\alpha (r_{0})\) for a photon coming from infinity to the closest approach distance \(r_{0}\) is defined as [83]

$$\begin{aligned} \alpha (r_{0})=I(r_{0})-\pi , \end{aligned}$$
(16)

where \(I(r_{0})\) is

$$\begin{aligned} I(r_0)=2\int ^{\infty }_{r_0}\frac{dr}{\sqrt{\frac{A(r) C(r)}{W(r)}} \sqrt{\frac{A(r_0)C(r)W(r_0)}{A(r)C(r_0)W(r)}-1}}. \end{aligned}$$
(17)

It is easy to observe that as the closest approach distance \(r_{0}\) decreases, the deflection angle increases. We also note that the deflection angle becomes \(2\pi \) for a certain value of \(r_{0}\), which means that the light ray makes a complete loop around the compact object before reaching the observer. When \(r_{0}\) is equal to the photon sphere radius \(r_{ps}\), we can find that the deflection angle diverges and the photon is captured by the black hole. In order to find the behavior of the deflection angle for photons closed to the photon sphere, we adopt the evaluation method proposed by BozzaFootnote 1 [9, 10] to work out the integral (17). Defining a new variable \( z=1-\frac{r_{0}}{r}, \) the integral (17) can be expressed as

$$\begin{aligned} I(r_{0})=\int ^{1}_{0}R(z,r_{0})f(z,r_{0})dz, \end{aligned}$$
(18)

with

$$\begin{aligned} R(z,r_0)= & {} 2\frac{r_0}{(1-z)^{2}} \frac{\sqrt{C(0,r_0)}}{C(z,r_0)} \frac{W(z,r_0)}{\sqrt{W(0,r_0)}}, \end{aligned}$$
(19)
$$\begin{aligned} f(z,r_0)= & {} \frac{1}{\sqrt{A(0,r_0)-A(z,r_0)\frac{C(0,r_0) W(z,r_0)}{C(z,r_0) W(0,r_0)}}}, \end{aligned}$$
(20)

where \(R(z,r_{0})\) is regular for all values of z and \(r_{0}\), but \(f(z,r_{0})\) diverges for \(z\rightarrow 0\). For the sake of finding the order of divergence of the integrand, we take a Taylor expansion for the argument of the square root in \(f(z,r_{0})\) to the second order in z, then we get

$$\begin{aligned} f_{0}(z,r_{0})=\frac{1}{\sqrt{p(r_{0})z+q(r_{0})z^{2}}}, \end{aligned}$$
(21)

with

$$\begin{aligned} p(r_0)= & {} \frac{r_0}{C(r_0)} \left[ \phantom {\frac{W'(r_0)}{W(r_0)}}A(r_0)C'(r_0)-A'(r_0)C(r_0)\right. \nonumber \\&\left. -\,A(r_0)C(r_0) \frac{W'(r_0)}{W(r_0)}\right] , \nonumber \\ q(r_0)= & {} \frac{r_0}{2C^{2}(r_0)W^{2}(r_0)} \left\{ \phantom {W'^{2}(r_0)}2[C(r_0)W(r_0)\right. \nonumber \\&-\,r_{0}(C'(r_0)W(r_0)-C(r_0)W'(r_0))]\nonumber \\&\times \,[A(r_0)(C'(r_0)W(r_0)-C(r_0)W'(r_0))\nonumber \\&-\,A'(r_0)C(r_0)W(r_0)]+r_{0}C(r_0)\nonumber \\&\times \,[A(r_0)(C''(r_0)W^{2}(r_0)\nonumber \\&-\,2C'(r_0)W(r_0)W'(r_0)-C(r_0)W(r_0)W''(r_0)\nonumber \\&\left. +\,2C(r_0)W'^{2}(r_0))-A''(r_0)C(r_0)W^{2}(r_0)] \right\} . \end{aligned}$$
(22)
Fig. 2
figure 2

Variation of the difference of minimum impact parameter \(\Delta u_{ps}\) with phantom hair b (left) and coupling constant \(\widetilde{\alpha }\) (right) in the regular phantom black hole

Full size image
Fig. 3
figure 3

Variation of the difference of the strong deflection limit coefficients \(\Delta \bar{a}\) with phantom hair b (left) and coupling constant \(\widetilde{\alpha }\) (right) in the regular phantom black hole

Full size image
Fig. 4
figure 4

Variation of the difference of deflection angle \(\Delta \alpha (\theta )\) evaluated at \(u=u_{ ps}+0.003\) with the phantom hair b (left) and coupling constant \(\widetilde{\alpha }\) (right) in the regular phantom black hole

Full size image

Comparing Eq. (15) with Eq. (22), we can find that if \(r_{0}\) tends to the radius of photon sphere \(r_{ps}\), the coefficient \(p(r_0)\) approaches zero, and then the integral (18) diverges logarithmical since the leading term of the divergence in \(f(z, r_{0})\) is \(\frac{1}{z}\). Thus, we can split the integral (18) into divergent part \(I_{D}(r_{0})\) and regular part \(I_{R}(r_{0})\)

$$\begin{aligned} I_{D}(r_{0})= & {} \int ^{1}_{0}R(0,r_{ps})f_{0}(z,r_{0})dz, \end{aligned}$$
(23)
$$\begin{aligned} I_{R}(r_{0})= & {} \int ^{1}_{0}[R(z,r_{0})f(z,r_{0})-R(0,r_{ps})f_{0}(z,r_{0})]dz.\nonumber \\ \end{aligned}$$
(24)

Afterwards, we solve the above two integrals separately, and sum up their results to get the deflection angle

$$\begin{aligned} \alpha (\theta )=-\bar{a}\log \left( \frac{\theta D_{OL}}{u_{ps}}-1\right) +\bar{b}+o(u-u_{ps}), \end{aligned}$$
(25)

with

$$\begin{aligned}&\bar{a}=\frac{R(0,r_{ps})}{2{\sqrt{q(r_{ps})}}},\qquad b_R=I_R(r_{ps}), \nonumber \\&\bar{b}= -\pi +b_R+\bar{a}\log {\frac{2q(r_{ps})}{A(r_{ps})}},\nonumber \\&u_{ps}={\sqrt{\frac{C(r_{ps})}{A(r_{ps})W(r_{ps})}}}, \end{aligned}$$
(26)

where \(D_{OL}\) denotes the distance between the observer and the gravitational lens, and \(\theta =\frac{u}{D_{OL}}\) is the angular image separation between the optical axis and the direction of image, \(u_{ps}\) is the minimum impact parameter which represents the impact parameter u evaluated at \(r_{ps}\), and the coefficients \(\bar{a}\) and \(\bar{b}\) are the so-called strong deflection limit coefficients. Making use of Eqs. (25) and (26), we can study the properties of strong gravitational lensing for the coupled photons in a regular phantom black hole spacetime. According to studying the difference between PPL case and PPM case, we define \(\Delta u_{ps}=u_{ps(PPL)}-u_{ps(PPM)}\), \(\Delta \bar{a}=\bar{a}_{(PPL)}-\bar{a}_{(PPM)}\) and \(\Delta \alpha (\theta )=\alpha (\theta )_{(PPL)}-\alpha (\theta )_{(PPM)}\). Then we plot them with phantom hair b for fixed \(\widetilde{\alpha }\) and with coupling constant \(\widetilde{\alpha }\) for fixed b in Figs. 2, 3, 4.

From Figs. 1 and 2, it is easy to find that the changes of the difference of minimum impact parameter \(\Delta u_{ps}\) are exactly similar to the difference of photon sphere radius \(\Delta r_{ps}\). It is due to that the impact parameter u is defined as the perpendicular distance between the path of the emergent ray and the gravitational lens, and it can be equated to the closest approach distance in some sense. Moreover, the light in the strong gravitational lensing that we are studying is in vicinity of the photon sphere and \(u_{ps}\) is the u evaluated at \(r_{ps}\), so \(\Delta u_{ps}\) and \(\Delta r_{ps}\) changes similarly. The Fig. 3 shows that \(\Delta \bar{a}\) increases for negative \(\widetilde{\alpha }\) and decreases for positive one with the increase of phantom hair b, and \(\Delta \bar{a}\) increases with the increase of coupling parameter \(\widetilde{\alpha }\) for fixed b. From Fig. 4, we find that the difference of deflection angle \(\Delta \alpha (\theta )\) in the strong deflection limit has similar behaviors to \(\Delta \bar{a}\). Furthermore, our calculation shows that the deflection angle \(\alpha (\theta )\) and strong deflection limit coefficient \(\bar{a}\) are similar too. These two cases imply that the deflection angle of the light rays is dominated by the logarithmic term. Next, let’s give a special analysis of \(\widetilde{\alpha }>0\) situation. We can get from Fig. 1 that \(r_{ps(PPL)}<r_{ps(PPM)}\) when \(\widetilde{\alpha }>0\), and there is no doubt about \(u_{ps(PPL)}<u_{ps(PPM)}\). Then, Fig. 4 shows that \(\alpha (\theta )_{(PPL)}>\alpha (\theta )_{(PPM)}\) for \(\widetilde{\alpha }>0\). For the \(\widetilde{\alpha }<0\) situation, the changes of physical quantities are contrary to that of \(\widetilde{\alpha }>0\). This is the same as our previous knowledge that the closer the light gets to the black hole, the larger the deflection angle will be. What we can’t forget is that all the above physical quantities have no difference for \(\widetilde{\alpha }=0\) due to the result recovers to the result of uncoupled case [68, 69]. And the absolute value of the difference of each physical quantities increase with the increase of the absolute value of the coupling constant \(\widetilde{\alpha }\) or with the decrease of phantom hair b. It implies that it is easy to distinguish the PPL case from PPM case when the effect of \(\widetilde{\alpha }\) is enhanced or the effect of b is reduced.

4 Observable in strong gravitational lensing

We are now in the position to calculate the observable in strong gravitational lensing for the coupled photons in a regular phantom black hole spacetime, including the difference of the angular image position \(\Delta \theta \) and the relative magnitudes \(\mathcal {R}\). Considering the source, lens, and observer are highly aligned, the lens equation in strong gravitational lensing can be written as [9, 10]

$$\begin{aligned} \beta =\theta -\frac{D_{LS}}{D_{OS}}\triangle \alpha _{n}, \end{aligned}$$
(27)

where \(\beta \) is called as angular source position which is the angle separation between the direction of the source and the optical axis. \(D_{LS}\) and \(D_{OS}\) are the lens-source distance and the observer-source distance, and they satisfy \(D_{OS}=D_{LS}+D_{OL}\). \(\triangle \alpha _{n}=\alpha (\theta )-2n\pi \) is the offset of the deflection angle, and n is an integer that indicates the number of loops done by the photon around the black hole. Since the angular source position \(\beta \) and the angular image position \(\theta \) are small, we obtain the position of the nth relativistic image

$$\begin{aligned} \theta _{n}\simeq \theta ^{0}_{n}+\frac{u_{ps}e_{n} (\beta -\theta _{n}^{0})D_{OS}}{\bar{a}D_{LS}D_{OL}}, \end{aligned}$$
(28)

with

$$\begin{aligned} \theta _{n}^{0}=\frac{u_{ps}}{D_{OL}}(1+e_{n}),\quad e_{n}=e^{\frac{\bar{b}-2n\pi }{\bar{a}}}, \end{aligned}$$
(29)

where \(\theta _{n}^{0}\) is the angular image position corresponding to \(\alpha (\theta )=2n\pi \). Another important information is the magnification of the \(n\hbox {th}\) relativistic image

$$\begin{aligned} \mu _{n}=\left. \frac{1}{\frac{\beta }{\theta }\frac{\partial \beta }{\partial \theta }}\right| _{\theta ^{0}_{n}} =\frac{u_{ps}^{2}e_{n}(1+e_{n})D_{OS}}{\bar{a}\beta D^{2}_{OL}D_{LS}}. \end{aligned}$$
(30)

It is not hard to find that the magnification decreases exponentially with n, so the first relativistic image is the brightest.

In order to analyze how the coupling constant, phantom hair and polarization affect the observable, we focus our attention on the difference between the PPL and PPM cases of the first relativistic image. We define the difference of angular image position \(\Delta \theta \) as \(\Delta \theta =\theta _{1(PPL)}-\theta _{1(PPM)}\), and the relative magnitudes \(\mathcal {R}\) as \(\mathcal {R}=2.5log \left[ \frac{\mu _{1(PPL)}}{\mu _{1(PPM)}}\right] \).

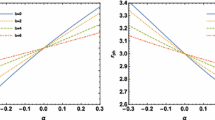
Now, we consider the supermassive black hole in the Galactic center can be described by this regular phantom black hole and the photon coupled to Weyl tensor. The mass of the central object is \(4.4\times 10^{6}M_{\odot }\) [81], and its distance from the Earth is \(8.5\hbox {kpc}\); so the ratio of the mass to the distance is \(\frac{M}{D_{OL}}\approx 2.4734\times 10^{-11}\). With this data, we can estimate the difference between PPL and PPM observable for strong gravitational lensing. From Fig. 5, we can easily find that \(\Delta \theta =0\) and \(\mathcal {R}=0\) when \(\widetilde{\alpha }=0\), which means that the image for PPL coincides with that of PPM. That is to say, the unique image represents the result of the phantom black hole for uncoupled case [68, 69]. And Fig. 5 shows that with the decrease of phantom hair b for fixed \(\widetilde{\alpha }\) or with the increase of \(|\widetilde{\alpha }|\) for fixed b, the absolute value of \(\Delta \theta \) and \(\mathcal {R}\) increase, which shows that two images for PPL and PPM will separate further and be distinguished more easily. We can also get from Fig. 5 that \(\Delta \theta <0\) and \(\mathcal {R}>0\) for \(\widetilde{\alpha }>0\), which implies that the image of PPL is closer to the optical axis and brighter than the image of PPM. However, \(\Delta \theta >0\) and \(\mathcal {R}<0\) for \(\widetilde{\alpha }<0\), which is opposite to the case of \(\widetilde{\alpha }>0\). In general, the image is brighter when it seats closer to the optical axis.

Fig. 5
figure 5

Variation of the difference of angular image position \(\Delta \theta \) (the top two panels) and relative magnitude \(\mathcal {R}\) (the bottom two panels) between PPL and PPM with phantom hair b and coupling constant \(\widetilde{\alpha }\) in the regular phantom black hole. The angular is expressed in \(\mu \) arc seconds

Full size image

5 Summary

We study strong gravitational lensing for photons coupled to Weyl tensor in a regular phantom black hole spacetime. We notice that photons with different polarizations have different trajectories when the photons coupled to the curvature of the spacetime, so there are two sets of relativistic images on each side of the object. The result is quite different from the uncoupled case which only has one set of relativistic images [68, 69]. Here, we only focus our attention on the two sets of relativistic images on one side of the object because the relativistic images on both sides of the object are symmetric when the angular source position is small, and we investigate the difference between PPL case and PPM case by discussing how the coupling constant and phantom hair affect the difference for all of the physical quantities in strong gravitational lensing, such as photon sphere radius, minimum impact parameter, deflection angle, angular image position and relative magnitudes.

From Figs. 1 and 2, it is easy to find that the changes of the difference of minimum impact parameter \(\Delta u_{ps}\) are exactly similar to the difference of photon sphere radius \(\Delta r_{ps}\). It is due to that the impact parameter u is defined as the perpendicular distance between the path of the emergent ray and the gravitational lens, and it can be equated to the closest approach distance in some sense. Additionally, the light in the strong gravitational lensing that we are studying is in vicinity of the photon sphere and \(u_{ps}\) is the u evaluated at \(r_{ps}\), so \(\Delta u_{ps}\) and \(\Delta r_{ps}\) changes similarly. Figures 3 and 4 show that the difference of deflection angle \(\Delta \alpha (\theta )\) in the strong deflection limit has similar behaviors to \(\Delta \bar{a}\). What’s more, our calculation shows that the deflection angle \(\alpha (\theta )\) and strong deflection limit coefficient \(\bar{a}\) are similar too. These two cases imply that the deflection angle of the light rays is dominated by the logarithmic term. From Figs. 1, 2, 3, 4, we can find that the absolute value of the difference of each physical quantities increase with the increase of the absolute value of the coupling constant \(\widetilde{\alpha }\) or with the decrease of phantom hair b. It implies that it is easy to distinguish the PPL case from PPM case when the effect of \(\widetilde{\alpha }\) is enhanced or the effect of b is reduced. Figs. 1, 2, 3, 4 also show that the green lines in the left panel couple to the axis, while all the lines in the right panel intersect at the origin. This is because that the result recovers to the result of uncoupled case [68, 69] when \(\widetilde{\alpha }=0\), then there is no difference between PPL case and PPM case. Next, let’s give a special analysis of \(\widetilde{\alpha }>0\) situation. We can get from Fig. 1 that \(r_{ps(PPL)}<r_{ps(PPM)}\) when \(\widetilde{\alpha }>0\), and there is no doubt about \(u_{ps(PPL)}<u_{ps(PPM)}\). Then, Fig. 4 shows that \(\alpha (\theta )_{(PPL)}>\alpha (\theta )_{(PPM)}\) for \(\widetilde{\alpha }>0\). For the \(\widetilde{\alpha }<0\) situation, the changes of physical quantities is contrary to that of \(\widetilde{\alpha }>0\). This is the same as our previous knowledge that the closer the light gets to the black hole, the larger the deflection angle will be.

By supposing that the gravitational field of the supermassive black hole at the centre of our Galaxy can be described by this solution, we obtain the numerical results for the difference of angular image position and the relative magnitudes of the first relativistic image between the PPL and PPM cases. We find that \(\Delta \theta =0\) and \(\mathcal {R}=0\) when \(\widetilde{\alpha }=0\) which means that the image for PPL coincides with that of PPM. That is to say, the unique image represents the result of the phantom black hole for uncoupled case [68, 69]. Then, the absolute value of \(\Delta \theta \) and \(\mathcal {R}\) increase with the decrease of phantom hair b for fixed \(\widetilde{\alpha }\) or with the increase of \(|\widetilde{\alpha }|\) for fixed b, which shows that two images for PPL and PPM will separate further and be distinguished more easily. We also find that \(\Delta \theta <0\) and \(\mathcal {R}>0\) for \(\widetilde{\alpha }>0\), which implies that the image of PPL is closer to the lens and brighter than the image of PPM. However, we notice that \(\Delta \theta >0\) and \(\mathcal {R}<0\) for \(\widetilde{\alpha }<0\), which is opposite to the case of \(\widetilde{\alpha }>0\). In general, the image is brighter when it seats closer to the optical axis.