1 Introduction

Up to present, Einstein’s general relativity is one of the most successful gravity theories. It coincides with the experiments at the highest achievable precision such as the perihelion precession of mercury, bending of light, radar echo delay, gravitational red-shift and so on. However, Einstein’s gravity theory may exist some problems in understanding gravity correctly at all scales. It cannot accurately describe the accelerated expansion of universe on large scales, and it is very difficult to establish a complete theory of quantum gravity at the micro-scale. This leads to various modifications of gravity theory, including Superstring theory [1], scalar-tensor theories [2], Lovelock gravity [3], Hořava–Lifshitz gravity [4], f(R) gravity [5], etc.

It is widely known that spacetime of Einstein’s general relativity is described by a Riemannian geometry. Since there exists some problems in general relativity, scientists have proposed to modify gravity theory by improving differential geometry. As the generalization of Riemannian geometry, Finsler geometry [6, 7] is the most general geometry, in which the line element is dependent on not only spacetime coordinates but also tangent vectors. Namely \(d{s^2} = f({x^\alpha }, d{x^\beta })\); \(d{s^2} = f({x^\alpha },\mu d{x^\beta }) = {\mu ^2}f({x^\alpha },d{x^\beta })\), and the metric can also be given by \(d{s^2} = {\mathcal{G}_{\alpha \beta }}d{x^\alpha }d{x^\beta }\), where noting that \({\mathcal{G}_{\alpha \beta }}\) is related to \(d{x^\alpha }\). This geometry can reduce to a Riemannian geometry when \(f({x^\alpha },d{x^\beta })\) becomes a quadratic form in the \(d{x^\beta }\). The applications of the Finsler geometry to general relativity and black hole physics have attracted a great deal of attention. Making use of Finsler geometry, Bekenstein discussed on the relation between gravitational and physical geometries within the two-geometries paradigm for gravitational theory [8]. An introduction to Finsler–Lagrange geometry in Einstein and string gravity was also presented [9]. In Ref. [10], Mavromatos pointed out the relationship between Finsler geometry and some methods to the Quantum Gravity problem. Recently, taking into account Finsler geometry can account for Planckian structure of relativistic particles’ configuration space , generalizing the results obtained in Ref. [11], Lobo, Loret and Nette studied the possibility to Planck-scale-deformed relativity in the context of Finsler geometry [12]. In addition, researchers have developed intensively some directions to construct various classes of Finsler black hole solutions [13,14,15,16,17]. Although gravity theory in the framework of Finsler geometry is still with great difficulties, the developments mentioned above have suggested that Finsler gravity theory has some potential to resolve some problems in general relativity, and the related works following this line of thought are constantly in progress.

On the other hand, based on the generalized uncertain principle (GUP), near Planck scale, the remnant of a black hole has generated enormous interest. Adler, Chen and Santiago argued that, just as the uncertainty principle can prevent the hydrogen atom from collapse, the GUP may effectively prevent a Schwarzschild black hole from evaporating completely when the radius arrives at the order of Planck length [18]. Based on this successful idea, applying the revised thermodynamics laws, Banerjee and Ghosh [19] proposed that the singularity can be avoided, since a black hole evaporation ceases at the remnant, and the singular mass is less than the remnant.

At the same time, utilizing GUP and the holographic principle, Scardigli, Gruber and Chen [20] numerically calculated the production of micro black holes remnants in the early pre-inflationary universe, and predicted that black hole can only evaporate down to Planck scale. Recently, via the generalized Dirac equation, incorporating GUP into the fermions’ tunneling method, Chen et al. showed how the remnant of a black hole arose according to the revised Hawking temperature-uncertainty relation, and estimated the reside mass. Following that, this process was generalized to the cases of scalar particles’ tunneling radiation [21]. More recently, close to the Planck scale in gravity’s rainbow, by employing the formation of remnant that is related to the form of rainbow functions, the remnants of black holes were discussed [22, 23]. All of these results predict that the existence of black hole remnant, however the stability of remnant has been comparatively less illustrated, and relevant problems still need to be resolved.

Motivated by mentioned above, in this paper, we would like to discuss the remnant and its stability of a Finsler black hole in the final stage of evaporation. As we all know, thermodynamics stability of a black hole is related to the heat capacity. To guarantee a black hole is in the thermal stability, when the black hole evaporates down to Planck scale, the black hole with negative heat capacity has to change to the black hole with positive heat capacity, which implies the black hole will undergo a phase transition. To explore whether there exists stable remnant in a Finsler spacetime, here, considering a simple Finsler black hole, namely Rutz-Schwarzschild black hole, we attempt to investigate the remnant and phase transition in detail.

2 A Finsler black hole and quantum tunneling

Now, let’s simply review a Rutz-Schwarzschild black hole solution in Finsler geometry. In 1993, Rutz discussed a vacuum gravity field equation in Finsler spacetime and resolved a Finsler black hole solution with spherical symmetry [13]

$$\begin{aligned} d{s^2} =&- \left( 1 - \frac{{2M}}{r}\right) \left( {1 - \frac{{\varepsilon d\Omega }}{{dt}}}\right) d{t^2} + {\left( 1 - \frac{{2M}}{r}\right) ^{ - 1}}d{r^2} \nonumber \\&+ {r^2}d{\Omega ^2}, \end{aligned}$$
(1)

where \(\varepsilon \ll 1\), and \( - \varepsilon d\Omega /dt\) is the Finsler correction on the Schwarzschild black hole. It is obvious that \({r_ + } = 2M\) is the event horizon of the Finsler black hole, and the time component of the line element is related to not only the spacetime coordinates but also the tangent vector \(d\Omega /dt\). Making use of the metric, let’s begin to investigate the fermion particle’s quantum tunneling. In a curved spacetime, based on the corrected commutation relations [24], the generalized Dirac equation can be presented as [25, 26]

$$\begin{aligned}&i\gamma ^0 \partial _0 + i\gamma ^i \partial _i \left( {1 - \beta m^2 } \right) + i\gamma ^i \beta \hbar ^2 \left( {\partial _j \partial ^j } \right) \partial _i \nonumber \\&+ \frac{m}{\hbar }\left( {1 + \beta \hbar ^2 \partial _j \partial ^j - \beta m^2 } \right) \nonumber \\&+ i\gamma ^\mu \frac{i}{\hbar }eA_\mu \left( {1 + \beta \hbar ^2 \partial _j \partial ^j - \beta m^2 } \right) \nonumber \\&+ i\gamma ^\mu \Omega _\mu \left( {1 + \beta \hbar ^2 \partial _j \partial ^j - \beta m^2 } \right) \psi = 0, \end{aligned}$$
(2)

where

$$\begin{aligned}&{\Omega _\mu } = \frac{i}{2}\omega _\mu ^{ab}{\sum _{ab}},{\sum _{ab}} = \frac{i}{4}\left[ {{\gamma ^a},{\gamma ^b}} \right] ,\left\{ {{\gamma ^a},{\gamma ^b}} \right\} = 2{\eta ^{ab}}, \nonumber \\&{\omega _\mu }{^a_b} = {e_\nu }^a{e^\lambda }_b\Gamma _{\mu \lambda }^\nu - {e^\lambda }_b{\partial _\mu }e_\lambda ^a,{\gamma ^\mu } = {e^\mu }_a{\gamma ^a},\nonumber \\ {}&\left\{ {\gamma ^\mu },{\gamma ^\nu } \right\} = 2{g^{\mu \nu }}, \end{aligned}$$
(3)

And the parameter \(\beta = {\beta _0}l_p^2/{\hbar ^2} = {\beta _0}/M_p^2{c^2}\), \({\beta _0}\left( { \le {{10}^{34}}} \right) \) is a dimensionless constant, here, \({l_p}\) and \({M_p}\) stand for the Planck length \(\left( { \sim {{10}^{ - 35}}m} \right) \) and Planck mass. With rational approximation, ignoring the small physical quantity, we can adopt the modified Dirac equation to discuss on the tunneling radiation from a Rutz-Schwarzschild black hole. For the spin-up case, the wave function of the generalized Dirac equation can be taking the following ansatz

$$\begin{aligned} \psi (t,r,\theta ,\varphi ) = \left( \begin{array}{l} A(t,r,\theta ,\varphi )\\ 0\\ B(t,r,\theta ,\varphi )\\ 0 \end{array} \right) \exp \left( {\frac{i}{\hbar }{I_ \uparrow }(t,r,\theta ,\varphi )} \right) \end{aligned}$$
(4)

The corresponding gamma matrices of the Finsler black hole are:

$$\begin{aligned}&\gamma ^t = \left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {1 - \frac{{\varepsilon d\Omega }}{{dt}}} \right) } \right] ^{ - \frac{1}{2}} \left( {\begin{array}{*{20}c} i &{} 0 \\ 0 &{} i \\ \end{array}} \right) , \nonumber \\&\gamma ^r = \sqrt{1 - \frac{{2M}}{r}} \left( {\begin{array}{*{20}c} 0 &{} {\sigma ^3 } \\ {\sigma ^3 } &{} 0 \\ \end{array}} \right) , \nonumber \\&\gamma ^\theta = \frac{1}{r}\left( {\begin{array}{*{20}c} 0 &{} {\sigma ^1 } \\ {\sigma ^1 } &{} 0 \\ \end{array}} \right) , \nonumber \\&\gamma ^\phi = \frac{1}{{r\sin \theta }}\left( {\begin{array}{*{20}c} 0 &{} {\sigma ^2 } \\ {\sigma ^2 } &{} 0 \\ \end{array}} \right) , \end{aligned}$$
(5)

and \({\sigma ^i}\left( {i = 1,2,3} \right) \) are Pauli sigma matrices.

$$\begin{aligned} {\sigma ^1} = \left( {\begin{array}{*{20}{c}} 0&{}1\\ 1&{}0 \end{array}} \right) ,{\sigma ^2} = \left( {\begin{array}{*{20}{c}} 0&{}{ - i}\\ { - i}&{}0 \end{array}} \right) ,{\sigma ^3} = \left( {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}{ - 1} \end{array}} \right) . \end{aligned}$$
(6)

Inserting the ansatz Eq. (4) and the matrices Eq. (5) into the equation Eq. (2), we employ the WKB approximation to resolve this equation, and neglect the higher-order terms of \(\hbar \). This gives the following equations:

$$\begin{aligned}&- iA\left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {1 - \frac{{\varepsilon d\Omega }}{{dt}}} \right) } \right] ^{ - \frac{1}{2}} \partial _t I_ \uparrow - B\sqrt{1 - \frac{{2M}}{r}} \nonumber \\&\times \left( {1 - \beta m^2 } \right) \partial _r I_ \uparrow - Am\beta \left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {\partial _r I_ \uparrow } \right) ^2 } \right. \nonumber \\&\left. { +\, \frac{1}{{r^2 }}\left( {\partial _\theta I_ \uparrow } \right) ^2 + \frac{1}{{r^2 \sin ^2 \theta }}\left( {\partial _\phi I_ \uparrow } \right) ^2 } \right] + Am\left( {1 - \beta m^2 } \right) \nonumber \\&+ B\beta \sqrt{1 - \frac{{2M}}{r}} \left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {\partial _r I_ \uparrow } \right) ^2 + \frac{1}{{r^2 }}\left( {\partial _\theta I_ \uparrow } \right) ^2 } \right. \nonumber \\&\left. { +\, \frac{1}{{r^2 \sin ^2 \theta }}\left( {\partial _\phi I_ \uparrow } \right) ^2 } \right] \partial _r I_ \uparrow = 0. \end{aligned}$$
(7)
$$\begin{aligned}&iB\left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {1 - \frac{{\varepsilon d\Omega }}{{dt}}} \right) } \right] ^{ - \frac{1}{2}} \partial _t I_ \uparrow - A\sqrt{1 - \frac{{2M}}{r}} \nonumber \\&\left( {1 - \beta m^2 } \right) \partial _r I_ \uparrow + A\beta \sqrt{1 - \frac{{2M}}{r}} \left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {\partial _r I_ \uparrow } \right) ^2 } \right. \nonumber \\&\left. { +\, \frac{1}{{r^2 }}\left( {\partial _\theta I_ \uparrow } \right) ^2 + \frac{1}{{r^2 \sin ^2 \theta }}\left( {\partial _\phi I_ \uparrow } \right) ^2 } \right] \partial _r I_ \uparrow - Bm\beta \times \nonumber \\&\left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {\partial _r I_ \uparrow } \right) ^2 + \frac{1}{{r^2 }}\left( {\partial _\theta I_ \uparrow } \right) ^2 } \right] + \frac{1}{{r^2 \sin ^2 \theta }}\left( {\partial _\phi I_ \uparrow } \right) ^2 \nonumber \\&+ Bm\left( {1 - \beta m^2 } \right) = 0. \end{aligned}$$
(8)
$$\begin{aligned}&\mathrm{{A}}\left\{ { - \left( {1 - \beta m^2 } \right) \frac{1}{r}\partial _\theta I_ \uparrow + \beta \frac{1}{r}\partial _\theta I_ \uparrow \left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {\partial _r I_ \uparrow } \right) ^2 } \right. } \right. \nonumber \\&\left. { +\, \frac{1}{{r^2 }}\left( {\partial _\theta I_ \uparrow } \right) ^2 + \frac{1}{{r^2 \sin ^2 \theta }}\left( {\partial _\phi I_ \uparrow } \right) ^2 } \right] - i\left( {1 - \beta m^2 } \right) \frac{1}{{r\sin \theta }}\partial _\phi I_ \uparrow \nonumber \\&+ i\beta \frac{1}{{r\sin \theta }}\partial _\phi I_ \uparrow \left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {\partial _r I_ \uparrow } \right) ^2 + \frac{1}{{r^2 }}\left( {\partial _\theta I_ \uparrow } \right) ^2 } \right. \nonumber \\&\left. {\left. { + \frac{1}{{r^2 \sin ^2 \theta }}\left( {\partial _\phi I_ \uparrow } \right) ^2 } \right] } \right\} = 0. \end{aligned}$$
(9)
$$\begin{aligned}&\mathrm{{B}}\left\{ { - \left( {1 - \beta m^2 } \right) \frac{1}{r}\partial _\theta I_ \uparrow + \beta \frac{1}{r}\partial _\theta I_ \uparrow \left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {\partial _r I_ \uparrow } \right) ^2 } \right. } \right. \nonumber \\&\left. { +\, \frac{1}{{r^2 }}\left( {\partial _\theta I_ \uparrow } \right) ^2 + \frac{1}{{r^2 \sin ^2 \theta }}\left( {\partial _\phi I_ \uparrow } \right) ^2 } \right] i\left( {1 - \beta m^2 } \right) \frac{1}{{r\sin \theta }}\partial _\phi I_ \uparrow \nonumber \\&+ i\beta \frac{1}{{r\sin \theta }}\partial _\phi I_ \uparrow \left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {\partial _r I_ \uparrow } \right) ^2 + \frac{1}{{r^2 }}\left( {\partial _\theta I_ \uparrow } \right) ^2 } \right. \nonumber \\&\left. {\left. { +\, \frac{1}{{r^2 \sin ^2 \theta }}\left( {\partial _\phi I_ \uparrow } \right) ^2 } \right] } \right\} = 0. \end{aligned}$$
(10)

We set the action

$$\begin{aligned} {I_ \uparrow } = - \omega t + W\left( r \right) + \Theta \left( {\theta ,\varphi } \right) . \end{aligned}$$
(11)

where \(\omega \) is the emitted particle’s energy. From Eq. (9) and Eq. (10), we have

$$\begin{aligned}&\quad \left( {\frac{1}{r}\partial _\theta I_ \uparrow + i\frac{1}{{r\sin \theta }}\partial _\phi I_ \uparrow } \right) \left\{ {\beta \left[ {\left( {1 - \frac{{2M}}{r}} \right) \left( {\partial _r I_ \uparrow } \right) ^2 } \right. } \right. \nonumber \\&+ \frac{1}{{r^2 }}\left( {\partial _\theta I_ \uparrow } \right) ^2 \left. {\left. { + \frac{1}{{r^2 \sin ^2 \theta }}\left( {\partial _\phi I_ \uparrow } \right) ^2 } \right] - \left( {1 - \beta m^2 } \right) } \right\} = 0. \end{aligned}$$
(12)

since \(\beta \) is a small quantity, the second term in Eq. (12) is not equal to zero. This means

$$\begin{aligned} \frac{1}{r}{\partial _\theta }{I_ \uparrow } + i\frac{1}{{r\sin \theta }}{\partial _\varphi }{I_ \uparrow } = 0. \end{aligned}$$
(13)

Namely,

$$\begin{aligned} \frac{1}{{{r^2}}}{\left( {{\partial _\theta }{I_ \uparrow }} \right) ^2} + \frac{1}{{{r^2}{{\sin }^2}\theta }}{\left( {{\partial _\varphi }{I_ \uparrow }} \right) ^2} = 0. \end{aligned}$$
(14)

Inserting Eqs. (11) and (14) into Eqs. (7) and (8), canceling A and B, we can get the following radial equation

$$\begin{aligned}&\beta ^2 \left( {1 - \frac{{2M}}{r}} \right) ^4 \left( {1 - \frac{{\varepsilon d\Omega }}{{dt}}} \right) \left( {\partial _r W} \right) ^6 + \beta \left( {1 - \frac{{2M}}{r}} \right) ^3 \nonumber \\&\quad \times \left( {1 - \frac{{\varepsilon d\Omega }}{{dt}}} \right) \left( {\partial _r W} \right) ^4 - \omega ^2 \nonumber \\&\quad + \left( {1 - \frac{{2M}}{r}} \right) ^2 \frac{{\varepsilon d\Omega }}{{dt}}\left( {1 - \beta ^2 m^4 } \right) \nonumber \\&\quad \times \left( {\partial _r W} \right) ^2 - m^2 \left( {1 - \beta m^2 } \right) ^2 \left( {1 - \frac{{2M}}{r}} \right) \left( {1 - \frac{{\varepsilon d\Omega }}{{dt}}} \right) = 0. \end{aligned}$$
(15)

It should be noted that, Eq. (15) is the modified Hamilton-Jacob equation, which can be derived from the Rarita-Schwinger equation, the Maxwell equations, and the gravitational wave equation. Thus, our results can be verified by those obtain from other spin particles cases [26,27,28,29].

We resolve above equation and integrate at the horizon \({r_ + }\), which we keep the leading order terms of \(\beta \). This yields

$$\begin{aligned} W_ \pm \left( r \right)&= \pm \int {\frac{{rdr}}{{\sqrt{1 - \varepsilon d\Omega /dt} \left( {r - r_ + } \right) }}} \nonumber \\&\times \sqrt{\frac{{\left( {1 - \frac{{\varepsilon d\Omega }}{{dt}}} \right) \left( {r - r_ + } \right) m^2 \left( {1 - 2\beta m^2 } \right) + \omega ^2 r}}{r}} \nonumber \\&\times \left[ {1 + \beta \left( {m^2 + \frac{{\omega ^2 r}}{{\left( {1 - \varepsilon d\Omega /dt} \right) \left( {r - r_ + } \right) }}} \right) } \right] \nonumber \\&= \pm i\frac{{2\pi M\omega }}{{\sqrt{1 - \frac{{\varepsilon d\Omega }}{{dt}}} }}\left[ {1 + \frac{1}{2}\beta \left( {3m^2 + \frac{{4\omega ^2 }}{{1 - \varepsilon d\Omega /dt}}} \right) } \right] \nonumber \\&+ \mathrm{{realpart}}. \end{aligned}$$
(16)

where the \(+(-)\)sign stands for the outgoing/ingoing radial solution. The invariant tunneling rate under canonical transformation is [30,31,32,33]

$$\begin{aligned} \Gamma&\propto \exp \left( { - {\mathop {\mathrm{Im}}\nolimits } \oint {Pdr} } \right) \nonumber \\&= \exp \left[ { - {\mathop {\mathrm{Im}}\nolimits } \left( {\int {{P_{out}}dr - \int {{P_{in}}dr} } } \right) } \right] \nonumber \\&= \exp \left[ - 2\pi \frac{{2M\omega }}{{\sqrt{1 - \varepsilon d\Omega /dt} }}\left( 1 \right. \right. \nonumber \\&\left. \left. + \frac{1}{2}\beta \left( {3{m^2} + \frac{{4{\omega ^2}}}{{1 - \varepsilon d\Omega /dt}}} \right) \right) \right] . \end{aligned}$$
(17)

where \(P = {\partial _r}W\left( r \right) \), \({P_{out}} = {\partial _r}{W_ + }\left( r \right) \), \({P_{in}} = {\partial _r}{W_ - }\left( r \right) \). However, by resolving the tunneling probability in this way, the contribution from the temporal part of the action is ignored [30]. In order to get the temporal contribution, we need to employ the Kruskal coordinates (T, R). The region exterior of the Rutz-Schwarzschild black hole is given by

$$\begin{aligned} T = {e^{\kappa {r^*}}}\sinh \left( {\kappa t} \right) ,~~~~R = {e^{\kappa {r^*}}}\cosh \left( {\kappa t} \right) . \end{aligned}$$
(18)

where \({r^*} = r + \frac{1}{{2\kappa }}\ln \frac{{r - {r_ + }}}{{{r_ + }}}\) is the tortoise coordinate and \(\kappa \) is the surface gravity of the black hole. As pointed out in [30,31,32,33], by rotating the time t as \(t \rightarrow t - i\kappa {\pi / 2}\), we can obtain the additional imaginary contribution of the temporal part, which is \({\mathop {\mathrm{Im}}\nolimits } \left( {\omega \Delta ^{\mathrm{{out,in}}} } \right) = {{\omega \pi } / {2\kappa }}\). Thus, by incorporating the temporal contribution, the tunneling rate can be expressed as

$$\begin{aligned} \Gamma&\propto \exp \left\{ {\left[ {{\mathop {\mathrm{Im}}\nolimits } \left( {\omega {t_{out}}} \right) + {\mathop {\mathrm{Im}}\nolimits } \left( {\omega {t_{in}}} \right) - {\mathop {\mathrm{Im}}\nolimits } \oint {Pdr} } \right] } \right\} \ \nonumber \\&= \exp \left[ - 4\pi \frac{{2M\omega }}{{\sqrt{1 - \varepsilon d\Omega /dt} }}\left( 1 \right. \right. \nonumber \\&\quad \left. \left. + \frac{1}{2}\beta \left( {3{m^2} + \frac{{4{\omega ^2}}}{{1 - \varepsilon d\Omega /dt}}} \right) \right) \right] . \end{aligned}$$
(19)

Therefore, the revised tunneling temperature is

$$\begin{aligned} T&= \frac{{\sqrt{1 - \varepsilon d\Omega /dt} }}{{8\pi M\left[ {1 + \frac{1}{2}\beta \left( {3{m^2} + \frac{{4{\omega ^2}}}{{1 - \varepsilon d\Omega /dt}}} \right) } \right] }} \nonumber \\&= {T_H}\left[ {1 - \frac{1}{2}\beta \left( {3{m^2} + \frac{{4{\omega ^2}}}{{1 - \varepsilon d\Omega /dt}}} \right) } \right] . \end{aligned}$$
(20)

where

$$\begin{aligned} {T_H} = \frac{{\sqrt{1 - \varepsilon d\Omega /dt} }}{{8\pi M}}. \end{aligned}$$
(21)

is Hawking temperature of the Rutz-Schwarzschild black hole. It is obvious that the nonlinear terms arise in Eq. (20). The modified tunneling temperature of the Rutz-Schwarzschild black hole is lower compared with. This implies that there exists a balance point , leading to the termination of the evaporation. As a consequence, the remnant arises naturally and is accompanied by the phase transition. In the following section, taking into account GUP, we will discuss on the phase transition and remnant of a Rutz-Schwarzschild black hole.

3 Phase transition and the remnant

Due to a black hole evaporation, the mass will decrease. When a black hole mass approaches the order of Planck mass, the quantum gravity effect should be considered. Here, we show that the GUP prevents black holes to evaporate totally and make it occur to phase transition, leading to stable remnant. Since all the particles via Hawking radiation near the event horizon are effectively massless, the mass of a tunneling particle does not be taken into in the following research procedure. Based on the uncertainty principle, during tunneling radiation, a lower bound on the energy of an emitted particle is given by [18, 34]

$$\begin{aligned} \omega \ge \hbar /x \end{aligned}$$
(22)

Near the event horizon, the uncertainty in position may take as the radius of a black hole [18, 34]

$$\begin{aligned} x \approx {r_{BH}} = {r_ + }. \end{aligned}$$
(23)

Substituting Eqs. (23) and (24) into Eq. (21), one gets

$$\begin{aligned} T&= \frac{{{T_H}}}{{1 + 2\beta {\omega ^2}/\left( {1 - \varepsilon d\Omega /dt} \right) }} \nonumber \\&= {T_H}\left( {1 - \frac{{2\beta {\omega ^2}}}{{1 - \varepsilon d\Omega /dt}}} \right) \nonumber \\&\approx {T_H}\left[ {1 - \frac{{2\beta {\hbar ^2}}}{{\left( {1 - \varepsilon d\Omega /dt} \right) {r_ + }^2}}} \right] . \end{aligned}$$
(24)

From above expression, we can find that the event horizon should satisfy \({r_{H}} \ge \sqrt{\frac{{2\beta {\hbar ^2}}}{{\left( {1 - \varepsilon d\Omega /dt} \right) }}}\) in order to guarantee the temperature of positivity. This means that a minimum radius can exist when the tunneling temperature becomes zero, namely,

$$\begin{aligned} {r_{\min }} = \sqrt{\frac{{2\beta {\hbar ^2}}}{{\left( {1 - \varepsilon d\Omega /dt} \right) }}} = {l_p}\sqrt{\frac{{2{\beta _0}}}{{\left( {1 - \varepsilon d\Omega /dt} \right) }}}. \end{aligned}$$
(25)

Making use of the relationship between event horizon and mass, we have

$$\begin{aligned} T \approx \frac{{\sqrt{1 - \varepsilon d\Omega /dt} }}{{8\pi GM}}\left( {1 - \frac{{\beta {\hbar ^2}}}{{2\left( {1 - \varepsilon d\Omega /dt} \right) {G^2}{M^2}}}} \right) . \end{aligned}$$
(26)

To guarantee the temperature, the black hole mass should satisfy

$$\begin{aligned} M \ge \sqrt{\frac{{\beta {\hbar ^2}}}{{2\left( {1 - \varepsilon d\Omega /dt} \right) {G^2}}}} . \end{aligned}$$
(27)

This yields the minimum mass of the black hole,

$$\begin{aligned} {M_i} = \sqrt{\frac{{\beta {\hbar ^2}}}{{2\left( {1 - \varepsilon d\Omega /dt} \right) {G^2}}}} = {M_p}\sqrt{\frac{{{\beta _0}{\hbar ^2}}}{{2{c^2}\left( {1 - \varepsilon d\Omega /dt} \right) }}}. \end{aligned}$$
(28)

This minimum mass is the remnant of the Finsler black hole, namely, \({M_i}={M_{res}}\). In order to further verify this issue, we need to discuss the heat capacity C, which is given by

$$\begin{aligned} C&= T\left( {\frac{{\partial S}}{{\partial T}}} \right) = T\frac{{\partial S}}{{\partial M}}\frac{{\partial M}}{{\partial T}} = T\frac{{\partial S}}{{\partial M}}{\left( {\frac{{\partial T}}{{\partial M}}} \right) ^{ - 1}} \nonumber \\&= \frac{{\left[ {2{G^2}{M^2}\left( {1 - \varepsilon d\Omega /dt} \right) - \beta {\hbar ^2}} \right] \left[ {16\pi {G^3}{M^4}\sqrt{1 - \varepsilon d\Omega /dt} } \right] }}{{\left[ {2{G^2}{M^2}\left( {1 - \varepsilon d\Omega /dt} \right) + \beta {\hbar ^2}} \right] \left[ {3\beta {\hbar ^2} - 2{G^2}{M^2}\left( {1 - \varepsilon d\Omega /dt} \right) } \right] }}. \end{aligned}$$
(29)

where

(30)

which is revised entropy of the Finslerer black hole. From Eq. (29), we find that

$$\begin{aligned} M&= {M_C} = {M_p}\sqrt{\frac{{3{\beta _0}{\hbar ^2}}}{{2{c^3}\left( {1 - \varepsilon d\Omega /dt} \right) }}}.\quad C \rightarrow \infty , \end{aligned}$$
(31)
$$\begin{aligned} M&= {M_i} = {M_{res}} = {M_p}\sqrt{\frac{{{\beta _0}{\hbar ^2}}}{{2{c^2}\left( {1 - \varepsilon d\Omega /dt} \right) }}}. \quad C = 0. \end{aligned}$$
(32)

That heat capacity is cutoff when \(M = {M_C}\), which implies the existence of phase transition. To illustrate the phase transition and remnant, according to Eqs. (26) and (29), we plot the related curved of the temperature, heat capacity with respect to mass in Figs. 1, 2, 3, 4. Here, for convenience, we order \(b = \varepsilon {d\Omega }/{dt}\) and \(M_{p} = c = \hbar = 1\) in the following pictures.

Fig. 1
figure 1

Plot of the temperature versus the mass for different \(\beta \). Green dashed curve corresponds to \(b=0.5\) and \(\beta =0\), red curve corresponds to \(b =0.5\) and \(\beta = 1\)

Full size image
Fig. 2
figure 2

Plot of the heat capacity with respect to the mass for different \( \beta \). Green dashed curve corresponds to \(b = 0.5\) and \(\beta = 0\), red curve corresponds to \(b = 0.5\) and \(\beta = 1\)

Full size image
Fig. 3
figure 3

Plot of the temperature versus the mass for different b. Above blue curve corresponds to \( \beta = 1 \) and \(b = 0.01\). Below red curve corresponds to \(\beta = 1\) and \(b = 0.5\)

Full size image
Fig. 4
figure 4

Plot of the heat capacity with respect to the mass for different b. Left blue curve corresponds to \(\beta = 1\) and \(b = 0.01\). Right red curve corresponds to \(\beta = 1\) and \(b = 0.5\)

Full size image

From these plots, we can clearly see that Finsler parameter b and GUP parameter \( \beta \) are effect on the phase transition and remnant. Or equivalently, from Eqs. (26) and (29), we can also see that the minimum mass \( M_{i} \) and heat capacity C are all dependent on b and \( \beta \).

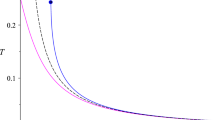
In Figs. 1 and 2, in case of \( \beta = 0 \), the temperature and the heat capacity correspond to the standard Hawking temperature and traditional heat capacity. In case of \( \beta = 1 \), the temperature and heat capacity correspond to revised Hawking temperature and modified heat capacity based on GUP. Obviously, in a large range of mass, for the two cases, the heat capacities tend to be consistent, and the temperatures are also the same. However, when the black hole mass is close to the Planck mass \( M _{p} \), they present the crucial difference for the two cases.

In case of \( \beta = 0 \), in Fig. 2, we know that the traditional heat capacity is always negative and the black hole does not exist phase transition. Namely, in Fig. 1, we see that the standard Hawking temperature monotonically increases with the mass decreasing, which implies that the black hole with negative capacity will evaporate completely.

In case of \( \beta = 1 \), in Fig. 2, we can see that, the modified heat capacity is negative when \( M > {M_C}\ \) and it is positive when \( M < {M_C}\), and the modified heat capacity is divergent when the mass attains the critical mass \( M_{C} \), which indicates that the phase transition take places at \( M_{C} \). Namely, as can be seen in Fig. 1, at \( M_{C} \), there exist an inflection point, which means that the black hole with negative heat capacity undergoes a phase transition to the black hole with positive heat capacity. From Fig. 1, we can observe that, as the mass decreases, the revised Hawking temperature increases, and it arrives at the maximum value (which is critical temperature \( T_{C} \)) at the critical mass \( M_{C} \) (which is marked by a red dot), then decreases to zero at the minimum mass \( M_{i} \) (which is marked by a blue dot). Furthermore, when \( M < {M_C}\), the revised Hawking temperature of monotonically decreases with the mass decreasing. When the mass is equal to the minimum mass \( M_{i} \), the revised Hawking temperature is zero and the modified heat capacity is also zero. Thus, the black hole becomes a stable one, which can be in thermal equilibrium with the surrounding environment. Therefore, at \( M_{i} \), evaporation of the black hole stops, resulting a stable remnant \( {M_{res}} = {M_i}\). For the case of \( \beta = 1 \) and \( \ b= 0.5 \), according to Eqs. (26), (31) and (32), we can get the corresponding critical values \( {M_C} = 1.7321\), \( {T_C} = 0.01083\), and the remnant \( {M_{res}} = {M_i} = 1\), which coincide with results obtained in Fig. 1 in our accuracy.

Fig. 5
figure 5

The relation between the temperature and entropy. We set \(b = 0.5\), \(\beta = 1\) and \(M_{p} = c = \hbar = 1\)

Full size image

In Figs. 3 and 4, we can also observe how the Finsler parameter b effects the remnant and phase transition. For different Finsler parameter, the related curves give a similar behavior not only in the \( T-M \) plane but also in the \( C-M \) plane. As b increases, the stable stage with positive heat capacity is longer. The critical temperature \( T_{C}\) decreases with b increasing, however the critical mass \( M_{C}\) and remnant \( M_{res}\) increase with b increasing.

In addition, in order to can better understand the phase transition in the later stage of evaporation, it is interesting to discuss phase transition of the Rutz-Schwarzschild black hole in the temperature T and entropy S plane. Here, we take \( \beta = 1 \) and \( b = 0.5 \) as example. Inserting Eq. (30) into Eq. (26) and eliminating the parameter M, we can get the relation between the temperature and entropy. According to Eq. (26), at the critical pointwe have \( S_{C} = 63.0766 \). The critical entropy and critical temperature are determined by the equation \( {\partial T /\partial S = 0 } \). Numerically, we have \( S_{C} = 63.0768 \) and \(T_{C} = 0.01083 \), which are consistent with the results obtained by using Eqs. (26) and (30). With the relation between the temperature and entropy, the phase transition curves can be plotted in the \( T-S \) plane in Fig. 5.

The phase structure in Fig. 5 is similar to one in Fig. 1 for the case. An inflection is also exhibited in the \( T-S \) plane, which corresponds to the critical temperature and critical entropy. Through the definition of a heat capacit, we know that C is negative when \( S > S_{C} \) and C is positive when \( S < S_{C} \). This implies that at \(M_C\), the black hole with negative heat capacity transits to one with positive heat capacity. The black hole’s evaporation stops until T is equal to zero and the entropy attains the minimum value.

4 Conclusion and discussion

In this paper, in the framework of the generalized uncertainty principle (GUP), near the Planck scale, we investigate the thermodynamic behavior of a Finsler black hole based on the fermion tunneling radiation. The Finsler black hole considered in this paper is an Einstein Vacuum field equation’s solution in the Finsler theory. We utilize this metric to investigate quantum corrections to the Hawking temperature and entropy as well as the heat capacity. Further, we analyze the phase transition and the remnant based on GUP, and also discuss on the impact of Finsler parameter on the phase transition and the remnant. Obviously, according to the plots, in a large range of mass, the phase transition curves tends to be the same but when the black hole mass is close to the Planck mass, there exists the crucial difference for the curves. Thus, we show that how the stable remnant forms for the Finsler black hole. GUP prevents black holes to evaporate totally, and close to the Planck scale, the black hole with negative heat capacity undergoes a phase transition to the black hole with positive heat capacity. As the mass decreases to the minimum value, the revised Hawking temperature and the modified heat capacity are all zero, and the black hole can be in thermal equilibrium with the surrounding environment. As a consequence, evaporation of the black hole ceases, leading to a stable remnant.