$Z_b(10610)$ in a hadronic medium

Abstract

In this work we investigate the $Z_b (10610)$ (called simply $Z_b$) abundance in the hot hadron gas produced in heavy ion collisions after the quark–gluon plasma phase. We use effective Lagrangians to calculate the thermally averaged cross sections of $Z_b$ production in processes such as $B^{(*)} + \bar{B}^{(*)} \rightarrow \pi + Z_b (10610)$ and also of its absorption in the corresponding inverse processes. We then solve the rate equation to follow the time evolution of the $Z_b$ multiplicity. We find that, if we neglect the $Z_b$ decay, the number of $Z_b$’s produced at the end of the quark–gluon plasma phase remains almost constant during the hadron phase. The introduction of the decay in the rate equation leads to a suppression in the final yield by a factor two.

1 Introduction

During the last decade the existence of exotic hadron states has been established [1,2,3,4,5,6,7,8]. In particular, in the bottomonium spectrum, the charged states $Z_b^\pm (10610)$ (from now on called simply $Z_b$) have been observed by the Belle Collaboration in the invariant mass spectra of the $\pi ^{\pm } \Upsilon (n S)\;(n=1, 2, 3)$ and $\pi ^{\pm } h_b (m P)\;(m = 1, 2)$ pairs that are produced in association with a single charged pion in $\Upsilon (5 S)$ decays [9, 10]. Their masses and decay widths have been estimated to be $m_{Z_b ^{\pm }} = 10607.2 \pm 2.0$ MeV and $\Gamma _{Z_b ^{\pm } } = 18.4 \pm 2.4$ MeV, respectively [7], and the favored quantum numbers are $I^G(J^P) = 1^+(1^+)$ [7]. The Belle Collaboration has also found evidence of the charge neutral partner $Z_b (10610)$ in the Dalitz plot analysis of $\Upsilon (5 S) \rightarrow \Upsilon (2 S) \pi ^{0} \pi ^{0}$, with the mass being $m_{Z_b ^{0}} = 10609 \pm 6$ MeV [11]. Since the $Z_b$ is an isotriplet state, it cannot be pure $b \bar{b}$ state, needing at least four quarks as minimal constituents.

The structure of these isospin triplets is still matter of debate. Due to the proximity to $B\bar{B}^*$ thresholds, a natural interpretation is to suppose that they are bound states of bottomed mesons [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Another plausible interpretation is that they could be compact tetraquark states, resulting from the binding of a diquark and an antidiquark [8].

The determination of the structure of the $Z_b$ states (meson molecule, tetraquark or a mixture, including bottomonium components) requires more experimental information. The study of the better known X(3872) state has led to the conclusion that the production in hadronic colliders may be more sensitive to the quark configuration. It has been claimed [30,31,32] that data on X(3872) production in proton–proton collisions are incompatible with a molecular interpretation (for a different point of view, see however [33, 34]).

Hadronic production of exotic states can be investigated in proton - proton collisions and in nucleus-nucleus reactions both in ultraperipheral [35] and central collisions [36, 37]. Indeed, heavy ion collisions (HIC) allow for a higher production rate of heavy quarks. Moreover, the formation of a quark–gluon plasma (QGP) phase allows heavy quarks to move freely and recombine to form exotic states. As described in [36, 37], heavy quarks coalesce to form bound states (and possibily exotic bound states) at the end of the QGP phase. After being produced, the multiquark states interact with other hadrons during the expansion and cooling of the hadronic matter. They can be destroyed in collisions with the comovinglight mesons, but they can also be produced through the inverse processes  [38,39,40,41,42]. The final multiplicity depends on the interaction cross sections, which, in turn, depend on the spatial configuration of the quarks. Therefore, the measurement of the $Z_b$ multiplicity would be very useful to determine the structure of these states. Theoretical studies reported in Ref. [41], for instance, suggest that the X(3872) multiplicity at the end of the QGP phase is reduced by a factor four due to the interactions with the hadron gas. Moreover the results found in [41] suggest that if the X(3872) was observed in HICs, it would be most likely a molecular state.

In heavy ion collisions there is, so far, no theory which tells us how to go from the initially formed heavy quarks to the X and Z hadrons. We need to use models. Following the papers of the EXHIC Collaboration, we assume that these hadrons are first formed at the end of the plasma phase. This process is described by the coalescence model. The estimates of the number of X’s and $Z_b$’s are given in Table 3.4 of Ref. [37]. Of course the X’s are always more abundant. The ratio of the yields $X/Z_b$ is $~10^4$ at RHIC ($\sqrt{s} = 200$ GeV), $~10^3$ at the LHC ($\sqrt{s} = 2.76$ TeV) and $~5 \times 10^2$ at the LHC ($\sqrt{s} = 5.02$ TeV) at a higher energy. As can be seen, as the energy increases it becomes more and more likely to produce $Z_b$.

Concerning the measurements, the X(3872) has been measured in pp collisions by the CDF, CMS and ATLAS collaborations. The $X_b$, the bottom analogue of the X(3872), is currently being searched in the $\Upsilon \pi ^+ \pi ^-$ decay channel. Due to their powerful muon detectors, the CMS and ATLAS groups have an excellent capability of measuring the $\Upsilon$ states.

In [43] the CMS reported the result of a dedicated search for $X_b$ in pp collisions at 8 TeV. More recently, in [44] the ATLAS Collaboration has reported the result of the search of the same particle in the same decay channel. A recent review of the status of these experimental searches can be found in [45]. The results are so far inconclusive but they show that the search is feasible. In principle the same experimental techniques can be applied to the search of $Z_b$.

In nucleus-nucleus collisions the production of bottom quark pairs is copious, even at RHIC (see the results of the STAR collaboration in [46]). In [47] CMS has presented cross sections for $\Upsilon (1S)$, $\Upsilon (2S)$ and $\Upsilon (3S)$ production measured in $Pb-Pb$ collisions at $\sqrt{s_{NN}} = 5.02$ TeV. The cross sections are in the nanobarn region. Based on our experimental knowledge from the charmonium case, we might expect that these cross sections should set the scale for the exotic bottomonium case. The $X_b$ and $Z_b$ should have production cross sections close to those of the excited bottomonium states $\Upsilon (2S)$ or $\Upsilon (3S)$. The $Z_b$ should be reconstructed in the analysis of the invariant mass of $\Upsilon {-}\pi$ final states. This involves the same level of complexity as the search for $X_b$ in the $\Upsilon {-}\pi {-}\pi$ final states.

These facts make us think that the search for $Z_b$ in heavy ion collisions is feasible and timely. Extending the study of the X(3872) abundance mentioned above, in this work we investigate the $Z_b$ abundance in the hot hadron gas produced in the late stage of heavy ion collisions. We will follow the previous works on the subject, where the interactions of the X(3872) with light mesons were addressed [39, 40]. As in Refs. [13,14,15, 26, 29], we assume that the $Z_b$ couples to $\bar{B} B^{*}$ and to $B \bar{B}$. We use effective Lagrangians to calculate the thermally averaged cross sections of the $Z_b$ production in processes such as $B^{(*)} + \bar{B}^{(*)} \rightarrow \pi + Z_b$, and also of the $Z_b$ absorption in the corresponding inverse processes. We then solve the rate equation to follow the time evolution of the $Z_b$ multiplicity and determine how it is affected by the considered reactions.

The paper is organized as follows. In Sect. 2 we describe the formalism and calculate the cross sections of $Z_b$ production and absorption. With these results, in Sect. 3 we calculate the thermally averaged cross sections of the processes above mentioned. Then, in Sect. 4 we solve the rate equation and follow the time evolution of the $Z_b$ abundance. Finally, in Sect. 5 we present some concluding remarks.

2 Cross sections

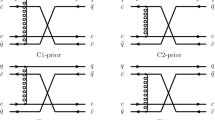
In this section we calculate the production and absorption cross sections involving the $Z_b$ and pions. We focus on the processes $\bar{B}B \rightarrow \pi Z_b$, $\bar{B}^* B \rightarrow \pi Z_b$ and $\bar{B}^* B^* \rightarrow \pi Z_b$ and the inverse reactions. In Fig. 1 we show the different diagrams contributing to each process, without the specification of the particle charges. The cross sections for these reactions were obtained in Ref.  [14] considering only the charged partner $Z_b ^{+}$. Thus, for completeness, here we compute the total cross section including all the components of the isospin triplet. Due to their large multiplicity (there are about ten pions for every particle of any other species), we expect that the reactions involving pions provide the main contributions to the study of the $Z_b$ abundance in hot hadronic matter.

Fig. 1

Diagrams contributing to the process $\bar{B} B \rightarrow \pi Z_b$ [diagrams (a) and (b)], $\bar{B}^* B \rightarrow \pi Z_b$ [diagram (c)] and $\bar{B}^* B^* \rightarrow \pi Z_b$ [diagrams (d) and (e)], without specification of the charges of the particles (from Ref. [14])

The amplitudes of the processes shown in Fig. 1 are calculated with the help of effective Lagrangians based on the extended hidden SU(4) local symmetry. For more details about explicit expressions of amplitudes and calculations, we refer the reader to Refs. [14, 39,40,41, 48,49,50,51,52]. The isospin-spin-averaged cross section for the processes $\bar{B}B, \bar{B}^*B, \bar{B}^*B^* \rightarrow \pi Z_b$ in the center of mass (CM) frame is given by

$$\begin{aligned} \sigma _r(s) = \frac{1}{64 \pi ^2 s } \frac{|\vec {p}_{f}|}{|\vec {p}_i|} \int d \Omega \overline{\sum _{S, I}}|\mathcal {M}_r(s,\theta )|^2, \end{aligned}$$

(1)

where $r = 1,2,3$ label processes $\bar{B}B, \bar{B}^*B, \bar{B}^*B^*$ respectivelly; $\sqrt{s}$ is the CM energy; $|\vec {p}_{i}|$ and $|\vec {p}_{f}|$ denote the tri-momenta of initial and final particles in the CM frame, respectively; the symbol $\overline{\sum _{S,I}}$ represents the sum over the spins and isospins of the particles in the initial and final state, weighted by the isospin and spin degeneracy factors of the two particles forming the initial state for the reaction r, i.e. [14, 39, 40]

$$\begin{aligned} \overline{\sum _{S,I}}|\mathcal {M}_r|^2\rightarrow & {} \frac{1}{(2I_{1i,r}+1)(2I_{2i,r}+1)} \nonumber \\&\times \frac{1}{(2S_{1i,r}+1)(2S_{2i,r}+1)} \sum _{S,I}|\mathcal {M}_r|^2, \end{aligned}$$

(2)

where

$$\begin{aligned} \sum _{S,I} |\mathcal {M}_r|^2 = \sum _{Q_{1i}, Q_{2i}} \left[ \sum _{S}\left| \mathcal {M}^{(Q_{1i},Q_{2i})}\right| ^2\right] . \end{aligned}$$

(3)

Notice that the charges of the two particles forming the initial state for the processes in Fig. 1 can be combined, giving a total charge $Q_r = Q_{1i} + Q_{2i} = -1, 0, +1$. We have then four possibilities: (0, 0), $(-,+)$, $(-,0)$ and $(0,+)$, giving

$$\begin{aligned} \sum _{S,I} |\mathcal {M}_r|^2= & {} \sum _{S}\left( \left| \mathcal {M}^{(0,0)}_r\right| ^2 + \left| \mathcal {M}^{(-,+)}_r\right| ^2 \right. \nonumber \\&\left. + \left| \mathcal {M}^{(-,0)}_r\right| ^2 + \left| \mathcal {M}^{(0,+)}_r\right| ^2\right) . \end{aligned}$$

(4)

As mentioned above, the expressions of the amplitudes and values of the coupling constants are given in Ref. [14]. The uncertainties in the couplings $g_{ZBB^*}$ will be taken into account and the results discussed below will be represented by shaded regions in the plots. Also, in the computations of the present work we have employed the isospin-averaged masses reported in Ref. [7]: $m_{\pi } = 137.3$ MeV; $m_{B} = 5279.4$ MeV; $m_{B^{*}} = 5324.8$ MeV; $m_{Z_b ^\pm } = 10607.2$ MeV; $m_{Z_b ^0} = 10609$ MeV.

In Fig. 2 the total $Z_b$ production cross sections are plotted as a function of the CM energy $\sqrt{s}$. We see that the cross sections are $\sim 6 \times 10^{-3} - 3 \times 10^{-2}$ mb for $10.80 \le \sqrt{s} \le 11.05$ GeV. Also, it can be noticed that the three processes have cross sections with the same order of magnitude. Another point worthy of mention is that, due to the inclusion of the contributions coming from processes with all the three components of the isospin triplet $(Z_b ^0, Z_b^+, Z_b^- )$, we obtain cross sections that are bigger (by a factor about 2–3) than those found in Ref. [14] with only the $Z_b^+$ component.

Fig. 2

Cross sections for the production processes $\bar{B} B \rightarrow \pi Z_b$ (medium shaded region), $\bar{B}^* B \rightarrow \pi Z_b$ (dark shaded region) and $\bar{B}^* B^* \rightarrow \pi Z_b$ (light shaded region), as function of CM energy $\sqrt{s}$

Using the detailed balance relation we also evaluate the cross sections related to the inverse processes, where the $Z_b$ is absorbed. In Fig. 3 the total $Z_b$ absorption cross sections are plotted as a function of the CM energy $\sqrt{s}$. Decreasing cross sections are expected because of the exothermic nature of these reactions. The sum of the $\Upsilon$ and $\pi$ masses is bigger than the sum of the masses in the final state. As it will be seen, the kinematic region where the two particles in the initial state are nearly at rest is at the edge of the phase space and it is unimportant for the calculation of the thermally averaged cross sections. They are found to be $\sim 5 \times 10^{-2} - 1$ mb for $10.80 \le \sqrt{s} \le 11.05$ GeV. As it can be seen, the reaction with the final $\bar{B}^* B^*$ state has the largest cross section (by a factor about 3-10, depending on the channel) in comparison with the other reactions. Again, the inclusion of the contributions coming from the processes with all the three components $(Z_b ^0, Z_b^+, Z_b^- )$ yields cross sections that are bigger (by a factor about 2–3) than those found in in Ref. [14] with only the $Z_b^+$ component.

The comparison between the $Z_b ^+$ production and absorption cross sections, shown in Figs. 2 and 3, suggests that the $Z_b$-production cross sections are smaller than the absorption ones by a factor about 3–100, depending on the specific channel and region of energy. This difference between production and absorption cross sections can be accounted for by kinematic effects.

Fig. 3

Cross sections for the absorption processes $\pi Z_b \rightarrow \bar{B} B$ (medium shaded region), $\pi Z_b \rightarrow \bar{B}^* B$ (dark shaded region) and $\pi Z_b \rightarrow \bar{B}^* B^*$ (light shaded region), as function of CM energy $\sqrt{s}$

In what follows we use the results reported above to compute the thermally averaged cross sections for the $Z_b$ production and absorption reactions.

3 Cross sections averaged over the thermal distribution

Let us introduce the cross section averaged over the thermal distribution for a reaction involving an initial two-particle state going into two final particles $ab \rightarrow cd$. It is given by [38, 41, 53]

$$\begin{aligned} \langle \sigma _{ab \rightarrow cd} \, v_{ab} \rangle= & {} \frac{\int d^3\vec {p}_a d^3\vec {p}_b f_a(\vec {p}_a) f_b(\vec {p}_b) \sigma _{ab \rightarrow cd}v_{ab} }{\int d^3\vec {p}_a d^3\vec {p}_b f_a(\vec {p}_a) f_b(\vec {p}_b)}, \end{aligned}$$

(5)

where $f_a$ and $f_b$ are Bose-Einstein distributions, $\sigma _{ab \rightarrow cd}$ are the cross sections evaluated in Sect. 2, $v_{ab}$ represents the relative velocity of the two interacting particles a and b.

In Figs. 4 and  5 we plot the thermally averaged cross sections for $Z_b$ absorption and production respectively, via the processes discussed in the previous section. All the three production reactions considered have similar magnitudes, especially at high temperatures. The absorption processes with $B \bar{B}$ and $B^* \bar{B}$ final states have comparable cross sections and these are smaller than in the case with $B^* \bar{B}^*$ final state (by a factor about 2–3). Comparing Figs. 4 and  5 we observe that absorption is stronger than production by a factor ranging from 20 to 100 in the energy region of interest.

Fig. 4

Thermally averaged cross section to the processes $\bar{B} B \rightarrow \pi Z_b$ (medium shaded region), $\bar{B}^* B \rightarrow \pi Z_b$ (dark shaded region) and $\bar{B}^* B^* \rightarrow \pi Z_b$ (light shaded region), as a function of temperature

Fig. 5

Thermally averaged cross section to the processes $\pi Z_b \rightarrow \bar{B} B$ (medium shaded region), $\pi Z_b \rightarrow \bar{B}^* B$ (dark shaded region) and $\pi Z_b \rightarrow \bar{B}^* B^*$ (light shaded region), as a function of temperature

In the next section we use these thermally averaged cross sections as input in the rate equation and study the time evolution of the $Z_b$ abundance.

4 Time evolution of $Z_b$ abundance

We complete the present investigation with the study of the time evolution of the $Z_b$ abundance in hadronic matter, using the thermally averaged cross sections estimated in the previous section. More precisely, we investigate the influence of $\pi {-} Z_b$ interactions on the abundance of $Z_b$ during the hadronic stage of heavy ion collisions. The momentum-integrated evolution equation for the abundances of particles included in processes previously discussed  [38, 41, 53] reads

$$\begin{aligned} \frac{ d N_{Z_b} (\tau )}{d \tau }= & {} \sum _{b,b^{\prime }} \bigg [ \langle \sigma _{b b^{\prime } \rightarrow \pi Z_b } v_{b b^{\prime }} \rangle n_{b} (\tau ) N_{b^{\prime }}(\tau ) \nonumber \\&- \langle \sigma _{ \pi Z_b \rightarrow b b^{\prime } } v_{ \pi Z_b} \rangle n_{\pi } (\tau ) N_{Z_b}(\tau ) \nonumber \\&- \Gamma _{Z_b} N_{Z_b} (\tau ) \bigg ], \end{aligned}$$

(6)

where $N_{Z_b} (\tau )$, $N_{b^{\prime }}(\tau )$, $n_{b} (\tau )$ and $n_{\pi } (\tau )$ are the abundances of $Z_b$, of bottomed mesons of type $b^{\prime }$, of bottomed mesons of type b and of pions at proper time $\tau$, respectively. In the last line $\Gamma _{Z_b}$ is the $Z_b$ decay width. We can see in the above equation that the $Z_b$ abundance at a proper time $\tau$ depends on the $\pi Z_b$ dissociation rate through the processes discussed previously, and also on the $\pi Z_b$ production rate from the inverse processes.

To solve Eq. (6) we assume that the pions and bottomed mesons in the reactions contributing to the abundance of $Z_b$ are in equilibrium. Accordingly, $n_{b} (\tau )$, $N_{b^{\prime }}(\tau )$ and $n_{\pi } (\tau )$ can be written as [38, 41, 53]

$$\begin{aligned} n_{b} (\tau )\approx & {} \frac{1}{2 \pi ^2} \, \gamma _{b} \, g_{B^{(*)}} \, m_{B^{(*)}}^2 \, T(\tau ) \, K_{2}\left( \frac{m_{B^{(*)}} }{T(\tau )}\right) , \nonumber \\ N_{b^{\prime }}(\tau )\approx & {} \frac{1}{2 \pi ^2} \, \gamma _{b} \, g_{B^{(*)}} \, m_{B^{(*)}}^2 \, T(\tau ) \, V(\tau ) \, K_{2}\left( \frac{m_{D^{(*)}} }{T(\tau )}\right) ,\nonumber \\ n_{\pi } (\tau )\approx & {} \frac{1}{2 \pi ^2} \, \gamma _{\pi } \, g_{\pi } \, m_{\pi }^2 \, T(\tau ) \, K_{2}\left( \frac{m_{\pi } }{T(\tau )}\right) , \end{aligned}$$

(7)

where $\gamma _i$ and $g_i$ are the fugacity factor and the degeneracy of particle i respectively.

As it can be seen in Eq. (7), the time dependence in Eq. (6) enters through the parametrization of the temperature $T(\tau )$ and volume $V(\tau )$ profiles suitable to describe the dynamics of the hot hadron gas after the end of the quark–gluon plasma phase. As in Refs. [38, 41, 53], we assume the $\tau$ dependence of $V(\tau )$ and T to be given by

$$\begin{aligned} V(\tau )= & {} \pi \left[ R_C + v_C \left( \tau - \tau _C\right) + \frac{a_C}{2} \left( \tau - \tau _C\right) ^2 \right] ^2 \tau c , \nonumber \\ T(\tau )= & {} T_C - \left( T_H - T_F \right) \left( \frac{\tau - \tau _H }{\tau _F - \tau _H}\right) ^{\frac{4}{5}} . \end{aligned}$$

(8)

These expressions are based on the boost invariant Bjorken picture with an accelerated transverse expansion. Since we focus on central Au–Au collisions at $\sqrt{s_{NN}} = 200$ GeV, in the above equation $R_C = 8.0$ fm denotes the final size of the quark–gluon plasma, while $v_C = 0.4 \, c$ and $a_C = 0.02 \, c^2$/fm are its transverse flow velocity and transverse acceleration at $\tau _C = 5.0$ fm/c  [38, 41, 54]. $T_H = T_C = 175$ MeV is the temperature of the hadronic matter at the end of the phase conversion, at $\tau _H = 7.5$ fm/c. The freeze-out takes place at the freeze-out time $\tau _F = 17.3$ fm/c, when the temperature drops to $T_F = 125$ MeV. The pseudocritical temperature of the quark–gluon plasma to hadronic matter crossover is $T_C=175$ MeV. We will stick to this choice in our calculations but we keep in mind that this temperature might be somewhat smaller, close to $T_C \simeq 155$ MeV. We have checked that changing $T_C$ from 175 to 155 does not change significantly our results.

We also solve the rate equation for a system formed at the LHC, where $\sqrt{s_{NN}} = 5.02$ TeV. In this case the parameters are [36, 37]: $R_c=13.11$ fm, $v_c=0.6 \, c$, $a_c = 0.044$ c$^2$/fm and $T_C = T_H = 175$ MeV.

We assume that the total number of bottom quarks in bottomed hadrons is conserved during the production and dissociation reactions, and that the total number of bottom quark pairs produced at the initial stage of the collisions at RHIC is 0.02, yielding the bottom quark fugacity factor $\gamma _b \approx 2.2 \times 10^6$ in Eq. (7) [36, 37]. In the case of pions, their total number at freeze-out is assumed to be 926  [38, 41, 54].

In spite of being useful, the model of the hot system formed in heavy ion collisions represented by Eqs. (7) and (8) has limitations both in its thermodynamical and hydrodynamical aspects.

We know that the fugacity is a function of the temperature T and of the chemical potential $\mu$. For fixed T and $\mu$, the quark fugacity is fixed and so is the quark density. If the system evolves in time (expands and cools down) the temperature and the chemical potential change with time and so does the fugacity. When we describe the time evolution of the system using a hydrodynamical code, we can follow step by step the changes in T, $\mu$ and $\gamma$. In contrast to this detailed (and time consuming) calculation, the model given by Eqs. (7) and (8) is a simple and schematic representation of hydrodynamics. Here the “fugacity parameter” $\gamma$ is just a normalization parameter, which is adjusted so as to reproduce the measured meson multiplicities.

The adopted formulas (Eqs. (7), (8)) and the fitting procedure were first introduced in [55] and then updated later in [54] and in subsequent papers. In the original papers the authors assumed that the firecylinder expands isentropically. In their model the fraction of hadronic matter during the phase conversion time increases approximately linearly. Before and after the change of phases the system is composed by noninteracting particles forming ideal gases. For the sake of consistency it would be interesting to calculate the entropy starting from the multiplicities at every time step and check whether it is conserved. However, to do this we would need to know more than Eq. (7). We would need to know the multiplicities of all particle species which are relevant for the computation of the entropy.

The Eq. (8) are an attempt to mimick in a simple way the hydrodynamical expansion of fluid. They lack many important features of a proper hydrodynamical expansion such as the dependence on the initial conditions (for example initial energy density and initial velocity distributions), the dependence on the details of the equation of state and also the dependence on the freeze-out criterion. Moreover, it is well known that Bjorken hydrodynamics is just an approximation. In particular, the predicted “plateau” in rapidity distributions was never really observed. Nevertheless, it remains useful because of its simplicity.

This kind of effective model can and should be improved, but this is outside the scope of this work. Moreover, we are not interested in the absolute multiplicity of $Z_b$. We just want to know how it changes during the hadron gas phase. We keep using it more as an exploratory tool and keep in mind that any findings observed in our calculations should be later confirmed, replacing (8) by a more realistic and fully numerical hydrodynamical simulation.

Fig. 6

a (upper panel) Time evolution of the $Z_b$ abundance as a function of the proper time in central Au–Au collisions at $\sqrt{s_{NN}} = 200$ GeV. Dark and light shaded bands represent the evolution with the number of $Z_b$’s produced at the end of the quark–gluon plasma phase calculated using statistical and four-quark coalescence models, respectively. b (lower panel) Same as a but including the decay of the $Z_b$

Fig. 7

a (upper panel) Time evolution of the $Z_b$ abundance as a function of the proper time in central Pb-Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. Dark and light shaded bands represent the evolution with the number of $Z_b$’s produced at the end of the quark–gluon plasma phase calculated using statistical and four-quark coalescence models, respectively. b (lower panel) Same as a but including the decay of the $Z_b$

In the present work we study the yields obtained for the $Z_b$ abundance within two different approaches: the statistical and the coalescence models. In the statistical model, hadrons are produced in thermal and chemical equilibrium, according to the expression of the abundance in Eq. (7) corresponding to the hadron considered. Therefore, the $Z_b$ yield at the end of the quark–gluon plasma phase is

$$\begin{aligned} N_{Z_b(Stat)} ^{0 } =N_{Z_b(Stat)} (\tau _H)\approx 2.1 \times 10^{-8}. \end{aligned}$$

(9)

Notice, however, that this model does not contain any information related to the internal structure of the $Z_b$. In the coalescence model the determination of the yield of a certain hadron is based on the overlap of the density matrix of the constituents in an emission source with the Wigner function of the produced particle. This model contains information on the internal structure of the considered hadron, such as angular momentum, multiplicity of quarks, etc. Then, following Refs. [36,37,38, 41], the number of $Z_b$’s produced at the end of the quark–gluon plasma phase can be written as :

$$\begin{aligned} N_{Z_{b}} ^{Coal}\approx & {} g_{Z_{b}} \prod _{j=1} ^{n} \frac{N_j}{g_j} \prod _{i=1} ^{n-1} \frac{(4 \pi \sigma _i ^2)^{\frac{3}{2}} }{V (1 + 2 \mu _i T \sigma _i ^2 )} \nonumber \\&\times \left[ \frac{4 \mu _i T \sigma _i ^2 }{3 (1 + 2 \mu _i T \sigma _i ^2 ) } \right] ^{l_i}, \end{aligned}$$

(10)

where $g_j$ and $N_j$ are the degeneracy and number of the j-th constituent of the $Z_b$ and $\sigma _i = (\mu _i \omega )^{-1/2}$. The quantity $\omega$ is the oscillator frequency (assuming an harmonic oscillator Ansatz for the hadron internal structure) and $\mu$ the reduced mass, given by $\mu ^{-1} = m_{i+1} ^{-1}+ \left( \sum _{j=1} ^{i} m_j \right) ^{-1}$. Finally, the angular momentum of the system, $l_i$, is 0 for an S-wave, and 1 for a P-wave. In order to calculate the $Z_b$ yield within the coalescence model, we consider it as a tetraquark state. Therefore, according to the coalescence model for $Z_b$ as a tetraquark, the time evolution of the abundance ($N_{Z_{b}}$) is determined by solving Eq. (6), with initial condition, at $\tau _H = 7.5$ fm/c, given by

$$\begin{aligned} N_{Z_{b}(4q)} ^{0 } =N_{Z_{b}(4q)} (\tau _H) \approx 2.1 \times 10^{-9}. \end{aligned}$$

(11)

The comparison between the values of $N_{Z_{b}(Stat)} ^{0 }$ and $N_{Z_{b}(4q)} ^{0}$ in Eqs. (9) and (11) indicates that the number of $Z_b$’s (produced at the end of the quark–gluon plasma phase) calculated with the statistical model is greater than the four-quark state (formed by quark coalescence) by one order of magnitude.

In Fig. 6 we show the time evolution of the $Z_b$ abundance as a function of the proper time in central Au–Au collisions at $\sqrt{s_{NN}} = 200$ GeV, using $N_{Z_{b}(Stat)} ^{0 }$ and $N_{Z_{b}(4q)} ^{0}$ as initial conditions. The results of the upper pannel suggest that the interactions between the $Z_b$’s and the pions during the hadronic stage of heavy ion collisions do not produce any relevant change in the $Z_b$ abundance, i.e. there is an approximate equilibrium between production and absorption and the number of $Z_b$’s throughout the hadron gas phase remains nearly constant. However, as it can be seen in the lower pannel of the same figure, when we take into account the spontaneous decay of the $Z_b$ there is a significant reduction of the abundance. In Fig. 7 we show the result of the same kind of calculation with initial conditions typical of the LHC. The conclusion is the same but the reduction is more pronounced.

5 Conclusions

In this work we have studied the $Z_b (10610)$ abundance in a hot pion gas produced in heavy ion collisions. Effective Lagrangians have been used to calculate the thermally averaged cross sections of the processes $B^{(*)} + \bar{B}^{(*)} \rightarrow \pi + Z_b (10610)$, as well as of the corresponding inverse processes. We have found that the magnitude of the thermally averaged cross sections for the dissociation and for the production reactions differ by factors up to 100, depending on whether the considered channel includes or not the $B^{(*)} + \bar{B}^{(*)}$ state. With the thermally averaged cross sections we have solved the rate equation to determine the time evolution of the $Z_b (10610)$ multiplicity. The results suggest that, if we neglect the $Z_b$ decay, its multiplicity is not significantly affected by the interactions with the pions and hence the number of $Z_b$’s would remain essentially unchanged during the hadron gas phase. However the introduction of the decay (included in the last line of Eq. (6) leads to a suppression of a factor two in the final yield. This amount of suppression is smaller (by a factor two) than the one found in similar conditions for the X(3872).

It is interesting to observe that the main cause of suppression is a vacuum property of the $Z_b$ resonance. This motivates the study of medium (density and temperature) effects on the decay width, which we plan to address in the future.

In the near future it will be interesting to refine the phenomenological description of the hadronic medium and perform a systematic study of the role played by this medium in “filtering” the particles produced at the end of the quark–gluon plasma phase.