$A_4$ realization of linear seesaw and neutrino phenomenology

Abstract

Motivated by the crucial role played by the discrete flavor symmetry groups in explaining the observed neutrino oscillation data, we consider the $A_4$ realization of linear seesaw by extending the standard model (SM) particle content with two types of right-handed (RH) neutrinos along with the flavon fields, and the SM symmetry with $A_4\times Z_4\times Z_3$ and a global symmetry $U(1)_X$, which is broken explicitly by the Higgs potential. We scrutinize this model to see if it can explain the recent results from neutrino oscillation experiments, by searching for parameter space that can accommodate the observables such as the reactor mixing angle $\theta _{13}$, the CP violating phase $\delta _\text {CP}$, sum of active neutrino masses $\Sigma _{i} m_i$, solar and atmospheric mass-squared differences, and the lepton number violating parameter called the effective Majorana mass parameter, in line with recent experimental results. We also discuss the scope of this model to explain the baryon asymmetry of the Universe through leptogenesis. We also investigate the possibility of probing the non-unitarity effect in this scenario, but it is found to be rather small.

1 Introduction

The Standard Model (SM) of particle physics predicts massless neutrinos, contradicting the experimental results on neutrino oscillation, according to which the three neutrino flavors mix with each other and at least two of the neutrinos have non-vanishing mass. Due to the absence of RH (RH) neutrinos in the SM, neutrinos do not have a Dirac mass like the other charged fermions and their mass generation in the SM is generally expected to arise from a dimension-five operator [1], which violates lepton number. However, very little is known about the origin of this operator and the underlying mechanism or its flavor structure. Hence, to generate non-zero neutrino mass, one resorts to some beyond the standard model scenarios. There are many such models where the SM is extended by including the RH neutrinos to its particle content. The inclusion of RH neutrinos $N_{R_i}$ not only generates the Dirac mass term but also leads to a Majorana mass for the RH neutrinos, which is of the form $\overline{N_{R_i}}N_{R_i}^c$ and violates $B-L$ symmetry. The smallness of the active neutrino mass is ensured by the high value of the Majorana mass of the RH neutrino [2,3,4,5,6]. In this class of models, if the Dirac masses of the neutrinos are of the order of lightest charged lepton mass i.e., electron mass, the Majorana mass has to be in TeV range to get the observed value of active neutrino mass [4]. But if such models have to be embedded in Grand Unified Theories (GUTs) where quarks and leptons are treated on the same footing, the Dirac mass of the neutrinos will be of the order of that of up-type quark [7] and the observed value of active neutrino mass requires the Majorana mass to be of the order of $10^{15} \, \hbox {GeV}$, which is beyond the reach of present and future experiments.

Many possibilities were proposed to have not so heavy Majorana mass and the existence of other types of neutrinos called sterile neutrinos (S) is one among them [8]. Now the neutrino mass can be expressed in the form of a $3\times 3$ matrix with each element representing a matrix. Depending on the position of the zero elements in the mass matrix in the basis $(\nu , N_R, S)$, active neutrinos receive masses through two different mechanisms called inverse seesaw [8, 9] and linear seesaw [10]. If the 11 and 13 elements are zero, then it is called the inverse seesaw model, and if 11 and 33 elements are zero with non-zero off-diagonal elements, then we have the linear seesaw model. The value of the 22 element could be either negligible or very large compared to all other elements of the mass matrix. In all those cases the smallness of the neutrino mass is independent of the ratio of Dirac mass to heavy neutrino mass and hence allows one to have heavy neutrinos in the TeV range and the bound on the ratio comes from the non-unitarity effect and neutrino-less double beta decay experiments.

All those seesaw mechanisms require some of the elements of the mass matrix to be zero or very small but none of them are prevented by the SM symmetry. All those terms except the 33 element in the matrix will be prohibited if the SM symmetry is extended to $\text {SU}(2)_L\times \text {SU}(2)_R\times \text {SU}(3)_C$ or $U(1)_{B-L}$, since in these symmetry groups RH neutrinos are no longer singlets. But linear seesaw requires the 33 element of the mass matrix to be zero or very small, which is difficult to realize with gauge symmetry, as sterile neutrinos are singlets in all gauge groups. However, if one considers the sterile neutrino as complex, such terms can be avoided by introducing suitable flavor symmetries.

The $A_4$ discrete symmetry group is the group of even permutations of four elements; it has attracted a lot of attention since it is the smallest one which admits one three-dimensional representation and three inequivalent one-dimensional representations. Then the choice of the $A_4$ symmetry is natural, since there are three families of fermions, i.e., the left-handed (LH) leptons can be unified in a triplet representation of $A_4$, while the RH leptons can be assigned to $A_4$ singlets. This set-up was first proposed in Ref. [11] to study the lepton masses and mixing obtaining nearly degenerate neutrino masses and allowing realistic charged leptons masses after the $A_4$ symmetry had been spontaneously broken. Later the $A_4$ symmetry was proved to be very successful in generating a tribimaximal mixing pattern for lepton mixing [12], being well supported by the trends of oscillation data at that time. The tribimaximal mixing pattern predicts solar mixing and atmospheric mixing angles consistent with the experimental data but yields a vanishing reactor mixing angle [13,14,15], contradicting the recent experimental results from various experiments, e.g., Daya Bay [16], T2K [17], MINOS [18], Double CHOOZ [19] and RENO [20] etc. In view of this, the tribimaximal mixing pattern has to be modified.

Here we consider the realization of the linear seesaw with $A_4$ symmetry. We extend the SM symmetry with $A_4\times Z_4\times Z_3$ along with an extra global symmetry $U(1)_X$, as discussed in Ref. [21]. The SM particle content has been extended by introducing three RH neutrinos, $N_{R_i}$, and three singlet fermions, $S_{R_i}$, along with the flavon fields ($\phi _S$, $\phi _T$, $\xi$, $\xi '$, $\rho$, $\rho '$), to understand the flavor structure of the lepton mixing. The proposed model gives an almost similar result to [21] in the context of neutrino oscillation, but it has a different physics aspect in the case of heavy neutrinos. In [21], the active neutrinos get their mass through an inverse seesaw mechanism with the prediction of six nearly degenerate heavy neutrinos, but in our case there are three very different mass states with each state being nearly doubly degenerate. Furthermore, in our model the lightest heavy neutrino mass is assumed to be around 5 TeV and there will be two heavy neutrinos around this energy. Thus, these two models can be distinguished by the structure and implications of the heavy neutrinos. Such implications include non-unitarity and a possible CP violation effect, which can be tested at the currently running long-baseline (NO$\nu$A) or upcoming DUNE experiments. Since all the six heavy neutrinos are almost degenerate in [21], the non-unitarity effect will be large there, whereas in our case the effect will be small as discussed in Sect. 6. Another possibility of distinguishing the two scenarios is the observation of lepton flavor violating (LFV) decay processes like $\mu \rightarrow e \gamma$, $\mu \rightarrow eee$, $\tau \rightarrow \mu \gamma$, etc. These processes are highly suppressed in the SM as they occur at one-loop level with the light neutrino flowing in the loop. Because of the large mixing between light and heavy neutrinos, the heavy neutrinos would flow in the loop and, hence, the rates are correspondingly enhanced as they are no longer suppressed by the light neutrino mass. However, the present model with the linear seesaw mechanism, invoked with $A_4$ symmetry, gives suppressed contributions to lepton flavor violating decay within the allowed model parameter although these contributions are a few orders of magnitude larger than the lepton flavor violating predictions in Ref. [21]. Thus, lepton flavor violation cannot distinguish between these inverse and linear seesaw scenarios with heavy sterile neutrinos. Moreover, our proposed scenario is very well suitable for leptogenesis, as discussed in [22, 23], where the analytic expression for CP asymmetry and corresponding baryon asymmetry for the case of three pairs of nearly degenerate heavy neutrinos can be found. In Ref. [23], the contributions of the absorptive part of the Higgs self-energy to CP violation in heavy particle decays, termed $\epsilon$-type CP violation, have been discussed elaborately. Such contributions are neglected in many cases as they are small compared to $\epsilon ^{\prime }$-type, the CP violation in heavy neutrino decays due to the overlapping of tree-level with one-loop vertex diagram. They have provided the formalism to deal with mixing of states during the decay of the particles and have shown that there is resonant enhancement of $\epsilon$-type CP violation, if the mixing states are nearly degenerate. The CP asymmetries due to both types of CP violations for a model with a pair of nearly degenerate heavy neutrinos were also calculated and it was shown that the CP asymmetry due to $\epsilon$-type CP violation is 100 times higher than that of due to $\epsilon ^{\prime }$-type, which in turn predicts the correct baryon asymmetry of the Universe.

The outline of the paper is as follows. In Sect. 2, we present the model framework for the linear seesaw mechanism. The $A_4$ realization of the linear seesaw mechanism and its implication for the neutrino oscillation parameters is discussed in Sect. 3. Section 4 contains a discussion of the neutrino masses and mixing in the context of $A_4$ symmetry and the results obtained are presented in Sect. 5. In Sect. 6, we present the discussion of leptogenesis and Sect. 7 contains a summary and the conclusions.

Table 1 The particle content and their charge assignments for an $A_4$ realization of the linear seesaw mechanism

2 The model framework for linear seesaw

We consider the minimal extension of the Standard Model ${\mathcal {G}}_{\mathrm{SM}} \equiv \text {SU}(2)_L \times U(1)_Y$, omitting the $\text {SU}(3)_C$ structure for simplicity, with two types of singlet neutrinos which are a complete singlet under ${\mathcal {G}}_{\mathrm{SM}}$ for the implementation of the linear seesaw mechanism. We denote these neutral fermion singlets as RH ($N_{R_i}$) and sterile ($S_{R_i}$) neutrinos. Both these neutral fermion species have a Yukawa coupling with the lepton doublet L. In addition, one can write down a mixing term connecting these two species of neutrinos. The bare Majorana mass terms for $N_{R_i}$ and $S_{R_i}$ are either assumed to be zero or forbidden by some symmetry arguments (Table 1). The leptonic Lagrangian for the linear seesaw mechanism is given by

$$\begin{aligned} -{\mathcal {L}}= & {} y {\overline{L}} {\tilde{H}} N_\text {R} + h {\overline{L}} {\tilde{H}} S_\text {R} + \overline{N_R} m_{RS} S^c_\text {R} + \text {~h.c.} \nonumber \\= & {} {\overline{\nu }}_\text {L} m_\text {D} N_\text {R} + {\overline{\nu }}_\text {L} m_\text {LS} S_\text {R} + {\overline{N}}_\text {R} m_{RS} S^c_\text {R} + \text {~h.c.}. \end{aligned}$$

(1)

The full mass matrix for neutral leptons in the basis $N = (\nu _\text {L}, ~N^c_\text {R}, ~S^c_\text {R})^\text {T}$ is given by

$$\begin{aligned} {\mathbb {M}} = \begin{pmatrix} 0 &{} m_\text {D} &{} m_\text {LS} \\ m_\text {D}^\text {T} &{} 0 &{} m_{RS} \\ m_\text {LS}^\text {T} &{} m^\text {T}_{RS} &{} 0 \end{pmatrix}. \end{aligned}$$

(2)

The resulting mass formula for light neutrinos is governed by the linear seesaw mechanism,

$$\begin{aligned} m_\nu&= m_\text {D} m_{RS}^{-1} m_\text {LS}^\text {T} + \text{ transpose }. \end{aligned}$$

(3)

3 An $A_4$ realization of linear seesaw

In this section, we wish to present an $A_4$ realization of the linear seesaw mechanism which has been discussed in the previous section. The particle content of the model and their representations under flavor symmetries are presented in Table 2.¹ The scalar potential of the model is presented in the appendix. We introduce an extra global symmetry $U(1)_X$, which is broken explicitly but softly by the potential $V_{\mathrm{ex}}(H, \phi _S, \phi _T,\xi ,\xi ', \rho ',\rho )$ given in (A11) in the appendix to prevent the Goldstone boson from occurring [24]. These terms not only break $U(1)_X$ symmetry but also give a non-zero vacuum expectation value to $\rho$, as shown in the appendix, which is found to be very small.

The Yukawa Lagrangian for the charged lepton sector is given as

$$\begin{aligned} {\mathcal {L}}_l= & {} -\left\{ \left[ \frac{\lambda _e}{\Lambda } \left( {\bar{L}}\phi _T\right) H e_{R}\right] + \left[ \frac{\lambda _{\mu }}{\Lambda } \left( {\bar{L}}\phi _T\right) ^{\prime }H\mu _{R}\right] \right. \nonumber \\&\qquad \left. + \left[ \frac{\lambda _{\tau }}{\Lambda }\left( {\bar{L}}\phi _T \right) ^{\prime \prime }H\tau _{R}\right] \right\} \,. \end{aligned}$$

After giving non-zero vacuum expectation values (VEVs) to SM Higgs as well as flavon fields, the $A_4$ symmetry in the charged lepton sector is broken to $Z_3$ with all other flavor symmetries remaining intact, while in the neutrino sector, the flavor symmetries are completely broken. Breaking of $A_4$ to $Z_3$ in the charged lepton sector makes the charged lepton mass matrix diagonal, which is given by

$$\begin{aligned} M_l=v\frac{v_T}{\Lambda }\mathrm{diag}\left( \lambda _e,\lambda _{\mu },\lambda _{\tau }\right) , \end{aligned}$$

(4)

where the couplings $\lambda _e$, $\lambda _\mu$ and $\lambda _\tau$ are considered to be hierarchical to give the correct physical charged lepton masses and the VEVs of the scalar fields are considered as

$$\begin{aligned} \langle H \rangle =(0,v)^T,~~\langle \phi _T\rangle =(v_T,0,0). \end{aligned}$$

(5)

Table 2 Vacuum expectation values of various fields

For the linear seesaw mechanism, the Lagrangian involved in the generation of the mass matrices for an $A_4$ flavor symmetric framework can be written as

$$\begin{aligned} -\mathcal {L_{\nu }}=&{\mathcal {L}}_{\nu N}+{\mathcal {L}}_{N S}+{\mathcal {L}}_{\nu S}\;, \end{aligned}$$

(6)

where

$$\begin{aligned} {\mathcal {L}}_{\nu N}&= y_1 {\overline{L}}{\widetilde{H}} N_R \frac{\rho ^{\prime }}{\Lambda }\;, \end{aligned}$$

(7)

$$\begin{aligned} {\mathcal {L}}_{\nu S}&= y_2 {\overline{L}} {\widetilde{H}} S_R\frac{\rho }{\Lambda }\;, \end{aligned}$$

(8)

$$\begin{aligned} {\mathcal {L}}_{N S}&= \left( \lambda _{NS}^{\phi }\phi _s+\lambda _{NS}^{\xi }\xi + \lambda _{NS}^{\xi ^{\prime }}\xi ^{\prime }\right) \overline{N_R} S^c_R\;. \end{aligned}$$

(9)

It should be noted that the terms ${\mathcal {L}}_{\nu N}$, ${\mathcal {L}}_{\nu S}$ and ${\mathcal {L}}_{N S}$ represent the contributions for Dirac neutrino mass connecting $\nu _L$–$N_R$, $\nu _L$–$S_R$ mixing and $N_R$–$S^c_R$ mixing terms. If one looks at the mass formula for light neutrinos governed by linear seesaw mechanism given in Eq. (3), one can use the mass hierarchy as $m_{RS} \gg m_D, m_{LS}$. That is the reason why we forbid ${\overline{\nu }} N$ and ${\overline{\nu }} S$ terms at tree level and generate them by a dimension-five operator while the heavy mixing term $N-S$ is generated at tree level.

Using the following VEVs for the scalar and flavon fields:

$$\begin{aligned}&\langle \phi _S \rangle = v_S(1,1,1),~~ \langle \xi \rangle =v_{\xi },~ \langle \xi ^{\prime }\rangle =v_{\xi ^{\prime }}, \\&\langle \rho \rangle =v_{\rho },~~ \langle \rho ^{\prime }\rangle =v_{\rho ^{\prime }}\;, \end{aligned}$$

the various mass matrices are found to be

$$\begin{aligned} m_\text {D}= & {} y_1v\frac{v_{\rho ^{\prime }}}{\Lambda }\left( \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} 0 &{}1 \\ 0 &{} 1 &{}0 \end{array} \right) , \nonumber \\ m_\text {LS}= & {} y_2v\frac{v_{\rho }}{\Lambda } \left( \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} 0 &{}1 \\ 0 &{} 1 &{}0 \end{array} \right) , \end{aligned}$$

(10)

$$\begin{aligned} m_{RS}= & {} \frac{a}{3}\left( \begin{array}{ccc} 2 &{} -1 &{} -1\\ -1 &{} 2 &{}-1 \\ -1 &{} -1 &{}2 \end{array} \right) + b\left( \begin{array}{ccc} 1 &{} 0&{} 0\\ 0 &{} 0 &{}1 \\ 0&{} 1 &{}0 \end{array} \right) \nonumber \\&+ d\left( \begin{array}{ccc} 0 &{} 0&{} 1\\ 0 &{} 1 &{}0 \\ 1&{} 0 &{}0 \end{array} \right) , \end{aligned}$$

(11)

where $a=\lambda _{NS}^{\phi }v_S$, $b=\lambda _{NS}^{\xi }v_{\xi }$ and $d=\lambda _{NS}^{\xi ^{\prime }}v_{\xi ^{\prime }}$.

The first term in Eq. (11) comes from $\lambda _1\phi _s\left( \overline{N_R}S_R^c\right) _{3s}$, where $\left( \overline{N_R}S_R^c\right) _{3s}$ is a triplet which is symmetric under exchange of $N_R$ and $S_R$. The product of two triplets can also form a triplet, which is antisymmetric under the exchange of the particles. In the linear seesaw mechanism, the mass of the light neutrino is represented as $m_{\nu }=m_\text {D}m_\text {RS}^{-1}m_\text {LS}^{T}$+transpose, and as seen from Eq. (10) the mass matrices $m_\text {D}$ and $m_\text {LS}$ are symmetric and are related as $m_\text {D} \propto m_\text {LS}$. Hence, in $m_{\nu }=m_\text {D}^{T}(m_\text {RS}^{-1}+{m_\text {RS}^{-1}}^T)m_\text {LS}$, the antisymmetric part cancels out and only the symmetric part survives.

In a natural scenario we expect the Yukawa couplings $y_{1,2}$ and the various $\lambda$ couplings to be just one or two orders of magnitude below unity, so that the different scales of the mass matrices should arise mainly through the VEVs of different scalars ($v,~v_{\rho '},~v_\rho ,~v_S,~v_\xi ,~ \mathrm{and} ~v_{\xi '}$). The VEV of the SM Higgs is considered to be $v=246 \, \hbox {GeV}$. For the TeV scale $m_{\mathrm{RS}}$, the VEVs $v_S,~v_\xi ,~ \mathrm{and} ~v_{\xi '}$ should be in the TeV range. Now considering $|y_1| ^2\approx |y_2|^2 \approx 10^{-3}$, and assuming the Dirac mass $m_D$ to be in the MeV range (say 70 MeV), one can obtain $\displaystyle {\frac{ v_{\rho '}}{\Lambda } }\approx 9 \times 10^{-3}$ from the expression $m_D \approx \displaystyle {\frac{y_1 v v_{\rho '}}{\Lambda }}$, which gives $v_{\rho '}\approx 9 \, \hbox {TeV}$ for $\Lambda =10^3 \, \hbox {TeV}$. Similarly for $m_{\mathrm{LS}}$ in the keV range (5 keV), one obtains $v_{\rho }\approx 6 \times 10^{-2} \, \hbox {GeV}$. Thus, a rather large spectrum of scales in the mass matrix arises through the VEVs of different scalar and flavon fields.

4 Neutrino masses and mixing

For calculation convenience one can rewrite the $m_\text {RS}$ mass matrix (11) as

$$\begin{aligned} m_{RS}= & {} \left( \begin{array}{ccc} 2a/3+b &{} -a/3&{} -a/3\\ -a/3 &{} 2a/3 &{}-a/3+b \\ -a/3&{} -a/3+b &{}2a/3 \end{array} \right) \nonumber \\&+ \left( \begin{array}{ccc} 0 &{} 0&{} d\\ 0 &{} d &{}0 \\ d&{} 0 &{}0 \end{array} \right) . \end{aligned}$$

(12)

Thus, with Eqs. (3), (10) and (11), one can obtain the light neutrino mass,

$$\begin{aligned} m_{\nu }= & {} m_\text {D} m_{RS}^{-1}m_\text {LS}^T+\text {transpose} \nonumber \\= & {} k_1k_2\left( \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} 0 &{}1 \\ 0 &{} 1 &{}0 \end{array}\right) m_{RS}^{-1}\left( \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} 0 &{}1 \\ 0 &{} 1 &{}0 \end{array}\right) , \end{aligned}$$

(13)

where the parameters $k_1$ and $k_2$ are related to the VEVs through

$$\begin{aligned} k_1=\sqrt{2} y_1v\frac{v_{\rho ^{\prime }}}{\Lambda }\;, ~~~~k_2=\sqrt{2}y_2v\frac{v_{\rho }}{\Lambda }. \end{aligned}$$

Hence, the inverse of the light neutrino mass matrix is given by

$$\begin{aligned} m_{\nu }^{-1}= & {} \frac{1}{k_1k_2}\left( \begin{array}{ccc} 2a/3+b &{} -a/3&{} -a/3\\ -a/3 &{} 2a/3 &{}-a/3+b \\ -a/3&{} -a/3+b &{}2a/3 \end{array} \right) \nonumber \\&+\frac{1}{k_1k_2}\left( \begin{array}{ccc} 0 &{} d&{} 0\\ d &{} 0 &{}0 \\ 0&{} 0 &{}d \end{array} \right) , \end{aligned}$$

(14)

which in the TBM basis will have the form $m_{\nu }^{-1^{\prime }}=U_\text {TBM}^T m_{\nu }^{-1}U_\text {TBM}$,

$$\begin{aligned} m_{\nu }^{-1^{\prime }}=\left( \begin{array}{ccc} a+b-d/2 &{} 0 &{} -\frac{\sqrt{3}}{2}d\\ 0 &{}~~ b+d~~ &{}0 \\ -\frac{\sqrt{3}}{2}d &{} 0 &{}a-b+d/2 \end{array}\right) \;. \end{aligned}$$

(15)

The inverse mass matrix $m_{\nu }^{-1^{\prime }}$ can be diagonalized by $U_{13}^*$. Hence, the matrix $m_\nu ^{-1}$ can be diagonalized by $U_\text {TBM}\cdot U_{13}^*$, and thus the matrix $m_{\nu }$ can be diagonalized by $U_\text {TBM}\cdot U_{13}$, and $m_{RS}$ by $U_\text {TBM}\cdot U_{13}^T$. The complex unitary matrix $U_{13}$ has the form

$$\begin{aligned} U_{13}=\left( \begin{array}{ccc} \cos \theta &{} 0 &{} \sin \theta e^{-i\psi }\\ 0 &{} 1 &{} 0 \\ -\sin \theta e^{i\psi }&{} 0 &{} \cos \theta \end{array} \right) , \end{aligned}$$

(16)

where the parameters $\theta$ and $\psi$ are expressed in terms of the mass matrix parameters $d/b=\lambda _1e^{\phi _{db}}$, $a/b=\lambda _2e^{\phi _{ab}}$ as

$$\begin{aligned} \tan 2\theta =-\frac{\sqrt{3}\lambda _1\cos \phi _{db}}{(\lambda _1 \cos \phi _{db}-2)\cos \psi +(2\lambda _2\sin \phi _{ab})\sin \psi }\;\nonumber \\ \end{aligned}$$

(17)

and

$$\begin{aligned} \tan \psi =\frac{\sin \phi _{db}}{\lambda _2\cos (\phi _{ab}-\phi _{db})}\;. \end{aligned}$$

(18)

The eigenvalues of $m_{\nu }$ and $m_{RS}$ are related by

$$\begin{aligned} {\tilde{m}}_i=\frac{k_1k_2}{{\tilde{M}}_i}\;, \end{aligned}$$

(19)

where ${\tilde{m}}_i$ and ${\tilde{M}}_i$ are $i\text {th}$ eigenvalues of $m_{\nu }$ and $m_{RS}$, respectively. The eigenvalues of $m_{RS}$ can be expressed as

$$\begin{aligned} {\tilde{M}}_1= & {} b\left[ \lambda _2 e^{i\phi _{ab}}-\sqrt{1+\lambda _1^2e^{2i\phi _{db}}-\lambda _1 e^{i\phi _{db}}}\right] , \nonumber \\ {\tilde{M}}_2= & {} b\left[ 1+\lambda _1 e^{i\phi _{db}}\right] , \nonumber \\ {\tilde{M}}_3= & {} b\left[ \lambda _2 e^{i\phi _{ab}}+\sqrt{1+\lambda _1^2e^{2i\phi _{db}}-\lambda _1 e^{i\phi _{db}}}\right] , \end{aligned}$$

(20)

which give the mass of the heavy neutrinos as $M_i=|\tilde{M_i}|$. Explicitly, one can write the heavy neutrino masses as

$$\begin{aligned} M_1= & {} |b|M_1^{\prime } \nonumber \\= & {} |b|\left[ (\lambda _2\cos \phi _{ab}-C)^2+(\lambda _2\sin \phi _{ab}-D)^2\right] ^{1/2} ,\nonumber \\ M_2= & {} |b|M_2^{\prime } =|b|\left[ 1+\lambda _1^2+2\lambda _1\cos \phi _{db}\right] ^{1/2}, \nonumber \\ M_3= & {} |b|M_3^{\prime } \nonumber \\= & {} |b|\left[ (\lambda _2\cos \phi _{ab}+C)^2+(\lambda _2\sin \phi _{ab}+D)^2\right] ^{1/2}\;,\nonumber \\ \end{aligned}$$

(21)

where

$$\begin{aligned} C= & {} \left[ \frac{A+\sqrt{A^2+B^2}}{2}\right] ^{1/2}\;, \nonumber \\ D= & {} \left[ \frac{-A+\sqrt{A^2+B^2}}{2}\right] ^{1/2}\;,\nonumber \\ A= & {} 1+\lambda _1^2\cos 2\phi _{db}-\lambda _1\cos \phi _{db}\;, \nonumber \\ B= & {} \lambda _1^2\sin 2\phi _{db}-\lambda \sin \phi _{db}\;, \end{aligned}$$

(22)

and the phases $\phi _i$ of ${{\tilde{M}}}_i$, i.e., ${{\tilde{M}}}_i=|\tilde{M}_i|e^{i \phi _i}$, as

$$\begin{aligned} \phi _1= & {} \tan ^{-1}\left[ \frac{\lambda _2\sin \phi _{ab}-D}{\lambda _2\cos \phi _{ab}-C}\right] \;,\nonumber \\ \phi _2= & {} \tan ^{-1}\left[ \frac{\lambda _1\sin \phi _{db}}{1+\lambda _1\cos \phi _{db}}\right] \;, \nonumber \\ \phi _3= & {} \tan ^{-1}\left[ \frac{\lambda _2\sin \phi _{ab}+D}{\lambda _2\cos \phi _{ab}+C}\right] . \end{aligned}$$

(23)

Thus, the active neutrino masses $m_i=|{\tilde{m}}_i|$ and the matrix which diagonalizes active neutrino mass matrix, $U_{\nu }$, are given by

$$\begin{aligned} m_i= & {} \frac{|k_1k_2|}{M_i}\;,\nonumber \\ U_{\nu }= & {} U_\text {TBM}\cdot U_{13}\cdot P\;, \end{aligned}$$

(24)

with $P=\text {diag}(e^{-i\phi _1/2},e^{-i\phi _2/2},e^{-i\phi _3/2})$.

The lepton mixing matrix, known as the PMNS matrix, is given by [25,26,27]

$$\begin{aligned} U_\text {PMNS}=U_l^{\dagger }\cdot U_{\nu }\;, \end{aligned}$$

(25)

where $U_l$ and $U_{\nu }$ are the matrices which diagonalize charged lepton and neutrino mass matrices. Here $U_l=I$ and $U_{\nu }=U_\text {TBM}\cdot U_{13}\cdot P$, hence

$$\begin{aligned} U_\text {PMNS}=U_\text {TBM}\cdot U_{13}\cdot P, \end{aligned}$$

(26)

which has been proved to be in good agreement with the experimental observations [28, 29]. The PMNS matrix can be parametrized in terms of three mixing angles ($\theta _{13}$, $\theta _{23}$ and $\theta _{12}$) and three phases (one Dirac phase, $\delta _\text {CP}$, and two Majorana phases, $\rho$ and $\sigma$) as

$$\begin{aligned} \begin{aligned}&U_\text {PMNS} \\&\quad =\left( \begin{array}{ccc} c^{}_{12} c^{}_{13} &{} s^{}_{12} c^{}_{13} &{} s^{}_{13} e^{-i\delta _\text {CP}} \\ -s^{}_{12} c^{}_{23} - c^{}_{12} s^{}_{13} s^{}_{23} e^{i\delta _\text {CP}} &{} c^{}_{12} c^{}_{23} - s^{}_{12} s^{}_{13} s^{}_{23} e^{i\delta _\text {CP}} &{} c^{}_{13} s^{}_{23} \\ s^{}_{12} s^{}_{23} - c^{}_{12} s^{}_{13} c^{}_{23} e^{i\delta _\text {CP}} &{} -c^{}_{12} s^{}_{23} - s^{}_{12} s^{}_{13} c^{}_{23} e^{i\delta _\text {CP}} &{} c^{}_{13} c^{}_{23} \end{array} \right) P^{}_\nu \;, \end{aligned}\nonumber \\ \end{aligned}$$

(27)

where $c_{ij}=\cos \theta _{ij}$ and $s_{ij}=\sin \theta _{ij}$ and $P_{\nu }=\text {diag}(1,e^{i\rho /2},e^{i\sigma /2})$. From Eqs. (26) and (27), one can find

$$\begin{aligned} \sin \theta= & {} \sqrt{\frac{3}{2}}\sin \theta _{13}~, \nonumber \\ \sin \delta _\text {CP}= & {} -\frac{\sin \psi }{\displaystyle {\sqrt{1-\frac{3(2-3\sin ^2\theta _{13})}{(1-\sin ^2\theta _{13})^2}\sin ^2\theta _{13}\cos ^2\psi }}} \nonumber \\\approx & {} -\sin \psi . \end{aligned}$$

(28)

The above expressions relate the parameters of the model, i.e., $\theta$ and $\psi$, to the mixing observables $\sin ^2\theta _{13}$ and $\delta _\text {CP}$, respectively. Since $\sin ^2\theta _{13}$ is known more precisely than $\delta _\text {CP}$, in our calculation we fix $\theta$ by fixing $\sin ^2\theta _{13}$ at its best-fit value while considering all possible value of $\psi$ for which $\delta _\text {CP}$ falls within its $3\sigma$ experimental range. Although in this case the solar mixing angle is slightly on the higher side of the observed central value, i.e., $\displaystyle {\sin ^2 \theta _{12} = 1/\left( 3-2\sin ^2 \theta \right) }$, it lies within the $3 \sigma$ range of the observed data.

5 Numerical results

Using Eqs. (19) and (21), the light neutrino masses are found to be

$$\begin{aligned} m_i=\frac{|k_1k_2|}{M_i}=\frac{|k_1k_2|}{|b|}\frac{1}{M_i^{\prime }}\;. \end{aligned}$$

(29)

Since only the mass-squared differences, $\Delta m^2_{21}$ (solar mass-squared difference) and $|\Delta m^2_{32}|$ (atmospheric mass-squared difference) are measured in neutrino oscillation experiments, we calculate the mass-squared differences from Eq. (29) as

$$\begin{aligned}&\Delta m^2_{21}=\left| \frac{k_1k_2}{b}\right| ^2 \left( \frac{1}{{M_2^{\prime }}^2}-\frac{1}{{M_1^{\prime }}^2}\right) \;, \nonumber \\&\left| \Delta m^2_{31}\right| =\left| \frac{k_1k_2}{b}\right| ^2 \left| \left( \frac{1}{{M_3^{\prime }}^2}-\frac{1}{{M_1^{\prime }}^2}\right) \right| \;. \end{aligned}$$

(30)

Substituting Eq. (21) in the above equations, we find the ratio of the two mass-squared differences:

$$\begin{aligned}&r=\frac{\Delta m_{21}^2}{|\Delta m_{31}^2|}=\left[ \frac{(\lambda _2\cos \phi _{ab}+C)^2+(\lambda _2\sin \phi _{ab}+D)^2}{1+\lambda _1^2+2\lambda _1\cos \phi _{db}}\right] \nonumber \\&\quad \times \left[ \frac{(\lambda _2\cos \phi _{ab}-C)^2+(\lambda _2\sin \phi _{ab}-D)^2-\left( 1+\lambda _1^2+2\lambda _1\cos \phi _{db}\right) }{4\lambda _2|C \cos \phi _{ab}+D\sin \phi _{ab}|}\right] \;.\nonumber \\ \end{aligned}$$

(31)

Now using Eqs. (17), (18), (21), (22) and (31), and by fixing the parameters $\phi _{db}$, $\psi$ and $\theta$, one can find the numerical values of the $M_i'$. Once the $M_i'$ are known $\left| \displaystyle {\frac{k_1k_2}{b}}\right|$ can be calculated from (30) as

$$\begin{aligned} \left| \frac{k_1k_2}{b}\right| =\sqrt{\frac{\Delta m^2_{21}}{\displaystyle { \left( \frac{1}{M_2^{\prime 2}}-\frac{1}{M_1^{\prime 2}}\right) }}} =\sqrt{\left| \frac{\Delta m^2_{31}}{\left( \frac{1}{M_3^{\prime 2}}-\frac{1}{M_1^{\prime 2}}\right) }\right| }\;, \end{aligned}$$

(32)

which will also give the absolute value of light neutrino masses as all the quantities on the right hand side of (29) are now known.

Fig. 1

Variation of $\lambda _2$, the lightest neutrino mass ($m_l$) and $\Sigma _im_i$ with $\phi _{ab}$, red lines are for the inverted hierarchy and green lines are for the normal hierarchy

Fig. 2

Variation of $\lambda _2$, $m_l$ and $\Sigma _im_i$ with $\phi _{ab}$, red points are for the inverted hierarchy and green points are for the normal hierarchy

We now rewrite the expression for $\tan \psi$ (18) in terms of $\phi _{db}$ as

$$\begin{aligned} \phi _{db}=0,\pi ,~~~\text {for}~ \tan \psi =0, \end{aligned}$$

(33)

and

$$\begin{aligned} \phi _{ab}=\phi _{db}+ \cos ^{-1}\left( \frac{\sin \phi _{db}}{\lambda _2\tan \psi }\right) ,~~~\text {for}~~ \tan \psi \ne 0, \end{aligned}$$

(34)

and consider the following cases to see the implications.

5.1 Correlation between model parameters with $\tan \psi =0$

In this case $\phi _{db}$ will be either 0 or $\pi$, and for $\phi _{db}=0$ one can obtain from Eq. (17)

$$\begin{aligned} \lambda _1=\frac{2\tan 2\theta }{\sqrt{3}+\tan 2\theta }\;, \end{aligned}$$

(35)

and the ratio of the mass-squared differences r (31), satisfies the relation

$$\begin{aligned} r= & {} \left[ \frac{\lambda _2^2+2\lambda _2C\cos \phi _{ab}+C^2}{(1+\lambda _1)^2}\right] \nonumber \\&\times \left[ \frac{\lambda _2^2-2\lambda _2C\cos \phi _{ab}+C^2-(1+\lambda _1)^2}{4\lambda _2|C\cos \phi _{ab}|}\right] , \end{aligned}$$

(36)

where $C=\sqrt{\frac{1-\lambda _1+\lambda _1^2}{2}}$. It should be noted from (36) that r will be divergent near $\phi _{ab}=\pi /2$ and, thus, the values of $\phi _{ab}$ around $\pi /2$ are not allowed. The eigenvalues of $m_{RS}$ in this case become

$$\begin{aligned} M_1= & {} |b|\sqrt{\lambda _2^2-2\lambda _2C\cos \phi _{ab}+C^2}\;, \nonumber \\ M_2= & {} |b|(1+\lambda _1),\nonumber \\ M_3= & {} |b|\sqrt{\lambda _2^2+2\lambda _2C\cos \phi _{ab}+C^2}\;. \end{aligned}$$

(37)

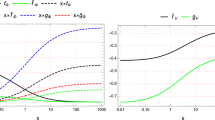
Now from Eq. (36), using the measured values of $r=0.0291 \pm 0.00085$ [30], variation of the parameter $\lambda _2$, the lightest neutrino mass ($m_l$) and the sum of active neutrino masses $\sum m_i$ with $\phi _{ab}$, consistent with the $3 \sigma$ range of the observed neutrino mixing parameters are shown in Fig. 1.

Fig. 3

Correlation plots between $\lambda _1$ and $\lambda _2$ for the normal hierarchy (top left panel), for the inverted hierarchy (top right panel) and between $\Sigma _im_i$ (red points), $m_l$ (green points) and $\delta _\text {CP}$ in the bottom left (right) panel for the normal (inverted) hierarchy. The vertical and horizontal bands represent the values of $\delta _\text {CP}$ beyond its $3\sigma$ range and $\Sigma _i m_i>0.23$ eV, the upper bound on the sum of active neutrino masses given by the Planck data, respectively

Fig. 4

Correlation plots between $\phi _{db}$, $\phi _{ab}$ and $\delta _\text {CP}$ for normal (left panel) and inverted (right panel) hierarchy. The vertical band represents the values of $\delta _\text {CP}$ beyond its $3\sigma$ range

Meanwhile for $\phi _{db}=\pi$

$$\begin{aligned} \lambda _1=\frac{2\tan 2\theta }{\sqrt{3}-\tan 2\theta }\;, \end{aligned}$$

(38)

and the ratio of the mass-squared differences r satisfies the relation

$$\begin{aligned} r= & {} \left[ \frac{\lambda _2^2+2\lambda _2C\cos \phi _{ab}+C^2}{(1-\lambda _1)^2} \right] \nonumber \\&\times \left[ \frac{\lambda _2^2-2\lambda _2C\cos \phi _{ab}+C^2 -(1-\lambda _1)^2}{4\lambda _2|C\cos \phi _{ab}|}\right] , \end{aligned}$$

(39)

with $C=\sqrt{\frac{1+\lambda _1+\lambda _1^2}{2}}$, and the eigenvalues of $m_{RS}$ are given as

$$\begin{aligned} M_1= & {} |b|\sqrt{\lambda _2^2-2\lambda _2C\cos \phi _{ab}+C^2}\;, \nonumber \\ M_2= & {} |b|(1-\lambda _1)\;,\nonumber \\ M_3= & {} |b|\sqrt{\lambda _2^2+2\lambda _2C\cos \phi _{ab}+C^2}\;. \end{aligned}$$

(40)

Analogous to Fig. 2, the variation of various parameters with $\phi _{ab}$ is shown in Fig. 2. From the plots it can be seen that, for normal ordering, the allowed parameter space is severely constrained.

5.2 Correlation between model parameters with $\tan \psi \ne 0$

With $\tan \psi \ne 0$, the analytic expression for $\lambda _1$ is given by

$$\begin{aligned} \lambda _1=\frac{2\lambda _2\tan 2\theta \cos \phi _{ab}\sin \psi }{\sin \phi _{ab}\left[ \sqrt{3}+\tan 2\theta \cos \psi \right] }\;. \end{aligned}$$

(41)

We obtain the correlation plots between various parameters as given in Figs. 3 and  4, by varying $\phi _{db}$ between 0 to $2\pi$ and $\delta _\text {CP}$ in its $3\sigma$ range $(0-0.17\pi \oplus 0.76\pi -2\pi )$, while fixing $\sin ^2\theta _{13}$ at its best-fit value [30].

Fig. 5

Correlation plots between Majorana phases $\sigma$ and $\rho$ for the case of normal (left pane) and inverted hierarchy (right panel) for $\tan \psi =0$

Fig. 6

Correlation plots between the Majorana phases $\sigma$ and $\rho$ for the case of the normal (left pane) and inverted hierarchy (right panel) for $\tan \psi \ne 0$

Fig. 7

Variation of the Majorana mass parameter $M_{ee}$, which is an observable in neutrino-less double beta decay with lightest neutrino mass for the case of the normal (left panel) and inverted hierarchy (right panel) for $\tan \psi =0$

Comment on neutrino-less double beta decay. The experimental observation of neutrino-less double beta decay would not only ascertain the Lepton Number Violation (LNV) in nature but it can also give an absolute scale of the lightest active neutrino mass. The experimental non-observation of such an event puts a bound on the half-life of this process on various isotopes which can be translated as a bound on the particle physics parameter called the effective Majorana mass. In the linear seesaw model, the light Majorana neutrinos contribute to neutrino-less double beta decay, while the heavy pseudo-Dirac neutrinos give a suppressed contribution.

The measure of LNV can be understood with the key parameter called the effective Majorana mass, which is defined as

$$\begin{aligned} \left| M_{ee} \right| \equiv \left| m^\nu _{ee} \right|= & {} \bigg | U^2_{e1}\, m_1 + U^2_{e2}\, m_2 e^{i \rho } + U^2_{e3}\, m_3 e^{i \sigma } \bigg |. \nonumber \\ \end{aligned}$$

(42a)

The light neutrino mass eigenvalues $m_1, m_2, m_3$ depend on input model parameters. These input model parameters are constrained to their allowed range in order to satisfy the oscillation data giving correct values of mass-squared differences and mixings. The Majorana phases $\rho$ and $\sigma$ are related to $\phi _{ab}$ and $\phi _{db}$ in some way and, thus, they are constrained to take limited values. A brief discussion on the allowed values of the Majorana phases is presented below.

Fig. 8

Variation of effective Majorana parameter $M_{ee}$, which is a measure of lepton number violation with the lightest neutrino mass for the case of the normal (left panel) and the inverted hierarchy (right panel) for $\tan \psi \ne 0$

Majorana phases: Majorana phases $\rho$ and $\sigma$ are related to the rephasing invariants $S_1=\mathrm{Im}\left\{ U_{e 1}^*U_{e 2} \right\}$, $S_2=\mathrm{Im}\left\{ U_{e 1}^*U_{e 3} \right\}$, and $S_3=\mathrm{Im}\left\{ U_{e 2}^*U_{e 3} \right\}$ of the leptonic mixing matrix [31] as

$$\begin{aligned}&\cos \rho =1-2\frac{S_1^2}{\left| U_{e1}\right| ^2\left| U_{e2}\right| ^2},\nonumber \\&\cos \sigma '=1-2\frac{S_2^2}{\left| U_{e1}\right| ^2\left| U_{e3}\right| ^2},\nonumber \\&\cos \left( \sigma '-\rho \right) =1-2\frac{S_3^2}{\left| U_{e2}\right| ^2\left| U_{e3}\right| ^2}\;, \end{aligned}$$

(43)

where $\sigma '= \sigma -2 \delta _\text {CP}$. The elements of the PMNS mixing matrix can be derived from the knowledge of the tribimaximal mixing multiplied by a rotation matrix in the 13 plane as shown in Eq. (26). Thus, the values of the various PMNS matrix elements in the proposed model are given as $\left| U_{e1}\right| =\frac{2}{\sqrt{6}}\cos \theta$, $\left| U_{e2}\right| =\frac{1}{\sqrt{3}}$ and $\left| U_{e3}\right| =\frac{2}{\sqrt{6}}\sin \theta$. It should be noted that the rephasing invariants associated with the Majorana phases are not uniquely determined. For example, instead of $S_1$ defined above, one could have chosen $S_1'=\mathrm{Im}\left\{ U_{\tau 1}^*U_{\tau 2} \right\}$, or $S_1{''}=\mathrm{Im}\left\{ U_{\mu 1}^*U_{\mu 2} \right\}$, and so on. With Eqs. (16) and (26), we obtain $S_1$, $S_2$ and $S_3$:

$$\begin{aligned} S_1= & {} \frac{\sqrt{2}}{3} \cos \theta \sin \left( \frac{\phi _1}{2}-\frac{\phi _2}{2}\right) , \nonumber \\ S_2= & {} \frac{1}{3} \sin 2 \theta \sin \left( \frac{\phi _1}{2}-\frac{\phi _3}{2} -\psi \right) ,\nonumber \\ S_3= & {} \frac{\sqrt{2}}{3} \sin \theta \sin \left( \frac{\phi _2}{2}-\frac{\phi _3}{2} -\psi \right) . \end{aligned}$$

(44)

The correlation plots between the Majorana phases $\rho$ and $\sigma$ are shown in Figs. 5 and 6 for $\tan \psi =0$ and $\tan \psi \ne 0$, respectively. The estimation of the effective Majorana mass parameter using these already constrained input model parameters with the variation of lightest neutrino mass is displayed in Fig. 7, where the left panel is for the NH and the right panel is for the IH pattern of light neutrino masses.

The current limit on the half-life, or the translated bound on the effective Majorana mass parameter ($m^\nu _{ee}$) from GERDA Phase-I [32], is $T_{1/2}^{0\nu }(^{76}\text {Ge}) > 2.3\times 10^{25}$ yr and this implies $|m_{ee}| \le 0.21\, \text{ eV }$ and from KamLAND-Zen [33] as $T_{1/2}^{0\nu }(^{136}\text {Xe}) > 1.07\times 10^{26}$ yr, and this implies $|m_{ee}| \le 0.15\, \text{ eV }$. There is also a bound from the CUORE experiment on the effective Majorana mass parameter as $|m_{ee}| \le 0.073\, \text{ eV }$ [34]. The expected reach of the future planned $0\nu \beta \beta$ experiments including the nEXO experiment gives $T_{1/2}^{0\nu }(^{136}\text {Xe}) \approx 6.6\times 10^{27}$ yr [35]. The variation of the effective mass parameter (in green points) with the lightest neutrino mass is shown in Fig. 7 for $\tan \psi =0$ and the same is plotted in Fig. 8 for $\tan \psi \ne 0$. The left panel is for the NH pattern and the right panel is for the IH pattern of the light neutrino masses. The horizontal lines represent the bounds on the effective Majorana mass from various neutrino-less double beta decay experiments, while the vertical shaded regions are disfavored by the Planck data. The present bound is $\Sigma _i m_i < 0.23$ eV from the Planck+WP+highL+BAO data (Planck1) at 95% CL.

As seen from the plots, the current bound on the effective mass parameters from GERDA Phase-I and KamLAND-Zen is not sensitive to the NH and IH patterns of the light neutrino mass ordering. However, the future planned nEXO experiment is sensitive to both patterns of light neutrinos.

6 Leptogenesis

It is well known that leptogenesis is one of the most elegant frameworks for dynamically generating the observed baryon asymmetry of the Universe. In the resonance leptogenesis scenarios, since the mass difference between two or more heavy neutrinos is much smaller than their individual masses and comparable to their widths, the CP asymmetry in their decays occurs primarily through self-energy effects ($\epsilon$-type) rather than vertex effects ($\epsilon '$-type) and gets resonantly enhanced. In the present $A_4$ realization, since the mass splitting between the two heavy neutrinos is rather tiny, it provides the opportunity for resonant leptogenesis, which will be discussed in this section.

During the calculation of light neutrino masses and mixing, we have neglected the higher order terms in the Lagrangian ${{{\mathcal {L}}}}_{\nu }$ as displayed in Eq. (6), which are given with an extra dimension-six operators as follows:

$$\begin{aligned}&-\left\{ \Big [\lambda _{N\phi }\phi _S+\lambda _{N\xi }\xi + \lambda _{N\xi ^{\prime }} \xi ^{\prime } \Big ]\frac{\rho \rho ^{\prime }}{\Lambda ^2}{\overline{N}}_RN_R^c \right. \nonumber \\&\quad \left. + \Big [\lambda _{S\phi }\phi _S+\lambda _{S\xi }\xi + \lambda _{S\xi ^{\prime }}{\xi ^{\prime }}\Big ] \frac{\rho ^\dagger {\rho ^{\prime }}}{\Lambda ^2}{\overline{S}}_R S_R^c \right\} . \end{aligned}$$

(45)

These extra terms do not make much difference in those calculations, but they lead to a tiny mass splitting in doubly degenerate mass states of heavy neutrinos. Including these additional terms, the Majorana mass matrix ${\mathbb {M}}_2$ becomes

$$\begin{aligned} {\mathbb {M}}_2=\left( \begin{array}{cc} m_R &{}m_{RS} \\ m_{RS}^T &{} m_S \end{array} \right) , \end{aligned}$$

(46)

where

$$\begin{aligned} m_R= & {} \frac{|v_{\rho }v_{\rho ^{\prime }}|}{\Lambda ^2} \left( \begin{array}{c c c} \frac{2}{3}\lambda _{N\phi }v_S+\lambda _{N\xi }v_{\xi }&{}-\frac{1}{3}\lambda _{N\phi }v_S&{}-\frac{1}{3}\lambda _{N\phi }v_S\\ -\frac{1}{3}\lambda _{N\phi }v_S &{}\frac{2}{3}\lambda _{N\phi }v_S &{} -\frac{1}{3}\lambda _{N\phi }v_S+\lambda _{N\xi }v_{\xi } \\ -\frac{1}{3}\lambda _{N\phi }v_S &{}-\frac{1}{3}\lambda _{N\phi }v_S+\lambda _{N\xi }v_{\xi } &{}\frac{2}{3}\lambda _{N\phi }v_S \end{array} \right) \\&+ {\frac{|v_{\rho }v_{\rho ^{\prime }}|}{\Lambda ^2}} \left( \begin{array}{ccc} 0 &{} 0 &{}\lambda _{N\xi ^{\prime }}v_{\xi ^{\prime }} \\ 0&{}\lambda _{N\xi ^{\prime }}v_{\xi ^{\prime }}&{}0\\ \lambda _{N\xi ^{\prime }}v_{\xi ^{\prime }}&{}0 &{}0 \end{array} \right) \; \end{aligned}$$

and

$$\begin{aligned} m_S= & {} \frac{|v_{\rho }v_{\rho ^{\prime }}|}{\Lambda ^2} \left( \begin{array}{c c c} \frac{2}{3}\lambda _{S\phi }v_S+\lambda _{S\xi }v_{\xi }&{}-\frac{1}{3}\lambda _{S\phi }v_S&{}-\frac{1}{3}\lambda _{S\phi }v_S\\ -\frac{1}{3}\lambda _{S\phi }v_S &{}\frac{2}{3}\lambda _{S\phi }v_S &{} -\frac{1}{3}\lambda _{S\phi }v_S+\lambda _{S\xi }v_{\xi } \\ -\frac{1}{3}\lambda _{S\phi }v_S &{}-\frac{1}{3}\lambda _{S\phi }v_S+\lambda _{S\xi }v_{\xi } &{}\frac{2}{3}\lambda _{S\phi }v_S \end{array} \right) \nonumber \\&+ {\frac{|v_{\rho }v_{\rho ^{\prime }}|}{\Lambda ^2}} \left( \begin{array}{ccc} 0 &{} 0 &{}\lambda _{S\xi ^{\prime }}v_{\xi ^{\prime }} \\ 0&{}\lambda _{S\xi ^{\prime }}v_{\xi ^{\prime }}&{}0\\ \lambda _{S\xi ^{\prime }}v_{\xi ^{\prime }}&{}0 &{}0 \end{array} \right) \;. \end{aligned}$$

(47)

The phase of $v_\rho$ has been absorbed in the couplings $\lambda$. The mass matrix ${\mathbb {M}}_2$ can be approximately block diagonalized by the unitary matrix $\frac{1}{\sqrt{2}} \left( \begin{array}{cc} I &{}-I \\ I &{}I \end{array} \right)$ (where we have neglected the small mass difference between $S_R$ and $M_R$) and becomes

$$\begin{aligned} {\mathbb {M}}_2^{\prime }= & {} \left( \begin{array}{cc} m_{RS}+\displaystyle {\frac{m_R+m_S}{2}} &{}m_S-m_R \\ m_S-m_R &{}-m_{RS}+\displaystyle {\frac{m_R+m_S}{2}} \end{array} \right) \nonumber \\\approx & {} \left( \begin{array}{cc} m_{RS}+\displaystyle {\frac{m_R+m_S}{2}} &{}0 \\ 0 &{}-m_{RS}+\displaystyle {\frac{m_R+m_S}{2}} \end{array} \right) , \end{aligned}$$

(48)

with eigenvalues

$$\begin{aligned} {M_1^{\prime }}^{\pm }\approx M_1\left( 1\pm \frac{v_{\rho }v_{\rho ^{\prime }}}{\Lambda ^2}\frac{m_1^{\prime }}{M_1}\right) \;, \nonumber \\ {M_2^{\prime }}^{\pm }\approx M_2\left( 1\pm \frac{v_{\rho }v_{\rho ^{\prime }}}{\Lambda ^2}\frac{m_2^{\prime }}{M_2}\right) \;, \nonumber \\ {M_3^{\prime }}^{\pm }\approx M_3\left( 1\pm \frac{v_{\rho }v_{\rho ^{\prime }}}{\Lambda ^2}\frac{m_3^{\prime }}{M_3}\right) \;, \end{aligned}$$

(49)

where

$$\begin{aligned} m_1^{\prime }= & {} 2\text {Re}\left\{ \left[ a^{\prime }-\left( \frac{bb^{\prime }-\frac{1}{2}\left( bd^{\prime }+b^{\prime }d\right) +dd^{\prime }}{\sqrt{b^2-bd+d^2}}\right) \right] e^{-i\phi _1}\right\} \;, \nonumber \\ m_2^{\prime }= & {} 2\text {Re}\left[ \left( b^{\prime }+d^{\prime } \right) e^{-i\phi _2}\right] \;,\nonumber \\ m_3^{\prime }= & {} 2\text {Re}\left\{ \left[ a^{\prime }+\left( \frac{bb^{\prime }-\frac{1}{2}\left( bd^{\prime }+b^{\prime }d\right) +dd^{\prime }}{\sqrt{b^2-bd+d^2}}\right) \right] e^{-i\phi _3}\right\} \;, \nonumber \\ a^{\prime }= & {} \frac{1}{2}\left( \lambda _{N\phi }+\lambda _{S\phi }\right) v_S ,~~ b^{\prime }=\frac{1}{2}\left( \lambda _{N\xi }+\lambda _{S\xi }\right) v_{\xi } \;,\nonumber \\ d^{\prime }= & {} \frac{1}{2}\left( \lambda _{N\xi ^{\prime }} +\lambda _{S\xi ^{\prime }}\right) v_{\xi ^{\prime }}\;, \end{aligned}$$

(50)

and $\phi _i$ is the phase associated with ${\tilde{M}}_i$. The above set of equations show that $m_i^{\prime }$ can be of the order of $M_i$ since a, $a^{\prime }$ are of the order of $v_S$, b, $b^{\prime }$ are of the order of $v_{\xi }$ and d, $d^{\prime }$ are of the order of $v_{\xi ^{\prime }}$.

The decay of nearly degenerate heavy neutrinos creates lepton asymmetry, and it is given as [22]

$$\begin{aligned} \epsilon _{N_i^{\pm }}= & {} -\frac{1}{4\pi A_{N_i^{\pm }}} \left[ \displaystyle {\left( \frac{{\tilde{m}}_{D}}{v}\right) ^{\dagger }\left( \frac{{\tilde{m}}_{D}}{v}\right) - \left( \frac{{\tilde{m}}_{LS}}{v}\right) ^{\dagger }\left( \frac{{\tilde{m}}_{LS}}{v}\right) } \right] _{ii} \nonumber \\&\times \displaystyle { \text {Im}\left[ \frac{{\tilde{m}}_{D}^{\dagger }{\tilde{m}}_{LS}}{v^2}\right] }_{ii} \nonumber \\&\times \frac{r_{N_i}}{\displaystyle {{r_{N_i}}^2+ \frac{1}{64\pi ^2}{A_{N_i^{\pm }}}^2}}\;, \end{aligned}$$

(51)

where

$$\begin{aligned} A_{N_i^{\pm }}= & {} \frac{1}{2}\left[ \left( \frac{{{\tilde{m}}_D}^{\dagger }}{v}\pm \frac{{{\tilde{m}}_{LS}}^{\dagger }}{v}\right) \left( \frac{{{\tilde{m}}_D}}{v}\pm \frac{{{\tilde{m}}_{LS}}}{v}\right) \right] _{ii} \end{aligned}$$

(52)

$$\begin{aligned} r_{N_i}= & {} \frac{{{M_i^{\prime }}^+}^2-{{M_i^{\prime }}^-}^2}{{{M_i^{\prime }}^+}{{M_i^{\prime }}^-}}\approx 4\left( \frac{v_{\rho }v_{\rho ^{\prime }}}{\Lambda ^2} \frac{m_i^{\prime }}{M_i}\right) \;,\nonumber \\ {\tilde{m}}_D= & {} m_D U_\text {TBM} U_{13}^T,~~~~{\tilde{m}}_{LS}=m_{LS}U_\text {TBM}U_{13}^T\;. \end{aligned}$$

(53)

It should be noted that $v_\rho$ is very small in comparison to other VEVs and $m_{LS}\approx y_2 v v_\rho /\Lambda$, while $m_D\approx y_1v v_{\rho '}/\Lambda$, where $y_1$ and $y_2$ are dimensionless coupling constants with $y_1 \approx y_2$, implying ${{\tilde{m}}}_{LS} \ll \tilde{m}_D$. We use $r_{N_i}\ll A_{N_i^{\pm }}$, ${r_{N_i}}^2+\frac{1}{64\pi ^2}A_{N_i^{\pm }}^2\approx \frac{1}{64\pi ^2}A_{N_i^{\pm }}^2$, and for ${\tilde{m}}_{LS}\ll {\tilde{m}}_D$

$$\begin{aligned} \epsilon _{N_i^{\pm }}\approx -128\pi \text {Im}\left[ {\tilde{m}}_{LS}^{\dagger } {\tilde{m}}_D\right] _{ii}\frac{r_{N_i}v^2}{\left( {\tilde{m}}_D^{\dagger }{\tilde{m}}_D\right) ^2}\;. \end{aligned}$$

(54)

Substituting ${\tilde{m}}_D^{\dagger }{\tilde{m}}_D\approx |y_1|^2\left( v v_{\rho ^{\prime }}/\Lambda \right) ^2$, ${\tilde{m}}_{D}^{\dagger }{\tilde{m}}_{LS}\approx y_1^*y_2 v^2 \left( v_{\rho } v_{\rho ^{\prime }}/{\Lambda }^2 \right)$ and $r_{N_i}\approx 4\left( v_{\rho }v_{\rho ^{\prime }}/{\Lambda ^2}\right) \left( m_i^{\prime }/{M_i}\right)$ in the above equation, we obtain

$$\begin{aligned} \epsilon _{N_i^{\pm }}\approx -512\pi \left( \frac{v_{\rho }}{v_{\rho ^{\prime }}}\right) ^2 \frac{\text {Im}\left[ y_1^*y_2 \right] }{|y_1|^4}\frac{m_i^{\prime }}{M_i}\;. \end{aligned}$$

(55)

Writing $y_1^*y_2=|y_1y_2|e^{i\theta _{\epsilon }}$, one can have

$$\begin{aligned} \epsilon _{N_i^{\pm }}\approx -512\pi \left( \frac{v_{\rho }}{v_{\rho ^{\prime }}}\right) ^2 \frac{|y_2|}{|y_1|^3}\frac{m_i^{\prime }}{M_i}\sin \theta _{\epsilon }\;. \end{aligned}$$

(56)

Here we calculate the baryon asymmetry for the case $M_3 \ll M_2< M_1$, i.e., the normal hierarchy in the active neutrino sector with $m_1<0.005$ eV. It is mainly the decay of $M_3^{\pm }$ that contributes to the final baryon asymmetry. Since the decay is in the strong wash-out region, the final baryon asymmetry is given by [22],

$$\begin{aligned} \eta _B=-\frac{28}{79}\left( \frac{0.3\epsilon _{N_3^{\pm }}}{g_*K_{N_3^{\pm }}\left( \ln K_{N_3^{\pm }}\right) ^{0.6}}\right) , \end{aligned}$$

(57)

where $K_{N_i^{\pm }}=\displaystyle {\frac{1}{8\pi } \left( \frac{8\pi ^3 g_*}{90}\right) ^{-1/2} }\left( \frac{M_{Pl}}{ M_{N_i^{\pm }}}\right) A_{N_i^{\pm }}$, $g_*\approx 106.75$ and $M_\text {Pl}=2.435\times 10^{18}~\text {GeV}$ are relativistic degrees of freedom of SM particles and Planck mass, respectively. Here

$$\begin{aligned} K_{N_3^{\pm }}=K_{N_3}\approx 0.234\left[ \frac{m_3~(\text {(eV)}}{10^{-2}}\right] \frac{v_{\rho ^{\prime }}}{v_{\rho }} \gg 1 , \end{aligned}$$

(58)

as $m_3$ is of the order of $10^{-2} ~\text {eV}$ and $\frac{v_{\rho ^{\prime }}}{v_{\rho }}\gg 1$. Substituting $K_{N_3^{\pm }}$ and $\epsilon _{N_3^{\pm }}$ in Eq. (57) gives

$$\begin{aligned} \eta _B\approx 0.174\left( \frac{\left( \displaystyle {\frac{m_3(\text {eV})}{10^{-2}}}\right) ^2}{K_{N_3}^3(\ln K_{N_3})^{0.6}}\right) \frac{|y_2|m_3^{\prime }}{|y_1|^3M_3}\sin \theta _{\epsilon }. \end{aligned}$$

(59)

For $y_1\approx y_2$ and $\displaystyle {\frac{m_3^{\prime }}{M_3}}\approx 1$ the above equation gives

$$\begin{aligned} \eta _B\le 0.174\left( \frac{\left( \displaystyle {\frac{m_3(\text {eV})}{10^{-2}}}\right) ^2}{|y_1|^2K_{N_3}^3(\ln K_{N_3})^{0.6}}\right) . \end{aligned}$$

(60)

With $m_3\approx 0.05~\text {eV}$, $|y_1|^2=10^{-3}$ and $\eta _B=6.9\times 10^{-10}$, from Eqs. (58) and (60) we found the minimum value of $\displaystyle {\frac{v_{\rho }}{v_{\rho ^{\prime }}}}$, which requires one to generate observed baryon asymmetry as

$$\begin{aligned} \left. \frac{v_{\rho }}{v_{\rho ^{\prime }}}\right| _{\text {min}}=5.07\times 10^{-5}\;. \end{aligned}$$

(61)

Comment on Non-unitarity in leptonic sector:

In the usual case, the light active Majorana neutrino mass matrix is diagonalized by the PMNS mixing matrix $U_{\mathrm{PMNS}}$ as $U_{\mathrm{PMNS}}^{\dagger }\, m_{\nu }\, U^*_{\mathrm{PMNS}} = \text {diag} \left( m_{1},m_{2},m_{3}\right)$ where $m_1,m_2,m_3$ are mass eigenvalues for light neutrinos. However, the diagonalizing mixing matrix in the case of the linear seesaw mechanism, where the neutral lepton sector comprises light active Majorana neutrinos plus two additional types of RH sterile neutrinos, is given by

$$\begin{aligned} {{\mathcal {N}}}\simeq (1-\eta )U_{\mathrm{PMNS}}\, , \end{aligned}$$

(62)

where the non-unitarity effect is parametrized as [36],

$$\begin{aligned} \eta =\frac{1}{2}m_D^*{m_{RS}^{\dagger ~ -1}} m_{RS}^{-1}m_D^T\;. \end{aligned}$$

(63)

In the linear seesaw framework under consideration, the N–S mixing matrix $m_{RS}$ is symmetric and, with $y_1\approx y_2$, the $\nu$–S mass term can be expressed as $m_{LS}^{\dagger }m_{LS}=\frac{1}{2}m_0 M_0 (v_{\rho }/v_{\rho ^{\prime }})$ where $m_0$ and $M_0$ are the masses of heaviest active and lightest heavy neutrinos, respectively. Thus, the above relation for $\eta$ can be written in terms of the light neutrino mass matrix and the other input model parameters as

$$\begin{aligned} \eta =\frac{m_{\nu }^*m_{\nu }^T}{4m_0M_0\frac{v_{\rho }}{v_{\rho {\prime }}}}\;. \end{aligned}$$

(64)

The maximum value of $\eta$ for the inverted mass hierarchy with lightest neutrino mass $m_l \simeq 0.005~\mathrm{eV}$, while considering the constrained value of the ratio of VEV $\frac{v_{\rho }}{v_{\rho ^{\prime }}}=5.07\times 10^{-5}$ as derived from the discussion of leptogenesis and using the representative value $M_0=5~\text {TeV}$, can be obtained as follows:

$$\begin{aligned} |\eta |\approx \frac{1}{2}\left[ \begin{array}{c c c} 4\times 10^{-12} &{} 10^{-11} &{} 10^{-11}\\ 10^{-11} &{} 5\times 10^{-11} &{}5\times 10^{-11}\\ 10^{-11} &{} 5\times 10^{-11} &{}5\times 10^{-11} \end{array}\right] . \end{aligned}$$

(65)

Using the representative set of model parameters $m_0$ and $M_0$, the mass matrices $m_D$ and $m_{LS}$ are expressed as follows:

$$\begin{aligned} m_D=\sqrt{\frac{M_0m_0}{v_{\rho }/v_{\rho ^{\prime }}}},~~~ m_{LS}=\sqrt{\frac{v_{\rho }}{v_{\rho ^{\prime }}}M_0m_0}\;. \end{aligned}$$

(66)

Using the constrained value of these model parameters $m_0$ and $M_0$, the Dirac neutrino mass connecting $\nu$–N is found to be $m_D\approx 70 \, \hbox {MeV}$ and the other mass term, connecting $\nu$–S, is $m_{LS}\approx 3.5 \, \hbox {keV}$.

7 Conclusion

In this paper we have considered the realization of the linear seesaw mechanism by extending the SM symmetry with $A_4\times Z_4\times Z_3$ along with a global symmetry $U(1)_X$, which is broken explicitly in the Higgs potential. In addition to the SM fermions, the model has six heavy fermions, three RH neutrinos $(N_{R_i})$ and three sterile neutrinos $(S_{R_i})$. We found that each mass state of the heavy neutrino is nearly doubly degenerate with a small mass splitting, which can be neglected for the calculation of active neutrino mass and mixing parameters. The masses of the active neutrinos are found to be inversely proportional to those of the heavy neutrinos. The model predicts lepton mixing matrix i.e., the PMNS as $U_\text {TBM}\cdot U_{13}\cdot P$, where $U_{13}$ is the rotation in the 13 plane and hence explains well the results on mixing angles and $\delta _\text {CP}$ from the oscillation experiments. We obtained the parameter space and correlation plots between various observables by fixing $\theta _{13}$ at its best-fit value and the ratio of mass-squared differences, $\Delta m^2_{21}/\left| \Delta m^2_{13}\right|$, at 0.0291 and varying $\delta _\text {CP}$ in its $3\sigma$ range.

We have demonstrated that pairs of nearly degenerate Majorana neutrinos in the model open the door to resonant leptogenesis to account for the baryon asymmetry of the Universe. We calculated the minimum value of $v_{\rho }/v_{\rho ^{\prime }}$ to generate the observed baryon asymmetry by fixing the mass of the lightest heavy neutrino in TeV for the case where the heavy neutrino masses are highly hierarchical, so that the only contribution to the baryon asymmetry is from the decay of the two lightest heavy neutrinos. The parameter space which satisfies this condition, predicts the normal hierarchy in the active neutrino sector with the lightest one being less than 0.005 eV. In this case the maximum non-unitarity value that the model can accommodate in the leptonic sector is very small and is of the order of $10^{-11}$ and the mass parameters are found to be $m_D\approx 70 \, \hbox {MeV}$ and $m_{LS}\approx 3.5 \, \hbox {keV}$.

Appendix A: The scalar potential

The most general renormalizable scalar potential of the model involving all the flavon fields which is invariant under $A_4 \times Z_4 \times Z_3$ and respecting $U(1)_X$ symmetry can be written as

$$\begin{aligned} V= & {} V(H)+V(\phi _S)+V(\phi _T)+V(\xi )+V(\xi ')+V(\rho ^{\prime }) \nonumber \\&+V(\rho ) +V(H,\phi _S,\phi _T,\xi ,\xi ',\rho )+V(\phi _S,\phi _T,\xi ,\xi ',\rho ')\nonumber \\&+ V_{\mathrm{ex}}(H,\phi _S,\phi _T,\xi ,\xi ^{\prime },\rho ^{\prime },\rho ), \end{aligned}$$

(A1)

where

$$\begin{aligned} V(H)= & {} \mu _H^2 H^{\dagger }H + \lambda _H (H^{\dagger }H)(H^{\dagger }H), \end{aligned}$$

(A2)

$$\begin{aligned} V(\phi _S)= & {} \mu _S^2 (\phi _S^{\dagger }\phi _S)_1 + \lambda _1^S ({\phi _S}^{\dagger }\phi _S)_1(\phi _S^{\dagger }\phi _S)_1 \nonumber \\&+\lambda _2^S (\phi _S^{\dagger }\phi _S)_{1'}(\phi _S^{\dagger }\phi _S)_{1''}\nonumber \\&+ \lambda _3^S (\phi _S^{\dagger }\phi _S)_{3S}(\phi _S^{\dagger }\phi _S)_{3S} \nonumber \\&+ \lambda _4^S (\phi _S^{\dagger }\phi _S)_{3A}(\phi _S^{\dagger }\phi _S)_{3A}\nonumber \\&+ \lambda _5^S (\phi _S^{\dagger }\phi _S)_{3S}(\phi _S^{\dagger }\phi _S)_{3A} , \end{aligned}$$

(A3)

$$\begin{aligned} V(\phi _T)= & {} \mu _T^2 (\phi _T^{\dagger }\phi _T)_1 + \lambda ^1_T (\phi _T^{\dagger }\phi _T)_1(\phi _T^{\dagger }\phi _T)_1 \nonumber \\&+\lambda ^2_T (\phi _T^{\dagger }\phi _T)_{1'}(\phi _T^{\dagger }\phi _T)_{1''}\nonumber \\&+ \lambda ^3_T (\phi _T^{\dagger }\phi _T)_{3S}(\phi _T^{\dagger }\phi _T)_{3S} \nonumber \\&+ \lambda ^4_T (\phi _T^{\dagger }\phi _T)_{3A}(\phi _T^{\dagger }\phi _T)_{3A}\nonumber \\&+ \lambda ^4_T (\phi _T^{\dagger }\phi _T)_{3S}(\phi _T^{\dagger }\phi _T)_{3A}, \end{aligned}$$

(A4)

$$\begin{aligned} V(\xi )= & {} \mu _{\xi }^2 {\xi }^{\dagger }\xi + \lambda _{\xi } ({\xi }^{\dagger }\xi )({\xi }^{\dagger }\xi ) , \end{aligned}$$

(A5)

$$\begin{aligned} V(\xi ')= & {} \mu _{\xi '}^2 {\xi '}^{\dagger }\xi ' + \lambda _{\xi '} ({\xi '}^{\dagger }\xi ')({\xi '}^{\dagger }\xi ') ,\end{aligned}$$

(A6)

$$\begin{aligned} V(\rho ^{\prime })= & {} \mu _{\rho ^{\prime }}^2 {\rho ^{\prime }}\rho ^{\prime } + \lambda _{\rho ^{\prime }} ({\rho ^{\prime }}\rho ^{\prime })({\rho ^{\prime }}\rho ^{\prime }), \end{aligned}$$

(A7)

$$\begin{aligned} V(\rho )= & {} \mu _{\rho }^2\rho ^{\dagger }\rho +\lambda _{\rho } \left( \rho ^{\dagger }\rho \right) \left( \rho ^{\dagger }\rho \right) , \end{aligned}$$

(A8)

$$\begin{aligned}&V(H,\phi _S,\phi _T,\xi ,\xi ',\rho ^{\prime },\rho ) \nonumber \\&\quad =\lambda _{HS} (H^{\dagger }H)(\phi _S^{\dagger }\phi _S)_1 + \lambda _{HT}(H^{\dagger }H)(\phi _T^{\dagger }\phi _T)_1\nonumber \\&\qquad + \lambda _{H\xi }(H^{\dagger }H)({\xi }^{\dagger }\xi ) +\lambda _{H\xi '}(H^{\dagger }H)({\xi '}^{\dagger }\xi ')\nonumber \\&\qquad +\lambda _{H\rho ^{\prime }}(H^{\dagger }H)({\rho }^{\prime }\rho ^{\prime }) +{\lambda }_{H\rho }\left( H^{\dagger }H\right) \left( \rho ^{\dagger }\rho \right) , \end{aligned}$$

(A9)

$$\begin{aligned}&V(\phi _S,\phi _T,\xi ,\xi ',\rho ^{\prime },\rho ) \nonumber \\&\quad = k_{11}(\phi _T\phi _T)_{3S} \phi _T+k_{12}(\phi _T\phi _T)_{3A}\phi _T \nonumber \\&\qquad +k_{31} (\phi _S^{\dagger }\phi _S)_{3S}\phi _T +k_{32} (\phi _S^{\dagger }\phi _S)_{3A}\phi _T \nonumber \\&\qquad +k_4 (\phi _S\phi _T)_{1}\xi ^{\dagger } +k_5 (\phi _S\phi _T)_{1'}\xi '^{\dagger }\nonumber \\&\qquad +k_6 (\phi _S^{\dagger }\phi _T)_{1}\xi +k_7 (\phi _S^{\dagger }\phi _T)_{1''}\xi '\nonumber \\&\qquad +k_8 (\phi _S\phi _T^{\dagger })_{1}\xi ^{\dagger } +k_9 (\phi _S\phi _T^{\dagger })_{1'}\xi '^{\dagger } \nonumber \\&\qquad +k_{10} (\phi _S^{\dagger }\phi _T^{\dagger })_{1}\xi +k'_{10} (\phi _S^{\dagger }\phi _T^{\dagger })_{1''}\xi '\nonumber \\&\qquad +\lambda ^1_{ST}(\phi _S^{\dagger }\phi _S)_1(\phi _T^{\dagger }\phi _T)_1 +\lambda ^2_{ST}(\phi _S^{\dagger }\phi _S)_{1'}(\phi _T^{\dagger }\phi _T)_{1''} \nonumber \\&\qquad + \lambda ^{22}_{ST}(\phi _S^{\dagger }\phi _S)_{1''}(\phi _T^{\dagger }\phi _T)_{1'} + \lambda ^3_{ST}(\phi _S^{\dagger }\phi _S)_{3S}(\phi _T^{\dagger }\phi _T)_{3S}\nonumber \\&\qquad + \lambda ^4_{ST}(\phi _S^{\dagger }\phi _S)_{3A}(\phi _T^{\dagger }\phi _T)_{3A} +\lambda ^5_{ST}(\phi _S^{\dagger }\phi _S)_{3S}(\phi _T^{\dagger }\phi _T)_{3A}\nonumber \\&\qquad + \lambda ^6_{ST}(\phi _S^{\dagger }\phi _S)_{3A}(\phi _T^{\dagger }\phi _T)_{3S} +\lambda '^{1}_{ST}(\phi _S^{\dagger }\phi _T)_1(\phi _T^{\dagger }\phi _S)_1\nonumber \\&\qquad +\lambda '^{2}_{ST}(\phi _S^{\dagger }\phi _T)_{1'}(\phi _T^{\dagger }\phi _S)_{1''} +\lambda '^{22}_{ST}(\phi _S^{\dagger }\phi _T)_{1''}(\phi _T^{\dagger }\phi _S)_{1'}\nonumber \\&\qquad +\lambda '^{3}_{ST}(\phi _S^{\dagger }\phi _T)_{3S}(\phi _T^{\dagger }\phi _S)_{3S} +\lambda '^{4}_{ST}(\phi _S^{\dagger }\phi _T)_{3A}(\phi _T^{\dagger }\phi _S)_{3A} \nonumber \\&\qquad +\lambda '^{5}_{ST}(\phi _S^{\dagger }\phi _T)_{3S}(\phi _T^{\dagger }\phi _S)_{3A} +\lambda '^{6}_{ST}(\phi _S^{\dagger }\phi _T)_{3A}(\phi _T^{\dagger }\phi _S)_{3S} \nonumber \\&\qquad + \lambda _{S\xi }(\phi _S^{\dagger }\phi _S)_1({\xi }^{\dagger }\xi ) +\lambda _{S\xi '}({\phi _S}^{\dagger }\phi _S)_{1}({\xi '}^{\dagger }\xi ') \nonumber \\&\qquad +\lambda _{S\rho ^{\prime }}(\phi _S^{\dagger }\phi _S)_1({\rho }^{\prime }\rho ^{\prime }) +\lambda _{S\rho }(\phi _S^{\dagger }\phi _S)_1({\rho }^{\dagger }\rho ) \nonumber \\&\qquad +\lambda _{T\xi }(\phi _T^{\dagger }\phi _T)_1({\xi }^{\dagger }\xi ) +\lambda _{T\xi '}(\phi _T^{\dagger }\phi _T)_{1}({\xi '}^{\dagger }\xi ') \nonumber \\&\qquad +\lambda _{T\rho ^{\prime }}(\phi _T^{\dagger }\phi _T)_1({\rho }^{\prime }\rho ^{\prime }) +\lambda _{T\rho }\left( \phi _T^{\dagger }{\phi _T}\right) _1\left( \rho ^{\dagger }\rho \right) \nonumber \\&\qquad +\lambda _{\xi \rho ^{\prime }}({\xi }^{\dagger }\xi )({\rho }^{\prime }\rho ^{\prime }) + \lambda _{\xi \rho }({\xi }^{\dagger }\xi )({\rho }^{\dagger }\rho )\nonumber \\&\qquad +\lambda _{\xi \xi '}({\xi }\xi ^{\dagger })_{1}({\xi '}\xi '^{\dagger })_{1} +\lambda _{\xi '\rho ^{\prime }}({\xi '}\xi '^{\dagger })({\rho }^{\prime }\rho ^{\prime })\nonumber \\&\qquad +\lambda _{\xi '\rho }({\xi '}\xi '^{\dagger })({\rho }^{\dagger }\rho ) \nonumber \\&\qquad +\lambda _{S\xi \xi '}(\phi _S^{\dagger }\phi _S)_{1''}({\xi }^{\dagger }\xi ')_{1'} +\lambda _{T\xi \xi '}(\phi _T^{\dagger }\phi _T)_{1''}({\xi }^{\dagger }\xi ')_{1'}\nonumber \\&\qquad +\lambda ^{2}_{S\xi \xi '}(\phi _S^{\dagger }\phi _S)_{1'}({\xi }\xi '^{\dagger })_{1''} +\lambda ^{2}_{T\xi \xi '}(\phi _T^{\dagger }\phi _T)_{1'}({\xi }\xi '^{\dagger })_{1''}\nonumber \\&\qquad +\lambda ^1_{SS\xi }(\phi _S^{\dagger }\phi _S)_{3S}({\phi _S}\xi ^{\dagger }) +\lambda ^2_{SS\xi }(\phi _S^{\dagger }\phi _S)_{3A}({\phi _S}\xi ^{\dagger })\nonumber \\&\qquad +\lambda ^1_{SS\xi '}(\phi _S^{\dagger }\phi _S)_{3S}({\phi _S}\xi '^{\dagger }) +\lambda ^2_{SS\xi '}(\phi _S^{\dagger }\phi _S)_{3A}({\phi _S}\xi '^{\dagger }) \nonumber \\&\qquad +\lambda ^1_{TS\xi }(\phi _T^{\dagger }\phi _T)_{3S}({\phi _S}\xi ^{\dagger }) +\lambda ^2_{TS\xi }(\phi _T^{\dagger }\phi _T)_{3A}({\phi _S}\xi ^{\dagger }) \nonumber \\&\qquad +\lambda ^1_{TS\xi '}(\phi _T^{\dagger }\phi _T)_{3S}({\phi _S}\xi '^{\dagger }) +\lambda ^2_{TS\xi '}(\phi _T^{\dagger }\phi _T)_{3A}(\phi _S\xi '^{\dagger })\nonumber \\&\qquad +\lambda ^{11}_{SS\xi }(\phi _S^{\dagger }\phi _S)_{3S}(\phi _S^{\dagger }\xi ) +\lambda ^{22}_{SS\xi }(\phi _S^{\dagger }\phi _S)_{3A}(\phi _S^{\dagger }\xi )\nonumber \\&\qquad +\lambda ^{11}_{SS\xi '}(\phi _S^{\dagger }\phi _S)_{3S}(\phi _S^{\dagger }\xi ') +\lambda ^{22}_{SS\xi '}(\phi _S^{\dagger }\phi _S)_{3A}(\phi _S^{\dagger }\xi ') \nonumber \\&\qquad +\lambda ^{11}_{TS\xi }(\phi _T^{\dagger }\phi _T)_{3S}(\phi _S^{\dagger }\xi ) +\lambda ^{22}_{TS\xi }(\phi _T^{\dagger }\phi _T)_{3A}(\phi _S^{\dagger }\xi ) \nonumber \\&\qquad +\lambda ^{11}_{TS\xi '}(\phi _T^{\dagger }\phi _T)_{3S}(\phi _S^{\dagger }\xi ') +\lambda ^{22}_{TS\xi '}(\phi _T^{\dagger }\phi _T)_{3A}(\phi _S^{\dagger }\xi '), \end{aligned}$$

(A10)

$$\begin{aligned}&V_{\mathrm{ex}}(H,\phi _S,\phi _T,\xi ,\xi ^{\prime },\rho ^{\prime },\rho ) \nonumber \\&\quad = \left[ \mu ^2_{\rho \xi }+\lambda _{H\rho \xi } H^{\dagger }H+\lambda _{T\rho \xi }\left( \phi _T^{\dagger }\phi _T\right) _1 +\lambda _{S\rho \xi }\left( \phi _s^{\dagger }\phi _s\right) _1\right. \nonumber \\&\qquad + \left. \lambda _{\xi \rho \xi }\xi ^{\dagger }\xi +\lambda _{\xi ^{\prime }\rho \xi }{\xi ^{\prime }}^{\dagger } \xi ^{\prime }+\lambda _{\rho ^{\prime }\rho \xi }{\rho ^{\prime }} \rho ^{\prime }\right] \rho \xi \nonumber \\&\qquad + \lambda _{S\rho \xi ^{\prime }}\left( \phi _S^{\dagger }\phi _S \right) _{1^{\prime \prime }}\rho \xi ^{\prime }+\lambda _{\rho \rho \xi } \left( \rho ^{\dagger }\rho \right) \rho \xi +\mathrm{h.c.}. \end{aligned}$$

(A11)

The potential $V_\mathrm{ex}(H,\phi _S,\phi _T,\xi ,\xi ^{\prime },\rho ^{\prime },\rho )$ breaks the $U(1)_X$ symmetry explicitly. As the potential presented above involves several free parameters, such a large number of free parameters should naturally allow the required VEV alignment of the flavons considered in this article, i.e., $\langle \phi _S \rangle =v_S(1,1,1), ~ \langle \phi _T \rangle =v_T(1,0,0),~ \langle \xi \rangle =v_{\xi },~ \langle \xi ' \rangle =v_{\xi '}, ~ \langle \rho ^{\prime } \rangle =v_{\rho ^{\prime }},~\langle \rho \rangle =v_{\rho }$.

The terms involving $\rho$ in the scalar potential are given by

$$\begin{aligned} V'(\rho )= & {} \left[ \mu _{\rho }^2+\lambda ^{\prime }_{H\rho } H^{\dagger }H+\lambda '_{T\rho }\left( \phi _T^{\dagger }\phi _T\right) _1+ \lambda '_{S\rho }\left( \phi _S^{\dagger }\phi _S\right) _1 \right. \nonumber \\&\quad \left. + \lambda '_{\xi \rho }\xi ^{\dagger }\xi +\lambda '_{\xi ^{\prime }\rho }{\xi ^{\prime }}^{\dagger } \xi ^{\prime }+\lambda '_{\rho ^{\prime }\rho }{\rho ^{\prime }} \rho ^{\prime }\right] \rho ^{\dagger }\rho \nonumber \\&\quad +\lambda _{\rho }\left( \rho ^{\dagger }\rho \right) ^2\nonumber \\&\quad + [(\mu ^2_{\rho \xi }+\lambda _{H\rho \xi } H^{\dagger }H+\lambda _{T\rho \xi } (\phi _T^{\dagger }\phi _T)_1 \nonumber \\&\quad +\lambda _{S\rho \xi } (\phi _s^{\dagger }\phi _s)_1 + \lambda _{\xi \rho \xi }\xi ^{\dagger }\xi \nonumber \\&\quad + \lambda _{\xi ^{\prime } \rho \xi }{\xi ^{\prime }}^{\dagger }\xi ^{\prime }+\lambda _{\rho ^{\prime } \rho \xi }{\rho ^{\prime }}\rho ^{\prime })\rho \xi \nonumber \\&\quad +\lambda _{S\rho \xi ^{\prime }} (\phi _S^{\dagger }\phi _S )_{1^{\prime \prime }}\rho \xi ^{\prime } \nonumber \\&\quad + \lambda _{\rho \rho \xi } (\rho ^{\dagger }\rho )\rho \xi +\mathrm{h.c.}]. \end{aligned}$$

(A12)

In terms of the VEVs of the fields, the above potential can be written as

$$\begin{aligned} V'(\rho )= & {} {\mu _{\rho }^{\prime }}^2v_{\rho }^{*}v_{\rho }+ \lambda _{\rho }(v_{\rho }^{*}v_{\rho })^2 \nonumber \\&+[({{\mu }^{\prime ~ 2}_{\rho \xi }}v_\xi +{\mu ^2_{\rho \xi ^{\prime }}}v_{\xi '})v_{\rho } \nonumber \\&\quad +\lambda _{\rho \rho } (v_{\rho }^{*}v_{\rho })v_{\rho }v_{\xi }+\mathrm{h.c.}], \end{aligned}$$

(A13)

where

$$\begin{aligned} {\mu _{\rho }^{\prime ~2}}= & {} \mu _{\rho }^2+\lambda ^{\prime }_{H\rho } v^2+\lambda ^{\prime }_{T\rho } v_{T}^{*}v_{T}+\lambda ^{\prime }_{S\rho } v_S^*v_S+\lambda ^{\prime }_{\xi \rho }v_{\xi }^{*}v_{\xi } \nonumber \\&+ \lambda ^{\prime }_{\xi ^{\prime }\rho }{v_{\xi ^{\prime }}}^{*} v_{\xi ^{\prime }}+\lambda ^{\prime }_{\rho '\rho } v_{\rho ^{\prime }}^2,\nonumber \\ {{\mu }^{\prime ~2}_{\rho \xi }}= & {} \mu ^2_{\rho \xi }+\lambda _{H\rho \xi }v^2+ \lambda _{T \rho \xi }v_T^{*}v_T+\lambda _{\xi \rho \xi } v_{\xi }^{*}v_{\xi } \nonumber \\&+\lambda _{\xi '\rho \xi }{v_{\xi ^{\prime }}}^{*} v_{\xi ^{\prime }}+\lambda _{\rho '\rho }{v_{\rho ^{\prime }}}^2+3 \lambda _{S\rho \xi }v_s^{*}v_s ,\nonumber \\ {\mu ^2_{\rho \xi ^{\prime }}}= & {} 3\lambda _{S\rho \xi '}v_{s}^*v_{s}\;. \end{aligned}$$

(A14)

For ${\mu ^{\prime }_{\rho }}^2>0$, $\lambda _{\rho }>0$ and $\mu ^{\prime }_{\rho \xi },\mu _{\rho \xi '}\ll {\mu ^{\prime }_{\rho }}^2$, $V'(\rho )$ (Eq. (A13)) has a minimum at

$$\begin{aligned} v_\rho ^*\approx -\frac{\left( {{\mu }^{\prime ~2}_{\rho \xi }} v_\xi +{\mu ^2_{\rho \xi ^{\prime }}}v_{\xi ^{\prime }}\right) ^{*}}{{\mu _{\rho }^{\prime }}^2}\;. \end{aligned}$$

(A15)

Estimate mass of flavon field. $\rho .$ From Eq. (A15), one can obtain the mass of the flavon field $\rho$ as

$$\begin{aligned} {\mu ^{\prime }_{\rho }} =\sqrt{\frac{{\mu ^{\prime }_{\rho \xi }}^2 v_{\xi }+{\mu ^{\prime }_{\rho \xi ^{\prime }}}^2v_{\xi ^\prime }}{v_{\rho }}}\;. \end{aligned}$$

(A16)

Substituting the VEVs given in Table 2 in Eq. (A16) gives the mass of the field $\rho$ ($\mu _{\rho }^{\prime }$) as $5.8 \, \hbox {TeV}$, for ${\mu ^{\prime }_{\rho \xi }},~\mu ^{\prime }_{\rho \xi ^{\prime }} \simeq 10 \, \hbox {GeV}$. The condition ${\mu ^{\prime }_{\rho \xi }}, \mu ^{\prime }_{\rho \xi ^{\prime }} \simeq 10\, \hbox {GeV}$ is satisfied for the parametric choice, $\mu _{\rho \xi }\simeq {{\mathcal {O}}}(10~\mathrm{GeV})$, and $\lambda _{H\rho \xi }$, $\lambda _{T\rho \xi }$, $\lambda _{\xi ^{\prime }\rho \xi }$, $\lambda _{\rho ^{\prime }\rho }$, $\lambda _{S\rho \xi }$, $\lambda _{S\rho \xi ^{\prime }} \simeq {\mathcal {O}}(10^{-6})$. Such small couplings as involved in those terms of the Higgs potential which break the $U(1)_X$ symmetry explicitly imply that the symmetry is softly broken.