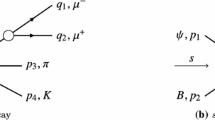Abstract
We discuss the differences between several partial-wave analysis formalisms used in the construction of three-body decay amplitudes involving fermions. Specifically, we consider the decay \(\Lambda _b \rightarrow \psi \,p K^-\), where the hidden charm pentaquark signal has been reported. We analyze the analytical properties of the amplitudes and separate kinematical and dynamical singularities. The result is an amplitude with the minimal energy dependence compatible with the S-matrix principles.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the recent years experiments such as BaBar, Belle, BESIII, CLAS, COMPASS, GlueX, LHCb, have produced significant amount of high-precision data on three-body hadron decays, garnering information on new hadronic states [1,2,3,4,5]. To put existence of such states on firm theoretical footing and to determine their physical properties rigorous amplitude analysis is needed. There are well established methods based on first principles of reaction theory for construction of reaction amplitudes describing three particle decays of hadrons [6, 8,9,10,11,12,13,14,15,16]. It appears, however that there is significant confusion as to the role of various approximations that these methods entail. In an earlier work [17], we pointed out that, contrary to the common wisdom, differences among the various approaches are dynamical rather than kinematical in nature, and we showed that the lore for the LS formalism to be nonrelativistic is unjustified. As an example, we discussed the decay \(B\rightarrow \psi \pi K\), which shows nontrivial structures appearing in the Belle and LHCb data in \(\psi (2S) \,\pi \) [18,19,20,21], and \(J/\psi \,\pi \) channels [22]. In the present paper, we extend the discussion to the more complicated fermion-boson case. Our main goal is to properly separate kinematical from dynamical singularities. In general, the analysis of kinematical singularities of amplitudes with fermions has to be handled with particular care, because of the additional branch point at vanishing value of the Mandelstam variables [23], and because fermions and antifermions have opposite intrinsic parities. Hence, one expects different behavior of the amplitudes at threshold and pseudothreshold. We thus believe that study of such amplitudes deserves an extended discussion. Moreover, because of the possible existence of hidden charm pentaquarks, there is particular interest in final states containing the nucleon, a light meson and a charmonium [1,2,3]. In this paper we thus study the amplitudes for the reaction \(\Lambda _b \rightarrow {\psi }p K^-\) in which a prominent pentaquark-like signal in the \({\psi }p\) invariant mass observed at LHCb [24, 25].
The paper is organized as follows. In Sect. 2 we discuss the canonical approach used to analyze the \(\Lambda _b \rightarrow \psi p K^-\) decay. By relating the helicity partial waves to the Lorentz scalar amplitudes via the partial-wave expansion, we derive constraints on the amplitudes and isolate the kinematical singularities. The results, and the comparison with the LS partial-wave amplitudes, are summarized in Sect. 3. In Sect. 4, we focus on the mass dependence of our solution, and the singularities at \(s=0\). In Sect. 5 we examine the Covariant Projection Method (CPM) approach and compare it to our results. Conclusions are given in Sect. 6. For ease of readability in the main text, most of the technical details are given in the appendices where we also give a practical parameterization of the amplitudes suitable for data analysis.
2 Analyticity constraints for \(\Lambda _b \rightarrow \psi p K^-\)
In Fig. 1 we specify the kinematics for the decay \(\Lambda _b \rightarrow \psi (\rightarrow \mu ^+\mu ^-) p K^-\). In the following, we follow the arguments presented in [17]. We will be able to identify and characterize all kinematical singularities as either pertaining to (pseudo)thresholds, or to the vanishing of particles’ energies. The particles \(\Lambda _b \), p, and \(K^-\) are stable against the strong interaction, and the \(\psi \) is narrow enough, allowing one to factorize its decay dynamics. Thus, we focus on the amplitude in which \(\psi \) is also considered as stable. In the following, we analyze the equivalent scattering problem \(\Lambda _b \psi \rightarrow p K^-\), and we refer to [17] for an extended discussion of crossing symmetry. We use \(p_i\), \(i=1, 2, 3\), and 4 to label the momenta of \(\Lambda _b \), \(\psi \), p, and \(K^-\) respectively. We call \({\bar{p}}_\psi = -p_\psi \) the momentum of the \(\psi \) in the decay kinematics. The helicity amplitude is denoted by \({\mathcal {A}}_{\lambda _p, \lambda _b\lambda _\psi } (s,t)\), where \(\lambda _p\), \(\lambda _b\) and \(\lambda _\psi \) are the helicities of p, \(\Lambda _b \) and \(\psi \), respectively. The amplitude depends on the standard Mandelstam variables \(s = (p_p+p_K)^2\), \(t = (p_b-p_p)^2\), and \(u = (p_b- p_K)^{2}\) with \(s + t + u = \sum _i m_i^2\).
The \(\Lambda _b \) baryon decays weakly, so \({\mathcal {A}}_{\lambda _p, \lambda _b\lambda _\psi } \) is given by the sum of a parity conserving (PC) and a parity violating (PV) amplitudes.
We discuss here the PC amplitude in the s-channel, and we refer to Appendix D for the summary of the PV amplitude. The s-channel resonances correspond to the \(\Lambda ^*\)’s and dominate the reaction [26]. As discussed in the previous section, the analysis of the experimental data indicates a possible signal of resonances in the exotic \(\psi p\) spectrum, which in our notation correspond to the u-channel.
In the center of mass of the s-channel scattering process, the momentum \(p_b\) defines the z-axis, the momenta \(p_p\) and \(p_K\) lie in the xz-plane, p and q denote magnitudes of relative momenta in the incoming (\(\Lambda _b\), \(\psi \)) and the outgoing (p, \(K^-\)) states. The scattering angle \(\theta _s\) is the polar angle of the proton (see Fig. 2). The quantities are expressed through the Mandelstam invariants,
with \(\lambda _{ik} \equiv \left( s - (m_i+m_k)^2\right) \left( s - (m_i-m_k)^2\right) \). The function \(4s\, n(s,t)\) is a polynomial in s and t.Footnote 1 To incorporate resonances in the \(p K^-\) system with a certain spin j, we expand the amplitude in partial waves,
where \({\mathcal {A}}_{\lambda _p, \lambda _b\lambda _\psi } ^j(s)\) are the helicity partial-wave amplitudes in the s-channel, \(\lambda = \lambda _b- \lambda _\psi \), \(\lambda ^\prime = \lambda _p\), and \(M= \max (|\lambda |,|\lambda ^\prime |)\) [9]. We use the definition of the Wigner d function as in [27], i.e. \(d_{\lambda \lambda ^\prime }^j(\cos \theta ) = \left\langle j, \lambda | \exp \left( -i J_y \theta \right) | j,\lambda ^\prime \right\rangle \), that differs from the one in [9] by \(\theta \rightarrow - \theta \). This results in a difference in our definition of the parity conserving helicity amplitudes given in Eq. (7) below.
Instead of working with an infinite number of helicity partial waves, we will consider the isobar model, customarily used in data analysis.Footnote 2 The dynamical singularities in s, t and u are taken into account explicitly by a sum of different terms,
with
and \(J_\text {max} < \infty \). In this model, it is assumed that the entire dynamical information is expressed by the isobar amplitudes, which are functions of a single Mandelstam variable: \(A^{(x)j} = A^{(x)j}(x)\), with \(x=s,t,u\). The expressions for the (t) and (u) isobars are similar to Eq. (4). In the following we focus on the s-channel isobars, and drop the (s) superscript. The u-channel isobars are described in the Appendices E, F).
In Eqs. (2), (4) the entire t dependence originates from the d functions. Specifically, the d functions have singularities in \(z_s\) which lead to kinematical singularities in t. We define the functions
with
being the so-called half angle factor that contains all the kinematic singularities in t. The reduced rotational function \({\hat{d}}_{\lambda \lambda ^\prime }^j(z_s)\) is a polynomial of n(s, t) / pq of order \(j - M\), see Eq. (1). For \(\lambda ,\lambda ^\prime \ne 0\), the functions \(d^j_{\lambda \lambda ^\prime }(z_s)\) have no definite parity. This means that the product \((pq)^{j-M} {\hat{d}}^j_{\lambda \lambda ^\prime }(z_s)\) contains terms with odd powers of pq that still have kinematic branch-point singularities in s. To be able to remove these singularities from the amplitude, we need to define the so-called parity-conserving helicity amplitudes (PCHAs),
where \(\eta _\psi = \eta _b = +\) are the naturality of the \(\psi \) and \(\Lambda _b \), respectively. These functions are free of kinematical singularities in t. Similarly, we can split the isobars into natural and unnatural ones
where we defined the definite-parity partial-wave/isobar amplitudes,
We introduce the definite-parity Wigner d functions by,
One can check that the function \({\hat{d}}^{j+}_{\lambda \lambda ^\prime }(z_s)\) is a definite-parity polynomial of order \(j-M\), i.e. \({\hat{d}}^{j+}_{\lambda \lambda ^\prime }(-z_s) = (-1)^{j-M} {\hat{d}}^{j+}_{\lambda \lambda ^\prime }(z_s)\).Footnote 3 Similarly, \({\hat{d}}^{j-}_{\lambda \lambda ^\prime }(z_s)\) is a definite parity polynomial of order \(j-M-1\), and therefore subleading in the \(z_s \rightarrow \infty \) limit. We refer the reader to Appendix B for a more detailed discussion on the (sub)leading behavior of the \({\hat{d}}^{j(\eta )}_{\lambda \lambda ^\prime }(z_s)\). In terms of these isobars, the PCHAs read
where we applied the parity relations in Eq. (9) in the transition from the first to second line. We note that, for given \(\eta \), isobars with both naturalities contribute to the \(A_{\lambda _p, \lambda _b\lambda _\psi } ^\eta (s,t)\).Footnote 4 The helicity isobars \(A_{\lambda _p, \lambda _b\lambda _\psi } ^j(s)\) have singularities in s, which have both dynamical and kinematical origin. The kinematical singularities in s, just like the t-dependent kinematical singularities, arise because of particle spin. We explicitly isolate the kinematic factors in s, and denote the kinematical singularity-free helicity isobar amplitudes by \({\hat{A}}_{\lambda _p, \lambda _b\lambda _\psi } ^j(s)\). First, we take out the factor \((p q)^{j - M}\) from the \(A_{\lambda _p, \lambda _b\lambda _\psi } ^j(s)\). This factor cancels the threshold and pseudothreshold singularities in s that appear in \({\hat{d}}^j_{\lambda \lambda ^\prime }(z_s)\). Second, we follow [9] and introduce the additional kinematic factor \(K^\eta _{MN}\). These factors are required to account for the mismatch between the j and L dependence in the angular momentum barrier factors in the presence of particles with spin. Specifically, it is expected that \(A_{\lambda _p, \lambda _b\lambda _\psi } ^{j\eta }(s) \sim p^{L_1}\) (\(A_{\lambda _p, \lambda _b\lambda _\psi } ^{j\eta }(s) \sim q^{L_2}\)) at \(\Lambda _b \psi \)-threshold (\(p K^-\)-threshold), where \(L_1\) and \(L_2\) are the lowest possible orbital angular momenta in the given helicity and parity combination. The definite-parity, kinematical-singularity-free helicity isobar amplitudes \({\hat{A}}_{\lambda _p, \lambda _b\lambda _\psi } ^{j \eta }(s)\) are defined by
with \(N= \min (|\lambda |,|\lambda ^\prime |) = \tfrac{1}{2}\), and
where the \({Q^{\pm ,1/2}}\) are regular functions for \(\sqrt{s}>0\). The functional form of the latter will be discussed in detail in Sect. 4. In addition, the K-factors have powers of \(\sqrt{s}\) as required to ensure factorization of the isobar amplitude into contributions from distinct vertices [9].
The isobar amplitudes \({\hat{A}}_{\lambda _p, \lambda _b\lambda _\psi } ^{j,\eta }(s)\) contain the dynamical information of the model. Often they are parameterized in terms of a sum of Breit-Wigner amplitudes with Blatt–Weisskopf barrier factors.
Once we have removed the kinematic singularities from the isobar amplitudes and the corresponding angular functions, we are now in a position to remove the singularities from the full amplitude. Therefore, we take out the factor \(K_{MN}^\eta \) and define the amplitudes F which are kinematic singularity-free PCHAs (KSF-PCHAs),
where the ratio \(K^{-\eta }_{MN}/K^\eta _{MN} = (-)^{M-N}\left( p m_p\big / q m_\psi \right) ^{\eta } {Q^{-\eta }}/{Q^{\eta }}\). While the KSF-PCHAs are free of kinematical singularities, they are not necessarily independent for all kinematics. Indeed, we will illustrate below that additional constraints must be fulfilled by the isobar amplitudes for certain kinematics. Therefore, as in [17], we seek a representation of \(A_{\lambda _p, \lambda _b\lambda _\psi } (s,t)\) in terms of a set of covariant structures that explicitly account for the kinematic part of the amplitude. For the PC amplitude, the basis with minimal energy dependence is given by
with


and the scalar functions \(C_i(s,t)\) are free from kinematical singularities. There are six independent \(M_{1\dots 6}^{\mu }\) tensors, and any other possible combination can be reduced to these using the Dirac equation for the spinors, or the orthogonality relation \(\epsilon _\mu (p_\psi ,\lambda _\psi )p_\psi ^\mu = 0\). Alternatively, one can use the CGLN basis defined in [28], for pseudoscalar-meson electro-production. However, these covariant structures enforce a gauge-invariance principle which does not apply here since \(\psi \) is a massive vector particle. Had we used the CGLN basis, there would be unnecessary kinematic zeros. The PC amplitude requires a \(\gamma ^5\) because of the unnatural \(K^-\) parity. The explicit expressions for the polarization vectors and spinors are given in Appendix A. We can match Eqs. (14) and (15), and express the scalar functions as a sum over kinematical singularity free helicity isobars. This yields
with \({\mathcal {M}}\) a \(6\times 6\) matrix that encodes all the kinematic factors and is provided in Appendix C.Footnote 5 The factors \(\sqrt{E_p+ m_p}\) and \(\sqrt{E_b+ m_b}\) are factored out to simplify the expression for \({\mathcal {M}}\). We stress that they have only singularities at \(s=0\). For example,
and the physical region of \(\sqrt{s}\) corresponds to \({{\mathrm{Re}}}\sqrt{s} > 0\). For \(m_b> m_\psi \), which is the case here, the first factor in Eq. (18) is always positive, and the only singularity is due to the branch point at \(s=0\). This would be different if the fermion was lighter than the boson. In that case, the factor will have a singularity at pseudothreshold that has to be considered separately. The relation in Eq. (17) can be inverted, leading to
where the matrices \({\mathcal {B}}\) and \(\text {Reg}\) are regular at \(p=0\). The explicit expression for the \({\mathcal {M}}^{-1}\) and the \({\mathcal {B}}\) matrices are in Appendix C. We just report a few terms here to ease the discussion,
Since the \(C_i\) functions must be regular at \(p=0\), i.e. for \(s = (m_b\pm m_\psi )^2 \equiv s_\pm \), the combinations of KSF-PCHAs \(F_{\lambda _p,\lambda _b\lambda _\psi }^\eta (s,t)\) in Eq. (19) must conspire to cancel the \(1/p^2\) pole. This translates into a relation between the various isobar amplitudes \({\hat{A}}_{\lambda _p, \lambda _b\lambda _\psi } ^{j\eta }(s)\). As an example, let us consider the last two rows in Eq. (19). Inspecting the matrix elements in Eq. (20) one finds that two emerging conditions are not independent and lead to,

where we mean here is that this combination must vanish as \(p^2\) for \(p \rightarrow 0\). The conspiracy relation can be written in terms of the isobar amplitudes by inserting the expression for the F’s in terms of the isobars, given in Eq. (14). Since the isobars of different spin are independent, we can consider each j individually. For \(j \ge \tfrac{3}{2}\) we obtain

When \(p \rightarrow 0\), \(z_s \rightarrow \infty \) and the leading \({\hat{d}}^{j+}_{-1/2,1/2}(z_s)\) and \({\hat{d}}^{j+}_{3/2,1/2}(z_s)\) diverge as \(1/p^{j-1/2}\) and \(1/p^{j-3/2}\), respectively. This divergence is canceled by the threshold factor \((pq)^{j-1/2}\), but an additional relation between \({\hat{A}}_{+,++}^{j+}(s)\) and \({\hat{A}}_{+,+-}^{j+}(s)\) is needed to cancel the additional \(1/p^2\) pole appearing in Eq. (19). On the other hand, the subleading \({\hat{d}}^{j-}_{-1/2,1/2}(z_s)\) and \({\hat{d}}^{j-}_{3/2,1/2}(z_s)\) diverge as \(1/p^{j-3/2}\) and \(1/p^{j-5/2}\) only, and together with the additional factor of p coming from the mismatch factors \(K_{MN}^\eta \) and the threshold factor, vanish as \(p^2\) to cancel the \(1/p^2\) pole. Therefore, the opposite-naturality waves do not contribute to this type of conspiracy relations. It is also straightforward to check that the expressions are regular when \(q\rightarrow 0\). One can use the asymptotic expansion of the Wigner d functions (the full expressions are in Appendix B),
and reduce Eq. (22) to
We now examine the conditions that emerge for the first and third rows in Eq. (20). These involve both natural and unnatural isobars. Although strictly speaking conspiracy relations might be realized by complicated cancellations involving all possible isobars, we again assume that isobars carrying different quantum numbers are independent. It is then possible to (i) break each one of the equations in Eq. (20) into separate equations for natural and unnatural isobars, and (ii) break them further by counting the powers of \(z_s\). This leads to the following conditions,




and using the asymptotic form of the d functions, for the natural isobars, we obtain
The conspiracy relation for the unnatural isobars are more cumbersome. We recall the relation between the helicity and the LS couplings. To ease the notation, we will write only the initial state in the LS form,Footnote 6
For the case at hand, this means
with \(G^{j-}_{LS}(s) = p^L q^{j-1/2} {\hat{G}}^{j-}_{LS}(s)\). We remark that these relations hold for the \(j=\tfrac{1}{2}\) case as well, and we do not need any separate consideration for it. There is only one LS coupling with nonminimal L, which calls for one conspiracy equation only. However, the equations obtained from the first and third line in Eq. (20) give


and it is easy to check the two equations to be independent out of (pseudo)threshold. We evaluate the constraints at both threshold and pseudothreshold,

with
By restoring the kinematic factors,

At threshold, this matches with the LS constraint. To interpolate with the pseudothreshold result, we replace  .
.
To summarize, we used analyticity constraints to derive relations between the different helicity isobars. At threshold, these relations are in agreement with the expectations derived from the LS decomposition. Similar constraints are derived at pseudothreshold. To interpolate between the two constraints, we add an energy dependent factor \(E_\psi /m_\psi \) in the \(\lambda _\psi = 0\) amplitude. This results in the minimal kinematic dependence as required by analyticity.
3 The generic parameterization for the s-channel isobars
In this section we derive a general parametrization for the isobar amplitude which takes into account the conspiracy relations derive in the preceding section. A generic parameterization for the natural isobars which fullfills Eqs. (24) and (29) is given by
where \(g^{(\prime ,\prime \prime )}_{j+}(s)\) and \(f^{(\prime ,\prime \prime )}_{j+}(s)\) are regular functions at \(s=s_\pm \), and \(g_{j+}(s_\pm )=g_{j+}^{\prime }(s_\pm )=g_{j+}^{\prime \prime }(s_\pm )\). The branch points at \(s=0\) are not constrained by the threshold relations. Their origin is dynamical and has to be addressed in the context of analyticity in j. We decided to include appropriate factors of \(\sqrt{s}\) to make these formulae more similar to the LS ones. For example, the additional factor of  in front of \(f_{j+}^{\prime \prime }(s)\) in Eq. (36c) is unconstrained by these relations, but it has been inserted by analogy with LS. Similarly, we decided the subleading \(f_{j+}^{(\prime ,\prime \prime )}(s)\) functions to appear with a factor \(p^2\) insted of \(\lambda _{b\psi }\), unlike in [17].
in front of \(f_{j+}^{\prime \prime }(s)\) in Eq. (36c) is unconstrained by these relations, but it has been inserted by analogy with LS. Similarly, we decided the subleading \(f_{j+}^{(\prime ,\prime \prime )}(s)\) functions to appear with a factor \(p^2\) insted of \(\lambda _{b\psi }\), unlike in [17].
Upon restoration of the kinematic factors, the original helicity isobars amplitudes read (\(j\ge \tfrac{3}{2}\))
A particular choice of the functions \(g^{(\prime ,\prime \prime )}_{j+}(s)\) and \(f^{(\prime ,\prime \prime )}_{j+}(s)\) constitutes a given hadronic model. For \(j = \tfrac{1}{2}\), no conspiracy constraint is needed. Indeed, the isobars \({\hat{A}}_{\lambda _p, \lambda _b\lambda _\psi } ^{j+}(s)\) always appears with an additional factor \(\propto p^2\), as shown in Eq. (12b), and the pole is automatically canceled.
We can immediately cast this expression in the LS basis. For the natural isobars considered, this reads
with \(G^{j+}_{LS}(s) = p^L q^{j+1/2} {\hat{G}}^{j+}_{LS}(s)\), and the dependence on \(\lambda _p\) is understood. We remark that there are two LS couplings having nonminimal L in Eq. (38), and at \(p=0\) the three helicity couplings will depend on one independent LS coupling only. This will require indeed two equations to be satisfied, ie Eqs. (24) and (29). This expression matches Eq. (36) by identifying
For the unnatural isobars, the minimal parameterization fulfilling Eq. (35) is
with \(g_{j-}(s_\pm ) - g'_{j-}(s_\pm ) = -g''_{j-}(s_\pm )\) and \(h_{j-}(s_\pm ) = h'_{j-}(s_\pm ) = -h''_{j-}(s_\pm )\). The identification with the LS couplings is straightforward,
As shown in Eqs. (39) and (41), care should be taken when choosing a parameterization of the LS amplitude so that the expressions are free from kinematical singularities, beyond the one at \(s=0\) discussed in Sect. 4. For example, if one takes the functions \({\hat{G}}^{j+}_{j-3/2, 3/2}(s)\), \({\hat{G}}^{j-}_{j-1/2, 1/2}(s)\) and \({\hat{G}}^{j-}_{j-1/2, 3/2}(s)\) to be proportional to Breit–Wigner functions with constant couplings, the amplitudes \(g'_{j+}(s)\), \(g'_{j-}(s)\) and \(h'_{j-}(s)\) would end up having a pole at \(s = m_b^2 - m_\psi ^2\). It is clear that using Breit–Wigner parameterizations, or any other model for helicity amplitudes, ie the left-hand sides of Eqs. (39) and (41), instead of the LS amplitudes helps prevent unwanted singularities. A practical use of these formulae, and the analogous forms for the PV amplitude and for the u-channel exchanges, are given in Appendix G.
4 MacDowell symmetry
Up to this point, we have mainly ignored singularities at \(s=0\). For the s-channel reaction, we choose the scattering configuration such that the pseudothresholds are positive: \(m_b- m_\psi > 0\) and \(m_p - m_K> 0\). Our current results therefore depend on the relative sizes of the meson and baryon masses. We then restricted our discussion to positive \({{\mathrm{Re}}}\sqrt{s}\), meaning that our expressions do not hold for negative \({{\mathrm{Re}}}\sqrt{s}\). The correct kinematic singularity free amplitudes cannot have this property, since the invariant amplitudes do not depend on relative masses either [29]. The restriction to \({{\mathrm{Re}}}\sqrt{s} > 0\) limits the reachable kinematic singularities of \(\sqrt{E_p+ m_p}\) and \(\sqrt{E_b+ m_b}\) in Eq. (18). For \({{\mathrm{Re}}}\sqrt{s} < 0\), however, these factors contain (pseudo)threshold branch points.
The above-mentioned complications arise only in the case of fermion-boson scattering, where the total angular momentum is half integer. In this type of process the obtained helicity amplitudes are not invariant under the transformation \(\sqrt{s} \rightarrow -\sqrt{s}\). It can be argued that for half-integer total angular momenta, the relevant kinematic variable is \(\sqrt{s}\) rather than s.
In order to construct a set of amplitudes that is free of kinematical singularities for negative \({{\mathrm{Re}}}\sqrt{s}\) as well. One must therefore verify that the new (pseudo)treshold singularities at \({{\mathrm{Re}}}\sqrt{s}<0\) are correctly accounted for by the kinematic factors \(K^\eta _{MN}\). We have already silently removed those factors in Eq. (13) by introducing the \(Q^\eta \), which take the form
Under \(\sqrt{s} \rightarrow -\sqrt{s}\), the terms \(p\sqrt{s}\) and \(q\sqrt{s}\) remain unchanged. However, the factors \(\sqrt{E_p+ m_p}\) and \(\sqrt{E_b+ m_b}\) will now contain branch points at (pseudo)threshold at positive \({{\mathrm{Re}}}\sqrt{s}\). An additional benefit of this analysis, is that the final amplitudes are now independent of the choice relative masses, i.e. the final form of the amplitudes are the same if we would have taken the configuration where the pseudothresholds are negative.
One can verify that no additional singularities are found at \({{\mathrm{Re}}}\sqrt{s} < 0\) for \(j>\frac{1}{2}\) that have not yet been accounted for. Indeed, this can be done by tracking down the factors of \(Q^{\pm }\) in the kinematic matrix \({\mathcal {M}}^{-1}\) in Eq. (19). In other words, the solution to the conspiracy relations for \({{\mathrm{Re}}}\sqrt{s}>0\) also solve the conspiracy relations for \({{\mathrm{Re}}}\sqrt{s}<0\). For \(j=\frac{1}{2}\) and \(\eta = +\), however, no conspiracy relation was needed since the isobars \({\hat{A}}_{\lambda _p, \lambda _b\lambda _\psi } ^{j+}(s)\) always appeared with an additional factor \(\propto p^2\) for \({{\mathrm{Re}}}\sqrt{s} > 0\). For \({{\mathrm{Re}}}\sqrt{s}<0\), however, only \((L=0,S=0)\) is possible in the initial state (\(\Lambda _b {\psi }\)), which requires a new conspiracy relation to be solved. This is indeed reflected by the factor \({Q^{1/2}}\) in the definition of \({\hat{A}}_{\lambda _p, \lambda _b\lambda _\psi } ^{\frac{1}{2}+}\) in Eq. (12a). The conspiracy relations read (remember that the \(\lambda _\psi =-\) contribution vanishes)


Since \(E_b= -m_b\) corresponds to \(-\sqrt{s}=m_b+m_\psi \), both relations are fulfilled by requiring that

Our KSF-PCHA are now free of singularities for both \({{\mathrm{Re}}}\sqrt{s}> 0\), and \({{\mathrm{Re}}}\sqrt{s}<0\), and are independent of the chosen mass configuration. Still, they contain remaining singularities at \(s=0\). However, MacDowell symmetry [30] (which is a consequence of CT invariance [31]) in principle allows one to remove these remaining singularities, resulting in amplitudes that are s- and t-singularity free [29, 32,33,34]. MacDowell symmetry for the KSF-PCHA reads
where \(\zeta = (-1)^{\lambda -\lambda '}\) with and the factor \((m_\psi /m_p)^{-\eta }\) is due to our definition of the kinematic factors \(K^\eta _{MN}(s)\) in Eq. (13). The MacDowell symmetry can be made explicit by considering the relation between the KSF-PCHA and the scalar amplitudes. For example, from Eq. (C1) it follows that
In other words, one only needs a single KSF-PCHA for a given helicity combination, say \(F_{\lambda _p,\lambda _b\lambda _\psi }^{+}(\sqrt{s},t)\), and the other one follows from \(F_{\lambda _p,\lambda _b\lambda _\psi }^{+}(-\sqrt{s},t)\). Additionally, the \({Q^{\eta }}\) factors defined in Eq. (42a) introduce a similar behavior for the kinematic factors
Considering the definite-parity partial-wave amplitudes in Eq. (7), MacDowell symmetry requires
This equation might seem odd at first: for a contribution of definite parity, the partial-wave amplitude of definite parity must be non-zero. N / D approaches have been developed, using \(\sqrt{s}\) as the relevant variables, rather than s [35,36,37]. In such a way, the resonances only ‘resonate’ in the definite-parity partial-wave amplitude with the corresponding parity for \({{\mathrm{Re}}}\sqrt{s}>0\). The origin of the singularity that gives rise to the symmetry relation in Eq. (49) can be explained as follows. For unequal masses only, the half-angle factor \(\xi _{\lambda \lambda '}(z_s)\) has a branch point at \(s=0\). This branch point originates from the factor \(\sqrt{1-z_s}^{\left| \lambda -\lambda ^\prime \right| }\) in Eq. (6).Footnote 7 Hence, taking \(\sqrt{s}\rightarrow -\sqrt{s}\) results in a phase \(\xi _{\lambda \lambda '}(z_s) \rightarrow (-1)^{\lambda -\lambda '} \xi _{\lambda \lambda '}(z_s)\). For the second contribution to the PCHA, one has \(\xi _{-\lambda \lambda '}(z_s) \rightarrow (-1)^{\lambda +\lambda '} \xi _{-\lambda \lambda '}(z_s)\). In particular, the phases \((-1)^{\lambda - \lambda '}\) and \((-1)^{\lambda + \lambda '}\) are the same in all but meson-baryon scattering reactions. Hence, by removing the physical boundary singularities (\(z_s = \pm 1\)) in forming the t-singularity free d-functions \({\hat{d}}^j_{\lambda ,\lambda ^\prime }\), we introduced singularities \(\sqrt{s}^{\left| \lambda -\lambda '\right| }\) as a consequence. For all but meson-baryon scattering reactions, this singularity is removed by dividing the amplitude by \(\sqrt{s}^{\left| \lambda \right| +\left| \lambda ^\prime \right| }=\sqrt{s}^{M+N}\). The additional requirement of factorization of the amplitude introduces an extra factor \(s^N\), resulting in \(\sqrt{s}^{M-N}\) in Eq. (13).
The remaining kinematical singularities at \(s=0\) can now be removed from the KSF-PCHA by exploiting the MacDowell symmetry. Indeed, we can build symmetric and antisymmetric combinations of the \(F_{\lambda _p,\lambda _b\lambda _\psi }^{\eta }(\sqrt{s},t) \), which are even and odd under \(\sqrt{s}\rightarrow -\sqrt{s}\) respectively, and define totally singularity free functions,
Interestingly enough, these \({\hat{B}}_{\lambda _p,\lambda _b\lambda _\psi }^{\pm }(s,t)\) are free of kinematic singularities in both s and \(\sqrt{s}\). We remark that [38] introduces an additional \(1/\sqrt{s}\) in the propagator to regularize its high-energy behavior. Such a singular factor cannot be disposed freely, and is incompatible with the MacDowell symmetry.
Despite the fact that we discussed a procedure to remove the singularities at \(s = 0\), Eq. (49) is clearly not compatible with the isobar model. The latter requires isobars with opposite naturalities to be independent, and such constraints cannot be imposed consistently. Although taking care of these singularities is mandatory when considering dispersive analyses, we renounce to do so, for the purpose of making this formalism usable by the isobar practitioners. We therefore set \(Q^{\pm ,1/2} = 1\) in our final form in Appendix G.
5 Comparison with the covariant projection method
The LS and helicity partial waves can now be compared to the CPM formalism. The latter builds LS-like partial-wave amplitudes, based on covariant structures that are interpreted as spin (S) and orbital-momentum (L) covariant tensors. We follow the methodology outlined by the Bonn–Gatchina partial-wave analysis group in [38]. We consider the example of a \(\Lambda ^*\) resonance with \(J^P=\tfrac{3}{2}^-\) in the s-channel. First, we consider the interaction in the scattering regime. In this case, all structures must be orthogonalized to the center-of-mass momentum \(P=p_b+p_\psi \). We define the relative four-momenta in the intial and final state \(p=(p_b- p_\psi )/2\) and \(q=(p_p- p_K)/2\), respectively. The orbital momentum component of the vertex \(\Lambda ^* \rightarrow p K^-\) is described by the D-wave tensor
with \(q_\perp ^\mu = q^\mu - P^\mu \,P\cdot q/s\), and \(g^{\rho \mu }_\perp = g^{\rho \mu } - P^\rho P^\mu /s\), such that \(q_\perp ^\mu P_\mu = q_\rho g_\perp ^{\rho \mu } P_\mu = 0\). Furthermore, we define \(\gamma _\perp ^\mu = g_\perp ^{\mu \nu } \gamma _\nu \). The initial state can be S-wave or D-wave. The orbital tensor structure for the latter reads
with \(p_\perp ^\mu = p^\mu - P^\mu \,P\cdot p/s\). The \(\frac{3}{2}^-\) contribution to the helicity amplitudes is therefore fully determined by the expressionFootnote 8
where we introduced the spin-\(\frac{3}{2}\) projector

with \(\sigma ^\perp _{\mu \nu } = \frac{1}{2}\left( \gamma ^\perp _\mu \gamma ^\perp _\nu - \gamma ^\perp _\nu \gamma ^\perp _\mu \right) \). Explicitly, the corresponding isobar amplitudes read
Notice that the expression in Eq. (55c) indeed does not contain a contribution from the \(D_{\frac{1}{2}}\) component, as expected from the LS in Eq. (30). As discussed in Sect. 2, the square roots have no singularities at (pseudo)threshold. The role of Clebsch–Gordan coefficients can be enlighted by writing
It is worth noticing that the Clebsch–Gordan multiplying the \(g_{D_{\frac{3}{2}}}(s)\) coupling is not the one expected according to the LS construction: the \({\psi }\) spin is coupled with the orbital angular momentum first, and only after with the spin of the the \(\Lambda _b\), while the canonical LS construction would couple the two spins first, and the angular momentum after. This is also evident by looking at the covariant structures the second line of Eq. (53), and explains why the various tensors are not orthogonal.
The same framework can be applied to the decay chain, where the tensor structures of the initial \(\Lambda _b \rightarrow {\psi }\Lambda ^*\) decay must be orthogonalized with the respect to the \(\Lambda _b \) momentum \(p_b\), rather than the isobar momentum P. The \({\psi }\) is now in the final state with momentum \({\bar{p}}_\psi = -p_\psi \) and polarization \(\epsilon ^*_\mu ({\bar{p}}_\psi , \lambda _\psi )\). We therefore obtain
In the above, the \(\gamma ^\perp (p_b)\) and \(\gamma ^\perp (P)\) are orthogonalized with respect to \(p_b\) and P respectively. We will show the results for the \(g_{D_{\frac{3}{2}}}\) only (equating the other couplings to zero), in the decay chain and scattering regime. In the isobar rest frame, the contribution in the decay chain reads
To summarize, the amplitudes that follow from the CPM method contain the factor \(E_\psi /m_\psi \) in the \(\lambda _\psi = 0\) isobar. This factor asserts the fulfillment of the conspiracy relation in Eq. (29). This factors was included in the canonical helicity amplitudes, but does not follow from the LS method. Additional energy dependent factors \(\sqrt{E_p+m_p}\sqrt{E_b+m_b}\) are found, which are not required by analyticity at \(\sqrt{s}>0\), since they are smooth. These factors have been discussed in Sect. 4. Even though they are not necessary in the isobar model, one can decide to include them anyways. Since for negative \({{\mathrm{Re}}}\sqrt{s}\) the minimal orbital angular momentum is given by a P-wave in the initial and final state, one expects the kinematic factors \(\sqrt{E_b+m_b} \sqrt{E_p+m_p}\), or similarly \(\sqrt{E_b+m_b}q^2/\sqrt{E_p+m_p} = {Q^{+}} q^2\) to appear. Notice, however, that \(\sqrt{E_p+m_p}\sqrt{E_b+m_b} = {Q^{+}}(E_p+m_p)\), and therefore, a redundant kinematic zero remains at \(E_p=-m_p\) in Eq. (58), which can be reached for negative \({{\mathrm{Re}}}\sqrt{s}\) only. As already pointed out in [17], the CPM formalism was shown to violate crossing symmetry, since the amplitudes in the decay and scattering kinematics differ. Also, the coupling of the external particle spins and orbital momentum occur in a different way than in the LS for the \(D_{\frac{3}{2}}\) component.
5.1 \(pK^-\) mass distribution in different approaches
We explore the difference between the various approaches and consider two intermediate natural parity, spin-\(\frac{3}{2}\) \(\Lambda ^*\) resonances in the s-channel (\(p K^-\)): the \(\Lambda (1520)\) with mass \(M_{\Lambda ^*}=1519.5{\mathrm {\,MeV}} \) and width \(\Gamma _{\Lambda ^*} = 156{\mathrm {\,MeV}} \) (artificially increased by a factor of 10 for illustration purposes), and the \(\Lambda (1690)\) with \(M_{\Lambda ^*}=1690{\mathrm {\,MeV}} \) and width \(\Gamma _{\Lambda ^*} = 60{\mathrm {\,MeV}} \). We denote the dynamical part of the amplitude as \(T_{\Lambda ^*}\). We consider the CPM formalism discussed in Eq. (55) and Eq. (58) (for scattering and decay respectively), setting \(g_{S_{\frac{3}{2}}}(s) = g_{D_{\frac{1}{2}}}(s) = 0\) and \(g_{S_{\frac{1}{2}}}(s) = g_{D_{\frac{5}{2}}}(s) = 0\) respectively. We assume \(g_{D_{\frac{3}{2}}}(s) = T_{\Lambda ^*}(s)\) to be identical in the scattering and decay kinematics, with
Comparison of the line shape of \(\Lambda (1520)\) (artificially broaden by a factor of 10) and \(\Lambda (1690)\) in the \(pK^-\) invariant mass distribution, constructed with the different formalisms. In the left panel we show the result with no barrier factors. In the right panel, we include the customary Blatt-Weisskopf factors
For the LS formalism, we choose the couplings in Eq. (30) to be \({\hat{G}}^{\frac{3}{2}+}_{0,\frac{3}{2}} = {\hat{G}}^{\frac{3}{2}+}_{2,\frac{1}{2}} = 0\) and \({\hat{G}}^{\frac{3}{2}+}_{2,\frac{1}{2}} = T_{\Lambda ^*}\). The LS amplitude in the decay kinematics differs from the one in the scattering kinematics only because of the breakup momentum of \(\Lambda _b \rightarrow {\psi }\Lambda ^*\), calculated in the \(\Lambda _b \) rest frame or in the \(\Lambda ^*\) rest frame, respectively. Finally, we show the results for our proposed amplitude given in Appendix G. The model is obtained by taking \(g_{\Lambda (1520)} + g_{\Lambda (1690)} = T_{\Lambda ^*}\) in Eq. (G3).
As in [17], we illustrate the effect of including Blatt-Weisskopf factors in the dynamic part of the amplitude. In the case at hand, this amounts to multiplying the dynamic amplitude \(T_{\Lambda ^*}\) by a factor \(B_2(p)B_2(q)\), where \(B_2\) is defined as \((x = p,q)\)
and assume \(R = 3{\mathrm {\,GeV}} ^{-1}\) as in [24]. The differential width is given by
where \(\rho (s) = \lambda _{b\psi }^{1/2}\lambda _{pK}^{1/2}/s\) and \(N_j\) is a normalization constant. The effect of the different kinematic structures is clearly observed in the invariant mass distributions in Fig. 3. Our proposed amplitudes from Appendix G, referred to as the JPAC amplitudes, differ from the LS amplitudes given in Eq. (39) by the factor of \(E_\psi /m_\psi \) in the \(\lambda _\psi = 0\) helicity partial-wave amplitude (cf. Eq. (G12)). This factor also follows naturally from the CPM formalism in the scattering kinematics. The CPM amplitudes in the scattering and decay frame (see Eq. (55) and Eq. (58) respectively) both include an additional factor of \(\sqrt{E_b+ m_b}\sqrt{E_p+ m_p}\) compared to the JPAC and LS formalism, which is related to the discussion in Sect. 4. In addition the CPM formalism applied to the decay kinematics introduces redundant kinematic factors of s in all partial-wave amplitudes. Additionally, the \(\lambda _\psi =0\) amplitude has a factor of \((s-m_b^2-m_\psi ^2)E_b/E_\psi \) in the decay kinematics. The differences shown in Fig. 3, particularly between the LS decay and the CPM scattering, are enough to significantly impact the extraction of the couplings.
6 Conclusions
We have expanded the discussion in [17] about the different approaches for constructing amplitudes for scattering and decay processes to the fermion-boson case. In particular, we have studied the \(\Lambda _b \rightarrow \psi p K^-\) decay, which is of interest for hidden charm pentaquark searches. The inclusion of fermion spins in the helicity formalism introduces mismatches between threshold and pseudothreshold, which makes the discussion more complicated and the equations cumbersome. We used analyticity as a guiding principle to examine the canonical helicity formalism [6, 8,9,10] and the covariant projection method [11,12,13,14]. We have shown how the latter violates crossing symmetry. The matching of the helicity amplitudes to the most general covariant expression allows us to identify the kinematical singularities, and to determine the minimal energy dependence required, summarized in Sect. 3. In order to factor out the kinematical singularities we need to build the hadronic part of the amplitudes with a well defined parity. A \(\sqrt{s}\) singularity cannot be removed with these considerations and needs to be taken care of through the corresponding dynamical model. As in our previous work [17], we find meaningful differences among the amplitude building methodologies which do affect the resonance pole position extraction, and consequently to the data analysis oriented to determine the existence and properties of the resonances. This is particularly relevant in situations where several resonances overlaps, and the quantum number assignment is not stable, as in [24]. Although there is no way to escape all model dependence, our analysis maximizes the consistency of a given model with the S-matrix principles. A practical formulation of the amplitudes, both in the s and u channels, and both for the parity-conserving and parity-violating case, can be found in Appendix G.
Notes
Note that the definition of n(s, t) given here differs from the one used in [17] by the factor 4s.
We remark that our discussion would be unchanged if applied to the untruncated partial-wave series.
Note that at leading order in \(z_s\), \(\xi _{\lambda \lambda ^\prime } (z_s) \propto z_s^M\).
The name “Parity-Conserving Helicity Amplitudes” arises from Regge theory, where in the limit \(t \rightarrow \infty \) (which implies \(z_s \rightarrow \infty \)) the contribution from the opposite naturality, \(-\eta \), is proportional to \({\hat{d}}^{j-}_{\lambda \lambda ^\prime }(z_s)\) which is negligible compared to \({\hat{d}}^{j+}_{\lambda \lambda ^\prime }(z_s)\). In the case at hand, however, we consider the limits \(q \rightarrow 0\) or \(p \rightarrow 0\), where the kinematic factors of the partial-wave amplitudes are also relevant to determine the leading behavior of the two contributions in Eq. (11).
\(F^+_{+,++}\) stands for \(F^+_{\lambda _p=+\tfrac{1}{2},\lambda _b=+\tfrac{1}{2}, \lambda _\psi = +1}\), and so on.
We remark that we used the convention \(\left\langle S,\lambda _b- \lambda _\psi ;L,0|j,\lambda _b- \lambda _\psi \right\rangle \) for the LS Clebsch-Gordan coefficients. However, up to signs one can use \(\left\langle L, 0; S,\lambda _b- \lambda _\psi |j,\lambda _b- \lambda _\psi \right\rangle \) to get equivalent results.
Actually, this happens if \((m_1 - m_2)(m_3 - m_4) > 0\), as in our s-channel case. If \((m_1 - m_2)(m_3 - m_4) < 0\), \(\sqrt{1-z_s}^{\left| \lambda -\lambda ^\prime \right| }\) is regular at \(s=0\), but the factor \(\sqrt{1+z_s}^{\left| \lambda +\lambda ^\prime \right| }\) in Eq. (6) is not. The following discussion proceeds accordingly, leading to the same conclusions.
We neglect overall factors of i.
This is, of course, apart from the uncontrolled branch point singularity at \(u=0\).
For the u-channel resonances \(\eta = (-1)^{j+L+1/2}\), for the s-channel resonances \(\eta = \eta _b(-1)^{j+L+1/2}\), where \(\eta _b = 1\) (\(-1\)) for PC (PV) processes.
References
A. Esposito, A. Pilloni, A.D. Polosa, Phys. Rept. 668, 1 (2016). arXiv:1611.07920 [hep-ph]
R.F. Lebed, R.E. Mitchell, E.S. Swanson, Prog. Part. Nucl. Phys. 93, 143 (2017). arXiv:1610.04528 [hep-ph]
S.L. Olsen, T. Skwarnicki, D. Zieminska, Rev. Mod. Phys. 90, 015003 (2018). arXiv:1708.04012 [hep-ph]
F.K. Guo, C. Hanhart, U.G. Meißner, Q. Wang, Q. Zhao, B.S. Zou, Rev. Mod. Phys. 90, 015004 (2018). arXiv:1705.00141 [hep-ph]
M. Karliner, J.L. Rosner, T. Skwarnicki, Ann. Rev. Nucl. Part. Sci 68, 5 (2018). https://doi.org/10.1146/annurev-nucl-101917-020902. arXiv:1711.10626 [hep-ph]
M. Jacob, G.C. Wick, Ann. Phys. 7, 404 (1959)
M. Jacob, G.C. Wick, Ann. Phys. 281, 774 (2000)
S.U. Chung, Spin formalisms (1971) (unpublished). https://suchung.web.cern.ch/suchung/spinfm1.pdf
P.D.B. Collins, An introduction to Regge theory and high-energy physics. Cambridge monographs on mathematical physics (Cambridge University Press, Cambridge, 2009). https://www.cambridge.org/core/books/an-introduction-to-regge-theory-and-high-energy-physics/E628F1657888F248E6BF236283350588
R. Kutsckhe, ‘An angular distribution cookbook’ (unpublished). http://home.fnal.gov/~kutschke/Angdist/angdist.ps
S.U. Chung, Phys. Rev. D 48, 1225 (1993). [Erratum: Phys. Rev. D56,4419(1997)]
S.-U. Chung, J. Friedrich, Phys. Rev. D 78, 074027 (2008). arXiv:0711.3143 [hep-ph]
V. Filippini, A. Fontana, A. Rotondi, Phys. Rev. D 51, 2247 (1995)
A.V. Anisovich, A.V. Sarantsev, Eur. Phys. J. A 30, 427 (2006). arXiv:hep-ph/0605135 [hep-ph]
A.V. Anisovich, R. Beck, E. Klempt, V.A. Nikonov, A.V. Sarantsev, U. Thoma, Eur. Phys. J. A 48, 15 (2012). arXiv:1112.4937 [hep-ph]
C. Adolph et al., (COMPASS), Phys. Rev. D 95, 032004 (2017). arXiv:1509.00992 [hep-ex]
M. Mikhasenko, A. Pilloni, J. Nys, M. Albaladejo, C. Fernández-Ramírez, A. Jackura, V. Mathieu, N. Sherrill, T. Skwarnicki, A.P. Szczepaniak, (JPAC), Eur. Phys. J. C 78, 229 (2018). arXiv:1712.02815 [hep-ph]
R. Mizuk et al. (Belle), Phys. Rev. D 80, 031104 (2009). arXiv:0905.2869 [hep-ex]
K. Chilikin et al. (Belle), Phys. Rev. D 88, 074026 (2013). arXiv:1306.4894 [hep-ex]
R. Aaij et al. (LHCb), Phys. Lett. B 747, 484 (2015). arXiv:1503.07112 [hep-ex]
R. Aaij et al. (LHCb), Phys. Rev. D 92, 112009 (2015). arXiv:1510.01951 [hep-ex]
K. Chilikin et al. (Belle), Phys. Rev. D 90, 112009 (2014). arXiv:1408.6457 [hep-ex]
G. Cohen-Tannoudji, A. Kotański, P. Saling, Phys. Lett. 27B, 42 (1968)
R. Aaij et al. (LHCb), Phys. Rev. Lett. 115, 072001 (2015). arXiv:1507.03414 [hep-ex]
R. Aaij et al. (LHCb), Phys. Rev. Lett. 117, 082002 (2016). arXiv:1604.05708 [hep-ex]
C. Fernández-Ramírez, I.V. Danilkin, D.M. Manley, V. Mathieu, A.P. Szczepaniak, Phys. Rev. D 93, 034029 (2016). arXiv:1510.07065 [hep-ph]
A. Martin, T. Spearman, Elementary particle theory (North-Holland Pub. Co., New York, 1970)
F.A. Berends, A. Donnachie, D.L. Weaver, Nucl. Phys. B 4, 1 (1967)
F.S. Henyey, Phys. Rev. 171, 1509 (1968)
S.W. MacDowell, Phys. Rev. 116, 774 (1959)
Y. Georgelin, Phys. Rev. D 1, 1782 (1970)
F. Arbab, J.D. Jackson, Phys. Rev. 176, 1796 (1968)
D.M. Levine, Nucl. Phys. B 11, 641 (1969)
A. Actor, Phys. Rev. D 6, 1625 (1972)
A. Gasparyan, M.F.M. Lutz, Nucl. Phys. A 848, 126 (2010). arXiv:1003.3426 [hep-ph]
A.M. Gasparyan, M.F.M. Lutz, B. Pasquini, Nucl. Phys. A 866, 79 (2011). arXiv:1102.3375 [hep-ph]
M.F.M. Lutz, I. Vidana, Eur. Phys. J. A 48, 124 (2012). arXiv:1111.1838 [hep-ph]
A. Anisovich, E. Klempt, A. Sarantsev, U. Thoma, Eur. Phys. J. A 24, 111 (2005). arXiv:hep-ph/0407211 [hep-ph]
L. Biedenharn, J. Louck, P. Carruthers, Angular momentum in quantum physics: theory and application. Encyclopedia of mathematics and its applications (Cambridge University Press, 2009) http://www.cambridge.org/gb/acadeHrBmic/subjects/mathematics/mathematical-physics/angular-momenHrBtum-quantum-physics-theory-and-application?format=PB
Wolfram Research Inc., “Mathematica, Version 11.3,” Champaign, IL, 2018
H. Chen, R.-G. Ping, Phys. Rev. D 95, 076010 (2017). arXiv:1704.05184 [hep-ph]
JPAC Collaboration, “JPAC Website,” http://www.indiana.edu/~jpac/
Acknowledgements
J.N. would like to thank Igor Danilkin for bringing Refs. [35,36,37] to our attention. This work was supported by BMBF, the U.S. Department of Energy under grants No. DE-AC05-06OR23177 and No. DE-FG02-87ER40365, PAPIIT-DGAPA (UNAM, Mexico) grant No. IA101717, CONACYT (Mexico) grant No. 251817, Research Foundation – Flanders (FWO), U.S. National Science Foundation under award numbers PHY-1507572, PHY-1415459 and PHY-1205019, and Ministerio de Economía y Competitividad (Spain) through grant No. FPA2016-77313-P.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: polarization vectors and spinors
In the s-channel center of mass frame the spinors are given by
and the \(\psi \) polarization by
We apply the ‘particle 2’ convention for a particle going into the \(-z\) direction, as in [6]. The energies \(E_i\) are calculated from the momenta and are fully determined by s.
Appendix B: leading and next-to-leading expansion of Wigner d-functions
The \({\hat{d}}^j_{\lambda \lambda '}(z_s)\) Wigner functions are polynomials in \(z_s\) of order \(j- M\), with the usual definition of \(M = \max (|\lambda |,|\lambda '|)\) and \(N = \min (|\lambda |,|\lambda '|)\). We use the relation between the Wigner d-functions and the Jacobi polynomials \(P_n^{(a,b)}\) given by equation (3.74) in [39]
Two useful relations to compare the above to the literature are \(\left| \lambda + \lambda ^\prime \right| + \left| \lambda - \lambda ^\prime \right| = 2 M\) and \(\left| \lambda \right| + \left| \lambda ^\prime \right| = M+N\). The leading and next-to-leading terms of the polynomial are given by
As we noted, this polynomial has no definite parity. We defined the parity-conserving Wigner d-functions as
With the substitution \(\lambda \rightarrow -\lambda \) in Eq. (B2), the second term between brackets obtains a minus sign, since \((\left| \lambda - \lambda ^\prime \right| - M) = -(\left| \lambda +\lambda ^\prime \right| - M)\), while the first term is unaffected. This illustrates the more general fact that even and odd powers of \(z_s\) obtain opposite sign under \(\lambda \rightarrow -\lambda \). In particular, the leading power in \(z_s\) obtains an extra phase \((-1)^{M-\lambda -|\lambda -\lambda ^\prime |}\) from the prefactor in front of the brackets. This phase factor is identically equal to \((-1)^{M-\lambda ^\prime }\) used in the definition B3. It follows that the \({\hat{d}}^{j\eta }_{\lambda \lambda ^\prime }(z_s)\) have definite parity, and asymptotic expressions
These can be expressed in terms of Clebsch–Gordan coefficients. Explicitly, for the case considered,
where
depends only on j.
For the u-channel process, we have the initial helicity fixed to 1 / 2, and the final one running. We can use the same formulae, upon
Appendix C: the matching matrices
The matrix \({\mathcal {M}}\), introduced in Eq. (17) to match the KSF-PCHAs and the covariant basis, is
with
The inverse matrix is calculated using Mathematica [40]. It is given by
with
and the \({\mathcal {B}}\) matrix introduced in Eq. (19), by
with
Appendix D: parity-violating s-channel amplitude
The calculation of the PV amplitude is very similar to the PC one carried out in Sect. 2. In practice, one effectively needs to consider the \(\Lambda _b\) to have \(J^P = \tfrac{1}{2}^-\). This turns out into switching the constraints for the natural and unnatural partial waves obtained before. We sketch the derivation. The covariant basis is given by


and the kinematical singularity-free helicity partial-wave amplitudes \({\hat{A}}_{\lambda _p, \lambda _b\lambda _\psi } ^j(s)\) by
with
such that \(K_{MN}^{-\eta }/K_{MN}^{\eta }=(-)^{M-N}(\tfrac{m_\psi m_p}{pqs})^\eta {Q^{\prime -\eta }}/{Q^{\prime \eta }}\). The \({Q^{\prime \eta }}\) are
if one considers MacDowell symmetry, as discussed in Sect. 4, or
as required by the isobar model and implemented in Appendix G.
The matching can be performed in the same way, giving a matching equation analogous to Eq. (19),
with the \({\mathcal {B}}'\) matrix
where \(D = -\sqrt{s}(1+E_p/m_p) {Q^{+}}/{Q^{-}}\), \({{\bar{D}}} = D^{-1} {Q^{+}} {Q^{\prime -}}\big / {Q^{-}} {Q^{\prime +}}\), the elements of the \({\mathcal {B}}\) matrix are defined in Appendix C, and \({\mathcal {B}}_{ij,k}\) stands for the term in \({\mathcal {B}}_{ij}\) of order \([n(s,t)]^k\). Up to irrelevant factors which do not enter the equations (as the multiplicative factors of D, or the terms \({\mathcal {R}}_{13,0} \ne {\mathcal {B}}_{13,0}\) and \({\mathcal {R}}_{33,0} \ne {\mathcal {B}}_{33,0}\)), the conspiracy relations are going to be the same as in Sec. 2, upon swapping the natural and unnatural partial waves. For completeness, we report the matrix elements of \(\text {Reg}'\):
and
Appendix E: the u-channel parity-conserving amplitude
We briefly review the u-channel process \(\Lambda _b K^+\rightarrow p \psi \) scattering process, where the pentaquark peak is observed. We call \({\bar{p}}_\psi = -p_\psi \), and \({\bar{p}}_K= -p_K\) the physical four-momenta of \(\psi \) and \(K^+\) in the u-channel scattering kinematics. The momentum \(p_b\) defines the z-axis, the momenta \(p_p\) and \({\bar{p}}_\psi \) lie in the xz-plane, \(p_u\) and \(q_u\) denote magnitudes of relative momenta in the incoming, \(\Lambda _b K^+\) and the outgoing, \(p\psi \) states. The scattering angle \(\theta _u\) is the polar angle of the proton. The kinematics is summarized in Fig. 4. The quantities are expressed through the Mandelstam invariants,
As before, the function \(4u\, n(u,t)\) is a polynomial in u, t. For the covariant amplitude, we have
with the same covariant basis \(M_i\) as in Eq. (16); the polarization spinors are the same as in Eq. (A1), with the obvious replacements \(\theta _s \rightarrow \theta _u\), \(E_{i}(s) \rightarrow E_{i}(u)\), with \(i=\psi ,b,p\). The \(\psi \) polarization is given by

We remark that, since in the final state the fermion (p) is lighter than the boson (\({\psi }\)), the factor \(\sqrt{E_p- m_p}\) will have the threshold singularity only, while \(\sqrt{E_p+ m_p}\) the pseudothreshold singularity only.Footnote 9 Therefore, the factorized kinematic factors will be different for the threshold and pseudothreshold. The latter is accounted for by the explicit factors of \(\sqrt{u-u_-}\) below. The PCHAs read
where now \(\lambda = \lambda _b\), \(\lambda ' = \lambda _p- \lambda _\psi \), and
and \(u_\pm = (m_\psi \pm m_p)^2\) the final-state (pseudo)threshold. The \({Q^{\prime \eta }}\) are
if one considers MacDowell symmetry, as discussed in Sect. 4, or
as required by the isobar model and implemented in Appendix G. Hence, \(\tfrac{K_{MN}^{-\eta }}{K_{MN}^{\eta }} = (-)^{M-N}\left( \tfrac{q m_b}{p m_p(u-u_-)}\right) ^{\eta } \frac{{Q^{-\eta }}}{{Q^{\eta }}}\). The matching equations yield
where the matrices \({\mathcal {B}}\), \({\mathcal {P}}\), and \(\text {Reg}\) are regular at (pseudo)threshold:
with
and
Notice that the factor \(\sqrt{(u-u_-)/(E_p+m_p)}\) is regular at pseudothreshold. Since the set of conspiracy equations does not have a nontrivial solution for general u, we follow the same argument we used for the unnatural isobars in Sect. 2. Imposing the constraints at threshold for the \({\hat{A}}_{\lambda _p\lambda _\psi , \lambda _b} \), and restoring the kinematic factors, we get the conspiracy relations expected from the LS analysis, analogous to the ones in Eqs. (24), (29) and (35)



where C was defined in Eq. (34). The  indicates that, for \(u \rightarrow u_+\), the left hand part of the equation vanishes as fast as \(q_u^{j+ 1 - \eta /2}\). These equations agree with the predictions for the LS couplings. The same conspiracy equations hold at pseudothreshold for the natural case, whereas for the unnatural isobars at threshold we find
indicates that, for \(u \rightarrow u_+\), the left hand part of the equation vanishes as fast as \(q_u^{j+ 1 - \eta /2}\). These equations agree with the predictions for the LS couplings. The same conspiracy equations hold at pseudothreshold for the natural case, whereas for the unnatural isobars at threshold we find


The latter system of equations overconstrains the relations between the unnatural isobars, which are expected from the LS in Eq. (E10c) to depend on two independent functions. To avoid this, we impose all these functions to vanish independently at pseudothreshold. All these constraints are satisfied by choosing
with \(g_{j+}(u_\pm ) = g'_{j+}(u_\pm ) = g''_{j+}(u_\pm )\), \(g_{j-}(u_\pm ) - g'_{j-}(u_\pm ) = g''_{j-}(u_\pm )\) and \(h_{j-}(u_\pm ) = h'_{j-}(u_\pm ) = h''_{j-}(u_\pm )\). Note that the choice of the factor \(E_p+m_p\) in the \(A_{+\lambda _\psi ,+}^{j-}(u)\) can be also justified through the singularity analysis for negative \(\sqrt{u}\) as well, as in Sect. 4.
Appendix F: the u-channel parity-violating amplitude
To carry out the analysis for the PV part of the u-channel amplitude, we remark that changing the spin-parity of the \(\Lambda _b \) from \(J^P = \dfrac{1}{2}^+\) to \(J^P = \dfrac{1}{2}^-\) only affects the arguments related to the initial state \(\Lambda _b K^+\). Since the arguments in the previous channel were based on the (pseudo)threshold of the final state \(p{\psi }\), the derivation of the conspiracy relations is unaffected. Therefore, the kinematical factors are identical to the ones for the PC u-channel amplitudes, and will not be discussed any further. For completeness, we report the matching matrices,
The \({Q^{\prime \eta }}\) are
if one considers MacDowell symmetry, as discussed in Sect. 4, or
as required by the isobar model and implemented in Appendix G. The matrices are given by
where
and
Appendix G: A practical covariant parameterization for the amplitude
We combine the s and u-channel PV and PC isobars. The full covariant amplitude reads Footnote 10
with \(x=s,u\). The tensors \(M_{1\cdots 6}\) have been introduced in Eq. (16), and we define the \(M_{7\cdots 12} \equiv M'_{1\cdots 6}\) for the PV tensors in Eq. (D1). We square the amplitude, contract with the leptonic tensor which describes the \(\psi \rightarrow \mu ^+ \mu ^-\) decay, and sum over polarizations

with \(l^1\) and \(l^2\) the momenta of \(\mu ^+\) and \(\mu ^-\), respectively. This amplitude is has bilinear form in the couplings of the intermediate resonances. We use \(R={x,j,\eta ,L,S,\eta _b}\) as a collective index, to indicate a resonance in the channel \(x=s,u\), having spin j, naturality \(\eta \), coupling to the \(\Lambda _b \psi , p \psi \) state in spin S and orbital momentum L, and naturality of the \(\Lambda _b\) \(\eta _b\).Footnote 11

The functions \(g_R(x)\) encode all the information about the dynamics, and may be parameterized as Breit–Wigners times the customary Blatt-Weisskopf factors. The scalar \({\mathcal {C}}^{R}_i\) functions depend only on kinematics
where

where \(\lambda \) is the Källén triangular function, and
The matrices \(\text {Mat}^{(\prime )}(x)\) will be available for download on the JPAC website [42]. The functions \(F^{R}_{i}\) contain the kinematical dependence of the KSF-PCHAs,
with
We remind the reader that the KSF-PCHAs contain contributions from partial waves of both naturalities, which we explained when we introduced these amplitudes in Eq. (14). Therefore, \({\bar{\eta }}\) is the index of the naturality of the PCHAs, related to the entries of the vector in Eq. (G10), and does not coincide with the naturality of the intermediate resonance \(\eta \). To make this compact form more understandable, we show the meaning of the factors in \(F^{R{\bar{\eta }}, \text {PC}}_{\lambda }(s,t)\). Let us consider the example of the \(\Lambda (1520)\) with \(j^P = \frac{3}{2}^-\) (and naturality \(\eta = +\)), and coupling to \(p K^-\) in \(L=2\) and \(S=3/2\). The factors in Eq. (G12a) are:
-
\((p_s q_s)^{j-\left| 1/2-\lambda \right| }\) is the factor \((p_s q_s)^{j-M}\) that cancels the threshold and pseudothreshold singularities of the \({\hat{d}}^{j+}_{1/2,1/2-\lambda }(z_s)\). It corresponds to the barrier factors compatible with the minimal L available in a given helicity;
-
\(\delta _{\eta ,{\bar{\eta }}} {\hat{d}}^{j+}_{1/2,1/2 - \lambda }(z_s)\): since the \(\Lambda (1520)\) is natural, it will appear as leading term in the natural \(F^{R +, \text {PC}}_{\lambda }(s,t)\);
-
\(\left( \frac{p_s \sqrt{s}}{m_\psi }\right) ^{(1 + \eta )\delta _{j,1/2}}\) is the special factor appearing for \(j^P = \frac{1}{2}^+\). In the case at hand, the factor is 1; see Eq. (12b);
-
\(\delta _{\eta ,-{\bar{\eta }}} \left( \frac{p_s m_p}{q_s m_\psi }\right) ^{{\bar{\eta }}} {\hat{d}}^{j-}_{1/2 - \lambda ,1/2}(z_s)\): since the \(\Lambda (1520)\) is natural, it will appear as subleading term in the \(F^{R -, \text {PC}}_{\lambda }(s,t)\), with \(\left( \frac{p_s m_p}{q_s m_\psi }\right) ^{-1}\) the mismatch factor between natural and unnatural KSF-PCHAs; see the factor \(K^{-\eta }_{MN}/K^{\eta }_{MN}\) Eq. (14);
-
\({\textstyle \left\langle \frac{1}{2}, \frac{1}{2}; 1, -\lambda \,\Big |\,S, \frac{1}{2} - \lambda \right\rangle \left\langle S,\frac{1}{2} - \lambda ; L ,0 \,\Big |\,j,\frac{1}{2} - \lambda \right\rangle }\) are the standard Clebsch–Gordan coefficients that appear in the LS construction. In our example, \(L=2,\,S=3/2\);
-
\(\left( \frac{E_\psi (s)}{m_\psi }\right) ^{(1-|\lambda |) (1 - \delta _{j,1/2}\delta _{\eta ,1})}\) is the energy-dependent factor derived via our construction. Since the \(j^P=\frac{1}{2}+\) case evades the conspiracy equation, there is no need to introduce that factor in that case. See Eq. (36b);
-
\(\left( \frac{m_\psi m_p}{\eta \bar{\eta }\sqrt{s}}\right) ^{\delta _{\lambda ,-1}}\) is the mismatch factor between the \({\hat{A}}^{j\eta }_{+,+-}(s)\) and \({\hat{A}}^{j\eta }_{+,++}(s)\). See Eq. (12a);
-
\((p_s)^{L-j+1 + \eta /2}= 1\) if L is minimal, or \(p_s^2\) if it is nonminimal. In our example \(L=2\) is nonminimal (the minimal L allowed is \(L=0\)) and the factor appears.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Pilloni, A., Nys, J., Mikhasenko, M. et al. What is the right formalism to search for resonances? II. The pentaquark chain. Eur. Phys. J. C 78, 727 (2018). https://doi.org/10.1140/epjc/s10052-018-6177-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6177-2