Abstract
In this paper we show that any static and spherically symmetric anisotropic solution of the Einstein field equations can be thought as a system sourced by certain deformed isotropic system in the context of Minimal Geometric Deformation-decoupling approach. To be more precise, we developed a mechanism to obtain an isotropic solution from any anisotropic solution of the Einstein field equations. As an example, we implement the method to obtain the sources of a simple static anisotropic and spherically symmetric traversable wormhole.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
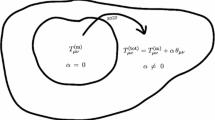
The Minimal Geometric Deformation (MGD) decoupling method, which was originally developed in the context of the brane-world [1, 2] (see also [3, 4]), has been successfully used to generate brane-world configurations from general relativistic perfect fluid solutions. Now we know that the utility of this method goes beyond this context [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30], and a new interpretation of it [18] in terms of the so-called gravitational decoupling, is being actively used [18, 22,23,24,25,26,27, 30]. This is precisely the scenario to study in this paper. In this sense, the MGD-decoupling represents the first systematic way to decoupling Einstein field equations, opening thus a new window in the analysis and study of these equations. By using this approach it is interesting to note how local anisotropy can be induced in well known spherically symmetric isotropic solutions of self-gravitating objects. Even more, the isotropic solution can be thought as a generator which, after gravitational interaction with certain decoupler matter content, lead through the MGD-decoupling to an anisotropic solution of the Einstein field equations.
Based on the above statement we may wonder if it can be possible to solve the inverse problem, namely, given any anisotropic solution of the Einstein field equations we can study if it is possible to obtain both its isotropic generator and its decoupler matter content. This inverse problem program could be implemented, for example, in situations where an anisotropic solution is known but the mechanisms behind such a geometry are unclear. Such is the case of traversable static and spherically symmetric wormholes [31,32,33,34,35,36,37,38,39,40] which in many cases are sourced by anisotropic fluids (for iso-tropic wormhole solutions see [41]). It is well known thattraversable wormhole solutions suffer from some issues related to their instability and violation of the energy conditions which has been explained in terms of the so–called exotic matter [38,39,40]. For these reasons, it could be interesting to explore the existence of isotropic solutions obeying suitable energy conditions which, after the MGD-decoupling, lead to wormholes geometries. Even more, it could be interesting to study if the MGD-decoupling could be considered as a kind of mechanism responsible for the breaking of the isotropy in the matter sector and for the appearance of the exotic source.
In this work we develop a method to obtain the isotropic generator of any anisotropic solution. More precisely, given any anisotropic solution we provide their sources through the MGD-decoupling (the generator perfect fluid and the decoupler matter content) and, as an example, we implement it to obtain the sources of a simple wormhole model.
This work is organized as follows. In the next section we briefly review the MGD-decoupling method. In Sect. 3 we develop the method to obtain the generator of any anisotropic solution of the Einstein field equations and then, we implement the method in a wormhole configuration in Sect. 4. The last section is devoted to final comments and conclusion.
2 Einstein equations and MGD–decoupling
Let us consider the Einstein field equations
and assume that the total energy-momentum tensor is given by
where \(T^{\mu (m)}_{\nu }=diag(-\rho ,p,p,p)\) is the matter energy momentum for a perfect fluid and \(\theta _{\mu \nu }\) is an additional source coupled with the perfect fluid by the constant \(\alpha \). Since the Einstein tensor is divergence free, the total energy momentum tensor \(T_{\mu \nu }^{(tot)}\) satisfies
Besides, we demand that the sources do not exchange energy–momentum between them but interact only gravitationally, which implies
In what follows, we shall consider spherically symmetric space–times with line element parametrized as
where \(\nu \) and \(\lambda \) are functions of the radial coordinate r only. Considering Eq. (5) as a solution of the Einstein field equations, we obtain
where the primes denote derivation respect to the radial coordinate and we have defined
It is well known that solutions of Eqs. (6), (7) and (8) can be obtained by the MGD–decoupling method [18, 22,23,24,25,26,27]. In particular, a well known isotropic system can be extended to, in some cases more realistic, anisotropic domains. The method consists in decoupling the Einstein field Eqs. (6), (7) and (8) by performing
where f is the geometric deformation undergone by the radial metric component \(\mu \) “controlled” by the free parameter \(\alpha \) which is a Lorentz and general coordinate invariant [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Doing so, we obtain two sets of differential equations: one describing an isotropic system sourced by the conserved energy–momentum tensor of a perfect fluid \(T^{\mu (m)}_{\nu }\) an the other set corresponding to quasi–Einstein field equations with a matter sector given by \(\theta _{\mu \nu }\). More precisely, we obtain
for the perfect fluid and
for the anisotropic system. It is worth noticing that the conservation equation \(\nabla _{\mu }\theta ^{\mu }_{\nu }=0\) leads to
which is a linear combination of Eqs. (16), (17) and (18). In this sense, there is no exchange of energy–momentum tensor between the perfect fluid and the anisotropic source as required.
As commented before, the MGD has been implemented to extend isotropic solutions by performing the following protocol: given the metric functions \(\{\nu ,\mu \}\) and the matter content \(\{\rho ,p\}\) that solve Eqs. (13), (14) and (15), the deformation function f is obtained from Eqs. (16), (17) and (18) after suitable conditions on the anisotropic source \(\theta _{\mu \nu }\) (a linear or barotropic equation of state, tracelessness of the corresponding sector, etc. [24]) are provided. With this information at hand, the “coupled” original set of Eqs. (6), (7) and (8) are finally solved. In this work we show that the scope of the MGD goes beyond the anisotropization of isotropic solution given that it allows to solve the inverse problem. To be more precise, we use the MGD-decoupling to obtain the isotropic generator and the decoupler matter content of any anisotropic solution of the original equations (6), (7) and (8) as it will be explained in the next section.
3 MGD-decoupling: the inverse problem
In this section we study how to obtain the isotropic generator and the decoupler matter content of any aniso-tropic system by the MGD-decoupling. The crucial point is to realize that given any anisotropic solution with metric functions \(\{\nu ,\lambda \}\), matter content \(\{\tilde{\rho },\tilde{p}_{r},\tilde{p}_{\perp }\}\) and definitions in Eqs. (9), (10) and (11), the following constraint must be satisfied
In this sense, we can combine Eqs. (17) and (18) in order to obtain the geometric deformation function f. With this information at hand we are able to use the geometry deformation \(e^{-\lambda }=\mu +\alpha f\) to obtain the remaining metric function of the perfect fluid \(\mu \) and its matter content. More precisely, the combination of Eqs. (17) and (18) with the constraint (20) leads to a differential equation for the decoupling function f given by
where we have introduced the auxiliary functions \(\mathcal {F}_{1}\) and \(\mathcal {F}_{2}\) as
From Eq. (21), it is straightforward that the deformation function f is given by
The next step consists in to obtain the metric function \(\mu \) by replacing Eq. (24) in the geometric deformation relation (12), from where
Now, from Eqs. (13), (14) and (15), the matter content for the isotropic system reads
where we have introduced four additional auxiliary functions
To determine the decoupler matter content we simply replace Eqs. (24) and (25) in (16), (17) and (18) to obtain
where
At this point the inverse problem program is completed. More precisely, Eqs. (25), (26) and (27) determine the isotropic generator \(\{\mu ,\rho ,p\}\) and Eqs. (32), (33) and (34) determine the decoupler matter content \(\{\theta ^{0}_{0},\theta ^{1}_{1},\theta ^{2}_{2}\}\) once any anisotropic solution \(\{\nu ,\lambda ,\tilde{\rho },\tilde{p}_{r},\tilde{p}_{\perp }\}\) is provided.
In the next section, as an example of the applicability of the method, we shall implement it to obtain the isotropic generator and the decoupler matter content corresponding to a static spherically symmetric wormhole.
4 Static spherically symmetric wormholes
Let us consider the static and spherically symmetric wormhole [38,39,40] line element given byFootnote 1
The metric functions \(\varPhi \) and b are arbitrary functions of the radial coordinate r. As \(\varPhi \) is related to the gravitational redshift, it has been named the redshift function, and b is called the shape function [38,39,40]. From Eq. (37) we identify \(\nu =2\varPhi \) and \(e^{-\lambda }=1-\frac{b}{r}\). The matter content associated to this geometry is given by
It is well known that the exotic matter content, as it has been usually coined, sustaining a traversable wormhole entails the violation of the weak energy condition. However, in order to minimize the use of such a source we can consider a distribution of matter which falls off rapidly with radius. As an example of the above mentioned case we can consider a simple wormhole [37] characterized by
where \(r_{0}\) is the minimum radius of the throat of the wormhole. From Eq. (41) the matter content reads
As pointed out by Morris and Thorne [37], the parameter \(\zeta =\frac{\tilde{p}_{r}}{\tilde{\rho }}-1\) quantifies the amount of exotic material needed to sustain the wormhole. In this particular case, although the exotic material decays rapidly with radius, \(\zeta \) is positive and huge. We may wonder if there exists some mechanism involving well behaved matter content (fulfilling the weak energy condition at least) which could lead to a wormhole geometry sustained by the matter content (43), (44) and (45). As we shall see later, the answer is affirmative and the mechanism involved is the MGD-decoupling of a perfect fluid which satisfies all the energy conditions.
In what follows, we shall implement the inverse problem program developed in the previous section to obtain the isotropic generator which after MGD-decoupling leads to the wormhole geometry described above. Replacing \(\nu =2\varPhi =0\) and \(e^{-\lambda }=1-\frac{r_{0}}{r}\) in Eq. (24) leads to
where \(c_{1}\) is a constant of integration with dimensions of inverse of length squared. Combining Eqs. (46) and (41) in (25) we obtain the metric function
Replacing Eqs. (47) and (41) in (26), (27) the matter content of the perfect fluid reads
Note that the system described by \(\{\mu ,\rho ,p\}\) corresponds to the isotropic generator of the wormhole geometry. To complete the inverse problem program we obtain the decoupler matter content which after gravitational interaction with the perfect fluid \(\{\rho ,p\}\) leads to the appearance of the exotic matter that sustains the wormhole geometry. Combining Eqs. (46) and (41) in (32), (33) and (34) the decoupler matter content reads
Henceforth we shall study the energy conditions fulfilled by the perfect fluid and the decoupler matter content by setting the parameter \(\alpha \) and the constant of integration \(c_{1}\). Let us start with the case \(c_{1}<0\) and \(\alpha <0\). Note that for this choice, the perfect fluid satisfies not only the weak but also the strong and the dominant energy conditions. In fact,
For the decoupler matter content the analysis is more subtle because the weak energy condition is satisfied whenever
It is worth noticing that the requirement in Eq. (57) is automatic but Eq. (56) leads to
In this case a suitable choice for \(c_{1}\) and \(\alpha \) would be
which implies
Remember that \(r_{0}\) is the minimum length allowed in the wormhole geometry so Eq. (60) does not contradict this fact. It is worth mentioning that with the above considerations the fulfilment of the strong and the dominant energy condition lead to \(r\ge r_{0}\). In this sense, the case \(\alpha <0\) and \(c_{1}<0\) corresponds to a perfect fluid and a decoupler matter satisfying all the energy conditions which after gravitational interaction leads to the appearance of the exotic matter sustaining the wormhole geometry. Even more, the exotic source could be thought as an effective matter arising as a consequence of the gravitational interaction between suitable fluids through the MGD decoupling.
Another case of interest could be to consider \(\alpha >0\) and \(c_{1}>0\). Note that for this choice the perfect fluid satisfy all the energy conditions listed above but the decoupler matter results in an exotic matter content. In this sense, if we insist in well behaved sources of the wormhole geometry, this case results unattractive. As a final case we could consider \(\alpha >0\) and \(c_{1}<0\) or \(\alpha >0\) or \(c_{1}<0\) but, as in the previous case, these choices are inadequate if we desire to avoid exotic content.
5 Conclusions
In this work we have developed the inverse problem program in the context of the Minimal Geometric Deformation method. Specifically, here we show that given any anisotropic solution of the Einstein field equations, its matter content can be decomposed into a perfect fluid sector interacting gravitationally with some decoupler matter content. As it was remarked in the manuscript, this inverse problem program could be implemented in cases where some anisotropic solution is known but the mechanism behind such a configuration remains obscure. Such is the case of traversable wormhole solutions where the matter sustaining it is the so called exotic matter which unavoidably violates all the energy conditions. Whether the exotic matter can be experimentally found or not, it could be interesting to provide a mechanism to explain its apparition. For this reason we illustrated how the inverse problem method works studying a simple model of a traversable wormhole space–time. We obtained that the exotic matter of the wormhole could be decomposed into a perfect fluid (the isotropic generator) and a matter (the decoupler matter) satisfying all the energy conditions. In this sense the emergence of the exotic matter could be thought a consequence of the gravitational interaction of reasonable (at least classically) matter content in the Minimal Geometric Deformation scenario.
The implementation of the method to obtain other anisotropic solutions both in general relativity and in extended theories of gravity is currently under study.
Notes
In what follows we sall assume \(\kappa ^{2}=8\pi \).
References
L. Randal, R. Sundrum, Phys. Rev. Lett. 83, 3370 (1999)
L. Randal, R. Sundrum, Phys. Rev. Lett. 83, 4690 (1999)
I. Antoniadis, Phys. Lett. B 246, 377 (1990)
I. Antoniadis, N. Arkani-Hamed, S. Dimopoulos, G. Dvali, Phys. Lett. B 436, 257 (1998)
J. Ovalle, Mod. Phys. Lett. A 23, 3247 (2008)
J. Ovalle, Int. J. Mod. Phys. D 18, 837 (2009)
J. Ovalle, Mod. Phys. Lett. A 25, 3323 (2010)
R. Casadio, J. Ovalle, Phys. Lett. B 715, 251 (2012)
J. Ovalle, F. Linares, Phys. Rev. D 88, 104026 (2013)
J. Ovalle, F. Linares, A. Pasqua, A. Sotomayor, Class. Quantum Gravity 30, 175019 (2013)
R. Casadio, J. Ovalle, R. da Rocha, Class. Quantum Gravity 30, 175019 (2014)
R. Casadio, J. Ovalle, Class. Quantum Gravity 32, 215020 (2015)
J. Ovalle, L.A. Gergely, R. Casadio, Class. Quantum Gravity 32, 045015 (2015)
R. Casadio, J. Ovalle, R. da Rocha, EPL 110, 40003 (2015)
J. Ovalle, Int. J. Mod. Phys. Conf. Ser. 41, 1660132 (2016)
R.T. Cavalcanti, A. Goncalves da Silva, R. da Rocha, Class. Quantum Gravity 33, 215007 (2016)
R. Casadio, R. da Rocha, Phys. Lett. B 763, 434 (2016)
J. Ovalle, Phys. Rev. D 95, 104019 (2017)
R. da Rocha, Phys. Rev. D 95, 124017 (2017)
R. da Rocha, Eur. Phys. J. C 77, 355 (2017)
R. Casadio, P. Nicolini, R. da Rocha, Class. Quantum Gravity 35, 185001 (2018)
J. Ovalle, R. Casadio, R. da Rocha, A. Sotomayor, Eur. Phys. J. C 78, 122 (2018)
M. Estrada, F. Tello-Ortiz. arXiv:1803.02344v3 [gr-qc]
J. Ovalle, R. Casadio, R. da Rocha, A. Sotomayor, Z. Stuchlik. arXiv:1804.03468 [gr-qc]
C. Las Heras, P. Leon, Fortschr. Phys. 66, 1800036 (2018)
L. Gabbanelli, A. Rincón, C. Rubio, Eur. Phys. J. C 78, 370 (2018)
M. Sharif, S. Sadiq. arXiv:1804.09616v1 [gr-qc]
A. Fernandes-Silva, A.J. Ferreira-Martins, R. da Rocha, Eur. Phys. J. C 78, 631 (2018)
A. Fernandes-Silva, R. da Rocha, Eur. Phys. J. C 78, 271 (2018)
E. Contreras, P. Bargueño, Eur. Phys. J. C 78, 558 (2018)
L. Flamm, Physik Z. 17, 448 (1916)
A. Einstein, N. Rosen, Phys. Rev. 48, 73 (1935)
C.W. Misner, J.A. Wheeler, Ann. Phys. 2, 525 (1957)
H. Ellis, J. Math. Phys. 14, 104 (1973)
K.A. Bronnikov, Acta Phys. Polonica B 4, 251 (1973)
H.G. Ellis, Gen. Relativ. Gravit. 10, 105 (1979)
M.S. Morris, K.S. Thorne, Am. J. Phys. 56, 395 (1988)
M.S. Morris, K.S. Thorne, U. Yurtsever, Phys. Rev. Lett. 61, 1446 (1988)
M. Visser, Lorentzian Wormholes: From Einstein to Hawking (AIP Press, New York, 1996)
F.S.N. Lobo, Wormholes, Warp Drives and Energy Conditions (Springer, New York, 2017)
M. Cataldo, L. Liempim, P. Rodriguez, Phys. Lett. B 757, 130 (2016)
Author information
Authors and Affiliations
Corresponding author
Additional information
Ernesto Contreras: On leave from Universidad Central de Venezuela.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Contreras, E. Minimal Geometric Deformation: the inverse problem. Eur. Phys. J. C 78, 678 (2018). https://doi.org/10.1140/epjc/s10052-018-6168-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6168-3