1 Introduction

The problem of spacetime singularities is a central one in classical and quantum theories of gravity. Given some general conditions, it was proven that general relativity leads to singularities, among which special significance is attributed to big bang and black hole singularities [1].

The occurrence of a singularity in a physical theory usually signals the breakdown of that theory. In the case of general relativity, the expectation is that its singularities will disappear after quantization. Although a theory of quantum gravity is not yet available in finite form, various approaches exist within which the question of singularity avoidance can be addressed [2]. Quantum cosmological examples for such an avoidance can be found, for example, in [3,4,5,6] and the references therein.

Independent of the quantum fate of singularities, the question of their exact nature in the classical theory, and in particular for cosmology, is of considerable interest and has a long history; see, for example [7, 8], for recent reviews. This is also the topic of the present paper.

Already in the 1940s, Evgeny Lifshitz investigated the gravitational stability of non-stationary isotropic models of universes. He found that the isotropy of space cannot be retained in the evolution towards singularities [10] (see [11] for an extended physical interpretation). This motivated the activity of the Landau Institute in Moscow to examining the dynamics of homogeneous spacetimes [12]. A group of relativists inspired by Lev Landau, including Belinski, Khalatnikov and Lifshitz (BKL), started to investigating the dynamics of the Bianchi VIII and IX models near the initial spacelike cosmological singularity [13]. After several years, they found that the dynamical behaviour can be generalized to a generic solution of general relativity [14]. They did not present a mathematically rigorous proof, but rather a conjecture based on deep analytical insight. It is called the BKL conjecture (or the BKL scenario if specialized to the Bianchi-type IX model). The BKL conjecture is a locality conjecture stating that terms with temporal derivatives dominate over terms with spatial derivatives when approaching the singularity (with the exception of possible ‘spikes’ [8, 9]). Consequently, points in space decouple and the dynamics then turn out to be effectively the same as those of the (non-diagonal) Bianchi IX universe. (In canonical gravity, this is referred to as the strong coupling limit, see e.g. [2, p. 127].)

The dynamics of the Bianchi IX towards the singularity are characterized by an infinite number of oscillations, which give rise to a chaotic character of the solutions (see e.g [15]). Progress towards improving the mathematical rigour of the BKL conjecture has been made by several authors (see e.g. [16]), while numerical studies giving support to the conjecture have been performed (see e.g. [17]).

The dynamics of the diagonal Bianchi IX model, in the Hamiltonian formulation, were studied independently from BKL by Misner [18, 19]. Misner’s intention was to search for a possible solution to the horizon problem by a process that he called “mixing”.Footnote 1 Ryan generalized Misner’s formalism to the non-diagonal case in [20, 21]. A qualitative treatment of the dynamics for all the Bianchi models may be found in the review article by Jantzen [22], and we make reference to it whenever we get similar results.

Part of the BKL conjecture is that non-gravitational (‘matter’) terms can be neglected when approaching the singularity. An important exception is the case of a massless scalar field, which has analogies with a stiff fluid (equation of state \(p=\rho \)) and, in Friedmann models, has the same dependence of the density on the scale factor as anisotropies (\(\rho \propto a^{-6}\)). As was rigorously shown in [23], such a scalar field will suppress the BKL oscillations and thus is relevant during the evolution towards the singularity. Arguments for the importance of stiff matter in the early universe were already given by Barrow [24].

In our present work, we shall mainly address the general (non-diagonal) Bianchi IX model near its singularity. Our main motivation is to provide support for a rather simple asymptotic form of the dynamics that can suitably model its exact complex dynamics. We expect this to be of relevance in the quantization of the general Bianchi IX model, which we plan to investigate in later papers; see, for example [25]. Apart from a few particular solutions that form a set of measure zero in the solution space, no general analytic solutions to the classical equations of motion are known. Therefore, we will restrict ourselves to qualitative considerations which will be supported by numerical simulations. The examination of the non-diagonal dynamics presented in [26], though it is mathematically satisfactory, is based on the qualitative theory of differential equations, which is of little use for our purpose.

Our paper is organized as follows. Section 2 contains the formalism and presents our main results for a general Bianchi IX model. We first specify the kinematics and dynamics. We then consider a matter field in the form of (tilted) dust. This is followed by investigating the asymptotic regime of the dynamics near the singularity. Our conclusions are presented in Sect. 3. The numerical methods used in our numerical simulations are described in the Appendix.

2 The general Bianchi IX spacetime

2.1 Kinematics

The general non-diagonal case describes a universe with rotating principal axes. The metric in a synchronous frame can be given as follows (see for the following e.g. [27, 28]):

$$\begin{aligned} d s^2=-N^2 d t^2 + h_{ij} \sigma ^i \otimes \sigma ^j , \end{aligned}$$
(1)

where N is the lapse function. Spatial hypersurfaces in the spacetime are regarded topologically as \(S^3\) (describing closed universes), which can be parametrized by using three angles \(\left\{ \bar{\theta },\bar{\phi },\bar{\psi } \right\} \in [0,\pi ]\times [0,2\pi ]\times [0,\pi ]\). The basis one-forms read

$$\begin{aligned} \begin{aligned} \sigma ^1&= -\sin (\bar{\psi }) d \bar{\theta } + \cos (\bar{\psi })\sin (\bar{\theta }) d \bar{\phi }, \\ \sigma ^2&= \cos (\bar{\psi }) d \bar{\theta } + \sin (\bar{\psi })\sin (\bar{\theta }) d \bar{\phi }, \\ \sigma ^3&= \cos (\bar{\theta }) d \bar{\phi } + d \bar{\psi }. \end{aligned} \end{aligned}$$
(2)

The \(\sigma ^i\), \(i=1,2,3\), are dual to the vector fields

$$\begin{aligned} \begin{aligned} X_1&= -\sin (\bar{\psi }) \partial _{\bar{\theta }} + \frac{\cos (\bar{\psi })}{\sin (\bar{\theta })} \left[ \partial _{\bar{\phi }} + \cos (\bar{\theta }) \partial _{\bar{\psi }} \right] , \\ X_2&= \cos (\bar{\psi }) \partial _{\bar{\theta }} + \frac{\sin (\bar{\psi })}{\sin (\bar{\theta })} \left[ \partial _{\bar{\phi }} + \cos (\bar{\psi }) \partial _{\bar{\psi }} \right] , \\ X_3&= \partial _{\bar{\psi }}, \\ \end{aligned} \end{aligned}$$
(3)

which together with \(X_0=\partial _t\) form an invariant basis of the Bianchi IX spacetime. The \(X_i\) are constructed from the Killing vectors that generate the isometry group \(SO(3,\mathbb {R})\) (see [27] for more details). The basis one-forms satisfy the relation

$$\begin{aligned} d \sigma ^i=-\frac{1}{2}C^i_{jk}\sigma ^j \wedge \sigma ^k \ , \end{aligned}$$
(4)

with \(C^i_{jk}=\varepsilon _{ijk}\) being the structure constants of the Lie algebra \(\mathfrak {so}(3, \mathbb {R})\). The \(X_i\) obey the algebra \([X_i,X_j]=-C^{k}_{ij}X_k\). We parametrize the metric coefficients in this frame as follows

$$\begin{aligned} h_{ij} = O_i{}^{k} O_j{}^{l} \bar{h}_{ k l }, \end{aligned}$$
(5)

where

$$\begin{aligned}&\bar{h}\equiv \left\{ \bar{h}_{i j} \right\} = e ^{2\alpha }\text {diag}\left( e ^{2\beta _+ + 2\sqrt{3}\beta _-}, e ^{2\beta _+ - 2\sqrt{3}\beta _-}, e ^{-4\beta _+ } \right) \nonumber \\&\quad \equiv \text {diag}\left( \Gamma _1 ,\Gamma _2 , \Gamma _3 \right) . \end{aligned}$$
(6)

The variables \(\alpha \), \(\beta _+\), and \(\beta _-\) are known as the Misner variables. The scale factor \(\exp (\alpha )\) is related to the volume, while the anisotropy factors \(\beta _+\) and \(\beta _-\) describe the shape of this model universe. The variables \(\Gamma _1\), \(\Gamma _2\) and \(\Gamma _3 \) were used by BKL in their original analysis [31].

We introduced here a matrix \(O\equiv \left\{ O_i{}^{j}\right\} \equiv O_{\theta }O_{\phi }O_{\psi }\) (i corresponding to rows and j corresponding to columns), which is an \(SO(3,\mathbb {R})\) matrix that can be parametrized by another set of Euler angles, \(\left\{ \theta ,\phi ,\psi \right\} \in [0,\pi ]\times [0,2\pi ]\times [0,\pi ]\). Explicitly,

$$\begin{aligned} \begin{aligned} O_{\psi }&=\left( \begin{array}{ccc} \cos ( \psi ) &{} \sin ( \psi ) &{} 0 \\ - \sin ( \psi ) &{} \cos ( \psi ) &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right) , \\ O_{\theta }&=\left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{}\cos ( \theta ) &{} \sin ( \theta ) \\ 0 &{}- \sin ( \theta ) &{} \cos ( \theta ) \end{array} \right) , \\ O_{\phi }&=\left( \begin{array}{ccc} \cos ( \phi ) &{} \sin ( \phi ) &{} 0 \\ - \sin ( \phi ) &{} \cos ( \phi ) &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right) \, . \end{aligned} \end{aligned}$$
(7)

The Euler angles \(\theta \), \(\phi \), and \(\psi \) are now dynamical quantities and describe nutation, precession, and pure rotation of the principal axes, respectively. In the case of Bianchi IX spacetime, the group \(SO(3,\mathbb {R})\) is the canonical choice for the diagonalization of the metric coefficients. For a treatment of other Bianchi models, see [22].

2.2 Dynamics

In the following, we shall discuss the Hamiltonian formulation of this model. In order to keep track of the diffeomorphism (momentum) constraints, we replace the metric (1) by the ansatz

$$\begin{aligned} \begin{aligned}&d s^2=- N^2 d t^2 + h_{ij}\left( N^i d t+\sigma ^i \right) \otimes \left( N^j d t+\sigma ^j \right) , \end{aligned} \end{aligned}$$
(8)

where \(N^i\) are the shift functions. The Hamiltonian formulation was first derived in a series of papers by Ryan: the symmetric (non-tumbling) case obtained by constraining \({\psi }\), \({\phi }\) to be constant and keeping \(\theta \) dynamical is discussed in [20], and the general case can be found in [21]. We write the Einstein–Hilbert action in the well known ADM form,

$$\begin{aligned} S_{EH}= & {} \frac{1}{16\pi G}\int \sigma ^1\wedge \sigma ^2\wedge \sigma ^3 \nonumber \\&\times \int d t\ N\sqrt{h} \left[ \left( h^{ik} h^{jl} -h^{ij}h^{kl}\right) K_{ij}K_{kl} +{}^{(3)} R \right] , \nonumber \\ \end{aligned}$$
(9)

where

$$\begin{aligned} K_{ij}=\frac{1}{2N}\left( \dot{h}_{ij}-2 D_{(i} N_{j}) \right) \end{aligned}$$

is the extrinsic curvature, and \(D_i\) is the spatial covariant derivative in the non-coordinate basis \(\left\{ X_i \right\} \). We will set \(\frac{3}{4\pi G}\int \sigma ^1\wedge \sigma ^2\wedge \sigma ^3=1\) for simplicity. The three-dimensional curvature \({}^{(3)}R\) on spatial hypersurfaces of constant coordinate time is given by

$$\begin{aligned} {}^{(3)} R= & {} -\frac{ e ^{-2\alpha }}{2} \left( e ^{-8\beta _+}-4 e ^{-2\beta _+} \cosh \left( 2\sqrt{3}\beta _- \right) \right. \nonumber \\&\left. +\, 2 e ^{4\beta _+} \left[ \cosh \left( 4\sqrt{3}\beta _- \right) -1 \right] \right) . \end{aligned}$$
(10)

We now turn to the calculation of the kinetic term and the diffeomorphism constraints. For this purpose, we define an antisymmetric angular velocity tensor \(\omega ^{i}{}_{j}\) by the matrix equation

$$\begin{aligned} \varvec{\omega }=\left\{ \omega ^{i}{}_{j} \right\} =\left( \begin{array}{ccc} 0 &{} \omega ^{1}{}_{2} &{} -\omega ^{3}{}_{1} \\ -\omega ^{1}{}_{2} &{} 0 &{} \omega ^{2}{}_{3} \\ \omega ^{3}{}_{1} &{} -\omega ^{2}{}_{3} &{} 0 \end{array} \right) \equiv O^{T}\dot{O}. \end{aligned}$$
(11)

An explicit calculation of the right-hand side gives, using (7),

$$\begin{aligned} \omega ^{2}{}_{3} =&\cos (\psi ) \dot{\phi }+\sin (\psi )\sin (\phi )\dot{\theta } \ , \end{aligned}$$
(12)
$$\begin{aligned} \omega ^{3}{}_{1} =&\sin (\psi )\dot{\phi }-\cos (\psi )\sin (\phi )\dot{\theta } \ , \end{aligned}$$
(13)
$$\begin{aligned} \omega ^{1}{}_{2} =&\dot{\psi }+\cos (\phi )\dot{\theta } \ . \end{aligned}$$
(14)

The Lagrangian in the gauge \(N^i=0\) then takes the form

$$\begin{aligned} \text {L}= & {} N e ^{3\alpha }\left[ \frac{-\dot{\alpha }^2+\dot{\beta }^2_+ + \dot{\beta }^2_- + I_1 \left( \omega ^{2}{}_{3}\right) ^2 + I_2 \left( \omega ^{3}{}_{1}\right) ^2 + I_3 \left( \omega ^{1}{}_{2}\right) ^2 }{2N^2}\right. \nonumber \\&\left. + \frac{{}^{(3)} R}{12}\right] , \end{aligned}$$
(15)

where the ‘moments of inertia’ are given by

$$\begin{aligned} 3 I_1\equiv & {} \sinh ^2 \left( 3\beta _+ - \sqrt{3}\beta _- \right) , \nonumber \\ 3 I_2\equiv & {} \sinh ^2 \left( 3\beta _+ + \sqrt{3}\beta _- \right) , \nonumber \\ 3 I_3\equiv & {} \sinh ^2 \left( 2\sqrt{3}\beta _- \right) . \end{aligned}$$
(16)

Note, in particular, that the term \(\frac{1}{2}\left[ I_1 \left( \omega ^{2}{}_{3}\right) ^2 + I_2 \left( \omega ^{3}{}_{1}\right) ^2 + I_3 \left( \omega ^{1}{}_{2}\right) ^2 \right] \) would formally correspond to the rotational energy of a rigid body if the moments of inertia were constant. The canonical momenta conjugate to the Euler angles are given by

$$\begin{aligned} \begin{aligned} p_{\theta }&= \frac{ e ^{3\alpha }}{N}\left[ I_1 \sin (\psi )\sin (\phi )\omega ^{2}{}_{3} \right. \\&\quad \left. -I_2\cos (\psi )\sin (\phi )\omega ^{3}{}_{1} +I_3 \cos (\theta )\omega ^{1}{}_{2} \right] , \\ p_{\phi }&= \frac{ e ^{3\alpha }}{N}\left[ I_1 \cos (\psi )\omega ^{2}{}_{3} +I_2 \sin (\psi )\omega ^{3}{}_{1} \right] , \\ p_{\psi }&= \frac{ e ^{3\alpha }}{N}\ I_3 \omega ^{1}{}_{2}. \end{aligned} \end{aligned}$$
(17)

It is convenient to introduce the following (non-canonical) angular momentum like variables:

$$\begin{aligned} l_1 \equiv \frac{ e ^{3\alpha }}{N}I_1 \omega ^{2}{}_3 , \quad l_2 \equiv \frac{ e ^{3\alpha }}{N}I_2 \omega ^{1}{}_3 \quad \text {and} \quad l_3 \equiv \frac{ e ^{3\alpha }}{N}I_3 \omega ^{2}{}_1 .\nonumber \\ \end{aligned}$$
(18)

The relation to the canonical momenta can now explicitly be given by

$$\begin{aligned} \begin{aligned} p_{\theta }&= \sin (\psi )\sin (\phi ) l_1 - \cos (\psi )\sin (\phi ) l_2 +\cos (\phi ) l_3 \ , \\ p_{\phi }&= \cos (\psi ) l_1 +\sin (\psi ) l_2 \ , \\ p_{\psi }&= l_3 \ . \end{aligned} \end{aligned}$$
(19)

It is readily shown that the variables \(l_i\) obey the Poisson bracket algebra \( \left\{ l_i,l_j \right\} =-C^k_{ij}{}l_k \). After the usual Legendre transform, we obtain the Hamiltonian constraint,

$$\begin{aligned} \mathcal {H}= & {} \frac{ e ^{-3\alpha }}{2} \nonumber \\&\times \left( -p_\alpha ^2 +p_+^2 +p_-^2 +\frac{l_1^2}{I_1}+\frac{l_2^2}{I_2}+\frac{l_3^2}{I_3} - \frac{ e ^{6\alpha }}{6} {}^{(3)}R \right) .\nonumber \\ \end{aligned}$$
(20)

From (9), we find that the diffeomorphism constraints (\(\partial L/\partial N^i=0\)) can be written as

$$\begin{aligned} \mathcal {H}_i = 2C^{j}{}_{il} h_{jk}p^{kl} , \end{aligned}$$
(21)

where

$$\begin{aligned} p^{ij}=\frac{\sqrt{h}}{24N}\left( h^{ik}h^{jl}-h^{ij}h^{kl} \right) K_{kl} \end{aligned}$$

is the ADM momentum. From this expression we can finally compute the diffeomorphism constraints in terms of the angular momentum-like variables and obtain

$$\begin{aligned} \mathcal {H}_i=O_{i}{}^{j}l_j, \end{aligned}$$
(22)

that is, we can identify the diffeomorphism constraints with a basis of the generators of \(SO(3,\mathbb {R})\). The full gravitational Hamiltonian then reads

$$\begin{aligned} H=N\mathcal {H}+N^i\mathcal {H}_i. \end{aligned}$$
(23)

From the diffeomorphism constraints (22) we conclude that in the vacuum case \(l_i=0\) and that therefore no rotation is possible, that is, we recover the diagonal case. If we want to obtain a Bianchi IX universe with rotating principal axes, we are thus forced to add matter to the system. A formalism for obtaining equations of motion for general Bianchi class A models filled with fluid matter was developed by Ryan [28]. For simplicity, we will only consider the case of dust as discussed by Kuchař and Brown in [29]. If we were, for example, interested in the study of the quantum version of this model, it would be desirable to introduce a fundamental matter field instead of an ideal fluid. Standard scalar fields alone cannot lead to a rotation for Bianchi IX models. The easiest way to achieve this is, to our knowledge, the introduction of a Dirac field [30].

2.3 Adding dust to the system

The energy momentum tensor for dust reads \(T_{\mu \nu } = \rho u_\mu u_\nu \). The local energy conservation \(\nabla _\mu T^{\mu \nu }=0\) leads to a geodesic equation for the positions of the dust particles. Let us start therefore by considering the geodesic equation for a single dust particle, whose four-velocity we can express in the non-coordinate frame \(\sigma ^i\) used above by the Pfaffian form

$$\begin{aligned} \mathbf {u}=u_0 d t + u_i \sigma ^i \quad \text {with} \ \ \langle \mathbf {u},\mathbf {u} \rangle =-1\ . \end{aligned}$$
(24)

We partially fix the gauge by setting \(N^i=0\). The normalization condition implies

$$\begin{aligned} u_0=- N \sqrt{1+h^{ij}u_i u_j}. \end{aligned}$$
(25)

We have chosen here the minus sign because this guarantees that the proper time in the frame of the dust particle has the same orientation as the coordinate time t. The geodesic equation for the spatial components of the four velocity can then be written as

$$\begin{aligned} u^0(\partial _t u_i) - C^k_{ij}u_k u^j = 0 \ . \end{aligned}$$
(26)

The geodesic equation implies the existence of a constant of motion. To see this explicitly, we compute the expression \(\sum \nolimits _{i=1,2,3}\dot{u}_i u_i\) and convince ourselves that it vanishes identically. Thus the Euclidean sum

$$\begin{aligned} C^2\equiv (u_1)^2+(u_2)^2+(u_3)^2 \end{aligned}$$
(27)

is a constant of motion. Defining \(\vec {u}\equiv (u_1, \ u_2, \ u_3)^{T}\), the geodesic equation (26) can be rewritten in vector notation,

$$\begin{aligned} \partial _t \vec {u}= \frac{N \left[ \vec {u}\times (O \bar{h}^{-1} O^T\vec {u})\right] }{\sqrt{1+\vec {u}^T O \bar{h}^{-1} O^T \vec {u}}} \ , \end{aligned}$$
(28)

where “\(\times \)” denotes the usual cross product in the three dimensional Euclidean space. Defining for convenience \(\vec {v}\equiv O^T \vec {u}/C\), we have \((v_1)^2+(v_2)^2+(v_3)^2 = 1\), and the geodesic equation simplifies to

$$\begin{aligned} \left( \partial _t+\varvec{\omega } \right) \vec {v} \ =\frac{ N C \left[ \vec {v}\times ({{\bar{h}}}^{-1}\vec {v} )\right] }{\sqrt{1+C^2 \vec {v}^T {{\bar{h}}}^{-1}\vec {v} }} . \end{aligned}$$
(29)

Note that we can also write \(\varvec{\omega }\vec {v}=\vec {v}\times \vec {\omega }\), where

$$\begin{aligned} \vec {\omega }\equiv \{ \omega ^i \}= \frac{N}{ e ^{3\alpha }} \left( \frac{l_1}{I_1},\ \frac{l_2}{I_2} ,\ \frac{l_3}{I_3} \right) ^T. \end{aligned}$$

It will thus be possible to eliminate \(\varvec{\omega }\) from the geodesic equation by using the diffeomorphism constraints.

We now add homogeneous dust to the system. The formalism developed in [29] leads to the following form of the Hamiltonian and diffeomorphism constraints for dust in a Bianchi IX universe,

$$\begin{aligned} \begin{aligned} \mathcal {H} + \mathcal {H}^{(m)}&= \frac{ e ^{-3\alpha }}{2}\left( -p_\alpha ^2 +p_+^2 +p_-^2 +\frac{l_1^2}{I_1}+\frac{l_2^2}{I_2}+\frac{l_3^2}{I_3} \right. \\&\quad \left. - \frac{ e ^{6\alpha }}{6} {}^{(3)}R + 2 e ^{3\alpha } p_T \sqrt{1+h^{ij}u_i u_j} \right) , \\ \mathcal {H}_i +\mathcal {H}^{(m)}_i&= O_i{}^j\left( l_j - C p_T v_j \right) , \end{aligned} \end{aligned}$$
(30)

where \(p_T\) denotes the momentum canonically conjugate to T, where T is the global ‘dust time’. Since the Hamiltonian does not explicitly depend on T, the momentum \(p_T\) is a constant of motion. The fact that \(l_1^2+l_2^2+l_3^2\) commutes with \(\mathcal {H}\) implies that \(l_1^2+l_2^2+l_3^2=(Cp_T)^2\) is a conserved quantity. This is consistent with (27). We note that a similar form of the constraints (30) was already presented in [20, 21]. The formalism is not entirely canonical and must be complemented by the geodesic Eq. (26).

For our numerical purposes, it will be convenient to rewrite the equations of motion in the variables \(\Gamma _i\) introduced in (6). We find that the choice of the variables \(\log \Gamma _i\) allow for a better control over the error in the Hamiltonian constraint. Moreover, we pick the quasi-Gaussian gauge \(N= e ^{3\alpha }=\sqrt{\Gamma _1 \Gamma _2 \Gamma _3}\), \(N^i=0\). Recall that the singularity is reached in a finite amount of comoving time (corresponding to the gauge \(N=1\)). The choice \(N= e ^{3\alpha }\) allows to resolve the oscillations in the approach towards the singularity. With these choices the Hamiltonian constraint becomes

$$\begin{aligned} \begin{aligned}&-(\log \Gamma _1)^{\cdot }(\log \Gamma _2)^{\cdot }-(\log \Gamma _2)^{\cdot }(\log \Gamma _3)^{\cdot } -(\log \Gamma _1)^{\cdot }(\log \Gamma _3)^{\cdot } \\&+\Gamma _1^2+\Gamma _2^2+\Gamma _3^2-2(\Gamma _1\Gamma _2+\Gamma _3\Gamma _1+\Gamma _2\Gamma _3) \\&+ 24 \left[ \frac{l_1^2}{I_1}+\frac{l_2^2}{I_2}+\frac{l_3^2}{I_3} \right. \\&\left. + 2 |p_T|\sqrt{\Gamma _1\Gamma _2\Gamma _3+ C^2 \left( \Gamma _2\Gamma _3 v_1^2+\Gamma _1\Gamma _3v_2^2+\Gamma _1\Gamma _2 v_3^2\right) } \right] \\&= 0, \end{aligned} \end{aligned}$$
(31)

where the moments of inertia are

$$\begin{aligned} I_1= & {} \frac{(\Gamma _3-\Gamma _2)^2}{12\Gamma _3\Gamma _2} , \quad I_2 = \frac{(\Gamma _1-\Gamma _3)^2}{12\Gamma _1\Gamma _3} , \nonumber \\ I_3= & {} \frac{(\Gamma _1-\Gamma _2)^2}{12\Gamma _1\Gamma _2} . \end{aligned}$$
(32)

The diffeomorphism constraints read \(l_i=p_T C v_i \) and can be used to eliminate the angular momentum variables from the equations of motion. These equations can then be written as

$$\begin{aligned} \begin{aligned}&(\log \Gamma _1)^{\cdot \cdot } = (\Gamma _2-\Gamma _3)^2-\Gamma _1^2 + 2p_T'^2C^2 \\&\quad \times \left[ \frac{\Gamma _1\Gamma _3(\Gamma _1+\Gamma _3)v_2^2}{(\Gamma _1-\Gamma _3)^3} +\frac{\Gamma _1\Gamma _2(\Gamma _1+\Gamma _2)v_3^2}{(\Gamma _1-\Gamma _2)^3} \right] \\&\quad + \frac{p_T'(\Gamma _1 \Gamma _2 \Gamma _3+2 C^2 v_1^2 \Gamma _2\Gamma _3)}{\sqrt{\Gamma _1\Gamma _2\Gamma _3+ C^2 \left( \Gamma _2\Gamma _3 v_1^2+\Gamma _1\Gamma _3v_2^2+\Gamma _1\Gamma _2 v_3^2\right) }}, \\&(\log \Gamma _2)^{\cdot \cdot }= (\Gamma _3-\Gamma _1)^2-\Gamma _2^2 \\&\quad +2p_T'^2C^2 \left[ \frac{\Gamma _1\Gamma _2(\Gamma _1+\Gamma _2)v_3^2}{(\Gamma _2-\Gamma _1)^3} +\frac{\Gamma _2\Gamma _3(\Gamma _2+\Gamma _3)v_1^2}{(\Gamma _2-\Gamma _3)^3} \right] \\&\quad + \frac{p_T'(\Gamma _1 \Gamma _2 \Gamma _3+2 C^2 v_2^2 \Gamma _1\Gamma _3)}{\sqrt{\Gamma _1\Gamma _2\Gamma _3+ C^2 \left( \Gamma _2\Gamma _3 v_1^2+\Gamma _1\Gamma _3v_2^2+\Gamma _1\Gamma _2 v_3^2\right) }}, \\&(\log \Gamma _3)^{\cdot \cdot } = (\Gamma _1-\Gamma _2)^2-\Gamma _3^2 \\&\quad + 2p_T'^2C^2\left[ \frac{\Gamma _1\Gamma _3(\Gamma _1+\Gamma _3)v_2^2}{(\Gamma _3-\Gamma _1)^3} +\frac{\Gamma _3\Gamma _2(\Gamma _3+\Gamma _2)v_1^2}{(\Gamma _3-\Gamma _2)^3} \right] \\&\quad + \frac{p_T'(\Gamma _1 \Gamma _2 \Gamma _3+2 C^2 v_3^2 \Gamma _1\Gamma _2)}{\sqrt{\Gamma _1\Gamma _2\Gamma _3+ C^2 \left( \Gamma _2\Gamma _3 v_1^2+\Gamma _1\Gamma _3v_2^2+\Gamma _1\Gamma _2 v_3^2\right) }}, \end{aligned}\nonumber \\ \end{aligned}$$
(33)

where we have set \(p_T'\equiv 12p_T\) for convenience. Note that these equations are exact. (In [13], the matter terms were neglected.) We use the diffeomorphism constraints to eliminate \(\vec {\omega }\) from the geodesic equation (29). If expressed in the gauge \(N= e ^{3\alpha }\) and using the \(\Gamma _i\), the geodesic Eq. (29) can be written as

$$\begin{aligned} \begin{aligned} \dot{\vec {v}}&= C\vec {v}\times \left( M\vec {v} \right) \quad \text {where} \\ M&=\frac{\text {diag}\left( \Gamma _2 \Gamma _3, \ \Gamma _1 \Gamma _3,\ \Gamma _1 \Gamma _2\right) }{\sqrt{\Gamma _1\Gamma _2\Gamma _3+ C^2 \left( \Gamma _2\Gamma _3 v_1^2+\Gamma _1\Gamma _3v_2^2+\Gamma _1\Gamma _2 v_3^2\right) }} \\&\quad + p_T' \text {diag}\left( \frac{\Gamma _2\Gamma _3}{\left[ \Gamma _2-\Gamma _3 \right] ^2} , \frac{\Gamma _1\Gamma _3}{\left[ \Gamma _3-\Gamma _1 \right] ^2}, \frac{\Gamma _1\Gamma _2}{\left[ \Gamma _1-\Gamma _2 \right] ^2}\right) . \end{aligned} \nonumber \\ \end{aligned}$$
(34)

Together with the constraint \(v_1^2+v_2^2+v_3^2=1\) this is all we need for numerical integration. Note that all dependence on the Euler angles and their momenta has dropped out from the equations of motion (33, 34). The numerical method we use is described in Appendix.

Fig. 1
figure 1

Potential picture for the tumbling case. The black contour lines represent the curvature potential while the dotted (blue) and dashed (red) lines represent the rotation and centrifugal walls, respectively

Full size image
Fig. 2
figure 2

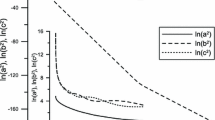
Numerical simulation of the tumbling case. In the region where \(0<t<5\times 10^5\) (arbitrary units) one can see a typical Kasner era. The solution bounces in the valley formed between the curvature and one of the centrifugal potential walls. Increasing t corresponds to evolution towards the singularity

Full size image

2.4 The tilted dust case

A qualitative picture for the dynamics of the universe can be obtained by considering the Hamiltonian (30) in the quasi-Gaussian gauge \(N= e ^{3\alpha }\), \(N_i=0\). The Hamiltonian can then be interpreted as the “relativistic energy” of a point particle (called the universe point) with “spacetime coordinates” \((\alpha ,\beta _+,\beta _-)\). The universe point is subject to the forces generated by the dynamical potential

$$\begin{aligned} \frac{l_1^2}{I_1}+\frac{l_2^2}{I_2}+\frac{l_3^2}{I_3} - \frac{ e ^{6\alpha }}{6} {}^{(3)}R + 2 e ^{3\alpha } p_T \sqrt{1+h^{ij}u_i u_j} \ , \end{aligned}$$
(35)

which is depicted in Fig. 1. The contour lines of the curvature potential \(-\frac{ e ^{6\alpha }}{12} {}^{(3)}R\) are represented by solid black lines. The curvature potential is exponentially steep and takes its minimum at the origin \(\beta _\pm =0\). When the universe evolves towards the singularity (\(\alpha \rightarrow -\infty \)), the curvature potential walls move away from the origin while becoming effectively hard walls in the vicinity of the singularity. The term \( e ^{3\alpha } p_T \sqrt{1+h^{ij}u_i u_j} \) can be interpreted as three rotational potential walls. These potentials are rather unimportant in the examination of the asymptotic dynamics, since they move away from the origin with unit speed. The term \(\frac{l_1^2}{I_1}+\frac{l_2^2}{I_2}+\frac{l_3^2}{I_3}\) can be interpreted as three singular centrifugal potential walls. They are represented by the dashed red lines. Asymptotically close to the singularity, these walls are expected to become static. In general, however, the centrifugal potential walls are dynamical and change in a complicated manner dictated by the geodesic Eq. (34). The centrifugal walls will prevent the universe point from penetrating certain regions of the configuration space. Misner [19] and Ryan [20, 21] employed these facts to obtain approximate solutions in a diagrammatic form. The other Bianchi models can be treated in a similar way [22].

2.4.1 Special classes of solutions

Before doing the numerics, we comment on particular classes of solutions: one class of solutions is obtained if we choose, for example, the initial conditions \(v_1=0=v_2\) and \(v_3 = 1\). The geodesic Eq. (34) implies now that the velocities stay constant in time. This implies that at all times \(l_1= 0= l_2\) and \(l_3 = p_\psi = p_T C\). This class of solutions is known as the non-tumbling case. Furthermore, there are classes of solutions which are rotating versions of the Taub solution. These solutions should be divided into two subclasses: one class that oscillates between the centrifugal walls and the curvature potential and one class that runs through the valley straight into the singularity. We set

$$\begin{aligned} v_1=v_2=\frac{1}{2},\quad v_3=0 \quad \text {and} \quad \beta _- = 0 . \end{aligned}$$
(36)

For the \(\Gamma _i\) variables it means that \(\Gamma _1= e ^{2\alpha } e ^{2\beta _+}=\Gamma _2\) and \(\Gamma _3= e ^{2\alpha } e ^{-4\beta _+}\). With this choice we obtain \(I_3=0\) and \(3I_1=3I_2=\sinh ^2\left( 3\beta _+ \right) \). Most importantly, the geodesic Eq. (34) is trivially satisfied, that is, \(v_1=v_2= 1/2\) and \(v_3=0\) for all times. When setting \(C=0\) we obtain the diagonal case which contains the isotropic case of a closed Friedmann universe. The simulation plotted in Fig. 2 was performed for the tumbling case, that is, the \(v_i\) are chosen to be non-zero.

2.4.2 The asymptotic regime close to the singularity

In order to simplify the dynamics of the general case, BKL made two assumptions based on qualitative considerations of the equations of motion. The first assumption states that anisotropy of space grows without bound. This means that the solution enters the regime

$$\begin{aligned} \Gamma _1\gg \Gamma _2\gg \Gamma _3 . \end{aligned}$$
(37)

The ordering of indices is irrelevant. In fact, there are six possible orderings of indices which each correspond to the universe point being constrained to one of the six regions bounded by the rotation and centrifugal walls sketched in Fig. 1. The region \(\Gamma _1> \Gamma _2> \Gamma _3\) corresponds to the right region above the line \(\beta _-=0\) in Fig. 1. More precisely, the inequality (37) means that

$$\begin{aligned} \Gamma _2 / \Gamma _1 \rightarrow 0 \quad \text {and}\quad \Gamma _3 / \Gamma _2 \rightarrow 0. \end{aligned}$$
(38)

Our numerical simulations support the validity of this assumption (see the plot of the ratios \(\Gamma _2 / \Gamma _1\) and \(\Gamma _3 / \Gamma _2\) in Fig. 3). We provide plots of the two ratios \(\Gamma _2/\Gamma _1\), \(\Gamma _3/\Gamma _2\) and the velocities \(\vec {v}\) in order to provide a sanity check of the approximation we will perform later on.

Fig. 3
figure 3

Plots of the ratios \(\Gamma _2/\Gamma _1\), \(\Gamma _3/\Gamma _2\) and the velocity \(\vec {v}\). The plots correspond to the numerical solution presented in Fig. 2. The peaks in the ratios appear during bounces of the universe point with the centrifugal walls. As we can see, the height of these peaks decreases in the evolution towards the singularity

Full size image

The second assumption made by BKL states that the Euler angles assume constant values:

$$\begin{aligned} (\theta ,\phi ,\psi )\rightarrow (\theta _0,\phi _0,\psi _0), \end{aligned}$$
(39)

that is, the rotation of the principal axes stops for all practical purposes and the metric becomes effectively diagonal. The analysis of BKL [31] supports the consistency of making both assumptions at the same time. Similar heuristic considerations can possibly be applied to other Bianchi models as well [22]. In the dust model under consideration, this assumption is equivalent to the statement that the dust velocities \(\vec {v}\) assume constant values \(\vec {v}\rightarrow \vec {v}^{(0)}\). Our numerical results indicate that this is in fact true (see Fig. 3). BKL then arrive at the simplified effective set of equations.

Let us now carry out the approximation and apply it to our equations of motion. The kinetic term stays untouched during the approximation. The first step in the approximation is to ignore the rotational potential. In view of the strong inequality (37), we approximate the curvature potential via

$$\begin{aligned} \Gamma _1^2+\Gamma _2^2+\Gamma _3^2-2(\Gamma _1\Gamma _2+\Gamma _3\Gamma _1+\Gamma _2\Gamma _3) \approx \Gamma _1^2 \ . \end{aligned}$$
(40)

Furthermore, we approximate the centrifugal potential by

$$\begin{aligned} \frac{l_1^2}{I_1}+\frac{l_2^2}{I_2}+\frac{l_3^2}{I_3} \approx 12C^2 p_T^2 \left[ \frac{\Gamma _3}{\Gamma _2}\left( v^{(0)}_1 \right) ^2+\frac{\Gamma _2}{\Gamma _1}\left( v^{(0)}_3 \right) ^2\right] .\nonumber \\ \end{aligned}$$
(41)

Note that one centrifugal wall was ignored completely. Having Fig. 1 in mind, this approximation is well motivated since only two of the centrifugal walls are expected to have a significant influence on the dynamics of the universe point. After defining the new variables

$$\begin{aligned} a\equiv & {} \Gamma _1, \quad b\equiv 2p_T'^2C^2\left( v^{(0)}_3\right) ^2\Gamma _2 , \nonumber \\ c\equiv & {} 4p_T'^4C^4\left( v^{(0)}_1v^{(0)}_3\right) ^2\Gamma _3, \end{aligned}$$
(42)

we arrive at a simplified Hamiltonian constraint and equations of motion,

$$\begin{aligned} \begin{aligned}&(\log a)^{\cdot }(\log b)^{\cdot } + (\log a)^{\cdot } (\log c)^{\cdot } + (\log b)^{\cdot } (\log c)^{\cdot } \\&\quad = a^2 + b/a +c/b , \\&(\log a)^{\cdot \cdot } = b /a - a^2 , \quad (\log b)^{\cdot \cdot } \\&\quad = a^2 - b/a + c/b , \quad (\log c)^{\cdot \cdot } = a^2 - c/b , \end{aligned} \end{aligned}$$
(43)

which coincides with the asymptotic form of equations obtained in [31]. Equation (43) can now be treated by the numerical methods which we have used in the previous sections. One must ensure that initial conditions are chosen such that the simulation starts close to the asymptotic regime (37).

3 Conclusions

The numerical simulations indicate that the non-diagonal Bianchi IX solutions, with tilted dust, evolve into the regime where \(\Gamma _1 \gg \Gamma _2 \gg \Gamma _3\) and \(v_i\approx \)const. The results motivate us to formulate the conjecture:

Given a tumbling solution to the general Bianchi IX model filled with pressureless tilted matter, there exists \(t_0\in \mathbb {R}\) such that the solution is well approximated by a solution to the asymptotic equations of motion for all times \(t>t_0\) describing the vicinity of the singularity.

Fig. 4
figure 4

The difference between the exact and the asymptotic solutions: a evolution towards the singularity, b evolution away from the singularity

Full size image

To make the notion of “approximation” mathematically more precise, a suitable measure of the “distance” on the set of solutions is needed. For this purpose, we propose to use the following simple measure:

$$\begin{aligned} \Delta (t)\equiv \sqrt{\left( \log \Gamma _1 (t) - \log \bar{a} (t) \right) ^2 +\left( \log \Gamma _2 (t) - \log \bar{b} (t)\right) ^2 +\left( \log \Gamma _3 (t) - \log \bar{c} (t) \right) ^2} , \end{aligned}$$
(44)

where \(\{\Gamma _1,\Gamma _2,\Gamma _3\} \) denotes the numerical solution to the exact equations of motion (33)–(34), and

$$\begin{aligned} a= & {} \bar{a}, \quad b=2p_T'^2C^2\left( v^{(0)}_3\right) ^2\bar{b}, \nonumber \\ c= & {} 4p_T'^4C^4\left( v^{(0)}_1 v^{(0)}_3\right) ^2\bar{c} \end{aligned}$$
(45)

denote the numerical solution to the asymptotic equations of motion (43).

We have evolved the exact system of equations from \(t=0\) forward in time until \(t=3 \times 10^6\). There we used the same initial conditions as the ones we used to obtain the solution shown in Fig. 2. We then took the final state at \(t=3 \times 10^6\) as an initial condition for the asymptotic system of equations and evolved it backwards in time towards the re-bounce until \(t=-980\).

Figure 4 presents the measure (44) as a function of time. We can see fast decrease of \(\Delta \) with increasing time (evolution towards the singularity) and fast increase of \(\Delta \) with decreasing time (evolution away from the singularity).

Our numerical simulations give strong support to the conjecture concerning the asymptotic dynamics of the general Bianchi IX spacetime put forward long ago by Belinski et al. [31]. We remark that approximating the diagonal or non-tumbling case by the asymptotic dynamics (43) is invalid (see [32] for more details).

It is sometimes stated that “matter does not matter” in the asymptotic regime, but this does not mean that one is allowed to use the dynamics of the purely diagonal case. One only encounters an effectively diagonal case, which is expressed in terms of the directional scale factors \(\{a,b,c\}\). So there exist serious differences between the purely diagonal and effectively diagonal cases (see [32] for more details).

Employing the asymptotic form of the equations of motion may enable one to study the chaotic behaviour and other properties of the solution space for the general model. This is also important for quantizing the general Bianchi IX model, where the quantization of the exact dynamics seems to be quite difficult, whereas the quantization of the asymptotic case seems to be feasible [25].