Abstract
In this paper, we study the complexity factor for a charged anisotropic self-gravitating object. We formulate the Einstein–Maxwell field equations, Tolman–Opphenheimer–Volkoff equation, and the mass function. We form the structure scalars by the orthogonal splitting of the Riemann tensor and then find the complexity factor with the help of these scalars. Finally, we investigate some astrophysical objects for the vanishing of complexity condition. It is found that the presence of the electromagnetic field decreases the complexity of the system.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The word complexity refers to a factor that includes all the terms inducing complications in a system. Many attempts have been dedicated towards a precise definition of complexity in various sectors of science [1,2,3,4,5,6,7,8,9,10,11]. However, an exact definition of complexity has not been obtained till now which defines it in every field accumulatively. It may be noted that the definition of complexity depends on the work established by Lopez-Ruiz et al. [7,8,9]. In view of different proposed definitions of complexity, it is related to the idea of information and entropy that describe the structure of the system.
In physics [7], the term complexity begins by examining the perfect crystal which has a periodic behavior and the isolated ideal gas with a random behavior. A perfect crystal is a completely ordered system of atoms that are arranged in a symmetric manner. A small segment of information is sufficient to define the perfect crystal which gives minimum information in the crystal. On the other hand, the isolated gas is totally disordered and all the segments have equal participation to give information related to the ideal gas such that it has a maximum information. These systems are examples of elementary models with zero complexity.
The definition of complexity should also include some other factors beyond information or order. Lopez-Ruiz et al. [7] proposed the abstract idea of disequilibrium which determines distance of the probable distribution in the system of accessible state. Thus disequilibrium should be maximum in case of perfect crystal and it should be zero for the ideal gas. Consequently, disequilibrium and information are introduced to describe the complexity by a quantity that is a result of these two notions.
The definition of disequilibrium and information which include probability distribution is redefined in [12,13,14,15,16,17] by the term energy density in the fluid distribution. However, the term energy density is not enough to describe the phenomenon of complexity because the pressure is absent which appears in the energy-momentum tensor and plays a vital role in the structure formation of the fluid distribution.
In literature [12,13,14,15,16,17], the idea of complexity has also been applied to the self-gravitating systems like neutron stars and white dwarfs. Recently, Herrera [18] introduced a quite different definition of complexity for a self-gravitating system. This definition is related to the notion of structure of the spherical system but is not related to disequilibrium or information. He used the notion of Tolman mass which may be considered the active gravitational mass for the fluid distribution. This mass depends on the inhomogeneity of the energy density along with anisotropy of the pressure. These two terms represent a single scalar function which is a complexity factor. This vanishes when the pressure is isotropic and energy density is homogenous and may also vanish when the two notions namely, inhomogeneous energy density and anisotropic pressure cancel each other. The variable which is responsible for a complexity factor appears in the structure scalars obtained from the orthogonal splitting of the Riemann tensor.
In literature, the study of charge in spherically symmetric self-gravitating system started with the pioneer work of Rosseland and Eddington [19]. Bonnor [20] examined the impact of charge on spherical collapse of dust cloud and concluded that the process of collapse slows down due to electric repulsion. Ray et al. [21] investigated the role of charge on compact stars and found that \(10^{20}\) Coulomb charge is present in the astrophysical objects producing an electric field of \(10^{21}~\mathrm{V/m}\). Sharif and Bhatti [22] studied the effect of charge on the instability of isotropic cylinder and deduced that the charge with other matter variables control the stable as well as unstable configuration. The same authors [23] investigated instability of charged spherical system with the viscous dissipative matter distribution and found the instability range from adiabatic index. Sharif and Sadiq [24] analyzed the effect of electromagnetic field on the stability of stellar object and concluded that it is stable for specific choice of polytropic index. The same authors [25] obtained exact solutions for anisotropic spherical system in the presence of electromagnetic field and found that stability increases with the effect of charge. Takisa and Maharaj [26] studied the charged anisotropic stellar solutions obeying polytropic equation of state and found that the behavior of energy density and pressure are consistent with the literature.
This paper studies the effects of charge on the definition of complexity proposed by Herrera [18]. The paper has the following format. In the next section, we formulate basic equations defining the structure of a stellar configuration. Section 3 gives brief review of the orthogonal splitting of the Riemann tensor as well as structure scalars. In Sect. 4, we introduce the complexity factor and obtain solutions of the Einstein–Maxwell field equations for vanishing complexity factor. Finally, we summarize our results in the last section.
2 Basic equations
Here we discuss physical variables as well as the equations necessary to define static charged stellar structure consisting of anisotropic fluid. We consider static spherically symmetric geometry in the interior of stellar structure defined by the line element
bounded by the hypersurface \(\Sigma \). We consider the energy-momentum tensor for anisotropic fluid distribution as
where \(\mu \) is the energy density and
The four velocity and four-vector are defined by
with the properties
The electromagnetic field tensor is given by
where \(F_{\beta \alpha }\) is the Maxwell field tensor described by \(F_{\beta \alpha } = \phi _{\alpha ,\beta }-\phi _{\beta ,\alpha }\) and \(\phi _{\alpha }\) is the four potential determined by \(\phi _{\beta } = \phi \delta ^{0}_{\beta }\).
The Maxwell field equations in four-vector formalism are given by
where \(\mu _{0}\) is the magnetic permeability and \(J^{\beta }\) is the four current defined by \(J_{\beta } = \xi u_{\beta }\), where \(\xi \) is the charge density. For the metric (1), the Maxwell field equations yield
Integration of the above equation gives
where
represents the total charge within the sphere. The Einstein–Maxwell field equations are
leading to
where prime represents derivative with respect to r. The conservation law gives the hydrostatic equilibrium equation
This is also called the generalized Tolman–Opphenheimer–Volkoff (TOV) equation for anisotropic charged fluid distribution. We consider the Reissner–Nordström metric for the exterior geometry defined by
where M and Q denote the total mass and total charge in the exterior region, respectively. The smooth matching of exterior and interior spacetimes yields
These equations are the necessary and sufficient conditions for matching of the two metrics (1) and (12) on hypersurface \(\Sigma \).
Now, we evaluate the mass function using two definition namely, Misner-Sharp mass and Tolman mass. The Misner-Sharp formula of mass function [27] yields
Differentiation and then integration of Eq. (14) and using Eq. (8), it follows that
Using the field equations and Eq. (14), we obtain
We simplify this expression using the Weyl tensor. The Weyl tensor consists of two parts one is the magnetic part which vanishes for spherical system while the other is the electric part defined as
where
with \(g_{\beta \alpha \mu \nu }=g_{\beta \mu }g_{\alpha \nu }-g_{\beta \nu }g_{\alpha \mu }\) and \(\eta _{\beta \alpha \mu \nu }\) represents the Levi-Civita tensor. \(E_{\alpha \beta }\) is defined as
with
Using Eq. (20) in (16), we have
Comparing Eqs. (15) and (21), it follows that
Substituting the above equation in (21), we obtain
Equation (22) expresses \(\mathcal {E}\) in terms of physical quantities namely, inhomogeneous density, anisotropic pressure as well as total charge and Eq. (23) represents the corresponding expression of mass function. Using Eq. (14) in (9), it follows that
Inserting Eq. (24) in (11), we obtain the following form of TOV equation
Tolman [28] proposed another definition of energy for static spherical system defined by
The total energy of the fluid within the sphere of radius r is
Using Eqs. (8)–(10) in (27), it follows that [29, 30]
Putting the value of \(\alpha '\) from Eq. (24) into (28), the Tolman mass becomes
Equation (28) can also be interpreted as active gravitational mass of the system. Another expression for \(m_{T}\) [29, 30] is
Using Eq. (22), this equation turns out to be
This represents the contribution of density inhomogeneity, charge and anisotropy of pressure in the Tolman mass.
3 Structure scalars
In this section, we use orthogonal splitting of the Riemann tensor introduced by Bel [31] and obtain scalar structures which help us to find the complexity factor. For the orthogonal splitting of the Riemann tensor, the following tensors are introduced [31,32,33]
where \(R^{*}_{\mu \nu \gamma \delta }=\frac{1}{2}\eta _{\epsilon \beta \gamma \delta }R^{\epsilon \beta }_{\mu \nu }\). These tensors can be expressed in the trace-free and trace parts as
Using the Einstein–Maxwell filed equations, we obtain these scalars as [33]
Also, using Eq. (22), we have
The expressions for \(Y_{T}\) and \(Y_{TF}\) are
Substitution of Eq. (22) in (40) yields
The scalars \(X_{TF}\) and \(Y_{TF}\) describe anisotropy of the pressure in the presence of charge as
Replacing Eq. (40) in (30), we obtain
Comparing Eq. (43) with (30), it follows that
This shows that \(Y_{ TF}\) is associated with the effect of the anisotropic pressure, inhomogeneity of the energy density and total charge of the fluid distribution, i.e., \(Y_{TF}\) describes the effect of these two quantities in the Tolman mass defined in Eq. (43). Also, the Tolman mass given in Eq. (26) can be written in terms of structure scalar as
4 The complexity factor
There are many factors producing complexity in a system for example, density inhomogeneity, pressure anisotropy, electromagnetic field, heat dissipation and viscosity. In general, any system having homogenous energy density as well as isotropic pressure and in the absence of the above mentioned factors is considered as the simplest system with negligible complexity. For our fluid, the causes of complexity are inhomogeneous energy density, anisotropic pressure and electromagnetic field. The structure scalar \(Y_{TF}\) defined in Eq. (41) contains these terms (inhomogeneous energy density, anisotropic pressure and charge) which are responsible for producing the complexity in the system. For this reason, the term complexity factor can be associated with the structure scalar \(Y_{TF}\).
Furthermore, the structure scalar \(Y_{TF}\) appears in the Tolman mass implying that these terms affect Tolman mass. Now, we discuss the vanishing complexity condition. The set of field equations leads to a system of three ordinary differential equations in which there are five unknown functions \(\alpha ,\gamma ,\mu ,P_{r},P_{\bot }\). Using the condition \(Y_{TF}=0\), we are left with four unknowns and need one more condition to have a unique solution. For this purpose, we take Eq. (41) and use \(Y_{TF}=0\). The vanishing complexity condition gives
In the following, we discuss some examples.
4.1 The Gokhroo and Mehra Ansatz
Gokhroo and Mehra [34] discussed the internal structure of the spherical configuration with the variable energy density for anisotropic spheres. Physically, these solutions have been used to discuss the behavior of compact objects. Here, we use the assumption proposed by Gokhroo and Mehra to discuss the behavior of stellar structures for vanishing complexity condition. The proposed energy density is
where \(K=(0,1)\). Using this value in Eq. (15), we have
Inserting this value in Eq. (14), we obtain
where \(\hat{\alpha }=8\pi \mu _{0}/3\). From Eqs. (9) and (10), it follows that
Introducing the new variables [18]
Using these variables, we obtain the following form of Eq. (49)
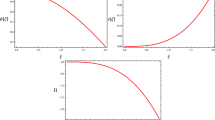
Its solution leads to the line element in terms of z and \(\Pi \) [35] as
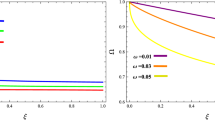
where C is an integration constant. Using the value of q(r) and Eq. (46), the vanishing complexity condition (45) becomes
The physical variables in the presence of charge yield
Equations (54)–(56) indicate the presence of charge in radial pressure, energy density and tangential pressure, respectively.
4.2 Polytropic equations with vanishing complexity factor
For self-gravitating system, the polytropic equation plays a vital role. Polytropes with anisotropic matter distribution have widely been discussed in literature [36,37,38]. Here, we discuss two different cases related to the polytropes. One of them is
where \(\mathcal {K}\) is called polytropic constant, \(\sigma \) is called polytropic exponent and n is called polytropic index. We take TOV Eq. (11) and convert it into the dimensionless form. For this purpose, we use dimensionless variables
where subscript c shows that the quantity is calculated at the center. At the boundary \(r=r_{\Sigma }\) (\(\zeta =\zeta _{\Sigma }\)), we have \(\Psi (\zeta _{\Sigma })=0\) [36]. Putting the values from Eqs. (24) and (57)–(59) in (11), we obtain
We also convert Eq. (15) in dimensionless variables as
Equations (60) and (61) are two ordinary differential equations with three unknown functions \(\Pi ,v,\Psi \). We still need one more condition to have a unique solution. For this purpose, we use the vanishing complexity condition (45) in dimensionless form given by
Now, we have three differential Eqs. (60)–(62) with three unknown functions \(\Pi ,v,\Psi \). For any of value of n and \(\beta \), this system can be integrated analytically or we can have a numerical solution using appropriate initial conditions. These equations physically describe the structure of stellar objects with the vanishing complexity condition. Any solution of this system gives the pressure, density, mass and radius of a specific stellar object for the chosen values of free parameters. We discuss another case of polytropes with the equation of state \(P_{r}=\mathcal {K}\mu ^{\sigma }_{d}=\mathcal {K}\mu ^{1+\frac{1}{n}}_{d},\) where \(\mu _{d}\) represents the baryonic mass density. Following the above procedure, we obtain
with
However, Eq. (61) remains the same for this equation of state. Again, we have a system of differential Eqs. [(61), (63), (64)] defining the structure of stellar configuration with specific equation of state and zero complexity factor.
5 Conclusions
In astrophysics, the study of stellar objects is an interesting phenomenon due to their physical features which motivate the researchers to explore these objects. Different aspects including mass-radius ratio, luminosity, anisotropy and stability or instability of stellar configurations have widely been studied in literature. However, the term complexity factor is not studied in detail for stellar objects. In this paper, we have studied the complexity factor for charged spherically symmetric stellar objects and the behavior of these objects in the context of vanishing complexity condition. This provides the effects of electromagnetic field on Herrera’s work [18]. We have formulated the Einstein–Maxwell field equations and found the mass function using Misner-Sharp as well as Tolman formalism. We have discussed structure scalars in the presence of electromagnetic field and obtained the complexity factor. The complexity factor \(Y_{TF}\) (41) contains the terms associated with energy density inhomogeneity, charge and anisotropic pressure. This equation indicates that the inclusion of charge decreases the complexity of the system.
Moreover, using the assumption \(Y_{TF}=0\) we have investigated the vanishing complexity condition [defined in Eq. (45)] for two examples of self-gravitating systems studied in the literature. Firstly, the stellar objects discussed by Gokhroo and Mehra [34] are considered in which a specific form of the energy density of the stellar system is assumed. We have observed that in our case the effect of charge appears in Eqs. (54)–(56) that describe the behavior of the system. Secondly, we have considered stellar systems obeying the polytropic equation of state and obtained a system of differential equations including the mass equation, TOV equation and vanishing complexity condition in terms of dimensionless variables. The solution of these equations for some physical conditions provide a better understanding of the charged stellar system with zero complexity factor. It is worthwhile to mention here that all our results reduce to uncharged case (\(q=0\)) [18].
References
A.N. Kolmogorov, Prob. Inform. Theory J. 1, 3 (1965)
P. Grassberger, Int. J. Theor. Phys. 25, 907 (1986)
S. Lloyd, H. Pagels, Ann. Phys. 188, 186 (1988)
J.P. Crutchfield, K. Young, Phys. Rev. Lett. 63, 105 (1989)
P.W. Anderson, Phys. Today 7, 54–61 (1991)
G. Parisi, Phys. World 6, 42 (1993)
R. Lopez-Ruiz, H.L. Mancini, X. Calbet, Phys. Lett. A 209, 321 (1995)
X. Calbet, R. Lopez-Ruiz, Phys. Rev. E 63, 066116 (2001)
R.G. Catalan, J. Garay, R. Lopez-Ruiz, Phys. Rev. E 66, 011102 (2002)
J. Sanudo, R. Lopez-Ruiz, Phys. Lett. A 372, 5283 (2008)
C.P. Panos, N.S. Nikolaidis, KCh. Chatzisavvasand, C.C. Tsouros, Phys. Lett. A 373, 2343 (2009)
J. Sanudo, A.F. Pacheco, Phys. Lett. A 373, 807 (2009)
KCh. Chatzisavvas, V.P. Psonis, C.P. Panos, ChC Moustakidis, Phys. Lett. A 373, 3901 (2009)
M.G.B. de Avellar, J.E. Horvath, Phys. Lett. A 376, 1085 (2012)
R.A. de Souza, M.G.B. de Avellar, J.E. Horvath, arXiv:1308.3519
M.G.B. de Avellar, J.E. Horvath, arXiv:1308.1033
M.G.B. de Avellar, R.A. de Souza, J.E. Horvath, D.M. Paret, Phys. Lett. A 378, 3481 (2014)
L. Herrera, Phys. Rev. D 97, 044010 (2018)
S. Rosseland, A.S. Eddington, Mon. Not. R. Astron. Soc. 84, 720 (1924)
W.B. Bonnor, Mon. Not. R. Astron. Soc. 129, 443 (1994)
S. Ray, M. Malheiro, J.P.S. Lemos, V.T. Zanchin, Braz. J. Phys. 34, 310 (2004)
M. Sharif, M.Z. Bhatti, Phys. Lett. A 378, 469 (2014)
M. Sharif, M.Z. Bhatti, Int. J. Mod. Phys. D 23, 1450085 (2014)
M. Sharif, S. Sadiq, Eur. Phys. J. C 76, 568 (2016)
M. Sharif, S. Sadiq, Eur. Phys. J. C 78, 410 (2018)
P.M. Takisa, S.D. Maharaj, Gen. Relativ. Gravit. 45, 1951 (2013)
C.W. Misner, D.H. Sharp, Phys. Rev. 136, B571 (1964)
R. Tolman, Phys. Rev. 35, 875 (1930)
L. Herrera, N.O. Santos, Phys. Rep. 286, 53 (1997)
L. Herrera, A. Di Prisco, J. Hernandez-Pastora, N.O. Santos, Phys. Lett. A 237, 113 (1998)
L. Bel, Ann. Inst. H Poincare 17, 37 (1961)
L. Herrera, J. Ospino, A. Di Prisco, E. Fuenmayor, O. Troconis, Phys. Rev. D 79, 064025 (2009)
L. Herrera, A. Di Prisco, J. Ibanez, Phys. Rev. D 84, 107501 (2011)
M.K. Gokhroo, A.L. Mehra, Gen. Relativ. Gravit. 26, 75 (1994)
L. Herrera, J. Ospino, A. Di Prisco, Phys. Rev. D 77, 027502 (2008)
L. Herrera, E. Fuemayor, P. Leon, Phys. Rev. D 93, 024047 (2016)
L. Herrera, W. Barreto, Phys. Rev. D 87, 087303 (2013)
L. Herrera, W. Barreto, Phys. Rev. D 88, 084022 (2013)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Sharif, M., Butt, I.I. Complexity factor for charged spherical system. Eur. Phys. J. C 78, 688 (2018). https://doi.org/10.1140/epjc/s10052-018-6121-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6121-5