New gauge boson $W^\prime$ and radiative leptonic decays of charged B and D mesons

Abstract

Considering the constraints on model parameters from the latest experimental data, we study the contributions of new gauge boson $W^\prime$ predicted by the general 221 models to the radiative leptonic decays of charged B and D mesons. It is found that the largest contributions of $W^\prime$ in the non-universal 221 model to the branching fractions occur in the decay modes $B^{-} \rightarrow \gamma \mu ^{-} \bar{\nu }_\mu$ and $B^{-} \rightarrow \gamma \tau ^{-} \bar{\nu }_\tau$, which can reach to about $8 \%$ of the corresponding SM values in the up-quark mixing scenario. In contrast, the relative corrections of $W^\prime$ predicted by the un-unified 221 model to the branching fractions are very tiny and identical for all the decay modes.

1 Introduction

In spite of the tremendous success of the standard model (SM), there are still open questions which imply the existence of new physics beyond it. One of the most common ways of building new physics models is to extend the gauge structure of the SM. An additional $U(1)_X$ gauge symmetry is introduced in the simplest extension. One of the next simplest extensions involves an additional SU(2) such as the left–right [1,2,3], leptophobic, hadrophobic, fermiophobic [4,5,6], non-universal [7,8,9,10,11] and un-unified models [12, 13], which are called the general 221 models in the literature [14]. The most important feature of these models is the existence of new heavy gauge bosons $W^\prime$ and $Z^\prime$ which are relevant to the low energy charged and neutral current processes, respectively. These new gauge bosons can have rich phenomenology in the current and future collider experiments.

The study of heavy meson decays is one of the most interesting and challenging fields in high energy physics, which involves both strong and weak interactions. In recent years, both experimental and theoretical studies have been improved greatly. However, the limitation in understanding and controlling the strong interactions in non-perturbative region is so far still a problem. Compared with hadronic decays, the leptonic decays are simpler due to the fact that strong interaction only occurs in the initial state. The pure leptonic decays of heavy mesons $H \rightarrow l \nu _l$ ($H=B, B_s, D, D_s$ and $l=e, \mu , \tau$) can be used to determine the decay constants $f_H$ if the CKM matrix elements $|V_{Qq}|$ ($Q=b, c$ and $q=u, d, s$) are known. Conversely, if we know the values of decay constants from other methods, e.g. the lattice calculation, these decays can also be used to extract the CKM matrix elements. In order to cancel the infrared divergences appearing in the loop calculations, the corresponding radiative leptonic decays $H \rightarrow \gamma l \nu _l$ should be considered. More importantly, the radiative leptonic decays are of interest in themselves, which may be separated properly and compared with measurements directly as long as the theoretical softness of the photon corresponds to the experimental resolutions. As well known, the measurement of pure leptonic decays is very difficult because of the helicity suppression and only one detected final state particle. However, having an extra real photon emitted in the final state, the radiative leptonic decays escape from the helicity suppression and therefore can be as large as, or even larger than the pure leptonic mode. Furthermore, with the extra photon to identify, the reconstruction of these decays is easier to do. For these reasons, the radiative leptonic decays have so far received a great deal of attention and been studied with various methods in the literature including the constituent quark model [15,16,17,18,19,20,21,22], light front quark model [23, 24], QCD factorization [25,26,27,28,29,30], pQCD [31], light cone sum rules [32, 33], dispersion approach [34,35,36,37] and so on, as a means of probing aspects of the strong and weak interactions in a heavy meson system. Concretely, the radiative leptonic decays have been used as an alternative and more viable way for the determination of $f_H$ and $|V_{Qq}|$. In addition, the branching fractions of these decays are sensitive to the inverse moment $\lambda _H$ of the leading twist light cone distribution amplitude of heavy mesons which also enters the QCD factorization formulae for hadronic decays. A measurement of $Br(H \rightarrow \gamma l \nu _l)$ thus provides a determination of $\lambda _H$ free of hadronic final state uncertainties. Moreover, the radiative leptonic decays play a peculiar role in understanding the dynamics of annihilation processes occurring in heavy meson decays which are relevant for many important quantities. Apart from the above, these decays also provide a good opportunity to study the factorization approach, where many ingredients required for the hadronic decays already appear but in a simplified setting.

Besides those aspects in the SM, these decays provide a way of probing possible new physics effects related to the charged current interactions. In Ref. [38], the effects of charged Higgs bosons in the two Higgs doublet model type II (2HDMII) on the radiative leptonic decays of charged B and D mesons were studied based on the factorization procedure. Using the constraints on the free parameters of the 2HDMII given in previous works, it was found that the corrections of charged Higgs boson to the decay $B \rightarrow \gamma \tau \nu _\tau$ could be as large as $13\%$. To our knowledge, there is little information available in the literature about the contributions of new charged gauge boson $W^\prime$ to the radiative leptonic decays of heavy mesons. In the present paper, we intend to study the corrections of $W^\prime$ predicted by the general 221 models to the radiative leptonic decays of charged B and D mesons. The extensions to the contributions of $W^\prime$ in other models to these decays are straightforward with simply changing the mass and relevant couplings. The remaining part of this paper is organized as follows. In Sect. 2, we describe the general 221 models briefly and give the corresponding couplings related to these decays. In Sect. 3, we give the formulae for the decay rates including the contributions of $W^\prime$ and define the relative corrections to the branching fractions. The numerical results and discussions are given in Sect. 4. Section 5 is our summary.

2 General 221 models and couplings relevant for the radiative leptonic decays of charged B and D mesons

As mentioned above, the general 221 models are extensions of the SM by introducing an additional SU(2) gauge symmetry. Here we only briefly revisit the basics and some aspects of particular importance to the present work and refer the reader to the original papers for a more thorough description [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. The most important feature of these models is the existence of new heavy gauge bosons $W^\prime$ and $Z^\prime$ which are relevant to the low energy charged and neutral current processes, respectively. According to the patterns of gauge symmetry breaking, the 221 models can be divided into two classes. The first stage gauge symmetry breaking in the models of class I and II are $SU(2)_2 \times U(1)_X \rightarrow U(1)_Y$ and $SU(2)_1 \times SU(2)_2 \rightarrow SU(2)_L$, respectively. The charge assignments of the SM fermions and the Higgs representation used to achieve the gauge symmetry breaking can be found in Ref. [14].

Table 1 The charged current $K^{+}_\mu$ for the LR, LP, HP, FP, NU and UU models. For the NU and UU models, the mixing angle of the extended gauge group $\theta _E$ is defined as $\tan \theta _E = g_1/g_2$

After gauge symmetry breaking, the Lagrangian involving the gauge boson masses and fermionic gauge interactions can be written as [14]

$$\begin{aligned} \mathcal{L} = \mathcal{L}_1 + \mathcal{L}_2 + \mathcal{L}_3 +\mathcal{L}_4 \end{aligned}$$

(1)

with

$$\begin{aligned} \mathcal{L}_1= & {} \frac{1}{2} \left( \tilde{M}^2_Z - \frac{\delta \tilde{M}^4_Z}{\tilde{M}^2_{Z^\prime } }\right) Z_\mu Z^\mu \nonumber \\&+\left( \tilde{M}^2_W - \frac{\delta \tilde{M}^4_W}{\tilde{M}^2_{W^\prime } }\right) W^{+\mu } W^{-}_\mu , \end{aligned}$$

(2)

$$\begin{aligned} \mathcal{L}_2= & {} \frac{1}{2} \left( \tilde{M}^2_{Z^\prime } + \varDelta \tilde{M}^2_{Z^\prime } + \frac{\delta \tilde{M}^4_Z}{\tilde{M}^2_{Z^\prime } } \right) Z^\prime _\mu Z^{\prime \mu } \nonumber \\&+ \left( \tilde{M}^2_{W^\prime } + \varDelta \tilde{M}^2_{W^\prime } + \frac{\delta \tilde{M}^4_W}{\tilde{M}^2_{W^\prime } } \right) W^{\prime + \mu } W^{\prime -}_\mu , \end{aligned}$$

(3)

$$\begin{aligned} \mathcal{L}_3= & {} Z_\mu \left( J^{0\mu } - \frac{\delta \tilde{M}^2_Z}{\tilde{M}^2_{Z^\prime }} K^{0 \mu } \right) \nonumber \\&+ Z^\prime _\mu \left( K^{0\mu } + \frac{\delta \tilde{M}^2_Z}{\tilde{M}^2_{Z^\prime }} J^{0 \mu } \right) + A_\mu J^\mu , \end{aligned}$$

(4)

$$\begin{aligned} \mathcal{L}_4= & {} \left[ W^{+}_\mu \left( J^{+ \mu } - \frac{\delta \tilde{M}^2_W}{\tilde{M}^2_{W^\prime }} K^{+ \mu } \right) \right. \nonumber \\&\left. + W^{\prime +}_\mu \left( K^{+ \mu } + \frac{\delta \tilde{M}^2_W}{\tilde{M}^2_{W^\prime }} J^{+ \mu } \right) + ( + \leftrightarrow - ) \right] . \end{aligned}$$

(5)

In Eqs. (1)–(5), the $\mathcal{L}_1$ and $\mathcal{L}_2$ correspond to the mass terms of the ordinary (Z, W) and heavy ($Z^\prime$, $W^\prime$) gauge bosons, respectively. The $\mathcal{L}_3$ denotes the neutral current fermionic gauge interactions and $\mathcal{L}_4$ represents the charged current gauge interactions. $\tilde{M}^2_{Z^\prime , W^\prime }$ are the mass squared of heavy gauge bosons obtained after the first stage symmetry breaking. The parameters $\varDelta \tilde{M}^2_{Z^\prime , W^\prime }$ denote the additional contributions to the mass squared of heavy gauge bosons after the second stage symmetry breaking, while $\delta \tilde{M}^2_{Z, W}$ are related to the mixing effects between the ordinary and heavy gauge bosons. Comparing with $\tilde{M}^2_{Z^\prime , W^\prime }$, these four parameters are all at the next leading order of $v^2/u^2$ expansion where v and u are the scales of the first and second stage symmetry breaking, respectively. Therefore, at the leading order of $v^2/u^2$ expansion, the heavy gauge bosons $W^\prime$ and $Z^\prime$ in the 221 model of class II are degenerate in mass,

$$\begin{aligned} M^2_{W^\prime }= & {} \tilde{M}^2_{W^\prime } = M^2_{Z^\prime }= \tilde{M}^2_{Z^\prime } \nonumber \\= & {} \frac{1}{4} ( g^2_1 + g^2_2 ) u^2 = \frac{1}{4} g^2 u^2 \frac{1}{ \sin ^2 \theta _E \cos ^2 \theta _E}. \end{aligned}$$

(6)

The $J^\pm _\mu$, $J^0_\mu$ and $J^\mu$ mainly couple to the ordinary gauge bosons (Z, W, A) and are corresponding to the weak and electromagnetic currents in the SM. The $K^\pm _\mu$ and $K^0_\mu$ mainly couple to the heavy gauge bosons, the explicit expressions of which depend on the specific models and can be found in Ref. [14].

Note that the subject of this work is to investigate the contributions of heavy gauge boson $W^\prime$ to the radiative leptonic decays of charged B and D mesons. We list the charged current $K^{+}_\mu$ for the left–right (LR), leptophobic (LP), hadrophobic(HP), fermiophobic (FP), non-universal (NU) and un-unified (UU) models in Table 1. The current $K^{-}_\mu$ is just the Hermitian conjugate of $K^{+}_\mu$. It is easily seen from Eqs. (1)–(5) and Table 1 that the heavy gauge boson $W^\prime$ in the LR, LP, HP, FP models does not couple to the ordinary left-handed neutrinos and therefore makes no contributions to these decays at the leading order of $v^2/u^2$ expansion. Therefore, we only need to consider the contributions from $W^\prime$ in the NU and UU models.

In the fermion mass eigenstate basis, the gauge couplings of $W^\prime$ with fermions in the NU and UU models have the following forms at the leading order of $v^2/u^2$ expansion [10, 11, 14],

$$\begin{aligned} g^{NU}(\bar{U},D, W^\prime )= & {} \frac{g}{\sqrt{2}} \gamma ^\mu \left[ \frac{\sin \theta _E}{\cos \theta _E} V_{CKM} \right. \nonumber \\&\left. - \frac{T^\dag _U \varDelta T_D}{ \sin \theta _E \cos \theta _E}\right] P_L, \end{aligned}$$

(7)

$$\begin{aligned} g^{NU} ( \bar{N}, E, W^\prime )= & {} \frac{g}{\sqrt{2}} \gamma ^\mu \left[ \frac{\sin \theta _E}{\cos \theta _E} - \frac{T^\dag _E \varDelta T_E}{ \sin \theta _E \cos \theta _E}\right] P_L, \nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned} g^{UU} ( \bar{U}, D, W^\prime )= & {} \frac{g}{\sqrt{2}} \gamma ^\mu \frac{\sin \theta _E}{\cos \theta _E} V_{CKM} P_L, \end{aligned}$$

(9)

$$\begin{aligned} g^{UU} ( \bar{N}, E, W^\prime )= & {} - \frac{g}{\sqrt{2}} \gamma ^\mu \frac{\cos \theta _E}{ \sin \theta _E} P_L, \end{aligned}$$

(10)

where $U = ( u, c, t)^T$, $D= (d ,s ,b )^T$, $N = ( \nu _e, \nu _\mu , \nu _\tau )^T$, $E= ( e, \mu , \tau )^T$, $\varDelta = \mathrm{diag} ( 0, 0, 1)$. $T_U$, $T_D$ and $T_E$ are unitary transformation matrices between the gauge and mass eigenstate basis for the up type quarks, down type quarks and charged leptons, respectively. $V_{CKM}= T^\dagger _U T_D$ is the usual CKM mixing matrix in the SM. The gauge couplings of W with fermions are the same as those in the SM at the leading order of $v^2/u^2$ expansion and therefore are not listed here.

For the quark sector, the unitary transformation matrices $T_U$, $T_D$ satisfy

$$\begin{aligned} T_U^\dagger \varDelta T_D= & {} T_U^\dagger T_D T_D^\dagger \varDelta T_D = V_{CKM} T_D^\dagger \varDelta T_D \nonumber \\= & {} T_U^\dagger \varDelta T_U T^\dagger _U T_D = T_U^\dagger \varDelta T_U V_{CKM}. \end{aligned}$$

(11)

As analyzed in Ref. [11], the flavor changing neutral currents must occur in the interaction of quarks to gauge bosons, which can be realized in three possible ways, i.e. in the down-quark sector only, in the up-quark sector only and in both sectors. Here we only consider the first two ways for simplicity, known as the down-quark mixing scenario and up-quark mixing scenario, respectively. In the down-quark mixing scenario,

$$\begin{aligned} T_U^\dagger \varDelta T_U = \varDelta \end{aligned}$$

(12)

and the additional charged currents mixing matrix for quarks

$$\begin{aligned} T_U^\dagger \varDelta T_D= & {} T_U^\dagger \varDelta T_U V_{CKM}= \varDelta V_{CKM} \nonumber \\= & {} \left( \begin{array}{c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ V_{td} &{} V_{ts} &{} V_{tb} \\ \end{array} \right) . \end{aligned}$$

(13)

In the up-quark mixing scenario,

$$\begin{aligned} T_D^\dagger \varDelta T_D = \varDelta \end{aligned}$$

(14)

and correspondingly

$$\begin{aligned} T_U^\dagger \varDelta T_D= & {} V_{CKM} T_D^\dagger \varDelta T_D = V_{CKM} \varDelta \nonumber \\= & {} \left( \begin{array}{c@{\quad }c@{\quad }c} 0 &{} 0 &{} V_{ub} \\ 0 &{} 0 &{} V_{cb} \\ 0 &{} 0 &{} V_{tb} \\ \end{array} \right) . \end{aligned}$$

(15)

For the lepton sector, the unitary transformation matrix $T_E$ can be written as

$$\begin{aligned} T_E = \left( \begin{array}{c@{\quad }c@{\quad }c} T_{11} &{} T_{12} &{} T_{13} \\ T_{21} &{} T_{22} &{} T_{23} \\ T_{31} &{} T_{32} &{} T_{33} \\ \end{array} \right) . \end{aligned}$$

(16)

It is easy to show that the currents mixing matrix for leptons

$$\begin{aligned} T_E^\dagger \varDelta T_E = \left( \begin{array}{c@{\quad }c@{\quad }c} |T_{31}|^2 &{} T_{31}^* T_{32} &{} T_{31}^* T_{33} \\ T_{32}^* T_{31} &{} |T_{32}|^2 &{} T_{32}^* T_{33} \\ T_{33}^* T_{31}&{} T_{33}^* T_{32} &{} |T_{33}|^2 \\ \end{array} \right) . \end{aligned}$$

(17)

Thus, the interaction of leptons to gauge bosons only depends on the third row of unitary matrix $T_E$, i.e. $T_{31}$, $T_{32}$ and $T_{33}$.

3 Decay rates and relative corrections to the branching fractions

Fig. 1

The Feynman diagrams of the radiative leptonic decays of charged B and D mesons at tree level in the SM

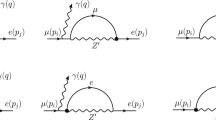
In the radiative leptonic decays of charged B and D mesons, the strong interactions are involved only in the initial states. The Feynman diagrams of these decays at tree level in the SM are given in Fig. 1. The tree level diagrams corresponding to the contributions of $W^\prime$ are similar to those in Fig. 1 with simply replacing W with $W^\prime$. Extending the expression for the amplitude in the SM given in Ref. [38] to include the contributions of $W^\prime$ by using Eqs. (7)–(10), we have

$$\begin{aligned} \mathcal{A}= & {} \frac{e G_F }{\sqrt{2}} \left[ V_{Qq} + \frac{m_W^2}{m_{W^\prime }^2} \left( f^{NU(UU)}_Q \right) _{Qq} \left( f^{NU(UU)}_L \right) _{l\nu _l} \right] \nonumber \\&\times \langle \gamma | \bar{q} \varGamma _\mu Q| P \rangle (\bar{l} \gamma ^\mu (1- \gamma _5) \nu _l ) \end{aligned}$$

(18)

with

$$\begin{aligned} f^{NU}_Q= & {} \frac{\sin \theta _E}{\cos \theta _E} V_{CKM} - \frac{T^\dag _U \varDelta T_D}{ \sin \theta _E \cos \theta _E}, \nonumber \\ f^{NU}_L= & {} \frac{\sin \theta _E}{\cos \theta _E} - \frac{T^\dag _E \varDelta T_E}{ \sin \theta _E \cos \theta _E}, \nonumber \\ f^{UU}_Q= & {} \frac{\sin \theta _E}{\cos \theta _E} V_{CKM}, \nonumber \\ f^{UU}_L= & {} - \frac{\cos \theta _E}{ \sin \theta _E}, \end{aligned}$$

(19)

and

$$\begin{aligned} \langle \gamma | \bar{q} \varGamma _\mu Q| P \rangle= & {} \epsilon _{ \mu \nu \rho \sigma } \varepsilon ^\nu p^\rho _P p^\sigma _\gamma (F_V + F_{c1}) \nonumber \\&+ i (\varepsilon _\mu p_P \cdot p_\gamma - p_{\gamma \mu } \varepsilon \cdot p_P ) ( F_A + F_{c1} ) \nonumber \\&+ F_{c2} p_{P \mu }. \end{aligned}$$

(20)

P denotes the charged B or D meson and $\varepsilon$ is the polarization vector of the photon in final state. $p_P$ and $p_\gamma$ are the 4-momentum of P and the photon, respectively. The form factors $F_V, F_A$ correspond to the contributions of diagrams (a), (b) in Fig. 1, while $F_{c1}, F_{c2}$ come from diagram (c). The contribution of (d) is suppressed by a factor of $1/m^2_W$ and thus is neglected here. Among these quantities,

$$\begin{aligned} F_{c1} = - \frac{f_P}{2 p_\gamma \cdot p_l}, \qquad F_{c2} = i f_P \left( \frac{\varepsilon \cdot p_P}{ p_\gamma \cdot p_P} - \frac{\varepsilon \cdot p_l}{ p_\gamma \cdot p_l} \right) .\nonumber \\ \end{aligned}$$

(21)

For the form factors $F_V, F_A$, the fitted numerical results based on the factorization procedure [38] are

$$\begin{aligned} F_V^B ( E_\gamma )= & {} \left[ 0.28 \frac{\varLambda _{QCD}}{ E_\gamma } - 0.73 \left( \frac{\varLambda _{QCD}}{ E_\gamma } \right) ^2 \,\,\,\right] \,\mathrm{GeV}^{-1}, \nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned} F_A^B ( E_\gamma )= & {} \left[ 0.25 \frac{\varLambda _{QCD}}{ E_\gamma } + 0.39 \left( \frac{\varLambda _{QCD}}{ E_\gamma } \right) ^2 \,\,\, \right] \mathrm{GeV}^{-1},\nonumber \\ \end{aligned}$$

(23)

$$\begin{aligned} F_V^D ( E_\gamma )= & {} \left[ 0.39 \frac{\varLambda _{QCD}}{ E_\gamma } + 0.04 \left( \frac{\varLambda _{QCD}}{ E_\gamma } \right) ^2 \,\,\,\right] \,\mathrm{GeV}^{-1}, \nonumber \\ \end{aligned}$$

(24)

$$\begin{aligned} F_A^D ( E_\gamma )= & {} \left[ -\,0.10 \frac{\varLambda _{QCD}}{ E_\gamma } + 0.76 \left( \frac{\varLambda _{QCD}}{ E_\gamma } \right) ^2 \right] \,\mathrm{GeV}^{-1},\nonumber \\ \end{aligned}$$

(25)

where $E_\gamma$ is the energy of the photon and $\varLambda _{QCD}$ denotes the characteristic energy scale of strong interaction.

In the present work, we only consider the contributions of $W^\prime$ to the leading order of $v^2/u^2$ expansion. Correspondingly, according to Eqs. (18) and (20), (21), the amplitude squared is

$$\begin{aligned} |\mathcal{M}|^2= & {} 4 e^2 G^2_F \left[ |V_{Qq}|^2 + 2 \frac{m^2_W}{m^2_{W^\prime }} \right. \nonumber \\&\left. \times \, Re \left( V_{Qq} \left( f^{NU(UU)}_Q \right) ^*_{Qq} \left( f^{NU(UU)}_L \right) ^*_{l\nu _l} \right) \right] \nonumber \\&\times \, \left\{ 2 \left[ m^2_P(p_\gamma \cdot p_l)^2 + (p_P \cdot p_\gamma )^2 ( p_P \cdot p_l)\right. \right. \nonumber \\&\left. -\, (p_P \cdot p_\gamma )^2 ( p_\gamma \cdot p_l ) -2 (p_P \cdot p_\gamma )(p_P \cdot p_l) \right. \nonumber \\&\times \, \left. ( p_\gamma \cdot p_l) \right] \left[ ( F_V+F_{c1} )^2 + ( F_A + F_{c1} )^2 \right] \nonumber \\&+\, 4 \left[ - ( p_P \cdot p_l)(p_P \cdot p_\gamma )^2 - ( p_\gamma \cdot p_l)(p_P \cdot p_\gamma )^2 \right. \nonumber \\&\left. +\, m^2_P (p_\gamma \cdot p_l)(p_P \cdot p_\gamma ) \right] ( F_V + F_{c1} ) ( F_A + F_{c1} )\nonumber \\&+ \,2 f_P ( F_V + F_{c1} ) \left[ -m^2_l \frac{ (p_P \cdot p_\gamma )^2}{ p_\gamma \cdot p_l} + 2 (p_P \cdot p_l )\right. \nonumber \\&\left. \times \, ( p_P \cdot p_\gamma ) -m^2_P p_\gamma \cdot p_l \right] + 2 f_P ( F_A + F_{c1} ) \nonumber \\&\times \, \left[ -2 \frac{ m^2_P (p_P \cdot p_l)( p_\gamma \cdot p_l)}{ p_P \cdot p_\gamma } + m^4_P \frac{p_\gamma \cdot p_l}{p_P \cdot p_\gamma }\right. \nonumber \\&+ \,4 (p_P \cdot p_l)^2 - m^2_P ( 2 p_P \cdot p_l + p_\gamma \cdot p_l) \nonumber \\&+ \,2 (p_P \cdot p_\gamma ) (p_P \cdot p_l ) -m^2_l \frac{(p_P \cdot p_\gamma )^2}{ p_\gamma \cdot p_l} \nonumber \\&\left. +\, m^2_P m^2_l \frac{p_P \cdot p_\gamma }{p_\gamma \cdot p_l} - 2 m^2_l \frac{(p_P \cdot p_\gamma )( p_P \cdot p_l )}{ p_\gamma \cdot p_l} \right] \nonumber \\&+\, f^2_P \left[ -2 (p_P \cdot p_l)^2 + m^2_P ( p_P \cdot p_l) \right. \nonumber \\&\left. -\,2 (p_P \cdot p_\gamma )(p_P \cdot p_l) + m^2_P ( p_\gamma \cdot p_l) +\, m^2_P m^2_l \right] \nonumber \\&\times \left[ - \frac{m^2_P}{(p_\gamma \cdot p_P)^2 } + 2 \frac{p_P \cdot p_l }{ (p_\gamma \cdot p_P)(p_\gamma \cdot p_l) } \right. \nonumber \\&\left. \left. - \,\frac{m^2_l}{(p_\gamma \cdot p_l )^2 } \right] \right\} . \end{aligned}$$

(26)

In the rest frame of P, the initial and final state 4-momenta can be written as

Fig. 2

The sketch for kinematics of the radiative leptonic decays of charged B and D mesons

$$\begin{aligned} p_P= & {} ( m_P, 0, 0, 0), \qquad p_\gamma = ( E_\gamma , 0, 0, -E_\gamma ), \nonumber \\ p_l= & {} ( E_l, p_{lx}, 0, p_{lz}), \end{aligned}$$

(27)

where the momentum of the photon has been chosen to be in the $-\,z$ direction as shown in Fig. 2. $E_l$ is the energy of the charged lepton in final state. Then, we have

$$\begin{aligned} p_P \cdot p_\gamma= & {} m_P E_\gamma , \qquad p_P \cdot p_l = m_P E_l, \nonumber \\ p_\gamma \cdot p_l= & {} E_\gamma ( E_l+p_{lz}). \end{aligned}$$

(28)

Note that the sum of momenta is conserved in the decay and the particles in the initial and final state are on mass shell, the $p_{lz}$ can be expressed in terms of $E_\gamma$ and $E_l$, i.e.

$$\begin{aligned} p_{lz} = \frac{2m_P E_\gamma + 2 m_P E_l -2E_\gamma E_l -m^2_P -m^2_l}{2 E_\gamma }. \end{aligned}$$

(29)

With the amplitude squared in Eq. (26) and relevant expressions given above, we can calculate the differential decay rates for radiative leptonic decays of charged B and D mesons by using the formula [39]

$$\begin{aligned} d \varGamma = \frac{1}{(2\pi )^3} \frac{1}{8m_P} |\mathcal{M}|^2 d E_l d E_\gamma . \end{aligned}$$

(30)

The total decay rates can be obtained by integrating the differential decay rates over $E_\gamma$ and $E_l$,

$$\begin{aligned} \varGamma= & {} \frac{1}{(2\pi )^3} \frac{1}{8m_P} \left[ \int ^{E_{l mid}}_{m_l} d E_l \int ^{E_{\gamma max}}_{E_{\gamma min}} d E_\gamma \right. \nonumber \\&\left. + \int ^{E_{lmax}}_{E_{l mid}} d E_l \int ^{E_{\gamma max}}_{\varDelta E_\gamma } d E_\gamma \right] |\mathcal{M}|^2 \end{aligned}$$

(31)

with the integral limits

$$\begin{aligned} E_{\gamma max}= & {} \frac{2 m_P E_l - m_P^2- m_l^2}{2 ( E_l - \sqrt{E_l^2- m_l^2} - m_P)}, \nonumber \\ E_{\gamma min}= & {} \frac{2 m_P E_l - m_P^2- m_l^2}{2 ( E_l + \sqrt{E_l^2- m_l^2} - m_P)}, \nonumber \\ E_{l mid}= & {} \frac{ 4 m_P \varDelta E_\gamma - 4 \varDelta E_\gamma ^2 - m_P^2 -m_l^2}{ 2 ( 2 \varDelta E_\gamma -m_P)}, \nonumber \\ E_{l max}= & {} \frac{m_P^2 + m_l^2}{2 m_P}. \end{aligned}$$

(32)

Note that since there are IR divergences in the radiative leptonic decays when the photon is soft or collinear with the emitted lepton, the total decay rates depend on the experimental resolution to the energy of the photon $\varDelta E_\gamma$. By using the lifetimes of charged B and D mesons, we can obtain the branching fractions from the total decay rates for all relevant decay modes.

To see the corrections of $W^\prime$ predicted by the NU and UU models more clearly and reduce the possible uncertainties stemming from the CKM matrix elements and form factors, we define the relative corrections of $W^\prime$ to the branching fractions of these decays

$$\begin{aligned} R= \frac{{Br}^{total}-{Br}^{SM}}{{Br}^{SM}}, \end{aligned}$$

(33)

where ${Br}^{total}$ and ${Br}^{SM}$ are the branching fractions of these decays with and without the contributions of $W^\prime$, respectively.

Table 2 The branching fractions of the decays $B^{-} \rightarrow \gamma l^{-} \bar{\nu }_l (l = e, \mu , \tau )$ and $D^{+} \rightarrow \gamma l^{+} \nu _l ( l= e, \mu )$ in the SM and corresponding experimental upper limits [39]

4 Numerical results and discussions

Before performing the actual calculations, we need to consider the constraints on the model parameters from the latest experimental data. As stated above, the mixing angle of the extended gauge group $\theta _E$ is defined as $\tan \theta _E = g_1/g_2$. Assuming the perturbativity of all the gauge couplings, $g_{1,2}^2/4\pi <1$, we have $0.03< \sin ^2 \theta _E < 0.96$ [40, 41]. It is easily seen from Eq. (6) that the mass of heavy gauge boson $m_{W^\prime }$ is relevant to $\sin ^2 \theta _E$. Considering the latest constraints from the CKM unitarity, lepton flavor violating processes and direct search for heavy gauge bosons at the LHC [40,41,42], $m_{W^\prime }$ can be chosen as $m_{W^\prime } > 1800\,\mathrm{GeV}$ and $m_{W^\prime } > 3000\,\mathrm{GeV}$ in the small and large $\sin ^2 \theta _E$ region, respectively. The $T_{31}, T_{32}, T_{33}$ in the currents mixing matrix for leptons $T_E^\dagger \varDelta T_E$ are constrained by considering the unitarity of $T_E$ and lepton flavor violating processes [40]. It is concluded that one of the matrix elements $T_{31}$, $T_{32}$, $T_{33}$ is close to 1 and the others are sufficiently small. It is more natural to assume the mixing strength between leptons to be directly related to their masses. So we only consider the cases that $T_{33}\approx 1$ or $T_{32}\approx 1$. Actually, we choose $T_{33} =1, T_{31}=T_{32}=0$ or $T_{32} =1, T_{31}=T_{33}=0$ for simplicity in our calculations.

Other input parameters are as follows [39],

$$\begin{aligned} \begin{array}{l@{\quad }l} m_{B^{-}} = 5.279\,\mathrm{GeV}, &{}\qquad m_{D^{+}}=1.870\,\mathrm{GeV}, \\ m_e = 0.511 \times 10^{-3}\,\mathrm{GeV}, &{} \qquad m_\mu = 0.106\,\mathrm{GeV}, \\ m_\tau = 1.777\,\mathrm{GeV}, &{}\qquad m_W = 80.385\,\mathrm{GeV}, \\ \tau _{B^{-}} = 1.638 \times 10^{-12}\,\mathrm{s}, &{}\qquad \tau _{D^{+}} = 1.04 \times 10^{-12} \,\mathrm{s}, \\ \varLambda _{QCD} = 0.2\,\mathrm{GeV}, &{}\qquad G_F= 1.166 \times 10^{-5}\,\mathrm{GeV}^{-2}, \\ |V_{ub}| = 4.09 \times 10^{-3}, &{}\qquad |V_{cd}| = 0.220. \end{array} \end{aligned}$$

For the decay constants of charged B and D mesons, we use the same values as Ref. [38], i.e. $f_{B^{-}}= 0.19357\,\mathrm{GeV}$, $f_{D^{+}} = 0.20498\,\mathrm{GeV}$, which are calculated using the same wave function and parameters as what used in calculating the form factors $F_V, F_A$. Considering that the characteristic energy scales of these decays are a few GeV, we choose the fine structure constant $\alpha = e^2/{4 \pi } = 1/132$.

With these considerations, we calculate the relative corrections of heavy gauge boson $W^\prime$ predicted by the NU and UU models to the branching fractions of the decays $B^{-} \rightarrow \gamma l^{-} \bar{\nu }_l (l = e, \mu , \tau )$ and $D^{+} \rightarrow \gamma l^{+} \nu _l ( l= e, \mu )$. First of all, we give the branching fractions of these decays in the SM and corresponding experimental upper limits [39] in Table 2. Since the branching fraction of $D^{+} \rightarrow \gamma \tau ^{+} \nu _\tau$ is too small due to the phase space suppression, we only consider the decay modes $D^{+} \rightarrow \gamma e^{+} \nu _e$ and $D^{+} \rightarrow \gamma \mu ^{+} \nu _\mu$ for the D decays. We can see that the branching fractions are all within their experimental upper limits and decrease slightly with the increase of $\varDelta E_\gamma$. The theoretical uncertainties can come from the CKM matrix elements $|V_{ub}|$, $|V_{cd}|$ and the form factors $F_V$, $F_A$, which are about 10–20% via roughly estimation. Considering that the main concern of this work is the relative corrections of $W^\prime$ and the uncertainties mentioned above can be canceled to a large extent in this quantity, we only give the central values for the branching fractions here.

In the NU model, it is easily seen from Eqs. (18) and (19) that the contributions of $W^\prime$ to the radiative leptonic decays of charged B and D mesons depend on the mixing angle of the extended gauge group $\theta _E$ and the charged currents mixing matrices $T_U^\dagger \varDelta T_D, T_E^\dagger \varDelta T_E$. Considering the relevant arguments given above, we obtain the relative corrections of $W^\prime$ to the branching fractions of these decays, which are all independent of the experimental resolution to the energy of the photon $\varDelta E_\gamma$ due to the fact that the relative corrections is defined via the ratio of branching fractions, c.f. Eq. (33), and therefore the effects of $\varDelta E_\gamma$ are canceled.

Fig. 3

The relative corrections of $W^\prime$ predicted by the NU model to the decay $B^{-} \rightarrow \gamma e^{-} \bar{\nu }_e$ as functions of $\sin ^2 \theta _E$ in the down-quark mixing scenario

Table 3 The numerical results for the relative corrections of $W^\prime$ predicted by the NU model to the decay $B^{-} \rightarrow \gamma e^{-} \bar{\nu }_e$ in the down-quark mixing scenario, in unit of $10^{-2}$

For the decay $B^{-} \rightarrow \gamma e^{-} \bar{\nu }_e$, we can see from Eqs. (17)–(19) that the contributions of $W^\prime$ to the branching fractions are related with $T_{31}$ which we have chosen to be zero as stated above. In the down-quark mixing scenario, the relative corrections R as functions of $\sin ^2 \theta _E$ are shown in Fig. 3. Apparently, the contributions of $W^\prime$ to this decay mode are positive and become more significant in the large $\sin ^2 \theta _E$ region. Hence we choose $0.5< \sin ^2 \theta _E < 0.96$ and $m_{W^\prime }>3000\,\mathrm{GeV}$. The numerical results for R corresponding to different values of $m_{W^\prime }$ and $\sin ^2 \theta _E$ in the above regions are given in Table 3. We can see that the relative corrections of $W^\prime$ to this decay mode in the down-quark mixing scenario are insignificant, $2\%$ for the largest possible case. In the up-quark mixing scenario, the corrections of $W^\prime$ to the branching fractions of $B^{-} \rightarrow \gamma e^{-} \bar{\nu }_e$ are independent of $\sin ^2 \theta _E$ which can be illuminated by scrutinizing Eqs. (15), (17)–(19), and we choose relatively low values for $m_{W^\prime }$, requiring $m_{W^\prime }>1800\,\mathrm{GeV}$. The corresponding numerical results for R are given in Table 4. We can observe that the corrections of $W^\prime$ to the branching fractions of this decay mode in the up-quark mixing scenario are negative and tiny, around $0.3 \%$ of the values in the SM for the largest possible case.

Table 4 The numerical results for the relative corrections of $W^\prime$ predicted by the NU model to the decay $B^{-} \rightarrow \gamma e^{-} \bar{\nu }_e$ in the up-quark mixing scenario, in unit of $10^{-2}$

For the decay $B^{-} \rightarrow \gamma \mu ^{-} \bar{\nu }_\mu$, the corrections of $W^\prime$ in the NU model to the branching fractions depend on the parameter $T_{32}$ which can be chosen to be 0 or 1 as stated above. Choosing $T_{32} =0$, it is found that the relative corrections of $W^\prime$ to the branching fractions of this decay mode are identical to those of $B^{-} \rightarrow \gamma e^{-} \bar{\nu }_e$ which are shown in Tables 3 and 4 for the down-quark and up-quark mixing scenario, respectively. This is due to the fact that the relative corrections R is defined via the ratio of branching fractions and thus the effects of the mass of charged lepton in the final state are canceled. For the same reason, we shall have the same results for the decay $B^{-} \rightarrow \gamma \tau ^{-} \bar{\nu }_\tau$ under the condition that $T_{33} =0$. Under the condition that $T_{32}=1$, the relative corrections of $W^\prime$ to the branching fractions are independent of $\sin ^2 \theta _E$ in the down-quark mixing scenario and this can be seen by inspecting Eqs. (13), (17)–(19). Requiring $m_{W^\prime }>1800\,\mathrm{GeV}$, we obtain the same numerical results for R as those shown in Table 4. It is worth mentioning that not only the relative corrections to the branching fractions but also the genuine ones are identical for the case $T_{32}=0$ in the up-quark mixing scenario and $T_{32}=1$ in the down-quark mixing scenario. In contrast, the relative corrections of $W^\prime$ to the branching fractions of $B^{-} \rightarrow \gamma \mu ^{-} \bar{\nu }_\mu$ decrease with the increase of $\sin ^2 \theta _E$ in the up-quark mixing scenario and therefore are more significant in the small $\sin ^2 \theta _E$ region as shown in Fig.4. Correspondingly, we choose $0.03<\sin ^2 \theta _E <0.5$ and $m_{W^\prime }>1800\,\mathrm{GeV}$. The numerical results for R are given in Table 5. We can observe that the largest possible corrections of $W^\prime$ to the decay $B^{-} \rightarrow \gamma \mu ^{-} \bar{\nu }_\mu$ are about $8 \%$ of the corresponding values in the SM.

Fig. 4

The relative corrections of $W^\prime$ in the NU model to the decay $B^{-} \rightarrow \gamma \mu ^{-} \bar{\nu }_\mu$ as functions of $\sin ^2 \theta _E$ with $T_{32}=1$ in the up-quark mixing scenario

Table 5 The numerical results for the relative corrections of $W^\prime$ predicted by the NU model to the decay $B^{-} \rightarrow \gamma \mu ^{-} \bar{\nu }_\mu$ with $T_{32}=1$ in the up-quark mixing scenario, in unit of $10^{-2}$

For the decay $B^{-} \rightarrow \gamma \tau ^{-} \bar{\nu }_\tau$, the corrections of $W^\prime$ predicted by the NU model to the branching fractions of this decay mode depend on the parameter $T_{33}$. As inferred above, under the condition that $T_{33}=0$, the relative corrections of $W^\prime$ to the branching fractions are the same as those of $B^{-} \rightarrow \gamma e^{-} \bar{\nu }_e$, c.f. Tables 3 and 4 for the down-quark and up-quark mixing scenario, respectively. By the same token, under the condition that $T_{33}=1$, the relative corrections of $W^\prime$ to this decay mode are identical to those of $B^{-} \rightarrow \gamma \mu ^{-} \bar{\nu }_\mu$ with $T_{32}=1$ which are shown in Tables 4 and 5 for the down-quark and up-quark mixing scenario, respectively. Similar to the decay $B^{-} \rightarrow \gamma \mu ^{-} \bar{\nu }_\mu$, the genuine corrections to the branching fractions of $B^{-} \rightarrow \gamma \tau ^{-} \bar{\nu }_\tau$ are the same for the case $T_{33}=0$ in the up-quark mixing scenario and $T_{33}=1$ in the down-quark mixing scenario.

For the decays $D^{+} \rightarrow \gamma l^{+} \nu _l (l = e, \mu )$, it is found that the relative corrections of $W^\prime$ predicted by the NU model to the branching fractions are the same in the down-quark and up-quark mixing scenarios, owing to the fact that the relevant matrix elements of $T^\dagger _U \varDelta T_D$ for the D decays are both zero in these two scenarios, c.f. Eqs. (13) and (15). With $T_{31}=0$, we have the same numerical results for the relative corrections of $W^\prime$ to the branching fractions of $D^{+} \rightarrow \gamma e^{+} \nu _e$ as those shown in Table 3. The effects of the mass difference between D and B mesons in the initial state are canceled due to the fact that the relative corrections R is defined via the ratio of branching fractions. As mentioned above, the effects of the mass of charged lepton in the final state are also canceled in the relative corrections. And indeed the numerical results for the relative corrections to the decay $D^{+} \rightarrow \gamma \mu ^{+} \nu _\mu$ with $T_{32}=0$ are identical to those shown in Table 3 as well. Under the condition that $T_{32}=1$, the contributions of $W^\prime$ to the branching fractions of this decay mode are independent of $\sin ^2 \theta _E$. Choosing $m_{W^\prime } >1800\,\mathrm{GeV}$, we obtain the same numerical results for the relative corrections as those given in Table 4.

Table 6 The numerical results for the relative corrections of $W^\prime$ predicted by the UU model to the decays $B^{-} \rightarrow \gamma l^{-} \bar{\nu }_l (l = e, \mu , \tau )$ and $D^{+} \rightarrow \gamma l^{+} \nu _l ( l= e, \mu )$, in unit of $10^{-2}$

Now we calculate the contributions of $W^\prime$ predicted by the UU model to the branching fractions of $B^{-} \rightarrow \gamma l^{-} \bar{\nu }_l (l = e, \mu , \tau )$ and $D^{+} \rightarrow \gamma l^{+} \nu _l ( l= e, \mu )$. For this model, it is easily seen from Eqs. (18) and (19) that the corrections of $W^\prime$ to the branching fractions of these decays are independent of $\sin ^2 \theta _E$ and the charged current mixing matrices $T_U^\dagger \varDelta T_D, T_E^\dagger \varDelta T_E$. In other words, our results in this model only depend on $m_{W^\prime }$. Moreover, the relative corrections of $W^\prime$ predicted by this model to the branching fractions are all the same for these decay modes owing to the fact that the effects of the mass difference between B and D in the initial state as well as those of the mass of charged lepton in the final state are all canceled. Choosing $m_{W^\prime } >1800\,\mathrm{GeV}$, we have the numerical results for R as shown in the Table 6. We can observe that the corrections of $W^\prime$ in the UU model to the branching fractions of $B^{-} \rightarrow \gamma l^{-} \bar{\nu }_l (l = e, \mu , \tau )$ and $D^{+} \rightarrow \gamma l^{+} \nu _l ( l= e, \mu )$ are negative and very insignificant, about $0.3 \%$ of the corresponding values in SM for the largest possible case.

5 Summary

In the present work, we study the contributions of new heavy gauge boson $W^\prime$ predicted by the general 221 models to the radiative leptonic decays of charged B and D mesons. Due to the fact that the heavy gauge boson $W^\prime$ in the LR, LP, HP and FP models does not couple to the ordinary left-handed neutrinos and therefore makes no contributions to these decays at the leading order of $v^2/u^2$ expansion, we only calculate the contributions of $W^\prime$ in the NU and UU models. To see the corrections of $W^\prime$ more clearly and reduce the uncertainties stemming from the CKM matrix elements and form factors, we define the relative corrections R via the ratio of branching fractions. Considering the constraints on the model parameters from the latest experimental data, we give the relative corrections of $W^\prime$ to the branching fractions of these decays. Due to the fact that the effects on R coming from the mass difference between B and D mesons in the initial state as well as those of the mass of charged lepton in the final state are all canceled, the numerical results for many decay modes are identical as noted above. Specially, the relative corrections of $W^\prime$ predicted by the NU model to the branching fractions of $B^{-} \rightarrow \gamma l^{-} \bar{\nu }_l (l=e,\mu , \tau )$ are all the same under the condition that $T_{31}=0$, $T_{32}=0$ and $T_{33}=0$, respectively. For the decays $D^{+} \rightarrow \gamma l^{+} \nu _l (l=e, \mu )$, the contributions of $W^\prime$ in the NU model are equal in the down-quark and up-quark mixing scenarios. The largest corrections of $W^\prime$ in the NU model to the branching fractions occur in the decay modes $B^{-} \rightarrow \gamma \mu ^{-} \bar{\nu }_\mu$ and $B^{-} \rightarrow \gamma \tau ^{-} \bar{\nu }_\tau$, which can reach to about 8% of the values in the SM in the up-quark mixing scenario under the condition that $T_{32}=1$ and $T_{33}=1$, respectively. For the time being, these effects are still smaller compared with the corresponding theoretical uncertainties of the SM branching fractions and thus difficult to discern in experiments. It is noteworthy that the near future BELLE II experiment at SuperB will be able to improve the accuracy of measurement on the CKM matrix element $|V_{ub}|$ significantly [43, 44]. In addition, it is possible to achieve a better control on the uncertainties of the form factors in the future. Under these circumstances, the theoretical uncertainties of branching fractions in the SM could be reduced to below 5% and our results may be tested by future more precise experiments such as BELLE II, LHCb upgraded. In contrast, the contributions of $W^\prime$ predicted by the UU model only depend on $m_{W^\prime }$ and the relative corrections to the branching fractions are the same for all the decay modes which are negative and very tiny, about 0.3% for the largest possible case.