Abstract
\(\phi \) meson measurements provide insight into strangeness production, which is one of the key observables for the hot medium formed in high-energy heavy-ion collisions. ALICE measured \(\phi \) production through its decay in muon pairs in Pb–Pb collisions at \(\sqrt{s_\mathrm {NN}} = 2.76\) TeV in the intermediate transverse momentum range \(2< p_\mathrm {T}< 5\) GeV/c and in the rapidity interval \(2.5<y<4\). The \(\phi \) yield was measured as a function of the transverse momentum and collision centrality. The nuclear modification factor was obtained as a function of the average number of participating nucleons. Results were compared with the ones obtained via the kaon decay channel in the same \(p_\mathrm {T}\) range at midrapidity. The values of the nuclear modification factor in the two rapidity regions are in agreement within uncertainties.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
At small values of the baryochemical potential and at extreme high temperatures, Quantum Chromodynamics (QCD) predicts chiral and deconfinement crossover transitions from hadronic matter to a state of strongly interacting medium, where dominant degrees of freedom are gluons and light quarks (Quark-Gluon Plasma, QGP). Ultrarelativistic heavy-ion collisions provide the tools to study this phase of matter in the laboratory. Strangeness production is a key tool to understand the properties of the medium formed in these collisions. Indeed, an enhanced production of strange particles with respect to elementary hadronic collisions was early proposed as one of the signatures of the QGP [1]. This enhancement is currently interpreted as resulting from the restoration of the chemical equilibrium between u, d and s quarks in sufficiently central heavy-ion collisions, with respect to ee and pp interactions, where strangeness production is expected to be canonically suppressed [2].
The \(\phi \) meson, due to its \(s \bar{s}\) valence quark content, provides insight into strangeness production. Since its cross section for interactions with non-strange hadrons can be assumed to be small, the \(\phi \) meson should be less affected by hadronic rescattering during the expanding hadronic phase, which follows the QGP phase. For this reason, the \(\phi \) meson better reflects the early evolution of the system [3]. Because of the long lifetime of the \(\phi \) meson, the rescattering effects that should affect the hadronic decay channels are negligible [4,5,6,7], making thus possible a direct comparison between the hadronic and dileptonic decay channels.
Moreover, the \(\phi \) meson may be sensitive to chiral symmetry restoration [8,9,10], that could be observed by measuring a mass shift of a few MeV/c\(^2\) or a broadening of the spectral function of the hadronic resonances up to several times their PDG value [11,12,13,14]. However, no experimental evidence of such a broadening or mass shift has been observed so far for the \(\phi \) meson in high-energy heavy-ion collisions neither in the hadronic nor in the dilepton decay channel [6, 15,16,17,18,19].
The measurement of hadrons in different \(p_\mathrm {T}\) ranges provides important information on the relative contribution of different possible hadronization mechanisms. Soft processes dominate the low transverse momentum region (\(p_\mathrm {T}\lesssim 2\) GeV/c), where the system evolution can be described on the basis of hydrodynamical models and particle yields follow the expectations of thermal models [20,21,22,23,24,25,26,27,28]. On the other side, for high transverse momenta (\(p_\mathrm {T}\gtrsim 5\) GeV/c), hard parton-parton scattering processes and subsequent fragmentation become the dominant production mechanisms. In the presence of a deconfined medium, additionally, parton energy loss via elastic collisions and gluon bremsstrahlung [29] modifies the spectral distributions, leading to a suppression of hadron production in central heavy-ion collisions with respect to the one measured in peripheral heavy-ion or in pp collisions, scaled by the number of binary collisions.
At intermediate transverse momenta (\(2< p_\mathrm {T}< 5\) GeV/c), measurements at RHIC showed an enhancement above unity of the ratio between the baryon and meson yields, the so-called “baryon anomaly”. This has been attributed to the recombination of quarks [30,31,32,33,34,35]. However, measurements at the LHC [36] showed that the proton-to-pion ratio from low to intermediate \(p_\mathrm {T}\) could be described by hydrodynamical models [25, 26]. The \(\phi \), being a meson and having a mass close to that of the proton, is an ideal probe to disentangle whether this effect is more related to the particle mass or to its valence quark content, since recombination scales with the number of quarks, while hydrodynamical models depend on the particle mass.
Recent measurements at the LHC [6] showed that the \(p/\phi \) ratio at midrapidity does not show a significant dependence on \(p_\mathrm {T}\), while the \(p/\pi \) and \(\phi /\pi \) ratios show similar increases as a function of the transverse momentum, indicating that particle radial flow and therefore the particle masses mainly determine the \(p_\mathrm {T}\) distributions of these particles. Hence, it is interesting to test whether there is a dependence of radial flow on rapidity and to compare the results at forward and midrapidity within the same experiment. A comparison with hydrodynamical models at forward rapidity would complement the results already obtained at midrapidity, where they have shown to describe the data even in the intermediate \(p_\mathrm {T}\) region.
This article presents a measurement of \(\phi \) production in Pb–Pb collisions at \(\sqrt{s_\mathrm {NN}}=2.76\) TeV at forward rapidity with the ALICE muon spectrometer at the LHC. The \(\phi \) meson was reconstructed in the rapidity range \(2.5< y < 4\) for intermediate transverse momenta in the range \(2< p_\mathrm {T}< 5\) GeV/c via its decay in muon pairs.
The evolution of the \(\phi \) yield with centrality and transverse momentum is discussed and compared with the measurement at midrapidity in the kaon decay channel [6]. Finally, the nuclear modification factors are determined.
2 Experimental apparatus
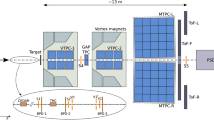
The ALICE detector is described in detail in [37]. The detectors relevant for this analysis are the forward muon spectrometer, the V0 detector, the silicon pixel detector (SPD) of the inner tracking system (ITS) and the zero degree calorimeters (ZDC).
The muon spectrometer covers the pseudorapidity region \(-4~< \eta <-2.5\);Footnote 1 its elements are a front hadron absorber, followed by a set of tracking stations, a dipole magnet, an iron wall acting as muon filter and a trigger system. The front hadron absorber is made of carbon, concrete and steel and is placed at a distance of 0.9 m from the nominal interaction point (IP). Its total length of material corresponds to ten hadronic interaction lengths. The 5 m long dipole magnet provides a magnetic field of up to 0.7 T in the vertical direction, which results in a field integral of 3 T m. A set of five tracking stations, each one composed of two cathode pad chambers, provides the muon tracking. The stations are located between 5.2 and 14.4 m from the IP, the first two upstream of the dipole magnet, the third in the middle of the dipole magnet gap and the last two downstream of it. A 1.2 m thick iron wall, corresponding to 7.2 hadronic interaction lengths, is placed between the tracking and trigger systems and absorbs the residual secondary hadrons emerging from the front absorber. The front absorber together with the muon filter stops muons with momenta lower than \(\sim \) 4 GeV/c. The tracking apparatus is completed by a muon triggering system (MTR) consisting of two detector stations, placed at 16.1 and 17.1 m from the IP. Each station is composed of two planes of resistive plate chambers.
The V0 detector is composed of two arrays of 32 scintillator sectors placed at 3.4 m and \(-0.9\) m from the IP and covering the pseudorapidity regions 2.8 \(< \eta<\) 5.1 (V0A) and \(-3.7< \eta < -1.7\) (V0C), respectively. It is used to reject the background from beam-gas interactions and estimate the collision centrality and event plane. The SPD, used for the determination of the primary vertex position, consists of two cylindrical layers of silicon pixel detectors, positioned at a radius of 3.9 and 7.6 cm from the beam axis. The pseudorapidity range covered by the inner and the outer layers is \(|\eta |<\) 2.0 and \(|\eta |<\) 1.4, respectively. The ZDC are located at \(\sim \) 114 m from the IP and cover the pseudorapidity region \(|\eta | > 8.7\). In this analysis they are used to reject electromagnetic interactions of lead ion beams.
3 Data analysis
The analysis presented in this paper is based on the data sample collected by ALICE in 2011 during the Pb–Pb run at \(\sqrt{s_\mathrm {NN}}= 2.76\) TeV.
The minimum bias (MB) trigger is defined as the coincidence of a signal in V0A and V0C, synchronized with the passage of two colliding lead bunches. Data were collected with a dimuon unlike-sign trigger (\(\mu \mu \)MB), which is defined as the coincidence of a MB trigger and at least a pair of opposite-sign (OS) tracks selected by the MTR system, each with a transverse momentum above the threshold,Footnote 2 \(p_{\mathrm {T},\mu }\gtrsim 1\) GeV/c.
The background events coming from beam interactions with the residual gas were reduced offline using the timing information on signals from the V0 and from the ZDC [38].
The number of OS dimuon triggers collected is 1.7 \(\times ~10^7\), corresponding to an integrated luminosity of \(L_\mathrm {int}=68.8\pm 0.9 \mathrm {(stat)}^{+6.0}_{-5.1}\mathrm {(syst)}~\mu \)b\(^{-1}\) [39].
The centrality determination is performed by fitting a distribution obtained with the Glauber model approach to the V0 amplitude distribution [40]. In the centrality range 0–90% the efficiency of the MB trigger is 100% and the contamination from electromagnetic processes is negligible. Events corresponding to the 90% most central collisions were thus selected. The centrality classes considered in this analysis were 0–20, 20–40, 40–60 and 60–90%.
The Glauber model fit to the V0 signal distribution also allows to extract variables related to the collision geometry, such as the average number of participating nucleons \(\left\langle N_\mathrm {part}\right\rangle \) and the nuclear overlap function \(\langle T_\mathrm {AA} \rangle \), as reported in Table 1.
Muon tracks were selected requiring a single muon \(p_{\mathrm {T},\mu }>\) 0.85 GeV/c, to reject muons with a transverse momentum much below the hardware \(p_{\mathrm {T},\mu }\) threshold imposed by the trigger system. The selection of the muon pseudorapidity \(-4< \eta _{\mu } < -2.5\) was applied in order to remove the tracks close to the acceptance borders. Tracks crossing the part of the front absorber with the highest material density were rejected by restricting the transverse radial coordinate of the track at the end of the absorber to the range \(17.6< R_\mathrm {abs} < 89.5\) cm. Each track reconstructed in the tracking chambers was required to match a track reconstructed in the trigger chambers.
Dimuons were selected requiring that their rapidity was in the range 2.5 \(< y<\) 4. The trigger threshold on the single muon transverse momentum strongly reduces the detection efficiency for low mass, low \(p_\mathrm {T}\) dimuons. Therefore, the analysis was limited to dimuon transverse momenta in the range \(2<p_{\mathrm {T}}<5\) GeV/c, where the upper limit is only set by the currently available statistics.
The opposite-sign dimuon invariant mass spectrum consists of correlated and uncorrelated pairs. The latter come mostly from the decay of pions and kaons and constitute the combinatorial background, which was evaluated via an event mixing technique, described in detail in [41]. Events were assigned to classes of similar vertex position, event plane orientation and centrality. Pairs were then formed with muons coming from different events belonging to the same classes. In this way, the resulting invariant mass spectrum consists of muon pairs which are uncorrelated by construction. The mixed events mass spectra were normalized to \(2R\sqrt{N_{++} N_{--}}\), where \(N_{++}\) (\(N_{--}\)) is the number of like-sign positive (negative) pairs integrated in the full mass range. The R factor takes into account the differences between the acceptances for like-sign and opposite-sign muon pairs and was estimated as \(R = N^\mathrm {mixed}_{+-} / (2 \sqrt{N^\mathrm {mixed}_{++} N^\mathrm {mixed}_{--}})\), where \(N^\mathrm {mixed}_{\pm \pm }\) is the number of mixed pairs for a given charge combination.
The quality of the combinatorial background determination was checked through a Monte Carlo (MC) simulation in which uncorrelated muon pairs were generated. The muon transverse momentum and rapidity distributions were parametrized to reproduce those from the experimental data. The detector response for these pairs was obtained with a simulation that uses GEANT3 [42]. The simulation results were then subjected to the same reconstruction and selection chain as the real data. In this way, all the possible correlations introduced by the detector were properly taken into account. The event mixing technique was then applied to the simulated pairs. The resulting opposite-sign mass spectrum was compared to the corresponding one obtained from the muon pairs in the same event. Differences within 2% in the two distributions were observed. The limited precision in the combinatorial background subtraction was taken into account in the evaluation of the systematic uncertainty, as described below.
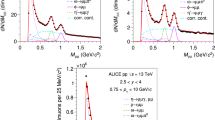
Figure 1 shows the invariant mass spectra for opposite-sign muon pairs in different centrality classes, before the combinatorial background subtraction, in the range \(2< p_\mathrm {T}< 5\) GeV/c. The combinatorial background, evaluated from opposite-sign pairs in mixed events, is also shown.
The ratio between the invariant mass spectra of correlated and uncorrelated pairs for the different centralities is shown in Fig. 2: for \(0.95< M_{\mu \mu } < 1.1\) GeV/c\(^2\) this ratio increases from \(\sim \) 0.07 in central collisions to \(\sim \) 2 in peripheral collisions.
The raw invariant mass spectrum after combinatorial background subtraction is shown in Fig. 3 in the four centrality classes considered in this analysis. The \(\phi \) peak is clearly visible in all the centrality bins, superimposed to a correlated background due to the dimuon two-body and Dalitz decays of the light resonances (\(\eta \), \(\eta '\), \(\rho \), \(\omega \)) and the semi-muonic decays of open charm and open beauty. To reproduce the different processes contributing to the dimuon mass spectrum, a Monte Carlo simulation was performed using the hadronic cocktail generator first developed for the analysis of pp collisions at \(\sqrt{s}=7\) TeV [41]. An exponential function
was used as input \(p_\mathrm {T}\) distribution of the \(\phi \) meson in the generator. In this formula \(m_\mathrm {T}\) is the transverse mass. The value of the parameter T was tuned iteratively to the results from the present analysis, as shown below, with \(T = (437 \pm 28)\) MeV, obtained from a fit to the \(p_\mathrm {T}\) distribution integrated over centrality.
The \(\phi \) rapidity distribution was based on a parametrization of PYTHIA 6.4 [43]. We assume that the rapidity and \(p_\mathrm {T}\) distributions factorize.
Invariant mass spectra in different centrality classes for 2 \(< p_\mathrm {T}<\) 5 GeV/c in Pb–Pb collisions at \(\sqrt{s_\mathrm {NN}} = 2.76\) TeV. The solid red line represents the result of the fit to the hadronic cocktail; the green dashed line represents the correlated background, given by the sum of all the MC sources other than \(\phi \), \(\rho \) and \(\omega \) mesons
The fit to the mass spectra obtained after the combinatorial background subtraction is also shown in Fig. 3. In this fit, the shape of each contribution was taken from the MC. The fit parameters allowed to vary freely were the normalizations of the \(\eta \rightarrow \mu ^+\mu ^- \gamma \), \(\omega \rightarrow \mu ^+\mu ^-\), \(\phi \rightarrow \mu ^+\mu ^-\) and open charm contributions. The other processes (\(\eta \rightarrow \mu ^+\mu ^-\), \(\eta ' \rightarrow \mu ^+\mu ^- \gamma \), \(\omega \rightarrow \mu ^+\mu ^-\pi ^0\), \(\rho \rightarrow \mu ^+\mu ^-\) and open beauty) were fixed to the ones mentioned above, according to the relative branching ratios or cross sections, as done in [41]. In particular, the normalization of the \(\rho \) relative to the \(\omega \) meson was fixed requiring that \(\sigma _\rho = \sigma _\omega \), as suggested both from models and pp data [41, 44,45,46], while the \(\eta '\) contribution was derived from the \(\eta \) cross section by applying the ratio of the corresponding cross sections \(\sigma _{\eta '}/\sigma _{\eta } = 0.3\) taken from the PYTHIA tunes ATLAS-CSC [47] and D6T [48]. The ratio between the open beauty and open charm was fixed according to the results from the LHCb Collaboration in pp collisions at 7 TeV [49, 50].
Invariant mass spectra for \(2.5< p_\mathrm {T}< 3\) GeV/c and \(3.6< p_\mathrm {T}< 4.2\) GeV/c in 0–90% Pb–Pb collisions at \(\sqrt{s_\mathrm {NN}} = 2.76\) TeV. The solid red line represents the result of the fit to the hadronic cocktail; the green dashed line represents the correlated background, given by the sum of all the MC sources other than \(\phi \), \(\rho \) and \(\omega \) mesons
Other contributions may be present in Pb–Pb collisions, such as the in-medium modification of the \(\rho \) meson or a thermal dilepton continuum. According to theoretical predictions based on [51,52,53], the magnitude of these contributions is expected to be below the sensitivity of our measurement [54]. However, in order to take their possible effect into account and to allow the \(\phi \) signal extraction to be studied under various hypotheses on the shape of the correlated background, two alternative empirical descriptions of the correlated background were used: the superposition of an exponential and a constant and of an exponential and a Landau distribution. In both cases, the peaks of the \(\phi \) and \(\rho +\omega \) were described with a Crystal Ball function [55] tuned on the MC. The differences among these two different background descriptions and the one obtained with the hadronic cocktail constitute one of the main sources of the systematic uncertainty in the signal extraction. The width of the reconstructed \(\phi \) peak is dominated by the detector resolution. From the MC simulation it was determined to be \(\sigma _{\phi } \approx 50\) MeV/c\(^{2}\) (Gaussian width). This width was used as a fixed parameter in the fits to the invariant mass spectra at all centralities, in order to reduce the sensitivity to statistical fluctuations. Performing the fits with the peak width as free parameter results in values compatible within uncertainties of about 10 MeV/c\(^2\) with the MC result. Likewise, if the \(\phi \) peak position is left free, the result is compatible with its PDG value within an uncertainty of about 10 MeV/c\(^2\). The present measurement does not allow to determine a broadening effect or a mass shift smaller than these uncertainties. More stringent limits are set in [6].
The fits of the mass spectra integrated over centrality and for 0–40 and 40–90% centrality classes, in different \(p_\mathrm {T}\) bins were performed as well. Two examples of these fits in two different \(p_\mathrm {T}\) bins (\(2.5~<~p_\mathrm {T}~<3\) GeV/c and \(3.6~<~p_\mathrm {T}~<4.2\) GeV/c), for 0–90% centrality, are shown in Fig. 4.
The raw number of \(\phi \) mesons decaying into muon pairs \(N_\phi ^\mathrm {raw}\) and the \(\phi \) yield dN/dy in the range \(2< p_\mathrm {T} < 5\) GeV/c are reported in Table 2 for the centrality classes considered in this analysis. Table 3 reports the \(\phi \) yield d\(^2N\)/(dyd\(p_\mathrm {T}\)) as a function of \(p_\mathrm {T}\) for 0–40 and 40–90% most central collisions. The systematic uncertainties will be discussed below.
The \(\phi \) yield for each centrality class has been calculated as
where A is the geometrical acceptance, \(\varepsilon \) the reconstruction efficiency, \(N_{MB}\) the number of minimum bias events in a given centrality class and \(BR_{\phi \rightarrow e^+e^-} = (2.954 \pm 0.030) \times 10^{-4}\) the branching ratio of the \(\phi \) meson decay into dielectrons [56]. Lepton universality allows to use this value instead of the one of the dimuon decay, which is known with a much larger uncertainty.
To estimate \(A \times \varepsilon \) as a function of centrality, Monte Carlo simulations were performed using the embedding technique, which consists in simulating a signal decay and adding the corresponding simulated detector response to the raw data of a real event. The resulting embedded event is then reconstructed as if it were a normal real event. This technique has the advantage of providing the most realistic background conditions, which is necessary if the high particle multiplicity environment alters the track reconstruction efficiency, as in central Pb–Pb collisions. The \(A \times \varepsilon \) is roughly independent from centrality, changing from 5.49 ± 0.31% (syst) in peripheral (60–90%) to 5.15 ± 0.30% (syst) in central (0–20%) collisions. The embedded simulations were used also to evaluate the \(A \times \varepsilon \) as a function of \(p_\mathrm {T}\). The \(A \times \varepsilon \) increases as a function of \(p_\mathrm {T}\) from \(\sim \) 2.5% for \(2< p_\mathrm {T}< 2.5\) GeV/c to \(\sim \) 21.4% for \(4.2< p_\mathrm {T}< 5\) GeV/c.
The number of minimum bias events has been obtained from the number of opposite-sign dimuon triggers, scaled by the normalization factor \(f_\mathrm {norm}\) [39], defined as the inverse of the probability of having a dimuon trigger in a MB event. Its value, averaged over the entire data sample, is \(f_\mathrm {norm} = 30.56 \pm 0.01 (\mathrm {stat.}) \pm 1.10 (\mathrm {syst.})\).
The systematic uncertainty on the \(\phi \) yield was evaluated taking into account several contributions:
-
Combinatorial background subtraction: this uncertainty was evaluated through a Monte Carlo simulation. The correlated muon pairs coming from the hadronic cocktail were added to the uncorrelated pairs, generated as described above. The relative abundance of correlated and uncorrelated muon pairs was chosen such that it reproduced the one in the data. The resulting mass spectrum was then subjected to the same analysis chain applied to the data, including background subtraction with the event mixing and fit with the hadronic cocktail. The number of raw \(\phi \) mesons obtained from the fit differs from the one actually injected in the spectrum, which is known a priori. This difference was taken as an estimate of the uncertainty related to the combinatorial background subtraction. It decreases from 9% in central collisions to less than 1% in peripheral collisions, while as a function of \(p_\mathrm {T}\), it amounts to 4.8% for 0–40% centrality and to 1.8% for 40–90% centrality.
-
Shape of the correlated background: this was evaluated using two alternative empirical descriptions of the correlated background, as previously described. The variations of \(N_\phi ^\mathrm {raw}\) decrease from 6.7% in central collisions to 2.2% in peripheral collisions. As a function of \(p_\mathrm {T}\), it varies from 1.9 to 8.2% for 0–40% centrality and from 1 to 4% for 40–90% centrality.
-
Range of the fit to the mass spectrum: three different fit ranges were tested: 0.2 \(< M_{\mu \mu } < 1.8\) GeV/c\(^{2}\), \(0.2< M_{\mu \mu } < 2.0\) GeV/c\(^{2}\) and \(0.2< M_{\mu \mu } < 2.2\) GeV/c\(^{2}\). The effect on \(N_\phi ^\mathrm {raw}\) is below 1% for all centralities, except for the most peripheral bin, where it amounts to 2.1%. As a function of \(p_\mathrm {T}\), it varies between 1.2 and 2.9% in central and semi-central collisions and from 1 to 2% in semi-peripheral and peripheral collisions.
-
Cut on single muon transverse momentum: this was evaluated by applying three different cuts, \(p_{\mathrm {T},\mu }>\) 0.7 GeV/c, \(p_{\mathrm {T},\mu }>\) 0.85 GeV/c and \(p_{\mathrm {T},\mu }>\) 1 GeV/c, which lead to variations of the corresponding \(A \times \varepsilon \) corrected \(N_\phi ^\mathrm {raw}\) ranging from 4 to 6.3% as a function of centrality, from 1.1 to 10.4% as a function of \(p_\mathrm {T}\) for 0–40% centrality, and from 1 to 5.7% as a function of \(p_\mathrm {T}\) for 40–90% centrality.
-
Systematic uncertainty of \(A \times \varepsilon \): to evaluate this contribution, the measured \(p_\mathrm {T}\) distribution, shown in the next section, was fitted with an exponential (Eq. 1). The value of the T parameter was used as an input to the simulation, that was then repeated varying T by one standard deviation \(\sigma _T\). The half of the difference between the \(A \times \varepsilon \) values obtained using \(T\pm \sigma _T\) as input parameter was taken as an estimation of its systematic uncertainty. As a function of centrality, it amounts to about 5.7% with no significant dependence on the collision centrality; it is \(<1\)% as a function of \(p_\mathrm {T}\).
-
Tracking and trigger efficiencies: the corresponding systematic uncertainties were determined from data and MC simulations as detailed in [39]. They are correlated as a function of centrality, amounting respectively to 11 and 2%, and uncorrelated as a function of \(p_\mathrm {T}\), varying in this case of 8–14 and 2–4% respectively.
-
Matching efficiency: the uncertainty on the matching efficiency between the tracks reconstructed in the tracking chambers and the ones reconstructed in the trigger chambers amounts to 1%. It is correlated as a function of centrality and uncorrelated as a function of \(p_\mathrm {T}\) [39].
-
Centrality limits: the effects of the uncertainty on the value of the V0 signal amplitude corresponding to 90% of the hadronic Pb–Pb cross section were estimated by varying such a value by ±0.5% [40] and redefining correspondingly the centrality intervals. The systematic effect of \(N_\phi ^\mathrm {raw}\) is negligible in all centrality bins, except for the most peripheral one, where it amounts to 3%. It is correlated as a function of \(p_\mathrm {T}\), amounting to less than 1%.
-
Uncertainty of the \(\phi \) branching ratio into dielectrons (\(\sim \) 1%) [56], correlated as a function of \(p_\mathrm {T}\) and centrality.
-
Uncertainty on \(f_\mathrm {norm}\) (\(\sim \) 3.6%), correlated as a function of \(p_\mathrm {T}\) and centrality [39].
These values are summarized in Table 4.
4 Results
\(\phi \) yield as a function of \(p_\mathrm {T}\) at forward rapidity in pp [57] and Pb–Pb collisions for different centralities. The distributions have been scaled differently for better visibility
Figure 5 shows the \(p_\mathrm {T}\) spectra in Pb–Pb collisions in the centrality ranges 0–40 and 40–90%. The pp spectrum [57] is also reported for comparison. The \(p_\mathrm {T}\) distribution in Pb–Pb collisions is softer than in pp in the measured transverse momentum range.
Top panel: comparison between the \(\phi \) yield as a function of \(p_\mathrm {T}\) with the EPOS 3.101 [26, 58, 59] and HIJING 2.0 [60] event generators, at forward and midrapidity [6], for 0–40% (left) and 40–90% centrality (right). The same scale factors applied to data were also used for the models. The transparent boxes represent the uncorrelated systematic uncertainties at forward rapidity and the total systematic uncertainties (including correlated and uncorrelated components) at midrapidity. Lower panels: ratios between the measured yields and the calculations by EPOS and HIJING
In Fig. 6 the \(p_\mathrm {T}\) spectra are compared with the EPOS 3.101Footnote 3 event generator [26, 58, 59], which utilizes a core–corona approach in which the core component undergoes a hydrodynamic expansion, and the HIJING 2.0 model [60], which does not include hydrodynamic effects in the calculation. The results obtained at midrapidity [6] are also shown. EPOS fairly reproduces the data at midrapidity for all centralities, although the \(p_\mathrm {T}\) spectra are slightly harder than the measured ones. At forward rapidity, the calculation underestimates the \(p_\mathrm {T}\) spectra at all centralities, approaching the data only at \(p_\mathrm {T}\sim \)4 GeV/c. It has to be noted that this disagreement is significantly worsened if the core component in EPOS were to be switched off. Qualitatively, this suggests that the steepness of the forward \(\phi \) spectra in Pb–Pb is a consequence of the interplay between radial flow at low- to mid-\(p_\mathrm {T}\), which increases the \(\phi \) yield in the lowest measured \(p_\mathrm {T}\) range, and a relatively unchanged contribution from hard processes at higher transverse momenta. HIJING underestimates the data and shows a harder \(p_\mathrm {T}\) shape at both mid- and forward rapidity. In particular, at forward rapidity, the disagreement with the data on the shape of the \(p_\mathrm {T}\) distribution is stronger than for EPOS.
Top panel: comparison between \((\mathrm {d}N_{\phi }/\mathrm {d}y)/\left\langle N_\mathrm {part}\right\rangle \) as a function of \(\left\langle N_\mathrm {part}\right\rangle \) measured in the muon decay channel at forward rapidity and in the kaon decay channel at midrapidity, in Pb–Pb collisions at \(\sqrt{s_\mathrm {NN}}= 2.76\) TeV, for \(2< p_\mathrm {T} <5\) GeV/c. The corresponding points in pp collisions at \(\left\langle N_\mathrm {part}\right\rangle = 2\) are also shown. Transparent boxes represent the uncorrelated systematic uncertainties at forward rapidity and the total systematic uncertainties (including correlated and uncorrelated components) at midrapidity. The shaded red box represents the correlated systematic uncertainties at forward rapidity, the shaded blue box represents the normalization uncertainty at midrapidity. Results from the EPOS 3.101 and HIJING 2.0 event generators are shown for comparison. The rapidity density per participant for pions at midrapidity is also reported, scaled to 0.1. Bottom panel: ratio between \(\phi \) rapidity densities per participant at mid- and forward rapidity, in pp (open circle) and Pb–Pb collisions (full circles)
Figure 7 shows the \(\phi \) rapidity density per participant as a function of \(\left\langle N_\mathrm {part}\right\rangle \). The result in pp collisions at the same energy [57] is also shown: the \(\phi \) yield per participant already grows by a factor of about 1.8 when going from pp to peripheral Pb–Pb collisions. This factor increases to about 4 when going from pp to central Pb–Pb collisions. No sizeable dependence on rapidity is observed. The ratio between the rapidity densities at mid- and forward rapidity is \(\sim 2\), both in pp and Pb–Pb collisions, where it is roughly constant as a function of centrality, as shown in the lower panel of the same figure.
The rapidity density per participant is also plotted in Fig. 7 for pions at midrapidity [61]. The rapidity density increases from pp to Pb–Pb collisions faster for the \(\phi \) than for pions. The increase of the \(\phi /\pi \) ratio in the intermediate \(p_\mathrm {T}\) region is interpreted in terms of radial flow, whose magnitude grows as a function of the collision centrality. The similar increase of the \(\phi \) at mid- and forward rapidity suggests that the magnitude of radial flow is similar in the two rapidity regions considered.
The comparison with HIJING and EPOS at forward rapidity shows that both calculations predict a similar evolution of the yield with the collision centrality. In this rapidity region, both models underestimate the yield by about a factor of two, independently of centrality. Different results are obtained at midrapidity, where HIJING largely underestimates the yield, while EPOS qualitatively reproduces the trend as a function of \(\left\langle N_\mathrm {part}\right\rangle \), even though it overestimates the data by about 30% in peripheral collisions and 13% in central collisions.
\(R_{\mathrm {AA}}\) of the \(\phi \) meson as a function of \(\langle N_{\mathrm {part}} \rangle \) for \(2.5<y<4\), compared with the ALICE measurement for \(|y|<0.5\). All the midrapidity points have been displaced by \(\left\langle N_\mathrm {part}\right\rangle = 10\) for better visibility. Transparent boxes represent the uncorrelated systematic uncertainties at forward rapidity and the total systematic uncertainties (including correlated and uncorrelated components) at midrapidity. The shaded red box represents the correlated systematic uncertainties at forward rapidity, the shaded blue box represents the normalization uncertainty at midrapidity. Results from PHENIX in Au-Au and Cu-Cu collisions at \(\sqrt{s_\mathrm {NN}} = 200\) GeV are also shown for comparison
The nuclear modification factor is defined as the yield ratio of nucleus–nucleus collisions to inelastic pp collisions, scaled with the average nuclear overlap function \(\left\langle T_\mathrm {AA} \right\rangle \). For a given centrality and integrated over the considered \(p_\mathrm {T}\) and y ranges, it is obtained as
where \(\mathrm {d}N/\mathrm {d}y\) is the \(\phi \) rapidity density and \(\mathrm {d} \sigma _\mathrm {pp} /\mathrm {d}y= 113 \pm 10 \mathrm {(stat)} \pm 7 \mathrm {(syst)}~\mu \)b [57] is the \(\phi \) production cross section in pp collisions at the same energy, integrated over the corresponding \(p_\mathrm {T}\) and rapidity range.
Figure 8 shows the \(R_\mathrm {AA}\) measured as a function of the average number of participants. The systematic uncertainties at forward rapidity are summarized in Table 5. In peripheral collisions, the nuclear modification factor is compatible with unity within uncertainties, indicating that these collisions behave as a superposition of incoherent pp collisions. In most central collisions, \(R_\mathrm {AA}\) at forward rapidity is reduced to about 0.65, showing a clear suppression of the \(\phi \) multiplicity with respect to the pp reference in the intermediate \(p_\mathrm {T}\) region. A qualitatively similar behaviour was observed also by the PHENIX experiment in Au-Au collisions at \(\sqrt{s_\mathrm {NN}}=200\) GeV for \(p_\mathrm {T}>2.2\) GeV/c at midrapidity [62].
The comparison with the ALICE results obtained at midrapidity shows that the two data sets agree within the present uncertainties.
5 Conclusions
\(\phi \) meson production was measured via its dimuon decay channel in Pb–Pb collisions at \(\sqrt{s_\mathrm {NN}} = 2.76\) TeV at forward rapidity. For intermediate transverse momenta (\(2<p_\mathrm {T}<5\) GeV/c) the \(p_\mathrm {T}\) spectra in Pb–Pb collisions are softer than in pp.
The yield per participant increases with the collision centrality, similarly to the yield measured in the kaon decay channel at midrapidity. The ratio between the yields in the two rapidity regions is constant as a function of centrality. The rapidity density increases from pp to Pb–Pb collisions faster for the \(\phi \) than for pions, suggesting the presence of radial flow, whose effect increases with the collision centrality with similar magnitudes at forward and midrapidity.
The measured yields as a function of \(p_\mathrm {T}\) or centrality were compared with results from the EPOS event generator and the HIJING Monte Carlo model. The two calculations predict similar centrality dependencies at forward rapidity, underestimating the measured yield by a factor of \(\sim \) 2 for all centralities. At midrapidity, EPOS qualitatively reproduces the trend as a function of the collision centrality, while HIJING largely underestimates the yield. Regarding the shape of the \(p_\mathrm {T}\) spectra, EPOS correctly reproduces the data at midrapidity, while it predicts harder transverse momentum distributions at forward rapidity. HIJING predicts harder \(p_\mathrm {T}\) distributions at both mid- and forward rapidity.
The integrated nuclear modification factor, measured as a function of \(\left\langle N_\mathrm {part}\right\rangle \), is compatible with unity for peripheral and semi-peripheral collisions, while in most central collisions it is reduced to about 0.65. The results at forward rapidity are in agreement within the uncertainties with the ones at midrapidity. The similarity of the two results hints for similar mechanisms driving the interaction of the \(\phi \) meson with the bulk and its hydrodynamical evolution, in the two rapidity ranges at intermediate \(p_\mathrm {T}\).
Notes
In the ALICE reference frame the muon spectrometer covers negative \(\eta \). However, we use positive values when referring to y.
The trigger threshold is not at a sharp value, but defined here as the \(p_\mathrm {T}\) value for which the trigger probability is 50%.
We used a version of the EPOS 3.101 generator, customized by the authors, in which the spectra for the \(\phi \) decaying into dimuons were determined by the kinematics of the \(\phi \) at the moment of its decay, assuming that the decay muons do not interact with the surrounding medium. On the other side, kaons originating from the \(\phi \) decay are allowed to rescatter inside the hadronic medium and thus emerge with an altered momentum distribution.
References
P. Koch, B. Müller, J. Rafelski, Strangeness in relativistic heavy ion collisions. Phys. Rep. 142, 167–262 (1986)
A. Tounsi, K. Redlich, Strangeness enhancement and canonical suppression. arXiv:hep-ph/0111159
A. Shor, \(\phi \)-meson production as a probe of the Quark-Gluon Plasma. Phys. Rev. Lett. 54, 1122–1125 (1985)
CERES Collaboration, D. Adamová, et al., Leptonic and charged kaon decay modes of the \(\phi \) meson measured in heavy-ion collisions at the CERN Super Proton Synchrotron. Phys. Rev. Lett. 96, 152301 (2006). arXiv:nucl-ex/0512007
NA60 Collaboration, R. Arnaldi et al., A comparative measurement of \(\phi \rightarrow K^+ K^-\) and \(\phi \rightarrow \mu ^+ \mu ^-\) in In-In collisions at the CERN SPS. Phys. Lett. B 699, 325–329 (2011). arXiv:1104.4060 [nucl-ex]
ALICE Collaboration, B.B. Abelev et al., \(K^*(892)^0\) and \(\phi (1020)\) production in Pb-Pb collisions at \(\sqrt{s{\rm NN}}\) = 2.76 TeV. Phys. Rev. C 91, 024609 (2015). arXiv:1404.0495 [nucl-ex]
A.G. Knospe, C. Markert, K. Werner, J. Steinheimer, M. Bleicher, Hadronic resonance production and interaction in partonic and hadronic matter in the EPOS3 model with and without the hadronic afterburner UrQMD. Phys. Rev. C 93, 014911 (2016). arXiv:1509.07895 [nucl-th]
D. Lissauer, E. Shuryak, K meson modification in hot hadronic matter may be detected via \(\phi \) meson decays. Phys. Lett. B 253, 15–18 (1991)
Y. Aoki, Z. Fodor, S. Katz, K. Szabó, The QCD transition temperature: results with physical masses in the continuum limit. Phys. Lett. B 643, 46–54 (2006). arXiv:0903.4155 [hep-lat]
M. Cheng, N.H. Christ, S. Datta, J. van der Heide, C. Jung, F. Karsch, O. Kaczmarek, E. Laermann, R.D. Mawhinney, C. Miao, P. Petreczky, K. Petrov, C. Schmidt, T. Umeda, Transition temperature in QCD. Phys. Rev. D 74, 054507 (2006). arXiv:hep-lat/0608013
F. Klingl, T. Waas, W. Weise, Modification of the \(\phi \)-meson spectrum in nuclear matter. Phys. Lett. B 431, 254–262 (1998). arXiv:hep-ph/9709210
S. Johnson, B. Jacak, A. Drees, Rescattering of vector meson daughters in high energy heavy ion collisions. Eur. Phys. J. C 18, 645–649 (2001). arXiv:nucl-th/9909075
R. Rapp, J. Wambach, H. van Hees, The chiral restoration transition of QCD and low mass dileptons. Landolt-Bornstein 23, 134 (2010). arXiv:0901.3289 [hep-ph]
V.L. Eletsky, M. Belkacem, P.J. Ellis, J.I. Kapusta, Properties of \(\rho \) and \(\omega \) mesons at finite temperature and density as inferred from experiment. Phys. Rev. C 64, 035202 (2001). arXiv:nucl-th/0104029
NA49 Collaboration, C. Alt, et al., Energy dependence of \(\phi \) meson production in central Pb+Pb collisions at \(\sqrt{s_{{\rm NN}}}\) = 6 to 17 GeV. Phys. Rev. C 78, 044907 (2008). arXiv:0806.1937 [nucl-ex]
NA60 Collaboration, R. Arnaldi, et al., \(\phi \) production in In-In Collisions at 158 A-GeV. Eur. Phys. J. C 64, 1–18 (2009). arXiv:0906.1102 [hep-ex]
STAR Collaboration, B. Abelev, et al., Measurements of \(\phi \) meson production in relativistic heavy-ion collisions at the BNL Relativistic Heavy Ion Collider (RHIC). Phys. Rev. C 79, 064903 (2009). arXiv:0809.4737 [nucl-ex]
STAR Collaboration, L. Adamczyk et al., Measurements of dielectron production in Au+Au collisions at \(\sqrt{{s}_{{\rm NN}}} = 200\) GeV from the STAR experiment. Phys. Rev. C 92, 024912 (2015). arXiv:1504.01317 [hep-ex]
PHENIX Collaboration, S.S. Adler et al., Production of \(\phi \) mesons at midrapidity in \(\sqrt{{s}_{\rm NN}} = 200\) GeV Au+Au collisions at relativistic energies. Phys. Rev. C. 72, 014903 (2005). arXiv:nucl-ex/0410012
J. Cleymans, I. Kraus, H. Oeschler, K. Redlich, S. Wheaton, Statistical model predictions for particle ratios at \(\sqrt{s_{\rm NN}} = 5.5\) TeV. Phys. Rev. C 74, 034903 (2006). arXiv:hep-ph/0604237
J. Rafelski, J. Letessier, G. Torrieri, Centrality dependence of bulk fireball properties at RHIC. Phys. Rev. C 72, 024905 (2005). arXiv:nucl-th/0412072
M. Petrán, J. Letessier, V. Petráček, J. Rafelski, Hadron production and Quark-Gluon Plasma hadronization in Pb-Pb collisions at \(\sqrt{s_{\rm NN}} = 2.76\) TeV. Phys. Rev. C 88, 034907 (2013). arXiv:1303.2098 [hep-ph]
A. Andronic, P. Braun-Munzinger, J. Stachel, Thermal hadron production in relativistic nuclear collisions: the hadron mass spectrum, the horn, and the QCD phase transition. Phys. Lett. B 673, 142–145 (2009). arXiv:0812.1186 [nucl-th]. [Erratum: Phys. Lett. B 678, 516 (2009)]
F. Becattini, P. Castorina, A. Milov, H. Satz, A comparative analysis of statistical hadron production. Eur. Phys. J. C 66, 377–386 (2010). arXiv:0911.3026 [hep-ph]
P. Bozek, I. Wyskiel-Piekarska, Particle spectra in Pb-Pb collisions at \(\sqrt{s_{{\rm NN}}}\) = 2.76 TeV. Phys. Rev. C 85, 064915 (2012). arXiv:1203.6513 [nucl-th]
K. Werner, I. Karpenko, M. Bleicher, T. Pierog, S. Porteboeuf-Houssais, Jets, bulk matter, and their interaction in heavy ion collisions at several TeV. Phys. Rev. C 85, 064907 (2012). arXiv:1203.5704 [nucl-th]
P. Braun-Munzinger, J. Stachel, J. Wessels, N. Xu, Thermal equilibration and expansion in nucleus-nucleus collisions at the AGS. Phys. Lett. B 344, 43–48 (1995). arXiv:nucl-th/9410026
P. Braun-Munzinger, J. Stachel, J. Wessels, N. Xu, Thermal and hadrochemical equilibration in nucleus-nucleus collisions at the SPS. Phys. Lett. B 365, 1–6 (1996). arXiv:nucl-th/9508020
D. d’Enterria, Jet quenching. Landolt-Bornstein 23, 471 (2010). arXiv:0902.2011 [nucl-ex]
R.C. Hwa, C.B. Yang, Scaling behavior at high \({p}_{T}\) and the \(p/\pi \) ratio. Phys. Rev. C 67, 034902 (2003). arXiv:nucl-th/0211010
R.J. Fries, B. Müller, C. Nonaka, S.A. Bass, Hadronization in heavy-ion collisions: recombination and fragmentation of partons. Phys. Rev. Lett. 90, 202303 (2003). arXiv:nucl-th/0301087
V. Greco, C.M. Ko, P. Lévai, Parton coalescence and the antiproton/pion anomaly at RHIC. Phys. Rev. Lett. 90, 202302 (2003). arXiv:nucl-th/0301093
PHENIX Collaboration, K. Adcox et al., Centrality dependence of \(\pi ^+\) / \(\pi ^-\), K\(^+\) / K\(^-\), p and \(\bar{\rm p}\) production from \(\sqrt{s_{\rm NN}} =\) 130 GeV Au+Au collisions at RHIC. Phys. Rev. Lett. 88, 242301 (2002). arXiv:nucl-ex/0112006
PHENIX Collaboration, S.S. Adler et al., Scaling properties of proton and anti-proton production in \(\sqrt{s_{\rm NN}} = 200\) GeV Au+Au collisions. Phys. Rev. Lett. 91, 172301 (2003). arXiv:nucl-ex/0305036
STAR Collaboration, J. Adams et al., Particle type dependence of azimuthal anisotropy and nuclear modification of particle production in Au+Au collisions at \(\sqrt{s_{\rm NN}} = 200\) GeV. Phys. Rev. Lett. 92, 052302 (2004). arXiv:nucl-ex/0306007
ALICE Collaboration, B. Abelev et al., Production of charged pions, kaons and protons at large transverse momenta in pp and Pb–Pb collisions at \(\sqrt{s_{{\rm NN}}}\) = 2.76 TeV. Phys. Lett. B 736, 196–207, (2014). arXiv:1401.1250 [nucl-ex]
ALICE Collaboration, K. Aamodt et al., The ALICE experiment at the CERN LHC. JINST 3, S08002 (2008)
ALICE Collaboration, B. Abelev et al., Performance of the ALICE experiment at the CERN LHC. Int. J. Mod. Phys. A 29, 1430044 (2014). arXiv:1402.4476 [nucl-ex]
ALICE Collaboration, B. Abelev et al., Centrality, rapidity and transverse momentum dependence of \(J/\psi \) suppression in Pb–Pb collisions at \(\sqrt{s_{{\rm NN}}}\) = 2.76 TeV. Phys. Lett. B 734, 314–327 (2014). arXiv:1311.0214 [nucl-ex]
ALICE Collaboration, B. Abelev et al., Centrality determination of Pb–Pb collisions at \(\sqrt{s_{{\rm NN}}}\) = 2.76 TeV with ALICE. Phys. Rev. C 88, 044909 (2013). arXiv:1301.4361 [nucl-ex]
ALICE Collaboration, B. Abelev et al., Light vector meson production in pp collisions at \(\sqrt{s} = 7\) TeV. Phys. Lett. B 710, 557–568 (2012). arXiv:1112.2222 [nucl-ex]
R. Brun, F. Bruyant, M. Maire, A.C. McPherson, P. Zanarini, GEANT 3: user’s guide Geant 3.10, Geant 3.11; rev. version. Tech. Rep. CERN-DD-EE-84-01, Geneva, 1987
T. Sjostrand, S. Mrenna, P.Z. Skands, PYTHIA 6.4 physics and manual. JHEP 05, 026 (2006). arXiv:hep-ph/0603175
LEBC-EHS Collaboration, M. Aguilar-Benitez et al., Inclusive particle production in 400 GeV/c pp-interactions. Z. Phys. C 50, 405–426 (1991)
G. Agakichiev et al., Neutral meson production in p-Be and p-Au collisions at 450 GeV beam energy. Eur. Phys. J. C 4, 249–257 (1998)
A. Uras for the NA60 Collaboration, Low mass dimuon production in pA collisions at \(\sqrt{s} = 27.5\) GeV with NA60. J. Phys. G Nucl. Part. Phys. 38, 124180 (2011). arXiv:1108.0970 [hep-ex]
C.M. Buttar, D. Clements, I. Dawson, A. Moraes, Simulations of minimum bias events and the underlying event, MC tuning and predictions for the LHC. Acta Phys. Pol. B 35, 433 (2004)
R. Field, Physics at the Tevatron. Acta Phys. Pol. B 39, 2611 (2008)
LHCb Collaboration, R. Aaij et al., Measurement of \(\sigma (pp \rightarrow b \bar{b} X)\) at \(\sqrt{s} = 7~{\rm TeV}\) in the forward region. Phys. Lett. B 694, 209–216 (2010). arXiv:1009.2731 [hep-ex]
LHCb Collaboration, R. Aaij et al., Prompt charm production in pp collisions at \(\sqrt{s}\) = 7 TeV. Nucl. Phys. B 871, 1–20 (2013). arXiv:1302.2864 [hep-ex]
R. Rapp, J. Wambach, Low-mass dileptons at the CERN-SpS: evidence for chiral restoration? Eur. Phys. J. A 6, 415–420 (1999). arXiv:hep-ph/9907502
H. van Hees, R. Rapp, Dilepton radiation at the CERN Super-Proton Synchrotron. Nucl. Phys. A 806, 339–387 (2008). arXiv:0711.3444 [hep-ph]
R. Rapp, Theory of soft electromagnetic emission in heavy-ion collisions. Acta Phys. Pol. B 42, 2823 (2011). arXiv:1110.4345 [nucl-th]
ALICE Collaboration, Addendum of the Letter of Intent for the upgrade of the ALICE Experiment: the Muon Forward Tracker. Tech. Rep. CERN-LHCC-2013-014, LHCC-I-022-ADD-1, CERN, Geneva, 2013
J.E. Gaiser, Charmonium Spectroscopy From Radiative Decays of the \(J/\psi \) and \(\psi ^\prime \). PhD thesis, SLAC, 1982. SLAC-0255, UMI-83-14449-MC, SLAC-R-0255, SLAC-R-255
Particle Data Group Collaboration, C. Patrignani et al., Review of particle physics. Chin. Phys. C 40, 100001 (2016)
ALICE Collaboration, J. Adam et al., \(\phi \)-meson production at forward rapidity in p-Pb collisions at \(\sqrt{s_{\rm NN}}\) = 5.02 TeV and in pp collisions at \(\sqrt{s}\) = 2.76 TeV. Phys. Lett. B 768, 203–217 (2017). arXiv:1506.09206 [nucl-ex]
H.J. Drescher, M. Hladik, S. Ostapchenko, T. Pierog, K. Werner, Parton based Gribov–Regge theory. Phys. Rep. 350, 93–289 (2001). arXiv:hep-ph/0007198
K. Werner, B. Guiot, I. Karpenko, T. Pierog, Analyzing radial flow features in p-Pb and p-p collisions at several TeV by studying identified-particle production with the event generator EPOS3. Phys. Rev. C 89, 064903 (2014). arXiv:1312.1233 [nucl-th]
X.-N. Wang, M. Gyulassy, HIJING: a Monte Carlo model for multiple jet production in pp, pA, and AA collisions. Phys. Rev. D 44, 3501–3516 (1991)
ALICE Collaboration, J. Adam et al., Centrality dependence of the nuclear modification factor of charged pions, kaons, and protons in Pb–Pb collisions at \(\sqrt{s_{\rm NN}} = 2.76\) TeV. Phys. Rev. C 93, 034913 (2016). arXiv:1506.07287 [nucl-ex]
PHENIX Collaboration, A. Adare et al., Nuclear modification factors of \(\phi \) mesons in d+Au, Cu+Cu and Au+Au collisions at \(\sqrt{s_{{\rm NN}}} = 200 GeV\). Phys. Rev. C 83, 024909 (2011). arXiv:1004.3532 [nucl-ex]
Acknowledgements
The ALICE Collaboration would like to thank all its engineers and technicians for their invaluable contributions to the construction of the experiment and the CERN accelerator teams for the outstanding performance of the LHC complex. The ALICE Collaboration gratefully acknowledges the resources and support provided by all Grid centres and the Worldwide LHC Computing Grid (WLCG) collaboration. The ALICE Collaboration acknowledges the following funding agencies for their support in building and running the ALICE detector: A. I. Alikhanyan National Science Laboratory (Yerevan Physics Institute) Foundation (ANSL), State Committee of Science and World Federation of Scientists (WFS), Armenia; Austrian Academy of Sciences and Nationalstiftung für Forschung, Technologie und Entwicklung, Austria; Ministry of Communications and High Technologies, National Nuclear Research Center, Azerbaijan; Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Universidade Federal do Rio Grande do Sul (UFRGS), Financiadora de Estudos e Projetos (Finep) and Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), Brazil; Ministry of Science & Technology of China (MSTC), National Natural Science Foundation of China (NSFC) and Ministry of Education of China (MOEC) , China; Ministry of Science and Education, Croatia; Ministry of Education, Youth and Sports of the Czech Republic, Czech Republic; The Danish Council for Independent Research | Natural Sciences, the Carlsberg Foundation and Danish National Research Foundation (DNRF), Denmark; Helsinki Institute of Physics (HIP), Finland; Commissariat à l’Energie Atomique (CEA) and Institut National de Physique Nucléaire et de Physique des Particules (IN2P3) and Centre National de la Recherche Scientifique (CNRS), France; Bundesministerium für Bildung, Wissenschaft, Forschung und Technologie (BMBF) and GSI Helmholtzzentrum für Schwerionenforschung GmbH, Germany; General Secretariat for Research and Technology, Ministry of Education, Research and Religions, Greece; National Research, Development and Innovation Office, Hungary; Department of Atomic Energy Government of India (DAE), Department of Science and Technology, Government of India (DST), University Grants Commission, Government of India (UGC) and Council of Scientific and Industrial Research (CSIR), India; Indonesian Institute of Science, Indonesia; Centro Fermi-Museo Storico della Fisica e Centro Studi e Ricerche Enrico Fermi and Istituto Nazionale di Fisica Nucleare (INFN), Italy; Institute for Innovative Science and Technology , Nagasaki Institute of Applied Science (IIST), Japan Society for the Promotion of Science (JSPS) KAKENHI and Japanese Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan; Consejo Nacional de Ciencia (CONACYT) y Tecnología, through Fondo de Cooperación Internacional en Ciencia y Tecnología (FONCICYT) and Dirección General de Asuntos del Personal Academico (DGAPA), Mexico; Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO), Netherlands; The Research Council of Norway, Norway; Commission on Science and Technology for Sustainable Development in the South (COMSATS), Pakistan; Pontificia Universidad Católica del Perú, Peru; Ministry of Science and Higher Education and National Science Centre, Poland; Korea Institute of Science and Technology Information and National Research Foundation of Korea (NRF), Republic of Korea; Ministry of Education and Scientific Research, Institute of Atomic Physics and Romanian National Agency for Science, Technology and Innovation, Romania; Joint Institute for Nuclear Research (JINR), Ministry of Education and Science of the Russian Federation and National Research Centre Kurchatov Institute, Russia; Ministry of Education, Science, Research and Sport of the Slovak Republic, Slovakia; National Research Foundation of South Africa, South Africa; Centro de Aplicaciones Tecnológicas y Desarrollo Nuclear (CEADEN), Cubaenergía, Cuba and Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas (CIEMAT), Spain; Swedish Research Council (VR) and Knut & Alice Wallenberg Foundation (KAW), Sweden; European Organization for Nuclear Research, Switzerland; National Science and Technology Development Agency (NSDTA), Suranaree University of Technology (SUT) and Office of the Higher Education Commission under NRU project of Thailand, Thailand; Turkish Atomic Energy Agency (TAEK), Turkey; National Academy of Sciences of Ukraine, Ukraine; Science and Technology Facilities Council (STFC), United Kingdom; National Science Foundation of the United States of America (NSF) and United States Department of Energy, Office of Nuclear Physics (DOE NP), United States of America.
Author information
Authors and Affiliations
Consortia
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Acharya, S., Acosta, FT., Adamová, D. et al. \(\phi \) meson production at forward rapidity in Pb–Pb collisions at \(\sqrt{s_\mathrm {NN}}=2.76\) TeV. Eur. Phys. J. C 78, 559 (2018). https://doi.org/10.1140/epjc/s10052-018-6034-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6034-3