Rare $\Lambda _c\rightarrow p \ell ^+\ell ^-$ decay in the relativistic quark model

Abstract

The relativistic quark model based on the quasipotential approach with the QCD-motivate potential is employed for the calculation of the form factors of the $\Lambda _c\rightarrow p$ rare weak transitions. Their momentum dependence is explicitly determined without additional assumptions and extrapolations in the whole kinematical range of the momentum transfer squared $q^2$. The differential $\Lambda _c\rightarrow p l^+l^-$ decay branching fractions and angular distributions are calculated on the basis of these form factors. Both the perturbative and effective Wilson coefficients, which include contributions of vector meson resonances, are used. The calculated branching fraction of the $\Lambda _c\rightarrow p \mu ^+\mu ^-$ rare decay is well consistent with the experimental upper limit very recently set by the LHCb Collaboration.

1 Introduction

In the standard model the $\Lambda _c\rightarrow p \ell ^+\ell ^-$ rare weak decays are governed by the $c\rightarrow u$ quark transitions which proceed through the flavour-changing neutral currents. The short-distance contributions to these decays are expected to be strongly suppressed by the Glashow–Iliuopoulos–Maiani (GIM) mechanism [1]. Indeed, the corresponding penguin diagrams get contributions only from the down-type quarks which have negligible masses compared to the electroweak scale thus providing almost complete GIM cancellation. Therefore a significant role is played by the long-distance effects which are expected to arise from the meson resonances decaying to the lepton pair. As a result process involving $c\rightarrow u l^+l^-$ transitions are far less explored than the corresponding $b\rightarrow s l^+l^-$ transitions both theoretically and experimentally. The exclusive decays proceeding through such transitions are mostly studied for the rare D-meson decays (see e.g. recent papers [2,3,4] and references therein). The baryon case $\Lambda _c\rightarrow p l^+l^-$ received substantially less attention. The estimates of the corresponding form factors and decay branching fractions in the light cone QCD sum rules are given in Refs. [5, 6]. The lattice QCD determination of the $\Lambda _c\rightarrow p$ form factors and the $\Lambda _c\rightarrow p \mu ^+\mu ^-$ rare decay observables was recently presented in Ref. [7]. Experimentally first constraints on the $\Lambda _c$ rare decay branching fractions were set by the BABAR Collaboration [8] and very recently they were significantly improved by the LHCb Collaboration [9].

In this paper we calculate the $\Lambda _c\rightarrow p$ transition form factors in the framework of the relativistic quark model based on quasipotential approach with QCD-motivated potential. We consider baryons to be the relativistic quark-diquark bound systems which wave functions were previously determined within the mass spectra calculations [10, 11]. Using the quasipotential approach we express the weak transition matrix elements through the overlap integrals of the initial and final baryon wave functions. It is important to emphasize that the momentum transfer dependence of the matrix elements and corresponding form factors is explicitly determined without additional assumptions and extrapolations in the whole available kinematical range. We previously successfully applied such approach for the study of the semileptonic and rare $\Lambda _b$ decays [12,13,14] and the semileptonic $\Lambda _c$ decays [15]. Then we use these form factors for the calculation of the differential and total decay branching fractions both with the perturbative and effective Wilson coefficients, which include the long-distance contributions from vector meson resonances, and confront the obtained results with the available experimental data.

2 Relativistic quark model

We employ the relativistic quark-diquark picture based on the quasipotential approach for the description of baryon properties. The diquark as a bound state of two quarks and the baryon as a quark-diquark bound system are described by the diquark wave function $\Psi _{d}$ and by the baryon wave function $\Psi _{B}$, which satisfy the relativistic quasipotential equation of the Schrödinger type [16,17,18]

$$\begin{aligned} {\left( \frac{b^2(M)}{2\mu _{R}}\!-\!\frac{\mathbf{p}^2}{2\mu _{R}}\right) \Psi _{d,B}(\mathbf{p})} \!=\!\int \frac{d^3 q}{(2\pi )^3} V(\mathbf{p,q};M)\Psi _{d,B}(\mathbf{q}). \end{aligned}$$

(1)

Here the relativistic reduced mass is defined as

$$\begin{aligned} \mu _{R}=\frac{M^4-(m^2_1-m^2_2)^2}{4M^3}, \end{aligned}$$

and the center-of-mass system relative momentum squared on mass shell is given by

$$\begin{aligned} {b^2(M) } =\frac{[M^2-(m_1+m_2)^2][M^2-(m_1-m_2)^2]}{4M^2}, \end{aligned}$$

where M is the bound state mass (diquark or baryon), $m_{1,2}$ are the masses of quarks ($q_1$ and $q_2$) which form the diquark or of the diquark (d) and quark (q) which form the baryon (B), and $\mathbf{p}$ is their relative momentum.

To construct the quasipotentials $V(\mathbf{p,q};M)$ of the quark-quark or quark-diquark interaction we use the off-mass-shell scattering amplitude, projected onto the positive energy states. The effective quark interaction is taken to be the sum of the one-gluon exchange term and the mixture of long-range vector and scalar linear confining potentials with the mixing coefficient $\varepsilon$. In the nonrelativistic limit they are given by

$$\begin{aligned} V_\mathrm{OG}(r)= & {} -\frac{4}{3}\frac{\alpha _s}{r}, \\V^V_\mathrm{conf}(r)= & {} (1-\varepsilon )(Ar+B),\\ V^S_\mathrm{conf}(r)= & {} \varepsilon (Ar+B), \end{aligned}$$

(2)

and their sum

$$\begin{aligned} V(r)=V_\mathrm{OG}(r)+V^V_\mathrm{conf}(r)+ V^S_\mathrm{conf}(r)=-\frac{4}{3}\frac{\alpha _s}{r}+Ar+B \end{aligned}$$

reproduce the widely used Cornell-like potential. Note that we use the freezing [19, 20] QCD coupling constant $\alpha _s$. As in the case of mesons [16,17,18], we also assume that the vector confining potential contains not only the Dirac term but the additional Pauli term, thus introducing the anomalous chromomagnetic quark moment $\kappa$:

$$\begin{aligned} \Gamma _{\mu }(\mathbf{k})=\gamma _{\mu }+ \frac{i\kappa }{2m}\sigma _{\mu \nu }\tilde{k}^{\nu }, \quad \tilde{k}=(0,\mathbf{k}). \end{aligned}$$

(3)

The explicit expressions for the quasipotentials are given in Refs. [21, 22].

All parameters of the model were fixed previously from calculations of meson and baryon properties [16,17,18, 21, 22]. We use the following values for the constituent quark masses: $m_u=m_d=0.33$ GeV, $m_s=0.5$ GeV, $m_c=1.55$ GeV and for the parameters of the linear potential: $A=0.18$ GeV$^2$ and $B=-0.3$ GeV. The value of the mixing coefficient of vector and scalar confining potentials $\varepsilon =-1$ has been determined from the consideration of the heavy quark expansion for the semileptonic heavy meson decays and the charmonium radiative decays [16,17,18]. While the universal Pauli interaction constant $\kappa =-1$ has been fixed from the analysis of the fine splitting of heavy quarkonia ${}^3P_J$-states [16,17,18]. Note that the long-range chromomagnetic contribution to the potential, which is proportional to $(1+\kappa )$, vanishes for the chosen value of $\kappa =-1$ in agreement with the flux tube model.

3 Form factors of the rare weak $\Lambda _c\rightarrow p$ transitions

To study the rare weak decays of the $\Lambda _c$ baryon we need to calculate the matrix element of the weak current between the $\Lambda _c$ and proton (p). This matrix element in the quasipotential approach is given by the expression

$$\begin{aligned}&\left\langle p(p_{p}) \vert J^W_\mu \vert \Lambda _c(p_{\Lambda _c})\right\rangle \nonumber \\&\quad =\int \frac{d^3p\, d^3q}{(2\pi )^6} \bar{\Psi }_{p\,\mathbf{p}_{{p}}}(\mathbf{p})\Gamma _\mu (\mathbf{p},\mathbf{q})\Psi _{\Lambda _c\,\mathbf{p}_{\Lambda _c}}(\mathbf{q}), \end{aligned}$$

(4)

where $\Gamma _\mu (\mathbf{p},\mathbf{q})$ is the two-particle vertex function and $\Psi _{B\,\mathbf{p}_{B}}$ are the B ($B=\Lambda _c,p$) baryon wave functions projected onto the positive-energy states of quarks. The vertex function $\Gamma$ receives relativistic contributions both from the impulse approximation diagram and from the diagrams with the intermediate negative-energy states [12]. Since the final proton is moving with the momentum $\mathbf{p}_{p}$ in the $\Lambda _c$ rest frame ($\mathbf{p}_{\Lambda _c}=0$) the boosts of the proton wave function are taken in to account by the wave function transformation [12]

$$\begin{aligned} \Psi _{{p}\,\mathbf{p }_p}(\mathbf{p})=D_{u}^{1/2}\left( R_{L_{\mathbf{p}_p}}^W\right) \Psi _{{p}\,\mathbf{0}}(\mathbf{p}), \end{aligned}$$

(5)

where $\Psi _{{p}\,\mathbf{0}}$ is the proton wave function in the rest frame, $R^W$ is the Wigner rotation, $L_\mathbf{p}$ is the Lorentz boost from the baryon rest frame to a moving one with the momentum $\mathbf{p}_p$, and $D^{1/2}_u(R^W)$ is the rotation matrix of the active (u) quark spin. Note that we consider a proton as the bound state of the u quark and scalar ud diquark.

Table 1 Form factors of the weak $\Lambda _c\rightarrow p$ transition

The hadronic matrix elements for the weak decay $\Lambda _c\rightarrow p\ell ^+\ell ^-$ can be parameterized by the following set of the invariant form factors [23,24,25]

(6)

Explicit expressions for the corresponding form factors in our model are given in Refs. [12,13,14]. The form factors are expressed through the overlap integrals of the baryon wave functions which we take from the mass spectrum calculations [10, 11]. All relativistic effects including transformations of the proton wave functions from the rest to moving reference frame (5) and contributions of the intermediate negative-energy states are consistently taken into account. It is important to point out that the momentum transfer $q^2$ behavior is explicitly determined in the whole kinematical range without extrapolations or additional assumptions which are used in most of other theoretical considerations. This fact improves the reliability of the form factor calculations.

The calculated form factors are well approximated by the following expressions

$$\begin{aligned} F(q^2)= \frac{1}{{1-q^2/{M_\mathrm{pole}^2}}} \left\{ a_0 + a_1 z(q^2) + a_2 [z(q^2)]^2 \right\} , \end{aligned}$$

(7)

where the variable

$$\begin{aligned} z(q^2) = \frac{\sqrt{t_+-q^2}-\sqrt{t_+-t_0}}{\sqrt{t_+-q^2}+\sqrt{t_+-t_0}}, \end{aligned}$$

(8)

$t_+=(M_D+M_\pi )^2$ and $t_0 = q^2_\mathrm{max} = (M_{\Lambda _c} - M_{p})^2$. The pole masses have the values: $M_\mathrm{pole}\equiv M_{D^*}=2.010$ GeV for $f_{1,2}^V$, $f_{1,2}^{TV}$; $M_\mathrm{pole}\equiv M_{D_{1}}=2.423$ GeV for $f_{1,2}^A$, $f_{1,2}^{TA}$; $M_\mathrm{pole}\equiv M_{D_{0}}=2.351$ GeV for $f_{3}^V$; $M_\mathrm{pole}\equiv M_{D}=1.870$ GeV for $f_{3}^A$. The fitted values of the parameters $a_0$, $a_1$, $a_2$ as well as the values of form factors at maximum $q^2=0$ and zero recoil $q^2=q^2_\mathrm{max}$ are given in Table 1. The difference of the approximated form factors from the calculated ones does not exceed 0.5%. Our model form factors are plotted in Fig. 1.

Fig. 1

Form factors of the rare $\Lambda _c\rightarrow p$ transition

We compare our results for the form factors $f^{V,A,TV,TA}_i$ at the maximum recoil point $q^2=0$ with the predictions of other approaches in Table 2. The covariant confined quark model was used in Refs. [24, 25]. The authors of Refs. [26, 27] employ the QCD light-cone sum rules. The calculations in Ref. [28] are based on full QCD sum rules at light cone. We find reasonable agreement with results of Refs. [24, 25, 27], while predictions of Ref. [28] are substantially different for most of form factors. Note that the tensor $f^{TV,TA^{}}_{1,2}$ form factors were not calculated in Refs. [24, 25, 27, 28]. It is not possible to present tensor form factors from the light-cone QCD sum rules [5], since the authors use a different parametrization for the matrix element involving tensor current which contains two extra form factors (6 instead of usual 4).

Table 2 Comparison of theoretical predictions for the form factors of weak baryon $\Lambda _c\rightarrow p$ decays at maximum recoil point $q^2=0$

Fig. 2

Helicity form factors of the rare $\Lambda _c\rightarrow p$ transition

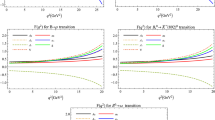
Recently the form factors of the weak $\Lambda _c\rightarrow p$ transitions were calculated on the lattice [7]. The author used the helicity-based definition of the form factors. The relation between these form factors and the ones defined by Eq. (6) are given in Refs. [13, 14]. We plot the helicity form factors of the rare $\Lambda _c\rightarrow p$ transition obtained in our model in Fig. 2. In Table 3 we compare our results for these form factors with the values calculated on the lattice [7] both at minimum $q^2=q^2_\mathrm{max}$ and maximum $q^2=0$ recoil of the final proton. We find that our and lattice form factors at $q^2=0$ have close values, while most of the lattice form factors at $q^2=q^2_\mathrm{max}$ have somewhat larger values than ours. Although we find the similar behaviour of the form factors, the lattice ones in general grow more rapidly than ours with the growth of the $q^2$.

4 Rare $\Lambda _c$ decays

The low-energy effective Hamiltonian for the $c\rightarrow u$ transitions can be written as follows [4]

$$\begin{aligned} {{\mathcal {H}}}_\mathrm{eff} =-\frac{4G_F}{\sqrt{2}}\left( V_{cb}^*V_{ub}{{\mathcal {H}}}_\mathrm{eff}^{(b)}+V_{cd}^*V_{ud}{{\mathcal {H}}}_\mathrm{eff}^{(d)}\right) , \end{aligned}$$

(9)

where

$$\begin{aligned} {{\mathcal {H}}}_\mathrm{eff}^{(b)}= & {} c_1{{\mathcal {O}}}_1^s+c_2{{\mathcal {O}}}_2^s+\sum _{i=3}^{10}c_i{{\mathcal {O}}}_i,\\ {{\mathcal {H}}}_\mathrm{eff}^{(d)}= & {} c_1\left( {{\mathcal {O}}}_1^s-{{\mathcal {O}}}_1^d\right) +c_2\left( {{\mathcal {O}}}_2^s-{{\mathcal {O}}}_2^d\right) , \end{aligned}$$

and $G_F$ is the Fermi constant, $V_{ij}$ denote the Cabibbo–Kobayashi–Maskawa matrix elements, $c_i$ are the Wilson coefficients and ${{\mathcal {O}}}_i^{(q)}$ are the standard model operators which expressions can be found e.g. in Ref. [4].

Table 3 Comparison of our predictions with lattice data for the helicity form factors of weak baryon $\Lambda _c\rightarrow p$ decays at minimum $q^2=q^2_\mathrm{max}$ and maximum $q^2=0$ recoil

Then the matrix element of the $c\rightarrow u l^+l^-$ transition amplitude between baryon states can be written in the form similar to the $b\rightarrow s l^+l^-$ transition [13, 14]

$$\begin{aligned} {{\mathcal {M}}}(\Lambda _c\rightarrow p l^+l^-)=\frac{G_F\alpha }{2\sqrt{2}\pi } \left[ T^{(1)}_\mu (\bar{l}\gamma ^\mu l)+T^{(2)}_\mu (\bar{l}\gamma ^\mu \gamma _5l)\right] , \end{aligned}$$

(10)

where

$$\begin{aligned} T^{(1)}_\mu= & {} c_9^\mathrm{eff}(q^2)\left\langle p|\bar{u} \gamma ^\mu (1-\gamma ^5)c|\Lambda _c\right\rangle \nonumber \\&-\frac{2m_c}{q^2}c_7^\mathrm{eff}(q^2)\left\langle p|\bar{u} i\sigma ^{\mu \nu } q_\nu (1+\gamma ^5)c|\Lambda _c\right\rangle ,\nonumber \\ T^{(2)}_\mu= & {} V_{cb}^*V_{ub}c_{10}\left\langle p|\bar{u} \gamma ^\mu (1-\gamma ^5)c|\Lambda _c\right\rangle . \end{aligned}$$

(11)

The expressions for $T^{(m)}$ ($m=1,2$) in terms of the form factors $f^{V,A,TV,TA}_i$ and the Wilson coefficients are given in Refs. [13, 14].

The effective Wilson coefficient $c_9^\mathrm{eff}$ contains additional effects from quark loops which can be treated within perturbation theory as well as long-distance contributions of the vector resonances $\rho ,\omega$ and $\phi$ decaying in to lepton pair $l^+l^-$. The perturbative part is given by [29]

$$\begin{aligned} c_9^\mathrm{eff}(q^2)= & {} \left( {V_{cd}^*V_{ud}}+{V_{cs}^*V_{us}}\right) \Biggl [c_9 +h(m_c, q^2)\nonumber \\&\times \left( 7c_3 + \frac{4}{3}c_4 + 76c_5 + \frac{64}{3} c_6\right) \nonumber \\&-\,h(m_s, q^2) (3 c_3 + 30 c_5)+\frac{4}{3} h(0,q^2) \nonumber \\&\times \left( 3c_3 + c_4 + \frac{69}{2} c_5 + 16 c_6\right) + \frac{8}{3} (c_3 + 10 c_5)\Biggr ]\nonumber \\&-\left( V_{cd}^*V_{ud} h(0,q^2)\right. \nonumber \\&\left. +\,V_{cs}^*V_{us}h(m_s, q^2)\right) \left( \frac{2}{3} c_1 + \frac{1}{2} c_2\right) , \end{aligned}$$

(12)

where

$$\begin{aligned}&h(m_q,q^2) = - \frac{8}{9}\ln \frac{m_q}{m_c} + \frac{8}{27} + \frac{4}{9} x \\&\quad - \frac{2}{9} (2+x) |1-x|^{1/2} \left\{ \begin{array}{ll} \ln \left| \frac{\sqrt{1-x} + 1}{\sqrt{1-x} - 1}\right| - i\pi , &{}\quad x \equiv \frac{4 m_q^2}{ q^2} < 1, \\ 2 \arctan \frac{1}{\sqrt{x-1}}, &{}\quad x \equiv \frac{4 m_q^2}{q^2} > 1, \end{array}\right. \\&\quad h(0, q^2) = \frac{8}{27} - \frac{4}{9} \ln \frac{q^2}{m_c^2} + \frac{4}{9} i\pi . \end{aligned}$$

From these expressions it is clearly seen that the perturbative contribution is strongly GIM suppressed. In the following calculations we take the values of the Wilson coefficients $c_i$ form Ref. [29] and the effective Wilson coefficient $c_7^\mathrm{eff}(q^2)$ from Ref. [3].

The contributions from the resonances can be modeled by the effective Wilson coefficient [3]

$$\begin{aligned}&c_9^\mathrm{R}(q^2)\nonumber \\&\quad =a_\rho e^{i\delta _\rho }\left( \frac{1}{q^2-M_\rho ^2 +iM_\rho \Gamma _\rho }-\frac{1}{3}\frac{1}{q^2-M_\omega ^2 +iM_\omega \Gamma _\omega }\right) \nonumber \\&\qquad +\frac{a_\phi e^{i\delta _\phi }}{q^2-M_\phi ^2 +iM_\phi \Gamma _\phi }, \end{aligned}$$

(13)

where $M_M$ and $\Gamma _M$ are masses and total widths of vector $M=\rho ,\omega ,\phi$ mesons which we take form Ref. [30]. The isospin relation between the $\rho$ and $\omega$ contributions was explicitly taken into account. The coupling $a_\phi$ can be determined from the experimental data [30]

$$\begin{aligned} \begin{aligned} Br(\Lambda _c\rightarrow p\phi )&=(1.08\pm 0.14)\times 10^{-3},\\ Br(\phi \rightarrow \mu ^+\mu ^-)&=(2.87\pm 0.19)\times 10^{-4}, \end{aligned} \end{aligned}$$

(14)

and $a_\rho$ from the recent LHCb measurement [9] of the ratio

$$\begin{aligned} \frac{Br(\Lambda _c\rightarrow p\omega )Br(\omega \rightarrow \mu ^+\mu ^-)}{Br(\Lambda _c\rightarrow p\phi )Br(\phi \rightarrow \mu ^+\mu ^-)}=0.23\pm 0.08\pm 0.03\nonumber \\ \end{aligned}$$

(15)

by approximating

$$\begin{aligned}&Br(\Lambda _c\rightarrow pV\rightarrow p\mu ^+\mu ^-)\nonumber \\&\quad = Br(\Lambda _c\rightarrow pV)Br(V\rightarrow \mu ^+\mu ^-), \quad (V=\phi ,\omega ).\nonumber \\ \end{aligned}$$

(16)

As a result the following values are obtained

$$\begin{aligned} a_\rho= & {} (0.21\pm 0.04)\ \mathrm{GeV^2},\\ a_\phi= & {} (0.13\pm 0.01)\ \mathrm{GeV^2}. \end{aligned}$$

These coefficients have close values to the ones found previously within the analysis of the rare D meson decays [3]. The relative strong phases $\delta _\rho$ and $\delta _\phi$ are not known and we vary them independently in 0 to $2\pi$ range.

The lepton angle differential decay distribution is given by

$$\begin{aligned}&\frac{d^2 \Gamma (\Lambda _c\rightarrow p l^+l^-)}{d q^2d\cos \theta }\nonumber \\&\quad =\frac{d\Gamma (\Lambda _c\rightarrow p l^+l^-)}{d q^2} \left[ \frac{3}{8}(1+\cos ^2\theta ) (1-F_L)\right. \nonumber \\&\qquad \left. + A_{FB}^\ell \cos \theta +\frac{3}{4}F_L\sin ^2\theta \right] , \end{aligned}$$

(17)

where $\theta$ is the angle between the $\Lambda _c$ baryon and the positively charged lepton in the dilepton rest frame, $A_{FB}^\ell$ is the lepton forward-backward asymmetry and $F_L$ is the fraction of the longitudinally polarized dileptons. The explicit expressions for the differential decay rates, forward-backward asymmetry and the fraction of the longitudinally polarized dileptons in terms of form factors can be straightforwardly obtained from the ones given in Refs. [13, 14].

Substituting in these expressions the decay form factors calculated within our model in the previous section we get predictions for the rare $\Lambda _c\rightarrow p l^+l^-$ decay observables. We calculate them separately both without and with the inclusion of the long-distance vector $\rho ,\omega ,\phi$ resonance contributions (LD). The obtained results for the branching fractions are given in Table 4 in comparison with other theoretical predictions. We see that our predictions agree well with recent lattice QCD calculations [7] especially for the $\Lambda _c\rightarrow p\mu ^+\mu ^-$ branching fraction with the account of the resonance contributions. On the other hand, the nonresonant branching fractions from Refs. [5, 6], which employ the light-cone sum rules, are 2 orders of magnitude lower than our predictions and 3 orders of magnitude lower than the lattice results [7]. Our prediction for the $\Lambda _c\rightarrow p\mu ^+\mu ^-$ nonresonant branching fraction is about a factor of 15 lower than the lattice QCD result [7]. Such deviation cannot be explained entirely by the above mentioned differences in the form factors, and could be additionally caused by the different choices for the perturbative effective Wilson coefficients. Thus lattice calculation includes the two-loop matrix elements of $O_1$ and $O_2$ from Ref. [31] which we do not take into account in the present consideration. We roughly estimate the uncertainty of our predictions for the nonresonant differential and total branching fractions to be about 15%. Its sources are the following: 10% comes from the uncertainties of our form factors and additional 5% emerges from the variation of the renormalization scale $\mu$ of the Wilson coefficients from $\mu =1.3\ \hbox {GeV}$ [29] to $\mu =1.5\ \hbox {GeV}$ [4].¹ Note that our value of the $\Lambda _c\rightarrow p\mu ^+\mu ^-$ nonresonant branching fraction is very close to the recent prediction [3] for the corresponding nonresonant branching fraction of the $D^+\rightarrow \pi ^+\mu ^+\mu ^-$ decay.

Table 4 Comparison of theoretical predictions for the $\Lambda _c$ rare decay branching fractions

Fig. 3

The differential branching fractions for the $\Lambda _c\rightarrow p\mu ^+\mu ^-$ rare decay. The area between dashed-dotted (orange) curves corresponds to the nonresonant predictions, while the (green) band shows resonance contributions including uncertainties in coefficients $a_\rho$ and $a_\phi$ as well as variations of the relative strong phases $\delta _\rho$ and $\delta _\phi$. The horizontal black line denotes the LHCb 90% CL upper limit [9]

Our result for the branching fraction of the $\Lambda _c\rightarrow p e^+e^-$ rare decay is well below the experimental upper limit set by the BABAR Collaboration $Br(\Lambda _c^+\rightarrow p e^+e^-)<5.5\times 10^{-6}$ [8].

In Fig. 3 we plot our predictions for the differential branching fractions of the $\Lambda _c\rightarrow p\mu ^+\mu ^-$ rare decay both without and with inclusion of the vector $\rho ,\omega ,\phi$ meson contributions. The LHCb 90% CL upper limit [9] is also given. We see that the calculated branching fraction with the account of resonances agree well with the experimental limit. If we calculate the branching fraction in a region with excluded ranges $\pm 40$ MeV around the $\omega$ and $\phi$ masses, we get the value $(1.9\pm 0.5)\times 10^{-8}$, which is in accord with experimental upper limit $Br(\Lambda _c^+\rightarrow p\mu ^+\mu ^-)<7.7\times 10^{-8}$ obtained with the same constraints. Note that the prediction with the account of resonances of Ref. [6] is significantly above this experimental limit.

In Fig. 4 we plot our prediction for the $q^2$-dependence of the fraction of the longitudinally polarized dimuons $F_L(q^2)$ for the central values of the decay parameters. The predicted value of the average longitudinal polarization fraction with the account of resonance contributions is $\langle F_L\rangle =0.52\,{\pm }\, 0.02$. The lepton forward-backward asymmetry $A_{FB}^\ell$ is proportional to the Wilson coefficient $c_{10}$ and thus vanishes in the standard model. Therefore, any experimental deviations from zero for $A_{FB}^\ell$ will be a signal of the new physics.

Fig. 4

Prediction for the fraction of longitudinally polarized dileptons $F_L(q^2)$ in the $\Lambda _c\rightarrow p \mu ^+\mu ^-$ decay. The dashed curve corresponds to the nonresonant predictions, while the solid curve shows results with the inclusion of the vector meson resonances

5 Conclusions

The $\Lambda _c\rightarrow p l^+l^-$ rare decays were investigated in the framework of the relativistic quark model. The quasipotential approach with the QCD-motivated interquark interaction was employed for the calculation of the $\Lambda _c\rightarrow p$ weak transition from factors. The relativistic effects including wave function transformations of the final proton from the rest to moving reference frame and contributions to decay processes of the intermediate negative-energy states are comprehensively taken into account. These form factors were expressed through the overlap integrals of the baryon wave functions and their $q^2$ dependence was consistently determined in the whole accessible kinematical range. No additional model assumptions and extrapolations were used thus improving the reliability of the obtained results. Reasonable agreement of the calculated helicity form factors at $q^2=0$ with recent lattice results [7] is found. However our form factors increase with growing $q^2$ slightly slowly than the lattice ones.

These form factors were used to calculate the differential and total branching fractions and angular distributions of the $\Lambda _c\rightarrow p l^+l^-$ rare decays. Both the perturbative and effective Wilson coefficients, which include the additional long-distance contributions from the vector $\rho ,\omega$ and $\phi$ resonances were used in the analysis. It was found that the perturbative term is strongly GIM suppressed and the main contribution comes from resonances modeled by a simple Breit–Wigner model, which coefficients are determined from available experimental data. The calculated branching fraction of the $\Lambda _c\rightarrow p\mu ^+\mu ^-$ decay is well consistent with the experimental upper limit $Br(\Lambda _c^+\rightarrow p\mu ^+\mu ^-)<7.7\times 10^{-8}$ at 90% confidence level recently reported by the LHCb [9].