Abstract
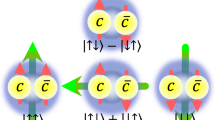
We demonstrate that spin flipping transitions occur between various quarkonium spin states due to transient magnetic field produced in non central heavy ion collisions (HICs). The inhomogeneous nature of the magnetic field results in non adiabatic evolution of (spin)states of quarkonia moving inside the transient magnetic environment. Our calculations explicitly show that the consideration of azimuthal inhomogeneity gives rise to dynamical mixing between different spin states owing to Majorana spin flipping. Notably, this effect of non-adiabaticity is novel and distinct from previously predicted mixing of the singlet and one of the triplet states of quarkonia in the presence of a static and homogeneous magnetic field.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of magnetic field in heavy ion collisions (HICs) has become an exciting trend in recent years. The existence of a strong time varying magnetic field is theoretically conjectured [1,2,3,4] and is awaiting experimental verification. Physicists are investing a lot of effort and interest to observe chiral magnetic effect [2, 5, 6]. Not only that, many other observables, too, will be affected should the magnetic field be produced. Therefore, it is quite natural to see how this magnetic field influences heavy quarkonia which, by themselves, constitute one of the major probes for the medium formed in high energy nucleus–nucleus collisions. It is obvious that the external magnetic field affects both the spatial and spin degrees of freedom of quarkonia. It is shown in some literature [7,8,9,10] how the presence of such a field impacts on the formation and dissociation of heavy quark-anti quark bound states. As far as the interaction between spin and magnetic field is concerned, the analogy with positronium atom [11,12,13] is adopted in studying the Zeeman splitting and spin mixing of quarkonium spin states. It shows that, for quarkonia also, there is spin mixing between ortho and para states, such as between 1S triplet (\(J/\Psi \) and \(\eta _c\)) and singlet (\(\Upsilon \) and \(\eta _b\)) states of charmonium and bottomonium respectively. This realisation is entirely based on the consideration of a homogeneous and constant magnetic field although a time dependent field has sometimes been considered [14]. The nature of spin mixing can radically change if we introduce an inhomogeneous magnetic field instead. Besides, the knowledge of the exact nature of this magnetic field is highly speculative till date. There are a few studies indicating that the field only lasts for a narrow span of time [1, 15], whereas, other investigations suggest that it can linger on for a longer time [16] due to the presence of the quark gluon plasma (QGP) medium formed after collision. Ergo, we decide to tackle the problem of quarkonium spin mixing from a general standpoint where the magnetic field varies both spatially and temporally. Notably, the centre of mass of quarkonia is not static, rather, it moves in the inhomogeneous magnetic environment. As the quarkonium travels from one space point to another, it experiences a varying interaction potential owing to the spatially changing magnetic field. Hence, the Hamiltonian of the system is changing with time. This time dependence becomes explicit when observed from the co-moving frame of quarkonia. Such a time dependent Hamiltonian invites us to check whether the nature of evolution of quarkonium spin states is adiabatic or non-adiabatic. Non-adiabaticity can cause spin flipping transitions (Majorana flipping) between different spin states. This sort of effect of non adiabaticity has, thus far, not been considered to the best of our knowledge. The time rate of change of the magnetic field, when observed from the rest frame of quarkonia, depends on the speed of quarkonia inside the inhomogeneous magnetic field. If the time scale of this varying field is much much smaller than that of the evolution of quarkonium spin states, the system will evolve adiabatically. On the other hand, if the magnetic field produced in HICs is rapidly decaying, it will guarantee the existence of a weak field regime where the Larmor frequency, being proportional to the field strength, is also negligibly small. As the time scale of evolution of quarkonium spin sates is inversely proportional to Larmor frequency, \(\omega \), the weak field or small \(\omega \) leads to a non-adiabatic evolution. In that case, one cannot naively hold fast to adiabaticity, rather, intricacies of non-adiabaticity may come into play.
In this article, the necessary and sufficient conditions for the occurrence of adiabatic evolution are discussed. To this end, the spin flipping transition probabilities for different spin states have been estimated by solving the Schrödinger equation with time dependent Hamiltonian. It has already been mentioned that previous works with a homogeneous field observed mixing between one of the triplet states and the singlet state of quarkonia [13]. Contrarily, considering an azimuthal inhomogeneity of magnetic field, we have explicitly witnessed the possibility of dynamical spin mixing, not only between two states, but amongst all possible states.
The magnetic field which people consider in this context is derived completely from a classical point of view by using Biot–Sovart law [17]. The magnetic field and its evolution therefore obey classical electrodynamics. This is justifiable as the field strength of the magnetic field produced in nucleus–nucleus collisions is expected to be much above the critical value [18, 19] of the field intensity where we can apply the classical equation. So the whole regime starting from strong to weak field, we can consider the magnetic field classically. In other words, when we say weak field regime, we mean the field intensity is much small compared to that of the initially produced magnetic field but still in the regime where the description through classical electrodynamics is possible. Never the less this semiclassical treatment to investigate the effect of magnetic field to quarkonium spin states can safely be used and has been employed many times in this context earlier with the justification which we just have mentioned.
2 Adiabatic and non-adiabatic spin mixing
The Hamiltonian of the system can be written as a summation of unperturbed part (\(H_{0}\)) and interaction part (\(H_I\)) due to the magnetic field. \(H_{0}\) only contains the spatial degrees of freedom because spin spin interaction has not been considered in the present work. Our point of interest is the spin-field interaction in \(H_I\) and any other term that might appear in H [8, 13] has not been taken into account here. So,
The quantity \(\vec {\mu } \) is the magnetic moment of the bound \(q{\bar{q}}\) pair. Singling out the interaction part, one can write
Here, g is the gyromagnetic ratio where, \(g=g_Q=-g_{{\bar{Q}}}\), \(\vec {S}\) is the spin and \(\mu _Q\) is the quark magneton given by \(Q/2m_Q\), \(m_Q\) being the mass of quark/antiquark. To start with, let us take the applied magnetic field to be constant and homogeneous. The field splits the otherwise degenerate energy eigenstates of the old Hamiltonian. The eigenstates of the new Hamiltonian (with magnetic field) can be written down as:
which are linear combinations of the eigenstates of the old Hamiltonian (without magnetic field), viz. \(|11\rangle \), \(|1-1\rangle \), \(|10\rangle \) and \(|00\rangle \). Equation 3 clearly shows the mixing between one of the triplet \(|10\rangle \) and singlet states \(| 00\rangle \). The discussion up to this point is just a recapitulation of previous work [12,13,14].
In the present treatment, we take a leap forward to consider the actual scenario which might be much more complicated. So, we refrain from considering a homogeneous magnetic field. In the co-moving frame of heavy quarkonia, moving in an inhomogeneous magnetic field, the interaction Hamiltonian \(H_{I}\) becomes solely time dependent as the magnetic field appears to be changing its magnitude and direction due to the inhomogeneity. Hence,
Here \(\omega =g\mu _QB\) is the Larmor frequency of the system and \(S_{u}\) is the spin along the direction \({\hat{u}}\) making an angle \(\theta \) with the z-axis and an azimuthal angle \(\phi \):
Unlike the case with homogeneous magnetic field where the field is considered to be applied in a fixed direction (say z), in the present circumstance (with inhomogeneous field) the field is changing its magnitude and direction. So, it is customary to introduce an arbitrary direction, \({\hat{u}}(t)\), along which the field would be aligned at any instant. It is worth noting that, in this case, \(H_I(t)\) and \(S_{{\hat{u}}(t)}\) have common set of eigenvectors.
The interaction Hamiltonian \(H_{I}(t)\) dictates the nature of the evolution of the energy eigenstates. Before we discuss the consequences of time dependence of the interaction Hamiltonian, let us check whether the evolution of spin states can really be adiabatic or not.
Instantaneous eigenstates of \(H_I(t)\) are given by
Here,
\(|\uparrow \rangle ^{{\hat{u}}(t)}_{Q/{\bar{Q}}}\) and \(|\downarrow \rangle ^{{\hat{u}}(t)}_{Q/{\bar{Q}}}\) are the up and down spins of the quark and antiquark along the direction \({\hat{u}}(t)\).
The magnetic field here is considered to have inhomogeneity in the azimuthal plane only. For the evolution to be adiabatic, \(\left| \frac{\langle \psi _m|{\dot{\psi }}_n\rangle }{E_m-E_n}\right| \) should be much less than 1 [20, 21]. In the lab frame, the ratio comes out to be:
\(E_m\) is the energy eigenvalue of the corresponding mth eigenstate \(|\psi _m\rangle \). As is reflected from the above expression, the ratio, in this context depends on the velocity \(\vec {v}\) of quarkonia as well as on the inhomogeneity of the magnetic field. Now, plugging in different energy eigenstates as given in Eq. (6) we have \(\left| \frac{\langle \psi _m|{\dot{\psi }}_n\rangle }{E_m-E_n}\right| = \frac{0}{0}\) for \(m, n=1,2 ; m\ne n \) as \(E_{1}\) and \(E_{2}\) are the equal eigenvalues of the states \(|\psi _1\rangle \) and \(|\psi _2\rangle \) respectively.
Other than these two cases, the value of the ratio is \(\frac{{\dot{\phi }}\sin \theta }{2\omega } \). So, the ratio is determined through the degree of inhomogeneity \({\dot{\phi }}\), the angle \(\theta \) and the Larmor frequency \(\omega \). For a non-zero value of \(\sin \theta \), the adiabatic evolution of the spin states is guaranteed if the Larmor frequency \(\omega \) is high enough to cope with the changing direction of magnetic field experienced by the moving \(q{\bar{q}}\) pair. This holds true for a very high value of magnetic field. However, in heavy ion collisions, though a very strong magnetic field is supposed to be created in the beginning, it might persist for a very short duration. So, no matter how small the quantity \({\dot{\phi }}\) is, the adiabaticity is bound to be broken as \(\omega \approx 0\) for vanishingly small magnetic field.
Survival probability P1 and spin flipping transition probabilities P2, P3, P4 to other spin states \(|\psi _2\rangle \), \(|\psi _3\rangle \), \(|\psi _4\rangle \) for different values of \(\theta \) as in a \(\theta = 0.5\), b \(\theta = 0.9\), c \(\theta = 1.6\), d \(\theta = 2.5\) as a function of time in the unit of fm / c
3 Spin flipping transitions in weak field regime
As is already evident from the preceding discussion, the non adiabaticity due to very small value of the magnetic field has an appreciable effect on the spin states of quarkonia. To quantify this effect, Schrödinger equation for the spin states needs to be solved. Spin state of quarkonia at any instant is the linear combination of the instantaneous eigenstates, \(|\psi _i(t)\rangle \), \(i=1, 2, 3, 4\) given by Eq. (6):
Equation 11 can be rewritten in terms of the basis \(| 11 \rangle ^{{\hat{u}}(t)}\), \(|1-1\rangle ^{{\hat{u}}(t)}\), \(|10\rangle ^{{\hat{u}}(t)}\) and \(| 00\rangle ^{{\hat{u}}(t)}\):
The coefficients \(C_i\)’s and the states are time dependent. These states can be written as the direct product of individual up and down spin states of the two spin 1/2 particles (heavy quark and its corresponding antiquark) bound to constitute a quarkonium. Time dependent Schrödinger equation for \(| \Psi (t)\rangle \) is,
where \(H_I(t)\) is the interaction Hamiltonian given by Eq. (4). Using Eqs. (12) and (4), we arrive at:
Here, dots on top of the coefficients and the states signify their respective time derivatives. Taking inner product of Eq. (14) with \(\langle 11|^{{\hat{u}}(t)}\), \(\langle 1-1|^{{\hat{u}}(t)}\), \(\langle 10|^{{\hat{u}}(t)}\) and \(\langle 00 |^{{\hat{u}}(t)}\) one at a time, we get four coupled first order differential equations for the coefficients \(C_1\), \(C_2\), \(C_3\) and \(C_4\) respectively. These equations take the following form when the magnetic field intensity takes a negligibly small value and azimuthal inhomogeneity is considered upto the first order in the Taylor series of \(\phi (t)\).
One can plot the probability of getting a particular state given by its corresponding \(\mid A_i(t)\mid ^2\) as a function of time with various initial conditions and different values of Larmor frequency and degree of inhomogeneity. Starting with the spin state \(|\psi _1\rangle \), we evaluate the survival probability \(P_1\) and spin flipping transitions \(P_2\), \(P_3\), \(P_4\) to other three states \(|\psi _2\rangle \), \(|\psi _3\rangle \) and \(|\psi _4\rangle \) as a function of time for charmonia by considering a regime of magnetic field around \(eB = 10^{-1} m_{\pi }^2\) . In Fig. 1, \(P_1\), \(P_2\), \(P_3\) and \(P_4\) have been represented by red, blue (dashed), green (dot dashed) and orange (dotted) for different values of \(\theta \). We have considered here the degree of inhomogeneity (\({\dot{\phi }}\)) as one order of magnitude higer than the Larmor frequency. The typical scale of the magnetic field (rather eB) is of the order of \(m_{\pi }^2\) and the corresponding scale of the time axis is fm / c which is a relevant scale to describe phenomenon in heavy ion collisions [15]. Similar plots can be obtained for the bottomonium states as well. It is quite clear from the plots that though we start with \(|\psi _1\rangle \), all other spin states get mixed with a mixing probability which changes with time. This phenomenon also occurs even if we start with any other initial states (\(|\psi _2\rangle \), \(|\psi _3\rangle \) or \(|\psi _4\rangle \)).
These plots confirm our previous assertion that if a rapidly decaying (with time) and inhomogeneous magnetic field exists, the evolution of spin states of quarkonia becomes nonadiabatic in the regime where the strength of the field is very weak. We have shown that this nonadiabaticity results in a dynamical spin mixing among all possible spin states of quarkonia, no matter which initial state we start with. We alreaday have mentioned that the phenomena of spin mixing was addressed earlier in the context of a magnetic field which is spatially homogeneous and does not depend of spatial degrees of freedom. The authors in one of those articles [13] already left the issue of inhomogeneous magnetic field as a future project which is now fulfilled through our analysis. It is difficult to measure the effect of spin mixing through the mass spectra of quarkonia with the current resolution of experiment as because the the typical gap between Zeeman levels are approximately 60–115 MeV. Still there is a possibility to observe this effect through the broadening of peak in the triplet sector of the quarkonium state. However, the deconfined medium, once formed in HICs, might drag the magnetic field along with it and help it maintain an appreciably large value for quite some time [16]. That being the scenario, the spin state evolution might have the possibility to be adiabatic and in turn, there will be no dynamical mixing occurring whatsoever. Hence, the manifestation or absence of this dynamical mixing among all the spin sates of quarkonia, as presented in this paper, can be a good way to decide the actual nature, strength and persistence of the magnetic field before and after the formation of the QCD medium in HICs.
References
V. Skokov, A Yu. Illarionov, V. Toneev, Int. J. Mod. Phys A24, 5925 (2009). arXiv:0907.1396 [nucl-th]
D.E. Kharzeev, L.D. McLerran, H.J. Warringa, Nucl. Phys. 803, A227 (2008). arXiv:0711.0950 [hep-ph]
J. Rafelski, B. Muller, Phys. Rev. Lett. 36, 517 (1976)
V. Voronyuk, V.D. Toneev, W. Cassing, E.L. Bratkovskaya, V.P. Konchakovski, S.A. Voloshin, Phys. Rev. C83, 054911 (2011). arXiv:1103.4239 [nucl-th]
D. Kharzeev, Phys. Lett. B633, 260 (2006). arXiv:hep-ph/0406125 [hep-ph]
J. Bloczynski, X.-G. Huang, X. Zhang, J. Liao, Phys. Lett. B718, 1529 (2013). arXiv:1209.6594 [nucl-th]
K. Marasinghe, K. Tuchin, Phys. Rev. C84, 044908 (2011a). arXiv:1103.1329 [hep-ph]
C. Bonati, M. D’Elia, A. Rucci, Phys. Rev. D92, 054014 (2015). arXiv:1506.07890 [hep-ph]
X. Guo, S. Shi, N. Xu, Z. Xu, P. Zhuang, Phys. Lett. B751, 215 (2015). arXiv:1502.04407 [hep-ph]
K. Marasinghe, K. Tuchin, Phys. Rev. C84, 044908 (2011b). arXiv:1103.1329 [hep-ph]
S .G. Karshenboim, Positronium physics. Proceedings, 1st International Workshop, Zuerich, Switzerland, May 30-31, 2003. Int. J. Mod. Phys. A19, 3879 (2004). arXiv:hep-ph/0310099 [hep-ph]
P. Filip, Proceedings, 8th international workshop on critical point and onset of deconfinement (CPOD 2013), Napa, 11–15 Mar 2013. PoS CPOD2013, 035 (2013)
J. Alford, M. Strickland, Phys. Rev. D88, 105017 (2013). arXiv:1309.3003 [hep-ph]
D.-L. Yang, B. Muller, J. Phys. G39, 015007 (2012). arXiv:1108.2525 [hep-ph]
K. Tuchin, Phys. Rev. C88, 024911 (2013a). arXiv:1305.5806 [hep-ph]
A. Das, S. S. Dave, P. S. Saumia, A. M. Srivastava, (2017), arXiv:1703.08162 [hep-ph]
K. Tuchin, Adv. High Energy Phys. 2013, 490495 (2013). arXiv:1301.0099 [hep-ph]
J.S. Schwinger, Phys. Rev. 82, 664 (1951)
J.S. Schwinger, Phys. Rev. 82, 116 (1951)
M.H.S. Amin, Phys. Rev. Lett. 102, 220401 (2009)
Y. Aharonov, J. Anandan, Phys. Rev. Lett. 58, 1593 (1987)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Dutta, N., Mazumder, S. Majorana flipping of quarkonium spin states in transient magnetic field. Eur. Phys. J. C 78, 525 (2018). https://doi.org/10.1140/epjc/s10052-018-6000-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6000-0