Real part of pp scattering amplitude in additive quark model at LHC energies

Abstract

Elastic pp scattering at LHC energies is treated in additive quark model together with Pomeron exchange theory. The obtained results are compared with the new experimental data on the ratio of real to imaginary part of the scattering amplitude at the small transverse momenta

Elastic pp scattering at the high energies including LHC energies has been treated in our previous papers [1,2,3] in the framework of additive quark model (AQM). The total interaction cross section $\sigma _{tot}$, differential cross section $d\sigma /dt$ at $\lesssim 1$ GeV$^2$ as well as its slope $B_{pp}(t=0)$ and the ratio of the real to the imaginary part of the amplitude,

$$\begin{aligned} \rho \,=\,\frac{\mathrm {Re}\,A}{\mathrm {Im}\,A}, \end{aligned}$$

(1)

have been in reasonable agreement with the experimental data. The ratio $\rho$ (1) has been recently measured by TOTEM collaboration [4]. For this reason we discuss here what value of $\rho$ results in AQM and how it depends on the model parameters.

To begin with we briefly recall the basics of AQM. In AQM baryon is treated as a system of three spatially separated compact objects – the constituent quarks. Each constituent quark is colored and has an internal quark–gluon structure and a finite radius that is much less than the radius of the proton, $r_q^2 \ll r_p^2$. The constituent quarks play the roles of incident particles in terms of which pp scattering is described in AQM. Elastic amplitudes for large energy $s=(p_1+p_2)^2$ and small momentum transfer t are dominated by Pomeron exchange. We neglect the small difference in pp and $p\bar{p}$ scattering coming from the exchange of negative signature Reggeons, such as $\omega$-Reggeon, since their contributions are suppressed by some power of s. The ratio of a possible Odderon to Pomeron contribution (see e.g. [5] and references therein) should also decreases with energy.

The single t-channel exchange results into the amplitude of constituent quarks scattering,

$$\begin{aligned} A_{qq}^{(1)}(s,t) = \gamma _{qq}(t) \cdot \left( \frac{s}{s_0}\right) ^{\alpha _P(t) - 1} \cdot \eta _P(t) \;, \end{aligned}$$

(2)

where $\alpha _P(t) = \alpha _P(0) + \alpha ^\prime _P\cdot t$ is the Pomeron trajectory specified by the intercept and slope values $\alpha _P(0)$ and $\alpha ^\prime _P$, respectively. The Pomeron signature factor,

$$\begin{aligned} \eta _P(t) \,=\, i \,-\, \tan ^{-1} \left( \frac{\pi \alpha _P(t)}{2}\right) , \end{aligned}$$

determines the complex structure of the amplitude. The factor $\gamma _{qq}(t)=g_1(t)\cdot g_2(t)$ has the meaning of the Pomeron coupling to the beam and target particles, the functions $g_{1,2}(t)$ being the vertices of the constituent quark-Pomeron interaction. In the following we assume the Pomeron trajectory to have the simplest form,

$$\begin{aligned} \left( \frac{s}{s_0}\right) ^{\alpha _P(t) - 1}\,=\,e^{\Delta \cdot \xi } e^{-r_q^2\,q^2}, ~~ \xi \equiv \ln \frac{s}{s_0},~~ r_q^2\equiv \alpha ^\prime \cdot \xi . \end{aligned}$$

The value $r_q^2$ defines the radius of the quark–quark interaction, while $S_0=(9~\mathrm{GeV})^2$ has the meaning of typical energy scale in Regge theory.

Fig. 1

The energy dependence of the ratio $\rho$. The experimental points are taken from [4, 11,12,13].

Fig. 2

The ratio $\rho$ as a function of parameter $\Delta$ (left) and as a function of parameter $a_1$ (right). The filled points indicate the parameters fixed in the set (7).

The scattering amplitude is presented in AQM as a sum over the terms with a given number of Pomerons,

$$\begin{aligned} A_{pp}(s,t)\,=\,\sum _n A_{pp}^{(n)}(s,t), \end{aligned}$$

(3)

where the amplitudes $A_{pp}^{(n)}$ collect all diagrams comprising various connections of the beam and target quark lines with n Pomerons. Similar to Glauber theory [6, 7] the multiple interactions between the same quark pair has to be ruled out. AQM permits the Pomeron to connect any two quark lines only once. It crucially decreases the combinatorics, leaving the diagrams with no more than $n=9$ effective Pomerons,

$$\begin{aligned}&A_{pp}^{(n)}(s,t)\,=\,i^{n-1}\biggl (\gamma _{qq}\eta _P(t_n) e^{\Delta \cdot \xi }\biggr )^n\, \nonumber \\&\quad \times \int \frac{d^2q_1}{\pi }\cdots \frac{d^2q_n}{\pi } \,\pi \,\delta ^{(2)}(q_1+\cdots +\,q_n-Q)\,\nonumber \\&\quad \times \,e^{-r_q^2(q_1^2+\cdots + q_n^2)}\, \frac{1}{n!}\nonumber \\&\quad \times \, \sum \limits _{n~\mathrm connections} F_P(Q_1,Q_2,Q_3)\,F_P(Q_1^{\,\prime },Q_2^{\,\prime },Q_3^{\,\prime }),\nonumber \\&\quad \times \, t_n\simeq t/n. \end{aligned}$$

(4)

The sum in this formula refers to all distinct ways to connect the beam and target quark lines with n Pomerons in the scattering diagram. The set of momenta $Q_i$ and $Q_l^{\,\prime }$ the quarks acquire from the attached Pomerons is particular for each connection pattern. It is worth pointing out that the reduced combinatorics ($n\le 9$) weakens the role of the screening correction in AQM compared to the widely applied eikonal models.

The function $F_P(Q_i)$ plays the role of a proton form factor for the strong interaction,

$$\begin{aligned}&F_P(Q_1,Q_2,Q_3)\,=\,\int dk_i\,\psi ^*(k_1,k_2,k_3)\, \nonumber \\&\quad \times \, \psi (k_1+Q_1,k_2+Q_2,k_3+Q_3). \end{aligned}$$

(5)

Here $\psi (k_1,k_2,k_3)$, is the initial proton wave function in terms of the quarks’ transverse momenta $k_i$, while $\psi (k_1+Q_1,k_2+Q_2,k_3+Q_3)$ is the wavefunction of the scattered proton. A more detailed description can be found in Ref. [1].

The quarks’ wave function has been taken in the simple form of Gaussian packets,

$$\begin{aligned}&\psi (k_1,k_2,k_3)\,=\,N\bigl [\,e^{-a_1(k_1^2+k_2^2+k_3^2)}\, \nonumber \\&\quad +\,C_1\,e^{-a_2(k_1^2+k_2^2+k_3^2)} +\,C_2\,e^{-a_3(k_1^2+k_2^2+k_3^2)}\bigr ], \end{aligned}$$

(6)

normalized to unity. The parameters have been chosen in [3] to fit the of $d\sigma /dt$ distribution, namely the slope at $t=0$ and the position of the minimum evidently seen in the experimental data for $\sqrt{s}=7$ TeV [8, 9]. They read

$$\begin{aligned} \Delta =0.14,~~~ \alpha ^\prime =0.116\,\mathrm{GeV}^{-2},~~~ \gamma _{qq}=0.45\,\mathrm{GeV}^{-2}. \end{aligned}$$

(7)

$$\begin{aligned}&a_1=9.0\,\mathrm{GeV}^{-2},~~~ a_2=0.29\,\mathrm{GeV}^{-2},\\&a_3=2.0\,\mathrm{GeV}^{-2},~~~ C_1=0.024,~~~ C_2=0.05. \end{aligned}$$

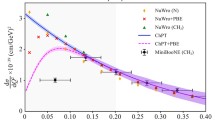
Here the same set of parameters is utilized to compare the energy behavior of $\rho$ (1) to the experimental data available now up to $\sqrt{s} = 13$ TeV, Fig. 1. The new measurement presented by TOTEM [10] gives two different $\rho$ values at $\sqrt{s} = 13$ TeV (connected to different assumptions made for the data analysis) shown in Fig. 1. Though our curve generally passes a little below the data it correctly reproduces the overall energy trend.

To demonstrate how the input parameters affect the result, the ratio $\rho$ is presented in Fig. 2(left) versus the intercept $\Delta$, i.e. the shift of bare Pomeron from the unity. The parameter $\gamma _{qq}$ is varied along with $\Delta$ to keep the fixed cross section $d\sigma /dt$ at $t=0$. The value $\rho$ is seen to substantially increase when $\Delta$ growths while another observables like $\sigma _{tot}$, $B_{pp}$ etc remain unchanged. Similarly, Fig. 2(right) shows $\rho$ as a function of parameter $a_1$, which determines the largest range of the quark–quark interaction in (6). Another physical quantities are again fixed to the values they have near $t=0$. The ratio $\rho$ increases with the growth of $a_1$.

To summarize, our approach yields the value $\rho$ (1) a little below the data but with the correct energy behavior. We would like to point put that our analysis in [3] had been fulfilled before the experimental $\rho$ value was reported. Generally we consider our description of $d\sigma _{pp}/dt$ at $|t|\lesssim 1$ GeV$^2$ as quite reasonable. It provides an additional argument for the applicability of AQM at the LHC energies. Similarly to Ref.[14] any C-odd exchange (including Odderon) is not needed within our accuracy. It was shown that the small change of the evaluated $\rho$ is achieved by the variation of model parameters without affecting another observable quantities at $t \approx 0$, namely, $d\sigma _{pp}/dt$, the slope and the total cross section. At the same time the behavior of the differential cross section near diffractive minimum could, of course, be modified and generally would needed additional corrections.