1 Introduction

In current scenario general relativity (GR) have discussed numerous critical issues, such as physical behavior of gravitating source, astrophysical bodies, gravitating physics, interstellar objects, rushing cosmology, neutron stars and clusters of galaxies. These provide us the key perception to the accelerating evolution of the cosmos. But at this time, there is need to explain more recent work for the vanishing of complexity factor in the significance of self-gravitating fluid distribution for relativistic structures. A lot of discussion about the complexity has been assessed in various fields of science. Now in this attention several researchers have given systematic work that is shown in [1,2,3,4,5,6,7,8,9,10].

Among the various definitions of complexity that have been planed up until now, a large portion of them depend on ideas, for example information and entropy, and depend on the natural thought that complexity should, somehow, amount a fundamental property showing the models, existing in the interior framework. Usually, the concept of complexity in material science paradigms by taking the ideal structure (episodic behavior) and the disengaged perfect gas, as cases of most straight forward structures and consequently as arrangements with null complexity. An ideal structure is totally arranged and the atoms are organized after particular principles of symmetry. The probability distribution for the conditions open to the ideal structure is based on a common condition of ideal symmetry, in other words it has minimum data fulfilment. On the other hand, the inaccessible perfect gas is totally scattered. The structure can be produced in any of its open condition by the similar prospect.

Lopez-Ruiz et al. [11] has investigated the concept of instability, which formulate the “distance” from the equiprobable scattering of the nearby situations of the structure. A lot of renowned astronomers [12,13,14,15] have developed the work in complexity for the self-gravitating objects. The notion of self-gravitating structure is naturally related to the interior fluid distribution, is not associated to instability, somewhat it comes from the essential presumption that the simplest configuration is shown with the homogeneous matter through ideal pressure. Having accepted this reality as an intuitive meaning of a terminating complexity structure, the real meaning of obscurity nature will rise in the advancement of the essential hypothesis of self-gravitating source dense paradigms, in regards of general relativity. Now the present work suggest to modify theory of gravity for self gravitating fluid distribution in static inhomogeneous region of complexity. The elementary incentive for this effort exits in complete detail for the state of complexity of the gravitating structure comprised in [1, 7, 16,17,18].

Herrera and Santos [19] studied the effects of anisotropy on the evolution of static gravitating source. Herrera et al. [8] modeled the spherically symmetric gravitating source accompanied with Ricci invariant arrived from orthogonal spliting of Riemann tensor. Also, Herrera et al. [20] examined the impacts of spherically symmetric dust on the structures of LTB metrics. Furthermore, Herrera et al. [21] discussed the constancy of shear free state which depends on the progression equation of the shear tensor and originate that the key factor is performed by Trace-Free tensor Y. Currently, Herrera and his coworkers [1, 22] conferred through results of self-gravitating paradigms under scalar functions. Sharif and Zaeem [4] have investigated the imperfect charged dissipative fluid distribution for cylindrically symmetric self-gravitating source with scalar structure defined by Riemann tensor. Sharif and Yousaf [23] evaluated the consequences of stable structures in spherically symmetric non-static spacetime under evolution of imperfect fluid. Herrera et al. [24] introduced perturbation system in disequilibrium dynamics of gigantic objects and one can determine the disequilibrium conditions of self-regulating of adiabatic index with considering heat flow transmission inside the interstellar bodies. Chan et al. [25] studied the spherically symmetric models accompanied by expansion-free perfect fluid source for the degree of gravitational collapse and also analyzed the results of newtonian effects approaching from degeneracy that rises in the disequilibrium area.

Nojiri and Odintsov [26] took the first initiate to present the notional and thoughtful idea in f(R) theory of gravity for the behavior of rushing universe. A motivational debate [27, 28] of dark matter regions on the configuration system, many feasible astral objects discussed in Einstein cosmology and modified theory of gravity f(R). Cembranos et al. [29] analyzed the impacts of huge-gauge body construction in rushing growth of universe in context of f(R) metric theory and also studied the gravitating contents in gravitational collapse with non-static inhomogeneous fluid. Santos et al. [30] established the feasibility conditions originating on general Ricci scalar function f(R). Their technique can be presumed to compel several probable modified gravity f(R) paradigms under appropriate corporal context. Durrer and Maartens [31] investigated the noteworthy solutions for celestial structure configuration in background of f(R) paradigms. Cognola et al. [32] concluded that insights of four major classifications taken from observationally unswerving dark energy (DE) f(R) metric gravity structures. Kainulainen et al. [33] explored the Tolman–Oppenheimer–Volkoff equation in framework of both metric f(R) and Palatini context with the formation of interior and exterior objects. Fay et al. [34] conferred the cosmological dynamics of Palatini type f(R) gravity with unlike modified metric f(R) models. Different researchers [35] presented local and cosmological parameters in distinct f(R) paradigms.

The symmetry of paper trails: in next section, we have established the geometry of the gravitating anisotropic fluid source, variables related to the spherically symmetric static interior region, the modified Einstein field equations in f(R) background and useful settlements used thoroughly in this paper. The debate on the orthogonal splitting of the curvature tensor and other scalar functions have been presented in detail in Sect. 3. Later section, express the exact results of Einstein field equation through disappearing of complexity factor. Finally, the last section includes the summary of the work.

2 Anisotropic self-gravitating fluid distribution and its interrelated variables

In this connection to present the physical significance of the gravitating source inside the celestial object formed by perfect fluid distribution and described with related variables under f(R) formalism. For this persistence to express the usual Einstein–Hilbert (EH) action in form of general relativity (GR),

$$\begin{aligned} S_{EH}=\frac{1}{2\kappa }\int d^4x\sqrt{-g}R. \end{aligned}$$
(1)

As for in f(R) context Einstein Hilbert (EH) action can be defined as

$$\begin{aligned} S_{modif}=\frac{1}{2\kappa }\int d^4x\sqrt{-g}(f(R)+L_{(matter)}). \end{aligned}$$
(2)

Here \(S_{M}\), \(\kappa \), \(L_{(matter)}\) and g denotes the modified action source of the generic function of Ricci scalar R, the coupling constant, determine the role of matter contents and the determinant of the metric tensor, respectively. The following field equations in background of metric f(R) notion are achieved by the variation of Eq. (2) w.r.t. \(g_{\alpha \beta }\),

$$\begin{aligned}&F(R)R_{\alpha \beta }-\frac{1}{2}f(R)g_{\alpha \beta }-\nabla _{\alpha }\nabla _{\beta }F(R)+g_{\alpha \beta }\nabla ^{\alpha }\nabla _{\alpha }F(R)\nonumber \\&\quad =\kappa T_{\alpha \beta }. \end{aligned}$$
(3)

where \(T_{\alpha \beta }\) stands for stress matter energy–momentum tensor, \(F(R)=\frac{d f(R)}{d R}\) , \(\nabla _{\alpha }\) and \(\nabla ^\alpha \nabla _\alpha \) are the covariant derivative operator and D’Alembertian, respectively. Above Eq. (3) can be re-manipulated as given under,

$$\begin{aligned} G_{\alpha \beta }=\frac{\kappa }{F} (T_{\alpha \beta }^m+T_{\alpha \beta }^D ), \end{aligned}$$
(4)

where

$$\begin{aligned} \begin{aligned} T_{\alpha \beta }^D&=\frac{1}{\kappa }\left[ \frac{f(R)-RF(R)}{2}g_{\alpha \beta }+\nabla _{\alpha }\nabla _{\beta }F(R)\right. \\&\quad \left. -g_{\alpha \beta }\nabla ^{\alpha }\nabla _{\alpha }F(R)\right] , \end{aligned} \end{aligned}$$
(5)

is the effective energy–momentum tensor of the self-gravitating source, bounded by interior region configuration inside the interstellar model with f(R) modified theory of gravity. We take an anisotropic matter bounded by spherically symmetric static spacetime. The interior metric representing the source of self-gravitating fluid is given by

$$\begin{aligned} ds^{2}=e^{\nu }dt^{2}-e^{\lambda }dr^{2}-r^{2} (d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(6)

where \(\nu \) and \(\lambda \) are dependable functions of r and coordinates are labeled with \((x^{0},x^{1},x^{2},x^{3})=(t,r,\theta ,\phi )\). Here the components of tensor \(T_{\alpha \beta }^m\) play an important role for the physical mechanism of the object and to evolve, some techniques are in [1, 36]. In this interpretation, following the Bondi approach [36], we presumed gently Minkowski coordinates \((\tau ,x,y,z)\)

$$\begin{aligned} d\tau = e^\frac{\nu }{2}dt; \quad dx = e^{\frac{\lambda }{2}}dr; \quad dy = rd\theta ; \quad dz = r sin\theta d\phi , \end{aligned}$$

Then, under given bar sign shows the energy momentum tensor of the Monkowskian components

$$\begin{aligned} \bar{T^{0}_{0}}={T^{0}_{0}}; \quad \bar{T^{1}_{1}}={T^{1}_{1}}; \quad \bar{T^{2}_{2}}={T^{2}_{2}}; \quad \bar{T^{3}_{3}}={T^{3}_{3}}. \end{aligned}$$

Now we consider that when seen with proper distance through fluid observer, the \(\mu \) is energy density of fluid source related with space, the \(P_{r}\) is radial pressure and \(P_{\bot }\) is tangential pressure. Consequently, in the Minkowski coordinates the matter tensor components are given as

$$\begin{aligned} \left( \begin{array}{cccc} \mu &{} 0 &{} 0 &{} 0 \\ 0 &{} P_{r} &{} 0 &{} 0 \\ 0 &{} 0 &{} P_{\bot } &{} 0 \\ 0 &{} 0 &{} 0 &{} P_{\bot } \\ \end{array} \right) . \end{aligned}$$

Hence

$$\begin{aligned} {T^{0}_{0}}= & {} \bar{T^{0}_{0}}=\mu ,\end{aligned}$$
(7)
$$\begin{aligned} {T^{1}_{1}}= & {} \bar{T^{1}_{1}}=-P_{r}, \end{aligned}$$
(8)
$$\begin{aligned} {T^{2}_{2}}= & {} {T^{3}_{3}}=\bar{T^{2}_{2}}=\bar{T^{3}_{3}}=-P_{\bot }. \end{aligned}$$
(9)

2.1 The modified field equations in context of f(R) metric theory

The relevant field equations with f(R) theory of gravity taken from equation (3) reads that

$$\begin{aligned}&-\left[ -\frac{1}{r^2}+e^{-\lambda }\left( \frac{1}{r^2}-\frac{\lambda '}{r}\right) \right] \nonumber \\&\quad =\frac{8\pi }{F}\left[ \mu +\frac{1}{\kappa }\left\{ \frac{f(R)-RF(R)}{2} +\frac{F''}{e^{\lambda }}\,{+}\,\frac{2F'}{re^{\lambda }}-\frac{\lambda F'}{2e^{\lambda }}\right\} \right] ,\nonumber \\\end{aligned}$$
(10)
$$\begin{aligned}&-\left[ \frac{1}{r^2}-e^{-\lambda }\left( \frac{1}{r^2}+\frac{\nu '}{r}\right) \right] \nonumber \\&\quad =\frac{8\pi }{F}\left[ P_{r}-\frac{1}{\kappa }\left\{ \frac{f(R)-RF(R)}{2} +\frac{\nu 'F'}{2e^{\lambda }}+\frac{2F'}{re^{\lambda }}\right\} \right] , \nonumber \\\end{aligned}$$
(11)
$$\begin{aligned}&\frac{e^{-\lambda }}{4}\left[ 2\nu ''+\nu '^2-\lambda '\nu '+2\frac{\nu '-\lambda '}{r}\right] \nonumber \\&\quad =\frac{8\pi }{F}\left[ P_{\bot }-\frac{1}{\kappa }\left\{ \frac{f(R)-RF(R)}{2} +\frac{F''}{e^{\lambda }}+\frac{\nu ' F'}{2e^{\lambda }}\right. \right. \nonumber \\&\qquad \left. \left. -\frac{\lambda ' F'}{2e^{\lambda }}+\frac{2F'}{re^{\lambda }}\right\} \right] \nonumber \\ \end{aligned}$$
(12)

Here \('=\frac{\partial }{\partial r}\). The conservation of modified energy–momentum tensor gives the following equations for the hydrostatic equilibrium

$$\begin{aligned} P'_{r}=-\frac{\nu '(\mu +P_{r})}{2}+\frac{2}{r}(P_{\bot }-P_{r})-D_{1}. \end{aligned}$$
(13)

where \(D_{1}\) is the component of dark source term due to f(R) gravity, which is given by

$$\begin{aligned} D_{1}= & {} \frac{1}{\kappa }\Bigg [\left\{ \frac{1}{e^{\lambda }}\left( -\frac{f(R)-RF(R)}{2}-\frac{\nu 'F'}{2e^{\lambda }}\right. \right. \nonumber \\&-\left. \left. \frac{2F'}{re^{\lambda }}\right) \right\} _{,1}+\frac{\nu '}{2e^{2\lambda }}\left\{ F''-\frac{\lambda ' F'}{2}-\frac{\nu ' F'}{2}\right\} \nonumber \\&+\frac{\lambda '}{e^{\lambda }}\left\{ -\frac{f(R)-RF(R)}{2}-\frac{\nu 'F'}{2e^{\lambda }}-\frac{2F'}{re^{\lambda }}\right\} \nonumber \\&\times \frac{2}{re^{2\lambda }}\left\{ F''-\frac{\lambda ' F'}{2}\right\} \Bigg ], \end{aligned}$$
(14)

This is the generalized Tolman–Oppenheimer–Volkoff equation [33], for anisotropic fluid in f(R) gravity.

Alternatively, using (11), we get

$$\begin{aligned} \nu '= & {} 2\frac{\left( m+\frac{4\pi P_{r}r^3}{F}\right) }{r(r-2m)}-\frac{r^3}{r(r-2m)F}\nonumber \\&\times \left\{ \frac{f(R)-RF(R)}{2}+\frac{\nu ' F'}{2e^{\lambda }}+\frac{2F'}{re^{\lambda }}\right\} . \end{aligned}$$
(15)

Equation (13) may be written in the following form

$$\begin{aligned} P'_{r}= & {} -\frac{(m+\frac{4\pi P_{r}r^3}{F})}{r(r-2m)}(\mu +P_{r})\nonumber \\&+\frac{r^2(\mu +P_{r})}{2(r-2m)F}\left\{ \frac{f(R)-RF(R)}{2}+\frac{\nu ' F'}{2e^{\lambda }}+\frac{2F'}{re^{\lambda }}\right\} \nonumber \\&+\frac{2}{r}(P_{\bot }-P_{r})-D_{1}. \end{aligned}$$
(16)

The general mass function m is as given below

$$\begin{aligned} R^{3}_{232}=\frac{2m}{r}=1-e^{-\lambda }. \end{aligned}$$
(17)

or,

$$\begin{aligned} m=4\pi \int ^{r}_{0}\frac{\tilde{r}^2\mu }{F}d\tilde{r}. \end{aligned}$$
(18)

Here the components of the four-velocity vector are

$$\begin{aligned} v^{\alpha }=(e^{-\frac{\nu }{2}},0,0,0). \end{aligned}$$
(19)

The four-acceleration \(a_{\alpha }=v_{\alpha ;\beta } v^{\beta }\), the only non-zero component is

$$\begin{aligned} a_{1}=-\frac{\nu '}{2}. \end{aligned}$$
(20)

From Eqs. (7)–(9), energy-momentum tensor for the gravitating fluid is

$$\begin{aligned} T^{\beta }_{\alpha }=\mu v^{\beta }v_{\alpha }-P h^{\beta }_{\alpha }+\Pi ^{\beta }_{\alpha }. \end{aligned}$$
(21)

with

$$\begin{aligned} \Pi ^{\beta }_{\alpha }= & {} \Pi (\psi ^{\beta }\psi _{\alpha }+\frac{1}{3}h^{\beta }_{\alpha }); \quad P=\frac{\tilde{P_{r}}+2P_{\bot }}{3};\nonumber \\ \Pi= & {} P_{r}-P_{\bot }; \quad h^{\beta }_{\alpha }=\delta ^{\beta }_{\alpha }-v^{\beta }v_{\alpha }, \end{aligned}$$
(22)

where non-zero component of \(\psi ^{\beta }\) is

$$\begin{aligned} \psi ^{\beta }=(0,e^{-\frac{\lambda }{2}},0,0), \end{aligned}$$
(23)

and its properties are \(\psi ^{\beta }v_{\beta }=0, \quad \psi ^{\beta }\psi _{\beta }=-1\).

2.2 The Riemann curvature and Weyl curvature tensor

It is convenient to express the Riemann curvature tensor in terms of conformal curvature tensor \(C^{\rho }_{\alpha \beta \mu }\), the Ricci tensor \(R_{\alpha \beta }\) and the Ricci scalar R, as

$$\begin{aligned} R^{\rho }_{\alpha \beta \mu }= & {} C^{\rho }_{\alpha \beta \mu }+\frac{1}{2}R^{\rho }_{\beta }g_{\alpha \mu }-\frac{1}{2}R_{\alpha \beta }\delta ^{\rho }_{\mu } +\frac{1}{2}R_{\alpha \mu }\delta ^{\rho }_{\beta }\nonumber \\&-\frac{1}{2}R^{\rho }_{\mu }g_{\alpha \beta }-\frac{1}{6}R(\delta ^{\rho }_{\beta }g_{\alpha \mu } -g_{\alpha \beta }\delta ^{\rho }_{\mu }). \end{aligned}$$
(24)

In case of spherically symmetric structure, the magnetic part of the conformal curvature tensor becomes identically zero and only it can be defined in form of electric part \((E_{\alpha \beta }=C_{\alpha \gamma \beta \delta }v^{\gamma }v^{\delta })\) as

$$\begin{aligned} C_{\mu \nu \kappa \lambda }=(g_{\mu \nu \alpha \beta }g_{\kappa \lambda \gamma \delta }-\eta _{\mu \nu \alpha \beta }\eta _{\kappa \lambda \gamma \delta })v^{\alpha }v^{\gamma }E^{\beta \delta }. \end{aligned}$$
(25)

where \( g_{\mu \nu \alpha \beta }= g_{\mu \alpha }g_{\nu \beta }-g_{\mu \beta }g_{\nu \alpha }\), and \(\eta _{\mu \nu \alpha \beta }\) is the Levi-Civita tensor. The formula of \(E_{\alpha \beta }\) is rewritten as

$$\begin{aligned} E_{\alpha \beta }=E\left( \psi _{\alpha }\psi _{\beta }+\frac{1}{3}h_{\alpha \beta }\right) , \end{aligned}$$
(26)

with

$$\begin{aligned} E=-\frac{e^{-\lambda }}{4}\left[ \nu ''+\frac{\nu ^{'2}-\lambda '\nu '}{2}-\frac{\nu ^{'}-\lambda '}{r}+\frac{2(1-e^{\lambda })}{r^2}\right] , \end{aligned}$$
(27)

and fulfill the following conditions:

$$\begin{aligned} E^{\alpha }_{\alpha }=0, \quad E_{\alpha \gamma }=E_{(\alpha \gamma )}, \quad E_{\alpha \gamma }v^{\gamma }=0. \end{aligned}$$
(28)

2.3 The formulation of Tolman mass and the mass function

This section, we introduce two definitions of mass for interior of object and their relationship with conformal curvature tensor. Later, will be used for justification of the complexity factor.

With the help of field equations (10)–(12) and the given mass function (17), we get

$$\begin{aligned} m= & {} \frac{4\pi r^3}{3F}(\mu +P_{\bot }-P_{r})+\frac{Er^3}{3}+\frac{r^3}{6F}\nonumber \\&\times \left\{ \frac{f(R)-RF(R)}{2}+\frac{2F'}{re^{\lambda }}\right\} , \end{aligned}$$
(29)

It may be written as

$$\begin{aligned} E= & {} -\frac{4\pi }{r^3}\int ^{r}_{0}\frac{\tilde{r}^3}{F}(\mu '-\frac{\mu F'}{F})d\tilde{r}+\frac{4\pi }{F}(P_{r}-P_{\bot })\nonumber \\&-\frac{1}{2F}\left\{ \frac{f(R)-RF(R)}{2}+\frac{2F'}{re^{\lambda }}\right\} , \end{aligned}$$
(30)

lastly, using (30) in (29), one gets

$$\begin{aligned} m(r)=\frac{4\pi r^3\mu }{3F}-\frac{4\pi }{3}\int ^{r}_{0}\frac{\tilde{r}^3}{F}(\mu '-\frac{\mu F'}{F})d\tilde{r}. \end{aligned}$$
(31)

The physical significance of the self-gravitating fluid dispersal of (30) is basically known by two quantities of density inhomogeneity and local anisotropy of pressure in f(R) getting through conformal curvature tensor, however in the instance of a homogeneous mass density distribution, desirable variation tempted through inhomogeneity to describe the mass function given in Eq. (31).

Another important conformation was presented by Tolman few decades ago in the explanation of energy source of the matter surface. For a static distribution of the spherically symmetric object the Tolman mass [1, 37] is given by

$$\begin{aligned} m_{T}=4\pi \int ^{r\Sigma }_{0}r^2e^\frac{(\nu +\lambda )}{2}\frac{1}{F}(T^{0}_{0}-T^{1}_{1}-2T^{2}_{2})dr. \end{aligned}$$
(32)

The purpose of Tolman’s formula to produce the estimation of the whole mass energy of the structure, through no assurance to its localization. Now we describe the mass function under f(R) context taken totaly interior of the spherically surface with radius r.

$$\begin{aligned} m_{T}=4\pi \int ^{r}_{0}\tilde{r}^2e^\frac{(\nu +\lambda )}{2}\frac{1}{F}(T^{0}_{0}-T^{1}_{1}-2T^{2}_{2})d\tilde{r}. \end{aligned}$$
(33)

The noticeable behavior of the “effective inertial mass” as named by \(m_{T}\) played with an extension on the universal theory of energy for the local surface , the detail is given in [8, 18, 19]

$$\begin{aligned} m_{T}= & {} e^\frac{(\nu +\lambda )}{2}\left\{ m(r)+\frac{4\pi P_{r}r^3}{F}-\frac{r^3}{2F}\right. \nonumber \\&\times \left. \left( \frac{f(R)-R F(R)}{2}+\frac{\nu ' F'}{2e^{\lambda }}+\frac{2 F'}{re^{\lambda }}\right) \right\} \nonumber \\&+\int ^{r}_{0}\frac{\tilde{r}^2}{F}e^\frac{(\nu +\lambda )}{2}\left( \frac{f(R)-R F(R)}{2}+\frac{F''}{2e^{\lambda }}-\frac{\lambda 'F'}{4e^{\lambda }}\right. \nonumber \\&\left. +\frac{3\nu 'F'}{4e^{\lambda }}+\frac{2F'}{re^{\lambda }}\right) d\tilde{r}. \end{aligned}$$
(34)

By the information of Eq. (15), one can also finds

$$\begin{aligned} m_{T}= & {} e^\frac{(\nu -\lambda )}{2}\nu '\frac{r^2}{2}+\int ^{r}_{0}\frac{\tilde{r}^2}{F}e^\frac{(\nu +\lambda )}{2}\left( \frac{f(R)-R F(R)}{2}\right. \nonumber \\&+\left. \frac{F''}{2e^{\lambda }}-\frac{\lambda 'F'}{4e^{\lambda }}+\frac{3\nu 'F'}{4e^{\lambda }}+\frac{2F'}{re^{\lambda }}\right) d\tilde{r}. \end{aligned}$$
(35)

The overhead expression gives the physical significance of the self-gravitating source of \(m_{T}\) is known as “effective inertial mass”. Definitely, used by Eq. (20), is the gravitational acceleration \((a=\psi ^{\alpha }a_{\alpha })\) of a test particle, in case of static gravitational field the test particle instantly at rest followed by [8]

$$\begin{aligned} a= & {} \frac{e^\frac{-\nu }{2}}{r^2}\left\{ m_{T}-\int ^{r}_{0}\frac{\tilde{r}^2}{F}e^\frac{(\nu +\lambda )}{2}\left( \frac{f(R)-R F(R)}{2}\right. \right. \nonumber \\&\left. \left. +\frac{F''}{2e^{\lambda }}-\frac{\lambda 'F'}{4e^{\lambda }}+\frac{3\nu 'F'}{4e^{\lambda }}+\frac{2F'}{re^{\lambda }}\right) d\tilde{r}\right\} . \end{aligned}$$
(36)

The more appealing debate will provide behavior of \(m_{T}\) in next section. Differentiate Eq. (35) with respect to r (for this attention slightly calculative work see in more detail [8]), using field equations and Eq. (34), we have

$$\begin{aligned}&r m'_{T}-3m_{T}=e^\frac{(\nu +\lambda )}{2}r^3\nonumber \\&\quad \times \left[ \frac{4\pi }{F}(P_{\bot }-P_{r})-E-\frac{F''}{2Fe^{\lambda }}+\frac{\lambda ' F'}{4Fe^{\lambda }}\right] \nonumber \\&\quad +\frac{r^2}{F}e^\frac{(\nu +\lambda )}{2}\nonumber \\&\quad \times \left( \frac{f(R)-R F(R)}{2}+\frac{F''}{2e^{\lambda }}-\frac{\lambda 'F'}{4e^{\lambda }}+\frac{3\nu 'F'}{4e^{\lambda }}+\frac{2F'}{re^{\lambda }}\right) .\nonumber \\ \end{aligned}$$
(37)

Here it is easy to formulate the integral form, so that

$$\begin{aligned}&m_{T}=(m_{T})_{\Sigma }\left( \frac{r}{r_{\Sigma }}\right) ^3\nonumber \\&\quad -r^3\int ^{r_{\Sigma }}_{r}\Big [\frac{e^\frac{(\nu +\lambda )}{2}}{\tilde{r}}\left\{ \frac{4\pi }{F}(P_{\bot }-P_{r})-E-\frac{(F'' -\frac{\lambda ' F'}{2})}{2Fe^{\lambda }}\right\} \nonumber \\&\quad + \frac{e^\frac{(\nu +\lambda )}{2}}{\tilde{r}^2F}\left( \frac{f(R)-R F(R)}{2}+\frac{F''}{2e^{\lambda }}-\frac{\lambda 'F'}{4e^{\lambda }}\right. \nonumber \\&\quad \left. +\frac{3\nu 'F'}{4e^{\lambda }}+\frac{2F'}{\tilde{r}e^{\lambda }}\right) \Big ]d\tilde{r}. \end{aligned}$$
(38)

Applying Eq. (30), which follows

$$\begin{aligned}&m_{T}=(m_{T})_{\Sigma }\left( \frac{r}{r_{\Sigma }}\right) ^3-r^3\int ^{r_{\Sigma }}_{r}\Big [e^\frac{(\nu +\lambda )}{2}\Big \{\frac{8\pi }{\tilde{r}F}(P_{\bot }-P_{r})\nonumber \\&\quad +\frac{4\pi }{\tilde{r}^4}\int ^{\tilde{r}}_{0}\frac{\tilde{r}^3}{F}\left( \mu '-\frac{\mu F'}{F}\right) d\tilde{r}\nonumber \\&\quad +\frac{1}{2F\tilde{r}}\left( \frac{f(R)-R F(R)}{2}+\frac{2F'}{\tilde{r}e^{\lambda }}\right) -\frac{(F'' -\frac{\lambda ' F'}{2})}{2\tilde{r}Fe^{\lambda }}\Big \}\nonumber \\&\quad +\frac{e^\frac{(\nu +\lambda )}{2}}{\tilde{r}^2F}\left( \frac{f(R)-R F(R)}{2}+\frac{F''}{2e^{\lambda }}-\frac{\lambda 'F'}{4e^{\lambda }}\right. \nonumber \\&\quad \left. +\frac{3\nu 'F'}{4e^{\lambda }}+\frac{2F'}{\tilde{r}e^{\lambda }}\right) \Big ]d\tilde{r}. \end{aligned}$$
(39)

Equation (39) conferred the noteworthy issues arrived in second integral defines the effects of density inhomogeneity and local anisotropy of the pressure on the Tolman’s mass in the background of f(R) gravity. We would like to mention that all the results reduce to Herrera [1], when we take \(f(R)=R\).

3 The orthogonal splitting of the curvature tensor

Bel [38] considered the orthogonal splitting of the curvature tensor. For that conjecture, we shall use slight changes in notation which are closely related to [39].

Now let us familiarize the under mentioned tensors, used by Bel:

$$\begin{aligned} Y_{\alpha \beta }=R_{\alpha \gamma \beta \delta }v^{\gamma }v^{\delta }, \end{aligned}$$
(40)
$$\begin{aligned} Z_{\alpha \beta }=^*R_{\alpha \gamma \beta \delta }v^{\gamma }v^{\delta }=\frac{1}{2}\eta _{\alpha \gamma \epsilon \mu }R^{\epsilon \mu }_{\beta \delta }v^{\gamma }v^{\delta }, \end{aligned}$$
(41)
$$\begin{aligned} X_{\alpha \beta }=^*R^{*}_{\alpha \gamma \beta \delta }v^{\gamma }v^{\delta }=\frac{1}{2}\eta ^{\epsilon \mu }_{\alpha \gamma }R^{*}_{\epsilon \mu \beta \delta }v^{\gamma }v^{\delta }. \end{aligned}$$
(42)

Here the sign \(*\) representing dual tensor, in other words, \(R^{*}_{\alpha \beta \gamma \delta }=\frac{1}{2}\eta _{\epsilon \mu \gamma \delta }R^{\epsilon \mu }_{\alpha \beta }\).

The orthogonal splitting of the curvature tensor are to be written in rewrite form of these tensors called curvature tensor (see [39]). Though, in substitution for using the explicit form of the splitting of curvature tensor (equation (4.6) in [39]), we shall keep as follows in the general non-static case detail given in [8].

Equation (24) takes the form, by using Einstein field equations

$$\begin{aligned} R^{\alpha \gamma }_{\beta \delta }=C^{\alpha \gamma }_{\beta \delta }+28\pi T^{[\alpha \gamma ]}_{[\beta ^{\delta } \delta ]}+8\pi T\left( \frac{1}{3}\delta ^{\alpha \gamma }_{[\beta ^{\delta } \delta ]}-\delta ^{[\alpha \gamma ]}_{[\beta ^{\delta }{\delta }]}\right) . \end{aligned}$$
(43)

Now split the curvature tensor, using (21) into (43), then we get

$$\begin{aligned} R^{\alpha \gamma }_{\beta \delta }=R^{\alpha \gamma }_{(I)\beta \delta }+R^{\alpha \gamma }_{(II)\beta \delta }+R^{\alpha \gamma }_{(III)\beta \delta }. \end{aligned}$$
(44)

Here

$$\begin{aligned} R^{\alpha \gamma }_{(I)\beta \delta }= & {} 16\pi \mu v^{[\alpha \gamma ]}v_{[\beta ^{\delta }{\delta }]}\nonumber \\&-28\pi P h^{[\alpha \gamma ]}_{[\beta ^{\delta } \delta ]} +8\pi (\mu -3P)\left( \frac{1}{3}\delta ^{\alpha \gamma }_{[\beta ^{\delta } \delta ]}-\delta ^{[\alpha \gamma ]}_{[\beta ^{\delta }{\delta }]}\right) ,\nonumber \\ \end{aligned}$$
(45)
$$\begin{aligned} R^{\alpha \gamma }_{(II)\beta \delta }=16\pi \Pi ^{[\alpha \gamma ]}_{[\beta ^{\delta } \delta ]}, \end{aligned}$$
(46)
$$\begin{aligned} R^{\alpha \gamma }_{(III)\beta \delta }=4v^{[\alpha \gamma ]}v_{[\beta ^E{\delta }]}-\epsilon ^{\alpha \gamma }_{\mu }\epsilon _{\beta \delta \nu }E^{\mu \nu }. \end{aligned}$$
(47)

with

$$\begin{aligned} \epsilon _{\alpha \gamma \beta }=v^{\mu }\eta _{\mu \alpha \gamma \beta }, \quad \epsilon _{\alpha \gamma \beta }v^{\beta }=0, \end{aligned}$$
(48)

In interpretation of spherical symmetric the splitting of the curvature tensor due to insertion of the magnetic part of the conformal curvature tensor \((H_{\alpha \beta }=^{*}C_{\alpha \gamma \beta \delta }v^{\gamma }v^{\delta })\).

From the above solutions, we can sort out three definite tensors in the form of the physical variables like \(Y_{\alpha \beta },Z_{\alpha \beta }\) and \(X_{\alpha \beta }\) expressed below:

$$\begin{aligned}&Y_{\alpha \beta }=\frac{4\pi }{3}(\mu +3P)h_{\alpha \beta }+4\pi \Pi _{\alpha \beta }+E_{\alpha \beta }, \end{aligned}$$
(49)
$$\begin{aligned}&Z_{\alpha \beta }=0, \end{aligned}$$
(50)
$$\begin{aligned}&X_{\alpha \beta }=\frac{8\pi }{3}\mu h_{\alpha \beta }+4\pi \Pi _{\alpha \beta }-E_{\alpha \beta }. \end{aligned}$$
(51)

The overhead expressions denotes the tensors and can describe it in form of structure scalars, the following study takes an account of scalar functions (see detail in [8]).

Surely, we may state that four structure scalars can attain through \(X_{\alpha \beta }\) and \(Y_{\alpha \beta }\) tensors and may also described these tensors with standard notations \(X_{T},X_{TF},Y_{T},Y_{TF}\) and last scalar related to the \(Z_{\alpha \beta }\) tensor removed in the static case (as shown in detail in [8])

so the structure scalar results are summarized as follows:

$$\begin{aligned} X_{T}= & {} 8\pi \mu ,\end{aligned}$$
(52)
$$\begin{aligned} X_{TF}= & {} 4\pi \Pi -E, \end{aligned}$$
(53)

by using (30) and get,

$$\begin{aligned} X_{TF}= & {} 4\pi (P_{r}-P_{\bot })+\frac{4\pi }{r^3}\int ^{r}_{0}\frac{\tilde{r}^3}{F}(\mu '-\frac{\mu F'}{F})d\tilde{r}\nonumber \\&-\frac{4\pi }{F}(P_{r}-P_{\bot })+\frac{1}{2F}\left\{ \frac{f(R)-RF(R)}{2}+\frac{2F'}{re^{\lambda }}\right\} ,\nonumber \\ \end{aligned}$$
(54)
$$\begin{aligned}&Y_{T}=4\pi (\mu +3P_{r}-2\Pi ),\end{aligned}$$
(55)
$$\begin{aligned}&Y_{TF}=4\pi \Pi +E, \end{aligned}$$
(56)

equivalently, with the help of (30)

$$\begin{aligned} Y_{TF}= & {} 4\pi (P_{r}-P_{\bot })-\frac{4\pi }{r^3}\int ^{r}_{0}\frac{\tilde{r}^3}{F}(\mu '-\frac{\mu F'}{F})d\tilde{r}\nonumber \\&+\frac{4\pi }{F}(P_{r}-P_{\bot })-\frac{1}{2F}\left\{ \frac{f(R)-RF(R)}{2}+\frac{2F'}{re^{\lambda }}\right\} .\nonumber \\ \end{aligned}$$
(57)

The above solutions of \(X_{TF}\) and \(Y_{TF}\) give the local anisotropy pressure

$$\begin{aligned} X_{TF}+Y_{TF}=8\pi \Pi , \end{aligned}$$
(58)

The solutions of \(Y_{T}\) and \(Y_{TF}\) arrange the physical meaning, for this instance utilizing (56) into (38) and we obtain

$$\begin{aligned}&m_{T}=(m_{T})_{\Sigma }\left( \frac{r}{r_{\Sigma }}\right) ^3\nonumber \\&\quad +r^3\int ^{{r_\Sigma }}_{r}\Big [\frac{e^\frac{(\nu +\lambda )}{2}}{\tilde{r}}\left\{ \frac{Y_{TF}}{F}-E(1-\frac{1}{F}) +\frac{(F''-\frac{\lambda ' F'}{2})}{2Fe^{\lambda }}\right\} \nonumber \\&\quad -\frac{e^\frac{(\nu +\lambda )}{2}}{\tilde{r}^2F}\left( \frac{f(R)-R F(R)}{2}+\frac{F''}{2e^{\lambda }}-\frac{\lambda 'F'}{4e^{\lambda }}+\frac{3\nu 'F'}{4e^{\lambda }}\right. \nonumber \\&\quad \left. +\frac{2F'}{\tilde{r}e^{\lambda }}\right) \Big ]d\tilde{r}. \end{aligned}$$
(59)

Analyzing the Eq. (59) by Eq. (39), \(Y_{TF}\) explains the impacts of self-gravitating source of the complexity factor in context of f(R) theory of gravity for the local anisotropy of pressure and density inhomogeneity on the Tolman mass. On the other hand, \(Y_{TF}\) explains how these two expressions alter the calculation of the Tolman mass with respect to its calculation of perfect fluid homogeneity. It is also worth evoking that \(Y_{TF}\) organized with \(X_{TF}\), explores the local anisotropy of the matter dispersion.

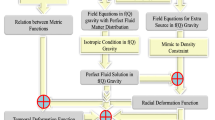
4 Matter distribution with disappearing complexity factor

In order to discuss the system of three ordinary differential equations (10)–(12), which are modified Einstein equations for static self-gravitating anisotropic fluid contribution in five unknown functions \((\nu ,\lambda ,\mu ,P_{r},P_{\bot })\) under metric f(R) theory of gravity. Hence, the off chance is that we implement the condition \(Y_{TF}=0\) which might still require one condition while keeping in mind the final goal to explain the structure.

Therefore from Eq. (57), the disappearing complexity factor condition is

$$\begin{aligned} \Pi= & {} \frac{1}{r^3(1+\frac{1}{F})}\int ^{r}_{0}\frac{\tilde{r}^3}{F}(\mu '-\frac{\mu F'}{F})d\tilde{r}\nonumber \\&+\frac{1}{8\pi (F+\frac{1}{F^2})}\left\{ \frac{f(R)-RF(R)}{2}+\frac{2F'}{re^{\lambda }}\right\} . \end{aligned}$$
(60)

After taking the expression (60), it can be seen that disappearing complexity factor condition suggest some homogeneous density and pressure isotropy, otherwise inhomogeneous energy density and pressure anisotropy. Likewise, it ought to be seen that (60) might be viewed as a non-local equation of state in f(R) gravity, another few researchers did work previously in [40] but this note is slightly different. It is interesting to mention that for \(f(R)=R\) above equation reduces to Eq.(58) of Herrera [1].

The preliminary idea to take the attention for those paradigms is the consideration for the formulation of the metric function \(\lambda \) which has the following [41] form

$$\begin{aligned} e^{-\lambda }=1-\alpha r^2+\frac{3K\alpha }{5r^{2}_{\Sigma }}r^{4}, \end{aligned}$$
(61)

here K is constant in the interval (0, 1) and and \(\alpha =\frac{8\pi \mu _{0}}{3}\).

Considering Eqs. (10) and (18), we get

$$\begin{aligned} \frac{\mu }{F}= & {} \mu _{0}\left( 1-\frac{K r^2}{r^{2}_{\Sigma }}\right) \nonumber \\&-\frac{\left( 1-\alpha r^2+\frac{3K\alpha }{5r^{2}_{\Sigma }}r^{4}\right) }{\kappa F} \Bigg \{\frac{f(R)-R F(R)}{2\left( 1-\alpha r^2+\frac{3K\alpha }{5r^{2}_{\Sigma }}r^{4}\right) }\nonumber \\&+F''+\frac{2F'}{r} -\frac{F'\left( 2\alpha r-\frac{12 K \alpha r^3}{5 R^{2}_{\Sigma }}\right) }{2\left( 1-\alpha r^2+\frac{3K\alpha }{5r^{2}_{\Sigma }}r^{4}\right) }\Bigg \}, \end{aligned}$$
(62)
$$\begin{aligned} m(r)= & {} \frac{4 \pi \mu _{0}r^3}{3}\left( 1-\frac{3K r^2}{5r^{2}_{\Sigma }}\right) \nonumber \\&-4\pi \int ^r_{0}\tilde{r}^2\frac{\left( 1-\alpha \tilde{r}^2+\frac{3K\alpha }{5\tilde{r}^2_{\Sigma }}\tilde{r}^4\right) }{\kappa F}\nonumber \\&\Bigg \{\frac{f(R)-R F(R)}{2\left( 1-\alpha \tilde{r}^2+\frac{3K\alpha }{5\tilde{r}^2_{\Sigma }}\tilde{r}^4\right) }\nonumber \\&+F''+\frac{2F'}{\tilde{r}} -\frac{F'\left( \alpha \tilde{r}-\frac{6 K \alpha \tilde{r}^3}{5 \tilde{r}^{2}_{\Sigma }}\right) }{\left( 1-\alpha \tilde{r}^2+\frac{3K\alpha }{5\tilde{r}^{2}_{\Sigma }}\tilde{r}^{4}\right) }\Bigg \}d\tilde{r}, \end{aligned}$$
(63)

introducing, because (11) and (12) we can get

$$\begin{aligned} \frac{8\pi \Pi (r)}{F}+\frac{1}{r^2}= & {} e^{-\lambda }\left[ -\frac{\nu ''}{2}-\left( \frac{\nu '}{2}\right) ^2+\frac{\nu '}{2r}+\frac{1}{r^2}\right. \nonumber \\&\left. +\frac{\lambda '}{2}\left( \frac{\nu '}{2}+\frac{1}{r}\right) \right] +\frac{1}{F}\left( \frac{-F''}{e^{\lambda }}+\frac{\lambda 'F'}{2e^{\lambda }}\right) ,\nonumber \\ \end{aligned}$$
(64)

Letting the variables

$$\begin{aligned} e^{\nu (r)}=e^{\int (2z(r)-\frac{2}{r})dr}, \end{aligned}$$
(65)

and

$$\begin{aligned} e^{-\lambda }=y(r). \end{aligned}$$
(66)

From Eq. (64), we get the following differential equation

$$\begin{aligned}&\left( 1+\frac{F'}{F z}\right) y'+y\left[ \frac{2z'}{z}+2z-\frac{6}{r}+\frac{4}{r^2z}+\frac{2F''}{F z}\right] \nonumber \\&\quad =-\frac{2}{z}\left( \frac{8\pi \Pi (r)}{F}+\frac{1}{r^2}\right) . \end{aligned}$$
(67)

In this illustration, the overhead solution is seeing to be a Ricatti expression and made with the assistance of the line element function \(\lambda \) held in form of variable y(r) given by (61) and also alongwith the solution of \(\Pi \) is obtained from (60) and (62). The final firm of the solution is providing z which can be taken through integration. Definitely, it becomes the solution of two functions z and \(\Pi \) in context of gravity f(R), the metric takes the formation [1, 42].

$$\begin{aligned} ds^2= & {} -e^{\int \big (2z(r)-\frac{2}{r}\big )dr}dt^2\nonumber \\&+\frac{z^2(r)e^{\int \Big (2z(r)+\frac{4}{r^2z(r)}+\frac{2F''}{F z(r)}\Big )dr}}{r^6\Big (-2\int \frac{z(r) \Big (F+8\pi \Pi (r) r^2\Big ) e^{\int \Big (2z(r)+\frac{4}{r^2z(r)}+\frac{2F''}{F z(r)}\Big )dr}}{r^8F}dr+C\Big )}dr^2\nonumber \\&+r^2d\theta ^2+r^2sin^2\theta d\phi ^2. \end{aligned}$$
(68)

where C is constant of integration.

Next, obtaining for physical variables

$$\begin{aligned} \frac{4\pi P_{r}}{F}= & {} \frac{z(r-2m)+\frac{m}{r}-1}{r^2}\nonumber \\&+\frac{(1-\frac{2m}{r})}{F}\left( \frac{f(R)-RF(R)}{2(1-\frac{2m}{r})}+(z+\frac{1}{r})F'\right) ,\nonumber \\ \end{aligned}$$
(69)
$$\begin{aligned} \frac{4\pi \mu }{F}= & {} \frac{m'}{r^2}-\frac{(1-\frac{2m}{r})}{2F}\nonumber \\&\left( \frac{f(R)-RF(R)}{2(1-\frac{2m}{r})}+F''+\frac{2F'}{r}-\frac{F'(\frac{m'}{r}-\frac{m}{r^2})}{(1-\frac{2m}{r})}\right) ,\nonumber \\ \end{aligned}$$
(70)

and

$$\begin{aligned} \frac{8\pi P_{\bot }}{F}= & {} \left( 1-\frac{2m}{r}\right) \left( z'+z^2-\frac{z}{r}+\frac{1}{r^2}\right) \nonumber \\&+z\left( \frac{m}{r^2}-\frac{m'}{r}\right) \nonumber \\&+\frac{1}{F}\Bigg [\frac{f(R)-RF(R)}{2}+F''(1-\frac{2m}{r})\nonumber \\&+(1-\frac{2m}{r})(z+\frac{1}{r})F'+\left( \frac{m}{r^2}-\frac{m'}{r}\right) F'\Bigg ]. \end{aligned}$$
(71)

Afterwards, fulfills these conditions \(\mu >0\) and \(\mu >P_{r}, P_{\bot }\), the progression is unvarying for prominent solutions to remove the complexity in the gravitating system. Next, to evade the nature of singularity for physical variables on the boundary surface \(\sum \), the solution must satisfy the Darmois junction conditions, by taking a vacumm solution solution in the exterior region of the compact object.

5 Conclusions

The concept of complexity factor for the static anisotropic gravitating has been present by Herrera [1]. This is very first step towards the understanding of complexity of a gravitating source in general relativity using the Bondi approach. We have found that in the frame of f(R) gravity, also the definition of complexity based on orthogonal splitting of the curvature tensor. Current work explains the innovative thoughts of the complexity of the system that frame with static spherically symmetric anisotropic gravitating matter under f(R) gravity. The purpose of f(R) gravity such a system is to see wether dark energy components lessens the complexity of the structure or enhance it.

We have investigated f(R) term agrees with an energy density homogeneity and its isotropic pressure to diminish the \(Y_{TF}\) scalar function. Our main objective is to estimate the amount of complexity that appears in the \(Y_{TF}\) scalar function with the effects of f(R). Present research discusses such motives that play the vital behavior in sense of applications:

  • The structure scalar \(Y_{TF}\) holds additions from the inhomogeneous energy density and the native anisotropy of pressure, joined in a systematic order.

  • The structure scalar \(Y_{TF}\) estimates the degree of the “effective inertial mass” in the departure state for the homogeneous and imperfect matter of the dark gravitating source, given by the inhomogeneity energy density and the anisotropy of pressure under f(R) formalism. The \(Y_{TF}\) includes the impacts of the electric charge in case of charged matter contribution.

  • The structure scalar also discuss the degeneracy of fluxes alongwith the contributions of inhomogeneity energy density and native anisotropic pressure in the presence of usual non-static dissipative gravitating source. In this case to remove the scalar function \(Y_{TF}\) is the essential parameter for the constancy of the shear free case(see in detail [21]).

  • It ought to be seen that the complexity is much eminent in prior frame, not just departure for the homogeneous case, perfect fluid, but here two factors display the worth role in Eq. (57) with f(R) notion and disappear indistinguishably, get additionally for all arrangements where the two factors in (57) cancel each other. The key role of these factors to disappear the complexity of the system configuration.

  • It merits telling us that though commitment of anisotropy of pressure to \(Y_{TF}\) is natural, the commitment of inhomogeneous energy density is not.

  • Consequently, to present the some valuable results that fulfilling the condition for disappearing of complexity. As suggested previously, the aim was not to furnish paradigms through particular celestial intrigue, but rather simply show how such paradigms might be attain, with examples.

  • It is very stimulating to note that for \(f(R)=R\) Eqs. (14, 15, 28, 29, 30, 33, 35, 38, 37, 53, 56, 58, 62, 67, 68–70) of the present paper reduce to Eqs. (10, 11, 28, 29, 30, 32, 34, 35, 36, 51, 54, 56, 61, 66, 67–69) Herrera Ref. [1].

The final form of the present work is designed for vanishing of complexity factor, in assistance of exact solutions of f(R) theory of gravity and also would like to confer in future with other modified concepts, such as f(G) Gauss–Bonnet gravity, f(T), f(R, T) and Rastall theory.