1 Introduction

The publication of Hubble’s 1929 article [1] marked a turning point in understanding the universe. In this interesting report, Hubble exposed the evidence for one of the great discoveries in 20th century science: the expanding universe. As soon as astrophysicists comprehend that Type Ia Supernovae (SNeIa) were standard candles, it appeared evident that their high luminosity should make it possible to extend the Hubble diagram, i.e. a plot of the distance-redshift relation, for interesting distance ranges. Inspired by this appealing consideration, two independent research groups started SNeIa surveys leading to the unexpected discovery that the Universe expansion is picking up speed, rather than slowing down as assumed by the Cosmological Standard Model [2,3,4,5,6]. This surprising finding has now been confirmed by more recent data coming from SNeIa surveys [7,8,9,10,11,12,13,14], large scale structure [15,16,17,18,19] and cosmic microwave background (CMBR) anisotropy spectrum [20,21,22,23,24,25,26]. This remarkable discovery has led cosmologists to hypothesize the presence of unknown form of energy called dark energy (DE), which is an exotic matter with negative pressure [27]. All current observations are consistent with a cosmological constant (CC); while this is in some sense the most economical possibility, the CC has its own theoretical and naturalness problems [28, 29], so it is worthwhile to consider alternatives.

In search for the solution of the riddle of dark energy two different ways are usually chosen. One is to modify Einstein’s theory of gravitation and the second is constructing various dark energy candidates. Thus some dark energy models like quintessence [30, 31] phantom energy [32, 33], k-essence [34], tachyon [35], Chaplygin gas [36] have been proposed. Also unified dark energy (UDE) models as an economical and attractive idea to unify the d ark sector of the universe have been studied by many authors [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]. Chaplygin gas is one of these UDE models which was introduced by Kamenshchik et al. [53]. Main idea of CG model comes from aerodynamics [54]. Its interesting characteristic is that it has a dual role as it gives density evolution of matter at high redshifts and dark energy at low redshifts [55, 56]. It obeys an equation of state (EOS) as \(p=-\frac{A}{\rho }\) where p and \(\rho \) are pressure and density respectively and A is a positive constant [57]. However Chaplygin gas model has a problem, in other words it has some inconsistency with observational datas [57,58,59], therefore Generalized Chaplygin gas (GCG) was introduced in order to establish an appropriate cosmological model with the equation of state \(p=-\frac{{A}}{\rho ^{\alpha }}\) where \(\alpha \) is a real number and it has a value in range (0, 1) and covers Chaplygin gas for \(\alpha =0\) [55, 56, 60, 61]. By presuming that there is a sufficiently high level of non-linear clustering on small scales, it has recently been shown that the GCG may be consistent with current observational constraints, over a wide region of parameter space [62,63,64,65,66]. Then, the modified Chaplygin gas (MCG) is proposed as a generalization of the GCG model. Modified Chaplygin gas obeying an equation of state \(p=A\rho -\frac{B}{\rho ^{\alpha }}\). Equation of state of dark energy (\(\omega _{x}\)) still cannot be determined exactly and the observational data show \(\omega _{x}\) is in the range of \((-1.46,-0.78)\) so Zhang et al. have generalized GCG model as possible X-type dark energy with constant \(\omega _{x}\) [67]. Therefore, they propose a new generalized Chaplygin gas (NGCG) scenario. Due to DM and DE are dominant component of universe, it is logical considering interaction between them. Moreover recent observation data from SNIa, CMB and galaxy cluster show this interaction [68, 69], Also The cosmic coincidence problem is solved for interacting models. Both dark energy models and modified gravity models may both fit observation. The question then arises whether the two scenarios can be distinguished. In fact Most of the observational constraints are model-dependent, thus, it not easy to distinguish dark energy models from modified gravity theories even by using the observations. These confusions suggest that a more conservative approach to the problem of the cosmic acceleration. Thus, various model-independent approaches have been proposed in the literature. A well-known one is the CPL parametrization [70, 71]. Another powerful model-independent approach is cosmography

2 Cosmography

Cosmography was first discussed by Weinberg [72] and extended by Visser [73] recently. Cosmography method, relies on the Copernican principle and lead to the Friedmann–Lematre–Robertson–Walker (FLRW) metric Cosmography is a mathematical framework for description of the universe. It relies on the Copernican principle [leading to the Friedmann–Lematre–Robertson–Walker (FLRW) metric]. By expansion of the scale factor with respect to cosmic time, cosmographical parameters obtained as [74,75,76,77,78,79,80,81,82,83]

$$\begin{aligned} H= & {} \frac{1}{a}\frac{da}{dt},\quad q=-\frac{1}{H^{2}}\frac{1}{a}\frac{d^{2}(a)}{dt^{2}},\quad j=\frac{1}{H^{3}}\frac{1}{a}\frac{d^{3}a}{dt^{3}},\nonumber \\ s= & {} \frac{1}{H^{4}}\frac{1}{a}\frac{d^{4}(a)}{dt^{4}},\quad l=\frac{1}{H^{5}}\frac{1}{a}\frac{d^{5}(a)}{dt^{5}} \end{aligned}$$
(1)

The coefficients in Eq. 1 are, by construction, model independent quantities, which are called the cosmographic set (CS). They are known in the literature as the Hubble rate (H), the acceleration parameter (q), the jerk parameter (j), the snap parameter (s), the lerk parameter (l) [75, 76] and the m parameter introduced in [76]. Present values of these parameters where is shown with subscript 0 characterize evolution of the universe. For example, \(q_{0}<0\) denotes an accelerated expansion and \(j_{0}\) discriminate various accelerating models. the cosmographic parameters can also be presented in terms of high derivatives of H as,

$$\begin{aligned}&q=-1-\frac{\dot{H}}{H^{2}} \end{aligned}$$
(2)
$$\begin{aligned}&j=\frac{\ddot{H}}{H^{3}}-3q-2 \end{aligned}$$
(3)
$$\begin{aligned}&s=\frac{\dddot{H}}{H^{4}}+4j+3q(q+4)+6 \end{aligned}$$
(4)
$$\begin{aligned}&l=\frac{H^{(4)}}{H^{5}}+5s-10j(q+2)-30q(q+2)-24. \end{aligned}$$
(5)

The luminosity distance relation can be obtained from the cosmographic approach [72, 74,75,76,77,78, 84,85,86,87];

$$\begin{aligned} d_{L}(z)= & {} \frac{c z}{H_{0}} \left\{ \mathcal {D}_{L}^{0} + \mathcal {D}_{L}^{1} \ z + \mathcal {D}_{L}^{2} \ z^{2}\right. \nonumber \\&\left. + \mathcal {D}_{L}^{3} \ z^{3} + \mathcal {D}_{L}^{4} \ z^{4} + O (z^{5}) \right\} . \end{aligned}$$
(6)

In which;

$$\begin{aligned} \mathcal {D}_{L}^{0}= & {} 1 \end{aligned}$$
(7)
$$\begin{aligned} \mathcal {D}_{L}^{1}= & {} - \frac{1}{2} \left( -1 + q_{0}\right) \end{aligned}$$
(8)
$$\begin{aligned} \mathcal {D}_{L}^{2}= & {} - \frac{1}{6} \left( 1 - q_{0} - 3q_{0}^{2} + j_{0} + \frac{k c^{2}}{H_{0}^{2}a_{0}^{2}}\right) \end{aligned}$$
(9)
$$\begin{aligned} \mathcal {D}_{L}^{3}= & {} \frac{1}{24} \left( 2 - 2 q_{0} - 15q_{0}^{2} - 15 q_{0}^{3} + 5 j_{0} \right. \nonumber \\&+ \left. 10 q_{0} j_{0} + s_{0} +\frac{2 k c^{2} (1 + 3 q_{0})}{H_{0}^{2} a_{0}^{2}}\right) \end{aligned}$$
(10)
$$\begin{aligned} \mathcal {D}_{L}^{4}= & {} \frac{1}{120} \left[ -6 + 6 q_{0} + 81 q_{0}^{2} + 165 q_{0}^{3} + 105 q_{0}^{4} \right. \nonumber \\&- 110 q_{0} j_{0}- 105 q_{0}^{2} j_{0} - 15 q_{0} s_{0} + - 27 j_{0} + 10 j_{0}^{2}\nonumber \\&\left. - 11 s_{0} - l_{0} - \frac{5kc^{2}(1 + 8 q_{0} + 9 q_{0}^{2} - 2 j_{0})}{a_{0}^{2}H_{0}^{2}}\right] . \end{aligned}$$
(11)

Despite of appealing features of this method, it has some shortcoming when trying to adequately reconstruct theories with higher-order derivatives [88]. It is worth noting that since the cosmography is based on series expansions, the basic problem of applying such an approach to fit the luminosity distance data using high redshift distance indicators are connected with the convergence and the truncation of the series. This problem may be a serious challenge for high redshift data set such as cosmic microwave background (CMB) and gamma ray bursts (GRBs). To avoid this problem Cattoen and Visser introduced new redshift variable so called y-redshift [84] :

$$\begin{aligned} y=\frac{z}{1+z}. \end{aligned}$$
(12)

Thus the y-redshift could potentially weaken this problem because, the redshift range \(z \in (0, \infty )\) can be mapped into \(y \in (0, 1)\), so that we are mainly inside the convergence interval of the series, even for CMB data \((z = 1089 \rightarrow y = 0.999)\). Alternatively, one can derive a new version of the luminosity distance in terms of the variable y as

$$\begin{aligned} d_{L}(y)&=\frac{c}{H_{0}}\left\{ y-\frac{1}{2}(q_{0}-3)y^{2}+\frac{1}{6}[11 -5q_{0} - j_{0}] y^{3} \right. \nonumber \\&\quad \left. +\, \frac{1}{24} [50 - 7j_{0} - 26q_{0} +10q_{0}j_{0} \right. \nonumber \\&\quad \left. +\, 21q_{0}^{2} - 15q_{0}^{3} + s_{0}] y^{4}\right\} \end{aligned}$$
(13)

In this paper, we are going to present a method to reconstruct cosmographic parameters from parameters of particular cosmological models. In this method inspired by dynamical system approach, we convert the equation of the cosmological model into an equivalent system of first order differential equations which is much easier to solve numerically. Then, we reproduce the cosmographic parameters in terms of these variables. Instead of constrain on cosmographic parameters using the luminosity distance relation (6), we best fit and estimate the parameters and initial conditions of the model by observational using the Luminosity distance relation

$$\begin{aligned} d_{L}(z)=(1+z)\int \frac{dz'}{H(z')}. \end{aligned}$$
(14)

Consequently, the cosmographic parameters which have been reproduced in terms of parameters and variables of the model will be constrained automatically. The advantage of this method is that, it is free of some of shortcomings reconstructing theories with higher-order derivatives.

3 Interacting new generalized Chaplygin gas model

The equations of motion corresponding to FRW spacetime filled with the two component fluid are

$$\begin{aligned}&\dot{H}=-\frac{\kappa ^{2}}{6}(p_{ncg}+\rho _{ncg}+\rho _{m}) \end{aligned}$$
(15)
$$\begin{aligned}&H^{2}=\frac{\kappa ^{2}}{3}(\rho _{ncg}+\rho _{m}) \end{aligned}$$
(16)

where \(\kappa ^{2}=8\pi G\) is the Einsteins gravitational constant. New generalized Chaplygin gas (NGCG) model is presented by Zhang et al. [67]. It is an extended form of the generalized Chaplygin gas. It is an exotic background with equation of state as follow

$$\begin{aligned} p_{ch}=-\frac{\tilde{A}(a)}{\rho _{ch}^{\alpha }} ,\quad \tilde{A}(a)=\omega _{x}Aa^{-3(1+\omega _{x})(1+\alpha )} \end{aligned}$$
(17)

where \(\alpha \) is a real number, \(\tilde{A}(a)\) is a function of scale factor a, A is a positive constant and the observational data favor \(\omega _{x}\) to have a value in range of \((1.46,-0.78)\) [89,90,91,92]. The energy density of NGCG is expressed as follow

$$\begin{aligned} \rho _{ch}=\left[ Aa^{-3(1+\omega _{x})(1+\alpha )}+Ba^{-3(1+\alpha )}\right] ^{\frac{1}{1+\alpha }} \end{aligned}$$
(18)

positive constant B is integration constant. The energy conservation equation is

$$\begin{aligned} \dot{\rho }_{ch}+\dot{\rho }_{m}+3H\left( \rho _{m}+\rho _{ch}+p_{ch}\right) =0 \end{aligned}$$
(19)

Because of unknown nature of dark matter and dark energy, it is more logical consuming interaction between DM and DE so energy conservation break into two non conserving equation as

$$\begin{aligned}&\dot{\rho }_{ch}+3H\rho _{ch}(p_{ch}+\rho _{ch})=-Q \end{aligned}$$
(20)
$$\begin{aligned}&\dot{\rho }_{m}+3H\rho _{m}=Q. \end{aligned}$$
(21)

Q is the energy exchange and it is clear that dimension of Q must be density into inverse time so we assume namely \(Q=Q(H\rho _{CG},H\rho _{m})\). By expanding about energy density, we have \(Q\simeq H(\rho _{ch}+\rho _{m})\) [86]. By inserting a coupling parameter c in Q we have

$$\begin{aligned} Q=3Hc(\rho _{ch}+\rho _{m}). \end{aligned}$$
(22)

From astrophysical data it is obtained that coupling parameter c have a positive value of the order unity [87]. Defining the e-folding x with definition \(x=lna=-ln(1+z)\), where z is redshift parameter. In addition density and pressure of NGCG can be represented by dimensionless parameter \(\chi \) and \(\zeta \) as

$$\begin{aligned} \chi =\frac{\rho _{ch}}{\rho _{cr}}=\Omega _{ch}=\frac{\kappa ^{2}\rho _{ch}}{3H^{2}},\quad \zeta =\frac{\kappa ^{2}p_{ch}}{3H^{2}}. \end{aligned}$$
(23)

The equation of state (EOS) of model can be obtained as

$$\begin{aligned} \omega _{x}(x)=\frac{\zeta }{\chi }. \end{aligned}$$
(24)

So density parameter of matter can be calculated as

$$\begin{aligned} \Omega _{m}=\frac{\kappa ^{2}\rho _{m}}{3H^{2}}=1-\Omega _{ch}=1-\chi . \end{aligned}$$
(25)

By substituting Eqs. (23), (24), (25) in (20), (21) we have

$$\begin{aligned} \frac{d\chi }{dx}&=-3c-3\zeta +3\zeta \chi \end{aligned}$$
(26)
$$\begin{aligned} \frac{d\zeta }{dx}&=3\frac{\alpha \zeta }{\chi }(\chi +\zeta +c)\nonumber \\&\quad +3\zeta (1+\alpha )\left( 1+\frac{\zeta }{\chi }\right) +3\zeta (1+\zeta ) \end{aligned}$$
(27)

we intend to solve these equation and fit parameters of model.

4 Reconstructing cosmographic parameters from NGCG model

In this subsection, we want to reconstruct cosmographic parameters from NGCG model. In order to relate this parameters with new variables, we derive the following equations.

$$\begin{aligned}&\frac{\dot{H}}{H^{2}}=\frac{1}{H}\frac{dH}{dx} \end{aligned}$$
(28)
$$\begin{aligned}&\frac{\ddot{H}}{H^{3}}=\frac{d}{dx}\left( \frac{\dot{H}}{H^{2}}\right) +2\left( \frac{\dot{H}}{H^{2}}\right) ^{2} \end{aligned}$$
(29)
$$\begin{aligned}&\frac{\dddot{H}}{H^{4}}=\frac{d}{dx}\left( \frac{\ddot{H}}{H^{3}}\right) +3\frac{\dot{H}}{H^{2}}\frac{\ddot{H}}{H^{3}} \end{aligned}$$
(30)
$$\begin{aligned}&\frac{H^{(4)}}{H^{5}}=\frac{d}{dx}\left( \frac{H^{(3)}}{H^{4}}\right) +4\frac{\dot{H}}{H^{2}}\frac{H^{(3)}}{H^{4}} \end{aligned}$$
(31)
$$\begin{aligned}&. \nonumber \\&. \nonumber \\&\frac{H^{(n)}}{H^{n+1}}=\frac{d}{dx}\left( \frac{H^{(n-1)}}{H^{n}}\right) +n\frac{\dot{H}}{H^{2}}\frac{ H^{(n-1)}}{H^{n}}. \end{aligned}$$
(32)

By extracting \(\frac{\dot{H}}{H^{2}}\) in terms of the new variables \((\chi ,\zeta )\), it is possible to obtain all cosmographic parameters in terms of these variables. From Eqs. (15), (16) and (23)

$$\begin{aligned} \frac{\dot{H}}{H^{2}}=-\frac{3}{2}(1+\zeta ) \end{aligned}$$
(33)

and consequently

$$\begin{aligned} q=-\left( 1+\frac{\dot{H}}{H^{2}}\right) =\frac{1}{2}(1+3\zeta ). \end{aligned}$$
(34)

The other cosmographical parameters j can be rewrite as

$$\begin{aligned} j=\frac{\ddot{H}}{H^{3}}-3q-2 =\frac{d}{dx}\left( \frac{\dot{H}}{H^{2}}\right) +2\left( \frac{\dot{H}}{H^{2}}\right) ^{2}-3q-2 \end{aligned}$$
(35)

From Eq. (34), \(\frac{d}{dx}\left( \frac{\dot{H}}{H^{2}}\right) =-\frac{3}{2}\frac{d\zeta }{dx}\). Thus using Eq. (27) the cosmographic parameter j can be obtain in terms of new variables as

$$\begin{aligned} j=-\frac{9}{2}\alpha \frac{\zeta }{\chi }(\zeta +\chi +c)-\frac{9}{2}\zeta (1+\alpha )\left( 1+\frac{\zeta }{\chi }\right) +1 \end{aligned}$$
(36)

Also, in terms of new variable

$$\begin{aligned} \frac{\ddot{H}}{H^{3}}=-\frac{9}{2}\alpha \frac{\zeta }{\chi }(\zeta +\chi +c)-\frac{9}{2}\zeta (1+\alpha )\left( 1+\frac{\zeta }{\chi }\right) +9\chi +\frac{9}{2} \end{aligned}$$
(37)

Same as we have done for j, the parameter, s, will be

$$\begin{aligned} s=\frac{d}{dx}\left( \frac{\ddot{H}}{H^{3}}\right) +3\frac{\dot{H}}{H^{2}}\frac{\ddot{H}}{H^{3}}+4j+3q(q+4)+6. \end{aligned}$$
(38)

Thus,

$$\begin{aligned} s&=\frac{1}{4\chi ^{2}}\left( -14\chi ^2+9\zeta ^2\chi -63\zeta \chi ^{2}+18\zeta ^{2}f(\chi ,\zeta )+81\chi \zeta ^{3} \right. \nonumber \\&\quad \left. +27\zeta ^{2}\chi ^{2}-36\alpha +g(\chi ,\zeta )+36\alpha \zeta ^{2}f(\chi ,\zeta )\right. \nonumber \\&\quad \left. -36\zeta \chi \zeta +18\alpha \zeta ^{2}\chi +18\alpha \zeta \chi ^{2}+162\chi \alpha \zeta ^{3}-72\alpha \zeta \chi \zeta \right. \nonumber \\&\quad \left. -18\alpha \zeta \chi c+18\alpha \zeta \chi c+9\chi \alpha c\zeta +81\chi \alpha c\zeta ^{2}\right) . \end{aligned}$$
(39)

Where, we have define \(f(\chi ,\zeta )=\frac{d\chi }{dx}\) and \(g(\chi ,\zeta )=\frac{d\zeta }{dx}\),which can be substituted from Eqs. (26) and (27). In the same procedure we can find the cosmo graphic parameter l.

Fig. 1
figure 1

The graph of the two dimensional likelihood distribution for parameters \(\alpha \) and c and h

Full size image

5 Cosmological constrain

The difference between the absolute and apparent luminosity of a distance object is given by, \(\mu (z)=25+5log_{10}d_{L}(z)\). The luminosity distance redshift is one of the basic relations in modern cosmology and cosmography. In this section we solve Eqs. (26), (27) and by best fitting parameters of model and initial condition with observational data from the Type Ia supernovae (SNeIa), we obtained best values for parameters. For this aim, we use a statistical method namely “\(\chi ^{2}\) method”. We constrain the parameters including initial conditions by minimizing the \(\chi ^{2}\) function that is given as

$$\begin{aligned} \chi ^{2}_{SN e}=\sum \frac{\left[ \mu _{i}^{the}-\mu _{i}^{obs}\right] ^{2}}{\sigma _{i}^{2}} \end{aligned}$$
(40)

where sum is over the SNeIa data. In relation (40), the theoretical distance modulus \(\mu _{i}^{the}\) is given by

$$\begin{aligned} \mu _{i}^{the}=5 log_{10}\frac{dl}{Mpc}+25=5log_{10}D_{L}(z_{i})+\mu _{0} \end{aligned}$$
(41)

where \(\mu _{0}=42.38-5 log_{10}h\) and h is the Hubble constant \(H_{0}\) in units of 100 km/s/Mpc. Also \(\mu _{i}^{obs}\) is the distance modulus parameters calculated from our model and \(\sigma \) is the estimated error of the \(\mu _{i}^{obs}\). In this paper, we use the Union2 data set, which contains 557 SNIa data. we have obtained the best values as \(\alpha =0.17^{+1}_{-4}\), \(c=0.12^{+0.04}_{-0.03}\)(at \(1\sigma \)), the best initial conditions as \(\chi _{0}=0.651\) and \(\zeta _{0}=-0.702\). and \(h=0.6976\) with the \(\chi ^{2}_{min}=540.8649642\). In Fig. 1, the two dimensional likelihood distribution, \(e^{-\chi ^{2}/2} \), for parameters \(\alpha \) and c and h have been plotted.

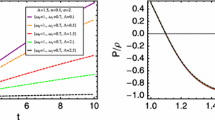
In order to understand the behavior of the universe and its dynamics we need to study the cosmological parameters such as EoS parameter which is given by \(\omega _{eff}=-1+(\frac{2}{3})(1+q)\). We have already verified our model with the current observational data via the distance modulus test. The EoS parameters analytically and/or numerically have been investigated by many authors for variety of cosmological models. The effective EOS parameter has been plotted as a function of redshift in Fig. 2.

Fig. 2
figure 2

The best fitted trajectory of Equation of State for NGCG, \(\Lambda CDM\) and CPL model in redshift range \(-1<z<3\)

Full size image

The calculated effective EoS parameter for the best fitted parameters \(\alpha \) and c and initial conditions, shows that the current effective EoS parameter is \(\omega _{eff}\simeq -0.706\). This value is very close to those obtained for \(\Lambda CDM\) and CPL models in [93, 94]. In Fig. 2 the comparison of the best fitted trajectory for NGCG, \(\Lambda CDM\) and CPL models and their current values have been shown.

Fig. 3
figure 3

The plot of cosmographic parameters as a function of redshift for best fitted parameters, \(\alpha =0.1\) and \(c=0.112\) and different initial conditions. The red dash line shows the trajectory for best fitted parameters and best fitted initial conditions

Full size image

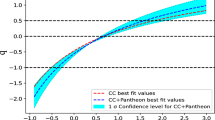
In Fig. 3 cosmographical parameters have been plotted for best fitted parameters c, \(\alpha \) and different initial conditions. The red dash line shows the plot for best values of \(\alpha \) and c and best fitted initial conditions.

Recently, the need of understanding at which time the decelerating–accelerating transition phase occurs has leads cosmologists to directly measure the corresponding transition redshift \(z_{tr} \) [95,96,97,98,99]. There exists a wide consensus, based on robust observational supports such as gamma ray bursts (GRBs), Hubble observational data H(z), BAO, CMB, galaxy clusters, lookback time etc, indicating transition redshift \(z_{tr} \) around the unity [95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111]. The plot of best fitted q(z) focused in transition redshift range in our study shows that the transition redshift \(z_{tr} = 0.825\) which is in good agreement with the recent Busca et al. [111] determination of \(z_{tr} = 0.820.08\), and [95] determination of \(z_{tr} = 0.740.05\) (Fig. 4).

Fig. 4
figure 4

The plot of deceleration parameter q(z) shows the deceleration–acceleration transition redshift

Full size image

6 Past and future of the cosmographic parameters

Some pervious studies have studied cosmographic parameters and constrained the present values of these parameters by various dataset [78, 83, 93, 112,113,114,115,116]. The Major part of the cosmographic analysis and their ability to reconstruct theories from cosmological data have been devoted on constraining on the current values of the cosmographic and cosmological parameters. However, in order to understanding the history of the universe, it could be interesting if we could estimate the future and past values of the cosmographic parameters. To do so, in this section we provide a procedure which not only enable us to evaluate the cosmographic parameters at present day but also it can explain evolution of cosmographic parameters and estimate the past and future values of cosmographic parameters. This method relies on dynamical system approach and the nature of the critical points of the system. For this purpose we refer to the Eqs. (26) and (27). The solution of these equations can provide us critical points of the system which can be related to the future and past values of cosmographic parameter. The critical points of the system are as

$$\begin{aligned}&P_{1}=\chi _{1c}=\infty ,\quad \zeta _{1c}=0 \end{aligned}$$
(42)
$$\begin{aligned}&P_{1}:=\chi _{1c}=-\frac{1}{2}-\frac{3}{4}c+\frac{1}{4}\sqrt{4+4c-15c^{2}},\nonumber \\&\zeta _{1c} =-\frac{1}{2}-\frac{1}{4}c+\frac{1}{4}\sqrt{4+4c-15c^{2}} \end{aligned}$$
(43)
$$\begin{aligned}&P_{2}:\chi _{2c}=-\frac{1}{2}-\frac{3}{4}c-\frac{1}{4}\sqrt{4+4c-15c^{2}},\nonumber \\&\zeta _{2c} =-\frac{1}{2}-\frac{1}{4}c-\frac{1}{4}\sqrt{4+4c-15c^{2}}. \end{aligned}$$
(44)

Subsisting the best value of parameters c, these critical points are simplified as

$$\begin{aligned}&P_{1} :=\chi _{1c}=\infty ,\quad \zeta _{1c}=0 \end{aligned}$$
(45)
$$\begin{aligned}&P_{2}:=\chi _{2c}=0.9,\quad \zeta _{2c}=-0.9 \end{aligned}$$
(46)
$$\begin{aligned}&P_{1}:=\chi _{1c}=0.1,\quad \zeta _{1c}=-0.1. \end{aligned}$$
(47)

Using the jacobian stability,one can determine the nature of the critical points. Here \(P_{1}\), \(P_{2}\) and \(P_{3}\) are unstable, saddle and stable respectively. Figure 5 shows that the best fitted trajectory beginning from unstable point in the past passes near the saddle point and reaches stable point in future.

Thus the cosmographic parameters beginning from their past values \(\{q_{i}=0.5,j_{i}=1,s_{i}=-3.5,l_{i}=17.479\}\) in unstable point \(P_{1}\) and pass the current value \(\{q_{0}=-0.559,j_{0}=0.732,s_{0}=-0.232,l_{0}=3.47\}\) and reaches their past values \(\{q_{f}=-0.916,j_{f}=0.76,s_{f}=0.571,l_{f}=0.379\}\) at unstable point (Fig. 6).

Fig. 5
figure 5

The two dimensional phase plane for \(\zeta ,\chi \). The trajectories entering the best fitted stable critical points with the model parameters \(\alpha \) and c are shown by black lines. The red dash trajectory approaching the stable point corresponds to the best fitted stability parameter and initial conditions

Full size image
Fig. 6
figure 6

The evolution of cosmographic parameters for best fitted parameters and initial conditions

Full size image
Table 1 Comparison of current values of cosmographical for different models
Full size table

7 Conclusions

In this paper we have presented a method to reconstruct cosmographic parameters from new generalized Chaplygin gas (NGCG) model. It is interesting to note that the most advantage of this method is that it is applicable for various cosmological models, although we have focused on (NGCG) ones. First we have introduced two dimensionless independent variables to simplify the obtained equations \((\chi ,\zeta )\). There are various reasons for doing this, one being that. The numerical solution of Eq. 15 even for simplest cosmological model is afflicted by the large uncertainties on the boundary conditions (i.e., the present day values of the scale factor and its derivatives up to the third order) that have to be set to find out the scale factor, while, introducing the equation of the system in terms of new variables solve this problem. It can help us to convert the equations into an equivalent system of first order differential equations which is much easier to solve numerically ( only the initial condition in first order must be constrained). This also help us to reconstruct cosmographic parameters, (q, j, s, l) in terms of new variables \((\chi ,\zeta )\). Thus by fitting the model with observations of type Ia supernovae, parameters of the model, \((\alpha ,c)\) and the initial conditions \((\chi _{0},\zeta _{0} )\), have been best fitted. Thus the cosmographic parameters and equation of state \(\omega _{eff}\) have been best fitted automatically.

The current values of cosmographic have been obtained as \(q_{0}=-0.559,j_{0}=0.732,s_{0}=-0.232,l_{0}=3.47\). Instead of best fitting the cosmographic parameters with observation directly, we best fit and estimate the parameters and initial conditions of the model by observational, then the cosmographic parameters will be constrained automatically. The advantage of this method is that, it is free of some of shortcomings reconstructing theories with higher-order derivatives. It also enable us to measure not only the current value of cosmographic parameters \(\{q_{0},j_{0},s_{0},l_{0}\}\) the past values, \(\{q_{i},j_{i},s_{i},l_{i}\}\), future values \(\{q_{f},j_{f},s_{f},l_{f}\}\) and their evolution. This can be a useful tool to test, compare and distinguish different cosmological models according to the reconstructed cosmographic parameters at different epoch of the universe. For previous studies, one focused on the current values of the cosmographic parameters, to distinguish different cosmological models, while now the past values (here obtained as \(\{q_{i}=0.5,j_{i}=1,s_{i}=-3.5,l_{i}=17.479\}\)) and past values (\(\{q_{f}=-0.916,j_{f}=0.76,s_{f}=0.571,l_{f}=0.379\}\)) can increase our knowledge about cosmological models

Our results for this specific cosmological model, explain the current acceleration of the universe, predict the cosmological deceleration–acceleration transition redshift as \(z_{tr} = 0.825\) which is in good agreement with those obtained in pervious studies based on robust observational supports and are in agreement with results obtained \(\Lambda CDM\) model and CPL parametrization. Also the current value of \(\omega _{eff}=-0.706\). This results are comparable with those obtained in [93] for \(\Lambda CDM\), DGP and Cardassian models and CPL parametrization (see Table 1). As a most advantage which distinguishes our study from previous ones, is that, it is possible to estimate cosmographic parameters in past and future.

We have discussed the cosmography of NGCG model so we obtain present value of them. We compare NGCG model with \(\Lambda CDM\), DPG, cardassian, CPL parametrization models.