1 Introduction

A conformal symmetry in spacetime places restrictions on the gravitational potentials. This happens because in the presence of a conformal Killing vector, null geodesics are mapped to null geodesics; the change in the metric is proportional to the metric as it is Lie dragged along a congruence of curves. A conformal symmetry generates conserved quantities for photons. Several researchers have studied the Einstein equations for neutral matter and the Einstein–Maxwell equations for charged matter with a conformal symmetry. Exact solutions generated in this way are useful in relativistic astrophysics and may be used to model dense stars. Most studies in conformal motions have been completed in spherically symmetric spacetimes because of potential applications in cosmology and astrophysics.

Conformal motions in static spherically symmetric spacetimes have been extensively studied by Maartens et al. [1, 2] and Tupper et al. [3]. It has been pointed out that static spherical geometries do admit conformal symmetries which are nonstatic. A recent comprehensive treatment of conformal symmetries in astrophysics, utilizing the Weyl tensor for conformally flat and non-conformally flat metrics, was completed by Manjonjo et al. [4]. Several authors have used conformal symmetries to model compact objects in a general relativistic setting. Herrera et al. [5] and Herrera and Ponce [6, 8], Maartens and Maharaj [9] and Mak and Harko [10] have modelled charged imperfect fluids in the presence of a conformal symmetry. New classes of compact stars with conformal symmetry and a linear equation of state were found by Esculpi and Aloma [11]. Rahaman et al. [12] and Shee et al. [13] studied anisotropic stars with a nonstatic conformal vector and a specific spacetime geometry. Clearly the assumption of a conformal symmetry has been useful in generating realistic astrophysical models.

In generating a stellar model, an equation of state should be imposed on the star based on physical considerations. However in our approach we have specified one of the gravitational potentials to yield an exact solution to the Einstein field equations with anisotropic matter distributions. This is an alternative approach using the gravitational metric rather than the equation of state arising from the microphysics. Our approach leads to an exact model with reasonable physical features. The presence of anisotropic pressure affects the values of the stellar mass, luminosity and other physical quantities. The investigations of Herrera and Santos [14] indicate that local anisotropic pressure provides stability to the stellar sphere. It was showed by Dev and Gleiser [15] that the structure and physical properties of stellar bodies are affected in the presence of anisotropy. The mass and surface redshift may vary depending on the nature of the anisotropic pressure. Gleiser and Dev [16] demonstrated for smaller adiabatic indices associated with anisotropy that the stellar sphere becomes more stable when compared with isotropic pressure. Ruderman [17] showed that in the high density range of order \(10^{15}\) g cm\(^{-3} \), where the nuclear interactions are relativistic, the distribution of matter is likely to be anisotropic. The presence of anisotropy has an important effect on the physical properties, stability and configuration of stellar matter distributions. It is interesting to observe that an equation of state may arise in particular models, involving the radial pressure, by assuming special forms of the metrics in the spacetime geometry. Mafa Takisa and Maharaj [18] showed that solutions are possible with a quadratic equation of state relating the radial pressure to the energy density. Varela et al. [19] established a general approach indicating the role played by an equation of state in the process of dealing with anisotropic matter. Linear relationships involving radial pressure and the energy density exist in anisotropic stellar models of Mafa Takisa et al. [20], Sunzu et al. [21, 22] and Kileba Matondo and Maharaj [23]. Recently, a new approach with anisotropic pressure has been investigated with the Finch and Skea geometry by Maharaj et al. [24] and Kileba Matondo et al. [25].

Anisotropic pressure plays a prominent role in many processes in relativistic astrophysics. Weber [26] has showed that the variation of the magnetic field intensity during the post main sequence of development of neutron stars, enables the matter distribution to produce pressure anisotropy. Several phenomena have been presented previously to describe the existence of anisotropic pressure inside the star. Kippenhahn and Weigert [27] argue that the presence of anisotropic pressure within a stellar object is likely due to the presence of a solid core or the stellar fluid is a type-3A superfluid. Within the stellar object, pressure anisotropy could have arisen from several phase transitions and pion condensation as showed by Sokolov [28] and Sawyer [29]. Sawyer and Scalapino [30] shown that when elementary particles such as pions condense, the anisotropic pressure has to be taken into account to describe a pion condensed phase configuration from the geometry of the \(\pi ^{-1}\) modes. Bowers and Liang [31] have studied the role played by the presence of anisotropy to describe stellar objects in relativistic astrophysics, and the effects arising on the physical quantities such as the compactness factor, redshift, mass and radius. Ivanov [32] pointed out the link between the anisotropy and the redshift, and obtained higher surface redshifts when the strong energy condition and the dominant energy condition are satisfied. For stellar objects with high densities greater than nuclear matter density, it is required that the Tolman–Oppenheimer–Volkov equation describing the equilibrium condition for charged fluid elements subject to gravitational, electric and hydrostatic forces, to be modified because of another interaction force due to the pressure anisotropy within the star. It was suggested by Usov [33] that the existence of strong electric field could be generated by the presence of anisotropy. Sharma and Maharaj [34] shown that in the presence of pressure anisotropy, compact stellar objects can be generated with a linear equation of state which can be applied to strange stars with quark matter. Recently, a class of static spherically symmetric objects with high anisotropic pressure in Tolman VII spacetime has been investigated by Bhar et al. [35]. A model for compact star with large pressure anisotropy which satisfies all physical requirements and causality conditions has been produced by Thirukkanesh and Ragel [36].

The usual approach in the modelling process is to restrict the conformal symmetry or assume a functional form for the metric functions. This approach is ad hoc. Manjonjo et al. [4] have shown that the existence of a conformal Killing vector implies a relationship relating the gravitational potentials. This provides a systematic method of generating solutions of the Einstein and Einstein–Maxwell systems of field equations. We use the relationship of Manjonjo et al. [4] to find new classes of exact solutions with an anisotropic matter distribution in terms of simple elementary functions and study their physical features. We show that the exact solutions obtained are physically reasonable and may be related to observed astrophysical objects.

Solutions of dense relativistic stars found with conformal symmetry often have a singularity at the stellar centre. We seek exact solutions of the Einstein field equations which are regular at the centre. We select forms of the metric functions that enable the conformal relation of Manjonjo et al. [4] to be integrated. This helps to eliminate the singularity at the centre. In Sect. 2 the Einstein field equations are given. In Sect. 3 we give the conformal relationship between the potentials derived in [4]. Polynomial forms for one of the potentials enable the conformal relation to be integrated. Three classes of metrics which are regular at the centre are found in Sects. 4, 5 and 6. In Sect. 7, we use the metric potentials obtained in Sect. 4 to generate an exact solution to Einstein field equations. In Sect. 8, we study the physical features of the model. The matter variables and other physical quantities are also plotted for a particular choice of parameter values. Concluding remarks are made in Sect. 9.

2 Field equations

The gravitational field in spherically symmetric spacetimes, modelling the interior of a static relativistic star, is given by

$$\begin{aligned} ds^2 = -e^{2\nu (r)}dt^{2}+e^{2\lambda (r)}dr^{2}+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(1)

The expressions \(\lambda (r)\) and \(\nu (r)\) are arbitrary functions and represent gravity. The tensor \(\mathbf{T}\) corresponds to energy momentum and has the general form

$$\begin{aligned} T_{ab}= & {} \text {diag}\left( -\rho ,~ p_{r} ,~ p_{t},~ p_{t} \right) , \end{aligned}$$
(2)

where the quantities \(\rho , p_{r}, p_{t}\) and E are the energy density, radial pressure and tangential pressure respectively. Then the Einstein system of equations can be written in the form

$$\begin{aligned} \frac{1}{r^2}\left[ r(1-e^{-2\lambda })\right] '= & {} 8\pi \rho , \end{aligned}$$
(3a)
$$\begin{aligned} -\frac{1}{r^2}(1-e^{-2\lambda }) + \frac{2\nu '}{r}e^{-2\lambda }= & {} 8\pi p_{r}, \end{aligned}$$
(3b)
$$\begin{aligned} e^{-2\lambda }\left( \nu '' +\nu '^{2} + \frac{\nu '}{r} - \nu '\lambda ' -\frac{\lambda '}{r}\right)= & {} 8\pi p_{t}, \end{aligned}$$
(3c)

in terms of the coordinate r. Primes denote differentiation with respect to r. We are using units in which \(G=c=1\).

The Durgapal and Bannerji  [37] form of the Einstein field equations is obtained if we introduce the transformation

$$\begin{aligned} x = Cr^{2},~~ Z(x) = e^{-2\lambda (r)},~~ A^{2}y^{2}(x) = e^{2\nu (r)}, \end{aligned}$$
(4)

where A and C are constants. In terms of the new variables the line element (1) has the form

$$\begin{aligned} ds^{2}= & {} -A^{2}y^{2}(x)dt^{2}+\frac{1}{4CxZ(x)}dx^{2}\nonumber \\&+\frac{x}{C}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}\right) . \end{aligned}$$
(5)

The field equations (3) become

$$\begin{aligned} \frac{8\pi \rho }{C}= & {} -2\dot{Z}+\frac{1-Z}{x}, \end{aligned}$$
(6a)
$$\begin{aligned} \frac{8\pi p_r}{C}= & {} 4Z\frac{\dot{y} }{y}+\frac{Z-1}{x}, \end{aligned}$$
(6b)
$$\begin{aligned} \frac{8\pi p_t}{C}= & {} 4xZ\frac{\ddot{y}}{y}+(4Z+2x\dot{Z})\frac{\dot{y} }{y}+\dot{Z}, \end{aligned}$$
(6c)

which is an equivalent form. The mass contained within a radius x of the spherical star is given by the expression

$$\begin{aligned} M(x)=\frac{2\pi }{ C^{3/2}}\int ^{x}_{0}\sqrt{\omega }\rho (\omega )\ d\omega , \end{aligned}$$
(7)

which is sometimes called the mass function.

3 Physical models

The field equations are highly nonlinear. If the spacetime manifold admits a symmetry then this often leads to simplification and an exact solution. For a conformal Killing vector to exist we have the requirement

$$\begin{aligned} \mathscr {L}_{\mathbf {X}}g_{ab}=2\psi g_{ab}, \end{aligned}$$
(8)

on the metric tensor field \(g_{ab}\). Here \(\mathscr {L}_{\mathbf {X}}\) is the Lie derivative along the integral curves of the vector field \(\mathbf {X}\) and \(\psi (x^a)\) is the conformal factor. The condition (8) places restrictions on the quantities associated with the spacetime curvature. In particular for the Ricci tensor \(R_{ab}\) and the Ricci scalar R we obtain respectively

$$\begin{aligned} \mathscr {L}_{\mathbf {X}}R_{ab}= & {} 2\psi _{;ab} - g_{ab}\Box \psi , \end{aligned}$$
(9a)
$$\begin{aligned} \mathscr {L}_{\mathbf {X}}R= & {} -2\psi R - 6\Box \psi , \end{aligned}$$
(9b)

where \(\Box \psi = g^{ab}\psi _{;ab}\). Then the Einstein field equations \(R_{ab}-\frac{1}{2}R g_{ab} = 8 \pi T_{ab}\) place restrictions on the matter variables in the presence of the conformal symmetry. The explicit conditions on the matter variables are given by Maartens et al. [38] and Coley and Tupper [39].

It is required to make a choice for the gravitational potentials to generate a new class of solution to the Einstein system of equations. A variety of choices can be made that lead to physical models. Here we use the fact that the line element (1) admits conformal symmetries. If a conformal symmetry exists then the potentials \(\nu \) and \(\lambda \) are related by

$$\begin{aligned} e^{\nu }=\tilde{a}r\cosh \left( b\int \frac{e^{\lambda }}{r}dr + c \right) , \end{aligned}$$
(10)

where \(\tilde{a}\), b, c are constants. The result (10) was established by Manjonjo et al. [4]. Combining (10) and the transformations (4), the relationship between y and Z can be written as

$$\begin{aligned} y = a \sqrt{x}\cosh \left( \frac{b}{2}\int \frac{dx}{x\sqrt{Z}} + c \right) , \end{aligned}$$
(11)

where \(a = \tilde{a}/A\sqrt{C}\) is a real constant. Particular choices of the gravitational potential Z allow us to integrate (11) and find exact solutions to the Einstein system of equations.

Table 1 Potentials for Class I models
Full size table

There have been several exact solutions with anisotropy and conformal symmetry that have been found including the recent works of Shee et al. [13] and Rahaman et al. [12]. Here we show that other classes of exact models are admitted by the field equations with this geometric feature. The advantage of our approach is that the gravitational potentials have a simple form: the function Z(x) can be written as a polynomial which helps to simplify the physical analysis. We consider the three polynomial functions:

  1. (a)

    Case I: \(Z=[(1 + d x)(1 + e x)]^2\)

  2. (b)

    Case II: \(Z=(1 + e x + d x^2)^2\)

  3. (c)

    Case III: \(Z=[(1 + n x)(1 + e x + d x^2)]^2\)

The coefficients and degree of the polynomial in Z(x) have been chosen so that integration is possible to yield elementary functions in (11). It is important to observe that the above choices for the function Z are physically reasonable. The forms for Z are all regular at the centre of the star and well behaved in the interior. They yield stellar models with desirable features which correspond to stellar objects as we show in Sect. 8. Many other forms of Z have been selected in the past as indicated in the works of Kiess [40], Fatema and Murad [41] and Murad [42]. Our polynomial forms for Z are new, make exact integration of the field equations possible and yield stars which are physically reasonable. The integration of the field equations is considered in the subsequent sections. It turns out that there are forms for the second gravitational potential y(x) which are also regular at the centre. Regularity at the centre is a desirable feature in a stellar model. Many of the exact solutions with conformal symmetry that have been found in the past exhibit singularities at the stellar centre for the potentials.

4 Class I metrics

In this case, we assume that the gravitational potential has the form

$$\begin{aligned} Z= & {} \left[ (1+dx) (1+ex) \right] ^2. \end{aligned}$$
(12)

Using the gravitational potential (12), the integration in (11) can be performed depending on the value of \(d-e\). When \(d\ne e\) we obtain

$$\begin{aligned} y(x)= & {} \frac{a\sqrt{x}}{2 K} \left[ K^2 x^{\frac{b}{2}}(1+dx)^{\frac{-bd}{2(d-e)}}(1+ex)^{\frac{eb}{2(d-e)}} \right. \nonumber \\&\left. +\, x^{-\frac{b}{2}}(1+ex)^{\frac{-be}{2(d-e)}}(1+dx)^{\frac{bd}{2(d-e)}} \right] , \end{aligned}$$
(13)

where K is new constant. When \(d=e\), the potential Z is

$$\begin{aligned} Z= & {} \left( 1 + e x\right) ^4, \end{aligned}$$
(14)

and (11) yields

$$\begin{aligned} y(x)= & {} \frac{a\sqrt{x}}{2 K} \left[ K^2\left( -\frac{b e x}{1 + e x}\right) ^{\frac{b}{2}}\exp \left( \frac{b}{2(1 + e x)}\right) \right. \nonumber \\&\left. + \left( -\frac{1 + e x}{b e x}\right) ^{\frac{b}{2}}\exp \left( -\frac{b}{2(1 + e x)}\right) \right] . \end{aligned}$$
(15)

We observe from (13) and (15) that when \(b=-1\) the potential y is regular at the centre \(x=0\). We present the metric potentials in Table 1 for \(d-e = \frac{1}{2}\), and \(d = e\) in terms of both variables x and r.

Table 2 Potentials for Class II models
Full size table

5 Class II solutions

In this case, we consider the gravitational potential in the form

$$\begin{aligned} Z= & {} \left( 1 + e x + d x^2 \right) ^2. \end{aligned}$$
(16)

The integration in (11) is possible depending on the value of \(e^2 - 4d\). It is convenient to introduce the new parameters

$$\begin{aligned} \alpha= & {} \frac{e - \sqrt{e^2 - 4d}}{2d}, \end{aligned}$$
(17a)
$$\begin{aligned} \beta= & {} \frac{e + \sqrt{e^2 - 4d}}{2d}, \end{aligned}$$
(17b)

in terms of e and d. When \(e^2 - 4d<0\) then complex quantities arise which we neglect. We take \(e^2 - 4d>0\). With \(e^2 > 4d\) we get

$$\begin{aligned} y(x)= & {} \frac{a\sqrt{x}}{2K} \left[ K^2 x^{\frac{b}{2\alpha \beta }}(\alpha +x)^{\frac{b}{2 \alpha (\alpha -\beta )}} ( \beta +x)^{-\frac{b}{2 \beta (\alpha -\beta )}} \right. \nonumber \\&\left. + x^{-\frac{b}{2\alpha \beta }} (\alpha +x)^{-\frac{b}{2 \alpha (\alpha -\beta )}} (\beta +x)^{\frac{b}{2 \beta (\alpha -\beta )}} \right] , \end{aligned}$$
(18)

where K is a new constant. We note from (18) that with \(b=-\alpha \beta \), the sphere is regular at the centre. When \(e^2 - 4d = 0\) the potential Z becomes

$$\begin{aligned} Z= & {} \left( 1 + 2\sqrt{d}x + d x^2\right) ^2, \end{aligned}$$
(19)

and (11) gives the function

$$\begin{aligned} y(x)= & {} \frac{a}{2K} \left[ \frac{K^2 x^{\frac{b+1}{2}}}{(1+\sqrt{d}x)^{\frac{b}{2}}}\exp \left( \frac{b}{2(1+\sqrt{d} x)} \right) \right. \nonumber \\&\left. + \frac{(1+\sqrt{d}x)^\frac{b}{2}}{x^{\frac{b-1}{2}}} \exp \left( -\frac{b}{2(1+\sqrt{d}x)} \right) \right] . \end{aligned}$$
(20)

In this situation (20) is regular at the centre when \(b=-1\). We present the metric potentials in Table 2 for \(e^2 - 4d = 0\) and \(e^2 - 4d > 0\) for both variables x and r.

6 Class III solutions

For this case we take the gravitational potential in the form

$$\begin{aligned} Z= & {} \left[ (1 + n x)(1 + e x + d x^2)\right] ^2. \end{aligned}$$
(21)

Then the integration in (11) can be done depending on the value of \(e^2 - 4d\). We take

$$\begin{aligned} \alpha= & {} \frac{e-\sqrt{e^2 - 4d}}{2d}, \end{aligned}$$
(22a)
$$\begin{aligned} \beta= & {} \frac{e+\sqrt{e^2 - 4d}}{2d}, \end{aligned}$$
(22b)

as the new parameters expressed in terms of e and d. When \( e^2 - 4d < 0 \) we obtain complex quantities, therefore this case is neglected in our study. With \( e^2 - 4d > 0 \) we have

$$\begin{aligned}&y(x)= \frac{a\sqrt{x}}{2K} \left[ \frac{K^2 x^{\frac{b}{2\alpha \beta }} (\beta +x)^{\frac{b}{2 \beta (\alpha -\beta )(n\beta -1 )}}}{(1 + n x)^{\frac{n^2 b}{2(n\alpha -1)( n\beta -1 )}} (\alpha + x )^{\frac{b}{2\alpha (n\alpha -1)(\alpha - \beta )}} } \right. \nonumber \\&\,\,\,\, \left. + \frac{(1 + n x)^{\frac{n^2 b}{2(n\alpha -1)(n\beta -1)}} (\alpha +x)^{ \frac{b}{2\alpha (n\alpha -1)(\alpha - \beta )}}}{ x^{\frac{b}{2\alpha \beta }}(\beta +x)^{-\frac{b}{2 \beta (\alpha -\beta )(n\beta -1)}}} \right] , \end{aligned}$$
(23)

where K is a new constant. It is convenient to know from (23) that with \(b=-\alpha \beta \) the potential is regular at the centre. For \( e^2 - 4d = 0 \), the potential Z takes the form

$$\begin{aligned} Z= & {} \left[ (1 + n x)(1 + 2\sqrt{d} x + d x^2)\right] ^2, \end{aligned}$$
(24)

and (11) becomes

$$\begin{aligned} y(x)= & {} \frac{a}{2K} \nonumber \\&\times \left[ \frac{ K^2 x^{\frac{b+1}{2}}(1 + \sqrt{d} x)^{ \frac{b(2n\sqrt{d} -d)}{2(\sqrt{d}-n)^2}}}{(1+nx)^{\frac{ bn^2}{2(\sqrt{d}-n)^2}}}\exp \left( E\right) \right. \nonumber \\&\left. + \frac{(1+nx)^{\frac{bn^2}{2(\sqrt{ d}-n)^2}}}{x^{\frac{b-1}{2}}(1+\sqrt{d} x)^{\frac{b(2n\sqrt{d}-d)}{2(\sqrt{d}-n)^2}} } \exp \left( E\right) \right] , \end{aligned}$$
(25)

where \(E= \frac{b\sqrt{d}}{2(\sqrt{d}-n)(1 + \sqrt{d}x)} \). So then, (25) is regular at the centre when we set \(b=-1\). We present the metric potentials in Table 3 for \(e^2 - 4d = 0\) and \(e^2 - 4d > 0\) for both variables x and r.

Table 3 Potentials for Class III models
Full size table

7 Exact solutions

We have generated a number of metrics in terms of elementary functions in Sects. 4–6. These metrics may be used to give the solution of the Einstein field equations for all geometrical and matter variables. We illustrate this with an example taken from Sect. 4. We use Case Ib from Table 1 with \(d-e<\frac{1}{2}\). Then the potentials and matter quantities can be written in terms of the coordinate r:

$$\begin{aligned} e^{2\lambda }= & {} \frac{1}{\left[ (1 + d C r^2)\left( 1 + e C r^2\right) \right] ^{2}}, \end{aligned}$$
(26a)
$$\begin{aligned} e^{2\nu }= & {} \frac{a^{2}A^2 }{4 K^2} \left[ K^2 \left( \frac{(1+d C r^2)^d}{(1+e C r^2)^e}\right) ^{\frac{1}{2(d-e)}} \right. \nonumber \\&\left. + C r^2 \left( \frac{(1+e C r^2)^e}{(1+d C r^2)^d}\right) ^{\frac{1}{2(d-e)}} \right] ^2, \end{aligned}$$
(26b)
$$\begin{aligned} \frac{8\pi \rho }{C}= & {} - d^2 C r^2 (1 + e C r^2) (5 + 9 e C r^2) \nonumber \\&- 2d(1 + e C r^2) (3 + 7 e C r^2 ) \nonumber \\&- e(6 + 5 e C r^2), \end{aligned}$$
(26c)
$$\begin{aligned} \frac{8\pi p_r}{C}= & {} d^2 e^2 C^3 r^6 + 2 d C^2 r^4 \left( d e + e^2\right) \nonumber \\&+ C r^2 \left( d^2+4 d e+e^2\right) + 2(d + e) \nonumber \\&+ \frac{2 (1 + d C r^2) (1 + e C r^2) }{k^2 (1 + d C r^2)^{\frac{d}{d-e}} + C r^2 (1 + e C r^2 )^{\frac{e}{d-e}}}\nonumber \\&\times \left[ (1 + e C r^2)^{\frac{e}{d-e}} (2 + (d + e + d e C r^2)C r^2) \right. \nonumber \\&\left. + k^2 (d + e + d e C r^2) (1 + d C r^2)^{\frac{d}{d-e}} \right] , \end{aligned}$$
(26d)
$$\begin{aligned} \frac{8\pi p_t}{C}= & {} d^2 (1 + e C r^2) (5 + 9 e C r^2)C r^2 \nonumber \\&+ 2 d (1 + e C r^2) (4 + 7 e C r^2) + e (8 + 5 e C r^2) \nonumber \\&+ \frac{1}{C r^2 (1 + d C r^2)^{\frac{d}{e-d}} (1 + e C r^2)^{\frac{e}{d-e}}+k^2}\nonumber \\&\times \left[ 4 (1 + d C r^2)^{\frac{d}{e-d}} (1 + e C r^2)^{\frac{e}{d-e}} \right. \nonumber \\&\left. - 4 d k^2 (1 + e C r^2)-4 e k^2 \right] , \end{aligned}$$
(26e)

in terms of elementary functions.

Table 4 Central density, radius, mass and compactification factor for \(\tilde{d}=-\,0.2\) and \(\tilde{e}=-\,0.1\)
Full size table

It is now possible to generate several physical quantities associated with the exact model (26). We can compute the mass function explicitly from (7). Then the total mass of the anisotropic star within the radius r has the form

$$\begin{aligned} M(r)= & {} -\frac{1}{6 } C r^3 \left[ 6(d+e) + 5 \left( d^2 + 4 d e + e^2\right) C r^2 \right. \nonumber \\&\left. + 14d e(d+e)C^2 r^4 + 9 d^2 e^2 C^3 r^6 \right] . \end{aligned}$$
(27)

The compactness factor is defined as

$$\begin{aligned} \mu =\frac{M(r)}{r}. \end{aligned}$$
(28)

For this model it is given by

$$\begin{aligned} \mu (r)= & {} -\frac{1}{6 }C r^2 \left[ 6(d+e) + 5 \left( d^2 + 4 d e + e^2\right) C r^2 \right. \nonumber \\&\left. + 14d e(d+e)C^2 r^4 + 9 d^2 e^2 C^3 r^6\right] . \end{aligned}$$
(29)

The surface redshift function corresponding to the compactness mass \(\mu \) is given by

$$\begin{aligned} Z_s=(1-2\mu )^{\frac{1}{2}}-1. \end{aligned}$$
(30)

Using (29), we obtain

$$\begin{aligned} Z_s= & {} \sqrt{3} \left[ 3 + \left( 9d^2 e^2 C^3 r^6 + 14 d e (d+e) C^2 r^4 \right) C r^2 \right. \nonumber \\&\left. + \left( 6(d+e) + 5(d^2 + 4 d e + e^2)C r^2 \right) C r^2 \right] ^{-\frac{1}{2}} \nonumber \\&- 1. \end{aligned}$$
(31)

It is possible to study the stability of the gravitating sphere in different ways. Firstly we can use the conservation matter related to the Tolman–Oppenheimer–Volkoff (TOV) equation which describes the equilibrium condition for an anisotropic fluid in the form

$$\begin{aligned} \frac{dp_r}{dr}=-(\rho + p_r)\frac{d\nu }{dr} + \frac{2}{r}(p_t - p_r). \end{aligned}$$
(32)

We introduce the terms for the gravitational force \(F_g =-(\rho + p_r)\frac{d\nu }{dr}\), hydrostatic force \(F_h = -\frac{dp_r}{dr}\) and anisotropic force \(F_a = \frac{2}{r}(p_t - p_r)\). Then the TOV equation can be expressed as

$$\begin{aligned} F_g + F_h + F_a = 0. \end{aligned}$$
(33)

In our model

$$\begin{aligned} F_a= & {} \frac{ C^2 r }{2\pi } \left( d^2 + 4 d e + e^2 + 4d e(d+e)C r^2 \right. \nonumber \\&\left. + 3d^2 e^2 C^2 r^4 \right) , \end{aligned}$$
(34)
$$\begin{aligned} F_g= & {} \frac{C^2 r}{4\pi } \nonumber \\&\times \left[ -\left( \frac{2 \left( 1 + e C r^2 \right) ^{\frac{ e}{d-e}}}{k^2 (1 + d C r^2)^{\frac{d}{d-e}} + C r^2 (1 + e C r^2)^{\frac{e}{d-e}}} \right) ^2 \right. \nonumber \\&\left. + d^2 (1 + e C r^2) (1 + 3e C r^2) + e^2 \right. \nonumber \\&\left. - \frac{4de K^2}{C r^2 \left( 1 + d C r^2\right) ^{\frac{d}{e-d}} \left( 1 + e C r^2\right) ^{\frac{e}{d-e}}+K^2 } \right. \nonumber \\&\left. +\, 2de(3+2e C r^2) \phantom {\left( \frac{2 \left( 1 + e C r^2\right) ^{\frac{ e}{d-e}}}{K^2 (1 + d C r^2)^{\frac{d}{d-e}} + C r^2 (1 + e C r^2)^{\frac{e}{d-e}}} \right) ^2} \right] , \end{aligned}$$
(35)
$$\begin{aligned} F_h= & {} \frac{C^2 r}{4\pi } \nonumber \\&\times \left[ \left( \frac{2 \left( 1 + e C r^2\right) ^{\frac{ e}{d-e}}}{K^2 (1 + d C r^2)^{\frac{d}{d-e}} + C r^2 (1 + e C r^2)^{\frac{e}{d-e}}} \right) ^2 \right. \nonumber \\&\left. -3d^2 \left( 1 + e C r^2\right) \left( 1 + 3e C r^2\right) -3e^2 \right. \nonumber \\&\left. + \frac{4de K^2}{C r^2 \left( 1 + d C r^2\right) ^{\frac{d}{e-d}} \left( 1 + e C r^2\right) ^{\frac{e}{d-e}}+K^2} \right. \nonumber \\&\left. - 2de(7 + 6e C r^2)\phantom {\left( \frac{2 \left( 1 + e C r^2\right) ^{\frac{ e}{d-e}}}{K^2 (1 + d C r^2)^{\frac{d}{d-e}} + C r^2 (1 + e C r^2)^{\frac{e}{d-e}}} \right) ^2} \right] , \end{aligned}$$
(36)

and the anisotropic star is in equilibrium. Secondly the stability is related to the adiabatic condition

$$\begin{aligned} \Gamma = \frac{\rho + p_r}{p_r}\frac{dp_r}{d\rho } >\frac{4}{3}. \end{aligned}$$
(37)

To maintain stability this condition has to be satisfied according to Herrera [43]. Thirdly the condition

$$\begin{aligned} \left| {v_{r}}^{2} - {v_{t}}^{2}\right| < 1, \end{aligned}$$
(38)

has to be satisfied to prevent cracking and overturning of the object.

Fig. 1
figure 1

Variation of metric potentials verses the radius

Full size image
Fig. 2
figure 2

Variation of energy density verses the radius

Full size image
Fig. 3
figure 3

Variation of tangential and radial pressures verses the radius

Full size image
Fig. 4
figure 4

Variation of anisotropy verses the radius

Full size image
Fig. 5
figure 5

Variation of speed of sound verses the radius

Full size image

8 Physical features

In this section we show that the particular solution to the Einstein field equations generated in Sect. 7 satisfies the physical requirements. To account for the physical units and dimensional homogeneity in the dynamical and geometrical variables it is convenient to rescale constants. Since the constants d and e are expressed in dimension \(length^{-2}\), and K in dimension \(length^{-1}\), we use the transformation

$$\begin{aligned} \tilde{d}=R^2 d,~~ \tilde{e}=R^2 e,~~ \tilde{K}=R K, \end{aligned}$$

where R is the parameter of geometry with dimension of length. The geometrical and matter variables are given in (26). A simpler form is obtained by considering a Taylor expansion. For the particular choices of parameter values \(C=0.00051\), \(\tilde{d}=-0.2\), \(\tilde{e}=-0.1\), \(A=5.3737\), \(\tilde{K}=1.1778\), \(a=2\) we get forms for the exact solution to the Einstein system by expanding them in terms up to order \(r^2\) such that

$$\begin{aligned} e^{2\lambda }\approx & {} 1 + 0.01226 r^2, \end{aligned}$$
(39a)
$$\begin{aligned} e^{2\nu }\approx & {} 1 + 0.02332 r^2, \end{aligned}$$
(39b)
$$\begin{aligned} \frac{8\pi \rho }{C}\approx & {} 0.03677 - 0.27 \times 10^{-3} r^2, \end{aligned}$$
(39c)
$$\begin{aligned} \frac{8\pi p_r}{C}\approx & {} 0.03439 - 0.72 \times 10^{-3} r^2, \end{aligned}$$
(39d)
$$\begin{aligned} \frac{8\pi p_t}{C}\approx & {} 0.03439 - 0.61 \times 10^{-3} r^2. \end{aligned}$$
(39e)

These quantities show clearly that the gravitational potentials and matter variables are finite and regular at the centre and in the region nearby the centre. Our model is not singular in the interior of the star. The behaviour of the model may be studied with the help of this particular choice of parameter values used above. It is important to observe that we can generate stars from the exact solution (26) which are physically reasonable. For particular choices of the parameters we generate the central density \(\rho _c\), radius r, mass M and compactness factor \(\frac{M}{r}\) for the stars SAX J1808.4-3658, EXO 1785, Cen X-3, 4U1820-30, PSR J1903+327, Vela X-1 and PSR J1614-2230 in Table 4. We find that these values fall in the observed range.

Fig. 6
figure 6

Variation of energy conditions verses the radius

Full size image
Fig. 7
figure 7

Variation of compactness factor verses the radius

Full size image
Fig. 8
figure 8

Variation of surface redshift function verses the radius

Full size image
Fig. 9
figure 9

Variation of the quantity \( |{v_r}^2-{v_t}^2|\) verses the radius

Full size image
Fig. 10
figure 10

Variation of adiabatic index verses the radius

Full size image
Fig. 11
figure 11

Variation of the forces verses the radius

Full size image
Fig. 12
figure 12

Variation of the mass verses the radius

Full size image

To analyse the behaviour of the matter variables and their stability throughout the star, we make a choice of two stars: PSR J1614-2230 and SAX J1808.4-3658. The choice of these two stellar bodies is motivated by the order of magnitude of their masses: the two masses correspond to the highest and lowest masses in Table 4. We keep the same values \(\tilde{d}=-0.2\) and \(\tilde{e}=-0.1\) while C, R and \(\tilde{K}\) are free, to generate numerical values of masses, radii and central density.

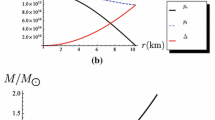
The metric potentials \(e^{2\nu }\) and \(e^{2\lambda }\) are plotted in Fig. 1 for PSR J1614-2230 and SAX J1808.4-3658 and the profiles are regular at the centre and continuous everywhere inside the star. The profiles of the energy density \(\rho \) for PSR J1614-2230 and SAX J1808.4-3658 are plotted in Fig. 2, and show that the density function is regular at the centre and monotonically decreasing with the radius. In Fig. 3 the radial and tangential pressures \(p_r\) and \(p_t\) are shown respectively for PSR J1614-2230 and SAX J1808.4-3658. They are positive, decreasing continuously inside the star. The radial pressure vanishes at \(r=10.79~\text {km}\) for PSR J1614-2230 and \(r=7.68~\text {km}\) for SAX J1808.4-3658. At the centre we observe that \(p_r=p_t\) which ensures stability of the star. Similar profiles for the pressure can be observed in the works of Bhar et al. [35] and Thirukkanesh and Ragel [36]. The variation of anisotropy \(\Delta \) is presented in Fig. 4. The profiles indicate for both bodies that the anisotropic pressure increases from the centre to the surface where it has a finite value. In our model the maximum values of the pressure anisotropy are \(0.37\times 10^{36}\,\text {dyne/cm}^{2}\) for PSR J1614-2230 and \(0.11\times 10^{36}\,\text {dyne/cm}^{ 2}\) for SAX J1808.4-3658 which are lower compared to the maximum value found by Thirukkanesh and Ragel [36] given as \(2.0978\times 10^{48}\,\text {dyne/cm}^{2} \). A lower bound on the anisotropy is a desirable feature.

In Fig. 5 it is shown that the radial and tangential speeds of sound are great than 0 and less than 1 for both stars PSR J1614-2230 and SAX J1808.4-3658. It is important to denote that the speed of sound is monotonically decreasing away from the centre and causality is maintained. It is clear that the null energy condition, the weak energy condition and the strong energy condition for PSR J1614-2230 and SAX J1808.4-3658 respectively are satisfied everywhere in the star. This is illustrated in Fig. 6. The variation of compactness factor and surface redshift are plotted in Figs. 7 and 8, respectively. The values of the compactness factor is consistent with real stars in Fig. 7. The redshift function is increasing with increase of \(\mu \) as shown in Fig. 8. The Buchdahl [44] limit \(\frac{2M(r)}{r} < \frac{8}{9}\) is satisfied and numerically, we have \(\frac{2M}{r}=0.5396\) for PSR J1614-2230 and \(\frac{2M}{r}=0.3476\) for SAX J1808.4-3658. The surface redshift turns out to be \(Z_s = 0.4739\) for PSR J1614-2230 and \(Z_s = 0.2381\) for SAX J1808.4-3658 respectively, which are compatible with observations.

Figure 9 refers to the cracking of the star as proposed by Herrera [43] for stability. We observe that \(0<{v_{r}}^{2} - {v_{t}}^{2}<1\) and \(-1<{v_{t}}^{2} - {v_{r}}^{2}<0\). We plotted the adiabatic index \(\Gamma \) in Fig. 10. As we can observe, everywhere inside these two compact stars \(\Gamma \) is greater than 4 / 3. We also investigated the stability of the model through TOV equation which describes the equilibrium condition for a anisotropic fluid subject to the gravitational, hydrostatic and anisotropic forces given in (33). Then Fig. 11 shows that the gravitational force is balanced by the joint action of hydrostatic and anisotropic forces for PSR J1614-2230 and SAX J1808.4-3658. Hence all three stability criteria are satisfied. In Fig. 12 we have plotted the variation of the mass versus radius for stellar objects PSR J1614-2230 and SAX J1808.4-3658. In both cases the mass function is a increasing quantity with increasing radius. In the first figure we find that the upper bound on the mass is \(1.971~M_{\bigodot }\), and for the second figure the upper bound is \(0.903~M_{\bigodot }\). These figures are consistent with observations and with our results in Table 4.

9 Conclusion

Manjonjo et al. [4] found an explicit relationship between the potentials \(e^{2\lambda (r)}\) and \(e^{2\nu (r)}\) if a conformal Killing vector is present. We used this relationship to generate three new classes of exact solutions to the Einstein field equations with an anisotropic fluid source. The gravitational potentials are regular in the centre. A particular exact solution was selected for a detailed physical analysis. We showed that this solution produces values for the central density, radius, mass and compactification factor consistent with the stars SAX J1808.3−3658, EXO 1785, Cen X-3, 4U 1820-30, PSR J1903+327, Vela X-1 and PSR J1614−2230. The stars PSR J1614−2230 and SAX J1808.4−3658 were chosen for further study as they correspond to the highest and smallest stellar masses in Table 4. We find that for PSR J1614−2230 the central density is \(\rho _c=1.97\times 10^{15}\,\text {g\,cm}^{-3}\) and for SAX J1808.4−3658 the value is \(\rho _c=1.27\times 10^{15}\,\text {g\,cm}^{-3}\). Such high density regime pushes the matter from the nuclear density to the quark matter density. This reinforces the idea of having a quark matter core inside a neutron star, i.e., a hybrid star or a purely strange quark star. In fact, some previous attempts have been made to classify these object as strange quark stars including the work of Gangopadhyay et al. [45]. Our present study on gravitating bodies using conformal symmetry reinforces these claims.

The stellar radius for PSR J1614−2230 is \(r_s=10.79~\text {km}\) and for SAX J1808.4−3658 the radius is \(r_s=7.68~\text {km}\). Our analysis of the features show clearly that the physical criteria of a realistic star are satisfied for our model. In particular the radial pressure \(p_r\) vanishes at the boundary, the anisotropic pressure \(\Delta \) vanishes at the centre, the radial speed of sound \({v_{sr}}^{2}\) and the tangential speed of sound \({v_{st}}^{2}\) have values less than 1 showing that causality is satisfied, the relativistic adiabatic index \(\Gamma \) is greater than 4 / 3 for stability [46], the energy conditions are satisfied everywhere in the star and the Buchdahl [44] limit is satisfied. For PSRJ1614-2230 we have \( \frac{2M}{r}=0.5396<\frac{8}{9}\) and for SAX J1808.4-3658 we have the condition \(\frac{2M}{r}=0.3476<\frac{8}{9}\). Furthermore we obtain bounds on the anisotropy which are lower than previous treatments such as Thirukkanesh and Ragel [36]. This is a desirable feature in a stellar model. Therefore we have showed that the conformal condition of Manjonjo et al. [4] can be integrated to lead to new solutions and they produce models of realistic stars.