Analysis of the structure of $\Xi (1690)$ through its decays

Abstract

The mass and pole residue of the first orbitally and radially excited $\Xi$ state as well as the ground state residue are calculated by means of the two-point QCD sum rules. Using the obtained results for the spectroscopic parameters, the strong coupling constants relevant to the decays $\Xi (1690)\rightarrow \Sigma K$ and $\Xi (1690) \rightarrow \Lambda K$ are calculated within the light-cone QCD sum rules and width of these decay channels are estimated. The obtained results for the mass of ${\widetilde{\Xi }}$ and ratio of the $Br(\widetilde{\Xi }\rightarrow \Sigma K)/Br(\widetilde{\Xi }\rightarrow \Lambda K)$, with $\widetilde{\Xi }$ representing the orbitally excited state in $\Xi$ channel, are in nice agreement with the experimental data of the Belle Collaboration. This allows us to conclude that the $\Xi (1690)$ state, most probably, has negative parity.

1 Introduction

Understanding the spectrum of baryons and looking for new baryonic states constitute one of the main research directions in hadron physics. Impressive developments of experimental techniques allow discovery of many new hadrons. Despite these developments, the spectrum of $\Xi$ baryon is still not well established. This is due to the absence of high intensity anti-kaon beams and small production rate of the $\Xi$ resonances. At present time only the ground state octet and decuplet baryons as well as $\Xi (1320)$ and $\Xi (1530)$ baryons are well established. Up to present time the quantum numbers of $\Xi (1690)$, $\Xi (1820)$ and $\Xi (1950)$ have not been determined. Theoretically, the spectrum of $\Xi$ baryon, within different approaches, have been studied intensively (see [1,2,3,4,5,6,7,8,9] and references therein).

The main results of these studies are that different phenomenological models explain successfully the nature of $\Xi (1320)$ and $\Xi (1530)$ states. However, these approaches predict controversially results for other excitations of $\Xi$ baryons. In [8] using the nonrelativistic quark model the mass of $\Xi (1690)$ is calculated and it is obtained that it might be radial excitation of $\Xi$ with $J^P=\frac{1}{2}^+$. This result was then supported by the quark model calculations in [5]. However within the relativistic quark model in [9] it was established that the first radial excitation should have mass around $1840~\mathrm {MeV}$. In [4] the authors suggested that the $\Xi (1690)$ state might be orbital excitation of $\Xi$ with $J^P=\frac{1}{2}^-$. This point of view was supported by calculations performed within Skyrme model [2] and chiral quark model [7]. The controversy results suggests independent analysis for establishing the nature of $\Xi (1690)$ state.

In the present study, within the light cone QCD sum rules, we estimate the widths of the $\Xi \rightarrow \Lambda K$ and $\Xi \rightarrow \Sigma K$ transitions. We suggest that $\Xi (1690)$ state may be radial ($\widetilde{\Xi }$) or orbital ($\Xi '$) excitation of $\Xi$ baryon. For establishing these decays we need to know the residue of $\Xi (1690)$ as well as the strong coupling constants for these decays. For calculation of the mass and residue of the $\Xi$ states as the main inputs of the calculations we employ the two point QCD sum rule method.

The paper is arranged as follows. In Sect. 2 the mass and residue of $\Xi (1690)$ baryon within both scenarios, namely considering $\Xi (1690)$ as the orbital and radial excitations of $\Xi$ baryon, are calculated. In Sect. 3 we present the calculations of the strong coupling constants defining the $\Xi (1690)\rightarrow \Sigma (\Lambda ) K$ transitions within both scenarios. By using the obtained results for the coupling constants we estimate the relevant decay widths and compare our predictions on decay widths with the existing experimental data in this section, as well. We reserve Sect. 1 for the concluding remarks and some lengthy expressions are moved to the Appendix.

2 Mass and pole residue of the first orbitally and radially excited $\Xi$ state

For calculation of the widths of $\Xi \rightarrow \Sigma K$ and $\Xi \rightarrow \Lambda K$ decays we need to know the residues of $\Xi$, $\Sigma$ and $\Lambda$ baryons. In present work we consider two possible scenarios about nature of the $\Xi (1690)$: (a) it is represented as radial excitation of the ground state $\Xi$. In other words it carries the same quantum numbers as the ground state $\Xi$, i.e. $J^P=\frac{1}{2}^+$. (b) The $\Xi (1690)$ state is considered as first orbital excitation of the ground state $\Xi$, i.e. it is negative parity baryon with $J^P=\frac{1}{2}^-$. In the following we will try to answer the question that which scenario is realized in nature? To answer this question we will calculate the mass of $\Xi (1690)$ state and decay width of the $\Xi \rightarrow \Sigma K$ and $\Xi \rightarrow \Lambda K$ transitions and then compare the ratio of these decays as well as the prediction on the mass with existing experimental data. Note that the BABAR Collaboration has measured the mass ($m=1684.7\pm 1.3^{+2.2}_{-1.6}$) MeV and width ($\Gamma =8.1 ^{+3.9+1.0}_{-3.5-0.9}$) MeV of $\Xi (1690)$ [10, 11] and Belle Collaboration has measured the mass ($m=1688\pm 2$) MeV and width ($\Gamma =11\pm 4$) MeV of this state as well as the ratio $\frac{B(\Xi (1690)^0\rightarrow K^-\Sigma ^+ )}{B(\Xi (1690)^0\rightarrow \bar{K}^0 \Lambda ^0 )}$. The experimental value for this ratio measured by Belle is $0.50\pm 0.26$ [12].

For determination of the mass and residue of $\Xi$ baryon, we start with the following two point correlation function:

$$\begin{aligned} \Pi (q)=i\int d^{4}xe^{iq\cdot x}\langle 0|\mathcal {T}\Big \{\eta _{\Xi }(x) \bar{\eta }_{\Xi }(0)\Big \}|0\rangle , \end{aligned}$$

(1)

where $\eta _{\Xi }(x)$ is the interpolating current for $\Xi$ state with spin $J^P=\frac{1}{2}^+$ and $\mathcal {T}$ indicates the time ordering operator. The general form of the interpolating current for the spin-${1\over 2}$ $\Xi$ baryon can be written as [13, 14]:

$$\begin{aligned} \eta _{\Xi }= & {} \epsilon ^{abc} \Big \{\Big (s^{T,a}(x)Cu^b(x)\Big )\gamma _5s^c(x) \nonumber \\&+\beta \Big (s^{T,a}(x)C\gamma _5u^b(x)\Big )s^c(x) \Big \}~, \end{aligned}$$

(2)

where a, b, c are the color indices and $\beta$ is an arbitrary parameter with $\beta =-1$ corresponding to the Ioffe current. C is the charge conjugation operator.

According to the general philosophy of QCD sum rules method, for calculation of the mass and residue of $\Xi$ baryons the correlation function needs to be calculated in two different ways: (a) in terms of hadronic degrees of freedom and (b) in terms of perturbative and vacuum-condensates contributions expressed as functions of QCD degrees of freedom in deep- Euclidian domain $q^2\ll 0$. After equating these two representations, the desired QCD sum rules for the physical quantities of the baryons under consideration are obtained. As already noted, the quantum numbers $J^P$ of $\Xi (1690)$ state have not been determined via experiments yet. Therefore, firstly we consider the case when $\Xi (1690)$ represents a negative parity baryon. The hadronic side of the correlation function is obtained by inserting complete sets of relevant intermediate states. For calculation of the hadronic side of the correlation function, we would like to note that the above interpolating current has nonzero matrix element with baryons of both parities. Taking into account this fact and saturating the correlation function by complete sets of intermediate states with both parities we obtain:

$$\begin{aligned} \Pi ^{\mathrm {Phys}}(q)= & {} \frac{\langle 0|\eta |\Xi (q,s)\rangle \langle \Xi (q,s)|\overline{\eta }|0\rangle }{m^{2}-q^{2}} \nonumber \\&+\frac{\langle 0|\eta |\widetilde{\Xi }(q,\widetilde{s})\rangle \langle \widetilde{\Xi }(q,\widetilde{s})|\overline{\eta }||0\rangle }{\widetilde{m} ^{2}-q^{2}} \nonumber \\&+\ldots , \end{aligned}$$

(3)

where m, $\widetilde{m}$ and s, $\widetilde{s}$ are the masses and spins of the ground and first orbitally excited $\Xi$ baryons, respectively. Here dots represent the contributions of higher states and continuum.

The matrix elements in Eq. (3) are determined as

$$\begin{aligned} \langle 0|\eta |\Xi (q,s)\rangle= & {} \lambda u(q,s), \nonumber \\ \langle 0|\eta |\widetilde{\Xi }(q,\widetilde{s})\rangle= & {} \widetilde{ \lambda }\gamma _{5}u(q,\widetilde{s}). \end{aligned}$$

(4)

Here $\lambda$ and $\widetilde{\lambda }$ are the residues of the ground and first orbitally excited $\Xi$ baryons, respectively. Using Eqs. (3) and (4) and performing summation over the spins of corresponding baryons, we obtain

We perform Borel transformation in order to suppress the contribution of higher state and continuum,

(5)

where $M^2$ is the square of Borel mass parameter.

The correlation function from QCD side can be calculated by inserting Eq. (2) to Eq. (1) and usage of Wick’s theorem to contract the quark fields. As a result we have an expression in terms of the involved quark propagators having perturbative and non-perturbative contributions. For calculation of these contributions we need explicit expressions of the light quark propagators. By using the light quark propagators in the coordinate space and performing the Fourier and Borel transformations, as well as performing the continuum subtraction by using the hadron-quark duality ansatz, after lengthy calculations, for the correlation function we obtain

(6)

where, the expressions for $\mathcal {B}\Pi _{1}^{\mathrm {QCD}}$ and $\mathcal {B}{\Pi _{2}}^{\mathrm {QCD}}$ are presented in Appendix.

Having calculated both the hadronic and QCD sides of the correlation function, we match the coefficients of the corresponding structures and I from these representations to find the following sum rules:

$$\begin{aligned} \lambda ^{2}e^{-\frac{m^{2}}{M^{2}}}+\widetilde{\lambda }^{2}e^{-\frac{ \widetilde{m}^{2}}{M^{2}}}= & {} \mathcal {B}\Pi _{1}^{\mathrm {QCD}}, \nonumber \\ \lambda ^{2}me^{-\frac{m^{2}}{M^{2}}}-\widetilde{\lambda }^{2}\widetilde{m}e^{-\frac{ \widetilde{m}^{2}}{M^{2}}}= & {} \mathcal {B}\Pi _{2}^{\mathrm {QCD}}. \end{aligned}$$

(7)

From these equations one can easily find:

$$\begin{aligned} \widetilde{m}^{2}= & {} \frac{\mathcal {B}\widetilde{\Pi } _{2}^{\mathrm {QCD}}-m\mathcal {B}\widetilde{\Pi } _{1}^{\mathrm {QCD}}}{\mathcal {B}\Pi _{2}^{\mathrm {QCD}}-m\mathcal {B}\Pi _{1}^{\mathrm {QCD}}},\nonumber \\ \widetilde{\lambda }^{2}= & {} \frac{m\mathcal {B}\Pi _{1}^{\mathrm {QCD}}-\mathcal {B}\Pi _{2}^{\mathrm {QCD}}}{m+\widetilde{m}}e^{\frac{\widetilde{m}^2}{M^2}},\nonumber \\ \lambda ^2= & {} \frac{\widetilde{m}\mathcal {B}\Pi _{1}^{\mathrm {QCD}}+\mathcal {B}\Pi _{2}^{\mathrm {QCD}}}{m+\widetilde{m}}e^{\frac{m^2}{M^2}}, \end{aligned}$$

(8)

where $\mathcal {B}\widetilde{\Pi } _{1(2)}^{\mathrm {QCD}}=-\frac{d}{d (1/M^2)}\mathcal {B}\Pi _{1(2)}^{\mathrm {QCD}}$.

The sum rules for mass and residue of the radially excited state $\Xi '$ are obtained from Eq. (8) by replacements $\widetilde{m}\rightarrow -m^{\prime }$ and $\widetilde{\lambda } \rightarrow \lambda ^{\prime }$. Note that, there are other approaches to separate the contributions of the positive and negative parity baryons (for instance see [15,16,17,18]).

Table 1 Some input parameters used in the calculations

The sum rules for the mass and residue of the orbitally and radially excited state of the $\Xi$ baryon as well as the residue of the ground state contain many input parameters. Their values are presented in Table 1. For performing analysis of widths of the $\Xi \rightarrow \Lambda K$ and $\Xi \rightarrow \Sigma K$ decays in next section, we also need the residues of the $\Lambda$ and $\Sigma$ baryons. We use the values of these residues calculated via QCD sum rules [20]. The mass of the ground state $\Xi$ is taken as input parameter, as well. Besides these input parameters, QCD sum rules contains three auxiliary parameters, namely the value of continuum threshold $s_0$, Borel mass square $M^2$ and $\beta$ arbitrary parameter. Obviously any measurable physical quantity must be independent of these parameters. Hence we need to find the working regions of these parameters, where physical quantities demonstrate good stability agains the variations of these parameters. The window for $M^2$ is obtained by requiring that the series of operator product expansion (OPE) in QCD side is convergent and the contribution of higher states and continuum is sufficiently suppressed. Numerical analyses lead to the conclusion that both conditions are satisfied in the domain

$$\begin{aligned} 1.8\ \mathrm {GeV}^{2}\le M^{2}\le & {} 2.2\ \mathrm {GeV}^{2}. \end{aligned}$$

(9)

The considerations of the pole dominance and OPE convergence lead to the following working window for the continuum threshold:

$$\begin{aligned} 1.9^2\,\,\mathrm {GeV}^{2}\le & {} s_{0}\le 2.1^2\,\,\mathrm {GeV}^{2}. \end{aligned}$$

(10)

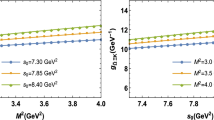
In Figs. 1, 2, 3 and 4 we present, as examples, the dependence of the mass of the $\widetilde{\Xi }$ state and residues of the $\Xi$, $\widetilde{\Xi }$ and $\Xi '$ baryons on $M^2$ and $s_0$ at fixed value of $\cos \theta =0.7$, with $\beta = \tan \theta$. From these figures we observe that the results shows quite good stability with respect to the variations of $M^2$ and $s_0$.

In order to find the working region of $\beta$, as an example in Fig. 5 we present the dependence of the ground-state $\Xi$ baryon’s residue on the $\cos \theta$. From this figure we see that the residue is practically insensitive to the variations of $\cos \theta$ in the domains

$$\begin{aligned} -1\le \cos \theta \le -0.3, \, \, \,0.3\le \cos \theta \le 1. \end{aligned}$$

(11)

Fig. 1

The mass of the $\widetilde{\Xi }$ baryon as a function of the Borel parameter $M^2$ at chosen values of $s_0$ (left panel), and as a function of the continuum threshold $s_0$ at fixed $M^2$ (right panel) with $\beta =0.7$

Fig. 2

The rediue of the $\Xi$ baryon as a function of the Borel parameter $M^2$ at chosen values of $s_0$ (left panel), and as a function of the continuum threshold $s_0$ at fixed $M^2$ (right panel) with $\beta =0.7$

Fig. 3

The same as in Fig. 2, but for the orbitally excited $\widetilde{\Xi }$ baryon with $\beta =0.7$

Fig. 4

The same as in Fig. 2, but for the radially excited $\Xi '$ baryon with $\beta =0.7$

We depict the numerical results of the masses and residues of the first orbitally and radially excited $\Xi$ baryon as well as the ground state residue in Table 2. The errors in the presented results are due to the uncertainties in determinations of the working regions of the auxiliary parameters as well as the errors of other input parameters. From this table we see that although consistent with the experimental data [10,11,12], the radial and orbital excitation of $\Xi$ receive the same mass, which prevent us to assign any quantum numbers to $\Xi (1690)$ only via mass calculations. The residue of these two states are obtained to be differ from each other by a factor of roughly three.

Fig. 5

The residue of the ground state $\Xi$ baryon as a function of the $\cos \theta$ at central values of the $s_0$ and $M^2$

3 ${\widetilde{\Xi }}$ and $\Xi '$ transitions To $\Lambda K$ and $\Sigma K$

In present section we calculate the strong couplings $g_{\widetilde{\Xi }\Sigma K}$, $g_{\widetilde{\Xi }\Lambda K}$, $g_{\Xi '\Sigma K}$ and $g_{\Xi '\Lambda K}$ defining the $\widetilde{\Xi }\rightarrow \Sigma K$, $\widetilde{\Xi }\rightarrow \Lambda K$, $\Xi ' \rightarrow \Sigma K$ and $\Xi ' \rightarrow \Lambda K$ transitions.

For this aim we introduce the correlation function

$$\begin{aligned} \Pi (p,q)=i\int d^{4}xe^{ipx}\langle K(q)|\mathcal {T}\{\eta _{\Sigma (\Lambda ) }(x) \bar{\eta }_{\Xi }(0)\}|0\rangle , \end{aligned}$$

(12)

where $\eta _{\Sigma }(x)$ and $\eta _{\Lambda }(x)$ are the interpolating currents for the $\Sigma$ and $\Lambda$ baryons, respectively. The general forms of these currents are taken as [13, 14]

$$\begin{aligned} \eta _{\Sigma }(x)= & {} -\frac{1}{\sqrt{2}}\epsilon _{abc} \sum _{i=1}^{2}\Big [\Big (u^{T,a}(x)CA_{1}^{i}s^{b}(x)\Big )A_{2}^{i}d^{c}(x)\nonumber \\&-\Big (d^{T,c}(x)CA_{1}^{i}s^{b}(x)\Big )A_{2}^{i}u^{a}(x)\Big ],\nonumber \\ \eta _{\Lambda }(x)= & {} \frac{1}{\sqrt{6}}\epsilon _{abc}\sum _{i=1}^{2} \Big [2\Big (u^{T,a}(x)CA_{1}^{i} d^{b}(x)\Big ) A_{2}^{i}s^{c}(x)\nonumber \\&+\Big (u^{T,a}(x)CA_{1}^{i}s^{b}(x)\Big )A_{2}^{i}d^{c}(x)\nonumber \\&+\Big (d^{T,c}(x)CA_{1}^{i}s^{b}(x)\Big )A_{2}^{i}u^{a}(x)\Big ], \end{aligned}$$

(13)

where a, b, c are color indices, C is the charge conjugation operator and $A_{1}^{1}=I$, $A_{1}^{2}=A_{2}^{1}=\gamma _5$, $A_{2}^{2}=\beta$. According to the method used, we again calculate the aforesaid correlation function in two representations: hadronic and QCD. Matching these two sides through a dispersion relation leads to the sum rules for the coupling constants under consideration.

Table 2 The sum rule results for the masses and residues of the first orbitally and radially excited $\Xi$ baryon as well as residue of the ground state

Firstly let us consider the $\widetilde{\Xi }\rightarrow \Sigma K$ transition. As we already noted, the interpolating currents for baryons can interact with both the positive and negative parity baryons. In what follows, we denote the ground state positive (negative) parity baryons with $\Sigma (\widetilde{\Sigma })$ and $\Lambda (\widetilde{\Lambda })$. Taking into account this fact, inserting complete sets of hadrons with the same quantum numbers as the interpolating currents and isolating the ground states, we obtain

$$\begin{aligned} \Pi ^{\mathrm {Phys}}(p,q)= & {} \frac{\langle 0|\eta _{\Sigma }|\Sigma (p,s)\rangle }{p^{2}-m_{\Sigma }^{2}}\langle K(q)\Sigma (p,s)|\Xi (p^{\prime },s^{\prime })\rangle \nonumber \\&\times \frac{\langle \Xi (p^{\prime },s^{\prime })|\bar{ \eta }_{\Xi }|0\rangle }{p^{\prime 2}-m_{\Xi }^{2}} \nonumber \\&+ \frac{\langle 0|\eta _{\Sigma }|\widetilde{\Sigma } (p,s)\rangle }{p^{2}-m_{\widetilde{\Sigma }}^{2}}\langle K(q)\widetilde{\Sigma }(p,s)|\Xi (p^{\prime },s^{\prime })\rangle \nonumber \\&\times \frac{\langle \Xi (p^{\prime },s^{\prime })|\bar{\eta }_{\Xi }|0\rangle }{p^{\prime 2}-m_{\Xi }^{2}} \nonumber \\&+\frac{\langle 0|\eta _{\Sigma }|\Sigma (p,s)\rangle }{p^{2}-m_{\Sigma }^{2}}\langle K(q)\Sigma (p,s)|\widetilde{\Xi } (p^{\prime },s^{\prime })\rangle \nonumber \\&\times \frac{\langle \widetilde{\Xi }(p^{\prime },s^{\prime })|\bar{ \eta }_{\widetilde{\Xi }}|0\rangle }{p^{\prime 2}-m_{\widetilde{\Xi }}^{2}} \nonumber \\&+ \frac{\langle 0|\eta _{\Sigma }|\widetilde{\Sigma }(p,s)\rangle }{p^{2}-m_{\widetilde{\Sigma }}^{2}}\langle K(q)\widetilde{\Sigma } (p,s)|\widetilde{\Xi } (p^{\prime },s^{\prime })\rangle \nonumber \\&\times \frac{\langle \widetilde{\Xi } _{c}(p^{\prime },s^{\prime })|\bar{\eta }_{\widetilde{\Xi }}|0\rangle }{p^{\prime 2}-m_{\widetilde{\Xi }}^{2}} +\cdots , \end{aligned}$$

(14)

where $p^{\prime }=p+q,\ p$ and q are the momenta of the $\Xi$, $\Sigma$ baryons and K meson, respectively. In this expression $m_{\Sigma }$ is the mass of the $\Sigma$ baryon. The dots in Eq. (14) stand for contributions of the higher resonances and continuum states.

The matrix elements in Eq. (14) are determined as

$$\begin{aligned} \langle 0|\eta _{\Sigma }|\Sigma (p,s)\rangle= & {} \lambda _{\Sigma } u(p,s), \nonumber \\ \langle 0|\eta _{\widetilde{\Sigma }}|\widetilde{\Sigma }(p,s)\rangle= & {} \lambda _{\widetilde{\Sigma }}\gamma _5 u(p,s), \nonumber \\ \langle K(q)\Sigma (p,s)|\Xi (p^{\prime },s^{\prime })\rangle= & {} g_{\Xi \Sigma K}\overline{u}(p,s)\gamma _{5}u(p^{\prime },s^{\prime }), \nonumber \\ \langle K(q)\Sigma (p,s)|\widetilde{\Xi } (p^{\prime },s^{\prime })\rangle= & {} g_{\widetilde{\Xi } \Sigma K}\overline{u}(p,s)u(p^{\prime },s^{\prime }), \nonumber \\ \langle K(q)\widetilde{\Sigma } (p,s)|\Xi (p^{\prime },s^{\prime })\rangle= & {} g_{\Xi \widetilde{\Sigma } K}\overline{u}(p,s) u(p^{\prime },s^{\prime }), \nonumber \\ \langle K(q)\widetilde{\Sigma } (p,s)|\widetilde{\Xi }(p^{\prime },s^{\prime })\rangle= & {} g_{\widetilde{\Xi }\widetilde{\Sigma } K}\overline{u}(p,s)\gamma _5 u(p^{\prime },s^{\prime }). \nonumber \\ \end{aligned}$$

(15)

where $g_i$ are the strong coupling constants for the corresponding transitions.

Using the matrix elements given in Eq. (15) and performing summation over spins of $\Sigma$ and $\Xi$ baryons and applying the double Borel transformations with respect $p^2$ and $p^{\prime 2}$ for physical side of the correlation function we get

(16)

where $M_{1}^{2}$ and $M_{2}^{2}$ are the Borel parameters.

From Eq. (16) it follows that we have different structures which can be used to obtain sum rules for the strong coupling constant of $\widetilde{\Xi }\rightarrow \Sigma K$ channel. We have four couplings (see Eq. 16), and in order to determine the coupling $g_{\widetilde{\Xi }\Sigma K}$ we need four equations. Therefore we select the structures and $\gamma _5$. Solving four algebraic equations for $g_{\widetilde{\Xi }\Sigma K}$, finally we get

$$\begin{aligned} g_{\widetilde{\Xi } \Sigma K}= & {} \frac{e^{\frac{m_{\widetilde{\Xi }}^2}{M_1^2}}e^{\frac{m_{\Sigma }^2}{M_2^2}}}{\lambda _{\widetilde{\Xi }}\lambda _{\Sigma }(m_{\Sigma } +m_{\widetilde{\Sigma }}) (m_{\Xi }+m_{\widetilde{\Xi }})} \nonumber \\&\times \left[ \Pi _{1}^{\mathrm {^{\prime }OPE}}\left( m_K^2+m_{\widetilde{\Sigma }}m_{\Xi }-m_{\Xi } m_{\widetilde{\Xi }}\right) \right. \nonumber \\&+\left. \Pi _{2}^{\mathrm {^{\prime }OPE}}\left( m_{\widetilde{\Xi }}-m_{\widetilde{\Sigma }} -m_{\Xi }\right) \right. \nonumber \\&+\left. \Pi _{3}^{\mathrm {^{\prime }OPE}}\left( m_{\widetilde{\Sigma }}-m_{\widetilde{\Xi }} \right) -\Pi _{4}^{\mathrm {^{\prime }OPE}}\right] , \end{aligned}$$

(17)

where $\Pi _{1}^{\mathrm {^{\prime }OPE}}$, $\Pi _{2}^{\mathrm {^{\prime }OPE}}$, $\Pi _{3}^{\mathrm {^{\prime }OPE}}$ and $\Pi _{4}^{\mathrm {^{\prime }OPE}}$ are the invariant amplitudes corresponding to the structures and $\gamma _{5}$ for $\widetilde{\Xi }\rightarrow \Sigma K$ decay, respectively.

If we carry out the same procedures for $\widetilde{\Xi }\rightarrow \Lambda K$ decay, for the coupling constant $g_{\widetilde{\Xi }\Lambda K}$ we obtain:

$$\begin{aligned} g_{\widetilde{\Xi } \Lambda K}= & {} \frac{e^{\frac{m_{\widetilde{\Xi }}^2}{M_1^2}}e^{\frac{m_{\Lambda }^2}{M_2^2}}}{\lambda _{\widetilde{\Xi }}\lambda _{\Lambda }(m_{\Lambda } +m_{\widetilde{\Lambda }}) (m_{\Xi }+m_{\widetilde{\Xi }})} \nonumber \\&\times \left[ \widetilde{\Pi } _{1}^{\mathrm {^{\prime }OPE}}\left( m_K^2+m_{\widetilde{\Lambda }}m_{\Xi }-m_{\Xi } m_{\widetilde{\Xi }}\right) \right. \nonumber \\&+\left. \widetilde{\Pi } _{2}^{\mathrm {^{\prime }OPE}}\left( m_{\widetilde{\Xi }}-m_{\widetilde{\Lambda }} -m_{\Xi }\right) \right. \nonumber \\&+\left. \widetilde{\Pi } _{3}^{\mathrm {^{\prime }OPE}}\left( m_{\widetilde{\Lambda }}-m_{\widetilde{\Xi }} \right) -\widetilde{\Pi } _{4}^{\mathrm {^{\prime }OPE}}\right] , \end{aligned}$$

(18)

where $\widetilde{\Pi }_{1}^{\mathrm {^{\prime }OPE}}$, $\widetilde{\Pi }_{2}^{\mathrm {^{\prime }OPE}}$, $\widetilde{\Pi } _{3}^{\mathrm {^{\prime }OPE}}$ and $\widetilde{\Pi } _{4}^{\mathrm {^{\prime }OPE}}$ are the invariant amplitudes corresponding to the structures and $\gamma _{5}$ for $\widetilde{\Xi }\rightarrow \Lambda K$ decay, respectively.

The general expressions obtained above contain two Borel parameters $M_1^{2}$ and $M_1^{2}$. In our analysis we choose

$$\begin{aligned} M_{1}^{2}=M_{2}^{2}= 2M^{2},\,\, M^2=\frac{M_1^{2}M_2^{2}}{M_1^{2}+M_2^{2}}, \end{aligned}$$

(19)

since the masses of the involved $\Xi$ and $\Sigma (\Lambda )$ are close to each other.

The sum rules for the coupling constants for $\Xi ' \rightarrow \Sigma K$ and $\Xi ' \rightarrow \Lambda K$ transitions can be easily obtained from Eqs. (17) and (18), by replacing $m_{\widetilde{\Xi }}\rightarrow - m_{\Xi ^{\prime }}$ and $\lambda _{\widetilde{\Xi }}\rightarrow \lambda _{\Xi ^{\prime }}$.

The OPE side of the correlation function $\Pi ^{\mathrm {OPE}}(p,q)$ can be obtained by inserting the corresponding interpolating currents to the correlation function, using Wick’s theorem to contract the quark fields, and inserting into the obtained expression the relevant quark propagators. The nonperturbative contributions in light cone QCD sum rules, which are described in terms of the K-meson distribution amplitudes (DAs), can be obtained by using Fierz rearrangement formula

$$\begin{aligned} \overline{s}_{\alpha }^{a}u_{\beta }^{b}=\frac{1}{4}\Gamma _{\beta \alpha }^{i}(\overline{s}^{a}\Gamma ^{i}u^{b}), \end{aligned}$$

where $\ \Gamma ^{i}=1,\ \gamma _{5},\ \gamma _{\mu },\ i\gamma _{5}\gamma _{\mu },\ \sigma _{\mu \nu }/\sqrt{2}$ is the full set of Dirac matrices. The matrix elements of these terms between the K-meson and vacuum states, as well as ones generated by insertion of the gluon field strength tensor $G_{\lambda \rho }(uv)$ from quark propagators, are determined in terms of the K-meson DAs with definite twists. The DAs are main nonperturbative inputs of light cone QCD sum rules. The K-meson distribution amplitudes are derived in [21,22,23] which will be used in our numerical analysis. All of these steps summarized above result in lengthy expression for the OPE side of correlation function. In order not to overwhelm the study with overlong mathematical expressions we prefer not to present them here. Apart from parameters in the distribution amplitudes, the sum rules for the couplings depend also on numerical values of the $\Sigma$ and $\Lambda$ baryon’s mass and pole residue, which are given in Table 1. Note that the working region of the Borel mass $M^2$, threshold $s_0$ and $\beta$ parameters for calculations of the relevant couplings are chosen the same as in the residue and mass computations.

Performing numerical analysis for the relevant coupling constants we get values presented in Table 3. Using the couplings $g_{\widetilde{\Xi } \Sigma K}$, $g_{\Xi ' \Sigma K}$ $g_{\widetilde{\Xi } \Lambda K}$ and $g_{\Xi ' \Lambda K}$ we can easily calculate the width of $\widetilde{\Xi } \rightarrow \Sigma K, \Xi ' \rightarrow \Sigma K, \widetilde{\Xi } \rightarrow \Lambda K$ and $\Xi ' \rightarrow \Lambda K$ decays. After some computations we obtain:

$$\begin{aligned} \Gamma \left( \widetilde{\Xi } \rightarrow \Sigma K\right)= & {} \frac{ g_{\widetilde{\Xi } \Sigma K}^{2}}{16\pi m_{\widetilde{\Xi }}^{3}}\left[ (m_{\widetilde{\Xi }} +m_{\Sigma })^{2}-m_{K}^{2}\right] \nonumber \\&\times \lambda ^{1/2}\left( m_{\widetilde{\Xi }}^2,m_{\Sigma }^2,m_{K}^2\right) , \end{aligned}$$

(20)

and

$$\begin{aligned} \Gamma \left( \Xi ^{\prime }\rightarrow \Sigma K\right)= & {} \frac{g_{\Xi ^{\prime }\Sigma K}^{2}}{16\pi m_{\Xi '}^{ 3}}\left[ (m_{\Xi '}-m_{\Sigma })^{2}-m_{K}^{2}\right] \nonumber \\&\times \lambda ^{1/2}\left( m_{\Xi '}^2,m_{\Sigma }^2,m_{K}^2\right) . \end{aligned}$$

(21)

In expressions above the function $\lambda (x^2,y^2,z^2)$ is given as:

$$\begin{aligned} \lambda (x^2,y^2,z^2)= x^{4}+y^{4}+z^{4}-2x^{2}y^{2}-2x^{2}z^{2}-2y^{2}z^{2}. \end{aligned}$$

The expressions for the widths of the $\widetilde{\Xi } \rightarrow \Lambda K$ and $\Xi ^{\prime } \rightarrow \Lambda K$ can be easily obtained from Eqs. (20) and (21), by the replacement $m_{\Sigma }\rightarrow m_{\Lambda }$.

Using the values of coupling constants and formulas for the decay widths we obtain the values of the partial width at different decay channels presented in Table 3.

Table 3 The sum rule results for the strong coupling constants and decay widths of the first orbitally and radially excited $\Xi$ baryon

Using the values of the partial decay widths from Table 3, we finally obtain the ratio of the branching fractions in $\widetilde{\Xi }$ channel as

$$\begin{aligned} \frac{Br\Big (\widetilde{\Xi } \rightarrow \Sigma K^- \Big )}{Br\Big (\widetilde{\Xi } \rightarrow \Lambda \overline{K}^0 \Big )}=0.50\pm 0.14, \end{aligned}$$

(22)

and for $\Xi ^{\prime }$ channel we get

$$\begin{aligned} \frac{Br\Big (\Xi ^{\prime } \rightarrow \Sigma K^- \Big )}{Br\Big (\Xi ^{\prime } \rightarrow \Lambda \overline{K}^0 \Big )}=0.17\pm 0.05. \end{aligned}$$

(23)

As is seen, the obtained value for the ratio of the branching fractions in $\widetilde{\Xi }$ channel is in nice consistency with the experimental data of Belle Collaboration [12]:

$$\begin{aligned} \frac{Br\Big (\Xi (1690) \rightarrow \Sigma ^+ K^- \Big )}{Br\Big (\Xi (1690) \rightarrow \Lambda ^0 \overline{K}^0 \Big )}=0.50\pm 0.26, \end{aligned}$$

(24)

Note that in [24], within the coupled channel approach, a very similar results has been found. The authors have concluded that the $\Xi (1690)$ has spin-1 / 2, but its parity has not been established. Our prediction for the corresponding ratio in $\Xi ^{\prime }$ channel is considerably small compared to the experimental data. From these results and those for the values of the corresponding masses we conclude that the $\Xi (1690)$ state, most probably, has quantum numbers $\frac{1}{2}^{-}$, i.e. it represents a negative parity spin-1/2 baryon.

Appendix: The QCD side of the correlation function in mass sum rules

In present Appendix we present explicit forms of the functions in QCD side of the two point correlation function used in mass sum rules:

$$\begin{aligned} \mathcal {B}\Pi ^{\mathrm {QCD}}_1(q)= & {} \int _{0}^{s_0}ds~ e^{-\frac{s}{M^2}} \frac{1}{2^7\pi ^2}\Bigg \{\frac{s^2(5\beta ^2+2\beta +5)}{2^4\pi ^2}\nonumber \\&+m_s \Big [\langle \bar{s}s\rangle (5\beta ^2+2\beta +5)+6\Big (\langle \bar{u}u\rangle +\langle \bar{d}d\rangle \Big )(\beta ^2-1)\Big ] \nonumber \\&+ \frac{\langle g_s^2 GG\rangle (5\beta ^2+2\beta +5)}{2^4\pi ^2}\nonumber \\&-\frac{3m_0^2\Big (\langle \bar{u}u\rangle +\langle \bar{d}d\rangle \Big )m_s(\beta ^2-1)}{M^2}\log \left[ \frac{s}{\Lambda ^2} \right] \nonumber \\&+\frac{\langle g_s^2 GG\rangle \Big (\langle \bar{u}u\rangle +\langle \bar{d}d\rangle \Big )}{3M^4} \nonumber \\&\times m_s(\beta ^2-1)\log \left[ \frac{s}{\Lambda ^2} \right] \Bigg \}\nonumber \\&-\frac{m_s}{3\cdot 2^8\pi ^2}\Big [3m_0^2\Big (\langle \bar{u}u\rangle +\langle \bar{d}d\rangle \Big )(\beta ^2-1)(6\gamma _E-13)\nonumber \\&-8m_0^2\langle \bar{s}s\rangle (\beta ^2+\beta +1)\Big ] \nonumber \\&+\frac{\beta -1}{24}\Big [3\Big (\langle \bar{s}s\rangle \langle \bar{d}d\rangle +\langle \bar{s}s\rangle \langle \bar{u}u\rangle \Big )(\beta +1)\nonumber \\&+\langle \bar{u}u\rangle \langle \bar{d}d\rangle (\beta -1)\Big ]\nonumber \\&+\frac{m_s(\beta +1)}{3\cdot 2^9\pi ^2M^2}\langle g_s^2 GG\rangle \Big [4\Big (\langle \bar{u}u\rangle +\langle \bar{d}d\rangle \Big )\nonumber \\&\times (\beta -1)-\langle \bar{s}s\rangle (\beta +1)\Big ]\nonumber \\&+e^{-\frac{s_0}{M^2}}\frac{\langle g_s^2 GG\rangle \Big (\langle \bar{u}u\rangle +\langle \bar{d}d\rangle \Big )}{3\cdot 2^7\pi ^2s_0M^2}m_s(\beta ^2-1)\nonumber \\&\times \Big (M^2+s_0\log \Big [\frac{s_0}{\Lambda ^2}\Big ]\Big )\nonumber \\&+\frac{(\beta -1)}{3\cdot 2^5M^2}m_0^2\Big [6\Big (\langle \bar{s}s\rangle \langle \bar{d}d\rangle \nonumber \\&+\langle \bar{s}s\rangle \langle \bar{u}u\rangle \Big )+(\beta -1)\langle \bar{u}u\rangle \langle \bar{d}d\rangle \Big ]\nonumber \\&+\frac{m_s(\beta ^2-1)}{3\cdot 2^(11)\pi ^2M^4}\langle g_s^2 GG\rangle m_0^2\Big (\langle \bar{u}u\rangle +\langle \bar{d}d\rangle \Big ),\nonumber \\ \end{aligned}$$

(A.1)

and

$$\begin{aligned} \mathcal {B}\Pi ^{\mathrm {QCD}}_2(q)= & {} \int _{0}^{s_0}ds~ e^{-\frac{s}{M^2}} \frac{1}{2^6\pi ^2}\left\{ \phantom {\left. +\frac{3m_0^2\Big (\langle \bar{u}u\rangle +\langle \bar{d}d\rangle \Big )}{2}(\beta ^2-1)\right\} }\frac{m_s s^2(\beta -1)^2}{2^3\pi ^2}\right. \nonumber \\&\left. +s(\beta -1)\Big [3\Big (\langle \bar{u}u\rangle +\langle \bar{d}d\rangle \Big )(\beta +1)+\langle \bar{s}s\rangle (\beta -1)\Big ]\right. \nonumber \\&\left. - \frac{\langle g_s^2 GG\rangle }{3\cdot 2^4\pi ^2}m_s(\beta -1)^2\Big (8+3\gamma _E-3\log \Big [ \frac{s}{\Lambda ^2}\Big ]\Big )\right. \nonumber \\&\left. +\frac{3m_0^2\Big (\langle \bar{u}u\rangle +\langle \bar{d}d\rangle \Big )}{2}(\beta ^2-1)\right\} +\frac{\langle g_s^2 GG\rangle }{2^{10}\pi ^4} \nonumber \\&\times \gamma _Em_sM^2(\beta -1)^2\Big (1-e^{-\frac{s_0}{M^2}} \Big )\nonumber \\&-\frac{m_s}{3\cdot 2^4}\Big [3\Big (\langle \bar{s}s\rangle \langle \bar{d}d\rangle +\langle \bar{s}s\rangle \langle \bar{u}u\rangle \Big )(\beta ^2-1) \nonumber \\&+2\langle \bar{u}u\rangle \langle \bar{d}d\rangle (5\beta ^2+2\beta +5)\Big ]\nonumber \\&+\frac{\beta -1}{3\cdot 2^8\pi ^2}\langle g_s^2 GG\rangle \Big [3\Big (\langle \bar{u}u\rangle +\langle \bar{d}d\rangle \Big )(\beta +1)\nonumber \\&-\langle \bar{s}s\rangle (\beta -1)\Big ]+\frac{\langle g_s^2 GG\rangle \langle \bar{u}u\rangle \langle \bar{d}d\rangle }{3^2\cdot 2^6M^4} \nonumber \\&\times m_s(5\beta ^2+2\beta +5)+\frac{m_0^2\langle \bar{u}u\rangle \langle \bar{d}d\rangle }{3\cdot 2^4M^2}m_s(3\beta ^2+2\beta +3)\nonumber \\&+\frac{\langle g_s^2 GG\rangle m_0^2\langle \bar{u}u\rangle \langle \bar{d}d\rangle }{3^2\cdot 2^6M^6}m_s(5\beta ^2+2\beta +5), \end{aligned}$$

(A.2)

where, to shorten the expressions, the terms proportional to $m_u$ and $m_d$ are not presented, although their contributions are taken into account in performing numerical analysis.