A non-perturbative exploration of the high energy regime in $N_{\mathrm{f}}=3$ QCD

Abstract

Using continuum extrapolated lattice data we trace a family of running couplings in three-flavour QCD over a large range of scales from about 4 to 128 GeV. The scale is set by the finite space time volume so that recursive finite size techniques can be applied, and Schrödinger functional (SF) boundary conditions enable direct simulations in the chiral limit. Compared to earlier studies we have improved on both statistical and systematic errors. Using the SF coupling to implicitly define a reference scale $1/L_0\approx 4$ GeV through $\bar{g}^2(L_0) =2.012$, we quote $L_0 \Lambda ^{N_\mathrm{f}=3}_{{\overline{\mathrm{MS}}}} =0.0791(21)$. This error is dominated by statistics; in particular, the remnant perturbative uncertainty is negligible and very well controlled, by connecting to infinite renormalization scale from different scales $2^n/L_0$ for $n=0,1,\ldots ,5$. An intermediate step in this connection may involve any member of a one-parameter family of SF couplings. This provides an excellent opportunity for tests of perturbation theory some of which have been published in a letter (ALPHA collaboration, M. Dalla Brida et al. in Phys Rev Lett 117(18):182001, 2016). The results indicate that for our target precision of 3 per cent in $L_0 \Lambda ^{N_\mathrm{f}=3}_{{\overline{\mathrm{MS}}}}$, a reliable estimate of the truncation error requires non-perturbative data for a sufficiently large range of values of $\alpha _s=\bar{g}^2/(4\pi )$. In the present work we reach this precision by studying scales that vary by a factor $2^5= 32$, reaching down to $\alpha _s\approx 0.1$. We here provide the details of our analysis and an extended discussion.

1 Introduction

The Standard Model seems to describe all high energy physics experiments carried out to date, in some cases with extraordinary accuracy (cf. [2] for the most recent PDG review). For processes involving the strong interactions the precision is usually less impressive, due to our limited ability to extract quantitative information from QCD. One of the main tools is perturbation theory (PT) in the strong coupling, $\alpha _s$, and there has been significant progress in high order perturbative QCD calculations, with renormalization group functions now available up to 5-loop order in the ${\overline{\mathrm{MS}}}$-scheme [3,4,5,6,7]. However, before a perturbative result can be confronted with experimental observables, the transition from quarks and gluons to hadronic degrees of freedom needs to be modelled in some way. Such models come in various shapes and forms, from “hadronisation Monte Carlo” in jet physics to “quark hadron duality” in QCD sum rules. A common problem then consists in assigning systematic errors to the model assumptions. A further issue is the reliability of PT itself, given that the series is only asymptotic. To some extent, the reliability can be assessed within PT itself, by comparing different orders of the expansion, or by increasing the energy scale, $\mu$, such that $\alpha _s(\mu )$ becomes small, due to asymptotic freedom. Unfortunately, the rapidly increasing complexity of higher order calculations means that typically only a few terms in the perturbative series are available. In addition, the energy scale is often defined by the kinematics of the physical process under consideration. The variation of the scale is then rather limited and to assign an error to the perturbative result is difficult.¹

In this work we carry out a systematic investigation into the reliability of PT. We do this by directly comparing non-perturbative QCD observables to their perturbative expansions, over a wide range of scales. Lattice QCD, together with a careful treatment of the continuum limit, is currently the only way to obtain such non-perturbative results, subject only to standard assumptions such as locality and universality. The main reason why this is rarely done is the usual limitation of any numerical approach: on a finite system it is very expensive to simultaneously resolve very different length scales. Most lattice QCD projects aim at hadronic low energy physics, and the space-time volume, $L^4$, must then measure several femto metres across in order not to distort the hadronic states of interest. At least for massive single particle states, the finite volume effects are exponentially suppressed [9] and one may then pretend to be in infinite space time volume, up to a systematic error which is often below the percent level. On the other hand, with current lattice resolutions of, say, $L/a < 100$ this means that the cutoff scale set by the inverse lattice spacing, 1 / a, reaches a few GeV at most, and the deep perturbative high energy regime seems out of reach. It is important to realize that this limitation is only due to the requirement that the lattice covers a physically large space-time volume. If this constraint is lifted, there is nothing that prevents simulations at very high energies, albeit in physically tiny space-time volumes. The observables² we consider in this situation are all normalized as effective couplings, which run with L, the scale set by the finite space-time volume. In order to achieve this we set all quark masses to zero and scale all other dimensionful parameters proportionally to L, thereby obtaining a mass-independent scheme. In the high-energy regime, PT can be used to relate to more commonly used schemes such as the ${\overline{\mathrm{MS}}}$ scheme of dimensional regularization. Moreover, by combining the idea of a finite volume scheme for the coupling with recursive step-scaling techniques [10, 11], one may both determine the scale L in units of some hadronic scale, and reach the perturbative high energy regime without ever requiring enormous lattice resolutions, L / a. Obviously, the finite space-time volume constitutes an integral part in the definition of these observables. PT must then be adapted to this situation. While the Euclidean space-time signature used in lattice QCD is advantageous in PT, all the sophisticated tools of standard PT in (infinitely extended) momentum space are of limited use.

As part of the project to determine $\alpha _s(m_Z)$ from low energy hadronic input in 3-flavour QCD [1, 12, 13], our collaboration has applied these techniques to a 1-parameter family of finite volume couplings in Schrödinger functional (SF) schemes, for which the 3-loop $\beta$-function is known [14,15,16,17]. We have measured these couplings in numerical simulations and for a range of lattice sizes with unprecedented precision. Extrapolation to the continuum limit of this data allows us to carry out stringent tests of renormalized perturbation theory for energy scales ranging from about 4 to $128\,\mathrm{GeV}$. A first account of our results has appeared in a letter [1] and we here provide the details of this work and a more extended analysis.

Fig. 1

The step scaling function $\sigma (u)$, a discrete version of the $\beta$-function, defined in Eq. (2.29). The combination shown here yields directly the lowest order coefficient, $b_0$ of the $\beta$-function as $(\sigma (u)-u)/u^2 = 2 b_0\ln \,2 +\mathrm{O}(u)$. The dashed lines show the perturbative 2-loop behavior. The purple 1-sigma band shows our result (fit C in Table 5). Data points for $N_\mathrm{f}=0,2,3,4$ are taken from the literature [18,19,20,21]

The technique, used earlier for between $N_\mathrm{f}=0$ and $N_\mathrm{f}=4$ quark flavours [18,19,20,21], allows one to non-perturbatively verify the close-to perturbative running of the coupling and observe the small effects of dynamical quarks, as illustrated in Fig. 1. A preview of our final result is included in the figure, demonstrating our advanced precision.

The paper is organized as follows: Sect. 2 uses a continuum language to explain how our QCD observables are defined and collects the relevant perturbative results from the literature. We also comment on “non-perturbative effects” which are associated with secondary minima of the action. Section 3 then presents the lattice set-up, the numerical simulations and statistics produced, and discusses the perturbative improvement of the data. The impatient reader might skip this section and directly pass to Sect. 4. There, after the discussion of the continuum extrapolated results and associated systematic errors, the comparison to renormalized perturbation theory is performed before we conclude in Sect. 5. Finally, a technical appendix presents the models we used for the sensitivity of the data to a variation of the two O(a) boundary counterterm coefficients $c_\mathrm{t}$ and $\tilde{c}_\mathrm{t}$.

2 SF couplings

In order to apply the recursive step-scaling techniques to lattice QCD, it is desirable to define renormalized QCD couplings in a finite space-time volume, $L^4$, and in the chiral limit. Such finite volume renormalization schemes are quark mass independent by construction [22], and the renormalization scale is set by $\mu =1/L$. It is then possible to apply recursive finite size scaling methods and trace the scale evolution over a wide range without the need for very large lattice sizes, L / a [10]. Still, these requirements leave many options, such as the boundary conditions for the fields and the exact choice of observable. We here choose Schrödinger functional boundary conditions [23, 24]: these introduce a gap in the spectrum of the Dirac operator, so that numerical simulations can be performed directly at zero quark masses, without the need for any chiral extrapolation. Moreover, perturbation theory remains tractable in this framework, as the absolute minimum of the action is unique up to gauge equivalence. For the observable we choose the traditional SF coupling [25, 26] and a 1-parameter family of close relatives [27]. The most important reason for this choice is the existence of a 2-loop calculation in this case [14, 15], which, in combination with [16, 17] allows to infer the 3-loop $\beta$-function for these schemes. Furthermore, the values of the 3-loop $\beta$-function coefficients are reasonable and enable us to make contact with the asymptotic perturbative regime at energy scales in the range O(10–100) GeV.

In the future one might also consider the more recent coupling definitions based on the gradient flow [28, 29]. The QCD 3-loop $\beta$-function is currently known in the case of infinite space-time volume [30], and there is progress for the case of a finite volume with SF boundary conditions [29] using numerical stochastic perturbation theory [31,32,33]. These results seem to point to a 3-loop $\beta$-function coefficient which is significantly larger than in the ${\overline{\mathrm{MS}}}$- and SF-schemes. This indicates that gradient flow couplings may not be ideal for matching with the asymptotic perturbative regime. Furthermore, cutoff effects are typically larger with the GF couplings than with the traditional SF coupling [13], so that larger lattice sizes are required. This partially offsets other computational advantages. Obviously, further studies are required and one should re-assess the situation once more perturbative information becomes available.

2.1 $\hbox {SF}_\nu$ schemes

In the continuum the Schrödinger functional is defined as the Euclidean path integral,

$$\begin{aligned} \mathcal{Z}[C,C']= \int D[\Lambda ] \int D[A,\psi ,\overline{\psi }]\mathrm{e}^{-S[A,\psi ,\overline{\psi }]}, \end{aligned}$$

(2.1)

with the Euclidean continuum action $S=S_g+S_f$,

$$\begin{aligned} S_g= & {} -\frac{1}{2g_0^2} \int _0^L\mathrm{d}x_0 \int _0^L\mathrm{d}^3\mathbf{x} \,\hbox {tr}\,\{F_{\mu \nu }(x) F_{\mu \nu }(x)\}, \end{aligned}$$

(2.2)

$$\begin{aligned} S_f= & {} \int _0^L\mathrm{d}x_0 \int _0^L\mathrm{d}^3\mathbf{x}\, \overline{\psi }(x)(\gamma _\mu D_\mu +m)\psi (x). \end{aligned}$$

(2.3)

Here, $g_0$ denotes the bare coupling constant, $F_{\mu \nu }$ is the field tensor associated with the gauge field $A_\mu$,

$$\begin{aligned} F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu +[A_\mu ,A_\nu ], \end{aligned}$$

(2.4)

and $D_\mu =\partial _\mu +A_\mu +i\theta _\mu /L$ is the covariant derivative acting on the quark fields. It includes a constant U(1) background field which we set to $\theta _\mu = (1-\delta _{\mu 0})\theta$, with the choice $\theta =\pi /5$. In the spatial directions L-periodic boundary conditions are imposed on all fields. At the time boundaries the fermionic fields satisfy [24]

$$\begin{aligned} P_+\psi \vert _{x_0=0}= & {} 0=P_-\psi \vert _{x_0=L},\nonumber \\ \overline{\psi }P_-\vert _{x_0=0}= & {} 0= \overline{\psi }P_+\vert _{x_0=L}, \end{aligned}$$

(2.5)

with the projectors $P_\pm =\frac{1}{2}(1\pm \gamma _0)$. For the gauge field one has

$$\begin{aligned} A_k|_{x_0=0} = C^{\Lambda }_k,\quad A_k|_{x_0=L} = C'_k,\quad k=1,2,3, \end{aligned}$$

(2.6)

with the boundary values $C_k$ and $C_k'$. The boundary condition at $x_0=0$ refers to the gauge transformed field,

$$\begin{aligned} C_k^{\Lambda }(\mathbf{x}) = \Lambda (\mathbf{x}) C_k(\mathbf{x}) \Lambda (\mathbf{x})^\dagger + \Lambda (\mathbf{x})\partial _k\Lambda (\mathbf{x})^\dagger . \end{aligned}$$

(2.7)

The integration over the SU(3)-valued and spatially periodic gauge functions $\Lambda (\mathbf{x})$ in Eq. (2.1) ensures gauge invariance of the Schrödinger functional. The spatially periodic $\Lambda (\mathbf{x})$ fall into different topological sectors labelled by an integer n,

$$\begin{aligned} n = \frac{1}{24\pi ^2} \int _0^L \mathrm {d}^3\mathbf{x}\, \epsilon _{ijk} \,\hbox {tr}\,\left\{ (\Lambda \partial _i\Lambda ^{-1}) (\Lambda \partial _j\Lambda ^{-1})(\Lambda \partial _k\Lambda ^{-1})\right\} , \end{aligned}$$

(2.8)

which is related to the topological charge of the gauge field,

$$\begin{aligned} Q[A] = -\dfrac{\epsilon _{\mu \nu \rho \sigma }}{32\pi ^2} \int \mathrm{d}^4x\, \mathrm{tr}\{F_{\mu \nu }(x) F_{\rho \sigma }(x)\}, \end{aligned}$$

(2.9)

through $n = - Q[A]$, provided the Chern–Simons action of the boundary gauge fields $C_k$, $C'_k$ vanishes (which is the case for the choice below). The value of the gauge action in each sector n is then subject to the usual instanton bound [23]

$$\begin{aligned} g_0^2 S_g[A] \ge 8\pi ^2|Q[A]|. \end{aligned}$$

(2.10)

Using the gauge invariance of the Schrödinger functional under the transformations,

$$\begin{aligned} A_\mu (x)\rightarrow & {} \Omega (x) A_\mu \Omega (x)^\dagger + \Omega (x) \partial _\mu \Omega (x)^\dagger , \end{aligned}$$

(2.11)

$$\begin{aligned} \Lambda (x)\rightarrow & {} \Omega (0,\mathbf{x}) \Lambda (\mathbf{x}), \end{aligned}$$

(2.12)

$$\begin{aligned} \psi (x)\rightarrow & {} \Omega (x) \psi (x), \end{aligned}$$

(2.13)

$$\begin{aligned} \overline{\psi }(x)\rightarrow & {} \overline{\psi }(x)\Omega (x)^\dagger , \end{aligned}$$

(2.14)

one may convert the integral over gauge functions $\Lambda$ to a sum over n, with $\Lambda$ in Eq. (2.6) replaced by fixed representatives $\Lambda _n$ for each topological sector. In particular one often sets $\Lambda _0 = 1$.

We now focus on Abelian and spatially constant boundary gauge fields,

$$\begin{aligned} C_k(\mathbf{x})=\frac{i}{L}\phi , \quad C'_k(\mathbf{x}) =\frac{i}{L}\phi ', \quad k=1,2,3, \end{aligned}$$

(2.15)

with traceless and diagonal $3\times 3$-matrices $\phi$ and $\phi '$. Their diagonal elements

$$\begin{aligned} \phi _1= & {} \eta -\frac{\pi }{3}, \quad \phi '_1 = -\eta -\pi , \nonumber \\ \phi _2= & {} \eta \left( \nu -\frac{1}{2}\right) , \quad \phi '_2 = \eta \left( \nu +\frac{1}{2}\right) +\frac{\pi }{3},\nonumber \\ \phi _3= & {} -\eta \left( \nu +\frac{1}{2}\right) +\frac{\pi }{3},\nonumber \\ \phi '_3= & {} -\eta \left( \nu -\frac{1}{2}\right) +\frac{2\pi }{3}, \end{aligned}$$

(2.16)

still depend on 2 real parameters, $\eta$ and $\nu$. In the temporal gauge and the topological charge zero sector the field equations with these boundary conditions are solved by,

$$\begin{aligned} B_0=0,\quad B_k= C_k + \frac{x_0}{L}\left( C_k'-C_k\right) , \quad k=1,2,3, \end{aligned}$$

(2.17)

which corresponds to a constant chromo-electric field,

$$\begin{aligned} G_{0k}=\partial _0 B_k = \frac{C_k'-C_k}{L}= \frac{i(\phi '-\phi )}{L^2}, \quad k=1,2,3. \end{aligned}$$

(2.18)

Inserting the field tensor into the gauge action, $S_g$, one obtains

$$\begin{aligned} S_g[B]= \frac{3}{g_0^2}\sum _{\alpha =1}^3(\phi '_\alpha -\phi _\alpha )^2 = \frac{18}{g_0^2}\left( \eta +\frac{\pi }{3}\right) ^2, \end{aligned}$$

(2.19)

which, for given $\eta$ (and independently of $\nu$) constitutes the absolute minimum of the action [23]. One may thus define the effective action as a function of this background field,

$$\begin{aligned} \Gamma [B]=-\ln \mathcal{Z}[C',C], \end{aligned}$$

(2.20)

and its perturbative expansion,

$$\begin{aligned} \Gamma [B] \, \buildrel g_0\rightarrow 0\over \sim \,\, \frac{1}{g_0^2}\Gamma _0[B]+ \Gamma _1[B]+\mathrm{O}(g_0^2), \end{aligned}$$

(2.21)

with $\Gamma _0[B]=g_0^2 S_g[B]$. The SF couplings $\bar{g}^2_\nu (L)$ can be defined through

$$\begin{aligned} {\frac{\partial \Gamma [B]}{\partial \eta }} \biggl \vert _{\eta =0}= \frac{k}{\bar{g}^2_\nu (L)}, \quad k={\frac{\partial \Gamma _0[B]}{\partial \eta }} \biggl \vert _{\eta =0}=12\pi . \end{aligned}$$

(2.22)

In fact the $\nu$-dependence is explicit,

$$\begin{aligned} \frac{1}{{\bar{g}}_\nu ^2(L)} = \frac{1}{{\bar{g}}^2(L)}-\nu \bar{v}(L), \end{aligned}$$

(2.23)

since both $1/\bar{g}^2(L)$ and $\bar{v}(L)$ are $\nu$-independent. In terms of the effective action, $\bar{v}(L)$ reads

$$\begin{aligned} \bar{v}(L) = -\frac{1}{k} \left. \frac{\partial ^2 \Gamma [B]}{\partial \nu \partial \eta }\right| _{\eta =\nu =0}. \end{aligned}$$

(2.24)

Note that the $\nu$-independence of $\Gamma _0[B]$, implies that $\bar{v}(L)$ has a perturbative expansion starting at O(1). This ensures the correct normalization of the whole 1-parameter family of couplings, namely $\bar{g}_\nu ^2=g_0^2$ to lowest order. Finally we remark that the entire 1-parameter family is determined by the expectation values,

$$\begin{aligned} \frac{k}{\bar{g}^2} = \left\langle \left. \frac{\partial S}{\partial \eta }\right| _{\eta =\nu =0} \right\rangle ,\quad \bar{v} = \frac{-1}{k}\left\langle \left. \frac{\partial ^2 S}{\partial \nu \partial \eta }\right| _{\eta =\nu =0} \right\rangle , \end{aligned}$$

(2.25)

defined in terms of the functional integral, Eq. (2.1), at $\nu =0$. Once the lattice regularization is in place both quantities will thus become observables in numerical simulations.

2.2 $\beta$-functions and perturbative relations to the ${\overline{\mathrm{MS}}}$-coupling

The SF couplings are defined independently of perturbation theory and thus the same is true for their $\beta$-functions,

$$\begin{aligned} \beta (\bar{g}_\nu ) = - L \frac{\partial \bar{g}_\nu }{\partial L} \buildrel {\bar{g}_\nu }\rightarrow 0\over \sim \, -\bar{g}_\nu ^3\sum _{k=0}^\infty b_k {\bar{g}_\nu }^{2k}, \end{aligned}$$

(2.26)

where the asymptotic expansion on the r.h.s. starts out with the standard universal coefficients $b_{0,1}$ for $N_\mathrm{f}=3$ QCD,

$$\begin{aligned} (4\pi )b_0= 9/(4\pi ), \quad (4\pi )^2b_1 = 4/\pi ^2, \end{aligned}$$

(2.27)

and the 3-loop coefficient is given by

$$\begin{aligned} (4\pi )^3b_{2}= & {} -\left( 0.064(27) + \nu \times 1.259(10)\right) . \end{aligned}$$

(2.28)

The 3-loop coefficient has been obtained by matching the coupling at the 2-loop level to the ${\overline{\mathrm{MS}}}$-scheme, where the $\beta$-function is now even known to 5-loop order ($b_3$ and $b_4$ in our notation) [3,4,5,6,7]. For later use we collect the numerical values for $N_\mathrm{f}=3$ QCD in Table 1, together with the $\hbox {SF}_\nu$ scheme results for the 3 choices of the parameter, $\nu =-0.5,0,0.3$, which we selected for more detailed analysis in Sect. 4.

Table 1 Coefficients in the asymptotic expansion of the $\beta$-function in different schemes. Note that the universal coefficients for $N_\mathrm{f}=3$ are $(4\pi )b_0 \approx 0.716197$, $(4\pi )^2b_1\approx 0.405285$

Comparing the ${\overline{\mathrm{MS}}}$ to the $\hbox {SF}_\nu$ scheme we note that the respective 3-loop $\beta$-functions coincide for $\nu \approx -0.3$. In general, $\nu$-values of O(1) are reasonable from a perturbative point of view.

Closely related to the $\beta$-functions are the step-scaling functions which connect couplings at scales which differ by a factor 2. Defining

$$\begin{aligned} \sigma (u) = \bar{g}^2(2L)\vert _{u=\bar{g}^2(L),m(L)=0}, \end{aligned}$$

(2.29)

the precise relationship is,

$$\begin{aligned} \int _{\sqrt{u}}^{\sqrt{\sigma (u)}}\frac{\mathrm{d}g}{\beta (g)} = -\ln 2, \end{aligned}$$

(2.30)

and the perturbative expansion of $\sigma (u)$,

$$\begin{aligned} \sigma (u) = u + s_0 u^2 + s_1 u^3 + s_2 u^4 + \cdots , \end{aligned}$$

(2.31)

is thus determined in terms of the coefficients of the $\beta$-function, with the first 3 given by

$$\begin{aligned} s_0= & {} 2b_0\ln 2,\quad s_1 = s_0^2 + 2b_1 \ln 2,\nonumber \\ s_2= & {} s_0^3 + 10 b_0 b_1 (\ln 2)^2 +2b_2 \ln 2. \end{aligned}$$

(2.32)

Finally, we quote the relation between the SF and the ${\overline{\mathrm{MS}}}$ couplings, in terms of $\alpha = \bar{g}^2/(4\pi )$ at the scales $\mu =1/L$ and $s\mu$, respectively, with $s>0$. One finds

$$\begin{aligned} \alpha _{\overline{\mathrm{MS}}}(s\mu ) = \alpha (\mu ) + c_1(s) \alpha ^2(\mu ) + c_2(s) \alpha ^3(\mu ) + \cdots \end{aligned}$$

(2.33)

with (for $N_\mathrm{f}=3$) [14,15,16,17, 23, 26]

$$\begin{aligned} c_1(s)= & {} - 8\pi b_0 \ln (s) + 1.3752097(26), \end{aligned}$$

(2.34)

$$\begin{aligned} c_2(s)-\left( c_1(s)\right) ^2= & {} - 32\pi ^2 b_1 \ln (s) + 1.320(30) . \end{aligned}$$

(2.35)

In order to connect to the $\hbox {SF}_\nu$ couplings for $\nu \ne 0$ we need the expansion of $\bar{v}$ in the coupling $\bar{g}$. Defining

$$\begin{aligned} \omega (u) = \bar{v}(L)\vert _{u=\bar{g}^2(L),m(L)=0}, \end{aligned}$$

(2.36)

the expansion is known to second order,

$$\begin{aligned} \omega (u) = v_1 + v_2\,u + \mathrm{O}(u^2), \end{aligned}$$

(2.37)

where the coefficients for $N_\mathrm{f}=3$ evaluate to

$$\begin{aligned} 4\pi v_1 = 1.797887(5), \quad (4\pi )^2v_2 = -0.741(14). \end{aligned}$$

(2.38)

Starting from

$$\begin{aligned} \bar{g}_\nu ^2(L) = \bar{g}^2(L) \left[ 1-\nu \bar{g}^2(L) \omega \left( \bar{g}^2(L)\right) \right] ^{-1}, \end{aligned}$$

(2.39)

we obtain the 2-loop relation,

$$\begin{aligned} \begin{aligned} \alpha _\nu (\mu )&= \alpha (\mu )+ (4\pi v_1\nu ) \alpha ^2(\mu ) \\&\quad + (4\pi )^2 \left( v_2\nu + v_1^2\nu ^2\right) \alpha ^3(\mu ) + \cdots . \end{aligned} \end{aligned}$$

(2.40)

Inverting perturbatively and combining with the previous equations we have

$$\begin{aligned} \alpha _{\overline{\mathrm{MS}}}(s\mu ) = \alpha _\nu (\mu ) + c_{1}^{\nu }(s) \alpha _\nu ^2(\mu ) + c_{2}^{\nu }(s) \alpha _\nu ^3(\mu ) + \cdots , \end{aligned}$$

(2.41)

where

$$\begin{aligned} c_1^{\nu }(s)= & {} c_1(s) -4\pi v_1 \nu , \end{aligned}$$

(2.42)

$$\begin{aligned} c_2^{\nu }(s) - \left( c_1^{\nu }(s)\right) ^2= & {} c_2(s) - \left( c_1(s)\right) ^2 - (4\pi )^2 v_2 \nu . \end{aligned}$$

(2.43)

In the perturbative matching of couplings one occasionally applies the principle of “fastest apparent convergence”, which implies that $s=s^\star$ is chosen such as to make the one-loop coefficient, $c_1^\nu (s^\star )$, vanish. This is the case for

$$\begin{aligned} \ln (s^\star ) = \dfrac{c_1^\nu (1)}{8\pi b_0} = \frac{2\pi }{9} c_1^\nu (1), \end{aligned}$$

(2.44)

and with this choice one obtains the relation,

$$\begin{aligned} \alpha _{\overline{\mathrm{MS}}}(s^\star \mu ) = \alpha _\nu (\mu ) + c_2^{\nu }(s^\star ) \alpha _\nu ^3(\mu ) + \mathrm{O}\left( \alpha _\nu ^4\right) . \end{aligned}$$

(2.45)

2.3 Perturbation theory and the $\Lambda$-parameter

There are various ways to define a target precision for $\alpha _s$. Instead of referring to the coupling in some scheme at some scale it is attractive to instead refer to the $\Lambda$-parameter. Given the coupling $\bar{g}_\mathrm{x}(L)$ in a scheme $\mathrm{x}$, the $\Lambda$-parameter in this scheme is a special solution of the Callan–Symanzik equation of the form

$$\begin{aligned} \Lambda _\mathrm{x}= & {} L^{-1} \varphi _\mathrm{x}(\bar{g}_\mathrm{x}(L)), \end{aligned}$$

(2.46)

with

$$\begin{aligned} \varphi _\mathrm{x}(\bar{g})= & {} ( b_0 \bar{g}^2 )^{-b_1/(2b_0^2)} \mathrm{e}^{-1/(2b_0 \bar{g}^2)} \nonumber \\&\times \exp \left\{ -\int \limits _0^{\bar{g}} \mathrm{d}g\ \left[ \frac{1}{\beta _\mathrm{x}(g)} +\frac{1}{b_0g^3} - \frac{b_1}{b_0^2g} \right] \right\} .\nonumber \\ \end{aligned}$$

(2.47)

Note that this definition is independent of perturbation theory provided the coupling and its $\beta$-function are defined non-perturbatively. In practice, however, one would like to evaluate the $\Lambda$-parameter at a large energy scale $\mu =1/L$ such that the integral in the exponent can be safely evaluated in perturbation theory. The exact scheme-dependence of the $\Lambda$-parameter is obtained by the one-loop matching of the respective couplings. Labelling the schemes by $\mathrm{x}$ and $\mathrm{y}$,

$$\begin{aligned} {\bar{g}}^2_\mathrm{x}(L) = {\bar{g}}^2_\mathrm{y}(L) + c_\mathrm{xy}{\bar{g}}_\mathrm{y}^4(L) + \cdots , \end{aligned}$$

(2.48)

one obtains the exact relationship

$$\begin{aligned} \Lambda _\mathrm{x}/\Lambda _\mathrm{y} = \mathrm{e}^{c_\mathrm{xy}/2b_0}. \end{aligned}$$

(2.49)

Note that this allows one to indirectly define $\Lambda _{\overline{\mathrm{MS}}}$ non-perturbatively, thereby justifying its use as a reference definition. With the perturbative matching coefficients of the previous subsection we obtain the relationships (for $N_\mathrm{f}=3$),

$$\begin{aligned} \Lambda /\Lambda _{\overline{\mathrm{MS}}}=0.38286(2)\quad \Lambda _\nu /\Lambda = \exp \left( \nu \times 1.255162(4)\right) , \end{aligned}$$

(2.50)

where $\Lambda$ and $\Lambda _\nu$ are the parameters for the SF and $\hbox {SF}_\nu$ scheme, respectively. In particular, the ratio $s^\star$ of scales used in Eq. (2.44) is given by the ratio of the respective $\Lambda$-parameters.

2.4 On exponentially suppressed corrections to perturbation theory

The perturbative expansion of the path integral generates an asymptotic series, with zero radius of convergence. In applications one then hopes that, for the accessible range of couplings, the perturbative series provides a good quantitative description of the observable. The observables we consider here, the couplings in the $\hbox {SF}_\nu$ schemes, are defined non-perturbatively in Euclidean space-time, with an infrared cutoff provided by the finite space-time volume. These properties are advantageous for perturbation theory, in particular, there should be no renormalon problem [34]. Lattice QCD provides very good non-perturbative control of these observables, for couplings $\alpha$ in the range 0.1–0.2 (cf. Sect. 3). Before testing perturbation theory, we would like to identify exponentially suppressed terms in the coupling which might preclude a good quantitative description of the non-perturbative data. Such terms are associated with local minima of the action, e.g. those corresponding to the classical solutions of the field equations. Given the instanton bound, Eq. (2.10), and the absolute minimum $S_g[B]=2\pi ^2/g_0^2$ of the action [Eq. (2.19), with $\eta =0$], contributions from the $|Q|=1$ instanton sector to our observables are accompanied by a suppression factor $\exp (-6\pi ^2/g_0^2)=\exp (-3\pi /(2\alpha ))$ and are therefore numerically irrelevant for our range of couplings. We may then ask the question whether there are further secondary minima of the action which are less strongly suppressed. Hence we are looking for a secondary minimum $B^*_\mu$ of the gauge action in the $Q=0$ sector, which satisfies

$$\begin{aligned} \Delta S = S_g[B^*] - S_g[B] < 6\pi ^2/g_0^2. \end{aligned}$$

(2.51)

In fact there are “large” gauge transformations at $x_0=0$ corresponding to gauge functions $\omega (\mathbf{x})$ which are topologically trivial but are not subject to the gauge fixing procedure around $B_\mu$ [23]. In order to find potential secondary minima we have resorted to a numerical experiment in the lattice discretized theory. More precisely, we have first performed numerical simulations of the pure SU(3) Yang-Mills theory on a lattice with linear extent $L/a=8$, (at $\beta \equiv 6/g_0^2= 5.7$), and generated a long Monte Carlo history of about 64.000 configurations, corresponding to 128.000 MDU, using the same simulation code as for our $N_\mathrm{f}=3$ QCD simulations (cf. Sect. 3). Every $5\text {th}$ gauge configuration has been taken as initial condition for the gradient flow equation [28], which we then integrated up to very large flow times t, corresponding to $c=\sqrt{8t}/L =10$; the gradient flow is a smoothing operation and drives the gauge field towards a local minimum of the action. At large flow times we selected the gauge field configurations in the $Q=0$ sector.³ Apart from the background field, Eq. (2.17), we have indeed found a single further local minimum. In order to check for its stability and to obtain its continuum limit, we have performed similar simulations on finer lattices with $L/a=12,16,24$, and bare couplings such as to keep $\bar{g}^2(L/2) =2.77$ approximately fixed. After extrapolation to the continuum and in the temporal gauge we find that this secondary minimum corresponds to the spatially constant Abelian field,

$$\begin{aligned} B^*_1(x)= & {} \dfrac{i\pi }{L}\left\{ \mathrm{diag}\left( -\frac{1}{3},\frac{1}{3},0\right) \right. \nonumber \\&\left. +\frac{x_0}{L}\mathrm{diag}\left( -\frac{2}{3},0,\frac{2}{3}\right) \right\} , \end{aligned}$$

(2.52)

$$\begin{aligned} B^*_2(x)= & {} B_1(x), \end{aligned}$$

(2.53)

$$\begin{aligned} B^*_3(x)= & {} \dfrac{i\pi }{L}\left\{ \mathrm{diag}\left( -\frac{7}{3},\frac{1}{3},2\right) \right. \nonumber \\&\left. +\frac{x_0}{L}\mathrm{diag}\left( -\frac{4}{3},0,\frac{4}{3}\right) \right\} . \end{aligned}$$

(2.54)

The boundary conditions at $x_0=0$ thus are given as

$$\begin{aligned} B^*_1(0,\mathbf{x}) = B^*_2(0,\mathbf{x}) = C_1^\omega = C_2^\omega = \dfrac{i\pi }{L}\mathrm{diag}\left( -\frac{1}{3},\frac{1}{3},0\right) , \end{aligned}$$

(2.55)

and

$$\begin{aligned} B^*_3(0,\mathbf{x}) = C_3^\omega = \dfrac{i\pi }{L}\mathrm{diag}\left( -\frac{7}{3},\frac{1}{3},2\right) . \end{aligned}$$

(2.56)

The gauge function $\omega (\mathbf{x})$ is thus non-constant in the $x_3$-direction, which induces the shift by $\pm 2\pi$ in 2 of the angles of $C_3^\omega$, in addition to the permutation of the colour 2- and 3-components of $\phi$, Eq. (2.16). Obviously the spatial directions can be permuted, so this minimum has a 3-fold degeneracy. Hence, the classical field $B^*_\mu$ is Abelian and spatially constant, but with boundary values, transformed by the gauge function

$$\begin{aligned} \omega (\mathbf{x}) = \begin{pmatrix} \exp \left( i\frac{2\pi }{L}x_3\right) &{} 0 &{} 0 \\ 0 &{} 0 &{} -1\\ 0 &{} \exp \left( -i\frac{2\pi }{L}x_3\right) &{} 0\\ \end{pmatrix}. \end{aligned}$$

(2.57)

To find the gap in the gauge action we insert the non-zero components of the field tensor

$$\begin{aligned} G^*_{0k} = \partial _0 B_k^*= \dfrac{i\pi }{L^2}\times {\left\{ \begin{array}{ll} \mathrm{diag}\left( -\frac{2}{3},0,\frac{2}{3}\right) , &{}\quad \text {if}\quad k=1,2,\\ \mathrm{diag}\left( -\frac{4}{3},0,\frac{4}{3}\right) , &{}\quad \text {if}\quad k=3, \end{array}\right. } \end{aligned}$$

(2.58)

into the gauge action Eq. (2.2), with the result

$$\begin{aligned} g_0^2 S[B^*] = -L^4 \sum _{k=1}^3\,\hbox {tr}\,\left\{ G^*_{0k}G^*_{0k}\right\} = \dfrac{16\pi ^2}{3}. \end{aligned}$$

(2.59)

Hence the gap, $\Delta S$, is found to be 10 / 3 in units of $\pi ^2/g_0^2$ which is 2 / 3 below the $Q=1$ instanton threshold. This leads to a suppression factor $\exp (-g_0^2 \Delta S/(4\pi \alpha )) = \exp (-5\pi /(6\alpha ))$. For the range of couplings in our study, this factor varies from a few times $10^{-6}$ to below $10^{-10}$, which renders such a non-perturbative contribution completely negligible.

3 Lattice set-up and simulations

In this section we briefly describe the main elements of the lattice set-up chosen for this study and discuss some details pertaining to the error treatment.

3.1 Lattice action

We choose the standard Wilson plaquette action for the gauge fields and three flavours of non-perturbatively O(a) improved Wilson fermions. The lattice action is then given by $S=S_g+S_f$, with

$$\begin{aligned} S_g[U]= & {} \frac{1}{g_0^2}\sum _{p}w(p)\,\,\hbox {tr}\,\{1-U(p)\}, \end{aligned}$$

(3.1)

$$\begin{aligned} S_f[U,\bar{\psi },\psi ]= & {} a^4\sum _{x}\bar{\psi }(x)(D+\delta D_b + m_0)\psi (x) . \end{aligned}$$

(3.2)

The gauge field action $S_g$ is a sum over all oriented plaquettes p on the lattice, with the weights w(p), and the parallel transporters U(p) around p. With the gauge field boundary conditions given in terms of the Abelian fields, Eq. (2.15),

$$\begin{aligned} U_k(0,\mathbf{x}) = \exp (a C_k),\quad U_k(L,\mathbf{x}) = \exp (a C'_k), \end{aligned}$$

(3.3)

the gauge part of the action is completely specified by setting $w(p)=1$ except for timelike plaquettes touching one of the boundaries for which $w(p)=c_\mathrm{t}$. The Dirichlet boundary conditions for the quark fields look exactly the same as in the continuum, cf. Sect. 2. Like in the continuum we take the fermionic fields to be spatially periodic and implement the phase $\theta =\pi /5$ via a constant U(1) background field $\lambda _\mu = \exp (ia\theta _\mu /L)$, with $\theta _\mu = (1-\delta _{\mu ,0})\theta$. With the covariant derivatives,

$$\begin{aligned} \nabla _\mu \psi (x)= & {} \frac{1}{a} \left[ \lambda _\mu U(x,\mu )\psi (x+a\hat{\mu })-\psi (x)\right] , \end{aligned}$$

(3.4)

$$\begin{aligned} \nabla _\mu ^{*}\psi (x)= & {} \frac{1}{a} \left[ \psi (x)-\lambda _\mu ^*U(x-a\hat{\mu },\mu )^{\dag }\psi (x-a\hat{\mu })\right] ,\nonumber \\ \end{aligned}$$

(3.5)

the Wilson-Dirac operator in the fermionic action (3.2) takes the form,

$$\begin{aligned} D= & {} \frac{1}{2} \sum _{\mu =0}^3 \left\{ \gamma _\mu (\nabla _\mu ^*+\nabla _\mu )- a\nabla _\mu ^*\nabla _\mu \right\} \nonumber \\&+\,\,c_\mathrm{sw}\,\frac{ia}{4}\sum _{\mu ,\nu =0}^3 \,\sigma _{\mu \nu }\mathcal{F}_{\mu \nu } , \end{aligned}$$

(3.6)

which includes the Sheikholeslami–Wohlert term [35]. For the clover leaf definition of the field strength tensor, $\mathcal{F}_{\mu \nu }$, we refer to [36] and the improvement coefficient $c_\mathrm{sw}(g_0)$ is set non-perturbatively using the result from [37]. Finally, the fermionic $\mathrm{O}(a)$ boundary counterterm action is specified by [36]

$$\begin{aligned} \delta D_b \psi (x) = (\tilde{c}_\mathrm{t}-1)\left( \delta _{x_0,a}+\delta _{x_0,L-a}\right) \psi (x). \end{aligned}$$

(3.7)

The 2 boundary counterterm coefficients, $c_\mathrm{t}(g_0)$ and $\tilde{c}_\mathrm{t}(g_0)$ are set to their perturbative two- and one-loop expressions, respectively [15, 25],

$$\begin{aligned} c_\mathrm{t}(g_0)= & {} 1+c_\mathrm{t}^{(1)}g_0^2+c_\mathrm{t}^{(2)}g_0^4+\mathrm{O}(g_0^6), \end{aligned}$$

(3.8)

$$\begin{aligned} \tilde{c}_\mathrm{t}(g_0)= & {} 1 + \tilde{c}_\mathrm{t}^{(1)}g_0^2 + \mathrm{O}(g_0^4), \end{aligned}$$

(3.9)

with the known perturbative coefficients for $N=3$ colours given by

$$\begin{aligned} c_\mathrm{t}^{(1)}= & {} -0.0890 + 0.019141\times N_\mathrm{f}\quad {\mathop {=}\limits ^{N_\mathrm{f}=3}} -0.0315, \end{aligned}$$

(3.10)

$$\begin{aligned} c_\mathrm{t}^{(2)}= & {} -0.0294+ 0.002\times N_\mathrm{f}\nonumber \\&+ 0.000(1)\times N_\mathrm{f}^2\quad {\mathop {=}\limits ^{N_\mathrm{f}=3}} -0.0234, \end{aligned}$$

(3.11)

$$\begin{aligned} \tilde{c}_\mathrm{t}^{(1)}= & {} -0.01795. \end{aligned}$$

(3.12)

We notice a significant cancellation in the one-loop term $c_\mathrm{t}^{(1)}$ between the gluon and fermion contributions. We interpret the resulting relative size of one- and two-loop terms for $N_\mathrm{f}=3$ as an accident and not a sign for a poor behaviour of the series in general.

3.2 Lattice observables

Like in the continuum, the basic observables $1/\bar{g}^2$ and $\bar{v}$ are given as expectation values, Eq. (2.25), of gauge invariant fields, which are now obtained as $\eta$- and $\nu$-derivatives of the lattice action⁴ (3.1, 3.2). The lattice version of the Abelian background field takes the form,

$$\begin{aligned} V_\mu (x) = \exp \left( a B_\mu (x)\right) , \end{aligned}$$

(3.13)

with $B_\mu (x)$ the continuum expression, Eq. (2.17). Cutoff effects with such Abelian gauge fields are known to be small [23]. Indeed, the $\eta$-derivative of $S_g[V]$ yields the lattice normalization constant

$$\begin{aligned} k = 12 (L/a)^2 [ \sin (\gamma )+\sin (2\gamma )], \quad \gamma =\frac{1}{3} \pi (a/L)^2, \end{aligned}$$

(3.14)

which converges to $12\pi$ with O($a^4$) corrections. We will use this lattice definition of k in order to ensure $\bar{g}^2=g_0^2$ exactly at lowest order. Note that this also holds for $\bar{g}_\nu ^2$, since $\bar{v}$ vanishes identically at tree level.

On the lattice with Wilson quarks, the chiral limit is not sharply defined, and one also needs to specify the exact definition used. For given bare coupling $g_0$, we require the PCAC quark mass,

$$\begin{aligned} m(L) = \left. \frac{\frac{1}{2}(\partial _0^{}+\partial _0^*) f_\mathrm{A}(x_0^{}) + c_\mathrm{A}(g_0^{}) a \partial _0^*\partial _0^{} f_\mathrm{P}(x_0^{})}{2 f_\mathrm{P}(x_0^{})}\right| _{x_0^{}=L/2}, \end{aligned}$$

(3.15)

to vanish on an $(L/a)^4$ lattice with the Abelian boundary conditions, Eq. (3.3). Here $f_\mathrm{A}(x_0)$ and $f_\mathrm{P}(x_0)$ are Schrödinger functional correlation functions defined e.g. in Eqs. (2.1) and (2.2) of [38], and $\partial _0$, $\partial _0^*$ are the forward and backward lattice time derivatives, respectively. Finally, the improvement coefficient, $c_\mathrm{A}$, is set to its perturbative 1-loop value [39, 40], since a non-perturbative estimate is not available for $N_\mathrm{f}=3$ and our choice of gauge action. Given that we do not attempt to reach the low energy, hadronic regime, we expect one-loop perturbation theory to work reasonably well for $c_\mathrm{A}$. The chiral limit is now defined by $m(L)=0$, and, for given bare coupling $g_0^2\equiv 6/\beta$, the bare mass $m_0$ for which this equation holds, defines the critical mass parameter or, equivalently, the critical $\kappa$,

$$\begin{aligned} am_0 = am_\mathrm{cr}(g_0) = 1/\left( 2\kappa _\mathrm{cr}(g_0)\right) -4. \end{aligned}$$

(3.16)

With these conventions we may now define the lattice observables. Specifying the value u of the coupling $\bar{g}^2(L)$ at vanishing quark mass defines our approach to the continuum limit, and other lattice observables are then well-defined functions of u. In particular $\bar{v}$ gives rise to 2 lattice observables

$$\begin{aligned} \Omega (u,a/L)= & {} \left. \bar{v}(L)\right| _{u=\bar{g}^2(L),m(L)=0}, \end{aligned}$$

(3.17)

$$\begin{aligned} \tilde{\Omega }(u,a/L)= & {} \left. \bar{v}(L)\right| _{u=\bar{g}^2(L),m(L/2)=0} , \end{aligned}$$

(3.18)

which differ by the chiral limit definition. The appearance of 2 lattice versions for $\omega (u)$ is a consequence of the definition of the lattice step-scaling functions through

$$\begin{aligned} \Sigma (u,a/L) = \left. \bar{g}^2(2L)\right| _{\bar{g}^2(L)=u,m(L)=0}, \end{aligned}$$

(3.19)

which requires simulations on lattices with resolutions L / a and 2L / a, at the same bare parameters. In particular, the simulations on the 2L / a-lattices are performed at the bare mass parameters for which the PCAC mass vanishes on the L / a lattice. Finally, we also consider the lattice step-scaling functions for $\bar{g}^2_\nu$,

$$\begin{aligned} \Sigma _\nu (u,a/L) = \left. \bar{g}_\nu ^2(2L)\right| _{\bar{g}_\nu ^2(L)=u,m(L)=0}, \end{aligned}$$

(3.20)

at non-zero values of $\nu$.

3.3 Perturbatively improved lattice observables

In order to accelerate the approach to the continuum limit one may use perturbation theory to subtract the lattice artefacts order by order in the coupling from the non-perturbative data [41]. The 2-loop calculation in [15] has been carried out in the very same lattice regularized theory, and the two-loop lattice artefacts in the $\nu =0$ step-scaling functions,

$$\begin{aligned} \delta (u,a/L)= & {} \frac{\Sigma (u,a/L) -\sigma (u)}{\sigma (u)} \nonumber \\= & {} \delta _1(a/L) u + \delta _2(a/L) u^2 + \mathrm{O}(u^3), \end{aligned}$$

(3.21)

are indeed available to this order. With the coefficients for $N_\mathrm{f}=3$ from Table 2, one may thus define the improved step-scaling functions,

$$\begin{aligned} \Sigma ^{(i)}(u,L/a) = \frac{\Sigma (u,L/a)}{1+ \sum _{k=1}^i \delta _k(L/a) u^k}, \end{aligned}$$

(3.22)

up to loop order $i=2$. By construction, the leading cutoff effects for $i=0,1,2$ are then given by⁵

$$\begin{aligned} \Sigma ^{(i)}(u,a/L) = \sigma (u) + \frac{a}{L}\times \mathrm{O}(u^4) +\frac{a^2}{L^2}\times \mathrm{O}(u^{2+i}), \end{aligned}$$

(3.23)

and are thus suppressed by additional powers of the coupling. The term linear in a / L is due to the incomplete cancellation of the O(a) boundary effects and could be eliminated by a non-perturbative determination of $c_\mathrm{t}$ and $\tilde{c}_\mathrm{t}$. We will come back to the question of remnant O(a) effects in Sect. 3.7.

For the observables $\Omega$ and $\tilde{\Omega }$ one parametrizes the cutoff effects by 2 functions, $\epsilon$ and $\tilde{\epsilon }$. For $\Omega$ we have

$$\begin{aligned} \Omega (u,a/L)= & {} \omega (u)\left[ 1+\epsilon (u,a/L)\right] , \end{aligned}$$

(3.24)

with perturbative expansion

$$\begin{aligned} \epsilon (u,a/L) = \epsilon _1(a/L) + \epsilon _2(a/L) u + \mathrm{O}(u^2), \end{aligned}$$

(3.25)

and analogous equations hold for $\tilde{\Omega }$ and $\tilde{\epsilon }$. Unfortunately, the published results of the 2-loop calculation do not allow for the extraction of the cutoff effects for this case, so that the perturbatively improved observables,

$$\begin{aligned} \Omega ^{(i)}(u,a/L)= & {} \frac{\Omega (u,a/L)}{1+\sum _{k=1}^i\epsilon _k(a/L) u^{k-1}}, \end{aligned}$$

(3.26)

$$\begin{aligned} \tilde{\Omega }^{(i)}(u,a/L)= & {} \frac{\tilde{\Omega }(u,a/L)}{1+\sum _{k=1}^i\tilde{\epsilon }_k(a/L) u^{k-1}}, \end{aligned}$$

(3.27)

are only available to 1-loop order, $i=1$, with the coefficients $\epsilon _1$ and $\tilde{\epsilon }_1$ given in Table 2.

The same remark applies to the step-scaling function $\Sigma _\nu$ for $\nu \ne 0$. Using the notation,

$$\begin{aligned} \delta _\nu (u,a/L) = \delta _1^\nu (a/L) u + \mathrm{O}(u^2), \end{aligned}$$

(3.28)

the one-loop coefficient is given by

$$\begin{aligned} \delta _1^\nu (L/a) = \delta _1(L/a) + \nu v_1 \left[ \tilde{\epsilon }_1(a/2L) - \epsilon _1(a/L)\right] , \end{aligned}$$

(3.29)

where $v_1$ is the expansion coefficient of the continuum function $\omega (u)$, Eq. (2.38). Values for $\delta _1^\nu$ can be inferred from Table 2, for $N_\mathrm{f}=3$ and the lattice sizes relevant for this study.

Table 2 Values of the coefficients for $N_\mathrm{f}=3$ and the relevant lattice sizes, as required for perturbative cancellation of lattice artefacts up to 2-loop order in $\Sigma$, and to one-loop order in $\Sigma _\nu$, $\Omega$ and $\tilde{\Omega }$, cf. text

3.4 Simulation parameters and statistics

Using the openQCD code [42, 43] we have simulated lattice sizes $L/a=4,6,8,10,12$ around 9 values of the coupling $\bar{g}^2(L)=u$ in the range 1.1–2.0, cf. Table 3. At the same bare coupling $g_0^2=6/\beta$ and bare quark mass $am_0 = 1/(2\kappa )-4$ we then doubled the lattice sizes and simulated for $2L/a=8,12,16$ and, in 3 cases also for $2L/a=24$, cf. Table 4. Starting from the $L/a=12$ lattices we have tried to approximately match the values of the coupling for $\nu =0$ at $L/a=4,6,8$, so as to be able to do continuum extrapolations of the step-scaling function at individual values of the coupling, without the necessity for large interpolations of the data.

As a target precision we chose the criterion,

$$\begin{aligned} \Delta \left( \frac{1}{\bar{g}^2}\right) = \frac{\Delta \bar{g}^2}{\bar{g}^4} \approx 0.001, \end{aligned}$$

(3.30)

which is reached for most of our data except for some $L/a=10$ lattices. These lattices were however not used for the step scaling procedure as we did not generate corresponding configurations on $2L/a=20$ lattices. Except for some checks we also refrained from using lattices as small as $L/a=4$ and thus do not list the results here. However, the $L/a=10$ data and the $2L/a=8$ data are used for the continuum extrapolation of $\Omega$ and $\tilde{\Omega }$, respectively, and are therefore included in the tables.

Table 3 Simulation parameters and results on the L-lattices. The hopping parameter $\kappa$ was tuned such that the PCAC mass m(L), Eq. (3.15), vanishes

Table 4 Simulation parameters and results on the doubled lattices. The hopping parameter $\kappa$ was tuned such that the PCAC mass m(L / 2) vanishes, cf. Eq. (3.15)

Note that the choice of the reference value $\nu _0=0.3$ is rather arbitrary. In fact, the data in the table for $\bar{g}^2$, $\bar{g}^2_{\nu _0=0.3}$ and $\bar{v}$, with their statistical errors enables the reconstruction of the coupling at any value of $\nu$, using Eq. (2.39) and straightforward error propagation,

$$\begin{aligned} \frac{\Delta \bar{g}^2_\nu }{\bar{g}^4_\nu }= & {} \left\{ \frac{\nu }{\nu _0} \left( \frac{\Delta \bar{g}^2_{{\nu _0}}}{\bar{g}^4_{\nu _0}}\right) ^2 + \left( \frac{\Delta \bar{g}^2}{\bar{g}^4}\right) ^2\left( 1-\frac{\nu }{\nu _0}\right) \right. \nonumber \\&\left. + \nu ^2 \left( \Delta \bar{v}\right) ^2\left( 1-\frac{\nu _0}{\nu }\right) \right\} ^{1/2}. \end{aligned}$$

(3.31)

We have checked that this reconstruction does indeed reproduce the result of a direct data analysis at a given $\nu$-value, provided that the treatment of autocorrelations is done consistently for the couplings at all $\nu$-values and $\bar{v}$. We find that the precision for the $\nu =0$ coupling, Eq. (3.30), translates to higher values for other choices of $\nu$, for instance we find an increase of 20 percent for $\nu =0.3$ (from Tables 3, 4), and ca. 50 percent for $\nu =-0.5$ from Eq. (3.31).

All statistical errors were determined using the $\Gamma$-method [44]. For our observables, one even has to be careful that one sums up the autocorrelation function sufficiently far. Still the final autocorrelation times range from values somewhat below 2 MDU for weak coupling and small L / a, to about 8 MDU at larger coupling and $L/a=24$. Further details on the performance of our algorithms will be reported in [45].

3.5 Treatment of statistical errors

When forming the step scaling function $\Sigma (u,a/L)$ there are statistical uncertainties both for $\bar{g}^2(L)$, Table 3, and for $\bar{g}^2(2L)$, Table 4. These are propagated to the error of $\Sigma (u,a/L)$ with u the central value of the estimate of $\bar{g}^2(L)$, via

$$\begin{aligned} (\Delta \Sigma (u,a/L))^2 = (\Delta \bar{g}^2(2L))^2 + \left( \frac{\partial \Sigma (u,a/L)}{\partial u} \Delta \bar{g}^2(L)\right) ^2. \end{aligned}$$

(3.32)

To estimate the required derivative $\partial \Sigma /\partial u$ we differentiate the 3-loop truncation of the continuum function, $\sigma (u)$, Eq. (2.31), corrected for the known lattice artefacts at one- and two-loop order for $\nu \ne 0$ and $\nu =0$, respectively, cf. Sect. 3.3. For $\nu =0$ this leads to

$$\begin{aligned} \frac{\partial \Sigma }{\partial u} \approx 1 + 2(s_0+\delta _1) u + 3(s_1+\delta _2+s_0 \delta _1)u^2 + 4 s_2 u^3, \end{aligned}$$

(3.33)

and similarly for $\nu \ne 0$ with $\delta _1^\nu$ from Eq. (3.29), the unknown $\delta _2^\nu$ set to zero and with the scheme dependence of $s_2$ [via $b_2$, Eq. (2.32)], taken into account. As a cross check, we also estimated the derivative directly from the data and found the differences to be negligible.

For the study of the observables $\Omega$ and $\tilde{\Omega }$ we proceed similarly: to obtain the derivative with respect to u we first perform a rough continuum extrapolation neglecting the errors on u. The resulting polynomial fit function

$$\begin{aligned} \omega (u)\approx & {} 0.14307 - 0.004693\times u + 0.0077906 \times u^2 \nonumber \\&-0.0105266 \times u^3 + 0.0023996 \times u^4, \end{aligned}$$

(3.34)

is then differentiated to provide an estimate for $\partial \Omega /\partial u$ and $\partial \tilde{\Omega }/\partial u$, neglecting any L / a-dependence of the derivative.

3.6 Quality of tuning to the chiral limit

An important aspect of Wilson fermions is the need to tune the bare quark mass parameter (parameterized by $\kappa$) to a critical value, such that chiral symmetry is restored up to cutoff effects. For our choice of condition $m(L)=0$, with the PCAC mass of Eq. (3.15), we have performed extensive tuning runs which enable a precision such that,

$$\begin{aligned} |z| < 0.001, \quad z= am(L)\times (L/a) = m(L)L, \end{aligned}$$

(3.35)

at all stages of the calculation [45]. The corresponding values for $\kappa$ are given in Table 3. What is the tolerance of a slight mistuning of the mass? Using 1-loop perturbative results from Ref. [26] for the mass dependence of $\bar{g}^2$ and $\bar{v}$ we obtain, in the continuum limit,

$$\begin{aligned} \left. \frac{\partial \bar{g}_\nu ^2}{\partial z}\right| _{z=0}= & {} N_\mathrm{f}\times \left[ 0.0095683(1) -0.01418(5)\times \nu \right] \bar{g}^4_\nu \, \nonumber \\&+\, \mathrm{O}(\bar{g}^6_\nu ). \end{aligned}$$

(3.36)

This should be compared with the target statistical precision, which is, for $\nu =0$, given in Eq. (3.30). We follow Ref. [19] and allow for an uncertainty of about 1 / 3 of the statistical error. Neglecting small cutoff effects in the mass derivative and for $N_\mathrm{f}=3$ this yields the bounds,

$$\begin{aligned} |z| < \frac{(1/3)\times \Delta \bar{g}^2_\nu }{\left( \partial \bar{g}^2_\nu /\partial z\right) _{z=0}} \approx {\left\{ \begin{array}{ll} 0.010, &{}\quad \nu =-0.5,\\ 0.012, &{}\quad \nu =0,\\ 0.025, &{}\quad \nu =0.3, \end{array}\right. } \end{aligned}$$

(3.37)

for the $\nu$-values that we chose for more detailed analysis in Sect. 4. We note that the achieved precision of the mass tuning, Eq. (3.35), stays well within these bounds, by at least a factor 10. Even if these perturbative estimates turned out to be significantly off the mark, e.g. by a factor 2, the systematic error associated with imperfect quark mass tuning would still be negligibly small and can thus be safely ignored.

3.7 Lattice artefacts linear in a / L

Despite the use of a non-perturbatively O(a) improved bulk action the very presence of the time boundaries in the Schrödinger functional creates lattice artefacts linear in a. In principle these could be cancelled by an appropriate non-perturbative tuning of the improvement coefficients $c_\mathrm{t}$ and $\tilde{c}_\mathrm{t}$, Eqs. (3.1, 3.7). In practice, however, we are currently limited to the use of perturbative estimates, Eqs. (3.8, 3.9). Hence some remnant linear a-effects in our data cannot be excluded. Instead of including a corresponding term in the fit ansatz for the continuum extrapolations we try to estimate the size of these uncertainties and include them as an additional systematic error. Using a combination of simulations and perturbation theory we have produced a model for the sensitivity of our data to a variation of $c_\mathrm{t}$ and $\tilde{c}_\mathrm{t}$. The details are deferred to Appendix A, where we obtain linearized shifts of the data, for instance,

$$\begin{aligned} \Sigma (u,a/L)\vert _{c_\mathrm{t}' = c_\mathrm{t}+\Delta c_\mathrm{t}} = \Sigma (u,a/L)\vert _{c_\mathrm{t}} + \Delta c_\mathrm{t}\times \delta _{c_\mathrm{t}}\Sigma (u,a/L), \end{aligned}$$

(3.38)

and analogously for a shift $\tilde{c}_\mathrm{t}'=\tilde{c}_\mathrm{t}+\Delta \tilde{c}_\mathrm{t}$. Hence, the model yields an estimate of the data that would have been obtained if the simulations had been performed at slightly different values $c_\mathrm{t}'$ and $\tilde{c}_\mathrm{t}'$. To complete the model we thus need an educated guess for $\Delta c_\mathrm{t}(g_0)$ and $\Delta \tilde{c}_\mathrm{t}(g_0)$ such that the difference between a fully non-perturbative definition of $c_\mathrm{t}$ and $\tilde{c}_\mathrm{t}$ and the perturbative estimates (3.8, 3.9) is likely to be covered. We here choose

$$\begin{aligned} \Delta c_\mathrm{t}(g_0) = c_\mathrm{t}^\mathrm{eff} g_0^6,\quad \Delta \tilde{c}_\mathrm{t}(g_0) = \tilde{c}_\mathrm{t}^\mathrm{eff} g_0^4, \end{aligned}$$

(3.39)

i.e. a term of the neglected order with an effective coefficient. In the case of $c_\mathrm{t}$ which is known to 2-loop order, cf. Sect. 3.1, we use a geometric progression and define

$$\begin{aligned} c_\mathrm{t}^\mathrm{eff} = \left( c_\mathrm{t}^{(2)}/c_\mathrm{t}^{(1)}\right) \times c_\mathrm{t}^{(2)} = 0.74104 \times c_\mathrm{t}^{(2)} = -0.01734. \end{aligned}$$

(3.40)

For $\tilde{c}_\mathrm{t}$ we simply use

$$\begin{aligned} \tilde{c}_\mathrm{t}^\mathrm{eff} = \tilde{c}_\mathrm{t}^{(1)} = -0.01795 . \end{aligned}$$

(3.41)

We note that particularly the choice for $\Delta c_\mathrm{t}$ is likely an overestimate, due to the accidental cancellation of the gluonic and fermionic terms observed in Sect. 3.1.

There are several options for the inclusion of this systematic error. We chose to proceed as follows: we first perform continuum extrapolations ignoring potential O(a) errors in both the original and the shifted data. We then take the spread of a given observable as an additional systematic error and add it in quadrature. Obviously this assumes that this systematic error is subdominant. We have therefore dismissed all continuum extrapolations where this turned out not to be the case. We will discuss the impact of these variations on the continuum extrapolations in the next section.

4 Continuum results

4.1 Continuum extrapolation of the step-scaling function

We now proceed with the continuum extrapolation of the data for the step-scaling function, for our default scheme with $\nu =0$. The 19 available data points for lattice resolutions $L/a=6,8,12$ are shown in Fig. 2. Simulation parameters have been chosen such as to have approximately matched u-values between different L / a, and this is seen in the vertical line-up of the data. The fact that the data are so close together at given u-value illustrates that cutoff effects in the SF scheme with the chosen lattice regularization are generally small, even without perturbative improvement.

Fig. 2

The step-scaling function for the $\nu =0$ SF-coupling. The band shows our result (fit C, cf. Table 5). The data points are the approximations at finite $L/a=6,8,12$ taken from Table 4 with errors from Eq. (3.32)

While our data enables a more traditional continuum extrapolation, u-value by u-value, we have done this only as a cross-check. Our preferred strategy is to simultaneously fit all data to a global ansatz of the form

$$\begin{aligned} \Sigma ^{(i)}(u,a/L)= & {} \sigma (u) + \rho ^{(i)}(u) \, (a/L)^2. \end{aligned}$$

(4.1)

Here $i=1,2$ denotes the order of perturbative improvement of $\Sigma$ and $i=0$ refers to unimproved data. In general, such global fits have the advantage that an interpolation of the data to common u-values is not required. More importantly, however, the expected smooth u-dependence of the step-scaling function both on the lattice and in the continuum limit, is automatically built into this ansatz. As anticipated in the last section, we assume leading cutoff effects to start at O($a^2$), with the linear a-effects being treated as systematic errors. Our fit ansätze for the cutoff effects thus are of the form,

$$\begin{aligned} \rho ^{(i)}(u)= & {} \sum _{k=1}^{n_\rho } \rho ^{(i)}_k u^{i+1+k}, \end{aligned}$$

(4.2)

and the assumption of no lattice artefacts, $\rho ^{(i)} = 0$, is referred to by $n_\rho =0$. For the continuum step scaling function we consider polynomial fits with $n_c=2$ parameters,

$$\begin{aligned} \sigma (u) = u + s_0 u^2 + s_1 u^3 + c_1 u^4 + c_2 u^5, \end{aligned}$$

(4.3)

or 1-parameter fits ($n_c=1$),

$$\begin{aligned} \sigma (u) = u + s_0 u^2 + s_1 u^3 + s_2 u^4 + c_1 u^5, \end{aligned}$$

(4.4)

where $s_{0,1,2}$ are fixed to their perturbative values Eq. (2.32). As the lattice artefacts are generally small at most $n_\rho =2$ parameters are required to obtain excellent fits to the data. A selection of our fits is given in Table 5. As an example we consider a 4-parameter fit (fit D) with $n_c=n_\rho =2$ to the 2-loop improved data at $\nu =0$,

$$\begin{aligned} \Sigma ^{(2)}(u,a/L)= & {} u + s_0 u^2 + s_1 u^3 + c_1 u^4 + c_2 u^5 \nonumber \\&+ (\rho _1 u^4 + \rho _2 u^5) (a/L)^2. \end{aligned}$$

(4.5)

Including all lattices with $L/a\ge 6$ there are thus 19 available data points and 4 fit parameters in the 5th order polynomial in u. The fit has an excellent $\chi ^2/\mathrm{d.o.f} = 14.5/15$ with the continuum parameters and their covariance given by

$$\begin{aligned}&c_1 = 0.0014(3),\quad c_2 = 0.0005(2) ,\nonumber \\&\mathrm{Cov}(c_1,c_2) = -0.38\times 10^{-5}. \end{aligned}$$

(4.6)

Note that the fit coefficient $c_1$ is not far from the perturbative value $s_2=0.001151$; it is therefore reasonable to fix this parameter to the perturbative one and only fit a next order coefficient. Hence the majority of fits in Table 5 only have $n_c=1$ continuum parameters, either $c_1$ in Eq. (4.4), or a 4-loop coefficient in the $\beta$-function, $b_3^\text {fit}$ (cf. Sect. 4.3 below).

Given the smallness of the cutoff effects, even fit G with $n_\rho =0$ parameters seems reasonable, if one restricts to data with $L/a\ge 8$. For the 2 continuum fit parameters of fit G the results are,

$$\begin{aligned}&c_1 = 0.0006(12),\quad c_2 = 0.0011(7),\nonumber \\&\mathrm{Cov}(c_1,c_2)= -0.86\times 10^{-6}. \end{aligned}$$

(4.7)

While the $\chi ^2/\mathrm{d.o.f} = 13/9 =1.44$ does not look too good, a comparison with fits B$'$ and F (with $n_\rho =1$) indicates that this may be an accident. In fact the $\chi ^2$-values are not a sharp criterion in our case, as these strictly refer only to the statistical errors of the data and the given fit functions used, and thus do not account for the systematic uncertainties from cutoff effects linear in a.

In order to quantify these systematic uncertainties we repeat the fits with the data shifted by varying either $c_\mathrm{t}$ or $\tilde{c}_\mathrm{t}$, as explained in Sect. 3.7. For fits with a single continuum parameter, $n_c=1$, we then take the spread in central values for this parameter as a systematic uncertainties due to either $c_\mathrm{t}$ or $\tilde{c}_\mathrm{t}$ variations and combine them in quadrature with the statistical error to obtain a total error of the fit parameter. Thus, in Table 5, the fits with $n_c=1$ show 2 errors, the first being the statistical and the second the total error. In all fits we find that the $c_\mathrm{t}$-uncertainty dominates the effect of the $\tilde{c}_\mathrm{t}$-uncertainty; for instance, for fit B we obtain

$$\begin{aligned} c_1= & {} [49(25)_{\text {stat.}}(15)_{\Delta c_\mathrm{t}}(6)_{\Delta \tilde{c}_\mathrm{t}}]\times 10^{-5} \nonumber \\= & {} 5(3)_\text {stat.}(3)_\text {total}\times 10^{-4}, \end{aligned}$$

(4.8)

where the r.h.s. takes the form given in Table 5. For fits with $n_c=2$ continuum parameters we proceed in the same way. However, rather than quoting a total error on the continuum fit parameters, we propagate these uncertainties to the observables in Table 6, where the results from the $n_c=2$ fits D and G are given with both a statistical and total error.

Table 5 Overview of the continuum fit functions and results. The naming convention is the same as in Ref. [1]. The two errors in the fit parameters are the statistical and the total error respectively, where the total error includes the systematic uncertainty from a variation of $c_\mathrm{t}$ and $\tilde{c}_\mathrm{t}$, added in quadrature

While the total errors for most fits are dominated by the statistical error, this is not the case of fit G, where the total errors are predominantly systematic, cf. Table 6. This indicates that fits with $n_\rho =0$ are too rigid to account for the O(a) variation of the data. While $n_\rho =1$ fits B$'$ and F are acceptable, we settled for fit ansätze with $n_\rho =2$ and $n_c=1$ to data with $L/a\ge 6$ as our preferred choice (fits A, B, C, E, H). Then, using the 2-loop improved data leaves us with fits C and E, which are essentially equivalent, and Fig. 2 shows $\sigma (u)$ from fit C with its error band.

4.2 The SF coupling for $\nu =0$ at scales $L_n=L_0/2^n$

We now use the continuum fit functions for the step-scaling function at $\nu =0$ to evaluate the coupling at different scales $L_n = L_0/2^n$, separated by factors of 2. Our starting point is the reference scale $L_0$, defined implicitly by

$$\begin{aligned} \bar{g}^2(L_0) = 2.012. \end{aligned}$$

(4.9)

The value 2.012 corresponds to the largest value of the coupling u for which the step-scaling function is known. In physical units the scale $L_0$ has been determined to be around $1/(4\,\mathrm{GeV})$ [12]. We note that $\sigma (2.012)$ defines the coupling $\bar{g}^2(2L_0)$, so that the lowest energy scale reached with the SF coupling is around 2 GeV.

Recursive application of the continuum step scaling function, $\sigma (u)$, allows us to obtain, in the continuum limit, the couplings at $L_n= L_0/2^n$, where $n=-1,0,1,2,\ldots$, via⁶

$$\begin{aligned} u_n = \sigma (u_{n+1}), \quad u_n = \bar{g}^2(L_n). \end{aligned}$$

(4.10)

This defines the couplings $u_n$ as a set of observables, with our data enabling the recursion up to $n=5$, thereby covering a total scale factor of $L_{-1}/L_5 = 2^6=64$. The results for $u_n$ are collected in Table 6, for the various fit functions representing $\sigma (u)$.

Table 6 Results for the couplings $u_n=\bar{g}^2_\nu (L_n)$, the $\Lambda$-parameter evaluated at $u_n$, cf. Eq. (4.15), in units of the reference scale, $L_0$ (4.9), and the effective $\beta$-function coefficient, $b_3^\mathrm{eff}$ (4.14), for most fits of Table 5. Results for $L_0\Lambda$ obtained with fits E, F and H are given in Table 7

4.3 Effective and fitted $\beta$-function

Given $\sigma (u)$ in terms of 1 or 2 continuum parameters $c_k$, one may translate this result into an effective 3-loop coefficient of the continuum $\beta$-function. For convenience we define $b(g^2) = -g\beta (g)$ so that

$$\begin{aligned} b(u)= & {} b_\mathrm{3loop}(u) + b_3^\mathrm{eff} u^5, \nonumber \\ b_\mathrm{3loop}(u)= & {} b_0 u^2 + b_1 u^3+ b_2 u^4. \end{aligned}$$

(4.11)

Then Eq. (2.30) becomes,

$$\begin{aligned} \int _{u}^{\sigma (u)} \frac{{\mathrm{d}} v}{b(v)} = 2\ln 2. \end{aligned}$$

(4.12)

Differentiation w.r.t. u yields

$$\begin{aligned} \frac{\sigma '(u)}{b(\sigma (u))} -\frac{1}{b(u)} =0, \end{aligned}$$

(4.13)

which can be solved for $b_3^\mathrm{eff}$, with the result,

$$\begin{aligned} b_3^\mathrm{eff} = \frac{b_\mathrm{3loop}(u)\sigma '(u)-b_\mathrm{3loop}(\sigma (u))}{ \sigma ^5(u)-u^5\sigma '(u)}. \end{aligned}$$

(4.14)

Note that $b_3^\mathrm{eff}$ will depend on the value u where it is measured. Extracting this coefficient at different values of u should yield consistent results in the perturbative regime, and this is indeed the case for the $\nu =0$ data, cf. Table 6.

This motivates a different parameterization of our fits with a single continuum parameter, namely via a 4-loop coefficient $b^\mathrm{fit}_3$ in the $\beta$-function as a fit parameter.⁷ This is the purpose of fits E, F and H, cf. Table 5, where we have taken $\sigma (u)$ to be defined by Eq. (4.12) with $b(u) = b_\mathrm{3loop}(u) + b_3^\mathrm{fit} u^5$ and inserted $\sigma (u)$ into Eq. (4.1). The resulting values for the fit parameter $b_3^\mathrm{fit}$ are given in Table 5. This representation of our continuum results is very practical. While the fit function in Eq. (4.4) allows us to find the couplings at scales which are separated by a factor 2, the $\beta$-function readily yields the scale ratio separating two given couplings.

4.4 Determination of the $\Lambda$-parameter

Once the coupling $u_n = \bar{g}^2(L_n)$ is small enough, it is justified to use three-loop perturbation theory for the $\beta$-function in the expression

$$\begin{aligned} L_0 \Lambda= & {} 2^{n} \left( b_0 \bar{g}^2(L_n) \right) ^{-b_1/(2b_0^2)} e^{-1/(2b_0 \bar{g}^2(L_n))} \nonumber \\&\times \exp \left\{ -\int \limits _0^{\bar{g}(L_n)}\mathrm{d}x\ \left[ \frac{1}{\beta (x)} +\frac{1}{b_0x^3} - \frac{b_1}{b_0^2x} \right] \right\} ,\nonumber \\ \end{aligned}$$

(4.15)

and determine the $\Lambda$-parameter in units of $L_n$ and thus in units of $L_0 = 2^n L_n$. Note that the expansion of the integral in the exponent

$$\begin{aligned} \int \limits _0^{\bar{g}}\mathrm{d}x\ \left[ \frac{1}{\beta (x)} +\frac{1}{b_0x^3} - \frac{b_1}{b_0^2x} \right]= & {} \frac{b_0b_2-b_1^2}{2b_0^3} \bar{g}^2 \nonumber \\&+\, \frac{b_0^2 b_3-2 b_0b_1b_2+b_1^3}{4b_0^4} \bar{g}^4\nonumber \\&+\, \mathrm{O}(\bar{g}^6), \end{aligned}$$

(4.16)

is unknown at order $\bar{g}^4$ as this term requires the knowledge of the 4-loop coefficient $b_3$ which is not available in the SF scheme. Provided such higher order terms are small, the result for $L_0\Lambda$ should be independent of n and the way the integral is evaluated. For completeness we note that our default evaluation consists in the direct numerical integration, using the truncated 3-loop $\beta$-function without expansion of the integrand or the exponential function. The results for $\Lambda$ in units of $L_0$ are given in Table 6, where Eq. (4.15) is evaluated for the coupling at scales $L_n$, for $n=0,\ldots ,5$ and for the various fit functions.

An alternative evaluation of the $\Lambda$-parameter is obtained with the fits E, F and H in terms of a fitted $\beta$-function. One simply inserts the $\beta$-function into Eq. (4.15) and evaluates the integral numerically between $\bar{g}^2(L_0)=2.012$ and $\bar{g}^2(0)=0$. The resulting $\Lambda$-parameters are given in Table 7 and show a remarkable consistency. We will discuss the results further in Sect. 4.6.

Table 7 $L_0\Lambda$ obtained with the fits to the coefficient $b_3^\mathrm {fit}$ in the $\beta$-function, cf. Table 5 and Sect. 4.4

4.5 Continuum extrapolation of $\Omega$ and $\tilde{\Omega }$

The continuum extrapolation for $\Omega (u,a/L)$ and $\tilde{\Omega }(u,a/L)$ proceeds along the same line as for the step-scaling function. A difference is that both data sets can be constrained to the same continuum limit but require separate fit coefficients for the cutoff effects. Moreover, the lattice resolutions L / a cover the range 6–24, i.e. a factor of 4 in scale and thus allow for an excellent control of the continuum limit.

Table 8 Results of the combined fits A and B for $\Omega ^{(i)}(u,a/L)$ and $\tilde{\Omega }^{(i)}(u,a/L)$ with ($i=1$) and without ($i=0$) improvement. The 2 errors given are the statistical and the total error, respectively, where the latter includes an estimate of the remnant uncertainty due to linear a-effects

The global fit ansätze used here are

$$\begin{aligned} \Omega ^{(i)}(u,a/L) = \omega (u) + \rho ^{(i)}(u,a/L), \end{aligned}$$

(4.17)

and analogously for $\tilde{\Omega }^{(i)}$ with $\tilde{\rho }^{(i)}$. Here, $i=1,0$ refers to 1-loop improved data (cf. Sect. 3.3) or unimproved data, respectively. In the models for the cutoff effects we just include 2 quadratic terms in a / L for either data set, with coefficients $\rho _{1,2}$ and $\tilde{\rho }_{1,2}$, e.g.

$$\begin{aligned} \rho ^{(i)}(u,a/L) = \left( \rho _1 u^i + \rho _2 u^{i+1}\right) \frac{a^2}{L^2}, \end{aligned}$$

(4.18)

and the powers of u are chosen according to the expectation from perturbation theory. As in the case of the step-scaling function, linear terms in a / L will be treated as systematic errors.

The continuum function $\omega (u)$ is parameterized by a fourth order polynomial in u,

$$\begin{aligned} \omega (u) = {\left\{ \begin{array}{ll} v_1+ v_2 u + \sum _{k=1}^3 d_k u^{k+1}, &{}\quad \text {fits type A}, \\ v_1+ \sum _{k=1}^4 d_k u^{k}, &{}\quad \text {fits type B}, \end{array}\right. } \end{aligned}$$

(4.19)

with fit parameters $d_k$, $k=1,\ldots ,4$ and $v_1$ and $v_2$ set to the known perturbative coefficients, Eq. (2.38). We have also experimented with separate fits to $\Omega ^{(i)}$ and $\tilde{\Omega }^{(i)}$ and find good overall consistency. Here, we restrict the discussion to combined fits of the $\Omega ^{(i)}$ and $\tilde{\Omega }^{(i)}$ data, with a common continuum fit function, $\omega (u)$. We distinguish fits of type A and B with 3 and 4 continuum fit parameters, respectively. Hence, fits of type A have $3+2\times 2 =7$ parameters, while type B fits have 8 parameters.

With these fit ansätze one obtains decent $\chi ^2/\mathrm{d.o.f.}$ values for the one-loop improved data, even when including all 52 data points with $L/a\ge 6$ (cf. Tables 3, 4). Given this much data we may afford to exclude the $L/a=6$ lattices, thereby reducing the number of data points to 44 . An example for the continuum function $\omega (u)$ thus obtained is

$$\begin{aligned} \omega (u)\vert _{\text {fit A}, i=1, L/a\ge 8}= & {} 0.14307 - 0.004693 u + 0.01284 u^2 \nonumber \\&-0.01480 u^3 + 0.003349 u^4. \end{aligned}$$

(4.20)

The fit has a $\chi ^2/\mathrm{d.o.f.} = 33.5/37$ and the covariance matrix for the fit parameters is given by

$$\begin{aligned} \mathrm{Cov}(d_i,d_j) = \begin{pmatrix} 1.286 &{} -1.244 &{} 0.2922\\ -1.244 &{} 1.231 &{} -0.2945\\ 0.2922 &{} -0.2945 &{} 7.153 \end{pmatrix}\times 10^{-5}. \end{aligned}$$

(4.21)

Note that the error encoded in the covariance matrix is only the statistical error. To account for the systematic effect estimated from the variation of the O(a) counterterm coefficients $c_\mathrm{t}$ and $\tilde{c}_\mathrm{t}$ (cf. Sect. 3.7), we here proceed in complete analogy with the analysis of the step-scaling function. In Table 8 we quote 2 errors, the first statistical, the second including the effect of a $c_\mathrm{t}$ and $\tilde{c}_\mathrm{t}$-variation. This only marginally increases the errors, as is evident from Table 8.

Fig. 3

The bands show the continuum fit functions for fits of type A and B to one-loop improved data for $L/a\ge 8$ and the data points are one-loop improved data with the cutoff effects subtracted using the models $\rho ^{(1)}(u,a/L)$ and $\tilde{\rho }^{(1)}(u,a/L)$ from the type A fit

The fits to the unimproved data have higher $\chi ^2/\mathrm{d.o.f.}$ values, emphasized in bold face in Table 8, unless the $L/a=6$ data are dropped. As mentioned above, $\chi ^2$ is not the full story, given that our fits assume the absence of a / L effects and this effect is taken into account afterwards by our $c_\mathrm{t},\tilde{c}_\mathrm{t}$-variation. However, we do see that (1) these variations have a tiny effect on the continuum values and (2) still, for example, $\omega (1.11)$ of the large $\chi ^2$ fits is off significantly. These fits have to be discarded. The other ones, which cover a remarkable range of lattice spacings, are entirely consistent.

These observations allow us to conclude that perturbative improvement works very well in our coupling range, our treatment of $c_\mathrm{t},\tilde{c}_\mathrm{t}$-variations is safe (maybe overly conservative), and most importantly, resolutions $a/L \le 1/6$ are sufficient to apply our continuum extrapolations which assume that $\mathrm{O}((a/L)^3)$ effects have a negligible effect. All this makes us very confident also in the continuum extrapolations of $\Sigma$, where the very small lattice spacings are not available, but where we have 2-loop perturbative improvement at our disposal.

We return to the specific discussion of $\omega$. As our best value at the reference coupling $u=2.012 = \bar{g}^2(L_0)$ we choose the result of fit A to 1-loop improved data with $L/a \ge 8$.

$$\begin{aligned} \omega (2.012) = 0.1199(10), \end{aligned}$$

(4.22)

which is required to define the starting point for the step-scaling procedure for $\hbox {SF}_\nu$ schemes with non-zero values of $\nu$ (s. below). Another interesting value is $\omega (u)$ at the largest available coupling, $u = 2.45$, which correspond to $\alpha =0.195$,

$$\begin{aligned} \omega (2.45) = 0.1117(13), \end{aligned}$$

(4.23)

using the same fit function. As discussed further in  [1], and as is evident from the large difference between 2-loop PT and the non-perturbative result in Fig. 3, an unnaturally large next order perturbative coefficient would be required to perturbatively describe the function $\omega (u)$ at such values of the coupling.

Finally, we comment on the different behaviour of the fits A and B, which is seen in Fig. 3 for small couplings, outside the range of the data. This illustrates the danger of using fit functions outside their range of validity. While fit A is constrained to produce the 2-loop perturbative result for $\omega (u)$, Eq. (2.37), fit B leaves the 2-loop coefficient $v_2$ as a fit parameter, $d_1$ (4.19). The result,

$$\begin{aligned} (4\pi )^2 d_1 = -0.9(2.9), \end{aligned}$$

(4.24)

should be compared with Eq. (2.38). While the central value is not too far off, the large error illustrates the difficulty to estimate such asymptotic coefficients, even if precise data is available over a wide range of couplings.

4.6 The step-scaling function for $\nu \ne 0$ and tests of perturbation theory

The step-scaling functions for $\nu \ne 0$ can be treated in the same way as for $\nu =0$. The fit ansätze we have considered for $\Sigma _\nu (u,a/L)$ and $\Sigma _\nu ^{(1)}(u,a/L)$ are analagous to the $\nu =0$ case, cf. Table 5. Choosing the values $\nu =-0.5,0.3$ for illustration and fits of type A, B, B$'$ we quote again the couplings at $L_n$, as well as the results for $L_0\Lambda$, cf. Table 6. Here, the $\Lambda$-parameter is again the one of the $\nu =0$ scheme, i.e. we use the known ratio of $\Lambda$-parameters (2.50) and evaluate, at $u_n= \bar{g}^2_\nu (L_n)$, the expression

$$\begin{aligned} L_0 \Lambda= & {} 2^{n} \frac{\Lambda }{\Lambda _\nu } \varphi _\nu \left( \bar{g}^2_\nu (L_n)\right) ,\quad n=0,\ldots ,5. \end{aligned}$$

(4.25)

The step-scaling procedure for $\nu \ne 0$ requires $\bar{g}^2_\nu (L_0)$ as starting point, which is given by

$$\begin{aligned} \frac{1}{\bar{g}_\nu ^2(L_0)} = \frac{1}{\bar{g}^2(L_0)} - \nu \omega \left( \bar{g}^2(L_0)\right) = \frac{1}{2.012} - \nu \times 0.1199(10) . \end{aligned}$$

(4.26)

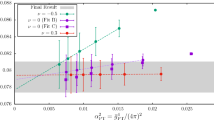
Note that this start value now has a small uncertainty, due to the fact that $L_0$ is still defined by Eq. (4.9) and the connection requires the result for $\omega (2.012)$ from Eq. (4.22). For our choices of $\nu$-values this uncertainty is a factor 2–3 below the statistical uncertainty, and will be neglected in the following. The propagation of errors to the couplings at scales $L_0/2^n$ and to $L_0\Lambda$ then proceeds in the same way as for $\nu =0$. Results are given in Table 6, and in Fig. 4. We observe a roughly linear behaviour in $\alpha ^2$, which suggests to directly fit to an effective 4-loop coefficient $b_3^\mathrm{fit}$ in the $\beta$-function. This is done in fits E, F and H, cf. Table 5. Not surprisingly, the resulting fit coefficients roughly agree with the effective 4-loop coefficients, Eq. (4.14), given in Table 6. We also note that schemes at different $\nu$-values behave quite differently; the 2 chosen non-zero values of $\nu$ illustrate this: while $\nu =0.3$ data shows no significant remnant $\alpha$-dependence even up to $\alpha \approx 0.2$, the slope in $\alpha ^2$ is very pronounced for $\nu =-0.5$. Therefore, it is a strong consistency check for our analysis that all values for $L_0\Lambda$ are compatible around $\alpha =0.1$, despite considerable deviations at larger couplings. This means we can confidently extract $L_0\Lambda$ in this regime. Our final value is obtained from fit C, taking the $n=4$ estimate at $\nu =0$, viz

$$\begin{aligned} L_0\Lambda = 0.0303(7) \quad \Rightarrow L_0\Lambda _{\overline{\mathrm{MS}}}^{N_\mathrm{f}=3} = 0.0791(19), \end{aligned}$$

(4.27)

which is slightly more precise than the result quoted in [1], due to a refined model for the O(a) boundary effects, cf. Sect. 3.7. For an even more conservative error estimate one could take fit D, again at $n=4$ and $\nu =0$, which yields $L_0\Lambda =0.0303(11)$.

Fig. 4

Determination of the $\Lambda$-parameter in units of $L_0$ at different values of $\alpha$. We compare the extraction in different schemes ($\nu =-0.5,0,0.3$), and show a comparison with our final result Eq. (4.27). As the reader can see when the extraction is performed at high enough energies ($\alpha \sim 0.1$), all schemes nicely agree. See the text for a full discussion

Using the fits E, F and H, in terms of the fitted $\beta$-function, the values in Table 7 are obtained. The fact that these are all compatible, with very similar central values further boosts the confidence that our final result is very robust. Finally, coming back to the question raised in Sect. 2 about exponentially suppressed contributions, we emphasize that the consistency of our analysis with fits taking the same functional form as higher order perturbative terms provides indirect evidence for the absence of such non-standard terms within our numerical precision.

4.7 Alternative tests

So far, our strategy has been to first determine $\Lambda$ in the SF scheme and then convert it to $\Lambda _{{\overline{\mathrm{MS}}}}$. However, one might also match the SF to the ${\overline{\mathrm{MS}}}$-coupling at 2-loop order using Eq. (2.41) and then extract the $\Lambda$-parameter within the ${\overline{\mathrm{MS}}}$-scheme. While the perturbative precision is parametrically the same as before, we present this alternative view here, as it is closer to the strategy often used in phenomenological applications.

Within the ${\overline{\mathrm{MS}}}$-scheme we have, with $\mu =s/L$, and $L_n=L_0/2^n$,

$$\begin{aligned}&\Lambda _{{\overline{\mathrm{MS}}}}L_0 = s \frac{L_0}{L_n} \varphi _{{\overline{\mathrm{MS}}}}\left( \bar{g}_{{\overline{\mathrm{MS}}}}(L_n/s)\right) \nonumber \\&= s\, 2^n \varphi _{{\overline{\mathrm{MS}}}}\left( \sqrt{\bar{g}^2_\nu (L_n){+}p^\nu _1(s) \bar{g}^4_\nu (L_n){+}p^\nu _2(s)\bar{g}^6_\nu (L_n) {+} \mathrm{O}\left[ \bar{g}_\nu ^8(L_n)\right] }\right) , \end{aligned}$$

(4.28)

where s is an additional scale parameter and $p_i^{\nu }(s) = c_i^\nu (s)/(4\pi )^i$, cf. Eq. (2.41). The unknown 3-loop and higher order terms in the argument of $\varphi _{{\overline{\mathrm{MS}}}}$ will be neglected in the following. The function $\varphi _{{\overline{\mathrm{MS}}}}$, Eq. (2.47) can be evaluated using up to 5-loop order for the $\beta$-function. For our range of $\alpha$-values, the numerical difference between 4- or 5-loop order evaluation is found to be negligible. The dominant uncertainty is due to the 2-loop truncation of the perturbative conversion to the ${\overline{\mathrm{MS}}}$ coupling,

$$\begin{aligned} \Delta g^2_{\overline{\mathrm{MS}}}= \mathrm{O}\left[ \bar{g}_\nu ^8(L_n)\right] = \mathrm{O}\left[ \bar{g}_{\overline{\mathrm{MS}}}^8(L_n/s)\right] , \end{aligned}$$

(4.29)

which multiplies the sensitivity to a change in the coupling,

$$\begin{aligned} \dfrac{d}{d g^2} \varphi _{{\overline{\mathrm{MS}}}}\left( g\right) \propto \frac{1}{g\beta _{\overline{\mathrm{MS}}}(g)} = \text {O}(g^{-4}), \end{aligned}$$

(4.30)

and thus induces an O($g^4$) or O($\alpha ^2$) uncertainty in the estimate of the $\Lambda$-parameter. As mentioned before, this is parametrically the same as previously, cf. Eq. (4.16).

Fig. 5

Determination of $L_0\Lambda _{\overline{\mathrm{MS}}}$ at different physical scales (parametrized by the value of $\alpha$ in the x-axes), and using different renormalization scales (value of s) to match with the ${\overline{\mathrm{MS}}}$ scheme. The left (right) panel uses the $\hbox {SF}_\nu$-scheme with $\nu =0$ ($\nu =-0.5$), cf. text

Fig. 6

Coefficients $c^\nu _1(s)$ and $c^\nu _2(s)$ for two different $\hbox {SF}_\nu$ schemes. Left $\nu =0$, right $\nu =-0.5$. The values $s^\star$ defined by the condition $c_1(s^\star )=0$ are approximately $s^\star \approx 3$ (left) and $s^\star \approx 5$ (right)

We now use the non-perturbative results for the $\hbox {SF}_\nu$-couplings from Table 6 as input in Eq. (4.28) and study the dependence of the $\Lambda$-parameter estimates on the choice of scale $L_n$, the scale factor s and the parameter $\nu$. Figure 5 shows some typical results; at fixed $\nu$ and s we observe again an approximate linearity in $\alpha ^2$, with the asymptotic values being compatible with our best estimate, Eq. (4.27). However, we note that the slope varies significantly as a function of s and $\nu$.

We find that the choice of $s=s^\star$, Eq. (2.44), which eliminates the one-loop term in the matching, Eq. (2.45), is often (but not always) a good one. For the cases $\nu =0$ and $\nu =-0.5$, Fig. 6 shows the 1- and 2-loop matching coefficients to the ${\overline{\mathrm{MS}}}$-coupling, Eq. (2.41), as functions of the scale factor s. The values for $s^\star$ are roughly around 3, 5 and 2 for $\nu =0$, $-0.5$ and 0.3, respectively. While for $\nu =0$ (similarly for $\nu =0.3$) the two-loop coefficient is near minimal around $s^\star$ and stays positive (Fig. 6, left panel), a more complicated pattern is seen for $\nu =-0.5$ (Fig. 6, right panel).

A common method to assign a systematic error to a perturbative uncertainty consists in a renormalization scale variation by a factor 2 in both directions, around some “optimal scale” (cf. the review of QCD in [2]). Taking the values $s^\star$ as our optimal values for the scale factor we can now assess how this method fares in our context. In Fig. 7 this systematic error is shown, together with the total errors, for the estimates of the $\Lambda$-parameter. As one might expect, this systematic error dominates the error at low energies, reduces proportional to $\alpha ^2$ and becomes negligible at higher energies. This is indeed the case for $\nu =0$ and $\nu =0.3$, where the systematic errors are seen to bracket the shaded area representing our reference result (4.27). However, this is not the case for $\nu =-0.5$, where a significant underestimation of the systematic error is observed, cf. Fig. 7.

Fig. 7

Statistical (interior error band) and total (exterior error band) uncertainties in the determination of $L_0\Lambda _{\overline{\mathrm{MS}}}$. The total uncertainty is computed by adding in quadratures the statistical and systematic uncertainties. The latter are computed varying the renormalization scale by a factor 2 above and below the value $s^\star$. See text for more details

However, in all cases we note that for $\alpha \sim 0.1$, the systematic uncertainty of the matching with perturbation theory, obtained by varying s is well below the statistical uncertainties. Moreover the latter are in line with the errors obtained with our previous strategy. This further reinforces our previous conclusions: thanks to the high energies reached with the step scaling method, our uncertainties are fully dominated by statistical errors, systematic uncertainties being negligible. The spread of results obtained by the variation of the perturbative matching scale provides a way to assess the systematic uncertainties which works well with the SF schemes at $\nu =0,0.3$, even at $\alpha \approx 0.2$ (although the systematic uncertainty there is large). But the failure of this method for the SF scheme with $\nu =-0.5$ indicates that this method may not always be reliable, particularly if the coupling is not small and cannot be varied. This illustrates that perturbative truncation errors are very difficult to estimate within perturbation theory, and that reaching high energies is crucial for a robust determination of the strong coupling. Indeed we see that for values $\alpha \approx 0.1$ there is nice agreement between all schemes and reasonable choices of the scale factor s within errors, which clearly allow us to meet the target accuracy of 3 per cent for the $\Lambda$-parameter.

5 Conclusions and outlook

Using numerical simulations and finite volume step-scaling techniques, we have studied a family of SF couplings, parameterized by $\nu$, over a range of scales corresponding to energies of 4–128 GeV, thus differing by a scale factor 32. This, together with an unprecedented control of statistical and systematic errors represents a luxury which we have exploited to test the accuracy of perturbation theory. Choosing the $\Lambda$-parameter for $\nu =0$ in units of $L_0 \approx 1/(4\,\text {GeV})$ as a reference, its evaluation requires the knowledge of a coupling and its $\beta$-function between a finite and the infinite energy scale, where the coupling vanishes by asymptotic freedom. Perturbation theory to 3-loop order is available for the asymptotic scale dependence beyond an energy scale 1 / L, which can be chosen anywhere in the range covered by our non-perturbative data, provided the ratio $L/L_0$ is known. By looking at the spread of values for $L_0\Lambda$ one therefore tests the accuracy of perturbation theory at the scale 1 / L. Moreover, the exact relation between $\Lambda$-parameters of different schemes requires a one-loop matching of couplings which is known in all cases considered. It is therefore also possible to test the robustness of the $\Lambda$-parameter determination by using SF-schemes at various values of $\nu$ as an intermediate step. The result is neatly illustrated in Fig. 4, where all data points should coincide up to a parametric uncertainty of order $\alpha ^2$. We conclude that a target precision of better than $3\%$ for $L_0\Lambda$ (which approximately corresponds to a $0.5\%$ precision for $\alpha _s(m_Z)$) requires non-perturbative data for a large enough range of couplings so that the perturbative truncation errors can be safely estimated. Our range of scales 4–128 GeV reaching down to $\alpha \approx 0.1$ allows us to reach such a precision. While some schemes may give compatible results even at $\alpha \approx 0.2$, it seems all but impossible to anticipate the quality of a given scheme if the coupling cannot be varied significantly.

With the hindsight of our $2.3\%$ precision result for $L_0\Lambda$, Eq. (4.27), we have also looked at an alternative test, which is close to procedures widely used in phenomenology. Namely, we have converted our non-perturbative observable, an $\hbox {SF}_\nu$-coupling with some choice for $\nu$ and L, to the ${\overline{\mathrm{MS}}}$-coupling where we allowed for a relative scale factor s in this perturbative conversion. Given the coupling in the ${\overline{\mathrm{MS}}}$-scheme the full machinery with up to 5-loops for the $\beta$-function [3,4,5,6,7] is available to extract the $\Lambda$-parameter. However, as in phenomenological applications, the limiting factor is the perturbative order in the conversion to the ${\overline{\mathrm{MS}}}$-scheme. We can perform this step at 2-loop order; for comparison we note that the 5-loop, O($\alpha ^4$) result for the R-ratio [46] translates to 3-loop order when formulated as a conversion between couplings. Looking at the dependence of the scale factor, a common method consists in identifying an “optimal scale factor”, $s^\star$, and then vary this factor between $s^\star /2$ and $2s^\star$ to obtain a systematic error estimate (c.f. the review of QCD in [2]). It is a bit of an art to determine the “optimal scale factor”, and some appeal to the kinematics or the physics of a given observable is often made in this context [2]. We here applied such a procedure, choosing $s^\star$ close to the ratio of $\Lambda$-parameters, which means the one-loop coefficient in the conversion to the ${\overline{\mathrm{MS}}}$ scheme is made very small. As illustrated in Fig. 7, this procedure gives an error that shrinks proportionally to $\alpha ^2$ and often brackets the correct result. However, we have also found cases (e.g. $\nu =-0.5$) where this procedure does not work and underestimates the systematic effect substantially, even at couplings around $\alpha =0.15$. We interpret this result as a warning: estimating errors within perturbation theory is notoriously difficult, and one may chance one’s luck by being too aggressive in this step.

The work presented in this paper constitutes a major step in the $\alpha _s$-determination by the ALPHA-collaboration [12]. Despite considerable improvements in the precision, this step currently still contributes the largest single error in this project. One may therefore hope for further progress, perhaps by combining the $\hbox {SF}_\nu$ schemes with alternative schemes. Gradient flow couplings are obvious candidates, provided the problems with large cutoff effects can be solved [13, 47], and the perturbative information is pushed at least to the same level as for the SF coupling. The latter step is possible based on numerical stochastic perturbation theory  [31,32,33]. Finally we note that, given the coupling results, similar non-perturbative tests of perturbation theory might also be performed using the quark mass parameters [48].

Appendix A: Modelling the sensitivity to \(c_\mathrm{t}\) and \(\tilde{c}_\mathrm{t}\)

In order to estimate the systematic error due to remnant O(a) effects stemming from an imperfect tuning of the counterterm coefficients $c_\mathrm{t}$ and $\tilde{c}_\mathrm{t}$ (cf. Sect. 3.7), we model how the data for the step-scaling functions $\Sigma (u,a/L)$ and $\Sigma _\nu (u_\nu ,a/L)$ were to change had the simulations been carried out at slightly shifted values of these coefficients. The basic observables in the simulations are the coupling at $u=\bar{g}^2(L)$ and $\bar{v}$ from which the couplings at $\nu \ne 0$ and the step-scaling functions are constructed. We therefore first obtain a model for the $c_\mathrm{t}$- and $\tilde{c}_\mathrm{t}$-dependence of u and $\bar{v}$. In a second step we translate this information to $u_\nu$ and finally to the step-scaling functions.

1.1 Linear a-effects in $\bar{g}^2$ and $\bar{v}$

We have carried out simulations at fixed $u=2.02$, lattice sizes $L/a=4,6,8$ and with $c_\mathrm{t}$- and $\tilde{c}_\mathrm{t}$-values varied around their perturbative default values. For instance, Fig. 8 shows the data for the $c_\mathrm{t}$-dependence of $u=\bar{g}^2(L)$.

Fig. 8

The left panel shows the dependence on $c_\mathrm{t}$ of the coupling $u=\bar{g}^2(L)$. The improvement coefficient is varied around its 2-loop value and the value of the coupling is $u\approx 2$. The right panel shows the slopes vs. a / L

These results are then used for numerical estimates of the respective derivatives which are collected in Table 9. Defining the functions

$$\begin{aligned} \delta _b(u) = \frac{L}{2a} \frac{1}{u} \frac{\mathrm {d}u}{\mathrm {d}c_\mathrm{t}} , \quad \varepsilon _b(u) = \frac{L}{a}\left. \frac{\mathrm {d}\bar{v}}{\mathrm {d}c_\mathrm{t}}\right| _{\bar{g}^2(L)=u} , \end{aligned}$$

(A.1)

and analogous functions $\tilde{\delta }_b(u)$ and $\tilde{\varepsilon }_b(u)$, with the derivative taken with respect to $\tilde{c}_\mathrm{t}$ instead of $c_\mathrm{t}$. From the simulations results one then infers their values at $u=2.02$,

$$\begin{aligned} \delta _b(2.02)= -2.15(6),\quad \varepsilon _b(2.02) = 0.22(11) , \end{aligned}$$

(A.2)

and, for the $\tilde{c}_\mathrm{t}$-dependence,

$$\begin{aligned} \tilde{\delta }_b(2.02) = 0.785(4),\quad \tilde{\varepsilon }_b(2.02) = -0.59(6). \end{aligned}$$

(A.3)

In order to obtain these functions for a range of u-values we interpolate these non-perturbative results with perturbation theory up to 2-loop order [15] and arrive at

$$\begin{aligned} \delta _b(u)= & {} -\left( 1 + 0.40 u + 0.085(14) u^2\right) , \end{aligned}$$

(A.4)

$$\begin{aligned} \varepsilon _b(u)= & {} 0.11(6)u, \end{aligned}$$

(A.5)

$$\begin{aligned} \tilde{\delta }_b(u)= & {} 0.25 u + 0.0686(7)u^2, \end{aligned}$$

(A.6)

$$\begin{aligned} \tilde{\varepsilon }_b(u)= & {} -1.35+0.38(3)u. \end{aligned}$$

(A.7)

We remark that the separation of the a / L- and the u-dependence is only approximate; in perturbation theory this neglects any logarithmic dependence on L / a in the coefficients. Furthermore, while we have indicated the error in the fit coefficients, the functions will be used with the central values throughout and these errors will not be propagated. We observe that the dominant effect for the coupling is the $c_\mathrm{t}$-dependence. In perturbation theory this is reflected by the fact that the fermionic $\tilde{c}_\mathrm{t}$-counterterm only contributes via loop effects and is thus suppressed by a relative factor u. For $\bar{v}$ the hierarchy is reversed, due to the fact that the $c_\mathrm{t}$-counterterm is $\nu$-independent and does not contribute to $v_1$, in contrast to the $\tilde{c}_\mathrm{t}$-counterterm.

With these definitions, we may now generalize the function $\delta _b(u)$ to the $\hbox {SF}_{\nu }$ coupling based on the relation $u_\nu = u/(1-\nu u \bar{v})$,

$$\begin{aligned} \delta _{b,\nu }(u_\nu ) = u_\nu \left( \frac{\delta _b(u)}{u} + \frac{1}{2} \nu \varepsilon _b(u)\right) , \end{aligned}$$

(A.8)

and the function $\tilde{\delta }_{b,\nu }$ is defined analogously. Here, explicit values for $\delta _{b,\nu }(u_\nu )$ require both u and $u_\nu$, which could be obtained from the data via $\beta$ and L / a. However, we prefer to define explicit functions of $u_\nu$ which is obtained by inverting numerically the function

$$\begin{aligned} u_\nu (u) = \frac{u}{1-\nu u \omega (u)},\quad \Rightarrow \quad u = u(u_\nu ), \end{aligned}$$

(A.9)

with $\omega (u)$ from Eq. (3.34), and by then substituting for u in Eq. (A.8). Obviously, this model for the $c_\mathrm{t}$- and $\tilde{c}_\mathrm{t}$-derivatives neglects some cutoff effects in the derivatives which are of higher than linear order in a / L.

1.2 Step-scaling functions

Given the models for the couplings $\bar{g}^2(L)$ we now translate this information to the step-scaling function, which is defined as the coupling $u'=\bar{g}^2(2L)$, taken as a function of $u=\bar{g}^2(L)$. Neglecting higher order cutoff effects we then find

$$\begin{aligned} \left. \frac{\mathrm {d}\Sigma (u,a/L)}{\mathrm {d}c_\mathrm{t}}\right| _{u=\bar{g}^2(L)}\approx & {} \frac{a}{L}\left( \sigma (u)\delta _b(\sigma (u))\right. \nonumber \\&\left. - 2u\sigma '(u)\delta _b(u)\right) , \end{aligned}$$

(A.10)

and analogous equations hold for $\nu \ne 0$ and the derivatives with respect to $\tilde{c}_\mathrm{t}$, with the obvious substitutions. We furthermore specify that we insert the continuum step-scaling functions to their known perturbative order,

$$\begin{aligned} \sigma (u) = u + s_0 u^2 + s_1 u^3 + s_2 u^4 \end{aligned}$$

(A.11)

with $s_{0,1,2}$ as given in Eq. (2.32). With this convention we then define the sensitivity in Eq. (3.38) as

Table 9 Non-perturbative estimates for the derivatives with respect to $c_\mathrm{t}$ and $\tilde{c}_\mathrm{t}$ at $u= 2.02$. The derivatives were obtained by numerical variation of the improvement coefficients around their perturbative 2-loop and 1-loop values, respectively

$$\begin{aligned} \delta _{c_\mathrm{t}}\Sigma _\nu (u_\nu ,a/L)= & {} \frac{a}{L}\left( \sigma _\nu (u_\nu ) \delta _{b,\nu }(\sigma _\nu (u_\nu ))\right. \nonumber \\&\left. - 2u_\nu \sigma '_\nu (u_\nu )\delta _{b,\nu }(u_\nu )\right) , \end{aligned}$$

(A.12)

and analogously for $\delta _{\tilde{c}_\mathrm{t}}\Sigma _\nu$, with the replacements $\delta _b \rightarrow \tilde{\delta }_b$. The case $\nu =0$ is included by omitting the index $\nu$. Furthermore, we define

$$\begin{aligned} \delta _{c_\mathrm{t}}\Omega (u,a/L) = \delta _{c_\mathrm{t}}\tilde{\Omega }(u,a/L) = \frac{a}{L}\varepsilon _{b}(u), \end{aligned}$$

(A.13)

and analogously for $\delta _{\tilde{c}_\mathrm{t}}\Omega = \delta _{\tilde{c}_\mathrm{t}}\tilde{\Omega }$ with the replacement $\varepsilon _b \rightarrow \tilde{\varepsilon }_b$. The functions $\varepsilon _b$ and $\tilde{\varepsilon }_b$ are given in Eqs. (A.5, A.7). The data $\tilde{\Omega }(u,a/L)$, obtained from the 2L-lattices, are treated exactly like $\Omega (u,a/L)$, as both the $c_\mathrm{t}$- and $\tilde{c}_\mathrm{t}$-variations were found to be rather insensitive to the precise definition of the critical mass (at least in perturbation theory).

We finally note that a slight extrapolation of our functions $\delta _b,\tilde{\delta }_b$ and $\varepsilon _b,\tilde{\varepsilon }_b$ beyond $u\approx 2$ is implicit due to the largest argument being $\sigma (2)\approx 2.45$. However, we expect that the model is not too far off, and are here not overly concerned about errors at the 10% level, which would add a corresponding uncertainty on our systematic error estimates. If future precision studies require a more refined model for these systematic effects, one might revisit the separation of the variables L / a and u in our models, and also check the non-perturbative derivatives at the largest relevant arguments. Finally we remark that this whole exercise would become redundant if the counterterm coefficients $c_\mathrm{t}$ and $\tilde{c}_\mathrm{t}$ could be determined non-perturbatively as functions of $g_0$.