The magnetic moment of the $Z_c(3900)$ as an axialvector tetraquark state with QCD sum rules

Abstract

In this article, we assign the $Z_c^\pm (3900)$ to be the diquark-antidiquark type axialvector tetraquark state, study its magnetic moment with the QCD sum rules in the external weak electromagnetic field by carrying out the operator product expansion up to the vacuum condensates of dimension 8. We pay special attention to matching the hadron side with the QCD side of the correlation function to obtain solid duality, the routine can be applied to study other electromagnetic properties of the exotic particles.

1 Introduction

In 2013, the BESIII collaboration studied the process $e^+e^- \rightarrow \pi ^+\pi ^-J/\psi$ at a center-of-mass energy of 4.260 GeV, and observed a structure $Z_c(3900)$ in the $\pi ^\pm J/\psi$ invariant mass distribution [1]. Then the $Z_c(3900)$ was confirmed by the Belle and CLEO collaborations [2, 3]. Recently, the BESIII collaboration determined the spin and parity of the $Z_c^\pm (3900)$ state to be $J^P = 1^+$ with a statistical significance more than $7\sigma$ over other quantum numbers in a partial wave analysis of the process $e^+e^- \rightarrow \pi ^+\pi ^-J/\psi$ [4]. If it is really a resonance, the assignments of tetraquark state [5,6,7,8,9,10,11] and molecular state [12,13,14,15,16,17,18,19] are robust according to the non-zero electric charge. The newly observed exotic states X, Y, Z, which are excellent candidates for the multiquark states, provide a good platform for studying the nonperturbative behavior of QCD and attract many interesting works of the particle physicists.

The QCD sum rules is a powerful nonperturbative tool in studying the ground state hadrons, and has given many successful descriptions of the hadronic parameters on the phenomenological side [20,21,22]. As far as the $Z_c(3900)$ is concerned, the mass and decay width of the $Z_c(3900)$ have been studied with the QCD sum rules in details [10, 11, 18, 19, 23, 24], while the magnetic moment of the $Z_c(3900)$ is only studied with the light-cone QCD sum rules [25]. The magnetic moment of the $Z_c(3900)$ is a fundamental parameter as its mass and width, which also has copious information about the underlying quark structure, can be used to distinguish the preferred configuration from various theoretical models and deepen our understanding of the underlying dynamics.

For example, although the proton and neutron have degenerated mass in the isospin limit, their electromagnetic properties are quite different. If we take them as point particles, the magnetic moments are $\mu _p=1$ and $\mu _n=0$ in unit of the nucleon magneton from Dirac’s theory of relativistic fermions. In 1933, Otto Stern measured the magnetic moment of the proton, which deviates from one significatively and indicates that the proton has under-structure. The neutron’s anomalous magnetic moment originates from the Pauli form-factor. So it is interesting to study the interaction of the $Z_c(3900)$ with the photon, which plays an important role in understanding its nature. In fact, the works on the magnetic moments of the exotic particles X, Y, Z are few, only the magnetic moments of the $Z_c(3900)$, X(5568) and $Z_b(10610)$ are studied with the light-cone QCD sum rules [25,26,27].

In this article, we tentatively assign the $Z_c(3900)$ to be the diquark-antidiquark type tetraquark state and study its magnetic moment with the QCD sum rules in the external weak electromagnetic field. In Ref. [28], Ioffe and Smilga (also in Ref. [29], Balitsky and Yung) introduce a static electromagnetic field which couples to the quarks and polarizes the QCD vacuum, and extract the nucleon magnetic moments from linear response to the external electromagnetic field with the QCD sum rules. This approach has been applied successfully to study the magnetic moments of the octet baryons and decuplet baryons [30,31,32,33,34]. Now we extend this approach to study the magnetic moment of the hidden-charm tetraquark state $Z_c(3900)$.

The article is arranged as follows: we derive the QCD sum rules for the magnetic moment $\mu$ of the $Z_c(3900)$ in Sect. 2; in Sect. 3, we present the numerical results and discussions; and Sect. 4 is reserved for our conclusion.

2 The magnetic moment of the $Z_c(3900)$ as an axialvector tetraquark state

In the following, we write down the two-point correlation function $\Pi _{\mu \nu }(p,q)$ in the external electromagnetic field F,

$$\begin{aligned}&\Pi _{\mu \nu }(p,q)=i\int d^4x e^{ip \cdot x} \langle 0|T\left\{ J_\mu (x)J_\nu ^{\dagger }(0)\right\} |0\rangle _F , \end{aligned}$$

(1)

$$\begin{aligned}&J_\mu (x)=\frac{\varepsilon ^{ijk}\varepsilon ^{imn}}{\sqrt{2}}\left\{ u^j(x)C\gamma _5c^k(x) {\bar{d}}^m(x)\gamma _\mu C {\bar{c}}^n(x)\right. \nonumber \\&\qquad \qquad \left. -u^j(x)C\gamma _\mu c^k(x){\bar{d}}^m(x)\gamma _5C {\bar{c}}^n(x) \right\} , \end{aligned}$$

(2)

the i, j, k, m, n are color indexes, the C is the charge conjugation matrix.

The correlation function $\Pi _{\mu \nu }(p,q)$ can be rewritten as

$$\begin{aligned}&\Pi _{\mu \nu }(p,q)=i\int d^4x e^{ip \cdot x} \Bigg \langle 0\Bigg |T\left\{ J_\mu (x)J_\nu ^{\dagger }(0)\right\} \Bigg |0\Bigg \rangle \nonumber \\&\quad +\,i\int d^4x e^{ip \cdot x} \Bigg \langle 0\Bigg |T\nonumber \\&\quad \times \, \left\{ J_\mu (x)\left[ -ie \int d^4y \,\eta _\alpha (y)\,A^\alpha (y) \right] J_\nu ^{\dagger }(0)\right\} \Bigg |0\Bigg \rangle +\cdots ,\nonumber \\ \end{aligned}$$

(3)

where the $\eta _\alpha (y)$ is the electromagnetic current and the $A_\alpha (y)$ is the electromagnetic field.

We can insert a complete set of intermediate hadronic states with the same quantum numbers as the current operator $J_\mu (x)$ into the correlation function $\Pi _{\mu \nu }(p,q)$ to obtain the hadronic representation [20,21,22]. After isolating the ground state and the first radial excited state contributions from the pole terms, we obtain

$$\begin{aligned}&\Pi _{\mu \nu }(p,q)=\frac{\lambda _{Z}^2}{M_{Z}^2-p^2} \zeta _\mu (p)\zeta _\nu ^*(p)+\frac{\lambda _{Z^\prime }^2}{M_{Z^\prime }^2-p^2} \zeta _\mu (p)\zeta _\nu ^*(p) \nonumber \\&\qquad -\,\lambda _{Z}^2 e \, \varepsilon ^*_\alpha (q)\,\zeta _\mu (p)\,\zeta ^*_\nu (p^\prime )\frac{1}{M_{Z}^2-p^2}\left\langle Z_c(p)|\eta ^\alpha (0)|Z_c(p^\prime )\right\rangle )\nonumber \\&\qquad \times \,\frac{1}{M_{Z}^2-p^{\prime 2}} -\lambda _{Z} \lambda _{Z^\prime }e \, \varepsilon ^*_\alpha (q)\,\zeta _\mu (p)\,\zeta ^*_\nu (p^\prime )\nonumber \\&\qquad \times \, \frac{1}{M_{Z^\prime }^2-p^2}\langle Z_c^\prime (p)|\eta ^\alpha (0)|Z_c(p^\prime )\rangle )\frac{1}{M_{Z}^2-p^{\prime 2}} \nonumber \\&\qquad -\,\lambda _{Z} \lambda _{Z^\prime }e \, \varepsilon ^*_\alpha (q)\,\zeta _\mu (p)\,\zeta ^*_\nu (p^\prime )\nonumber \\&\qquad \times \, \frac{1}{M_{Z}^2-p^2}\langle Z_c(p)|\eta ^\alpha (0)|Z_c^\prime (p^\prime )\rangle )\frac{1}{M_{Z^\prime }^2-p^{\prime 2}} +\cdots \nonumber \\&\quad =\frac{\lambda _{Z}^2}{M_{Z}^2-p^2} \left( -g_{\mu \nu } \right) +\frac{\lambda _{Z^\prime }^2}{M_{Z^\prime }^2-p^2} \left( -g_{\mu \nu } \right) \nonumber \\&\qquad +\,\frac{\lambda _{Z}^2}{\left( M_{Z}^2-p^2\right) \left( M_{Z}^2-p^{\prime 2}\right) } \,G_2(0)\,ie\,F_{\mu \nu }\nonumber \\&\qquad +\,\frac{\lambda _{Z^\prime }\lambda _{Z}}{\left( M_{Z^\prime }^2-p^2\right) \left( M_{Z}^2-p^{\prime 2}\right) } \,{\widetilde{G}}_2(0)\,ie\,F_{\mu \nu }\nonumber \\&\qquad +\,\frac{\lambda _{Z}\lambda _{Z^\prime }}{\left( M_{Z}^2-p^2\right) \left( M_{Z^\prime }^2-p^{\prime 2}\right) } \,{\widetilde{G}}_2(0)\,ie\,F_{\mu \nu }+\,\cdots \nonumber \\&\quad =\Pi (p^{\prime 2},p^2)i\,e\,F_{\mu \nu }+\cdots , \end{aligned}$$

(4)

where $F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu$, the pole residue (or coupling) $\lambda _{Z^{(\prime )}}$ is defined by

$$\begin{aligned} \langle 0|J_\mu (0)|Z^{(\prime )}(p)\rangle =\lambda _{Z^{(\prime )}} \, \zeta _\mu (p) , \end{aligned}$$

(5)

the $\varepsilon _\alpha$ and $\zeta _\mu$ are the polarization vectors of the photon and the axial-vector meson $Z_c^{(\prime )}$, respectively. The hadronic matrix element $\langle Z_c(p)|\eta _\alpha (0)|Z_c(p^\prime )\rangle$ can be parameterized by three form-factors,

$$\begin{aligned}&\left\langle Z_c(p)|\eta _\alpha (0)|Z_c(p^\prime )\right\rangle =G_1(Q^2)\,\zeta ^*(p)\cdot \zeta (p^\prime )\left( p_\alpha +p^\prime _\alpha \right) \nonumber \\&\quad +G_2(Q^2)\left[ \zeta _\alpha (p^\prime )\zeta ^*(p)\cdot q-\zeta ^*_\alpha (p)\zeta (p^\prime )\cdot q \right] \nonumber \\&\quad -G_3(Q^2)\frac{1}{2M_{Z}^2}\zeta ^*(p)\cdot q \, \zeta (p^\prime )\cdot q \left( p_\alpha +p^\prime _\alpha \right) , \end{aligned}$$

(6)

with $Q^2=-q^2$, $p^\prime =p+q$ [35]. The Lorentz-invariant form-factors $G_1(Q^2)$, $G_2(Q^2)$ and $G_3(Q^2)$ are related to the charge, magnetic and quadrupole form-factors,

$$\begin{aligned}&G_C=G_1+\frac{2}{3}\eta G_Q,\nonumber \\&G_M=-G_2,\nonumber \\&G_Q=G_1+G_2+(1+\eta )G_3, \end{aligned}$$

(7)

respectively, where $\eta =\frac{Q^2}{4M_{Z}^2}$ is a kinematic factor. At zero momentum transfer, these form-factors are proportional to the usual static quantities of the charge e, magnetic moment $\mu _Z$ and quadrupole moment $Q_1$,

$$\begin{aligned} e\, G_C(0)= & {} e,\nonumber \\ e\, G_M(0)= & {} 2M_{Z}\,\mu _Z,\nonumber \\ e\, G_Q(0)= & {} M_{Z}^2\,Q_1\, . \end{aligned}$$

(8)

The hadronic matrix elements $\langle Z_c(p)|\eta _\alpha (0)|Z^\prime _c(p^\prime )\rangle$ and $\langle Z_c^\prime (p)|\eta _\alpha (0)|Z_c(p^\prime )\rangle$ are parameterized analogously by the form-factors ${\widetilde{G}}_1(Q^2)$, ${\widetilde{G}}_2(Q^2)$ and ${\widetilde{G}}_3(Q^2)$. In this article, we choose the tensor structure $F_{\mu \nu }$ for analysis.

The current $J_\mu (x)$ also has non-vanishing couplings with the scattering states $D D^*$, $J/\psi \pi$, $J/\psi \rho$, etc [36]. In the following, we study the contributions of the intermediate meson-loops to the correlation function $\Pi _{\mu \nu }(p,q)$,

$$\begin{aligned}&\Pi _{\mu \nu }(p,q)=\frac{{\widehat{\lambda }}_{Z}^2}{{\widehat{M}}_{Z}^2+\Sigma (p) -p^2} \left( -g_{\mu \nu } \right) \nonumber \\&\quad +\,\frac{\lambda _{{\widehat{Z}}^\prime }^2}{{\widehat{M}}_{Z^\prime }^2+\Sigma (p)-p^2} \left( -g_{\mu \nu } \right) \nonumber \\&\quad +\,\frac{{\widehat{\lambda }}_{Z}^2}{\left( {\widehat{M}}_{Z}^2+\Sigma (p)-p^2\right) \left( {\widehat{M}}_{Z}^2+\Sigma (p^\prime )-p^{\prime 2}\right) } \,G_2(0)\,ie\,F_{\mu \nu }\nonumber \\&\quad +\,\frac{{\widehat{\lambda }}_{Z^\prime }{\widehat{\lambda }}_{Z}}{\left( {\widehat{M}}_{Z^\prime }^2+\Sigma (p)-p^2\right) \left( {\widehat{M}}_{Z}^2+\Sigma (p^\prime )-p^{\prime 2}\right) } \,{\widetilde{G}}_2(0)\,ie\,F_{\mu \nu }\nonumber \\&\quad +\,\frac{{\widehat{\lambda }}_{Z}{\widehat{\lambda }}_{Z^\prime }}{\left( {\widehat{M}}_{Z}^2+\Sigma (p)-p^2\right) \left( {\widehat{M}}_{Z^\prime }^2+\Sigma (p^\prime )-p^{\prime 2}\right) } \,{\widetilde{G}}_2(0)\,ie\,F_{\mu \nu }\nonumber \\&\quad +\,\cdots , \end{aligned}$$

(9)

where the self-energy $\Sigma (p)=\Sigma _{DD^*}(p)+\Sigma _{J/\psi \pi }(p)+\Sigma _{J/\psi \rho }(p)+\cdots$. The ${\widehat{\lambda }}_{Z/Z^\prime }$ and ${\widehat{M}}_{Z/Z^\prime }$ are bare quantities to absorb the divergences in the self-energies $\Sigma (p)$ and $\Sigma (p^\prime )$. The renormalized self-energies contribute a finite imaginary part to modify the dispersion relation,

$$\begin{aligned}&\Pi _{\mu \nu }(p,q)=\frac{\lambda _{Z}^2}{M_{Z}^2-i\sqrt{p^2}\,\Gamma (p^2) -p^2} \left( -g_{\mu \nu } \right) \nonumber \\&\quad +\frac{\lambda _{Z^\prime }^2}{M_{Z^\prime }^2-i\sqrt{p^2}\,\Gamma ^\prime (p^2)-p^2} \left( -g_{\mu \nu } \right) \nonumber \\&\quad +\frac{\lambda _{Z}^2}{\left( M_{Z}^2-i\sqrt{p^2}\,\Gamma (p^2)-p^2\right) \left( M_{Z}^2-i\sqrt{p^{\prime 2}}\,\Gamma (p^{\prime 2})-p^{\prime 2}\right) } \,G_2(0)\,ie\,F_{\mu \nu }\nonumber \\&\quad +\frac{\lambda _{Z^\prime }\lambda _{Z}}{\left( M_{Z^\prime }^2-i\sqrt{p^2}\,\Gamma ^\prime (p^2)-p^2\right) \left( M_{Z}^2 -i\sqrt{p^{\prime 2}}\,\Gamma (p^{\prime 2})-p^{\prime 2}\right) } \,{\widetilde{G}}_2(0)\,ie\,F_{\mu \nu }\nonumber \\&\quad +\frac{\lambda _{Z}\lambda _{Z^\prime }}{\left( M_{Z}^2-i\sqrt{p^2}\,\Gamma (p^2)-p^2\right) \left( M_{Z^\prime }^2 -i\sqrt{p^{\prime 2}}\,\Gamma ^\prime (p^{\prime 2})-p^{\prime 2}\right) } \,{\widetilde{G}}_2(0)\,ie\,F_{\mu \nu }\nonumber \\&\quad +\cdots , \end{aligned}$$

(10)

the physical width of the ground state $\Gamma (M_Z^2)=\Gamma _{Z_c(3900)}=(28.1\pm 2.6)\, \mathrm {MeV}$ is small enough [36], while the effect of the large width of the first radial excited state $\Gamma ^\prime (M^2_{Z^\prime })=\Gamma _{Z(4430)}=181\pm 31\,\mathrm {MeV}$ can be absorbed into the continuum states (the Z(4430) can be tentatively assigned to be the first radial excitation of the $Z_c(3900)$ based on the QCD sum rules [37]), the zero width approximation in the hadronic spectral density works, the contaminations of the intermediate meson-loops are expected to be small and can be neglected safely [38]. In fact, even the effect of the large width of the $Z_c(4200)$ ($\Gamma _{Z_c(4200)}=370\pm 70{}^{+ 70}_{-132}\,\mathrm {MeV}$) can be safely absorbed into the pole residue [39]. For detailed discussions about this subject, one can consult Refs. [10, 39].

In the following, we briefly outline the operator product expansion for the correlation function $\Pi _{\mu \nu }(p,q)$ in perturbative QCD. We contract the quark fields in the correlation function $\Pi _{\mu \nu }(p,q)$ with Wick theorem, obtain the result,

$$\begin{aligned} \Pi _{\mu \nu }(p,q)= & {} -\frac{i\varepsilon ^{ijk}\varepsilon ^{imn}\varepsilon ^{i^{\prime }j^{\prime }k^{\prime }}\varepsilon ^{i^{\prime }m^{\prime }n^{\prime }}}{2} \nonumber \\&\times \int d^4x e^{ip \cdot x} \Bigg \{\mathrm{Tr}\left[ \gamma _5C^{kk^{\prime }}(x)\gamma _5 CU^{jj^{\prime }T}(x)C\right] \nonumber \\&\times \,\mathrm{Tr}\left[ \gamma _\nu C^{n^{\prime }n}(-x)\gamma _\mu C D^{m^{\prime }mT}(-x)C\right] \nonumber \\&+\,\mathrm{Tr}\left[ \gamma _\mu C^{kk^{\prime }}(x)\gamma _\nu CU^{jj^{\prime }T}(x)C\right] \nonumber \\&\times \,\mathrm{Tr}\left[ \gamma _5 C^{n^{\prime }n}(-x)\gamma _5 C D^{m^{\prime }mT}(-x)C\right] \nonumber \\&+\,\mathrm{Tr}\left[ \gamma _\mu C^{kk^{\prime }}(x)\gamma _5 CU^{jj^{\prime }T}(x)C\right] \nonumber \\&\times \, \mathrm{Tr}\left[ \gamma _\nu C^{n^{\prime }n}(-x)\gamma _5 C D^{m^{\prime }mT}(-x)C\right] \nonumber \\&+\,\mathrm{Tr}\left[ \gamma _5 C^{kk^{\prime }}(x)\gamma _\nu CU^{jj^{\prime }T}(x)C\right] \nonumber \\&\times \, \mathrm{Tr}\left[ \gamma _5 C^{n^{\prime }n}(-x)\gamma _\mu C D^{m^{\prime }mT}(-x)C\right] \Bigg \} \nonumber \\= & {} \Pi (p^{\prime 2},p^2)\,i\,e\,F_{\mu \nu }+\cdots , \end{aligned}$$

(11)

where the $U_{ij}(x)$, $D_{ij}(x)$ and $C_{ij}(x)$ are the full u, d and c quark propagators, respectively (the $U_{ij}(x)$ and $D_{ij}(x)$ can be written as $S_{ij}(x)$ for simplicity),

$$\begin{aligned}&S_{ij}(x)= \frac{i\delta _{ij}\!\not \!{x}}{ 2\pi ^2x^4}-\frac{\delta _{ij}\langle {\bar{q}}q\rangle }{12} \nonumber \\&\quad -\,\frac{\delta _{ij}x^2\langle {\bar{q}}g_s\sigma Gq\rangle }{192} -\frac{ig_sG^{a}_{\alpha \beta }t^a_{ij}\left( \!\not \!{x} \sigma ^{\alpha \beta }+\sigma ^{\alpha \beta } \!\not \!{x}\right) }{32\pi ^2x^2} \nonumber \\&\quad -\,\frac{1}{8}\langle {\bar{q}}_j\sigma ^{\mu \nu }q_i \rangle \sigma _{\mu \nu }+\frac{i \delta _{ij}\, e e_q F_{\alpha \beta }\left( \!\not \!{x} \sigma ^{\alpha \beta }+\sigma ^{\alpha \beta } \!\not \!{x}\right) }{32\pi ^2x^2}\nonumber \\&\quad -\,\frac{\delta _{ij}\langle {\bar{q}}q\rangle \,\chi \, \sigma ^{\alpha \beta }\, e e_q F_{\alpha \beta }}{24}\nonumber \\&\quad +\,\frac{\delta _{ij}\langle {\bar{q}}q\rangle \,e e_q F_{\alpha \beta } }{288}\left( \sigma ^{\alpha \beta }x^2-2x_{\lambda }x^{\beta }\sigma ^{\lambda \alpha } \right) \nonumber \\&\quad +\,\frac{\delta _{ij}\langle {\bar{q}}q\rangle \,e e_q F_{\alpha \beta } }{576}\nonumber \\&\quad \times \,\left[ \sigma ^{\alpha \beta }x^2\left( \kappa +\xi \right) -2x_\lambda x^\beta \sigma ^{\lambda \alpha }\left( \kappa -\frac{\xi }{2} \right) \right] +\cdots , \end{aligned}$$

(12)

$$\begin{aligned}&C_{ij}(x)=\frac{i}{(2\pi )^4}\int d^4k e^{-ik \cdot x} \nonumber \\&\quad \times \,\left\{ \frac{\delta _{ij}}{\!\not \!{k}-m_c} -\frac{g_sG^n_{\alpha \beta }t^n_{ij}}{4}\frac{\sigma ^{\alpha \beta }(\!\not \!{k}+m_c)+(\!\not \!{k}+m_c) \sigma ^{\alpha \beta }}{(k^2-m_c^2)^2}\right. \nonumber \\&\quad \left. +\,\frac{\delta _{ij} e e_q F_{\alpha \beta } }{4}\frac{\sigma ^{\alpha \beta }(\!\not \!{k}+m_c)+(\!\not \!{k}+m_c) \sigma ^{\alpha \beta }}{(k^2-m_c^2)^2}+\cdots \right\} ,\nonumber \\ \end{aligned}$$

(13)

and $t^n=\frac{\lambda ^n}{2}$, the $\lambda ^n$ is the Gell-Mann matrix [10, 22, 28, 31, 33, 34, 40]. We retain the term $\langle {\bar{q}}_j\sigma _{\mu \nu }q_i \rangle$ originates from Fierz re-ordering of the $\langle q_i {\bar{q}}_j\rangle$ to absorb the gluons emitted from other quark lines to form $\langle {\bar{q}}_j g_s G^a_{\alpha \beta } t^a_{mn}\sigma _{\mu \nu } q_i \rangle$ to extract the mixed condensate $\langle {\bar{q}}g_s\sigma G q\rangle$ [10]. The new condensates or vacuum susceptibilities $\chi$, $\kappa$ and $\xi$ induced by the external electromagnetic field are defined by

$$\begin{aligned}&\langle 0|{\bar{q}}\sigma _{\alpha \beta }q|0\rangle _F= e\,e_q\,\chi \, \langle {\bar{q}}q\rangle \, F_{\alpha \beta }, \nonumber \\&\langle 0|{\bar{q}}g_s G_{\alpha \beta }q|0\rangle _F= e\,e_q\,\kappa \, \langle {\bar{q}}q\rangle \, F_{\alpha \beta }, \nonumber \\&\varepsilon _{\alpha \beta \lambda \tau }\langle 0|{\bar{q}}g_s G^{\lambda \tau }\gamma _5q|0\rangle _F=i e\,e_q\,\xi \, \langle {\bar{q}}q\rangle \, F_{\alpha \beta }, \end{aligned}$$

(14)

with the convention $\varepsilon ^{0123}=-\varepsilon _{0123}=1$ [28, 31, 33, 34]. Then we compute the integrals both in the coordinate and momentum spaces, and obtain the correlation function $\Pi (p^{\prime 2},p^2)\,F_{\mu \nu }$ therefore the spectral density at the level of quark-gluon degrees of freedom. Furthermore, we take into account contributions of the new condensates originate from the quark interacting with the external electromagnetic field as well as the vacuum gluons,

$$\begin{aligned}&\langle 0| q^i(x){\bar{q}}^j(0)G^n_{\alpha \beta }(x)|0\rangle _F \nonumber \\&\quad =-\frac{\langle {\bar{q}}q\rangle }{16}\,t^n_{ij}\,e e_q \left( \kappa \, F_{\alpha \beta }-\frac{i}{4}\xi \, \gamma _5 \,\varepsilon _{\alpha \beta \lambda \tau }F^{\lambda \tau }\right) , \end{aligned}$$

(15)

see the Feynman diagrams shown in Figs. 1 and 2.

Fig. 1

The contributions $\langle {\bar{q}}q\rangle \, F_{\alpha \beta }$ come from the terms $\langle 0| q^i(x){\bar{q}}^j(0)G^n_{\alpha \beta }(x)|0\rangle _F$, where the external lines denote the photon field. Other diagrams obtained by interchanging of the heavy quark lines (dashed lines) or light quark lines (solid lines) are implied

Fig. 2

The contributions $\langle {\bar{q}}q\rangle \langle {\bar{q}}g_s \sigma Gq\rangle \, F_{\alpha \beta }$ come from the terms $\langle 0| q^i(x){\bar{q}}^j(0)G^n_{\alpha \beta }(x)|0\rangle _F$, where the external lines denote the photon field. Other diagrams obtained by interchanging of the heavy quark lines (dashed lines) or light quark lines (solid lines) are implied

We have to be cautious in matching the QCD side of the correlation function $\Pi (p^{\prime 2},p^2)$ with the hadron side of the correlation function $\Pi (p^{\prime 2},p^2)$, as there appears the variable $p^{\prime 2}=(p+q)^2$. We rewrite the correlation function $\Pi _H(p^{\prime 2},p^2)$ on the hadron side into the following form through dispersion relation,

$$\begin{aligned} \Pi _{H}(p^{\prime 2},p^2)=\int _{4m_c^2}^{s_{Z}^0}ds^\prime \int _{4m_c^2}^{s^0_{Z}}ds \frac{\rho _H(s^\prime ,s)}{(s^\prime -p^{\prime 2})(s-p^2)}+\cdots ,\nonumber \\ \end{aligned}$$

(16)

where the $\rho _H(s^\prime ,s)$ is the hadronic spectral density,

$$\begin{aligned} \rho _H(s^\prime ,s)= & {} {\lim _{\epsilon _2\rightarrow 0}}\,\,{\lim _{\epsilon _1\rightarrow 0}} \,\,\frac{ \mathrm{Im}_{s^\prime }\, \mathrm{Im}_{s}\,\Pi _H(s^\prime +i\epsilon _2,s+i\epsilon _1) }{\pi ^2} \nonumber \\= & {} \lambda _Z^2\, G_2(0)\,\delta \left( s^\prime -M_Z^2\right) \delta \left( s -M_Z^2\right) \nonumber \\&+ \lambda _{Z^\prime }\lambda _Z\, {\widetilde{G}}_2(0)\,\delta \left( s^\prime -M_{Z^\prime }^2\right) \delta \left( s -M_Z^2\right) \nonumber \\&+\lambda _{Z^\prime }\lambda _Z\, {\widetilde{G}}_2(0)\,\delta \left( s^\prime -M_{Z}^2\right) \delta \left( s -M_{Z^\prime }^2\right) +\cdots ,\nonumber \\ \end{aligned}$$

(17)

the $s_Z^0$ is the continuum threshold parameter, we add the subscript H to denote the hadron side. However, on the QCD side, the QCD spectral density $\rho _{QCD}(s^\prime ,s)$ does not exist,

$$\begin{aligned} \rho _{QCD}(s^\prime ,s)= & {} {\lim _{\epsilon _2\rightarrow 0}} \,\,{\lim _{\epsilon _1\rightarrow 0}}\,\,\frac{ \mathrm{Im}_{s^\prime }\, \mathrm{Im}_{s}\,\Pi _{QCD}(s^\prime +i\epsilon _2,s+i\epsilon _1) }{\pi ^2} \nonumber \\= & {} 0, \end{aligned}$$

(18)

because

$$\begin{aligned} {\lim _{\epsilon _2\rightarrow 0}}\,\,\frac{ \mathrm{Im}_{s^\prime }\,\Pi _{QCD}(s^\prime +i\epsilon _2,p^2) }{\pi }= & {} 0, \end{aligned}$$

(19)

we add the subscript QCD to denote the QCD side.

On the QCD side, the correlation function $\Pi _{QCD}(p^2)$ (the $\Pi _{QCD}(p^{\prime 2},p^2)$ is reduced to $\Pi _{QCD}(p^2)$ due to lacking dependence on the variable $p^{\prime 2}$) can be written into the following form through dispersion relation,

$$\begin{aligned} \Pi _{QCD}(p^2)= & {} a_n\, p^{2n}+ \int _{4m_c^2}^{s^0_{Z}}ds \frac{\rho _{QCD}(s)}{s-p^2}+\cdots , \end{aligned}$$

(20)

where the $\rho _{QCD}(s)$ is the QCD spectral density,

$$\begin{aligned} \rho _{QCD}(s)= & {} \,\,{\lim _{\epsilon _1\rightarrow 0}}\,\,\frac{ \mathrm{Im}_{s} \,\Pi _{QCD}(s+i\epsilon _1) }{\pi } , \end{aligned}$$

(21)

which is independent on the variable $p^{\prime 2}$, the coefficients $a_n$ with $n=0,\,1,\,2, \ldots$ are some constants, the terms $a_n\, p^{2n}$ disappear after performing the Borel transform with respect to the variable $P^2=-p^2$, we can neglect the terms $a_n\, p^{2n}$ safely.

We math the hadron side with the QCD side of the correlation function, and carry out the integral over $ds^\prime$ firstly to obtain the solid duality,

$$\begin{aligned} \int _{4m_c^2}^{s^0_{Z}}ds \frac{\rho _{QCD}(s)}{s-p^2}= & {} \int _{4m_c^2}^{s^0_{Z}}ds \frac{1}{s-p^2} \left[ \int _{4m_c^2}^{\infty }ds^\prime \frac{\rho _H(s^\prime ,s)}{s^\prime -p^{\prime 2}} \right] \nonumber \\= & {} \frac{\lambda _{Z}^2\,G_2(0)}{\left( M_{Z}^2-p^2\right) \left( M_{Z}^2-p^{\prime 2}\right) }\nonumber \\&+ \int _{4m_c^2}^{s^0_{Z}}ds \frac{1}{s-p^2} \left[ \int _{s^0_Z}^{\infty }ds^\prime \frac{\rho _H(s^\prime ,s)}{s^\prime -p^{\prime 2}} \right] \nonumber \\= & {} \frac{\lambda _{Z}^2\,G_2(0)}{\left( M_{Z}^2-p^2\right) \left( M_{Z}^2-p^{\prime 2}\right) }+ \frac{\lambda _Z^2\, C}{M_Z^2-p^2},\nonumber \\ \end{aligned}$$

(22)

where we introduce the unknown parameter C to denote the transition between the ground state and the excited states,

$$\begin{aligned} \lambda _Z^2\, C= & {} \int _{4m_c^2}^{s^0_{Z}}ds \int _{s^0_Z}^{\infty }ds^\prime \frac{\rho _H(s^\prime ,s)}{s^\prime -p^{\prime 2}}=\frac{\lambda _{Z^\prime }\lambda _Z\, {\widetilde{G}}_2(0)}{M_{Z^\prime }^2-p^{\prime 2}}+\cdots .\nonumber \\ \end{aligned}$$

(23)

In numerical calculation, we smear dependency of the C on the momentum $p^{\prime 2}$ and take it as a free parameter, and choose the suitable value to eliminate the contaminations from the high resonances and continuum states to obtain the stable QCD sum rule with respect to the variation of the Borel parameter $T^2$.

Now we set $p^{\prime 2}=p^2$ and perform the Borel transform with respect to the variable $P^2=-p^2$ to obtain the following QCD sum rule:

$$\begin{aligned}&\left[ \frac{G_2(0)}{T^2}+C\right] \, \lambda _{Z}^2\, \exp \left( -\frac{M_{Z}^2}{T^2}\right) \nonumber \\&\quad = \int _{4m_c^2}^{s_0} ds\, \rho _{QCD}(s) \, \exp \left( -\frac{s}{T^2}\right) , \end{aligned}$$

(24)

where

$$\begin{aligned} \rho _{QCD}(s)= & {} \rho _0(s)+\rho _3(s)+\rho _5(s)+\rho _6(s)+\rho _8(s), \end{aligned}$$

(25)

$$\begin{aligned} \rho _{0}(s)= & {} \frac{1}{256\pi ^6}\int _{y_i}^{y_f}dy \int _{z_i}^{1-y}dz \, yz\, (1-y-z)\nonumber \\&\times \left( s-{\overline{m}}_c^2\right) ^2\left( 4s-{\overline{m}}_c^2 \right) , \end{aligned}$$

(26)

$$\begin{aligned} \rho _{3}(s)= & {} -\frac{m_c\langle {\bar{q}}q\rangle }{96\pi ^4}\int _{y_i}^{y_f}dy \int _{z_i}^{1-y}dz \, (y+z)\, s \nonumber \\&+\,\frac{m_c\langle {\bar{q}}q\rangle \,\chi }{64\pi ^4}\int _{y_i}^{y_f}dy \int _{z_i}^{1-y}dz \, (y+z)\,(1-y-z) \nonumber \\&\times \,\left( s-{\overline{m}}_c^2\right) \left( 2s-{\overline{m}}_c^2 \right) \nonumber \\&+\,\frac{m_c\langle {\bar{q}}q\rangle \,\kappa }{384\pi ^4}\int _{y_i}^{y_f}dy \int _{z_i}^{1-y}dz \, (y+z)\, \left( 4s-3{\overline{m}}_c^2\right) \nonumber \\&+\,\frac{m_c\langle {\bar{q}}q\rangle \,\xi }{768\pi ^4}\int _{y_i}^{y_f}dy \int _{z_i}^{1-y}dz \, (y+z)\, \left( 5s-3{\overline{m}}_c^2\right) \nonumber \\&-\,\frac{m_c\langle {\bar{q}}q\rangle \,(2\kappa +\xi )}{256\pi ^4}\int _{y_i}^{y_f}dy \int _{z_i}^{1-y}dz \nonumber \\&\times \,\left( \frac{y}{z}+\frac{z}{y}\right) \,(1-y-z) \left( 3s-2{\overline{m}}_c^2\right) \nonumber \\&-\,\frac{m_c\langle {\bar{q}}q\rangle \,\kappa }{256\pi ^4}\int _{y_i}^{y_f}dy \int _{z_i}^{1-y}dz \,(2-y-z) \left( 2s-{\overline{m}}_c^2\right) \nonumber \\&+\,\frac{m_c\langle {\bar{q}}q\rangle \,\xi }{512\pi ^4}\int _{y_i}^{y_f}dy \int _{z_i}^{1-y}dz \nonumber \\&\times \,\left[ \left( \frac{y}{z}+\frac{z}{y}\right) \,(1-y-z) -(y+z)\right] \left( s-{\overline{m}}_c^2\right) ,\nonumber \\ \end{aligned}$$

(27)

$$\begin{aligned} \rho _{5}(s)= & {} \frac{m_c\langle {\bar{q}}g_s\sigma Gq\rangle }{256\pi ^4}\int _{y_i}^{y_f}dy \, \left[ 1+s\,\delta \left( s-{\widetilde{m}}_c^2 \right) \right] \nonumber \\&-\frac{m_c\langle {\bar{q}}g_s\sigma Gq\rangle }{1536\pi ^4}\int _{y_i}^{y_f}dy \int _{z_i}^{1-y}dz \, \left[ 1+s\,\delta \left( s-{\overline{m}}_c^2 \right) \right] \nonumber \\&-\frac{5m_c\langle {\bar{q}}g_s\sigma Gq\rangle }{1536\pi ^4}\int _{y_i}^{y_f}dy \int _{z_i}^{1-y}dz \,\left( \frac{z}{y}+\frac{y}{z} \right) \nonumber \\&\times \left[ 1+s\,\delta \left( s-{\overline{m}}_c^2 \right) \right] , \end{aligned}$$

(28)

$$\begin{aligned} \rho _{6}(s)= & {} -\,\frac{m_c^2\langle {\bar{q}}q\rangle ^2\,\chi }{24\pi ^2}\int _{y_i}^{y_f}dy -\frac{\langle {\bar{q}}q\rangle ^2\,\xi }{384\pi ^2}\int _{y_i}^{y_f}dy \nonumber \\&-\,\frac{m_c^2\langle {\bar{q}}q\rangle ^2\,(\kappa +2)}{72\pi ^2}\int _{y_i}^{y_f}dy\, \left( 1+\frac{s}{2T^2} \right) \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&-\,\frac{m_c^2\langle {\bar{q}}q\rangle ^2\,\xi }{288\pi ^2}\int _{y_i}^{y_f}dy\, \left( 1+\frac{2s}{T^2} \right) \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&+\,\frac{\langle {\bar{q}}q\rangle ^2\,(3\kappa +\xi )}{192\pi ^2}\int _{y_i}^{y_f}dy\, s\, \delta \left( s-{\widetilde{m}}_c^2 \right) , \end{aligned}$$

(29)

$$\begin{aligned} \rho _{8}(s)= & {} \frac{m_c^2\langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \,\chi }{96\pi ^2}\int _{y_i}^{y_f}dy \, \left( 1+\frac{s}{T^2} \right) \nonumber \\&\times \delta \left( s-{\widetilde{m}}_c^2 \right) +\frac{m_c^2\langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \,(\kappa +2)}{576\pi ^2T^2}\nonumber \\&\times \int _{y_i}^{y_f}dy \left( 1+\frac{s}{T^2}+\frac{s^2}{T^4} \right) \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&-\frac{m_c^2\langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \, \xi }{1152\pi ^2T^2}\int _{y_i}^{y_f}dy \nonumber \\&\times \left( 1+\frac{s}{T^2}-\frac{2s^2}{T^4} \right) \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&-\frac{ 13\langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \,\chi }{2304\pi ^2}\int _{y_i}^{y_f}dy \, s\, \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&-\frac{13\langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \, (\kappa +2)}{13824\pi ^2}\int _{y_i}^{y_f}dy\nonumber \\&\times \left( \frac{s}{T^2}+\frac{s^2}{T^4} \right) \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&+\frac{13\langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \, \xi }{27648\pi ^2}\int _{y_i}^{y_f}dy \nonumber \\&\times \left( \frac{s}{T^2}-\frac{2s^2}{T^4} \right) \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&+\frac{ \langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \,\chi }{768\pi ^2}\int _{y_i}^{y_f}dy \nonumber \\&\times \left[ 1+ \frac{2s}{3}\, \delta \left( s-{\widetilde{m}}_c^2 \right) \right] \nonumber \\&+\frac{ \langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \,(\kappa +2)}{3456\pi ^2}\int _{y_i}^{y_f}dy \nonumber \\&\times \left( 1+\frac{s}{T^2}+\frac{s^2}{2T^4} \right) \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&+\frac{ \langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \,\xi }{13824\pi ^2}\nonumber \\&\times \int _{y_i}^{y_f}dy \left( 1+\frac{5s}{2T^2}+\frac{2s^2}{T^4} \right) \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&-\frac{ \langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \,(3\kappa +\xi )}{768\pi ^2}\nonumber \\&\times \int _{y_i}^{y_f}dy \frac{s^2}{T^4} \, \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&+\frac{ \langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \,\xi }{768\pi ^2}\nonumber \\&\times \int _{y_i}^{y_f}dy \left( 1+\frac{s}{2T^2} \right) \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&+\frac{59 \langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \,(2\kappa +\xi )}{18432\pi ^2}\nonumber \\&\times \int _{y_i}^{y_f}dy \frac{s}{T^2} \, \delta \left( s-{\widetilde{m}}_c^2 \right) \nonumber \\&-\frac{11 \langle {\bar{q}}q\rangle \langle {\bar{q}}g_s\sigma Gq\rangle \,\kappa }{4608\pi ^2}\nonumber \\&\times \int _{y_i}^{y_f}dy \frac{s}{T^2} \, \delta \left( s-{\widetilde{m}}_c^2 \right) , \end{aligned}$$

(30)

$y_{f}=\frac{1+\sqrt{1-4m_c^2/s}}{2}$, $y_{i}=\frac{1-\sqrt{1-4m_c^2/s}}{2}$, $z_{i}=\frac{y m_c^2}{y s -m_c^2}$, ${\overline{m}}_c^2=\frac{(y+z)m_c^2}{yz}$, ${\widetilde{m}}_c^2=\frac{m_c^2}{y(1-y)}$, $\int _{y_i}^{y_f}dy \rightarrow \int _{0}^{1}dy$, $\int _{z_i}^{1-y}dz \rightarrow \int _{0}^{1-y}dz$ when the $\delta$ functions $\delta \left( s-{\overline{m}}_c^2\right)$ and $\delta \left( s-{\widetilde{m}}_c^2\right)$ appear, we neglect the small contributions of the gluon condensate.

According to Eqs. (22, 23), the non-diagonal transitions between the ground state and the excited states can be written as

$$\begin{aligned} \frac{\lambda _Z^2\, C}{M_Z^2-p^2}= & {} \frac{\lambda _{Z^\prime }\lambda _Z\, {\widetilde{G}}_2(0)}{\left( M_Z^2-p^2\right) \left( M_{Z^\prime }^2-p^{\prime 2}\right) }+\cdots . \end{aligned}$$

(31)

If we set $p^{\prime 2}=p^2$ and perform the Borel transform with respect to the variable $P^2=-p^2$, we can obtain

$$\begin{aligned} \frac{\lambda _{Z^\prime }\lambda _Z\, {\widetilde{G}}_2(0)}{M_{Z^\prime }^2-M_Z^2}\left[ \exp \left( -\frac{M_{Z}^2}{T^2}\right) -\exp \left( -\frac{M_{Z^\prime }^2}{T^2}\right) \right] +\cdots .\nonumber \\ \end{aligned}$$

(32)

In Ref. [37], we observe that the Z(4430) can be tentatively assigned to be the first radial excitation of the $Z_c(3900)$ based on the QCD sum rules. If we set $Z^\prime =Z(4430)$, then

$$\begin{aligned} \frac{\exp \left( -\frac{M_{Z^\prime }^2}{T^2}\right) }{\exp \left( -\frac{M_{Z}^2}{T^2}\right) }= & {} 0.11\sim 0.17, \end{aligned}$$

(33)

for the Borel parameter $T^2=(2.2-2.8)\,\mathrm {GeV}^2$. So the terms $\exp \left( -\frac{M_{Z^\prime }^2}{T^2}\right)$, $\exp \left( -\frac{M_{Z^{\prime \prime }}^2}{T^2}\right) , \ldots$ can be neglected approximately, the non-diagonal transitions can be approximated as $\lambda _Z^2 C \exp \left( -\frac{M_{Z}^2}{T^2}\right)$.

3 Numerical results and discussions

The input parameters on the QCD side are taken to be the standard values $\langle {\bar{q}}q \rangle =-(0.24\pm 0.01\, \mathrm {GeV})^3$, $\langle {\bar{q}}g_s\sigma G q \rangle =m_0^2\langle {\bar{q}}q \rangle$, $m_0^2=(0.8 \pm 0.1)\,\mathrm {GeV}^2$, at the energy scale $\mu =1\, \mathrm {GeV}$ [20,21,22, 31, 32, 41], and $m_{c}(m_c)=(1.28\pm 0.03)\,\mathrm {GeV}$ from the Particle Data Group [36]. Furthermore, we set $m_u=m_d=0$ due to the small current quark masses. For the new condensates or vacuum susceptibilities $\chi$, $\kappa$ and $\xi$ induced by the external electromagnetic field, we take two set parameters:

(I):

the old values $\chi =-3\,\mathrm {GeV}^{-2}$, $\kappa =-0.75$, $\xi =1.5$ at the energy scale $\mu =1\, \mathrm {GeV}$ fitted in the QCD sum rules for the magnetic moments of the p, n and $\Lambda$ [31, 32];

(II):

the new values $\chi =-(3.15\pm 0.30)\,\mathrm {GeV}^{-2}$, $\kappa =-0.2$, $\xi =0.4$ at the energy scale $\mu =1\, \mathrm {GeV}$ determined in the detailed QCD sum rules analysis of the photon light-cone distribution amplitudes [42].

The existing values of the vacuum susceptibilities $\chi$, $\kappa$ and $\xi$ are quite different from different determinations, the old values $\chi (\mathrm{1\, GeV})=-(4.4\pm 0.4)\,\mathrm {GeV}^{-2}$ [44] or $-(5.7\pm 0.6)\,\mathrm {GeV}^{-2}$ [45] determined in the QCD sum rules combined with the vector meson dominance, while the most recent value $\chi (\mathrm{1\, GeV})=-(2.85\pm 0.50)\,\mathrm {GeV}^{-2}$ determined in the light-cone QCD sum rules for the radiative heavy meson decays [43]. The old values $\chi =-6\,\mathrm {GeV}^{-2}$, $\kappa =-0.75$, $\xi =1.5$ at the energy scale $\mu =1\, \mathrm {GeV}$ determined in the QCD sum rules for the octet and decuplet baryon magnetic moments [33, 34] are also different from the parameters (I) determined in analysis of the magnetic moments of the p, n and $\Lambda$ [31, 32]. The most popularly used values are the parameters (II) [42], which are consistent with the most recent values determined in Ref. [43]. In the parameters (I), we choose the value $\chi (\mathrm{1\, GeV})=-3\,\mathrm {GeV}^{-2}$ [31, 32] instead of $\chi (\mathrm{1\, GeV})=-6\,\mathrm {GeV}^{-2}$ [33, 34] according to the most recent value $\chi (\mathrm{1\, GeV})=-(2.85\pm 0.50)\,\mathrm {GeV}^{-2}$ [43].

Fig. 3

The form-factor $G_2(0)$ with variation of the Borel parameter $T^2$, where the (I) and (II) denote the parameters (I) and parameters (II), respectively

We take into account the energy-scale dependence of the input parameters from the renormalization group equation,

$$\begin{aligned}&\langle {\bar{q}}q \rangle (\mu )=\langle {\bar{q}}q \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{12}{25}},\nonumber \\&\langle {\bar{q}}g_s \sigma Gq \rangle (\mu )=\langle {\bar{q}}g_s \sigma Gq \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{2}{25}}, \nonumber \\&\chi (\mu )=\chi (Q)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(Q)}\right] ^{\frac{16}{25}} ,\nonumber \\&\kappa (\mu )=\kappa (Q)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(Q)}\right] ^{\frac{36}{25}} ,\nonumber \\&\xi (\mu )=\xi (Q)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(Q)}\right] ^{\frac{36}{25}} ,\nonumber \\&m_c(\mu )=m_c(m_c)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_c)}\right] ^{\frac{12}{25}} ,\nonumber \\&\alpha _s(\mu )=\frac{1}{b_0t}\left[ 1-\frac{b_1}{b_0^2}\frac{\log t}{t} +\frac{b_1^2(\log ^2{t}-\log {t}-1)+b_0b_2}{b_0^4t^2}\right] ,\nonumber \\ \end{aligned}$$

(34)

where $t=\log \frac{\mu ^2}{\Lambda ^2}$, $b_0=\frac{33-2n_f}{12\pi }$, $b_1=\frac{153-19n_f}{24\pi ^2}$, $b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}$, $\Lambda =210\,\mathrm {MeV}$, $292\,\mathrm {MeV}$ and $332\,\mathrm {MeV}$ for the flavors $n_f=5$, 4 and 3, respectively [36, 42, 46, 47], and evolve all the input parameters to the optimal energy scale $\mu =1.4\,\mathrm {GeV}$ to extract the form-factor $G_2(0)$ [10, 24, 48].

The hadronic parameters are taken as $\sqrt{s^0_{Z}}=4.4\,\mathrm {GeV}$, $M_{Z}=3.899\,\mathrm {GeV}$, $\lambda _{Z}=2.1\times 10^{-2}\,\mathrm {GeV}^5$ [10, 48]. In the scenario of tetraquark states, the QCD sum rules indicate that the $Z_c(3900)$ and Z(4430) can be tentatively assigned to be the ground state and the first radial excited state of the axialvector tetraquark states, respectively [37]. We choose the value $\sqrt{s^0_{Z}}=4.4\,\mathrm {GeV}$ to avoid contamination of the Z(4430) and reproduce the experimental value of the mass $M_{Z}=3.899\,\mathrm {GeV}$ from the QCD sum rules. The unknown parameter is fitted to be $C=0.97\,\mathrm {GeV}^{-2}$ and $0.94\,\mathrm {GeV}^{-2}$ for the parameters (I) and (II) respectively to obtain platforms in the Borel window $T^2=(2.2-2.8)\,\mathrm {GeV}^2$.

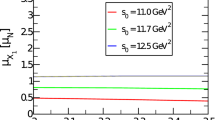
We take into account uncertainties of the input parameters, and obtain the value of the form-factor $G_2(0)$ therefore the magnetic moment $\mu _Z$ of the $Z_{c}(3900)$, which is shown explicitly in Fig. 3,

$$\begin{aligned} |\mu _{Z}|= & {} G_2(0) \,\,\frac{e}{2M_{Z}} \nonumber \\= & {} 1.46^{+0.98}_{-0.80} \,\,\frac{e}{2M_{Z}} \nonumber \\= & {} 0.35^{+0.24}_{-0.19}\,\mu _{N} \quad \mathrm{for} \, \mathrm{parameters}, \mathrm{(I)}, \end{aligned}$$

(35)

$$\begin{aligned}= & {} 1.96^{+1.14}_{-0.91} \,\,\frac{e}{2M_{Z}} \nonumber \\= & {} 0.47^{+0.27}_{-0.22}\,\mu _{N}\quad \mathrm{for} \, \mathrm{parameters}\, \mathrm{(II)}, \end{aligned}$$

(36)

where the $\mu _N$ is the nucleon magneton. The present prediction can be confronted to the experimental data in the future.

As the vacuum susceptibilities $\kappa$ and $\xi$ are less well studied compared to the vacuum susceptibility $\chi$, in Fig. 4, we plot the value of the $G_2(0)$ with variation of the parameter $y=-\kappa (\mathrm{1\,GeV})=\xi (\mathrm{1\,GeV})/2$ for the parameters $T^2=2.5\,\mathrm {GeV}^2$, $\chi (\mathrm{1\,GeV})=-3.15\,\mathrm {GeV}^{-2}$ and $C=0.94\,\mathrm {GeV}^{-2}$. From the figure, we can see that the value of the $G_2(0)$ decreases monotonously with increase of the absolute values of the $\kappa$ and $\xi$. Once the value of the magnetic moment $\mu _Z$ is precisely measured, we can obtain a powerful constraint on the values of the $\kappa$ and $\xi$.

Fig. 4

The form-factor $G_2(0)$ with variation of the parameter $y=-\kappa (\mathrm{1\,GeV})=\xi (\mathrm{1\,GeV})/2$

In Ref. [25], Ozdem and Azizi obtain the magnetic moment $\mu _{Z}=0.67 \pm 0.32\,\mu _N$ from the light-cone QCD sum rules, where the $\mu _{Z}$ decreases monotonously with increase of the Borel parameter, the Borel window is not flat enough. Compared to the QCD sum rules in the external electromagnetic field, the light-cone QCD sum rules have more parameters with limited precision. Furthermore, there exists no experimental data on the electromagnetic multipole moments of the exotic particles X, Y and Z, so theoretical studies play an important role, more theoretical works are still needed. For example, the magnetic moment of the $Z_c(3900)$ as a molecular state is still not studied with the QCD sum rules or light-cone QCD sum rules, a comparison of the two possible assignments is not possible at the present time. We can diagnose the nature of the $Z_c(3900)$ as a genuine resonance or anomalous triangle singularity in the photoproduction process [49]. Experimentally, the COMPASS collaboration observed the X(3872) in the subprocess $\gamma ^*N\rightarrow N^\prime X(3872)\pi ^\pm$ in the process $\mu ^+N\rightarrow \mu ^+ N^\prime X(3872)\pi ^\pm \rightarrow \mu ^+ N^\prime \pi ^+\pi ^- \pi ^\pm$ [50], but have not observed the $Z_c^\pm (3900)$ in the subprocess $\gamma ^*N\rightarrow N^\prime Z_c(3900)^\pm$ in the process $\mu ^+N\rightarrow \mu ^+ N^\prime Z_c(3900)^\pm \rightarrow \mu ^+ N^\prime J/\psi \pi ^\pm$ yet [51]. We can study the photon associated production $\gamma ^*N\rightarrow N^\prime Z_c(3900)^\pm \gamma$ or other processes with the final states $Z_c^\pm (3900)\gamma$ to study the electromagnetic multipole moments of the $Z_c^\pm (3900)$, although it is a difficult work.

4 Conclusion

In this article, we tentatively assign the $Z_c^\pm (3900)$ to be the diquark-antidiquark type axialvector tetraquark state, study its magnetic moment with the QCD sum rules in the external weak electromagnetic field by carrying out the operator product expansion up to the vacuum condensates of dimension 8, and neglect the tiny contributions of the gluon condensate. We pay special attention to matching the hadron side of the correlation function with the QCD side of the correlation function to obtain solid duality, the routine can be applied to study other electromagnetic properties of the exotic particles X, Y and Z directly. Finally, we obtain the magnetic moment of the $Z_c(3900)$, which can be confronted to the experimental data in the future and shed light on the nature of the $Z_c(3900)$.