Is pulsar timing a hopeful tool for detection of relic gravitational waves by using GW150914 data?

Abstract

The inflation stage has a behaviour as power law expansion like $S(\eta )\propto \eta ^{1+\beta }$ where $\beta$ constrained on the $1+\beta <0$. If the inflation were preceded by a radiation era, then there would be thermal spectrum of relic gravitational waves at the time of inflation. Based on this idea we find new upper bound on $\beta$ by comparison the thermal spectrum with strain sensitivity of single pulsar timing. Also we show that sensitivity curve of single pulsar timing may be hopeful tool for detection of the spectrum in usual and thermal case by using the GW150914 data.

1 Introduction

The inflation stage has a behaviour as power law expansion like $S(\eta )\propto \eta ^{1+\beta }$. The S and $\eta$ are scale factor and conformal time respectively and $\beta$ constrained on the $1+\beta <0$¹ [1, 2]. If the inflation were preceded by a radiation era, then there would be thermal spectrum of gravitational waves at the time of inflation [3,4,5]. Based on this idea we have shown in [6] that there is some more chances for the detection of relic gravitational waves (RGWs) in usual and thermal spectrum by using the data of GW150914. On the other hand, there is an important procedure for direct detection of RGWs that called pulsar timing (PT). This procedure is based on the investigation of fluctuation of the pulses of the pulsars due to RGWs. The frequency range of PT is $10^{-9}$–$10^{-6}$ Hz [7]. The authors in [7] have found an upper bound on $\beta$ and shown that there is so low chance for the detection of RGWs by using the mentioned method. But we think that the upper bound on $\beta$ will modify if we use the thermal spectrum. Also the chance of detection of RGWs based on the strain sensitivity of PT will increase by using the obtained $\beta$ for GW150914 [6] in usual and thermal case. Therefore the main purpose of this work is investigation of this detection. In the present work, we use the unit $c=\hbar = k_{B} =1$.

Fig. 1

The spectrum $h_{mc}(\nu )\sqrt{F/\nu }$ of RGWs in usual case (solid line) and thermal case (dashed line) compared to the strain sensitivity of PT (green line)

2 The spectrum of gravitational waves in usual and thermal case

The perturbed metric for a homogeneous isotropic flat Friedmann–Robertson–Walker universe can be written as

$$\begin{aligned} d s^{2}= S^{2}(\eta )\left( d\eta ^{2}-(\delta _{ij}+h_{ij})dx^{i}dx^{j}\right) , \end{aligned}$$

(1)

where $\delta _{ij}$ is the Kronecker delta symbol and $h_{ij}$ are metric perturbations with the transverse-traceless properties i.e; $\nabla _i h^{ij} =0, \delta ^{ij} h_{ij}=0$. The gravitational waves are described with the linearized field equation given by

$$\begin{aligned} \nabla _{\mu } \left( \sqrt{-g} \, \nabla ^{\mu } h_{ij}(\mathbf {x}, \eta )\right) =0. \end{aligned}$$

(2)

The tensor perturbations have two independent physical degrees of freedom $(h^{+}, h^{\times })$ that called polarization modes. We can write $h^{+}$ and $h^{\times }$ in terms of the creation ($a^{\dagger }$) and annihilation (a) operators then,

$$\begin{aligned} h_{ij}(\mathbf{x},\eta )= & {} \frac{\sqrt{16\pi } l_{pl}}{S(\eta )} \sum _\mathbf{{p}} \int \frac{d^{3}k}{(2\pi )^{3/2}} {\varepsilon }_{ij} ^\mathbf{{p}}(\mathbf {k}) \nonumber \\&\times \frac{1}{\sqrt{2 k}} \Big [a_\mathbf{{k}}^\mathbf{{p}}h_\mathbf{{k}}^\mathbf{{p}}(\eta ) e^{i \mathbf {k}.\mathbf {x}} +a^{\dagger }_\mathbf{{k}} {^\mathbf{{p}}} h^{*}_\mathbf{{k}}{^\mathbf{{p}}} (\eta )e^{-i\mathbf {k}.\mathbf {x}}\Big ], \end{aligned}$$

(3)

where $\mathbf {k}$ is the comoving wave number with $k=|\mathbf {k}|$, $l_{pl}= \sqrt{G}$ is the Planck’s length and $\mathbf { p}= +, \times$ are polarization modes. The polarization tensors $\varepsilon _{ij} ^{\mathbf{p}}(\mathbf{k})$ are symmetric and transverse-traceless $k^{i} \varepsilon _{ij} ^{\mathbf{p}}(\mathbf{k})=0, \delta ^{ij} \varepsilon _{ij} ^{\mathbf{p}}(\mathbf{k})=0$ and satisfy the conditions $\varepsilon ^{ij \mathbf{p}}(\mathbf{k}) \varepsilon _{ij}^{\mathbf{p}^{\prime }}(\mathbf{k})= 2 \delta _{ \mathbf{p}{\mathbf{p}}^{\prime }}$ and $\varepsilon ^{\mathbf{p}}_{ij} (\mathbf{-k}) = \varepsilon ^{\mathbf{p}}_{ij} (\mathbf{k})$. Also the creation and annihilation operators satisfy $[a_{\mathbf{k}}^{\mathbf{p}},a^{\dagger }_{\mathbf{k} ^{\prime }} {{^{\mathbf{p}}}^{\prime }}]= \delta _{{\mathbf{p}} \mathbf{{p}}^{\prime } }\delta ^{3}(\mathbf{k}-{\mathbf{k}}^{\prime })$ and the initial vacuum state is defined as

$$\begin{aligned} a_\mathbf{{k}}^\mathbf{{p}}|0\rangle = 0, \end{aligned}$$

(4)

for each $\mathbf {k}$ and $\mathbf {p}$. For a fixed wave number $\mathbf {k}$ and a fixed polarization state $\mathbf {p}$ the Eq. (2) gives coupled Klein–Gordon equation as follows:

$$\begin{aligned} f^{\prime \prime }_{k}+\Big (k^{2}-\frac{S^{\prime \prime }}{S} \Big )f_{k}=0. \end{aligned}$$

(5)

where $h_{k}(\eta )=f_{k}(\eta )/S(\eta )$ [1, 2] and prime means derivative with respect to the conformal time. Since the polarization states are same, we consider $f_{k}(\eta )$ without the polarization index. The solution of the above equation for the different stages of the universe are given in [6]. There is another state that called ‘thermal vacuum state’ see [8] for more details. The strain amplitude of the RGWs in thermal vacuum state are as follows [6, 8]:

$$\begin{aligned} h_{m}(k,\eta _{0})=A\Big (\frac{k_{2}}{k_{H}}\Big )^{\beta } \frac{1}{(1+z_{E})^{3}} \Big ( \frac{k}{k_{2}} \Big )^{\rho },\;\;\;k _{2}\le k \le k _{s}, \end{aligned}$$

(6)

with $\rho =\frac{\log _{10}(h_{2T})_{k_{s}}-\log _{10}(h_{1T})_{k_{2}}}{\log _{10}(k_{s})-\log _{10}(k_{2})}$

$$\begin{aligned} =\dfrac{\log _{10}\Big ( \Big (\frac{k_{s}}{k_{2}} \Big )^{1+\beta } \mathrm {{coth}^{1/2}\Big [\frac{k_{s}}{2T_{g}}\Big ]}\Big )}{\log _{10}\Big ( \frac{k_{s}}{k_{2}}\Big )}, \end{aligned}$$

(7)

where $h_{m}$ is an enhanced amplitude that is called modified amplitude in [8] , $T_{g}=1.52\times 10^{25}\; Mpc^{-1}\simeq 0.905\;K$ [9] see Appendix A for more details, $\gamma$ is $\varOmega _{\varLambda }$ dependent parameter, and $\varOmega _{\varLambda }$ is the energy density contrast. We take the value of redshift $z_{E}\sim 0.3$ and $\gamma \simeq 1.05$ [10] for $\varOmega _{\varLambda }=0.692$ from Planck 2015 [11]. By taking the reduced wavelength $\lambda /2\pi =1/H$ [12, 13], we can obtain $\nu _{2}\simeq 1.4\times 10^{-17}$ Hz, $\nu _{s}\simeq 1.5\times 10^{9}$ Hz. One can get the constant A without scalar running as follows [14]

$$\begin{aligned} A=\dfrac{\varDelta _{R}(k_{0})r^{1/2}}{(1+z_{E})^{\frac{-2-\gamma }{\gamma }}} \left( \frac{\nu _H}{\nu _0}\right) ^{\beta }, \end{aligned}$$

(8)

where $\varDelta ^{2}_{R}(k_{0})$ is the power spectrum of the curvature perturbation evaluated at the pivot wave number $k^{p}_{0}=k_{0}/a(\eta _{0})=0.002$ Mpc$^{-1}$ [15] with corresponding physical frequency $\nu _{0}\simeq 4.9\times 10^{-19}$ Hz and $\nu _{H}\simeq 3.6\times 10^{-19}$ Hz. The $\varDelta ^{2}_{R}(k_{0})=(2.464\pm 0.072\times 10^{-9})$ is given by WMAP9$+$eCMB$+$BAO$+$ $H_{0}$ [16]. The tensor to scalar ratio $r< 0.11 (95 \%CL)$ is based on Planck measurement [17]. We take $r\simeq 0.1$ and also value of redshift $z_{E}=0.3$ for TT, TE, EE+lowP+lensing contribution in this work [11].

Fig. 2

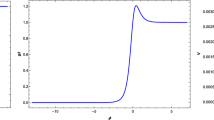
The spectrum $h_{mc}(\nu )\sqrt{F/\nu }$ of RGWs in usual case (solid lines) and thermal case (dashed lines) for two obtained $\beta$ based on GW150914 data [6] compared to the strain sensitivity of PT (green line)

3 The analysis of the spectrum

The expression of the noise spectral density of the relative frequency fluctuations for single pulsar timing is [7]

$$\begin{aligned} S(\nu )=[4.0\times 10^{-31}\nu ^{-1}+3.41\times 10^{-8}\nu ^{2}] Hz^{-1}, \end{aligned}$$

(9)

where the $\nu$ is frequency. We consider the spectrum of RGWs in usual and thermal case in the range $(10^{-9}-10^{-6})$ Hz corresponding to the frequency range of PT. The spectrum of RGWs is related to characteristic strain spectrum like $h_{mc}(\nu )\equiv h_{m}(\nu , \eta _{0})/\sqrt{2}$ [18, 19]. We are interested to $h_{mc}(\nu )\sqrt{F/\nu }$ for SNR $=1$, where we consider the factor $F=1/3$ in this work see [7] for more details. We plot $h_{mc}(\nu )\sqrt{F/\nu }$ of RGWs compared to the strain sensitivity of PT based on Eqs. (6, 9) in Fig. 1, respectively. We can see the obtained upper bound on $\beta =-1.955$ is modified compared to the $\beta =-1.9$ that obtained in [7] corresponds to the thermal spectrum for the lower frequency. Also we plot the spectrum $h_{mc}(\nu )\sqrt{F/\nu }$ of RGWs for the obtained $\beta$ based on the GW150914 data [6] compared to the strain sensitivity of PT in Fig. 2. The obtained results tell us that there is more chance for detection of RGWs for the spectrum in usual and thermal case.

Therefore based on the our results, the PT may be more hopeful tool for the detection of RGWs.

4 Discussion and conclusion

The thermal spectrum of RGWs causes an enhanced amplitude that called ‘modified amplitude’. The obtained results based on the thermal spectrum cause new upper bound on $\beta$ which can give us more information about the inflation. Also using the obtained amounts of $\beta$ based on the GW150914 data tell us that PT may be more hopeful tool for detection of RGWs in usual and thermal case.

Appendix A: extra-dimensional scenario and thermal gravitons

Cosmology with extra dimensions has been motivated by Kaluza and Klein (KK) [20,21,22]. The modern scenarios involving extra dimensions are being explored in particle physics, with most models possessing either a large volume or a large curvature. Although there exist different models of extra dimensions, there are some general features and signals common to all of them. In the presence of D extra spatial dimensions, the $(3+D+1)$-dimensional action for gravity can be written as

$$\begin{aligned} S=\int d^{4}x \Big [\int d^{D}y\sqrt{-g_{D}}\frac{R_{D}}{16\pi G_{D}}+\sqrt{-g}L_{m}\Big ], \end{aligned}$$

(A.1)

where

$$\begin{aligned} G_{D}=G_{N}\frac{m^{2}_{pl}}{m^{2+D}_{D}}, \end{aligned}$$

(A.2)

and $m_{pl}$ is Planck mass, g is the four-dimensional metric, $G_{N}$ is Newton’s constant, $g_{D}, G_{N}$ and $R_{D}$ denote the higher dimensional counterparts of the metric, Newton’s constant, and the Ricci scalar, respectively. The factor $m_{D}$ is the fundamental scale of the extra-dimensional theory.

Since the gravitational interactions are not strong enough to produce a thermal gravitons at temperatures below the Planck scale $(m_{pl}\sim 1.22\times 10^{19}$ GeV), the standard inflationary cosmology predicted the existence of the cosmic gravitational wave backgrounds which are non-thermal in nature. However if the universe contains extra dimensions that can generate the thermal gravitational waves, then its shape and amplitude of the stochastic cosmic background of gravitational waves (CGWB) may change significantly. This can happen when energies in the universe are higher than the fundamental scale $m_{D}$. The gravitational coupling strength increases significantly as the gravitational field spreads out into the full spatial volume. Instead of freezing out at $O(m_{pl})$, as in $3+1$ dimensions, gravitational interactions freeze-out at $\sim O (m_{D})$. If the gravitational interactions become strong at an energy scale below the reheat temperature $(m_{D}< T_{RH})$, gravitons get the opportunity to thermalize, creating a thermal CGWB. The creation of a thermal CGWB if $(m_{D}< T_{RH})$, is unchanged by the type of extra dimensions chosen [9].

Thus, if extra dimensions do exist and the fundamental scale of those dimensions is below the reheat temperature, a relic thermal CGWB ought to exist today. Compared to the relic thermal photon background (CMB), a thermal CGWB would have the same shape, statistics and high degree of isotropy and homogeneity. The energy density ($\rho _{g}$) and fractional energy density ($\varOmega _{g}$) of a thermal CGWB are

$$\begin{aligned} \rho _{g}= & {} \frac{\pi ^{2}}{15}\Big (\frac{3.91}{g_{*}}\Big )^{4/3}T^{4}_{CMB}, \end{aligned}$$

(A.3)

$$\begin{aligned} \varOmega _{g}= & {} \frac{\rho _{g}}{\rho _{c}}\simeq 3.1\times 10^{-4}(g_{*})^{4/3}, \end{aligned}$$

(A.4)

where $\rho _{c}$ is the critical energy density today, $T_{CMB}$ is the present temperature of the CMB and $g_{*}$ is the number of relativistic degrees of freedom at the scale of $m_{D}$. $g_{*}$ is dependent on the particle content of the universe, i.e. whether (and at what scale) the universe is supersymmetric, has a KK tower, etc. Other quantities, such as the temperature (T), peak frequency ($\nu$), number density (n), and entropy density (s) of the thermal CGWB can be derived from the CMB if $g_{*}$ is known, as

$$\begin{aligned} n_{g}= & {} n_{CMB}\Big (\frac{3.91}{g_{*}}\Big ),\;\;\;\;s_{g}=s_{CMB}\Big (\frac{3.91}{g_{*}}\Big ), \end{aligned}$$

(A.5)

$$\begin{aligned} T_{g}= & {} T_{CMB}\Big (\frac{3.91}{g_{*}}\Big )^{1/3},\;\;\;\;\nu _{g}=\nu _{CMB}\Big (\frac{3.91}{g_{*}}\Big )^{1/3}. \end{aligned}$$

(A.6)

These quantities are not dependent on the number of extra dimensions, as the large discrepancy in size between the three large spatial dimensions and the D extra dimensions suppresses those corrections by at least a factor of $\sim 10^{-29}$. If $m_{D}$ is just barely above the scale of the standard model, then $g_{*}=106.75$. The thermal CGWB then has a temperature of $T_{g}=1.52\times 10^{25} Mpc ^{-1}\simeq 0.905 \;K$ and a peak frequency of 19 GHz [9].