Abstract
We study the width of a two-body resonance in a coupled-channel system. We demonstrate how the width does not come only determined by the available phase space for its decay to the detection channel, but it greatly depends on the relative position of the mass of the resonance with respect to the masses of the coupled-channels generating the state. Our results are consistent with the experimental observation of narrow hadrons lying well above their lowest decay threshold.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During the last years we have witnessed a flurry of new resonances in the heavy hadron spectra with unexpected properties, see the compilation of theoretical and experimental works in Refs. [1,2,3,4,5] for a comprehensive overview. Apart from the fact that some of these states have exotic flavor character or quantum numbers, in several cases another striking result is the lack of a clear relation between the phase space available for the decay in the detection channel and the width of the resonance. For example, in the case of the lower LHCb pentaquark \(P^+_c(4380)\) [6,7,8] with a mass of \(4380\, \pm \, 8 \, \pm \, 29\) MeV, it is seen to decay to the \(J/\Psi p\) channel with a width \(\Gamma = 205 \, \pm \, 18 \, \pm \, 86\) MeV. The phase space is of the order of 345 MeV. Some of these states share the common feature that they have been suggested as possible coupled-channel hadronic resonances [1,2,3,4,5], and thus the coupled-channel dynamics may play a basic role to understand their main features, in particular the width.
In this work we show how the width of a two-body resonance generated in a coupled-channel approach does not come only determined by the available phase space for its decay to the detection channel, but it substantially depends on the relative position of the mass of the resonance with respect to the masses of the coupled-channels generating the state. Thus, one could expect the existence of narrow hadrons lying well above their lowest decay threshold, in agreement with experimental observations.
2 Formalism
We have studied the behavior of the width of a resonance for those cases where it is produced between two thresholds, thanks to a coupling between the two corresponding configurations within the resonance as suggested, for example, in Refs. [9, 10]. For this purpose, we have modelled the system as a coupled-channel problem obeying the non-relativistic Lippmann–Schwinger equation. Channel 1, the lower in mass, consists of two particles with masses \(m_1\) and \(m_2\), and channel 2, the upper in mass, is made of two particles with masses \(m_3\) and \(m_4\). The Lippmann–Schwinger equation in the case of S-wave interactions is written as,
where \(\mu _1=m_1 m_2/(m_1+m_2)\) and \(\mu _2=m_3 m_4/(m_3+m_4)\) are the reduced masses of channels 1 and 2, and \(\Delta E=m_3+m_4-m_1-m_2\) with \(m_3+m_4 > m_1+m_2\). The interactions in momentum space are given by,
where the two-body potentials, which are the inputs to our present study, consist of an attractive and a repulsive Yukawa term, i.e.,
This type of parametrization is known to work rather well for the study of two-, three-, and few-baryon systems [11, 12] and, thus, it is adopted here. We have considered scenarios where a resonance exists at an energy \(E=E_R\) such that the phase shift \(\delta (E_R)=90^\circ \), for energies between the thresholds of channels 1 and 2, i.e., \(0< E_R < \Delta E\). The mass of the resonance would be given by \(W_R=E_R + m_1 +m_2\). The width of the resonance is calculated using the Breit–Wigner formula as [13,14,15,16],
3 Interacting model
We have parametrized the scenario depicted above, that might be applied to several heavy resonances recently reported in the heavy hadron spectra [1,2,3,4,5]. Without loss of generality, we make use of the same thresholds recently considered in a more involved three-body calculation [17]: \(m_1=m_2=1115.7\) MeV/c\(^2\), \(m_3=938.8\) MeV/c\(^2\), and \(m_4=1318.2\) MeV/c\(^2\). None of the results we will later on discuss critically depend on the choice of the masses of the particles constituting the thresholds. As said above, the interaction in the different channels is described by Yukawa potentials consisting of an attractive and a repulsive term. By varying the parameters one is able to control the existence of a bound state or a resonance and its relative position with respect to the thresholds, in the cases where the dynamics is dominated by two channels. We have chosen as starting point the set of parameters given in Table 1.
They are adjusted such that in a single-channel calculation, the upper channel (channel 2) has a bound state just at threshold, while in a coupled-channel calculation, the full system has a bound state just at the lower threshold (channel 1).
4 Results
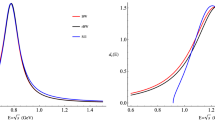
If one increases, for example, the magnitude of the repulsive term in the lower channel, \(B(1\leftrightarrow 1)\) in Table 1, the bound state of the coupled-channel system moves up and actually becomes a resonance into the continuum. Thus, one can study the behavior of the width of the resonance when its mass evolves from the lower threshold, channel 1, to the upper one, channel 2. The result is shown in Fig. 1.
As one can see, the width of the resonance starts increasing quickly when getting away from the lower threshold, but about a third of the way towards the upper channel, the width starts to decrease although the phase space with respect to the threshold where the resonance is observed still increases.Footnote 1 When the resonance approaches the upper threshold, it becomes narrow and seemingly ignores the existence of the lower threshold. The wave function of the \((m_3,m_4)\) bound state of vanishing energy has, indeed, little overlap with the \((m_1,m_2)\) configuration. The same trend is obtained for different strengths of the coupling interaction in Table 1, channel \(1\leftrightarrow 2\), or by diminishing the repulsion in the upper channel, \(B(2\leftrightarrow 2)\). Hence, in this region, the dynamics is dominated by the attraction in the upper channel and the second channel is mainly a tool for the detection. This mechanism is somewhat related to the ’synchronization of resonances’ proposed by Bugg [18].
The mechanism we have discussed could help to understand the narrow width of some experimental resonances found in the heavy hadron spectra with a large phase space in the detection channel, whose assumed internal structure allow them to split into different subsystems [1, 3, 9, 10]. In this case the transition potential between the upper and lower channels would come from the quark rearrangements allowed by the color structure of a multiquark state [4, 19]. In particular, it has been explained in Ref. [19] how hadrons with a \(Q\bar{Q} n\bar{n}\) internal structure, where n stands for a light quark and Q for a heavy one, could split either into \((Q \bar{n}) - (n \bar{Q})\) or \((Q \bar{Q}) - (n \bar{n})\). For \(Q=c\) and \(Q=b\), the \((Q \bar{Q}) - (n \bar{n})\) threshold is lower than the \((Q \bar{n}) - (n \bar{Q})\), the mass difference augmenting when increasing the mass of the heavy quark (see Fig. 1 of Ref. [19]). Such experimental behavior can be simply understood within quark models with a Cornell-like potential [20, 21]. Each configuration can indeed evolve into the other one, so they cannot be considered one at a time: we are dealing with a compact object, whose quark color quantum numbers are not separately conserved during time evolution. This state is not a simple bound state of mesons. Thus, the possibility of finding meson–antimeson molecules, \((Q \bar{n}) - (n \bar{Q})\), contributing to the heavy meson spectra becomes more and more difficult when increasing the mass of the heavy flavor, due to the lowering of the mass of the \((Q \bar{Q}) - (n\bar{n})\) threshold.Footnote 2 This would make the system to dissociate immediately. In such cases, the presence of an attractive meson–antimeson upper threshold together with the arguments we have drawn in this work, hint to a possible explanation of a narrow width of some of the XYZ states lying close to the \((Q \bar{n}) - (n \bar{Q})\) upper threshold as a meson–antimeson molecule, emphasizing the basic role of coupled-channel dynamics [23]. The situation described above would be similar to a Feshbach resonance, where the open channel is represented by the \((Q \bar{Q}) - (n\bar{n})\) state that would get trapped in a molecular state supported by the closed channel potential \((Q \bar{n}) - (n \bar{Q})\) [24, 25].
An interesting case appears when the thresholds generating the resonance come rather close, because in this case one would find small decay widths for the resonance in between the thresholds, that would become even smaller when approaching any of them. This is illustrated in Fig. 2, where we have reduced the mass difference between the upper and lower thresholds up to 5.6 MeV. This situation may apply directly to the width of one the most elusive exotic states, that however has been firmly established by different collaborations and whose properties seem to be hardly accommodated in the quark–antiquark scheme, this is the X(3872) [26,27,28,29].Footnote 3 Its small width, \(\Gamma < 1.2\) MeV, would fit our reasoning seeing as a coupled-channel of \({D}^0\bar{D}^{*0} - D^+\bar{D}^{*-}\), with a mass difference of 7−8 MeV and being rather close to the lowest threshold [24, 31]. There also could be a contribution from other channels, like \(J/\Psi \omega \) [31, 32], that it is almost degenerate with the upper threshold \(D^+\bar{D}^{*-}\), and thus our conclusions would remain. Similar arguments could be handled for the LHCb pentaquarks, which require a careful analysis in the models used for their study.
It is obvious that the situation may become even more involved in the case of a resonance that appears in a coupled-channel system with a larger number of channels. However, the described systematic of our findings would not be modified, requiring a proper knowledge of the structure of the resonance before estimating its decay width. The other way around, one may conclude that an unexpected behavior of the width of the resonance may be indicating an important contribution of coupled-channel dynamics and the knowledge of the decay width in a particular channel would hint to the upper threshold contributing to the formation of the resonance. This has been illustrated in Fig. 3, where we have calculated the width of the resonance for a fixed value of its mass with respect to the lower threshold, \(\Delta E_{Th} = W_R-m_1-m_2=\) 6.5 MeV, but increasing the distance with respect to the upper threshold, \(\Delta E^\prime _{Th} = m_3+m_4-W_R\). For this purpose, we have diminished the mass of the lower channel in steps of 5 MeV, thus increasing the distance between thresholds, \(m_3+m_4-m_1-m_2\), and we have increased \(A(1\leftrightarrow 1)\) in Table 1 in such a way that \(\Delta E_{Th} =W_R-m_1-m_2=\) 6.5 MeV remains constant. The result is striking, being the phase space fixed for the detection channel, the width increases when the upper threshold moves away. Thus the width provides also with basic information about the coupled channels that may contribute to the formation of a resonance.
5 Conclusion
In this work we have studied the width of a two-body resonance in a coupled-channel system. We have demonstrated how the width does not come only determined by the available phase space for its decay to the detection channel, but it greatly depends on the relative position of the mass of the resonance with respect to the masses of the coupled-channels generating the state. Our results are consistent with the experimental observation of narrow hadrons lying well above their lowest decay threshold. Thus, they may be relevant to understand the basic features of some of the recently reported resonances in the heavy hadron spectra which are suggested to be generated by coupled-channel effects. We have also demonstrated how an unexpected behavior of the width of the resonance may be indicating an important contribution of coupled-channel dynamics. The other way around, the observation of a small width in a detection channel hints to a dominant contribution of some upper channel to the formation of the resonance. Hence, in this region, the dynamics is dominated by the attraction in the upper channel and the second channel is mainly a tool for the detection.
Let us finally note that although the exact shape of the dependence of the width on its position with respect to the detection channel would depend on the specific dynamics of the coupled-channel system, the gross features obtained in this study might be a relevant and basic hint to explore the nature of some of the exotic states.
Notes
Note, however, that there exist some studies [30] finding a good fit of the data with mainly a \(c\bar{c}\) structure.
References
H.-X. Chen, W. Chen, X. Liu, Y.-R. Liu, S.-L. Zhu, Rep. Prog. Phys. 80, 076201 (2017)
H.-X. Chen, W. Chen, X. Liu, S.-L. Zhu, Phys. Rep. 639, 1 (2016)
A. Esposito, A. Pilloni, A.D. Polosa, Phys. Rep. 668, 1 (2016)
J.-M. Richard, Few Body Syst. 57, 1185 (2016)
A. Hosaka, T. Iijima, K. Miyabayashi, Y. Sakai, S. Yasui, Prog. Theor. Exp. Phys. 062C01 (2016)
R. Aaij et al., LHCb Collaboration. Phys. Rev. Lett. 115, 072001 (2015)
R. Aaij et al., LHCb Collaboration. Phys. Rev. Lett. 117, 082002 (2015)
R. Aaij et al., LHCb Collaboration. Phys. Rev. Lett. 117, 082003 (2015)
H. Huang, J. Ping, F. Wang, Phys. Rev. C 87, 034002 (2013)
H. Huang, C. Deng, J. Ping, F. Wang, Eur. Phys. J. C 76, 624 (2016)
R.A. Malfliet, J.A. Tjon, Nucl. Phys. A 127, 161 (1969)
I. Filikhin, V.M. Suslov, B. Vlahovic, Math. Model. Geom. 5, 1 (2017)
G. Breit, E. Wigner, Phys. Rev. 49, 519 (1936)
S. Ceci, M. Korolija, B. Zauner, Phys. Rev. Lett. 111, 112004 (2013)
S. Ceci, A. Švarc, B. Zauner, D.M. Manley, S. Capstick, Phys. Lett. B 659, 228 (2008)
S. Ceci, M. Vukšić, B. Zauner, arXiv:1408.2437
H. Garcilazo, A. Valcarce, Phys. Lett. B 772, 394 (2017)
D.V. Bugg, Int. J. Mod. Phys. A 24, 394 (2009)
T.F. Caramés, A. Valcarce, J. Vijande, Phys. Lett. B 709, 358 (2012)
N. Isgur, Phys. Rev. D 60, 054013 (1999)
F. Close, AIP Conf. Proc. 717, 919 (2004)
J.-M. Richard, A. Valcarce, J. Vijande, Phys. Rev. D 95, 054019 (2017)
J. Vijande, A. Valcarce, Phys. Lett. B 736, 325 (2014)
E. Braaten, M. Kusunoki, Phys. Rev. D 69, 074005 (2004)
A. Pilloni, Acta Phys. Pol. B Proc. Suppl. 7, 463 (2014)
S.K. Choi et al., Belle Collaboration. Phys. Rev. Lett. 91, 262001 (2003)
D. Acosta et al., CDF Collaboration. Phys. Rev. Lett. 93, 072001 (2004)
V.M. Abazov et al., D0 Collaboration. Phys. Rev. Lett. 93, 162002 (2004)
B. Aubert et al., BaBar Collaboration. Phys. Rev. D 71, 071103 (2005)
C. Meng, J.J. Sanz-Cillero, M. Shi, D.-L. Yao, H.-Q. Zheng, Phys. Rev. D 92, 034020 (2015)
E. Braaten, M. Lu, Phys. Rev. D 77, 014029 (2008)
T. Fernández-Caramés, A. Valcarce, J. Vijande, Phys. Rev. Lett. 103, 222001 (2009)
Acknowledgements
This work has been partially funded by COFAA-IPN (México), by Secretaría de Estado de Investigación, Desarrollo e Innovación, Ministerio de Economía, Industria y Competitividad and EU FEDER under Contracts nos. FPA2016-77177-C2-2-P and FPA2015-69714-REDT, and by Consejería de Educación, Junta de Castilla y León under Contract no. SA041U16.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Garcilazo, H., Valcarce, A. Width of a two-body coupled-channel resonance. Eur. Phys. J. C 78, 259 (2018). https://doi.org/10.1140/epjc/s10052-018-5747-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5747-7