1 Introduction

What is the origin of mass? This question has attracted a lot of interests as a big mystery in elementary particle physics. It has been established by the Large Hadron Collider (LHC) [1, 2] that there exists a scalar particle, namely, the Higgs boson, which, as a result of the spontaneous symmetry breaking, gives the particles in the standard model (SM) a finite mass. It is, however, unknown how the Higgs field acquires a finite vacuum expectation value. This is still an open question for a deeper understanding of the origin of the mass of the SM particles.

The Higgs boson mass parameter is the only dimensionful parameter and breaks the scale invariance in the SM. Its breaking is soft and from this reason Bardeen [3] argued that “the SM does not, by itself, have a fine tuning problem due to the approximate scale invariance of the perturbative expansion”.Footnote 1 The recent idea of a scale invariant extension of the SM in fact goes back to this observation of Bardeen. Since the scale invariant classical SM action does not provide the EW scale, it has to be generated by quantum effects. We here call it “scalegenesis”.

A possible way to realize scalegenesis in perturbation theory is the Coleman–Weinberg mechanism [5], where the origin of scale is the renormalization scale that has to be introduced unless scale anomaly is cancelled. This mechanism cannot, however, yield a stable EW vacuum in the SM without contradicting with the observed Higgs boson mass. Therefore, extensions of the Higgs sector are required. Along this line of thought, numerous studies have been dedicated to explain the origin of the EW vacuum.

An alternative approach to realize scalegenesis relies on non-perturbative dynamics. As is well known, in Quantum chromodynamics (QCD), whose action is given as a scale invariant form except for the current quark mass term, a non-trivial vacuum is generated by the strong dynamics of non-Abelian gauge interactions in the infrared energy regime. The classically scale invariant extensions of the SM based on the hidden QCD and their phenomenological implications have been recently discussed in [6,7,8,9,10,11,12,13,14,15,16,17,18,19].

In this paper, we consider scalegenesis realized by another non-perturbative dynamics. We introduce a scale invariant hidden sector, which is described by an \(SU(N_c)\) non-Abelian gauge theory coupled with \(N_f\) complex scalar fields \(S_i\) in the fundamental representation of \(SU(N_c)\), where the index i denotes the flavor species. Due to the strong dynamics in the hidden sector, the scalar bi-linear condensate \(\langle S_i^\dagger S_j\rangle \) forms, triggering the EW symmetry breaking via the Higgs portal coupling \(\lambda _{HS,ij}S_i^\dagger S_jH^\dagger H\) [20, 21]. That is, the dynamical scale symmetry breaking takes place in the hidden sector. Even though analytic treatments of non-perturbative dynamics are highly complicated, several approaches are available: One of the possibilities is an effective theory approach to the non-perturbative dynamics. Indeed, the Nambu–Jona-Lasinio (NJL) model [22, 23] has been successfully employed to understand the dynamical chiral symmetry breaking in QCD. It seems obvious that the basic idea of the NJL model in QCD can be applied to formulate an effective theory that describes the dynamical scale symmetry breaking. The first attempt was made in Ref. [21], in which the hidden sector is effectively described by a scale invariant scalar field theory. Since the \(U(N_f)\) flavor symmetry is unbroken by the scalar bi-linear condensate (i.e., \(\langle S_i^\dagger S_j\rangle \propto \delta _{ij})\), the excited states above the vacuum with \(\langle S_i^\dagger S_j\rangle \ne 0\) are stable and can be identified with a weakly interacting massive particle (WIMP) dark matter (DM). The DM relic abundance \(\Omega h^2\) and its spin-independent cross section off the nucleon \(\sigma _{\mathrm{SI}}\) have been computed by using the mean-field approximation [21]. It has been found there that \(\sigma _{\mathrm{SI}}\) of the model is bounded from below and is just at the border of the experimental upper bound of XENON100 [24, 25]. Since then there have been progresses in experiments [26,27,28], so that the minimal model may be running into problems with experimental constraints in future. The reason why \(\sigma _{\mathrm{SI}}\) cannot be made small while maintaining a correct value of \(\Omega h^2\) is that the portal coupling \(\lambda _{HS}\) acts on \(\Omega h^2\) and \(\sigma _{\mathrm{SI}}\) in an opposite direction. Therefore, as long as the \(U(N_f)\) flavor symmetry is intact, we cannot avoid this problem.

The main feature of the modified model presented in the present work is that the \(U(N_f)\) flavor symmetry is explicitly broken by the quartic scalar couplings. Specifically, we consider the case of the U(2) flavor symmetry, which is broken by the quartic scalar couplings down to \(U(1)\times U(1)\). In the \(U(1)\times U(1)\) invariant model there is one complex scalar for the DM candidate, while there are three real stable scalars in the U(2) invariant model. The benefit of the explicit breaking of U(2) is that due to the presence of the would-be DM candidate (the third scalar in the U(2) invariant model) a new annihilation process for DM at finite temperature becomes available, which is independent of \(\lambda _{HS}\).

In the following section we start by modifying the minimal model and elucidate our mean field approximation to the strong dynamics, which is successively applied to compute effective interactions of DM in Sect. 4. They are finally used to obtain \(\Omega h^2\) and \(\sigma _{\mathrm{SI}}\) in Sect. 5. The last section is devoted to our conclusion.

2 The model

We extend the classical scale invariant extension of the SM, which has been studied in [21, 29, 30]. The hidden sector, in which the EW scale originates, is described by an \(SU(N_c)\) gauge theory with the scalar fields \(S_i^{a}\) (\(a=1,\ldots ,N_c\), \(i=1,\ldots ,N_f\)) in the fundamental representation of \(SU(N_c)\). Instead of the \(U(N_f)\) flavor symmetry, which was assumed in [21, 29, 30], we assume here only \(U(1)^{N_f}\) symmetry. The total \(U(1)^{N_f}\) invariant Lagrangian for the extended model is given by

$$\begin{aligned} {{\mathcal {L}}}_{\mathrm{H}}&= -\frac{1}{2}\text{ tr }\,\{F_{\mu \nu }F^{\mu \nu }\} +\left( [D^\mu S_i]^\dag D_\mu S_i \right) \nonumber \\&\quad -{\hat{\lambda }}_{S_{ij}}(S_i^\dag S_i) (S_j^\dag S_j)\nonumber \\&\quad -\hat{\lambda '}_{S_{ij}} (S_i^\dag S_j)(S_j^\dag S_i) +{\hat{\lambda }}_{HS_{i}}(S_i^\dag S_i)H^\dag H\nonumber \\&\quad -\lambda _H ( H^\dag H)^2+{{\mathcal {L}}}'_{\mathrm {SM}}, \end{aligned}$$
(1)

where the parenthesis (  ) stands for \(SU(N_c)\) invariant products, \(D_\mu S_i = \partial _\mu S_i -ig_H G_\mu S_i\), \(G_\mu \) is the matrix-valued \(SU(N_c)\) gauge field, \(F_{\mu \nu }\) is the field strength tensor of \(G_\mu \), the SM Higgs doublet field is denoted by H, and \({{\mathcal {L}}}'_{\mathrm {SM}}\) contains the SM gauge and Yukawa interactions. The scale-invariance violating Higgs mass term is absent in (1).

Our basic assumption is as before that the origin of the EW scale is a scalar-bilinear condensation,

$$\begin{aligned} \langle (S^\dag _i S_j) \rangle = \langle \sum _{a=1}^{N_c} S^{a\dag }_i S^a_j \rangle =f_{ij}, \end{aligned}$$
(2)

which forms due to the \(SU(N_c)\) gauge interaction and triggers the EW symmetry breaking through the Higgs portal coupling \({\hat{\lambda }}_{HS_i}\). The condensation (2) will also generate the mass term (constituent mass) for \(S_i\) dynamically. In [21, 29, 30] we have proposed to describe this non-perturbative phenomena of condensation approximately by using an effective theory. As in the case of the NJL theory, which can effectively describe the dynamical chiral symmetry breaking in QCD, the effective Lagrangian contains only the “constituent” scalar fields \(S_i^{a}\). Furthermore, in writing down the effective Lagrangian at the tree level, we have ignored the presence of scale anomaly, because its breaking is only logarithmic and cannot generate a mass term. That is, the breaking of scale invariance is hard, but not soft. Here we restrict ourself to the minimal model, i.e., to \(N_f=2\). The effective Lagrangian then can be written as

$$\begin{aligned} {{\mathcal {L}}}_{\mathrm{eff}}= & {} ([\partial ^\mu S_i]^\dag \partial _\mu S_i)- \lambda _{1}(S_1^\dag S_1) (S_1^\dag S_1)\nonumber \\&\quad - \lambda _{2}(S_2^\dag S_2) (S_2^\dag S_2) -\lambda _{12} (S_1^\dag S_1)(S_2^\dag S_2)\nonumber \\&\quad -\lambda '_{12}(S_1^\dag S_2) (S_2^\dag S_1) +\lambda _{HS_i}(S_i^\dag S_i)H^\dag H \nonumber \\&\quad -\lambda _H ( H^\dag H)^2, \end{aligned}$$
(3)

where all coupling constants are positive, and

$$\begin{aligned} \lambda _{1}&= \lambda _{{S11}} + \lambda _{{S11}}^{\prime } ,\quad \lambda _{2} = \lambda _{{S22}} + \lambda _{{S22}}^{\prime } ,\nonumber \\&\quad \lambda _{{12}} = \lambda _{{S12}} + \lambda _{{S21}} ,\quad \lambda _{{12}}^{\prime } = \lambda _{{S12}}^{\prime } + \lambda _{{S21}}^{\prime }. \end{aligned}$$
(4)

The effective Lagrangian \({{\mathcal {L}}}_{\mathrm{eff}}\) is the most general form which is consistent with the global \(SU(N_c)\times U(1)^{N_f}\) symmetry and the classical scale invariance.Footnote 2 Needless to say that \({{\mathcal {L}}}_\mathrm{eff}\) has the same global symmetry as \({{\mathcal {L}}}_{\mathrm{H}}\) even at the quantum level. Note also that, though the structure of the quartic couplings of S in \( {{\mathcal {L}}}_{\mathrm{eff}}\) is the same as that in \( {{\mathcal {L}}}_{\mathrm{H}}\), the couplings \({\hat{\lambda }}_{S_{ij}}, \hat{\lambda '}_{S_{ij}}\), and \({\hat{\lambda }}_{HS_i}\) in \(\mathcal{L}_{\mathrm{H}}\) are not the same as \(\lambda _{S}, \lambda '_{S}\), and \(\lambda _{HS}\) in \( {{\mathcal {L}}}_{\mathrm{eff}}\), because the unhatted ones are dressed by the \(SU(N_c)\) gauge field contributions.

3 Physical quantities within mean field approximation

We employ the auxiliary field method to investigate the vacuum structure of the effective Lagrangian \({{\mathcal {L}}}_{\mathrm{eff}}\). In particular, we here would like to see that the non-perturbative dynamics described by \({{\mathcal {L}}}_{\mathrm{eff}}\) actually realizes the non-trivial vacuum (2) in the hidden sector. To this end, we introduce auxiliary fields \(f_i\) and \(\phi ^{\pm }\) (\(\phi ^+=(\phi ^-)^*\)) and add

$$\begin{aligned} {{\mathcal {L}}}_{\mathrm{ax}}= \lambda _1 f_{1}^2+\lambda _2 f_{2}^2+ \lambda _{12} f_{1} f_{2}+ \frac{1}{2}\lambda '_{12} \phi ^+ \phi ^-, \end{aligned}$$
(5)

to the effective Lagrangian (3). Note that since the path integrals of \(f_i\), \(\phi ^\pm \) are Gaussian ones, at the tree-level, the contributions from these fields have no effects on the effective theory. We then shift them according to

$$\begin{aligned}&f_{1} \rightarrow f_{1} -(S_1^\dag S_1), f_{2} \rightarrow f_{2} -(S_2^\dag S_2),\nonumber \\&\quad \phi ^+ \rightarrow \phi ^+ -\sqrt{2}(S_2^\dag S_1), \phi ^- \rightarrow \phi ^- -\sqrt{2}(S_1^\dag S_2), \end{aligned}$$
(6)

to obtain the mean-field Lagrangian

$$\begin{aligned} {{\mathcal {L}}}_{\mathrm{MFA}}&= ([\partial ^\mu S_i]^\dag \partial _\mu S_i) -M_{i0}^2(S_i^\dag S_i) + \lambda _1 f_{1}^2 \nonumber \\&\quad + \lambda _2 f_{2}^2 + \lambda _{12} f_{1}f_{2}\nonumber \\&\quad -\lambda _H(H^\dag H)^2+\frac{\lambda _{12}'}{2}\phi ^+\phi ^-\nonumber \\&\quad -\frac{\lambda '_{12}}{\sqrt{2}}\phi ^+(S^\dag _1 S_2) -\frac{\lambda '_{12}}{\sqrt{2}}\phi ^-(S^\dag _2 S_1), \end{aligned}$$
(7)

where

$$\begin{aligned} M_{10}^2&= 2\lambda _1 f_{1}+\lambda _{12} f_{2}- \lambda _{HS_1} H^\dag H,\nonumber \\ M_{20}^2&=2\lambda _2 f_{2}+\lambda _{12} f_{1} - \lambda _{HS_2} H^\dag H. \end{aligned}$$
(8)

Note that the mean-field Lagrangian reduces to \({{\mathcal {L}}}_{\mathrm{eff}}\) when the tree-level equations of motion for the auxiliary fields, \(f_{i} =(S_i^\dag S_i),~\phi ^+ =\sqrt{2}(S_2^\dag S_1)\), are plugged into (7).

To proceed with the mean-field approximation, we have to derive the effective potential \(V_\text {MFA}\) for our problem. By assumption the non-perturbative effect of the original gauge theory breaks neither the hidden \(SU(N_c)\) color symmetry nor the \(U(1)\times U(1)\) flavor symmetry , which means that \(\langle S_i \rangle =0\) and \(\langle (S_2^\dag S_1) \rangle =\langle \phi ^+ \rangle /\sqrt{2} = \langle (S_1^\dag S_2) \rangle =\langle \phi ^- \rangle /\sqrt{2} =0\). Therefore, we ignore the last three terms involving \(\phi ^\pm \) in (7) and calculate the \(V_\text {MFA}\) by integrating out the scalar fields S whose integration is Gaussian. Then, we find the effective potential:

$$\begin{aligned} V_\text {MFA}\!\left( f,H\right)&= - \lambda _1 f_{1}^2 - \lambda _2 f_{2}^2 -\lambda _{12} f_{1}f_{2}+\lambda _H (H^\dag H)^2 \nonumber \\&\quad +\frac{N_c}{32\pi ^2}M_{10}^4 \ln \frac{M_{10}^2}{\Lambda _H^2}+ \frac{N_c}{32\pi ^2}M_{20}^4 \ln \frac{M_{20}^2}{\Lambda _H^2}, \end{aligned}$$
(9)

where \(M_{i0}^2\) are given in (8), the ultraviolet divergence was subtracted with the \(\overline{\mathrm{MS}}\) scheme, and \(\Lambda _H=\mu e^{-3/4}\) is a renormalization scale at which the quantum corrections vanish.

We here stress that the scale is generated by quantum effects within the scaleless effective theory (3).Footnote 3 This scale characterizes the origin of the scales of both the hidden sector and the EW.

The minima of the effective potential (9) can be obtained from the solution of the gap equationsFootnote 4

$$\begin{aligned} 0&= \frac{\partial }{\partial f_{i}}V_{\mathrm{MFA}} =\frac{\partial }{\partial H_l}V_\mathrm{MFA},&(i,l&=1,2).&\end{aligned}$$
(10)

The first Eq. in (10) yields

$$\begin{aligned} N_c \langle M_{i0}^2\rangle \left[ \ln \left( \langle M_{i0}^2 \rangle /\Lambda _H^2 \right) +\frac{1}{2} \right] = 16 \pi ^2 \langle f_{i} \rangle , \end{aligned}$$
(11)

which implies that \(\langle M_{i0}^2\rangle =0\) if \(\langle f_{i} \rangle =0\). In the case that \(\ln (\langle M_{i0}^2 \rangle /\Lambda _H^2)+1/2 <0\), (11) is inconsistent unless \(\langle M_{i0}^2\rangle =\langle f_{i} \rangle =0\), because \(\langle M_{i0}^2\rangle \) are \(\langle f_{i} \rangle \) are not allowed to be negative. Then the second Eq. of (10) gives

$$\begin{aligned} 2\lambda _H \langle H^\dag H\rangle = \lambda _{HS_1}\langle f_{1}\rangle +\lambda _{HS_2} \langle f_{2}\rangle . \end{aligned}$$
(12)

Using (11) and (12), we find the potential at the minimum:

$$\begin{aligned} \langle V_{\mathrm{MFA}}\rangle =-\frac{N_c}{64\pi ^2}\left( \langle M_{10}^2\rangle ^2+ \langle M_{20}^2\rangle ^2\right) . \end{aligned}$$
(13)

From (12) we see that, if \(\langle H^\dag H\rangle \) vanishes, \(\langle f_{1}\rangle \) and \(\langle f_{2}\rangle \) also have to vanish, because we assume that \(\lambda _H, \lambda _{HS_i}\) are positive. \(\langle H^\dag H\rangle =0\) cannot be at a local minimum unless both \(\langle f_{i} \rangle \) vanish, which can be seen from the Higgs mass squared

$$\begin{aligned} m_{h0}^2&= 6\lambda _H \langle H^\dag H\rangle + \frac{ N_c(\lambda _{HS_1}^2+\lambda _{HS_2}^2) \langle H^\dag H\rangle }{8\pi ^2}\nonumber \\&\quad -\lambda _{HS_1} \langle f_{1}\rangle -\lambda _{HS_2} \langle f_{2}\rangle +2\langle H^\dag H\rangle \nonumber \\&\quad \times \left( \lambda _{HS_1}^2 \frac{\langle f_{1}\rangle }{ M_1^2}+ \lambda _{HS_2}^2 \frac{\langle f_{2}\rangle }{ M_2^2}\right) \nonumber \\&\rightarrow -(\lambda _{HS_1}\langle f_{1}\rangle +\lambda _{HS_2}\langle f_{2}\rangle ) < 0 ~\text{ as }~\langle H^\dag H\rangle \rightarrow 0, \end{aligned}$$
(14)

where we have not used (12). Therefore, \(\langle H^\dag H\rangle =0\) is possible only if \(\langle f_{1}\rangle =\langle f_{2}\rangle =0\), which is consistent with (12). Furthermore, one can convince oneself that Eqs. (11) and (12) cannot be simultaneously satisfied if one of \(\langle f_{i} \rangle \) vanishes, unless we make a precise fine-tuning of the quartic coupling constants. From the discussions above we may therefore conclude that, as long as \(\ln (\langle M_{i0}^2 \rangle /\Lambda _H^2)+1/2 > 0\) is satisfied, the non-vanishing VEV of H and \(f_{i}\) correspond to the true minimum of the potential (9).Footnote 5

To proceed with our mean-field approximation, we introduce fluctuations about the mean-field vacuum (11)–(13) as

$$\begin{aligned} f_{i}&= \langle f_{i}\rangle +\sigma _i. \end{aligned}$$
(15)

Note that \(\phi ^\pm \) are also fluctuations and also that the canonical dimension of \(\sigma _i\) and \(\phi ^\pm \) is two. Similarly, we expand the Higgs doublet around the vacuum value as

$$\begin{aligned} H = \frac{1}{\sqrt{2}} \begin{pmatrix} \chi ^1+i\chi ^2\\ v_h+h +i\chi ^0\end{pmatrix}, \frac{v_h}{\sqrt{2}} =(\langle H^\dagger H\rangle )^{1/2}, \end{aligned}$$
(16)

where \(\chi ^i\) are would-be Nambu–Goldstone fields and we will suppress them in the following discussions. Then the mean-field Lagrangian (7) can be finally written as

$$\begin{aligned} {\mathcal {L}}_\text {MFA}&= ([\partial ^\mu S_i]^\dag \partial _\mu S_i) -M_i^2(S_i^\dag S_i)+\frac{\lambda _{12}'}{2} \phi ^+\phi ^- \nonumber \\&\quad + \lambda _1 \sigma _1^2 + \lambda _2 \sigma _2^2 + \lambda _{12} \sigma _1\sigma _2\nonumber \\&\quad + \lambda _1 f_1^2 + \lambda _2 f_2^2 + \lambda _{12} f_1f_2\nonumber \\&\quad -(2\lambda _1 \sigma _1+ \lambda _{12} \sigma _2)(S_1^\dag S_1)\nonumber \\&\quad - (2\lambda _2 \sigma _2+ \lambda _{12} \sigma _1)(S_2^\dag S_2) -\frac{\lambda _{12}'}{\sqrt{2}}\phi ^+(S^\dagger _1 S_2)\nonumber \\&\quad -\frac{\lambda _{12}'}{\sqrt{2}}\phi ^-(S^\dagger _2 S_1) \nonumber \\&\quad +\frac{\lambda _{HS_i}}{2}(S_i^\dag S_i) h (2v_h +h) -\frac{\lambda _H}{4}h^2(6v_h^2 +4v_h h \partial + h^2), \end{aligned}$$
(17)

where

$$\begin{aligned} M_1^2&= \langle M_{10}^2\rangle =2\lambda _1 \langle f_{1}\rangle +\lambda _{12} \langle f_{2}\rangle -\frac{ \lambda _{HS_1}}{2} v_h^2, \end{aligned}$$
(18)
$$\begin{aligned} M_2^2&=\langle M_{20}^2\rangle = 2\lambda _2 \langle f_{2}\rangle +\lambda _{12}\langle f_{1}\rangle -\frac{\lambda _{HS_2}}{2} v_h^2. \end{aligned}$$
(19)

At this level the mean fields \(\sigma _i\) and \(\phi ^{\pm }\) are classical fields, but we reinterpret them as quantum fields after their kinetic terms are generated at the loop level. More specifically, the auxiliary fields, \(\sigma _i\) and \(\phi ^\pm \), are not dynamical in the Lagrangian at the classical level (17). As will be seen in the next subsection, these fields become dynamical by integrating out the fundamental fields \(S_i\). Note that within the present effective model approach to dynamical scale symmetry breaking described by (1), the confinement effects cannot be taken into account.

Here, we briefly introduce the one-loop contribution from the SM sector to the effective potential (9) and evaluate the correction to the Higgs mass (14). The one-loop contribution to the effective potential is calculated as

$$\begin{aligned} V_\text {CW}\!\left( h\right)&= \sum _{I=W,Z,h} \frac{n_I}{2}\int \frac{d^4k}{(2\pi )^4} \ln \!\left( k^2 + m_I^2\!\left( h\right) \right) \nonumber \\&\quad - \frac{n_t}{2}\int \frac{d^4k}{(2\pi )^4} \ln \!\left( k^2 + m_t^2\!\left( h\right) \right) +\text{ c.t. }, \end{aligned}$$
(20)

where \(n_I\) (\(I=W,Z,t,h\)) is the degrees of freedom of the corresponding particle, i.e., \(n_W=6\), \(n_Z=3\), \(n_t=12\) and \(n_h=1\), and c.t. denotes the counter terms. We work in the Landau gauge, and the contributions from the would-be Goldstone bosons in the Higgs field have been neglected. We employ the dimensional regularization in order to respect scale invariance and choose the counter terms such that the following normalization conditions with \(v_h=246\) GeV are satisfied:

$$\begin{aligned} V_{\mathrm{CW}}\!\left( h=v_h\right)&=0,&\frac{d V_{\mathrm{CW}}\!\left( h\right) }{d h}\bigg |_{h=v_h}&=0.&\end{aligned}$$
(21)

Then, we obtain the one-loop corrections (20) as the Coleman–Weinberg potential [5]

$$\begin{aligned} V_{\mathrm{CW}}\!\left( h\right)= & {} C_0 (h^4-v_h^4)+\frac{1}{64 \pi ^2} \nonumber \\&\quad \bigg [ ~6 {\tilde{m}}_W^4 \ln ({\tilde{m}}_W^2/m_W^2)+ 3 {\tilde{m}}_Z^4 \ln ({\tilde{m}}_Z^2/m_Z^2)\nonumber \\&\quad + {\tilde{m}}_h^4 \ln ({\tilde{m}}_h^2/m_h^2) -12{\tilde{m}}_t^4 \ln ({\tilde{m}}_t^2/m_t^2)~\bigg ], \end{aligned}$$
(22)

where

$$\begin{aligned} C_0&\simeq -\frac{1}{64 \pi ^2 v_h^4}\left( 3m_W^4+(3/2)m_Z^4+(3/4) m_h^4-6 m_t^4\right) , \end{aligned}$$
(23)
$$\begin{aligned} {\tilde{m}}_W^2&=(m_W/v_h)^2h^2,~~~ {\tilde{m}}_Z^2=(m_Z/v_h)^2 h^2,~~~ \nonumber \\ {\tilde{m}}_t^2&=(m_t/v_h)^2 h^2,~~~ {\tilde{m}}_h^2 =\frac{\partial ^2 V_\text {MFA}}{\partial h^2}, \end{aligned}$$
(24)

and \(m_I\) (masses given at the vacuum \(v_h=246\) GeV) are

$$\begin{aligned} m_W&=80.4~\text{ GeV },\quad m_Z=91.2~\text{ GeV },\nonumber \\ m_t&=173.2~\text{ GeV },\quad m_h=125~\text{ GeV }. \end{aligned}$$
(25)

We find that the Coleman–Weinberg potential (22) yields a one-loop correction to the Higgs mass squared (14)

$$\begin{aligned} \delta m_h^2 = \frac{d^2V_\text {CW}}{dh^2}\bigg |_{h=v_h} \simeq -16 C_0 v_h^2. \end{aligned}$$
(26)

This correction modifies the Higgs mass (14) slightly.

3.1 Inverse propagators and masses

The inverse propagators should be computed to obtain the masses and the corresponding wave function renormalization constants. We also have to define canonically normalized fields with a canonical dimension of one. To this end, we integrate out the constituent scalars \(S^a\) and up to and including one-loop order to obtain the inverse propagators:

$$\begin{aligned} \Gamma _\phi (p^2)= & {} \frac{1}{2}\lambda '_{12} \left[ 1+ \lambda '_{12} N_c\Gamma (M_1^2,M_2^2,p^2)\right] , \end{aligned}$$
(27)
$$\begin{aligned} \Gamma _{11}(p^2)= & {} 2\lambda _{1}\left[ 1+ 2 N_c \lambda _{1}\Gamma (M_1^2,M_1^2,p^2)\right] \nonumber \\&+\, N_c \lambda _{12}^2\Gamma (M_2^2,M_2^2,p^2), \end{aligned}$$
(28)
$$\begin{aligned} \Gamma _{22}(p^2)= & {} 2\lambda _{2}\left[ 1+ 2 N_c \lambda _{2}\Gamma (M_2^2,M_2^2,p^2)\right] \nonumber \\&+\, N_c \lambda _{12}^2\Gamma (M_1^2,M_1^2,p^2), \end{aligned}$$
(29)
$$\begin{aligned} \Gamma _{12}(p^2)= & {} \lambda _{12}\left[ 1+ 2 N_c \lambda _{1}\Gamma (M_1^2,M_1^2,p^2)\right. \nonumber \\&\left. +\, 2 N_c \lambda _{2}\Gamma (M_2^2,M_2^2,p^2) \right] , \end{aligned}$$
(30)
$$\begin{aligned} \Gamma _{h1}(p^2)= & {} -v_h\left[ 2\lambda _{HS_1}\lambda _{1} N_c \Gamma (M_1^2,M_1^2,p^2) \right. \nonumber \\&\left. +\,\lambda _{HS_2}\lambda _{12} N_c \Gamma (M_2^2,M_2^2,p^2) \right] , \end{aligned}$$
(31)
$$\begin{aligned} \Gamma _{h2}(p^2)= & {} -v_h\left[ 2\lambda _{HS_2}\lambda _{2} N_c \Gamma (M_2^2,M_2^2,p^2) \right. \nonumber \\&\left. +\,\lambda _{HS_1}\lambda _{12} N_c \Gamma (M_1^2,M_1^2,p^2) \right] , \end{aligned}$$
(32)
$$\begin{aligned} \Gamma _h(p^2)= & {} p^2-m_{h}^2+(v_h \lambda _{HS_i})^2 N_c\nonumber \\&\times \left[ \Gamma (M_i^2,M_i^2,p^2) - \Gamma (M_i^2,M_i^2,0)\right] , \end{aligned}$$
(33)

with \(m_{h}^2=m_{h0}^2+\delta m_h^2\), where \(m_{h0}^2\) is given in (14), \(\delta m_h^2\) is the SM correction given in (26), and we defined the loop function,

$$\begin{aligned} \Gamma (M_1^2,M_2^2,p^2)&=\frac{-1}{16\pi ^2} \left( \int _0^1 dx \ln \{ 1-x(1-r)-x(1-x)t\} \right. \nonumber \\&\quad \left. +\ln \left[ \frac{M_2^2}{\Lambda _H^2 \exp (-3/2)}\right] \right) , \end{aligned}$$
(34)

with \(r=M_1^2/M_2^2\) and \(t=p^2/M_2^2\). Note that we have included the canonical kinetic term for H, but its wave function renormalization constant is ignored, because it is approximately equal to one within the approximation here. Note that the fundamental fields \(S_i\) have been integrated out, so that they are no longer fields as degrees of freedom in low energy regimes (below the confinement scale). Instead, the auxiliary fields associated with the composite fields could behave as dynamical fields with degrees of freedom in low energy regimes. The DM mass is the momentum squared at which the inverse propagator of \(\Gamma _\phi \!\left( p^2\right) \) vanishes, i.e.,

$$\begin{aligned} \Gamma _{\phi }(p^2 = {m_{\mathrm{DM}}}^2)=0, \end{aligned}$$
(35)

and \(Z_{\phi }\) (which has a canonical dimension of two) can be obtained from

$$\begin{aligned} Z_{\phi }^{-1}&= \frac{d \Gamma _\phi }{d p^2}\bigg |_{p^2=m_\mathrm{DM}^2}. \end{aligned}$$
(36)

The Higgs and \(\sigma _i\) masses can be similarly obtained from the eigenvalues of the following \(h-\sigma \) mixing matrix

$$\begin{aligned} \mathbf{\Gamma }(p^2)&= \begin{pmatrix} \Gamma _{11}(p^2) &{}\quad \Gamma _{12}(p^2) &{}\quad \Gamma _{h1}(p^2)\\ \Gamma _{12}(p^2) &{}\quad \Gamma _{22}(p^2) &{}\quad \Gamma _{h2}(p^2) \\ \Gamma _{h1}(p^2) &{}\quad \Gamma _{h2}(p^2) &{}\quad \Gamma _{h}(p^2) \end{pmatrix}. \end{aligned}$$
(37)

The squared masses \(m^2_a~(a=H,L,h)\) are given as the momenta at which \(\det \mathbf{\Gamma }(p^2)\) becomes zero, where we assume that

$$\begin{aligned} m_H> m_L > m_h. \end{aligned}$$
(38)
Fig. 1
figure 1

One-loop diagrams contributing to the effective interactions among \(\phi ^\pm , \sigma _L\) and \(h'\), where the external momenta are set equal to zero

Full size image

Further, the wave function renormalization constants can be computed in the following way. We first compute the squared masses from \(\det \mathbf{\Gamma }(p^2) =0\). Then we diagonalize \(\mathbf{\Gamma }(p^2)\) at each \(p^2=m_a^2\) and denote the eigenvector with zero eigenvalue by \({\mathbf {\xi }}^{(a)}~(a=H,L,h)\), i.e., \(\mathbf{\Gamma }(p^2=m_a^2){\mathbf {\xi }}^{(a)}=0\). Then the matrix U that links \(\sigma _i\) and the Higgs h to the mass eigenstates, denoted by \(\sigma _H,\sigma _L, h'\), is given by

$$\begin{aligned} U&= \begin{pmatrix} \xi ^{(H)}_1 &{}\quad \xi ^{(L)}_1 &{}\quad \xi ^{(h)}_1\\ \xi ^{(H)}_2 &{}\quad \xi ^{(L)}_2 &{}\quad \xi ^{(h)}_2\\ \xi ^{(H)}_3 &{}\quad \xi ^{(L)}_3 &{}\quad \xi ^{(h)}_3 \end{pmatrix}, \end{aligned}$$
(39)

where the canonical dimension of \(\xi ^{(a)}_1\) and \(\xi ^{(a)}_2\) is one, while that of \(\xi ^{(a)}_3\) is zero. This implies

$$\begin{aligned} \lim _{p^2 \rightarrow m^2_a} {\mathbf {\xi }}^{(a)}\Gamma (p^2){\mathbf {\xi }}^{(a)}&= Z_a^{-1}(p^2-m_a^2), \end{aligned}$$
(40)

and hence

$$\begin{aligned} \begin{pmatrix} \sigma _1\\ \sigma _2\\ h \end{pmatrix}&=\begin{pmatrix} \xi ^{(H)}_1 Z_H^{1/2}&{}\quad \xi ^{(L)}_1 Z_L^{1/2}&{}\quad \xi ^{(h)}_1\\ \xi ^{(H)}_2 Z_H^{1/2}&{}\quad \xi ^{(L)}_2 Z_L^{1/2}&{}\quad \xi ^{(h)}_2\\ \xi ^{(H)}_3 Z_H^{1/2}&{}\quad \xi ^{(L)}_3 Z_L^{1/2}&{}\quad \xi ^{(h)}_3 \end{pmatrix}\begin{pmatrix} \sigma _H\\ \sigma _L\\ h' \end{pmatrix}. \end{aligned}$$
(41)

The wave function renormalization constants \(Z_a\) are dimensionless so that \(\sigma _H\), \(\sigma _L\) and \(h'\) are canonically normalized fields with the canonical dimension of one. The Lagrangian (17) is rewritten in terms of the fields \(\sigma _H\), \(\sigma _L\) and \(h'\).

If \(m_{\mathrm{DM}} (m_{H,L}) >2 M_{1,2}\), \(\phi ^\pm (\sigma _{H,L})\) would decay into \(S_1\) and \(S_2\) (the inverse propagators \(\Gamma \)s have an imaginary part) within the framework of the effective theory, because the effective theory cannot incorporate confinement. Therefore, we will consider only the parameter space with \(m_\mathrm{DM}\), \(m_{H,L}< 2 M_{1,2}\).

3.2 Effective interactions

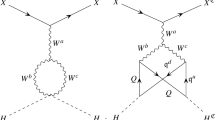
To calculate the relic abundance of DM and also the interaction of DM with the SM particles, we need to compute the diagrams shown in Fig. 1. The corresponding effective interactions can be obtained by setting the external momenta equal to zero:

$$\begin{aligned} {{\mathcal {L}}}_{\mathrm{DM}}&=\frac{1}{2}G_{\phi \sigma }\phi ^+\phi ^- (\sigma _L)^2+ \frac{1}{2}G_{\phi h}\phi ^+\phi ^- h'^2 \nonumber \\&\quad + \frac{1}{4}G_{\sigma h}\sigma _L^2 h'^2\nonumber \\&\quad + v_h G_{\phi h}\phi ^+\phi ^- h' +\frac{1}{2}v_h G_{\sigma h}\sigma _L^2 h' \nonumber \\&\quad +\frac{1}{2}{\hat{G}}_{\sigma h}\sigma _L h'^2, \end{aligned}$$
(42)

where the effective vertices up to and including \(O(\lambda _{HS_i})\) are

$$\begin{aligned} G_{\phi \sigma }&= \frac{Z_\phi Z_L N_c}{16 \pi ^2} (\lambda '_{12})^2 \left[ \lambda _{1L}^2 F_1(M_1,M_2)\right. \nonumber \\&\quad \left. + \lambda _{2L}^2 F_1(M_2,M_1)+ 2\lambda _{1L} \lambda _{2L} F_2(M_1,M_2)\right] , \end{aligned}$$
(43)
$$\begin{aligned} G_{\phi h}&= \frac{Z_\phi N_c}{32 \pi ^2} (\lambda '_{12})^2\left[ \lambda _{HS_1} F_3(M_1,M_2)\right. \nonumber \\&\quad \left. + \lambda _{HS_2} F_3(M_2,M_1)\right] , \end{aligned}$$
(44)
$$\begin{aligned} G_{\sigma h}&= \frac{Z_L N_c}{16 \pi ^2} \left[ \lambda _{1L}^2\lambda _{HS_1}/M_1^2+ \lambda _{2L}^2\lambda _{HS_2}/M_2^2\right] , \end{aligned}$$
(45)
$$\begin{aligned} {\hat{G}}_{\sigma h}&= \frac{Z_L^{1/2} N_c}{16 \pi ^2} \left[ \lambda _{1L}\lambda _{HS_1}\ln \left( \frac{M_1^2}{\Lambda _H^2\exp (-3/2)}\right) \right. \nonumber \\&\quad \left. + \lambda _{2L}\lambda _{HS_2} \ln \left( \frac{M_2^2}{\Lambda _H^2\exp (-3/2)}\right) \right] , \end{aligned}$$
(46)

with

$$\begin{aligned} \lambda _{1L}&=(2\lambda _1\xi _1^{(L)} +\lambda _{12}\xi _2^{(L)}),\nonumber \\ \lambda _{2L}&=(2\lambda _2\xi _2^{(L)} +\lambda _{12}\xi _1^{(L)}), \end{aligned}$$
(47)

and

$$\begin{aligned} F_1(M_1,M_2)&=\frac{M_1^2+M_2^2}{(M_1^2-M_2^2)^2 M_1^2} -\frac{2M_2^2}{(M_1^2-M_2^2)^3}\ln (M_1^2/M_2^2)&\nonumber \\&= \frac{1}{3M_1^4},~~~\text{ for }~M_2=M_1,&\end{aligned}$$
(48)
$$\begin{aligned} F_2(M_1,M_2)&= -\frac{2}{(M_1^2-M_2^2)^2} +\frac{M_1^2+M_2^2}{(M_1^2-M_2^2)^3} \ln (M_1^2/M_2^2)&\nonumber \\&= \frac{1}{6M_1^4},~~~\text{ for }~M_2=M_1,&\end{aligned}$$
(49)
$$\begin{aligned} F_3(M_1,M_2)&= \frac{1}{M_1^2-M_2^2} -\frac{M_2^2}{(M_1^2-M_2^2)^2} \ln (M_1^2/M_2^2)&\nonumber \\&= \frac{1}{2 M_1^2},~~~\text{ for }~M_2=M_1.&\end{aligned}$$
(50)

In the next section, the vertices (43)–(46) are used to evaluate the thermal averaged cross sections for the annihilation processes of \(\sigma _L\), \(\phi ^\pm \) and the decay width of \(\sigma _L\).

4 Dark matter

4.1 Relic abundance

Let us evaluate the relic abundance of the DM candidates in the model. To this end, we have to follow the temperature-evolution of the number densities of the particles \(\sigma _L\) and \(\phi ^\pm \), denoted by \(n_{\sigma _L}\) and \(n_\phi \). These quantities are functions of temperature T. Here, we introduce convenient quantities \(Y_{\sigma _L,\phi }=n_{\sigma _L,\phi }/s\), where s is the entropy density of the universe. Then, the evolution of \(Y_{\sigma _L}\) and \(Y_\phi \) can be described by the following coupled Boltzmann equation [35,36,37,38]:

$$\begin{aligned} \frac{d Y_{\sigma _L}}{dx}=&-0.264~ g_*^{1/2} \left[ \frac{\mu M_\mathrm{PL}}{x^2} \right] \Bigg \{\langle \sigma (\sigma _L\sigma _L;\text{ SM }) v\rangle \nonumber \\&\quad \times \left( Y_{\sigma _L}Y _{\sigma _L}-{\bar{Y}}_{\sigma _L} {\bar{Y}}_{\sigma _L}\right) +\langle \sigma (\sigma _L\sigma _L;\phi ^+ \phi ^- )v\rangle \nonumber \\&\quad \times \left( Y_{\sigma _L} Y _{\sigma _L}-\frac{Y_{\phi } Y_{\phi }}{{\bar{Y}}_{\phi }{\bar{Y}}_{\phi }} {\bar{Y}}_{\sigma _L}{\bar{Y}}_{\sigma _L} \right) \Bigg \}\nonumber \\&\quad -0.602~ g_*^{-1/2} \left[ \frac{x M_{\mathrm{PL}}}{\mu ^2} \right] \langle \gamma (\sigma _L)\rangle (Y_{\sigma _L}-{\bar{Y}}_{\sigma _L}), \end{aligned}$$
(51)
$$\begin{aligned} \frac{d Y_{\phi }}{dx}&=-0.264~ g_*^{1/2} \left[ \frac{\mu M_\mathrm{PL}}{x^2} \right] \Bigg \{ \frac{1}{2}\langle \sigma (\phi ^+ \phi ^- ;\text{ SM }) v\rangle \nonumber \\&\quad \times \left( Y_{\phi } Y _{\phi }-{\bar{Y}}_{\phi }{\bar{Y}}_{\phi }\right) \nonumber \\&\quad -\langle \sigma (\sigma _L\sigma _L;\phi ^+ \phi ^- )v\rangle \nonumber \\&\quad \times \left( Y_{\sigma _L} Y _{\sigma _L}-\frac{Y_{\phi } Y_{\phi }}{{\bar{Y}}_{\phi }{\bar{Y}}_{\phi }} {\bar{Y}}_{\sigma _L} {\bar{Y}}_{\sigma _L} \right) \Bigg \}, \end{aligned}$$
(52)

where \({\bar{Y}}_{\sigma _L,\phi }\) is \(Y_{\sigma _L,\phi }\) in equilibrium, \(M_{\mathrm{PL}}=1.22\times 10^{19}~\text {GeV}\) and \(g_*=106.75\) are the reduced Planck mass and the total number of effective degrees of freedom, respectively, and \(1/\mu =1/m_L+1/m_{\mathrm{DM}}\). \(Y_{\sigma _L,\phi }\) are written as functions of \(x=\mu /T\). Note that \(m_{\mathrm{DM}}\) is the mass of \(\phi ^\pm \): \(m_\text {DM}\equiv m_\phi \). The thermal averaged cross sections and the decay width given in (51) and (52) are computed as

$$\begin{aligned} \langle \sigma (\sigma _L\sigma _L;\phi ^+ \phi ^- ) v\rangle&=\frac{{G^2_{\phi \sigma }}}{32\pi m_\sigma ^2} \left( 1-m_{\mathrm{DM}}^2/m_\sigma ^2\right) ^{1/2}, \end{aligned}$$
(53)
$$\begin{aligned} \langle \sigma (\phi ^+ \phi ^- ;\text{ SM }) v\rangle&=\frac{{1}}{32\pi m_{\mathrm{DM}}^2}~\sum _{I=W,Z,t,h} \left( 1-m_I^2/m_{\mathrm{DM}}^2\right) ^{1/2} \nonumber \\&\quad \times a_I(G_{\phi h},m_{\mathrm{DM}}), \end{aligned}$$
(54)
$$\begin{aligned} \langle \sigma (\sigma _L\sigma _L;\text{ SM }) v\rangle&=\frac{{1}}{32\pi m_L^2}~\sum _{I=W,Z,t,h} \left( 1-m_I^2/m_L^2\right) ^{1/2} \nonumber \\&\quad \times a_I(G_{\sigma h},m_L), \end{aligned}$$
(55)
$$\begin{aligned} \langle \gamma (\sigma _L)\rangle&= \frac{{1}}{16\pi m_L}~\sum _{I=W,Z,t} \left( 1-4m_I^2/m_L^2\right) ^{1/2}\nonumber \\&\quad \times a_I({\hat{G}}_{\sigma h},m_L/2)\nonumber \\&\quad + \frac{{\hat{G}}^2_{\sigma h}}{32\pi m_L}~ \left( 1-4m_h^2/m_L^2\right) ^{1/2}\nonumber \\&\quad \times \left( 1+ 24 \lambda _H \Delta _{h}(m_L/2) \frac{m_W^2}{g^2}\right) , \end{aligned}$$
(56)
Fig. 2
figure 2

Left: \(Y_i\) as a function of x. Right: The total relic abundance \(\Omega h^2\) against the decay width \(\langle \gamma (\sigma _L)\rangle \) in the range \((0.1-- 2.0)\times 10^{12}\) GeV. We have used: \(m_{\mathrm{DM}}=500\) GeV, \(m_L=550\) GeV, \(\langle \sigma (\sigma _L\sigma _L;\phi ^+ \phi ^- ) v\rangle =5.2\times 10^{-6}\,\text{ GeV }^{-2}\), \(\langle \sigma (\sigma _L\sigma _L;\text{ SM }) v\rangle =10^{-11}\,\text{ GeV }^{-2}\), \(\langle \sigma (\phi ^+ \phi ^- ;\text{ SM }) v\rangle =10^{-11}\,\text{ GeV }^{-2}\) for both the left- and right-hand panels, while \(\langle \gamma (\sigma _L)\rangle =10^{-9}\) GeV is assumed for the left-hand panel

Full size image

where \(m_W\), \(m_Z\), and \(m_t\) are the W, Z bosons and the top-quark masses given in (25), respectively, the effective coupling constants are in (43)–(46), and we defined

$$\begin{aligned} a_{W(Z)}(G,m)= & {} 4 (2) G^2\Delta _{h}^2(m) m_{W(Z)}^4 \nonumber \\&\times \left( 3+4\frac{m^4}{m_{W(Z)}^4}-4 \frac{m^2}{m_{W(Z)}^2}\right) ,\nonumber \\ a_t(G,m)= & {} 24G^2\Delta _{h}^2 (m) m_t^2(m^2-m_t^2), \nonumber \\ a_h (G,m)= & {} \frac{1}{2}G^2\nonumber \\&\times \left( 1+24 \lambda _H \Delta _{h}(m) \frac{m_W^2}{g^2}+ 8G\Delta _{h}^t(m) \frac{m_W^2}{g^2} \right) ^2.\nonumber \\ \end{aligned}$$
(57)

Here, \(g=0.65\) is the \(SU(2)_L\) gauge coupling constant, and \( \Delta _{h}(m)=(4 m^2-m_h^2)^{-1}\) (\( \Delta _{h}^t(m)=(-2 m^2+m_h^2)^{-1}\)) is the Higgs propagator in the s(t)-channel. From the solutions \(Y_{\sigma _L;\,\infty }\equiv Y_{\sigma _L}\!\left( x=\infty \right) \) and \(Y_{\phi ;\,\infty }\equiv Y_\phi \!\left( x=\infty \right) \) to the coupled Boltzmann equations (51), (52), we obtain the relic abundances for \(\sigma _L\) and \(\phi ^\pm \):

$$\begin{aligned} \Omega _{\sigma _L, \phi }h^2=\frac{g_{\sigma _L,\phi }m_\text {DM} Y_{\sigma _L, \phi ;\,\infty } s_0 }{\rho _c/h^2}, \end{aligned}$$
(58)

where \(g_{\sigma _L,\phi }\) is the degrees of freedom of \(\sigma _L\), \(\phi ^\pm \), and \(s_0=2890\,\text {cm}^{-3}\) and \(\rho _c/h^2=1.05\times 10^{-5}\,\text {GeV}/\text {cm}^3\) are the entropy density and the critical energy density over the dimensionless Hubble constant at present, respectively [39].

Before we solve the evolution equations numerically, we consider what we would expect. If the decay width \( \langle \gamma (\sigma _L)\rangle \) of \(\sigma _L\) is large, \(Y_{\sigma _L}\) may be approximated by its equilibrium value \({\bar{Y}}_{\sigma _L}\), which is illustrated in Fig. 2 for a representative set of the parameters. From the left-hand side panel of Fig. 2 we see that \(Y_{\sigma _L}\) (solid line) can be well approximated by its equilibrium value \({\bar{Y}}_{\sigma _L}\) (dotted line) to compute the final value of for \(Y_{\phi }\) (dot-dashed line). In the right-hand side panel of Fig. 2 we plot the total relic abundance \(\Omega h^2= (\Omega _{\sigma _L}+\Omega _{\phi }) h^2\) against the decay width \(\langle \gamma (\sigma _L)\rangle \) with the same input parameter (except for \(\langle \gamma (\sigma _L)\rangle \)) as for the left-hand side panel of Fig. 2, where we varied \(\langle \gamma (\sigma _L)\rangle \) between (0.1 and 2.0) \(\times 10^{-12}\) GeV. We see that the total relic abundance approximately coincides with \(\Omega _{\phi } h^2\) if \(\langle \gamma (\sigma _L)\rangle \times 10^{12}\,\text {GeV}>0.5\). Therefore, if \(\langle \gamma (\sigma _L)\rangle \) is sufficiently large, we may approximate the expression in the braces \(\{~\}\) in the right-hand side of (52) by

$$\begin{aligned}&\left[ \frac{1}{2}\langle \sigma (\phi ^+ \phi ^- ;\text{ SM }) v\rangle +\frac{1}{4}\langle \sigma (\sigma _L\sigma _L;\phi ^+ \phi ^- )v\rangle \right. \nonumber \\&\quad \left. \frac{m^3_{\sigma _L}}{m_{\mathrm{DM}}^3} \exp \left( 2x\frac{m^2_{\mathrm{DM}} -m^2_L}{m_{\mathrm{DM}} m_L}\right) \right] \left( Y_{\phi } Y _{\phi }-{\bar{Y}}_{\phi }{\bar{Y}}_{\phi }\right) , \end{aligned}$$
(59)

which also appears in the co-annihilation of DM with an unstable particle [40]. From (59) we see that if \(m_L\) is close to \(m_{\mathrm{DM}}\) the second term of (59) effectively increases the annihilation rate of DM. The reason why \(m_L > m_{\mathrm{DM}}\) is assumed is that \(G_{\phi \sigma }\) given in (43) is so large that the second term in the bracket [  ] of (59) should be suppressed by \(\exp \left( 2x\frac{m^2_{\mathrm{DM}} -m^2_L}{m_{\mathrm{DM}} m_L}\right) \). Apart from this mass relation the mechanism is similar to the secluded DM mechanism [41]. We use this mechanismFootnote 6 to overcome the constraint from the direct detection experiment, as we explain below. On one hand, \(G_{\phi h}\) enters in the spin-independent elastic cross section \(\sigma _{SI}\) (60), so that it cannot be made small. The annihilation cross section \(\langle \sigma (\phi ^+ \phi ^- ;\text{ SM }) v\rangle \), on the other hand, depends on \(G_{\phi h}\), so that there would be a lower bound on the relic abundance \(\Omega _{\mathrm{DM}}\) of DM, if there would be no effect from \(\sigma _L\) on \(\Omega _{\mathrm{DM}}\). As we have seen above, the \(\sigma _L\) effect is an increase of the annihilation cross section of DM, and consequently, the lower bound on \(\Omega _\mathrm{DM}\) can be lowered.

Solving the Boltzmann equation (52) with the replacement (59) for large \(\langle \gamma (\sigma _L)\rangle \), we obtain the DM relic abundance \(\Omega _{\mathrm{DM}}h^2\). The latest observation by the Planck satellite tells us that \(\Omega _{\mathrm{DM}}h^2= 0.1188\pm 0.0010\) [44].

4.2 Direct detection

In order to compare with the WIMP DM direct-detection search experiments [26,27,28], we evaluate the spin-independent elastic cross section off the nucleon \(\sigma _{SI}\). As we can see from \({{\mathcal {L}}}_{\mathrm{DM}}\) in (42) the localized interaction of DM with the SM is that of the Higgs portal. Consequently, the spin-independent elastic cross section off the nucleon \(\sigma _{SI}\) is given by [45]

$$\begin{aligned} \sigma _{SI}&=\frac{{1}}{4\pi } \left( {\hat{r}} \frac{G_{\phi h} m_N ^2}{m_{\mathrm{DM}}m_h^2} \right) ^2 \left( \frac{m_{\mathrm{DM}}}{m_N+m_\mathrm{DM}} \right) ^2, \end{aligned}$$
(60)

where \(G_{\phi h}\) is given in (44), \(m_N\simeq 940\,\text {MeV}\) is the nucleon mass, and \({\hat{r}}\sim 0.3\) stems from the nucleonic matrix element [46,47,48]. We search the parameter space where the following observed values are satisfied: \(v_h=246\,\text {GeV}\), \(m_h\simeq 125\,\text {GeV}\), \(\Omega _\text {DM}h^2\simeq 0.12\) [39, 44].

So far we have assumed the \(U(1)\times U(1)\) flavor symmetry, where one of U(1) symmetries is a subgroup of SU(2). It is possible to enlarge the flavor symmetry, while maintaining the new DM annihilation process, and add the permutation symmetry \(Z_2\) of \(S_1\) and \(S_2\), which requires \(\lambda _1=\lambda _2\) and \( \lambda _{HS_1}= \lambda _{HS_2}\) in \({{\mathcal {L}}}_{\mathrm{eff}}\) given in (3). We have computed the spin-independent elastic cross section \(\sigma _\text {SI}\) of DM off the nucleon for three different flavor symmetries \(U(2), U(1)\times U(1)\) and \(U(1)\times U(1)\times Z_2\) with \(N_c=6\). This is shown in Fig. 3, where the red, blue and pink points show the predicted regions in the model with U(2), \(U(1)\times U(1)\times Z_2\) and \(U(1)\times U(1)\), respectively. For comparison the case of the single-scalar DM is also included (brown points). These theoretical predictions should be compared with the resent experimental constraints of LUX [49], XENON1T [50] and PandaX-II [51], where the green and yellow bands denote the \(1\sigma \) and \(2\sigma \) bands of XENON1T [50], respectively. We see from Fig. 3 that the model with the unbroken U(2) flavor symmetry is at the border of the experimental upper bound and future experiments can exclude the model. We also see that, in contrast to the U(2) case, the model with \(U(1)\times U(1)\times Z_2\) and \(U(1)\times U(1)\) can clear more stringent constraints.

Fig. 3
figure 3

The spin-independent elastic cross section \(\sigma _\text {SI}\) of DM off the nucleon as a function of the DM mass \(m_\text {DM}\) for the case of \(N_f=2\), \(N_c=6\). The red, blue and pink points show the predicted regions in the model with U(2), \(U(1)\times U(1)\times Z_2\) and \(U(1)\times U(1)\), respectively. The brown points show the predicted region of the single-scalar DM. The black dashed, solid and dotted lines stand for the current upper bound from the direct detection experiments, LUX [49], XENON1T [50] and PandaX-II [51], respectively. The green and yellow bands denote the \(1\sigma \) and \(2\sigma \) bands of XENON1T [50], respectively. The gray dot-dashed and dotted lines stands for sensitivities of XENON experiment in the future [27]. The orange line and band stands for the cosmic neutrino background [52]

Full size image

5 Conclusion

We have considered the scale invariant extension of the SM proposed in [21], while relaxing the assumption on the \(U(N_f)\) flavor symmetry. Specifically, we have investigated the model with the U(2) flavor symmetry, which is broken explicitly down to \(U(1)\times U(1)\) by the scalar quartic couplings. This breaking opens a completely new possibility of reducing the relic abundance of DM: One of the three DM candidates in the U(2) case becomes neutral under \(U(1)\times U(1)\), so that the other two ones can annihilate into a pair of the neutral ones, which subsequently decay in the SM particles. The result is given in Fig. 3, which shows that the model could satisfy more stringent constraints of the future experiments of DM direct detection. A salient feature of the model is that the DM of the present model (which is the lightest scalar in the hidden sector) can be significantly heavier than about 500 GeV, which is the upper bound for a certain class of classically scale invariant extensions of the SM [53].

The solution of the hierarchy problem within the framework of the classically scale invariant extension of the SM is directly connected to the scale invariance properties of its Planck scale embedding. We have assumed the classical scale invariance to act in such a way that the Planck scale does not enter as a physical scale into the SM. This sounds like a strong assumption, but might be realistic in asymptotically safe gravity which could be one of candidates for quantum gravity [54,55,56,57].