The $Z_c(3900)$ peak does not come from the “triangle singularity”

Abstract

We compare contributions from the triangle diagram and the $D\bar{D}^*$ bubble chain with the processes of $e^{+}e^{-}\rightarrow J/\psi \pi ^{+}\pi ^{-}$ and $e^{+}e^{-}\rightarrow (D\bar{D}^*)^\mp \pi ^{\pm }$. By fitting the $J/\psi \pi$ maximum spectrum and the $D\bar{D}^*$ spectrum, we find that the triangle diagram cannot explain the new experimental results from BESIII Collaboration at center of mass at 4.23 and 4.26 GeV, simultaneously. On the contrary, the molecular assignment of $Z_c(3900)$ gives a much better description.

1 Introduction

The charged charmonium-like state $Z_c(3900)$ was observed in $J/\psi \pi ^\pm$ mass spectrum by BES III Collaboration in $e^+e^-\rightarrow J/\psi \pi \pi$ process [1], and confirmed by Belle [2] and CLEO [3] Collaborations in the same processes. Afterwards, it was also observed in the $(D\bar{D}^*)^\pm$ invariant mass spectrum in the process of $e^{+}e^{-}\rightarrow D\bar{D}^*\pi ^\mp$, and the quantum number of $Z_c(3900)$ was determined to be $\mathrm{I}(J^P)=1(1^+)$ by angular distribution analysis of the $\pi Z_c(3900)$ system [4]. The experimental discovery has stimulated a lot of discussion because of the unique nature of $Z_c(3900)$, as it could be (together with $Z_b$) an unambiguous candidate of the long wished-for tetra-quark state.

In a recent paper [5], we have made a detailed comparison between the $D\bar{D}^*$ molecule picture and the “elementary” picture, and we concluded that $Z_c(3900)$ is of $D\bar{D}^*$ molecular nature, using the pole counting method [6, 7].

However, there is also found in the literature another possible mechanism, called the anomalous triangle singularity (ATS), to explain the singularity structure at $Z_c(3900)$. ATS refers to a branch cut in a three-point loop function other than the normal threshold. The study of ATS can be traced back to about 60 years ago. In Ref. [8] Mandelstam worked out the ATS branch point and discussed its effects on the deuteron electromagnetism form factor, and in Ref. [9] the Landau equations were used to analyze ATS in triangle diagrams. Extensive studies on the triangle singularity using dispersion techniques can also be found in Refs. [10,11,12,13,14,15]. Especially in the paper by Lucha, Melikhov and Simula of Refs. [10,11,12,13,14,15], a detailed dispersive analysis is given on different variables. Some similar analyses of triangle singularity based on the non-relativistic expression can be found in Ref. [16].

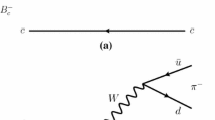
ATS has attracted renewed interests, recently, because it may contribute to peaks in some certain invariant-mass spectra. In other words, some so-called “exotic hadron states” could be just the ATS peak rather than real particles; or even if real exotic hadron states exist, there may be some non-negligible contributions from ATS. For example, it is suggested in Refs. [17,18,19] that the singularity structure of the triangle diagram (see Fig. 1), which contains both the normal threshold effect and the anomalous threshold effect, may lead to the peak at 3900 MeV. In Refs. [20, 21] it is emphasized that the anomalous triangle singularity may have significant impact in understanding the nature of the near-threshold state. The possible impact of triangle singularity on $Z_c(3900)$ has also been discussed in Refs. [22].

This paper is devoted to the study of the triangle diagram contribution to the $Z_c(3900)$ peak. In Sect. 2 we give a pedagogical analysis of general three-point loop functions using the Feynman parameter representation that can be found in most textbooks, and we discuss the properties of the ATS. In Sect. 3 we calculate the triangle diagram corresponding to $e^{+}e^{-}\rightarrow J/\psi \pi ^{+}\pi ^{-}$ and $e^{+}e^{-}\rightarrow (D\bar{D}^*)^\mp \pi ^{\pm }$ processes and fit the experimental data to test whether the $Z_c(3900)$ peak comes from the triangle diagram. In Sect. 4 the major conclusion of the present paper is reached: basically, it is found that the new experimental results from Refs. [23, 24] play a crucial role in clarifying the issue of the triangle diagram contribution: the experimental data indicate that the peak at 4.23 GeV is higher than that at 4.26 GeV, whereas the triangle diagram predicts an opposite behavior. Our analysis reveals that the $Z_c(3900)$ peak cannot be explained from the triangle diagram contribution from Fig. 1. Hence, combining with our previous analysis in Ref. [5], the molecular nature of $Z_c(3900)$ is firmly established.

2 Theoretical framework

To start let us first look upon a general triangle diagram as shown in Fig. 1.

Fig. 1

A general triangle diagram. The external and internal momenta are denoted as $p_i$ and $k_i$, and the internal and external masses are labeled $m_i$ and $M_i$ ($i=1,2,3$), respectively

The amplitude for such a triangle diagram contains the following scalar three-point function:

$$\begin{aligned}&T(s_1,s_2,s_3) \nonumber \\&\quad =-i\int \frac{\mathrm{d}^4q}{(2\pi )^4}\frac{1}{ (k_1^2-m_1^2+i \epsilon ) (k_2^2-m_2^2+i \epsilon ) (k_3^2-m_3^2+i \epsilon )}, \end{aligned}$$

(1)

where $k_1=q-p_2,k_2=p_1-q,k_3=q$, $s_i=p_i^2(i=1,2,3)$, and $\epsilon \rightarrow 0^+$ is a small positive parameter. This scalar three-point function could be evaluated using the standard method as follows. First one can rewrite it in terms of the Feynman parameters x, y and z,

$$\begin{aligned}&T(s_1,s_2,s_3)=-i\int _0^1 \mathrm{d}x\mathrm{d}y\mathrm{d}z\int \frac{\mathrm{d}^4q}{(2\pi )^4} \frac{2\delta (x+y+z-1)}{ [x(k_1^2-m_1^2)+y(k_2^2-m_2^2)+z(k_3^2-m_3^2)+i(x+y+z)\epsilon ]^3}. \end{aligned}$$

(2)

After a straightforward calculation, the function can be represented as

$$\begin{aligned}&T(s_1,s_2,s_3)=-i\int _0^1\mathrm{d}x\int _0^{1-x}\mathrm{d}y \nonumber \\&\quad \times \int \frac{\mathrm{d}^4q}{(2\pi )^4} \frac{2}{[(q-xp_2-yp_1)^2-\Delta (x,y)+i \epsilon ]^3}, \end{aligned}$$

(3)

where

$$\begin{aligned} \Delta (x,y)&=x^2s_2+y^2s_1+xy(s_1+s_2-s_3) \nonumber \\&\quad -x (s_2-m_1^2+m_3^2 )-y (s_1-m_2^2+m_3^2 )+m_3^2. \end{aligned}$$

(4)

One can perform a momentum translation $q=l+xp_2+yp_1$, then

$$\begin{aligned}&T(s_1,s_2,s_3)=-i\int _0^1\mathrm{d}x\int _0^{1-x}\mathrm{d}y \nonumber \\&\quad \times \int \frac{\mathrm{d}^4l}{(2\pi )^4} \frac{2}{ [l^2-\Delta (x,y)+i \epsilon ]^3}. \end{aligned}$$

(5)

To evaluate the integration, a Wick rotation is done:¹ $l^0\rightarrow i l^0_E, l^2\rightarrow -l^2_E$ and we have

$$\begin{aligned}&T(s_1,s_2,s_3)=-\int _0^1\mathrm{d}x\int _0^{1-x} \mathrm{d}y \nonumber \\&\quad \times \int \frac{\mathrm{d}^4l_E}{(2\pi )^4} \frac{2}{ [l_E^2+\Delta (x,y)-i \epsilon ]^3}. \end{aligned}$$

(6)

Then the integration in momentum space can be worked out anyway regardless of the sign of $\Delta (x,y)$²

$$\begin{aligned} T(s_1,s_2,s_3)=-\frac{1}{16\pi ^2}\int _0^1 \mathrm{d}x\int _0^{1-x} \mathrm{d}y \frac{1}{\Delta (x,y)-i \epsilon } . \end{aligned}$$

(7)

Further, the integration of y is then calculated analytically (for simplicity we omit the term $- i \epsilon$ in the following discussion),

$$\begin{aligned}&T(s_1,s_2,s_3)=-\frac{1}{8\pi ^2}\int _0^1 \frac{\mathrm{d}x}{a(s_3,x)} \nonumber \\&\quad \times \bigg \{\arctan \bigg [\frac{(-s_1+s_2-s_3)x+s_1+m_2^2-m_3^2}{a(s_3,x)}\bigg ] \nonumber \\&\quad -\arctan \bigg [\frac{(s_1+s_2-s_3)x-s_1+m_2^2-m_3^2}{a(s_3,x)}\bigg ]\bigg \}, \end{aligned}$$

(8)

with

$$\begin{aligned}&a(s_3,x)= \{ [\lambda (s_1,s_2,s_3)+\lambda (s_1,m_2^2,m_3^2) \nonumber \\&\quad +4s_1 m_1^2-(s_2-s_3+m_2^2-m_3^2)^2 ]x \end{aligned}$$

(9)

$$\begin{aligned}&\quad -\lambda (s_1,s_2,s_3)x^2-\lambda (s_1,m_2^2,m_3^2) \}^{1/2}, \end{aligned}$$

(10)

where

$$\begin{aligned} \lambda (a,b,c)=a^2+b^2+c^2-2ab-2bc-2ac\ . \end{aligned}$$

(11)

Now it is not difficult to analyze the singularity structures of $T(s_1,s_2,s_3)$ based on Eqs. (8) and (9), and for simplicity we only study the singularities of $s_3$ variable. There are two “$\arctan$” terms in Eq. (8); the singularity of the first term is given by the $\pm \ i$ branch points of the $\arctan$ function, i.e.

$$\begin{aligned} \frac{(-s_1+s_2-s_3)x+s_1+m_2^2-m_3^2}{a(s_3,x)}=\pm \ i . \end{aligned}$$

Its solution with respect to the integration variable x is

$$\begin{aligned} x= \frac{-m_1^2+m_2^2+s_3\pm \sqrt{\lambda (s_3,m_1^2,m_2^2 )}}{2s_3}. \end{aligned}$$

(12)

If $\lambda (s_3,m_1^2,m_2^2)\rightarrow 0^-$, a pinch singularity occurs. Especially when $s_3\rightarrow (m_1+m_2)^2-0^+$, the two singularities from Eq. (12),

$$\begin{aligned} x=\frac{m_2}{m_1+m_2}\pm i0^+, \end{aligned}$$

will pinch the integration interval [0, 1], while $a(s_3,x)$ stays finite, hence it is reasonably concluded that $s_3=(m_1+m_2)^2$ is a singularity of $T(s_1,s_2,s_3)$.³ In fact, that result is nothing but the well-known normal threshold of the three-point function. One can do analogous analyses on the second $\arctan$ term of Eq. (8), and it is found that the solution of x,

$$\begin{aligned} x=\frac{-m_1^2+m_3^2+s_2\pm \sqrt{\lambda (m_1^2,s_2,m_3^2 )}}{2s_2}, \end{aligned}$$

is independent of $s_3$, so the second term has no contribution to the singularities of $T(s_1,s_2,s_3)$ with respect to the variable $s_3$.

On the other hand, if the singularities occur in the denominator $a(s_3,x)=0$, then the solution for x variable is

$$\begin{aligned}&x=\frac{-N(s_1,s_2,s_3)\pm \sqrt{N^2(s_1,s_2,s_3)-\lambda (s_1,m_2^2,m_3^2)\lambda (s_1,s_2,s_3)}}{\lambda (s_1,s_2,s_3)}, \nonumber \\&N(s_1,s_2,s_3)=\lambda (s_1,s_2,s_3)+\lambda (s_1,m_2^2,m_3^2 )+4s_1 m_1^2 \nonumber \\&\quad - (s_2-s_3+m_2^2-m_3^2 )^2. \end{aligned}$$

(13)

When s approaches the following two points:

$$\begin{aligned} s^{\pm }&=\frac{1}{2 m_3^2} \Big [2m_3^2(s_1+s_2)-(s_1-m_2^2+m_3^2)(s_2-m_1^2+m_3^2)\nonumber \\&\quad \pm \sqrt{\lambda (s_2,m_1^2,m_3^2)\lambda (s_1,m_2^2,m_3^2)} \Big ], \end{aligned}$$

(14)

a pinch singularity occurs in $T(s_1,s_2,s_3)$. However, that singularity may not always appear on the physical Riemann sheet (i.e. the first sheet). Actually there exist two cases leading to a singularity on the un-physical (the second) sheet: firstly, when the pinch points in Eq. (13) lie off the integral interval [0, 1]; secondly, when the numerator of the integrand in Eq. (8) approaches 0 simultaneously as $a(s_3,x)\rightarrow 0$, giving a well-defined value of the integrand. We will meet examples of these two cases below.

To proceed, in the following we discuss two situations; one is that all particles are stable, the other is that some particles are unstable like the case we meet in the real situation ($X(4260)\rightarrow J/\psi \pi \pi , D D^* \pi$).

Fig. 2

The trajectory of the anomalous threshold $s^-$: a all particles are stable; b the kinematics from Eq. (15)

Fig. 3

Invariant mass distributions of the process $X(4260)\rightarrow \pi \pi J/\psi$ from the triangle diagram for different $\sqrt{s_1}$: a the ATS is on the second sheet; b the ATS is on the first sheet, and above the normal threshold

Fig. 4

Feynman diagrams of Fit I

For the first situation, $(m_i-m_k)^2<s_j<(m_i+m_k)^2$ (i, j, k are permutations of 1,2,3). When we substitute the $s^+$ in Eq. (14) for $s_3$ in Eq. (13), it will be found that x is not in the integral interval, thus $s^+$ is located on the second sheet. But the situation is more complicated when we focus on $s^-$, which is usually called an “anomalous threshold” or “anomalous triangle singularity”. Since the pinch points in Eq. (13) stay in [0, 1] when $s\rightarrow s^-$, one has to test whether the numerator of the integrand in Eq. (8) approaches 0. We make the following observations:

• when $s_1<(m_2+m_3)^2+\frac{m_2}{m_1}[(m_3-m_1)^2-s_2]$, the $s^-$ is located on the second sheet and is below the normal threshold;

• when $s_1=(m_2+m_3)^2+\frac{m_2}{m_1}[(m_3-m_1)^2-s_2]$, the $s^-$ just rides on the normal threshold;

• when $s_1>(m_2+m_3)^2+\frac{m_2}{m_1}[(m_3-m_1)^2-s_2]$, the $s^-$ is located on the first sheet and is below the normal threshold.

To obtain the above results, one needs to analyze the behavior of the numerator of the integral in Eq. (8) at $s^-$ by looking at the arguments of the two $\arctan$ functions. For example, when $s_1<(m_2+m_3)^2+\frac{m_2}{m_1}[(m_3-m_1)^2-s_2]$, it is found that for the first argument

$$\begin{aligned} \lim _{s_3\rightarrow s^-}\lim _{x\rightarrow x_1}\frac{(-s_1+s_2-s_3)x+s_1+m_2^2-m_3^2}{a(s_3,x)}=-\infty \ , \end{aligned}$$

while for the second argument

$$\begin{aligned} \lim _{s_3\rightarrow s^-}\lim _{x\rightarrow x_1}\frac{(s_1+s_2-s_3)x-s_1+m_2^2-m_3^2}{a(s_3,x)}=-\infty \ , \end{aligned}$$

using $\arctan (-\infty )=-\pi /2$, one finds that the two $\arctan$ terms cancel each other in Eq. (8) when $s_3\rightarrow s^-$, so in this case $s^-$ is not on the physical sheet. But when $s_1>(m_2+m_3)^2+\frac{m_2}{m_1}[(m_3-m_1)^2-s_2]$ the first argument becomes $+\infty$, leading to a nonzero numerator,

$$\begin{aligned} \lim _{s_3\rightarrow s^-}\lim _{x\rightarrow x_1} \arctan [\cdots ]-\arctan [\cdots ]=\pi /2-(-\pi /2)=\pi ; \end{aligned}$$

thus $s^-$ appears on the first sheet. In the above discussion the behavior of $s^-$ is actually the classical example discovered long ago by Mandelstam in Ref. [8], being used to explain the long tail of the deuteron wave function.

Fig. 5

Feynman diagrams of Fit II

Fig. 6

Feynman diagrams of Fit III

In reality, however, the stability condition in obtaining the above results may not hold. For example, one may consider the following kinematics (which corresponds to the kinematics of Fig. 4):

$$\begin{aligned} 0<s_2{<}(m_1-m_3)^2 ,\;(m_1+m_2)^2<s_3<(\sqrt{s_1}-\sqrt{s_2})^2. \end{aligned}$$

(15)

After some analyses similar to the situation of stable particles, we find that when $s_1$ satisfies

$$\begin{aligned} (m_2+m_3)^2<s_1<(m_2+m_3)^2+\frac{m_2}{m_1} [(m_3-m_1)^2-s_2 ], \end{aligned}$$

(16)

$s^-$ is located on the physical sheet, and it is above the normal threshold. Otherwise, $s^{-}$ would be on the un-physical sheet.

In addition, to understand the dependence of $s^-$ on $s_1$, one gives $s_1$ a small positive imaginary part, $s_1\rightarrow s_1+i0^+$. Then $s^-$ can be expressed as $s^-(s_1+i0^+)=s^-(s_1)+i\frac{\partial s^-}{\partial s_1}0^+$ derived from Eq. (14). As $s_1$ increases, the near-threshold trajectory of $s^-$ both in the classical stable case (see Fig. 2a) and under the kinematics of Eq. (15) (see Fig. 2b) can thus be drawn.

The aim of this paper is to investigate whether the $Z_c(3900)$ peak is mainly from the triangle singularity or not, so the processes $X(4260)\rightarrow \pi ^{+}\pi ^{-} J/\psi , D \bar{D}^* \pi$ are considered, with respect to the triangle diagrams shown in Fig. 4 as suggested by Refs. [17,18,19,20,21]. We set $s_1$ to be the square of the X(4260) 4-momentum, and the pertinent masses to the masses of those particles; then according to Eq. (16), it is found that the ATS lies on the second sheet when $\sqrt{s_1}$ lies between 4230 and 4260 MeV. Hence the $Z_c(3900)$ peak cannot be a direct manifestation of the anomalous threshold. We plot the modulus-square of the amplitude in Eq. (8) with different center-of-mass energies $\sqrt{s_1}$, as shown in Fig. 3.

It is, however, found that the location and effect of the anomalous threshold are very sensitive to the energy of X(4260). When the anomalous threshold is on the second sheet as shown in Fig. 3a, the closer it is to normal threshold, the more influence it has on the amplitude. Since the anomalous threshold (on the second sheet) can be rather close to the normal threshold, one still needs to check whether the (anomalous and normal) threshold effects can cause the experimentally observed $Z_c(3900)$ peak.

The discussions above are only brief qualitative analyses aiming at studying the dependence of ATS peak on $s_1$ variable, and what we have calculated above is not the whole amplitude of that process to fit the experimental data, since in the full amplitude there exists a X(4260) production process, a X(4260) propagator, spin structures, and derivative couplings. The detailed formulas can be found in Appendices A and B; with these the numerical discussions are presented in the next section.

3 Numerical analyses and discussions

3.1 Fit to the data of Refs. [1, 4]

As pointed out in Refs. [20], the ATS contribution to the decay of X(4260) to $J/\psi \pi \pi$ (see Fig. 3b) may have a strong dependence on the center-of-mass energy. However, Ref. [20] just presented a discussion without data fit. On the other side, the result in Ref. [5] supports a molecular state interpretation rather than an “elementary” state explanation. Since the aim of this paper is to test whether the triangle diagram can provide the $Z_c(3900)$ peak, we make three independent fits to compare the fit quality:

• Fit I: X(4260) decays to final states only through triangle diagram as depicted in Fig. 4.

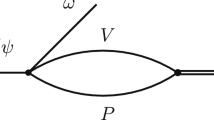
• Fit II: the final states are only produced by $D\bar{D}^*$ rescattering, and the Feynman diagram is shown in Fig. 5.

• Fit III: the mixed situation by combining the triangle diagram and $D\bar{D}^*$ bubble chains, as shown in Fig. 6.

Recall that both the bubble and the triangle diagrams are ultraviolet divergent. We use the $\overline{\text {MS}}-1$ scheme of the dimensional renormalization method to deal with the divergences, which leaves another somewhat arbitrary parameter: the renormalization scale $\mu$ (see Appendix B). Considering the physical process we are studying, it is reasonable to expect that the $\mu$ parameter should be around or not much different from the mass of X(4260). Indeed, we find that when we set the renormalization scale at the reasonable value $\mu =5$ GeV, the bubble chains give a satisfactory fit result as shown in the following, and it is verified that the fit quality is not sensitive to the variation of $\mu$ parameter. On the contrary, the triangle diagram does not give a good description of the data when $\mu$ is set at 5 GeV. The fit results shown in the following correspond to an unreasonably small $\mu$ (in getting the Figs. 9 and 10).⁴

In the numerical fit two sets of data including $J/\psi \pi$ maximum invariant mass spectrum [1] and $D\bar{D}^*$ invariant mass distribution [4] are taken into account.

Fig. 7

The dominant contribution to the $J/\psi \pi \pi$ process. a S-wave $D^*\pi$ interaction in $D_1 D^*\pi$ vertex; b D-wave $D^*\pi$ interaction in $D_1 D^*\pi$ vertex

Fig. 8

The cross section of the $D D^*\pi$ channel amplitude (divided by $\frac{32\pi \alpha |c_1\lambda _1 h_1h_2|^2}{f_\pi ^2}$). a S-wave $D_1 D^*\pi$ interaction; b D-wave $D_1 D^*\pi$ interaction. Note that the vertical scale in b is ten times smaller in magnitude than that in a

Fig. 9

Data fit using two different parameterizations (Fit I, II) of the amplitudes. a The $J/\psi \pi$ maximum invariant mass distribution from Ref. [1]; b the $D\bar{D}^*$ invariant mass distribution from Ref. [4]

The Lagrangian we use is taken from Ref. [5], with three additional pieces,

$$\begin{aligned} \mathcal {L}_{XD_1D}= & {} h_1X_\mu \langle D_{1}^\mu \bar{D}+ h.c.\rangle , \end{aligned}$$

(17)

$$\begin{aligned} \mathcal {L}_{D_1D^*\pi }= & {} h_2\langle \bigtriangledown ^\mu D_1^{\nu }\cdot \bar{D}^{*}_\nu u_\mu \rangle , \end{aligned}$$

(18)

and

$$\begin{aligned} \mathcal {L}_{\gamma ^*X}=c_\gamma F_{\mu \nu }X^{\mu \nu }\ , \end{aligned}$$

(19)

where $X^{\mu \nu }=\partial ^\mu X^\nu -\partial ^\nu X^\mu$. The corresponding Feynman rules can be found in Appendix. A.

Note that in reality the $D_1D^*\pi$ interaction can be either through the S-wave or D-wave (of the $D^* \pi$ system). Equation (18) is in S-wave form, while the D-wave vertex can be found in Eq. (5) of Ref. [17]. Here we adopt the S-wave form, for the reason that the D-wave interaction would lead to a higher order momentum dependence in the numerator of the amplitude, which suppresses the contribution from the near-threshold region and increases too fast when the energy goes higher; in other words, it wrecks the line shape of the triangle diagram peak and gives a much worse fit result, as discussed in the following.

We may focus on the dominant contribution $\Lambda _{22}$ to the $J/\psi \pi \pi$ process,⁵ which contains no free parameters like the coupling constants; see Eq. (42) in Appendix B. With the $D_1 D^* \pi$ vertex in S-wave and D-wave, this dominant term is depicted in Fig. 7a, b, respectively.

It is found that the D-wave interaction behaves worse when the energy increases—it cannot even give the correct shape of the peak when $\sqrt{s_1}=4.23$ GeV. As for the $D D^*$ spectrum, the D-wave interaction of $D_1D^*\pi$ also makes the line shape worse; see Fig. 8. Furthermore, one may discuss the situation of S-wave $D_1D^*\pi$ interaction with a large $D_1$ width ($\simeq 400$ MeV as inspired by PDG), and it is found that the structure of the $DD^*$ spectrum are totally destroyed. Hence such a scenario is completely ruled out.

With these preparations, it is possible to make a combined fit on the $J/\psi \pi$ maximum spectrum and $D\bar{D}^*$ mass distribution [1, 4]. Except for various coupling parameters, two parameters for the $D\bar{D}^*$ incoherent background and two normalization constants are further introduced. In total, there are 8 and 10 free parameters for Fit I and Fit II, respectively.

Since the value of the center-of-mass energy of $X(4260)/\gamma ^*$ severely influences the ATS contribution as discussed previously, we in the fit also carefully analyze the effect of energy resolution. However, it is found, through numerical tests, that the effect of the energy resolution does not obviously improve the fit quality, since the energy resolution parameters $\sigma =4.2$ MeV in $J/\psi \pi \pi$ channel [1], $\sigma =1.0$ MeV in $D\bar{D}^*\pi$ channel [4], and $\sigma =3.0$ MeV for the energy spread of X(4260), are much smaller than the particle widths ($\sim 30$ MeV).⁶

The fit results are shown in Fig. 9. The $\chi ^2/dof$ of Fit I and Fit II are 2.5 and 0.96, respectively. In Fit II we find a bound state pole of $DD^*$, $\sqrt{s}=3.8747\pm 0.0148i$ GeV, which is consistent with our previous result in Ref. [5]. Further, Fit III gives a very similar $\chi ^2$ to Fit II with the pole located at $\sqrt{s}=3.8749\,\pm \,0.0145i$ GeV, which suggests that the triangle diagram plays only a minor role when compared with the bubble chain contribution. In Fit II and Fit III, the denominators of the amplitudes of the processes $e^{+}e^{-}\rightarrow J/\psi \pi \pi (D\bar{D}^*\pi )$ take the form

$$\begin{aligned} 1-i\lambda _1 (D(l)+c_0), \end{aligned}$$

(20)

where the $\lambda _1$ represents the $D\bar{D}^*\bar{D}D^*$ contact coupling constant, and $c_0$ simulates the contribution from other lighter channels to the $Z_c(3900)$ width. The function D(l) is the $D\bar{D}^*$ meson loop integral. The parameters $\lambda _1$ and $c_0$, which determine the pole positions, are listed in Table 1.⁷

Table 1 The parameters which determine the pole positions of Fit II and Fit III

Although the bubble chains (the molecule picture) fit the data better than the triangle diagram, the latter still cannot be firmly excluded here. Generally speaking, one believes that the cusp effects are much weaker singularities than the poles, and the triangle diagram does not generate poles except branch point singularities. However, the undetermined overall normalization factor in the present fit makes up the defect of branch cuts (i.e., being weak in general), and hence prevents us from excluding the triangle diagram mechanism.

Fig. 10

Simultaneous fit to data at $\sqrt{s_1}=4.23$ GeV and data at $\sqrt{s_1}=4.26$ GeV. The integrated luminosity of these two data sets are renormalized to be equal. a Fit I’, triangle diagram; b Fit II’, bubble chains. Data are from Refs. [23, 24]

3.2 Fit to the new data

Fortunately, the new data from BESIII Collaboration [23, 24] indicates that there are more events in $Z_c(3900)$ peak at $\sqrt{s_1}=4.23$ GeV (with an integrated luminosity of $L=1092$ pb$^{-1}$) than at $\sqrt{s_1}=4.26$ GeV (with $L= 827$ pb$^{-1}$), after background subtraction (see Fig. 10). On the contrary, the magnitude of the triangle diagram in Fig. 4 at the $Z_c$ peak is smaller when $\sqrt{s_1}=4.23$ GeV compared with the magnitude when $\sqrt{s_1}=4.26$ GeV.⁸ It is noticed that the $s_1$ dependence of the triangle diagram will be slightly balanced by the $s_1$ dependence of X(4260) propagator, which takes the standard Breit–Wigner form of the constant width taken from PDG, and the mass of X(4260) is chosen to be 4.23 GeV.⁹ If the mass of X(4260) is set to be 4.26 GeV, the propagator would also suppress the cross section when $\sqrt{s_1}=4.23$ GeV, making the fit with a pure triangle diagram even worse. On the other side, different from the triangle diagram, the bubble chain amplitude is not sensitive to $s_1$ in the energy region of interests. New fits to both the $\sqrt{s_1}=4.23$ GeV and the $\sqrt{s_1}=4.26$ GeV data are performed.

The results are shown in Fig. 10. The $\chi ^2_{dof}=5.3$ for a pure triangle diagram (Fit I’) and the $\chi ^2_{dof}=1.6$ for pure bubble resummation (Fit II’). The pole of Fit II’ is located at $\sqrt{s}=3.8804\pm 0.0150i$ GeV. Hence the triangle diagram gives a much worse fit compared with the bubble chain diagram, and hence can be ruled out. Apparently, the new data [23, 24] are crucial in supporting of the $D\bar{D}^*$ molecule explanation of $Z_c(3900)$.

We also fit the new data of Fig. 10 in the mixed situation (Fit III’); however, it does not obviously improve the total $\chi ^2$ compared with Fit II’. That is, the $\chi ^2_\mathrm{dof}$ is almost the same as Fit II’, with the pole location $\sqrt{s}=3.8822\pm 0.0119i$ GeV; see Table 2. Hence we may draw the conclusion that the bubble chain mechanism plays a dominant role in reproducing the experimentally observed peak structure.

Table 2 The parameters which decide the pole position of Fit II’ and Fit III’

Here we should mention that in the above fit using triangle diagrams, the renormalization scale $\mu$ runs to a ridiculously small number, $\sim 10^{-7}$ GeV. If we fix $\mu$ at 5 GeV, the fit quality of triangle diagrams gets even worse.

4 Conclusion

To summarize, we have investigated whether the triangle singularity mechanism proposed in the literature can be responsible for the experimentally observed $Z_c(3900)$ peak. It is found that, though the triangle diagram could barely explain the line shape, up to an arbitrary normalization constant, it fails to explain the dependence of the process $e^{+}e^{-}\rightarrow J/\psi \pi ^{+}\pi ^{-}$ on the center-of-mass energy, not to mention the weird value of the renormalization scale it requires. Therefore, we conclude that the $Z_c(3900)$ peak is dominantly contributed by the pole of the $D \bar{D}^*$ molecular state.

Note added: when this paper was being completed, we became aware of a recent paper [27], where the authors also attacked the same problem using four different amplitude parameterizations. They reached the conclusion that at this stage they cannot have a preference on one of these parameterizations, which contradicts our conclusion. We point out here that they were only able to use the old data (at c.m. energy 4.23 GeV) in the neutral channel of $J/\psi \pi ^0$ [28], which is much worse in statistics compared with the data of [23, 24]. Hence we urge the authors of Ref. [27] to redo their analysis with the new data incorporated and compare with our result.

Appendices

Appendix A: The pertinent Feynman rules

For charged final state $DD^*$ or $J/\psi \pi$, the Feynman vertices in Fig. 4 are given as follows:

$$\begin{aligned}&iV_{X^\mu DD_1^\nu }=i h_1 g^{\mu \nu }\ , \end{aligned}$$

(21)

$$\begin{aligned}&iV_{D_1^\mu D^{*\nu }\pi }=-\frac{i\sqrt{2}h_2}{f_\pi }g^{\mu \nu }(p_{D_1}\cdot p_{\pi }),\end{aligned}$$

(22)

$$\begin{aligned}&iV_{DD^{*\mu }J/\psi ^\nu \pi }= \frac{i\sqrt{2}}{f_\pi } \nonumber \\&\quad \times [g^{\mu \nu } (\lambda _2p_{J/\psi }\cdot p_\pi -\lambda _3p_{D^*}\cdot p_\pi ) \nonumber \\&\quad + (\lambda _4p_{J/\psi }^{\mu } p_\pi ^\nu -\lambda _5p_{D^*}^\nu p_\pi ^{\mu } ) ], \end{aligned}$$

(23)

$$\begin{aligned}&\quad iV_{DD^{*\mu }DD^{*\nu }}=2i\lambda _1g^{\mu \nu }, \end{aligned}$$

(24)

where $\mu , \nu$ are the Lorentz indices of spin − 1 particles, $f_\pi$ is the pion decay constant, the flat space-time metric is $g^{\mu \nu }=\text {diag}\{1,- \ 1,- \ 1,- \ 1\}$, and $p_{A}$ denotes the four-momentum of particle A in the vertex. As for the propagators of $D^*,\ D_1$ and $J/\psi$, we adopt the standard formula of Proca fields with four-momentum k and mass $M_P$, i.e.

$$\begin{aligned} iD_{F\,\rho \sigma }(k)=\frac{-i\left( g_{\rho \sigma }-\frac{k_\rho k_\sigma }{M_P^2}\right) }{k^2-M_P^2}. \end{aligned}$$

(25)

When one calculates the modulus-square of the amplitudes, the polarization summing of the final state $D^*$ and $J/\psi$ is needed, and the formula of the Proca field physical polarization summation is as follows:

$$\begin{aligned} \sum \varepsilon ^*_{\alpha }\varepsilon _{\beta }=-g_{\alpha \beta }+\frac{k_{\alpha }k_{\beta }}{M_P^2}, \end{aligned}$$

(26)

with $\varepsilon (k)$ being the final state Proca field polarization vector and k being the four-momentum of the Proca field.

The initial $e^+e^-\rightarrow \gamma ^*(\mu )$ QED process is written as

$$\begin{aligned} \bar{v}(p_+,s)(-i e\gamma ^\mu )u(p_-,r), \end{aligned}$$

(27)

with the initial positron 4-momentum being $p_+$ and the polarization being s, and the electron’s $p_-$ and r. Moreover, the $\gamma ^*$ ($\mu$) and X(4260) ($\nu$) two-point coupling is

$$\begin{aligned} iV_{\gamma ^{*\mu } X^\nu }=2i (g^{\mu \nu }p_1^2-p_1^\mu p_1^\nu )c_\gamma , \end{aligned}$$

(28)

with $p_1=p_++p_-$. That form ensures the QED Ward identity.

Appendix B: Amplitudes of the total process

In this section we denote the 4-momentum of X(4260) as $p_1$, the 4-momentum of the final state $\pi$ in the 3-vertex as $p_2$, and 4-momenta of the final state $\pi$ and $J/\psi$ in the $4-$ vertex as $p_\pi$ and $p_{J/\psi }$, respectively, and similar for the final state D and $D^*$ (see Fig. 11). The total amplitudes with triangle diagrams of $DD^*\pi$ or $J/\psi \pi \pi$ final states can be written as

$$\begin{aligned} i\mathcal {M}= & {} \bar{v}(p_+,s)\gamma ^\alpha u(p_-,r)\frac{2ie c_1(p_1^2g_{\alpha \mu }-p_{1\alpha }p_{1\mu })}{p_1^2 [p_1^2-M_X^2+iM_X\Gamma (p_1^2) ]} \nonumber \\&\quad \times (iT_{DD^*,J/\psi \pi }^{\mu \sigma } ) \cdot \varepsilon ^*_\sigma (p_{D^*,J/\psi },f ), \end{aligned}$$

(29)

while the triangle parts are

$$\begin{aligned}&\begin{aligned}&iT^{\mu \sigma }_{DD^*}=\frac{-2\sqrt{2}\lambda _1 h_1h_2}{f_\pi }it^{\mu \sigma }_{\lambda _1}, \end{aligned} \end{aligned}$$

(30)

$$\begin{aligned}&\quad iT^{\mu \sigma }_{J/\psi \pi }=-\frac{2h_1h_2}{f_\pi ^2}\left( \sum _{j=2}^{5}\lambda _jit^{\mu \sigma }_{\lambda _j}\right) , \end{aligned}$$

(31)

with

$$\begin{aligned} \begin{aligned}&it^{\mu \sigma }_{\lambda _1}=\int \frac{\mathrm{d}^Dq\nu ^{2\epsilon }}{(2\pi )^D}\frac{(q\cdot p_2) \bigg \{g ^{\mu \sigma }-\frac{1}{M_{D_1}^2M_{D^*}^{2}} [M_{D_1}^2(q-p_2)^\mu (q-p_2)^\sigma +M_{D^*}^{2}q^\mu q^\sigma -q\cdot (q-p_2)q^\mu (q-p_2)^\sigma ] \bigg \}}{(q^2-M_{D_1}^{2}) [(q-p_1)^2-M_{D}^{2} ] [(q-p_2)^2-M_{D^*}^{2} ]}, \end{aligned} \end{aligned}$$

(32)

$$\begin{aligned} \begin{aligned} it^{\mu \sigma }_{\lambda _2}&=\int \frac{\mathrm{d}^Dq\nu ^{2\epsilon }}{(2\pi )^D}(p_{J/\psi }\cdot p_{\pi })g^{\rho '\sigma } \frac{g_{\rho \rho '}-\frac{(q-p_2)_\rho (q-p_2)_{\rho '}}{M_{D^*}^{2}}}{(q-p_2)^2-M_{D^*}^{2}} \\&\quad \times [g^{\rho \nu '}(q\cdot p_2) ] \times \frac{g_{\nu '\nu }-\frac{q_\rho q_{\rho '}}{M_{D_1}^{2}}}{q^2-M_{D_1}^{2}}g^{\mu \nu }\frac{1}{(q-p_1)^2-M_{D}^{2}}, \end{aligned} \end{aligned}$$

(33)

$$\begin{aligned} \begin{aligned} it^{\mu \sigma }_{\lambda _3}&=-\int \frac{\mathrm{d}^Dq\nu ^{2\epsilon }}{(2\pi )^D}p_{\pi }\cdot (q{-}p_2)g^{\rho '\sigma } \frac{g_{\rho \rho '}{-}\frac{(q{-}p_2)_\rho (q{-}p_2)_{\rho '}}{M_{D^*}^{2}}}{(q-p_2)^2-M_{D^*}^{2}} \\&\quad \times [g^{\rho \nu '}(q\cdot p_2) ] \times \frac{g_{\nu '\nu }-\frac{q_\rho q_{\rho '}}{M_{D_1}^{2}}}{q^2-M_{D_1}^{2}}g^{\mu \nu }\frac{1}{(q-p_1)^2-M_{D}^{2}}, \end{aligned} \end{aligned}$$

(34)

$$\begin{aligned} \begin{aligned} it^{\mu \sigma }_{\lambda _4}&=\int \frac{\mathrm{d}^Dq\nu ^{2\epsilon }}{(2\pi )^D}p_{J/\psi }^{\rho '}p_{\pi }^\sigma \frac{g_{\rho \rho '}-\frac{(q-p_2)_\rho (q-p_2)_{\rho '}}{M_{D^*}^{2}}}{(q-p_2)^2-M_{D^*}^{2}} \\&\quad \times [g^{\rho \nu '}(q\cdot p_2) ] \times \frac{g_{\nu '\nu }{-}\frac{q_\rho q_{\rho '}}{M_{D_1}^{2}}}{q^2{-}M_{D_1}^{2}}g^{\mu \nu }\frac{1}{(q{-}p_1)^2-M_{D}^{2}}, \end{aligned} \end{aligned}$$

(35)

$$\begin{aligned} \begin{aligned} it^{\mu \sigma }_{\lambda _5}&=-\int \frac{\mathrm{d}^Dq\nu ^{2\epsilon }}{(2\pi )^D}p_{\pi }^{\rho '}(q-p_2)^\sigma \frac{g_{\rho \rho '}-\frac{(q-p_2)_\rho (q-p_2)_{\rho '}}{M_{D^*}^{2}}}{(q-p_2)^2-M_{D^*}^{2}} \\&\quad \times [g^{\rho \nu '}(q\cdot p_2) ] \times \frac{g_{\nu '\nu }{-}\frac{q_\rho q_{\rho '}}{M_{D_1}^{2}}}{q^2-M_{D_1}^{2}}g^{\mu \nu }\frac{1}{(q{-}p_1)^2{-}M_{D}^{2}}. \end{aligned} \end{aligned}$$

(36)

Fig. 11

The process of $e^+e^-\rightarrow J/\psi \pi \pi (D\bar{D}^*\pi )$

We should mention that in Eqs. (30) and (31) there are three-point tensor functions, which could be reduced to one-point, two-point and three-point functions. The latter is convergent, while the former two can be divergent. Besides, each bubble in the bubble chains contains divergence as well. In this paper we use the dimensional regularization method with the $\overline{\text {MS}}-1$ scheme to handle the divergences. The subtraction constant of the $\overline{\text {MS}}-1$ scheme is

$$\begin{aligned} R=-\frac{1}{\epsilon }+\gamma _E-\ln (4\pi )-1, \end{aligned}$$

where $\epsilon =2-D/2$ with D being the number of dimensions, and $\gamma _E$ is the Euler constant. A renormalization scale $\mu$ is also indispensable. The expressions of Eqs. (30) and (31) after Passarino–Veltman reduction are too complicated to be shown here, but the R and $\mu$ dependence of general one- and two-point functions are as follows: for the one-point functions we have

$$\begin{aligned} \begin{aligned} A_0\left( M_a^2\right)&= \frac{\mu ^{2\epsilon }}{i}\int \frac{\mathrm{d}^Dk}{(2\pi )^D}\frac{1}{k^2-M_a^2+i0^+}\\&=-\frac{M_a^2}{16\pi ^2}\left( R+\ln \frac{M_a^2}{\mu ^2}\right) ; \end{aligned} \end{aligned}$$

(37)

and for the two-point functions

$$\begin{aligned}&B_0 (p^2,M_a^2,M_b^2 ) \nonumber \\&\quad =\frac{\mu ^{2\epsilon }}{i}\int \frac{\mathrm{d}^Dk}{(2\pi )^D} \frac{1}{(k^2{-}M_a^2{+}i0^+) [(p{-}k)^2-M_b^2{+}i0^+ ]} \nonumber \\&\quad =\frac{1}{16\pi ^2}\bigg [-R+1-\ln \frac{M_a^2}{\mu ^2}+\frac{M_a^2-M_b^2-p^2}{2p^2}\ln \frac{M_b^2}{M_a^2} \nonumber \\&\qquad +\frac{p^2-(M_a-M_b)^2}{p^2}\alpha (p^2)\ln \frac{\alpha (p^2)-1}{\alpha (p^2)+1}\bigg ], \end{aligned}$$

(38)

with $\alpha (p^2)=\sqrt{\frac{p^2-(M_a+M_b)^2}{p^2-(M_a-M_b)^2}}$.

Finally, the non-polarized modulus-square can be written as

$$\begin{aligned} |\overline{\mathcal {M}}|^2= & {} -\frac{4\pi \alpha |c_1|^2g^{\alpha \beta }}{3p_1^2 | p_1^2-M_X^2+iM_X\Gamma (p_1^2 )|^2}\nonumber \\&\times \bigg (g_{\alpha \mu }-\frac{p_{1\alpha }p_{1\mu }}{M_X^2}\bigg )T_{DD^*,J/\psi \pi }^{\mu \sigma }\bigg (g_{\beta \nu }-\frac{p_{1\beta }p_{1\nu }}{M_X^2}\bigg ) \nonumber \\&\times T_{DD^*,J/\psi \pi }^{\nu \rho *}\bigg (g_{\sigma \rho }-\frac{p_{D^*,J/\psi \sigma }p_{D^*,J/\psi \rho }}{M_{J/\psi ,D^*}^2}\bigg ), \end{aligned}$$

(39)

while the cross sections of the $DD^*\pi$ and $J/\psi \pi \pi$ final states are

$$\begin{aligned}&\sigma _{e^+e^-\rightarrow DD^*\pi }=\frac{32\pi \alpha |c_1h_1h_2|^2}{f_\pi ^2}\lambda _1\lambda _1\Lambda _{11}(s,s_1), \end{aligned}$$

(40)

$$\begin{aligned}&\quad \sigma _{e^+e^-\rightarrow J/\psi \pi \pi }=\frac{16\pi \alpha |c_1h_1h_2|^2}{f_\pi ^4} \sum _{ij=2}^{5}\lambda _i\lambda _j\Lambda _{ij}(s,s_1),\nonumber \\ \end{aligned}$$

(41)

where

$$\begin{aligned} \begin{aligned}&\Lambda _{ij}(s,s_1)=-\int (2\pi )^2\delta ^{(4)}(p_1-p_2-p_3) \\&\quad \times \prod _f\frac{\mathrm{d}^3\mathbf {p}_f}{(2\pi )^3 2E_f}\frac{1}{3p_1^2 | p_1^2-M_X^2+iM_X\Gamma (p_1^2)|^2} \\&\quad \times \bigg (g_{\alpha \mu }-\frac{p_{1\alpha }p_{1\mu }}{M_X^2}\bigg )t^{\mu \sigma }_{\lambda _i} \bigg (g_{\alpha \nu }-\frac{p_{1\alpha }p_{1\nu }}{M_X^2}\bigg )t^{\nu \rho *}_{\lambda _j} \\&\quad \times \bigg (g_{\sigma \rho }-\frac{p_{J/\psi \sigma }p_{J/\psi \rho }}{M_{J\psi }^2}\bigg ). \end{aligned} \end{aligned}$$

(42)